第12章 算法与程序框图
算法与程序框图基础题
第十二章 算法与程序框图A一选择题1. （12.2）下列对算法的描述中，正确的是（ ）A.算法只能用自然语言描述B.算法只能用程序框图描述C.同一问题可以有不同的算法D.同一问题不同的算法会得到不同的算法 2. （12.2）在程序框图中，判断框的进口数和出口数分别为 （ ）A.1和1B.1和2C.2和1D.2和2 3. （12.2）下列给出的赋值语句中正确的是 （ ）A. 21i =B. M M -=C.M M =-D. 0x y += 4. （12.2）程序框图中表示判断框的是 （ ）A.矩形框B.菱形框C.圆形框D. 椭圆形框 5. （12.2）下列关于算法的叙述中，正确的是 （ ）A.算法是一种运算符合B.算法是一种对数进行运算的方法C.算法是指用来解决问题的一系列明确而有效的步骤D.算法是一种计算机程序.6. （12.2）下列关于算法的说法中，不正确的是（）A.求解某一类问题的算法是唯一的B.算法必须在执行有限个步骤后停止C.算法的每一个步骤必须是确切的，不能有歧义D.算法执行后一定要输出结果7．（12.2）下面描述的算法：第一步X=3第二步Y=4第三步X=X+Y 第四步输出X，Y输出的结果为 ( )A．7，4 B．7，7 C．7，3 D．3，48．（12.2）下列流程图是循环结构的是 .①②③④9．（12.2）下列程序框中，出口可以有两个流向的是( )A．终止框B．输入输出框C．处理框D．判断框二．填空题1.（12.2）如图所示是某个函数求值的程序框图，则该程序表示的函数解析式为 .（第12. （3.（第34.程序框图有顺序结构，_________和循环结构。
三．解答题1. （12.2）写出求任意两个数的平均数的算法，并画出程序框图.2. （12.2）如果三角形的三边长分别为a,b,c,那么这个三角形的面积S=p 为三角形的半周长，即2a b cp ++=.这就是着名的海伦公式.请利用海伦公式设计一个求三角形面积的算法，并画出程序框图.3. （12.2）设计一个求任意实数的绝对值的算法，并画出程序框图.4 （12.2）已知一个学生的语文成绩为89分，数学成绩为96分，外语成绩为99分，请将“求他的平均成绩的一个算法”补充完整,并画出程序框图．第一步：A =89，B=96，C =99； 第二步：S =A +B +C ；第三步：x = ； 第四步：输出x ．B一选择题1．（12.2）看下面的四段话，其中不是解决问题的算法的是 ( )A．从济南到北京旅游，先坐火车，再坐飞机抵达B．方程x2-1=0有两个实根C．解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1D．求1+2+3+4+5的值，先计算1+2=3，再求3+3=6，6+4=10，10+5=15，最终结果为2．（12.2）下列关于算法的说法①求解某一类问题的算法是唯一的；②算法必须在有限步操作之后停止；③算法的每一步操作必须是明确的，不能有歧义或模糊；④算法执行后一定产生确定的结果．其中正确的有（）A．1个 B．2个 C．3个 D．4个二填空题1（12.2）已知一个学生的语文成绩为89分，数学成绩为96分，外语成绩为99分，请将“求他的平均成绩的一个算法”补充完整．第一步：A=89，B=96，C=99；第二步：S=A+B+C；第三步：x= ；第四步：输出x．2（12.2）阅读下面的流程图中，若输入的数据,,a b c 分别是7,9,6，则输出的结果是( )A. 6B. 9C. 7D. 7,9,6二解答题1. （12.2）某班有40名学生，依次输入这40名学生的数学考试成绩，输出全班学生的数学总分和平均分.请画出解决这个问题的算法的程序框图.2. （12.2）设计一个算法，计算123...100++++的值，并画出程序框图.3. （12.2）设计一个算法，计算123...100⨯⨯⨯⨯的值，并画出程序框图.4. （12.2）设计一个算法，计算1111+++...+23100的值，并画出程序框图. 5. （12.2）画出求三个数的平均数的算法的程序框图.6. （12.2）已知摄氏温度()o x C 与华氏温度()o y F 的换算关系为9325y x =+，设计一个算法，输入摄氏温度，输出相应的华氏温度，并画出程序框图.7. （12.2）任意定三个正数，设计一个算法，判断分别以这三个数为三边长能否构成直角三角形，并画出程序框图.8. （12.2）设计一个算法，计算135 (2011)++++的值，并画出程序框图.9. （12.2）设计一个算法，计算135 (2011)⨯⨯⨯⨯的值，并画出程序框图.C一选择题1. （12.2）算法共有三种逻辑结构，即顺序结构、条件结构和循环结构，下列说法中正确的是（）A.一个算法只能含有一种逻辑结构B.一个算法最多可以包含两种逻辑结构C.一个算法必须含有上述三种逻辑结构D.一个算法可以含有上述三种逻辑结构的任意组合2．（12.2）某程序框图如下图所示，该程序运行后输出的k的值是（）A.4B.5C.6D.73. （12.24. （12.2a,b,c三个数中的最大数B. 求a,b,cC.将a,b,c按从小到大排列D.将a,b,c按从大到小排列二解答题1. （12.2）设计一个算法，输入一个正整数，输出它的所有正因数，并计算正因数的个数和所有正因数的和.请画出算法的程序框图.2.某厂今年的利润为100万元，假设今后10年该厂的利润以每年5%的增幅递增，设计一个算法，计算10年后该厂的利润及今后10年该厂的总利润.请画出算法的程序框图.3. （12.2）数列{}n a 满足：10a =，21a =，122(3)n n n a a a n --=+≥，设计一个算法，列出数列{}n a 的前20项，并画出程序框图.4. （12.2）如图所示为某个函数求值的程序框图，如果输入的实数分别为5-，0,2和，那么输出的函数值分别为多少?5（12.2.6. （12.2n ，并画出程序框图.7. （12.2.8. （12.2.9（12.3）.已知函数231(1),23(1),(){x xx xf x+>-≤=设计一个求函数值的算法，并画出程序框图.10. （12.3）已知函数221,0,32,0,(){x xx xf x->+≤=设计一个求函数值的算法，并画出程序框图.11. （12.3）设计一个算法，输出1到100之间所有的3的倍数，并画出程序框图.12. （12.3）验证存在自然数n，使11111 (100000)234n+++++>，画出算法的程序框图.13. （12.3）输入3个正数，如果以这3个数为三边长的三角形存在，则输出这个三角形的面积，否则提示输入出错，并重新输入.画出这个算法的程序框图.。
12.2程序框图(第5课时循环结构)
第12章 算法与程序框图
§12.2程序框图(循环结构)
学习目标
理解基本算法结构——循环结构 会设计简单的循环结构程序框图 能够读懂循环结构程序框图
新课教学
三种基本逻辑结构中，顺序结构是最简单的结构，也 是最基本的结构，循环结构必然包括条件结构。这三种结 构是相互支撑的，他们共同构成了算法的基本结构。 三者共同特点为： （1）只有一个入口和一个出口。 （2）基本逻辑结构内的每一部分都有机会被执行到，即对 每 一个框来说，都应当有一条从入口到出口的的路径通 过它。 （3）基本逻辑结构内不允许存在死循环，所以循环结构中 必定包含一个条件结构，用以判断循环是否结束。
课堂小结：
理解基本算法结构——循环结构。 会设计简单的循环结构程序框图。 能够读懂循环结构程序框图。
例题讲解
例1、设计一个算法，输入一个正整数，输出它的 所有正因数，并计算正因数的个数和所有正因数 的和。画出算法程序框图。
分析：如果整除，则为正因数，所以要求出正整数的所有正因
数，只要对1～
n这 n
个正因数逐一判断是都能整除即可。
练习1：设计一个算法，输出1～100之间所有的偶数，并
画出程序框图。
例题讲解
例2、某厂今年的利润为100万元，假设今后10年该
厂的利润以每年5％的增幅递增，设计一个算法，计 算10年后该厂的利润及今后10年该厂的总利润。画出 算法程序框图。
1 1 1 练习2、设计一个算法，计算 1 3 100 的值，并画出程序框图。 2
学生练习
3、下图是求
12 22 32 …+1002Βιβλιοθήκη 开始值的程序框图，则正整数
12.1 算法与程序框图
(2)框中y=-x2+mx的含义是什么？
(3)该程序框图解决的是怎样的一个问题？ (4)若输入的x值为0和4时，输出的值相等，则 ①当输入的x值为3时，输出的值为多大？ ②要想使输出的值最大，输入的x值应为多少？ ③按照这个程序框图，当输入的x的值都大于 2时，x值大的输出的y值反而小，为什么？
解
该算法对应的程序框图如图所示：
探究提高 顺序结构的算法写好后，按顺序依次
画出流程图.在变量赋值时，以后赋的为准，前边 赋过值的变量，有新的数值时，原来的值无效.
知能迁移2
如图所示的框图是解决某个
问题而绘制的程序框图，仔细分析各 图框内的内容及图框之间的关系，回 答下面的问题： (1)框中x=a的含义是什么？
并画出程序框图.
解
算法如下：
第一步：令S=1,i=1； 第二步：若i≤99成立，则执行第三步； 否则输出S，结束算法； 第三步：S=S×i； 第四步：i=i+2，返回第二步. 程序框图：
方法一 当型循环程序框图
方法二 直到型循环程序框图
思想方法 感悟提高
方法与技巧
1.在设计一个算法的过程中要牢记它的五个特征:
第五步，输出d.
Z2
程序框图:
探究提高 给出一个问题，设计算法应注意：
(1)认真分析问题，联系解决此问题的一般数学
方法； (2)综合考虑此类问题中可能涉及的各种情况； (3)将解决问题的过程划分为若干个步骤； (4)用简练的语言将各个步骤表示出来.
知能迁移1
解
写出求过两点M(-2,-1）、N(2,3)的
第三步：输出函数值y.
相应的程序框图如图所示.
探究提高 利用条件结构解决算法问题时，要引入
算法与程序框图
算法与程序框图算法的概念和程序框图学习目标目标一:学会用自然语言描述算法1、写出求1+2+3+4+5+6的一个算法。
2、写出求1至1000的正整数中的3倍数的一个算法。
23、写出解不等式x-2x-3<0的一个算法。
4、求过P(x,y)、Q(x,y)两点的直线的斜率。
1122目标二:学会用框图语言描述算法5、已知点P(x，y)和直线l:Ax+By+C=0，试用程序框图描述求点P(x，y)到直线l0000的距离d的算法。
6、给出A(x,y)、B(x,y)两点坐标，试设计一个算法，求直线AB的斜率，并画出程序框图。
11227、设x为为一个正整数，规定如下运算:若x为奇数，则求3x+2;若x为偶数，则为5x，写出算法，并画出程序框图。
- 1 -目标三:掌握循环结构中的“当型”和“直到型”1231008、试分别用“直到型”和“当型”循环结构画出求2+2+2+…2的值的程序框图。
9、设计一个求1+2+3+…+n,200的最小正整数n的算法，并画出相应的程序框图。
- 2 -目标四:正确阅读程序框图10、如图所示的程序框图所表示的算法是: 。
开始开始S=1 输入n，mi=3 k=1,p=1i=i+2p=p(n-m+k)是i?99? S=S×I k=k+1否是 k,m?输出S否结束输出p第10题图结束第11题图11、(10年辽宁卷)如果执行右侧的程序框图，输入n=6，m=4，那么输出的p等于 12、如图所示的程序框图输出的结果是S=720，则判断框内应填的条件是( ) 开始i=10,S=1i=i-1S=S×i是否输出S结束A.i?7B.i,7C.i?9D.i,9- 3 -。
算法与程序框图
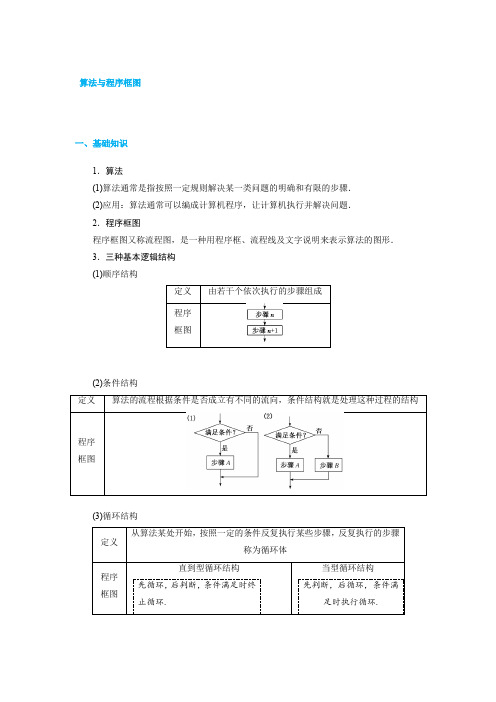
算法与程序框图一、基础知识1．算法(1)算法通常是指按照一定规则解决某一类问题的明确和有限的步骤． (2)应用：算法通常可以编成计算机程序，让计算机执行并解决问题． 2．程序框图程序框图又称流程图，是一种用程序框、流程线及文字说明来表示算法的图形． 3．三种基本逻辑结构 (1)顺序结构(2)条件结构(3)循环结构三种基本逻辑结构的适用情境(1)顺序结构：要解决的问题不需要分类讨论． (2)条件结构：要解决的问题需要分类讨论．(3)循环结构：要解决的问题要进行许多重复的步骤，且这些步骤之间有相同的规律．考点一 顺序结构和条件结构[例1] (2019·沈阳质检)已知一个算法的程序框图如图所示，当输出的结果为0时，输入的实数x 的值为( )A ．－3B ．－3或9C ．3或－9D ．－3或－9[解析] 当x ≤0时，y ＝⎝⎛⎭⎫12x －8＝0，x ＝－3；当x >0时，y ＝2－log 3x ＝0，x ＝9.故x ＝－3或x ＝9，选B.[答案] B[例2] 某程序框图如图所示，现输入如下四个函数，则可以输出的函数为( )A ．f (x )＝cos x x ⎝⎛⎭⎫－π2<x <π2，且x ≠0 B ．f (x )＝2x －12x ＋1C ．f (x )＝|x |xD ．f (x )＝x 2ln(x 2＋1)[解析] 由程序框图知该程序输出的是存在零点的奇函数，选项A 、C 中的函数虽然是奇函数，但在给定区间上不存在零点，故排除A 、C.选项D 中的函数是偶函数，故排除D.选B.[答案] B[解题技法] 顺序结构和条件结构的运算方法(1)顺序结构是最简单的算法结构，语句与语句之间、框与框之间是按从上到下的顺序进行的．解决此类问题，只需分清运算步骤，赋值量及其范围进行逐步运算即可．(2)条件结构中条件的判断关键是明确条件结构的功能，然后根据“是”的分支成立的条件进行判断．(3)对于条件结构，无论判断框中的条件是否成立，都只能执行两个分支中的一个，不能同时执行两个分支．[题组训练]1．半径为r 的圆的面积公式为S ＝πr 2，当r ＝5时，计算面积的流程图为( )解析：选D 因为输入和输出框是平行四边形，故计算面积的流程图为D. 2．运行如图所示的程序框图，可输出B ＝______，C ＝______.解析：若直线x＋By＋C＝0与直线x＋3y－2＝0平行，则B＝3，且C≠－2，若直线x＋3y＋C＝0与圆x2＋y2＝1相切，则|C|12＋(3)2＝1，解得C＝±2，又C≠－2，所以C＝2.答案：3 2考点二循环结构考法(一)由程序框图求输出(输入)结果[例1](2018·天津高考)阅读如图所示的程序框图，运行相应的程序，若输入N的值为20，则输出T的值为()A．1B．2C．3 D．4[解析]输入N的值为20，第一次执行条件语句，N＝20，i ＝2，Ni ＝10是整数，∴T ＝0＋1＝1，i ＝3＜5；第二次执行条件语句，N ＝20，i ＝3，N i ＝203不是整数，∴i ＝4＜5；第三次执行条件语句，N ＝20，i ＝4，Ni ＝5是整数，∴T ＝1＋1＝2，i ＝5，此时i ≥5成立，∴输出T ＝2. [答案] B[例2] (2019·安徽知名示范高中联考)执行如图所示的程序框图，如果输出的n ＝2，那么输入的 a 的值可以为( )A ．4B ．5C ．6D ．7[解析] 执行程序框图，输入a ，P ＝0，Q ＝1，n ＝0，此时P ≤Q 成立，P ＝1，Q ＝3，n ＝1，此时P ≤Q 成立，P ＝1＋a ，Q ＝7，n ＝2.因为输出的n 的值为2，所以应该退出循环，即P >Q ，所以1＋a >7，结合选项，可知a 的值可以为7，故选D.[答案] D[解题技法] 循环结构的一般思维分析过程 (1)分析进入或退出循环体的条件，确定循环次数．(2)结合初始条件和输出结果，分析控制循环的变量应满足的条件或累加、累乘的变量的表达式．(3)辨析循环结构的功能． 考法(二) 完善程序框图[例1] (2018·武昌调研考试)执行如图所示的程序框图，如果输入的a 依次为2,2,5时，输出的s 为17，那么在判断框中可以填入( )A ．k <n?B ．k >n?C ．k ≥n?D ．k ≤n?[解析] 执行程序框图，输入的a ＝2，s ＝0×2＋2＝2，k ＝1；输入的a ＝2，s ＝2×2＋2＝6，k ＝2；输入的a ＝5，s ＝2×6＋5＝17，k ＝3，此时结束循环，又n ＝2，所以判断框中可以填“k >n ？”，故选B.[答案] B[例2] (2018·全国卷Ⅱ)为计算S ＝1－12＋13－14＋…＋199－1100，设计了如图所示的程序框图，则在空白框中应填入( )A ．i ＝i ＋1B ．i ＝i ＋2C ．i ＝i ＋3D ．i ＝i ＋4[解析] 由题意可将S 变形为S ＝⎝⎛⎭⎫1＋13＋…＋199－⎝⎛⎭⎫12＋14＋…＋1100，则由S ＝N －T ，得N ＝1＋13＋…＋199，T ＝12＋14＋…＋1100.据此，结合N ＝N ＋1i ，T ＝T ＋1i ＋1易知在空白框中应填入i ＝i ＋2.故选B.[答案] B[解题技法] 程序框图完善问题的求解方法(1)先假设参数的判断条件满足或不满足；(2)运行循环结构，一直到运行结果与题目要求的输出结果相同为止； (3)根据此时各个变量的值，补全程序框图．[题组训练]1．(2018·凉山质检)执行如图所示的程序框图，设输出的数据构成的集合为A ，从集合A 中任取一个元素a ，则函数y ＝x a ，x ∈[0，＋∞)是增函数的概率为( )A.47B.45C.35D.34解析：选C 执行程序框图，x ＝－3，y ＝3；x ＝－2，y ＝0；x ＝－1，y ＝－1；x ＝0，y ＝0；x ＝1，y ＝3；x ＝2，y ＝8；x ＝3，y ＝15；x ＝4，退出循环．则集合A 中的元素有－1,0,3,8,15，共5个，若函数y ＝x a ，x ∈[0，＋∞)为增函数，则a >0，所以所求的概率为35.2．(2019·珠海三校联考)执行如图所示的程序框图，若输出的n 的值为4，则p 的取值范围是( )A.⎝⎛⎦⎤34，78B.⎝⎛⎭⎫516，＋∞C.⎣⎡⎭⎫516，78D.⎝⎛⎦⎤516，78解析：选A S ＝0，n ＝1；S ＝12，n ＝2；S ＝12＋122＝34，n ＝3；满足条件，所以p >34，继续执行循环体；S ＝34＋123＝78，n ＝4；不满足条件，所以p ≤78.输出的n 的值为4，所以34<p ≤78，故选A.3．(2019·贵阳适应性考试)某程序框图如图所示，若该程序运行后输出的值是137，则整数a 的值为( )A ．6B ．7C ．8D ．9解析：选A 先不管a 的取值，直接运行程序．首先给变量S ，k 赋值，S ＝1，k ＝1，执行S ＝S ＋1k (k ＋1)，得S ＝1＋11×2，k ＝2；执行S ＝1＋11×2＋12×3，k ＝3；……继续执行，得S ＝1＋11×2＋12×3＋…＋1k (k ＋1)＝1＋⎝⎛⎭⎫1－12＋⎝⎛⎭⎫12－13＋…＋⎝⎛⎭⎫1k －1k ＋1＝2－1k ＋1，由2－1k ＋1＝137得k ＝6，所以整数a ＝6，故选A.考点三 基本算法语句[典例] 执行如图程序语句，输入a ＝2cos 2 019π3，b ＝2tan 2 019π4，则输出y 的值是( )A ．3B ．4C ．6D ．－1[解析] 根据条件语句可知程序运行后是计算y ＝⎩⎪⎨⎪⎧a (a ＋b )，a <b ，a 2－b ，a ≥b ，且a ＝2cos 2 019π3＝2cos π＝－2，b ＝2tan 2 019π4＝2tan 3π4＝－2.因为a ≥b ，所以y ＝a 2－b ＝(－2)2－(－2)＝6， 即输出y 的值是6. [答案] C[变透练清]1. 执行如图所示的程序，输出的结果是________．i ＝11S ＝1DOS ＝S*ii ＝i －1LOOP UNTIL i<9PRINT S END解析：程序反映出的算法过程为 i ＝11⇒S ＝11×1，i ＝10； i ＝10⇒S ＝11×10，i ＝9； i ＝9⇒S ＝11×10×9，i ＝8；i ＝8<9退出循环，执行“PRINT S ”． 故S ＝990. 答案：9902．阅读如图所示的程序．a 的值是________． 解析：由题意可得程序的功能是计算并输出a ＝⎩⎪⎨⎪⎧2＋a ，a >2，a ×a ，a ≤2的值， 当a >2时，由2＋a ＝9得a ＝7； 当a ≤2时，由a 2＝9得a ＝－3， 综上知，a ＝7或a ＝－3. 答案：－3或7[课时跟踪检测]1．(2019·湖北八校联考)对任意非零实数a ，b ，定义a *b 的运算原理如图所示，则(log222)*⎝⎛⎭⎫18－23＝( )A ．1B ．2C ．3D ．4解析：选A 因为log222＝3，⎝⎛⎭⎫18－23＝4,3<4，所以输出4－13＝1，故选A. 2．执行如图所示的程序框图，则输出的x ，y 分别为( )A ．90,86B ．94,82C ．98,78D ．102,74解析：选C 第一次执行循环体，y ＝90，s ＝867＋15，不满足退出循环的条件，故x ＝90；第二次执行循环体，y ＝86，s ＝907＋433，不满足退出循环的条件，故x ＝94；第三次执行循环体，y ＝82，s ＝947＋413，不满足退出循环的条件，故x ＝98；第四次执行循环体，y ＝78，s ＝27，满足退出循环的条件，故x ＝98，y ＝78.3．(2018·云南民族大学附属中学二模)执行如图所示的程序框图，若输出的k 的值为6，则判断框内可填入的条件是( )A ．s >12？B ．s >710？C ．s >35？D ．s >45？解析：选B s ＝1，k ＝9，满足条件；s ＝910，k ＝8，满足条件；s ＝45，k ＝7，满足条件；s ＝710，k ＝6，不满足条件．输出的k ＝6，所以判断框内可填入的条件是“s >710？”．故选B.4．(2019·合肥质检)执行如图所示的程序框图，如果输出的k 的值为3，则输入的a 的值可以是( )A ．20B ．21C ．22D ．23解析：选A 根据程序框图可知，若输出的k ＝3，则此时程序框图中的循环结构执行了3次，执行第1次时，S ＝2×0＋3＝3，执行第2次时，S ＝2×3＋3＝9，执行第3次时，S ＝2×9＋3＝21，因此符合题意的实数a 的取值范围是9≤a <21，故选A.5．(2019·重庆质检)执行如图所示的程序框图，如果输入的x ＝0，y ＝－1，n ＝1，则输出x ，y 的值满足( )A ．y ＝－2xB ．y ＝－3xC ．y ＝－4xD ．y ＝－8x解析：选C 初始值x ＝0，y ＝－1，n ＝1，x ＝0，y ＝－1，x 2＋y 2<36，n ＝2，x ＝12，y＝－2，x 2＋y 2<36，n ＝3，x ＝32，y ＝－6，x 2＋y 2>36，退出循环，输出x ＝32，y ＝－6，此时x ，y 满足y ＝－4x ，故选C.6．(2018·南宁二中、柳州高中联考)执行如图所示的程序框图，若输出的结果s ＝132，则判断框中可以填( )A．i≥10? B．i≥11?C．i≤11? D．i≥12?解析：选B执行程序框图，i＝12，s＝1；s＝12×1＝12，i＝11；s＝12×11＝132，i ＝10.此时输出的s＝132，则判断框中可以填“i≥11？”．7．(2019·漳州八校联考)执行如图所示的程序，若输出的y的值为1，则输入的x的值为() INPUT xIF x>＝1THENy＝x2ELSEy＝－x2＋1END IFPRINT yENDA．0 B．1C．0或1 D．－1,0或1解析：选C当x≥1时，由x2＝1得x＝1或x＝－1(舍去)；当x<1时，由－x2＋1＝1得x＝0.∴输入的x的值为0或1.)8．执行如图所示的程序框图，若输入的n＝4，则输出的s＝(C．20 D．35解析：选C执行程序框图，第一次循环，得s＝4，i＝2；第二次循环，得s ＝10，i ＝3； 第三次循环，得s ＝16，i ＝4； 第四次循环，得s ＝20，i ＝5.不满足i ≤n ，退出循环，输出的s ＝20.9.(2018·洛阳第一次统考)已知某算法的程序框图如图所示，则该算法的功能是( )A ．求首项为1，公差为2的等差数列的前2 018项和B ．求首项为1，公差为2的等差数列的前2 019项和C ．求首项为1，公差为4的等差数列的前1 009项和D ．求首项为1，公差为4的等差数列的前1 010项和解析：选D 由程序框图得，输出的S ＝(2×1－1)＋(2×3－1)＋(2×5－1)＋…＋(2×2 019－1)，可看作数列{2n －1}的前2 019项中所有奇数项的和，即首项为1，公差为4的等差数列的前1 010项和．故选D.10．(2018·郑州第一次质量测试)执行如图所示的程序框图，若输出的结果是7，则判断框内m 的取值范围是( )A ．(30,42]B ．(30,42)C ．(42,56]D ．(42,56)解析：选A k ＝1，S ＝2，k ＝2；S ＝2＋4＝6，k ＝3；S ＝6＋6＝12，k ＝4；S ＝12＋8＝20，k ＝5；S ＝20＋10＝30，k ＝6；S ＝30＋12＝42，k ＝7，此时不满足S ＝42<m ，退出循环，所以30<m ≤42，故选A.11．(2019·石家庄调研)20世纪70年代，流行一种游戏——角谷猜想，规则如下：任意写出一个自然数n ，按照以下的规律进行变换，如果n 是奇数，则下一步变成3n ＋1；如果n 是偶数，则下一步变成n2.这种游戏的魅力在于无论你写出一个多么庞大的数字，最后必然会落在谷底，更准确地说是落入底部的4－2－1循环，而永远也跳不出这个圈子，下列程序框图就是根据这个游戏而设计的，如果输出的i 值为6，则输入的n 值为( )A ．5或16B ．16C ．5或32D ．4或5或32解析：选C 若n ＝5，执行程序框图，n ＝16，i ＝2；n ＝8，i ＝3；n ＝4，i ＝4；n ＝2，i ＝5；n ＝1，i ＝6，结束循环，输出的i ＝6.若n ＝32，执行程序框图，n ＝16，i ＝2；n ＝8，i ＝3；n ＝4，i ＝4；n ＝2，i ＝5；n ＝1，i ＝6，结束循环，输出的i ＝6.当n ＝4或16时，检验可知不正确，故输入的n ＝5或32，故选C.12．(2018·贵阳第一学期检测)我国明朝数学家程大位著的《算法统宗》里有一道闻名世界的题目：“一百馒头一百僧，大僧三个更无争．小僧三人分一个，大小和尚各几丁？”如图所示的程序框图反映了对此题的一个求解算法，则输出的n 的值为( )A ．20B ．25C ．30D ．35解析：选B 法一：执行程序框图，n ＝20，m ＝80，S ＝60＋803＝8623≠100；n ＝21，m ＝79，S ＝63＋793＝8913≠100；n ＝22，m ＝78，S ＝66＋783＝92≠100；n ＝23，m ＝77，S ＝69＋773＝9423≠100；n ＝24，m ＝76，S ＝72＋763＝9713≠100；n ＝25，m ＝75，S ＝75＋753＝100，退出循环．所以输出的n ＝25.法二：设大和尚有x 个，小和尚有y 个， 则⎩⎪⎨⎪⎧x ＋y ＝100，3x ＋13y ＝100，解得⎩⎪⎨⎪⎧x ＝25，y ＝75， 根据程序框图可知，n 的值即大和尚的人数，所以n ＝25.13．已知函数y ＝lg|x －3|，如图所示程序框图表示的是给定x 值，求其相应函数值y 的算法．请将该程序框图补充完整．其中①处应填________，②处应填________．解析：由y ＝lg|x －3|＝⎩⎪⎨⎪⎧lg (x －3)，x >3，lg (3－x )，x <3及程序框图知，①处应填x <3？，②处应填y＝lg(x －3)．答案：x <3？ y ＝lg(x －3)14．执行如图所示的程序框图，若输入的N ＝20，则输出的S ＝________.解析：依题意，结合题中的程序框图知，当输入的N ＝20时，输出S 的值是数列{2k －1}的前19项和，即19(1＋37)2＝361.答案：36115．执行如图所示的程序框图，则输出的λ是________．解析：依题意，若λa ＋b 与b 垂直，则有(λa ＋b )·b ＝4(λ＋4)－2(－3λ－2)＝0，解得λ＝－2；若λa ＋b 与b 平行，则有－2(λ＋4)＝4(－3λ－2)，解得λ＝0.结合题中的程序框图可知，输出的λ是－2.答案：－216．执行如图所示的程序框图，如果输入的x ，y ∈R ，那么输出的S 的最大值为________．解析：当条件x ≥0，y ≥0，x ＋y ≤1不成立时，输出S 的值为1，当条件x ≥0，y ≥0，x ＋y ≤1成立时，输出S ＝2x ＋y ，下面用线性规划的方法求此时S 的最大值．作出不等式组⎩⎪⎨⎪⎧x ≥0，y ≥0，x ＋y ≤1表示的平面区域如图中阴影部分所示，由图可知当直线S ＝2x ＋y 经过点M (1,0)时S 最大，其最大值为2×1＋0＝2，故输出S 的最大值为2.答案：2。
12章算法与程序框图
(24,18) (18,6)
(6,12) (6,6)
6就是24和18的最大公约数
循环变量初始化 循环终止条件 循环体
实例四
题意: 某城市对居民的生活用水 实行阶梯式收费，标准为： 每月每户生活用水20m3以 内（含20m3 ）为第一级， 按居民生活用水的供水价 格收费；每月每户生活用 水超过20m3且低于或等于 30m3为第二级，超出部分 按供水价格的1.5倍收费； 每月每户生活用水超过 30m3，超过部分按供水价 格的2倍收费，如果该市 居民生活用水的供水价格 为1.24元m3/，另加收城市 附加费用0.06/m3，污水处 理费1.3/m3，水资源费 0.2/m3，请设计一个算法， 输入某户居民某个月的用 水量，输出这个月该户居 民所需缴纳的水费。
当赋予它新的数值，原来的值就被取代。
• 注意： • 1、赋值号左边只能出现变量名，如: x=2,a=b+c,不能出现 2=b, c+1=2 • 2、赋值语句中，只能给一个变量赋值，不能同时给两个变量赋值，如：a=b=5是错误的 。 • 3、赋值号不同于“等号”，赋值号左右可以现现同一个变量，如n=n+1,而等式n=n+1是错误的。 • 4、一个变量可多次赋值，但运算时只跟最后一次赋值相关
题目
起止框 第一步 输入两个数a,b；(输入输出框） 第二步 计算c=a+b；（处理框） 第三步 计算m=c÷2；（处理框） 第四步 输出m；（输入输出框） 起止框
算法
程序框图
实例
起止框
例2： 如图所示程序框图 的功能是（ ） A. 求a-b的值 B.求b-a的值 C.求|a-b|的值 D.求 -|a-b|的值
例题
一杯白开水一杯茶水，设计一个算法，将两个怀子中的水对调 ②
算法与程序框图PPT优秀课件
算法与程序框图
算法 程序框图
算法的三种基本逻辑 结构和框图表示
顺序结构 条件分支结构
循环结构
算法
可以理解为由基本运算及规定的运 算顺序所构成的完整的解题步骤，或
者看成按照要求设计好的有限的确切
的计算序列，并且这样的步骤或序列
能够一类问题解决.
自然语言、数学语言、形式语言、框图。
程序框图 用一些通用图形符号构成一张图来 表示算法，这种图称作程序框图 （简称框图）.
――[阿萨·赫尔帕斯爵士] 115.旅行的精神在于其自由，完全能够随心所欲地去思考.去感觉.去行动的自由。――[威廉·海兹利特]
116.昨天是张退票的支票，明天是张信用卡，只有今天才是现金；要善加利用。――[凯·里昂] 117.所有的财富都是建立在健康之上。浪费金钱是愚蠢的事，浪费健康则是二级的谋杀罪。――[B·C·福比斯] 118.明知不可而为之的干劲可能会加速走向油尽灯枯的境地，努力挑战自己的极限固然是令人激奋的经验，但适度的休息绝不可少，否则迟早会崩溃。――[迈可·汉默] 119.进步不是一条笔直的过程，而是螺旋形的路径，时而前进，时而折回，停滞后又前进，有失有得，有付出也有收获。――[奥古斯汀] 120.无论那个时代，能量之所以能够带来奇迹，主要源于一股活力，而活力的核心元素乃是意志。无论何处，活力皆是所谓“人格力量”的原动力，也是让一切伟大行动得以持续的力量。――[史迈尔斯] 121.有两种人是没有什么价值可言的：一种人无法做被吩咐去做的事，另一种人只能做被吩咐去做的事。――[C·H·K·寇蒂斯] 122.对于不会利用机会的人而言，机会就像波浪般奔向茫茫的大海，或是成为不会孵化的蛋。――[乔治桑] 123.未来不是固定在那里等你趋近的，而是要靠你创造。未来的路不会静待被发现，而是需要开拓，开路的过程，便同时改变了你和未来。――[约翰·夏尔] 124.一个人的年纪就像他的鞋子的大小那样不重要。如果他对生活的兴趣不受到伤害，如果他很慈悲，如果时间使他成熟而没有了偏见。――[道格拉斯·米尔多] 125.大凡宇宙万物，都存在着正、反两面，所以要养成由后面.里面，甚至是由相反的一面，来观看事物的态度――。[老子]
(完整版)人教版高中数学必修5《算法与程序框图》教案(有答案)
第 9 页 共 13 页
8．解析： S 2 4 6 L 100 2550
三、解答题 9． 请阅读下面程序框图，说明此程序的功能
解：程序功能是求 s 的值． s 1 2 22 ... 26 ，并输出 s
10．已知函数 y
( x 2)2 ( x 0)
解析： 首先要理解各程序框的含义，输入 a，b，c 三个数之后，接着判断 a，b 的大小，若 b 小，则
把 b 赋给 a，否则执行下一步，即判断 a 与 c 的大小，若 c 小，则把 c 赋给 a， 否则执行下一步，
这样输出的 a 是 a， b， c 三个数中的最小值．所以该程序框图所表示的功能是求
是
输出①
是
输出②
当工资薪金所得不超过 3600元，计算个人所得税的一个算法框图如图．
则输出①、输出②分别为 ( )．
A． 0.05 x; 0.1x
B． 0.05 x; 0.1x 185
C． 0.05 x 80; 0.1x;
D． 0.05x 80; 0.1x 185
5．解析 : 设全月总收入金额为 x 元， 所得税额为 y 元，则 y 与 x 之间的函数关系为
1 变式训练 画出求 1 42
解： 程序框图如下 :
1 72 L
1 1002 的值的程序框图．
第 4 页 共 13 页
例 5．某工厂 2005 年的生产总值为 200 万元，技术改进后预计以后后每年的年生产总值都比上一年
增长 5%．设计一个程序框图，输出预期年生产总值超过
300 万元的最早年份及 2005 年到此年份之
D ．算法执行步骤的次数不可以很大，否则无法实施．
12算法与程序框图
邗江职业技术教育中心教案一、引言：说起算法，大家有可能觉得有点陌生，但事实上，我们几乎每天都会和它打交道，例如，青菜的价格是4.8元/kg，买了1.2kg,如果我们用计算器计算该付多少钱，我们做法是：第一步按计算机的开启键；第二步按数字键输入4.8；第三步按乘号键；第四步按数字键输入1.2；第五步按等号键得出结果。
这就是解决这个问题的算法；二、新课讲授：（一）探究小李想用银行卡从自动取款机上取500元钱，由于他第一次用银行卡取钱，所以向你求助，你能写出用银行卡取钱的具体步骤，帮助他顺利取出钱吗？第一步插入银行卡；第二步输入取款密码；第三步输入取款金额；第四步从出钞口取走钱；第五步取回银行口；（二）算法1、定义：算法是指用来解决问题的一系列明确而有效的步骤，是解决问题清晰的指令。
即能够对一定规范的输入，在有限的时间内获得所要求的答案。
2、设计算法的要求：写出的算法必须能够解决某一类问题；要使算法尽量的简单，步骤尽量少；要保证算法正确，且计算能够执行。
（三）例题讲解例1：设计一个算法，求出1+2+3+4+5……+10的值。
解：算法为：第一步计算1+2，得出结果3；第二步计算3+3，得出结果6；第三步计算6+4，得出结果10；第四步计算10+5，得出结果15；……第九步 计算45+10，得出结果55。
所以：1+2+3+……+10=55例2：现有一杯开水和一杯茶，你能设计一个算法，将两个杯子中的开水和茶对调吗？ 试一试。
解：设原来装开水的是A 杯，装茶的是B 杯，空杯子为C 杯 将开水和茶对调的算法为: 第一步 将A 杯中的开水倒入C 杯； 第二步 将B 杯中的茶倒入A 杯; 第三步 将C 杯中的开水倒入B 杯；完成练习（1） 设计一个算法，求出10321⨯⨯⨯⨯ 的值。
（2） 写出从12,3，-1,2,6,9,18,5，-3,17中搜索出数据5的一个算法。
（四） 变量和赋值（1）变量：在解决问题的过程中，可以取不同数值的量叫做变量。
1.1.2算法与程序框图
循环结构分为当型循环结构和 循环结构分为当型循环结构和直到型循环结构 当型循环结构
循环体 循环体 是 满足条件？ 满足条件？ 否 当型循环结构 满足条件？ 满足条件？ 是 直到型循环结构 否
差异:循环终止条件不同 检验条件是否成立的先后次序也不同 差异 循环终止条件不同,检验条件是否成立的先后次序也不同 循环终止条件不同 检验条件是否成立的先后次序也不同. 当型循环结构:先判断后执行循环体 先判断后执行循环体. 当型循环结构 先判断后执行循环体 直到型循环结构:先执行循环体后判断条件是否成立 先执行循环体后判断条件是否成立. 直到型循环结构 先执行循环体后判断条件是否成立
1.1.2 程序框图 与 算法的基本逻辑结构
程序框
名称
终端框 起止框） （起止框） 输入、 输入、输出框 处理框 执行框） （执行框）
功能
表示一个算法的起始和结束 表示一个算法输入和 输出的信息 赋值、 赋值、计算
判断框
判断某一条件是否成立, 判断某一条件是否成立,成立 时在出口处标明“ 时在出口处标明“是”或“Y”； ； 不成立时标明“ 不成立时标明“否”或“N”. . 连接程序框
结束
判断整数n(n>2)是否为质数”的算法： 判断整数n(n>2)是否为质数”的算法： n(n>2)是否为质数
开始 输入n 输入 i=2 设n是一个大 是一个大 的整数. 于2的整数 的整数
一般用i=i+1 一般用 表示. 表示
除以i的余数 求n除以 的余数 除以 的余数r
i=i+1 i的值增加 仍用 表示 的值增加1仍用 的值增加 仍用i表示
循环结构一定包含条件结构,用以控制循环过程 避免出现 循环结构一定包含条件结构 用以控制循环过程,避免出现 用以控制循环过程 死循环” 判断框内写上条件 判断框内写上条件,两个出口分别对应终止条件成 “死循环”.判断框内写上条件 两个出口分别对应终止条件成 立与否,其中一个指向循环体 经过循环体回到判断框的入口处. 其中一个指向循环体,经过循环体回到判断框的入口处 立与否 其中一个指向循环体 经过循环体回到判断框的入口处
人教版高中数学【必修三】[知识点整理及重点题型梳理]_算法与程序框图_基础
![人教版高中数学【必修三】[知识点整理及重点题型梳理]_算法与程序框图_基础](https://img.taocdn.com/s3/m/9e4474cff90f76c661371ac8.png)
人教版高中数学必修三知识点梳理重点题型（常考知识点）巩固练习算法与程序框图【学习目标】1.初步建立算法的概念；2.让学生通过丰富的实例体会算法的思想；3.让学生通过对具体问题的探究，初步了解算法的含义；4.掌握程序框图的概念；5.会用通用的图形符号表示算法，掌握算法的三个基本逻辑结构；6.掌握画程序框图的基本规则，能正确画出程序框图.【要点梳理】【算法与程序框图 397425 知识讲解1】要点一、算法的概念1、算法的定义：广义的算法是指完成某项工作的方法和步骤，那么我们可以说洗衣机的使用说明书是操作洗衣机的算法，菜谱是做菜的算法等等.在数学中，现代意义的算法是指可以用计算机来解决的某一类问题的程序和步骤，这些程序或步骤必须是明确和有效的，而且能够在有限步之内完成.2、算法的特征：（1）确定性：算法的每一步都应当做到准确无误、“不重不漏”.“不重”是指不是可有可无的、甚至无用的步骤，“不漏”是指缺少哪一步都无法完成任务.（2）逻辑性：算法从开始的“第一步”直到“最后一步”之间做到环环相扣，分工明确，“前一步”是“后一步”的前提，“后一步”是“前一步”的继续.（3）有穷性：算法要有明确的开始和结束，当到达终止步骤时所要解决的问题必须有明确的结果，也就是说必须在有限步内完成任务，不能无限制的持续进行.（4）不唯一性：求解某一个问题的算法不一定是唯一的，对于一个问题可以有不同的算法．3、设计算法的要求（1）写出的算法，必须能解决一类问题（如：判断一个整数35是否为质数；求任意一个方程的近似解……），并且能够重复使用．（2）要使算法尽量简单、步骤尽量少．（3）要保证算法正确．且计算机能够执行，如：让计算机计算1×2×3×4×5是可以做到的．4、算法的描述：（1）自然语言：自然语言就是人们日常使用的语言，可以是汉语、英语或数学语言等.用自然语言描述算法的优点是通俗易懂，当算法中的操作步骤都是顺序执行时比较容易理解.缺点是如果算法中包含判断和转向，并且操作步骤较多时，就不那么直观清晰了.（2）程序框图：所谓框图，就是指用规定的图形符号来描述算法，用框图描述算法具有直观、结构清晰、条理分明、通俗易懂、便于检查修改及交流等特点.（3）程序语言：算法最终可以通过程序的形式编写出来，并在计算机上执行.要点诠释：算法的特点:思路简单清晰，叙述复杂，步骤繁琐，计算量大，完全依靠人力难以完成，而这些恰恰就是计算机的特长，它能不厌其烦地完成枯燥的、重复的繁琐的工作，正因为这些，现代算法的作用之一就是使计算机代替人完成某些工作，这也是我们学习算法的重要原因之一.事实上，算法中出现的程序只是用基本的语句把程序的主要结构描述出来，与真正的程序还有差距，所以算法描述的许多程序并不能直接运行，要运行程序，还要把程序按照某种语言的严格要求重新改写才行.【算法与程序框图 397425 知识讲解2】要点二、程序框图1、程序框图的概念：程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形.23一个程序框图包括以下几部分：实现不同算法功能的相对应的程序框；带箭头的流程线；程序框内必要的说明文字.4、算法的三种基本逻辑结构(1)顺序结构顺序结构是最简单的算法结构，语句与语句之间，框与框之间是按从上到下的顺序进行的.它是由若干个依次执行的步骤组成的，它是任何一个算法都离不开的一种基本算法结构.见示意图和实例：顺序结构在程序框图中的体现就是用流程线将程序框自上而下地连接起来，按顺序执行算法步骤.如在示意图中，A框和B框是依次执行的，只有在执行完A框指定的操作后，才能接着执行B框所指定的操作.(2)条件结构如下面图示中虚线框内是一个条件结构，此结构中含有一个判断框，算法执行到此判断给定的条件P 是否成立，选择不同的执行框(A框、B框).无论P条件是否成立，只能执行A框或B框之一，不可能既执行A框又执行B框，也不可能A框、B框都不执行.A框或B框中可以有一个是空的，即不执行任何操作.见示意图要点诠释：条件结构中的条件要准确，不能含混不清，要清楚在什么情况下需要作怎样的判断，用什么条件来区分．(3)循环结构在一些算法中要求重复执行同一操作的结构称为循环结构.即从算法某处开始，按照一定条件重复执行某一处理过程.重复执行的处理步骤称为循环体.循环结构有两种形式：当型循环结构和直到型循环结构.①当型循环结构，如左下图所示，它的功能是当给定的条件P成立时，执行A框，A框执行完毕后，返回来再判断条件P是否成立，如果仍然成立，返回来再执行A框，如此反复执行A框，直到某一次返回来判断条件P不成立时为止，此时不再执行A框，离开循环结构，继续执行下面的框图.②直到型循环结构，如右下图所示，它的功能是先执行重复执行的A框，然后判断给定的条件P是否成立，如果P仍然不成立，则返回来继续执行A框，再判断条件P是否成立，依次重复操作，直到某一次给定的判断条件P成立为止，此时不再返回来执行A框，离开循环结构，继续执行下面的框图.见示意图要点诠释：循环结构中使用什么样的条件控制循环的开始和结束，要清楚满足某个条件的变量的次数与循环次数的联系与区别.误区提醒1、框图中的流程线不能出现交叉的现象.若有交叉，则程序语句无法写出；2、各种框图有其固定的格式和作用，不要乱用.如条件结构中不要忘了“是”与“否”，流程线不要忘记画箭头；3、条件分支结构的方向要准确；4、循环结构中，计数变量要赋初值，计数变量的自加不要忘记，自加多少不能弄错.另外计数变量一般只负责计数任务；5、循环结构中循环的次数要严格把握，区分“＜”与“≤”等.循环变量的取值与循环结构(当型与直到型)有关，需区分清楚.另外，同一问题用两种不同的结构解决时，其判断条件恰是相反的；6、程序框图不要出现死循环(无限步的循环).【典型例题】类型一：算法的概念例1．（1）下列描述不能看作算法的是（）．A．做米饭需要刷锅，淘米，添水，加热这些步骤B．洗衣机的使用说明书C．解方程2x2+x－1=0D．利用公式S=πr2，计算半径为4的圆的面积，就是计算π×42（2）下列关于算法的说法：①求解某一类问题的算法是唯一的；②算法必须在有限步操作之后停止；③算法的每一步操作必须是明确的，不能有歧义或模糊；④算法执行后一定产生明确的结果．其中正确的有（）．A．1个B．2个C．3个D．4个【答案】（1）C （2）C【解析】（1）A、B、D都描述了解决问题的过程，可以看作算法．而C只描述了一个事实，没说明怎么解决问题，不是算法．（2）根据算法的特征可以知道，算法要有明确的开始与结束，每一步操作都必须是明确而有效的，必须在有限步内得到明确的结果，所以②③④正确．而解决某一类问题的算法不一定是唯一的，故①错误．【总结升华】算法一般是机械的，有时需要进行大量的重复计算，只要按部就班去做，总能算出结果.通常把算法过程称为“数学机械化”，数学机械化的最大优点是它可以借助计算机来完成.实际上处理任何问题都需要算法，如：中国象棋有中国象棋的棋谱、走法、胜负的评判准则；而国际象棋有国际象棋的棋谱、走法、胜负的评判准则；再比如申请出国有一系列的先后手续，购买物品也有相关的手续…….举一反三：【变式1】我们已学过的算法有求解一元二次方程的求根公式，加减消元法求二元一次方程组的解，二分法求出函数的零点等，对算法的描述有：①对一类问题都有效；②算法可执行的步骤必须是有限的；③算法可以一步一步地进行，每一步都有确切的含义；④是一种通法，只要按部就班地做，总能得到结果．以上算法的描述正确的有（）．A．1个B．2个C．3个D．4个【答案】D类型二：算法的描述例2．写出求方程组32142x yx y-=⎧⎨+=-⎩①②的解的算法．【解析】可利用消元法或代入法求解．算法一：第一步：②×2+①，得到5x=14－4．③第二步，解方程③，可得x=2．④第三步，将④代入②，可得2+y=－2．⑤第四步，解⑤得y=－4．第五步，得到方程组的解为24 xy=⎧⎨=-⎩算法二：第一步，由②式移项可以得到x=－2－y．③第二步，把③代入①，得y=－4．④第三步，把④代入③，得x=2．第四步，得到方程组的解为24 xy=⎧⎨=-⎩．【总结升华】通过求解二元一次方程组可知，求解某个问题的算法不一定唯一．对于具体的实例可以选择合适的算法，尽量做到“省时省力”，使所用的算法是最优算法．举一反三：【变式1】试描述求解三元一次方程组1233162x y zx y zx y z++=⎧⎪--=⎨⎪--=-⎩①②③的算法步骤．【解析】算法1：第一步，①+③，得x=5．④第二步，将④分别代入①式和②式可得73 1y zy z+=⎧⎨+=-⎩⑤⑥．第三步，⑥－⑤，得y=－4．⑦第四步，将⑦代入⑤可得z=11．第五步，得到方程组的解为5411xyz=⎧⎪=-⎨⎪=⎩．算法2：第一步，①+②，得2x －y=14． ④ 第二步，②－③，得x －y=9． ⑤ 第三步，④－⑤，得x=5． ⑥第四步，将⑥代入⑤式，得y=－4． ⑦ 第五步，将⑥和⑦代入①式，得z=11．第六步，得到方程组的解为5411x y z =⎧⎪=-⎨⎪=⎩．类型三：算法的设计【算法与程序框图 397425 算法中的例1】例3．设计一个算法，从3个互不相等的数中选出最小的一个数．，并用数学语言表达． 【解析】第一步：假定这3个数中第一个是“最小值”；第二步：将第二个数与“最小值”比较，如果它小于此“最小值”，那么就用这个数取代“最小值”； 第三步：再重复第二步，将第三个数与最小值比较，如果它小于此“最小值”，那么就用这个数取代“最小值”；第四步：此时的“最小值”就是三个数中的最小值，输出最小值．所谓的算法，就是解决该类问题的一般步骤. 举一反三：【变式1】任意给定一个正整数n ，设计出判断n 是否为质数的一个算法． 【解析】第一步，当n =1时，n 既不是质数，也不是合数； 第二步，当n =2时，n 是质数；第三步，当n ≥3时，从2到n －1依次判断是否存在n 的因数（因数1除外），若存在，则n 是合数；若不存在，则n 是质数．类型四：顺序结构的应用【算法与程序框图 397425 程序框图中的例1】 例4．对于一个二次函数2y ax bx c =++，求出顶点坐标．【解析】算法步骤：S1 用户输入二次函数的系数a,b,c ；S2 计算顶点坐标24,24b ac b x y a a-=-=（赋值）；S3 输出顶点坐标．举一反三：【变式1】已知x=40，y=3．画出计算z=15x+8y 的值的程序框图． 【答案】程序框图如下图所示．类型五：条件结构的应用例5．已知函数232 1 (0)1 (01)2 (1)x x y x x x x x -<⎧⎪=+≤<⎨⎪+≥⎩，写出求该函数的函数值的算法，并画出程序框图．【解析】该函数是分段函数，因此当给出一个自变量x 的值时，需先判断x 的范围，然后确定利用哪一段的解析式求函数值．画程序框图时，必须采用条件分支结构，因为函数解析式分了三段，所以需要两个判断框，即进行两次判断．算法如下：第一步，输入x ．第二步，如果x ＜0，那么使y=2x －1，输出y ；否则，执行第三步． 第三步，如果0≤x ＜1，那么使y=x 2+1，输出y ；否则，执行第四步．第四步，y=x 2+2x 第五步，输出y ．程序框图如下图所示．【总结升华】凡是必须先根据条件作出判断，然后再决定进行哪一个步骤的问题，在画程序框图时，必须引入判断框，采用条件结构．而像本题求分段函数的函数值的程序框图的画法，如果是分两段的函数，只需引入一个判断框；如果是分三段的函数，需引入两个判断框；分四段的函数需引入三个判断框，依此类推．判断框内的内容是没有固定顺序的．举一反三：【变式1】已知函数 1 (0)()0 (0)1 (0)x f x x x ->⎧⎪==⎨⎪<⎩， 写出求函数()f x 的任一函数值的一个算法并画出程序框图．【解析】记y=f (x)．算法：第一步：输入x ．第二步：如果x ＞0，那么使y=－1；如果x=0，那么使y=0；如果x ＜0，那么使y=1． 第三步：输出函数值y ． 程序框图如下图所示．【变式2】如果学生的成绩大于或等于60分，则输出“及格”，否则输出“不及格”.用程序框图表示这一算法过程.【答案】开始结束类型六：循环结构的应用例6．设计一个计算1+3+5+7+…+999的值的算法，并画出程序框图．【解析】算法一：当型循环：第一步，令S=0，i=1．第二步，若i≤999成立，则执行第三步；否则输出S，结束算法．第三步，S=S+i．第四步，i=i+2，返回第二步，程序框图如图（1）．算法二：直到型循环：第一步，令S=0，i=1．第二步，S=S+i．第三步，i=i+2．第四步，若i不大于999，转第二步；否则，输出S，结束算法．程序框图如图1-1-8（2）．【总结升华】注意直到型循环和当型循环的区别．直到型循环先执行i=i+2，再判断i＞999是否成立，若成立才输出S；而当型循环先判断i≤999是否成立，若成立，则执行i=i+2，直到条件i≤999不成立才结束循环，输出S．举一反三：【变式1】给出30个数：1,2,4,7,11，…，要计算这30个数的和，现已给出了该问题的程序框图如图所示，那么框图中判断框处①和执行框②处应分别填入（）A．i≤30？；p=p+i－1 B．i≤31？；p=p+i+1C．i≤31？；p=p+i D．i≤30？；p=p+i【答案】D【解析】由于要计算30个数的和，故循环要执行30次，由于循环变量的初值为1，步长为1，故终值应为30即①中应填写i≤30；又由第1个数是1；第2个数比第1个数大1，即1+1=2；第3个数比第2个数大1，即2+2=4；第4个数比第3个数大1，即4+3=7；…故②中应填写p=p+i故选：D．【变式2】（2016春河南周口期中）设计求1+3+5+7+…+31的算法，并画出相应的程序框图．【解析】第一步：S=0；第二步：i=1；第三步：S=S+i；第四步：i=i+2；第五步：若i不大于31，返回执行第三步，否则执行第六步；第六步：输出S值．程序框图如图：类型七：利用算法和程序框图解决实际问题例7．北京获得了2008年第29届奥运会主办权．你知道在申办奥运会的最后阶段，国际奥委会是如何通过投票决定主办权归属的吗？对选出的5个申办城市进行表决的操作程序是：首先进行第一轮投票，如果有一个城市得票超过总票数的一半，那么该城市就获得主办权；如果所有申办城市得票数都不超过总票数的一半，则将得票最少的城市淘汰，然后重复上述过程，直到选出一个申办城市为止．试画出该过程的程序框图．【解析】本题为算法中与现实生活相联系的题目，从选举的方法看，应选择循环结构来描述算法．如图所示：【总结升华】解决与现实相关的问题时首先要理清题意，此循环结构中对用哪一个步骤控制循环，哪一个步骤作为循环体，要有清晰的思路．举一反三：【变式1】儿童乘坐火车时，若身高不超过1.1 m，则无需购票；若身高超过1.1 m，但不超过1.4 m，可买半票；若超过1.4 m，应买全票，请设计一个算法，并画出程序框图．【解析】根据题意，该题的算法中应用条件结构，首先以身高为标准，分成买和免票，在买票中再分出半票和全票．买票的算法步骤如下：第一步：测量儿童身高h．第二步：如果h≤1.1 m，那么免费乘车，否则若h≤1.4 m，则买半票，否则买全票．精品文档 用心整理资料来源于网络 仅供免费交流使用 程序框图如下图所示．【总结升华】本题的程序框图中有两个判断点，一个是以1.1 m 为判断点，1.1 m 把身高分为两段，在大于1.1 m 的一段中，1.4 m 又将其分两段，因此1.4 m 这个判断是套在1.1 m 的判断里的．所以我们用到两个条件结构．。
必修三算法与程序框图优秀教案
算法与程序框图教学目的：明确算法的含义，熟识算法的三种根本构造。
教学重点：算法的根本学问与算法对应的程序框图的设计.教学难点：与算法对应的程序框图的设计及算法程序的编写.教学过程：1.算法的定义：广义的算法是指完成某项工作的方法和步骤，现代意义的算法是指可以用计算机来解决的某一类问题的程序和步骤，这些程序或步骤必需是明确和有效的，而且可以在有限步之内完成.2.流程图的概念：流程图是用一些规定的图形、指向线及简洁的文字说明来表示算法几程序构造的一种图形程序．它直观、清晰，便于检查和修改.其中，图框表示各种操作的类型，图框中的文字和符号表示操作的内容，带箭头的流程线（指向线）表示操作的先后次序．构成流程图的图形符号及其作用3．标准流程图的表示：①运用标准的框图符号；②框图一般按从上到下、从左到右的方向画，流程线要标准；③除推断框外，大多数框图符号只有一个进入点和一个退出点.④在图形符号内描绘的语言要特别简练、清晰.4、算法的三种根本逻辑构造：课本中例题的讲解得出三种根本逻辑构造：依次构造、条件构造、循环构造（1）依次构造：依次构造描绘的是是最简洁的算法构造，语句与语句之间，框与框之间是按从上到下的依次进展的。
例1：已知一个三角形的三边分别为2、3、4，利用海伦公式设计一个算法，求出它的面积，并画出算法的程序框图。
算法分析：这是一个简洁的问题，只需先算出p的值，再将它代入公式，最终输出结果，只用依次构造就可以表达出算法。
解：程序框图：点评：依次构造是由若干个依次执行的步骤组成的，是任何一个算法都离不开的根本构造。
（2）条件构造：依据条件选择执行不同指令的限制构造。
例2：随意给定3个正实数，设计一个算法，推断分别以这3个数为三边边长的三角形是否存在，画出这个算法的程序框图。
算法分析：推断分别以这3个数为三边边长的三角形是否存在，只需要验收这3个数当中随意两个数的和是否大于第3个数，这就需要用到条件构造。
高中数学_算法与程序框图
算法与程序框图知识图谱算法与程序框图知识精讲一．算法的概念1.算法的定义由基本运算及规定的运算顺序所构成的完整的解题步骤，或者看成按照一定规则，解决某一类问题的明确的和有限的步骤，称为算法．通常可以编成计算机程序，让计算机执行并解决问题．2.算法的特征：（1）有穷性：算法必须在执行有限步后结束，通常还理解为实际上能够容忍的合理限度；（2）确定性：算法的每一个步骤必须有确定的含义；（3）可行性：组成算法的每个步骤和操作必须是相当基本的，原则上都是能精确地执行的；（4）输入：有零个或多个输入；（5）输出：有一个或多个输出．二．算法的描述1．用自然语言；2．用数学语言；3．用算法语言（程序设计语言）；4．用程序框图（流程图）．三．程序框图的概念：用一些通用的图形符号构成的一张图来表示算法，称为程序框图（简称框图）．1.常用图形符号：图形符号名称符号表示的意义起、止框框图的开始或结束输入、输出框数据的输入或者结果的输出处理框赋值、执行计算语句、结果的传送判断框根据给定条件判断流程线流程进行的方向连结点连结另一页或另一部分的框图四．算法的三种基本逻辑结构：顺序结构、条件（分支）结构和循环结构．1.顺序结构：最简单的算法结构，语句与语句之间，框与框之间是按从上到下的顺序进行的．如下图，只有在执行完A 框指定的操作后，才能接着执行B 框指定的操作；2.条件（分支）结构：在一个算法中，用来处理需要根据条件是否成立有不同的流向的结构．常见的条件结构的程序框图有下面两种形式：否否是是BA A P PB A3.循环结构：从某处开始，按照一定的条件反复执行某些步骤的情况，就是循环结构，其中反复执行的步骤称为循环体．常见的循环结构的框图对应为：否是A P三点剖析一．注意事项：1.在画程序框图时，从开始框沿箭头必须能到达结束框，特别是条件分支结构应沿每条支路都能到达结束框，流程线必须加箭头表示顺序．2．对于循环结构有如下需要注意的情况：（1）循环结构非常适合计算机处理，因为计算机的运算速度非常快，执行成千上万次的重复计算，只不过是一瞬间的事，且能保证每次的结果都正确；（2）循环结构要有中止循环体的条件，不能无休止的运算下去，循环结构中一定包含条件结构，如i n ≤就是中止循环的条件；（3）循环结构的关键是，要理解“累加变量”和“用1i 代替i ”，S 是一个累加变量，i 是计数变量，每循环一次，S 和i 都要发生变化，这两步要重复计算若干次；（4）一种循环结构是先判断i n ≤是否成立，若是，执行循环体；若否，则中止循环，像这样，每次执行循环体前对控制循环条件进行判断，条件满足时执行循环体，不满足则停止，称为当型循环．除了当型循环外，常用的循环结构还有直到型循环．二．方法点拨1．画程序框图的规则：（1）使用标准的框图的符号；（2）框图一般按从上到下、从左到右的方向画；（3）除判断框外，大多数框图符号只有一个进入点和一个退出点．判断框是具有超过一个退出点的惟一符号；（4）一种判断框是“是”与“不是”两分支的判断，而且有且仅有两个结果；另一种是多分支判断，有几种不同的结果；（5）在图形符号内描述的语言要非常简练清楚．2．画程序框图要注意的几点：（1）起、止框是任何流程不可少的，表示程序的开始和结束；（2）输入、输出框可以用在算法中任何需要输入、输出的位置；（3）算法中间要处理数据或计算，可分别写在不同的处理框内；（4）当算法要求你对两个不同的结果进行判断时，要写在判断框内；（5）一个算法步骤到另一个算法步骤用流程线连结；（6）如果一个框图需要分开来画，要在断开处画上连结点，并标出连结的号码．程序框图例题1、下列说法正确的是（）A.算法就是某个问题的解题过程；B.算法执行后可以产生不同的结果；C.解决某一个具体问题算法不同结果不同；D.算法执行步骤的次数不可以为很大，否则无法实施．例题2、指出下列哪一个不是算法（）A.解方程260x -=的过程是移项和系数化为1B.从济南到温哥华需要先乘火车到北京，再从北京乘飞机到温哥华C.解方程2210x x +-=D.利用公式2πS r =，计算半径为3的圆的面积为2π3⨯例题3、下列语句中是算法的个数为（）①从济南到巴黎：先从济南坐火车到北京，再坐飞机到巴黎；②统筹法中“烧水泡茶”的故事；③测量某棵树的高度，判断其是否是大树；④已知三角形的一部分边长和角，借助正余弦定理求得剩余的边角，再利用三角形的面积公式求出该三角形的面积A.1B.2C.3D.4随练1、下面四种叙述能称为算法的是（）A.在家里一般是妈妈做饭B.做米饭要需要刷锅．添水．加热这些步骤C.在野外做饭叫野炊D.做饭必需要有米随练2、下列关于算法的说法正确的有（）①求解某一类问题的算法是唯一的；②算法必须在有限步操作之后停止；③算法的每一步操作必须是明确的，不能有歧义或模糊；④算法执行后产生确定的结果．A.1个B.2个C.3个D.4个随练3、早上从起床到出门需要洗脸刷牙（5min）．刷水壶（2min）．烧水（8min）．泡面（3min）．吃饭（10min）．听广播（8min）几个步骤，下列选项中最好的一种算法为（）A.s1洗脸刷牙s2刷水壶s3烧水s4泡面s5吃饭s6听广播B.s1刷水壶s2烧水的同时洗脸刷牙s3泡面s4吃饭s5听广播C.s1刷水壶s2烧水的同时洗脸刷牙s3泡面s4吃饭的同时听广播D.s1吃饭的同时听广播s2泡面s3烧水的同时洗脸刷牙s4刷水壶算法的三种逻辑结构和框图表示例题1、如果执行如图所示的程序框图，那么输出的a=（）A.2B.12 C.﹣1 D.以上都不正确例题2、如果执行如图所示的程序框图，那么输出的a=（）A.2B.12 C.﹣1 D.以上都不正确例题3、阅读右边的程序框图，运行相应的程序，输出的S的值是（）A.26B.40C.57D.无法确定随练1、如图是某算法的流程图，则执行该算法输出的结果是S=____．随练2、执行如图所示的程序框图，如果输入a=2，那么输出的a值为（）A.4B.16C.256D.log316随练3、执行如图所示的程序框图，则输出的k=（）A.4B.5C.6D.7拓展1、算法的有穷性是指（）A.算法最后包含输出B.算法的每个操作步骤都是可执行的C.算法的步骤必须有限D.以上都不正确2、下面对算法描述正确的一项是（）A.算法只能用自然语言来描述B.算法只能用图形方式来表示C.同一问题可以有不同的算法D.同一问题的算法不同，结果必然不同3、看下面的四段话，其中不是解决问题的算法的是（）A.从上海到北京旅游，先坐火车，再坐飞机抵达B.解一元一次方程的步骤是去分母．去括号．移项．合并同类项．系数化为1C.方程210x -=有两个实根D.求12345++++的值，先计算123+=，再由于336+=，6410+=，10515+=，4、根据如图程序框图，输出k 的值为（）A.3B.4C.5D.65、给出计算12+14+16+…+120的值的一个程序框图如图，其中判断框内应填入的条件是（）A.i ＞10B.i ＜10C.i ＞20D.i ＜206、如图所示的流程图表示一函数，记作y=f （x ），若x 0满足f （x 0）＜0，且f （f （x 0））=1，则x 0=____．。
高二数学算法与程序框图
N
y x 2 3x 1
输出
y
x x 0 .1
结束
开始
P15习题1—1（B）
1：
b d 输入分数 , a c
bc x ad bc 约简 x ad
输出
x
结束
开始
P15习题1—1（B） 2：
S=0,i=1
i 50
Y
N
S=S+i i=S+(i+1)
输ቤተ መጻሕፍቲ ባይዱS 结束
3：
开始
P15习题1—1（B）（1）：
P15习题1—1（A）
3：
设两位小数为a.bc ，其 中 a, b, c 都为整数，且 0 b 9,0 c 9 .
开始 输入实数
x a.bc
N
Y
c5
x a 0.1 b
输出
x a 0.1 b 1
x
结束
开始
P15习题1—1（A）
4：
x 3
x3
程序框图
用一些通用图形符号构成一张图来 表示算法，这种图称作程序框图 （简称框图）.
四种图框类型 输入、输出框 处理框 判断框 起止框
算法的三种基本逻辑结构和框图表示
顺序结构 条件分支结构 循环结构
A B A
Y
p
N B
p
Y
N
A
开始
P14练习A
1：
S=0,i=1
i 10
Y
N
S=S+i i=i+1
疑。神秘人冲着这股劲，接着说道，“帮主给我们下了命令，趁着傅家四公子娶妾之事，傅宗哲必然会回到傅家来，趁机务必将傅宗哲 的人头给取来！”说罢，神秘人咻地一声就消失了。不得了啊，这就是电视剧中经典到不能再经典的桥段吗？而且我又恰好充当了那个 偷听者的角色！而且，从说话的内容，我基本上可以断定出这个女剑侠就是之前遇到的那个帮大看宅子的女看护，傅烨！这就是传说中 的混进大宅然后杀人大作战吗？怎么办？我的小命危在旦夕啊！待神秘人走后，傅烨在原地歇了一会，紧接着也离开了。好险啊！差点 就瞎闯着把自己的命搭上去了，还好他们俩都已经走了。在我万分感慨了之后，才想起自己依旧被困在禁地之林里，还没有找到出去的 路。虽然高手们已经走掉了，但是走不出这鬼地方我还是要死啊。想到这，我又开始摸索着路走了起来。不料，刚开始走了一小步，突 然感到有人在我身后敲了我一下，顿时就昏了过去。5傅大少的宅子|“小琴，你在那作甚？”不出所料，厅内传出丑妇人的声音。小琴 听罢，也不敢继续和我闲聊，乖乖地往屋里走去，边应和道，“夫人，奴婢这就过来。”说罢，小琴已经进屋子去了。我站在原地，看 着小琴的背影离我远去，蓦地觉得好好的一个救生圈就这么走掉了，又是一阵凉意传来。不久，丑妇人从屋里再次走了出来，小琴也跟 在她的身后。丑妇人今天的打扮甚是奇葩。稍微瞄了一眼，只见头顶着一堆不知道是发簪还是夹子的闪亮亮的东西，全身被五颜六色的 衣服裹着，真有一种现代人超级非主流的打扮韵味；而她的脸部还是老样子，光从她头部周围依旧飘着那些粉末状的小颗粒就知道她今 天擦的粉底还是那么的厚。正当我看着这丑妇人的装扮且不小心露出一脸不屑模样之际，丑妇人对我叫道，“你这厮就是新来的家丁 吗？”什么！厮？好啊丑妇人，一出口就不把我当一般人看，我脸上就刻着“厮”这字吗？你睁大你的眼睛看看我的样子吧，长得这么 秀气，你丫的你们这年代是找不出能超越我样貌的美男的了，但是我也拿他们的审美观没辙，也许别的模样在他们眼中才算是好看吧。 一不小心在心里吐槽得火热，忘记答话了，这回丑妇人生气地提高了说话语气对我再次吼道，“你这畜生聋的吗？说话啊。”也许这声 音大得有些扭曲，我果真被她的吼叫从我的心理世界换了回来。这时我心里大惊，难道丑夫人要杀掉我了？急中生智，连忙跪下，低下 头回答，“是的，大夫人。”一边说道一边把头埋得更深，一来是尽显我的卑下，二来一不小心给她看出来我在鄙视她的表情就更遭了。 “这厮真是个废物，小琴，你把他带出去。”说完，丑妇人转身再次走进了屋里。听着丑妇人的脚步声越来越远，接着，小琴的脚步声 越来
[Word]算法框图知识点和练习
![[Word]算法框图知识点和练习](https://img.taocdn.com/s3/m/d92b9e1417fc700abb68a98271fe910ef12dae79.png)
一、知识网络知识点一：算法与程序框图一、算法1．算法的概念：算法通常是指按一定规则解决某一类问题的明确和有限的步骤。
2.算法的描述方式有：自然语言、程序框图、程序语言。
3.算法的基本特征：①明确性：算法的每一步执行什么是明确的；②顺序性：算法的“前一步”是“后一步”的前提，“后一步”是“前一步”的继续；③有限性：算法必须在有限步内完成任务，不能无限制的持续进行；④通用性：算法应能解决某一类问题。
二、程序框图(一)程序框图基本概念程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形。
一个程序框图包括以下几部分：表示相应操作的程序框；带箭头的流程线；程序框外必要文字说明。
(二)构成程序框的图形符号及其作用程序框名称功能起止框表示一个算法的起始和结束，是任何流程图不可少的。
输入、输出框表示一个算法输入和输出的信息，可用在算法中任何需要输入、输出的位置。
处理框赋值、计算，算法中处理数据需要的算式、公式等分别写在不同的用以处理数据的处理框内。
算法初步算法与程序框图算法语句算法案例算法概念框图的逻辑结构输入语句赋值语句循环语句条件语句输出语句顺序结构循环结构条件结构判断框判断某一条件是否成立，成立时在出口处标“是”或“Y ”；不成立时标明“”或“N ”。
画程序框图的规则如下：①、使用标准的图形符号。
②框图一般按从上到下、从左到右的方向画。
③除判断框外，大多数流程图符号只有一个进入点和一个退出点。
判断框具有超过一个退出点的唯一符号。
④判断框分两大类，一类判断框“是”与“否”两分支的判断，而且有且仅有两个结果；另一类是多分支判断，有几种不同的结果。
⑤在图形符号内描述的语言要非常简练清楚。
(三)、程序框图的三种基本逻辑结构是：顺序结构、条件结构、循环结构。
1、顺序结构：顺序结构在程序框图中的体现就是用流程线将程序框自上而 下地连接起来，按顺序执行算法步骤。
如在示意图中，A 框和B框是依次执行的，只有在执行完A 框指定的操作后，才能接着执行B 框所指定的操作。
高考总复习理数(北师大版)第12章第1节算法与程序框图
第一节算法与程序框图考点高考试题考查内容核心素养程序框图2017·全国卷Ⅰ·T8·5分填充程序框图数学运算2017·全国卷Ⅱ·T8·5分循环结构框图逻辑推理2017·全国卷Ⅲ·T7·5分循环结构框图逻辑推理2016·全国卷Ⅰ·T9·5分框图的功能逻辑推理2016·全国卷Ⅱ·T8·5分循环结构框图逻辑推理2016·全国卷Ⅲ·T7·5分循环结构框图逻辑推理命题分析本节是高考的必考内容，常以选择题、填空题形式出现，考查题型有输出结果，完善程序框图以及判断程序运行功能.1．算法在解决某类问题时，所要执行的一系列可操作或可计算的步骤.现代算法的作用之一是使计算机能代替人完成某些工作.2．算法框图中的符号意义图形符号名称符号表示的意义起止框表示一个算法的起始和结束□输入、输出框表示一个算法输入和输出的信息处理框赋值、执行计算、结果传送判断框判断某一条件是否成立流程线流程进行的方向为了使算法结构更加清晰，可借助图来帮助描述算法．图的特点是直观、清楚，便于检查和交流.通常这样的图叫作框图．4．算法的基本结构名称内容顺序结构选择结构循环结构定义按照步骤依次执行的一个算法，称为具有“顺序结构”的算法，或者称为算法的顺序结构在算法的执行过程中，需要对条件进行判断，判断的结果决定后面的步骤，像这样的结构通常称作选择结构在一些算法中，经常会出现从某处开始，按照一定的条件，反复执行某一处理步骤的情况，像这种需要反复执行循环体的结构称为循环结构算法框图提醒：1．辨明两个易误点(1)易混淆处理框与输入、输出框，处理框主要是赋值、计算，而输入、输出框只是表示一个算法输入或输出的信息．(2)易忽视循环结构中必有选择结构，其作用是控制循环进程，避免进入“死循环”，是循环结构必不可少的一部分．2．识别三种结构的关系顺序结构是每个算法结构都含有的，而对于循环结构有重复性，选择结构具有选择性没有重复性，并且循环结构中必定包含一个选择结构，用于确定何时终止循环体，循环结构和选择结构都含有顺序结构．1．判断下列结论的正误(正确的打“√”，错误的打“×”)(1)算法只能解决一个问题，不能重复使用．()(2)程序框图中的图形符号可以由个人来确定．()(3)输入框只能紧接开始框，输出框只能紧接结束框．()(4)选择结构的出口有两个，但在执行时，只有一个出口是有效的．()答案：(1)×(2)×(3)×(4)√2．(教材习题改编)给出如图算法框图，其功能是()A ．求a －b 的值B ．求b －a 的值C ．求|a －b |的值D ．以上都不对解析：选C 由算法框图知其功能是求|a －b |的值．3．阅读如图所示的程序框图，运行相应的程序，输出s 的值等于( )A ．－3B ．－10C ．0D ．－2解析：选A 第一次循环：k ＝0＋1＝1，满足k ＜4，s ＝2×1－1＝1； 第二次循环：k ＝1＋1＝2，满足k ＜4，s ＝2×1－2＝0； 第三次循环：k ＝2＋1＝3，满足k ＜4，s ＝2×0－3＝－3； 第四次循环：k ＝3＋1＝4，不满足k ＜4，故输出的s ＝－3. 4．(2018·济宁模拟)执行如图所示的程序框图，则输出的S 为( )A ．－2B ．12C ．43D ．3解析：选D 程序运行如下： S ＝3，k ＝1；S ＝43，k ＝2；S ＝12，k ＝3；S ＝－2，k ＝4； S ＝3，k ＝5；……发现此程序中的S 值4个一循环，2 017÷4＝504……1，则输出的S ＝3，故选D ．顺序结构与选择结构 [明技法]应用顺序结构和选择结构的注意点(1)顺序结构是最简单的算法结构，语句与语句之间、框与框之间是按从上到下的顺序进行的．(2)解决此类问题，只需分清运算步骤，赋值量及其范围进行逐步运算即可．(3)选择结构中条件的判断关键是明确选择结构的功能，然后根据“是”的分支成立的条件进行判断．(4)对选择结构，无论判断框中的条件是否成立，都只能执行两个分支中的一个，不能同时执行两个分支．[提能力]【典例】 (1)运行如图所示程序框图，若输入a ，b 的值分别为log 23和log 32，则输出M 的值是( )A ．0B ．1C ．2D ．－1解析：选C∵log23>log32，即a>b，故M＝a×b＋1＝log23×log32＋1＝2.(2)(2017·山东卷)执行两次如图所示的程序框图，若第一次输入的x的值为7，第二次输入的x的值为9，则第一次、第二次输出的a的值分别为()A．0,0B．1,1C．0,1D．1,0解析：选D当x＝7时，∵b＝2，∴b2＝4＜7＝x.又7不能被2整除，∴b＝2＋1＝3.此时b2＝9＞7＝x，∴退出循环，a＝1，∴输出a＝1.当x＝9时，∵b＝2，∴b2＝4＜9＝x.又9不能被2整除，∴b＝2＋1＝3.此时b2＝9＝x，又9能被3整除，∴退出循环，a＝0.∴输出a＝0.故选D．[刷好题]1．阅读如图所示的程序框图，运行相应的程序，若输入x的值为1，则输出y的值为() A．2B．7C ．8D ．128解析：选C 由程序框图知，y ＝⎩⎪⎨⎪⎧2x ，x ≥2，9－x ，x <2.∵输入x 的值为1，比2小，∴执行的程序要实现的功能为9－1＝8，故输出y 的值为8.2．执行下面的程序框图，如果输入的t ∈[－1,3]，则输出的s 属于( )A ．[－3,4]B ．[－5,2]C ．[－4,3]D ．[－2,5]解析：选A 由框图知s 是关于t 的分段函数s ＝⎩⎪⎨⎪⎧3t ，－1≤t <1，4t －t 2，1≤t ≤3，当t ∈[－1,1)时，s ∈[－3,3)；当t ∈[1,3]时，s ＝4t －t 2＝4－(t －2)2∈[3,4]，故s ∈[－3,4]，故选A ．循环结构 [析考情]循环结构是高考命题的一个热点问题，多以选择题、填空题的形式呈现，试题难度不大，多为容易题或中档题．[提能力]命题点1：求程序运行后的结果【典例1】(2016·全国卷Ⅱ)中国古代有计算多项式值的秦九韶算法，如图是实现该算法的程序框图，执行该程序框图，若输入的x ＝2，n ＝2，依次输入的a 为2,2,5，则输出的S ＝( )A．7B．12C．17D．34解析：选C由框图可知，输入x＝2，n＝2，a＝2，S＝2，k＝1，不满足条件；a＝2，S＝4＋2＝6，k＝2，不满足条件；a＝5，S＝12＋5＝17，k＝3，满足条件，输出S＝17，故选C．命题点2：确定控制循环的变量【典例2】(2017·全国卷Ⅰ)如图所示的程序框图是为了求出满足3n－2n＞1 000的最小偶数n，那么在和两个空白框中，可以分别填入()A．A＞1 000和n＝n＋1B．A＞1 000和n＝n＋2C．A≤1 000和n＝n＋1D．A≤1 000和n＝n＋2解析：选D因为题目要求的是“满足3n－2n＞1 000的最小偶数n”，所以n的叠加值为2，所以内填入“n＝n＋2”．由程序框图知，当内的条件不满足时，输出n，所以内填入“A≤1 000”．故选D．命题点3：辨析程序框图的功能【典例3】如图所示的程序框图，该算法的功能是()A．计算(1＋20)＋(2＋21)＋(3＋22)＋…＋(n＋1＋2n)的值B．计算(1＋21)＋(2＋22)＋(3＋23)＋…＋(n＋2n)的值C．计算(1＋2＋3＋…＋n)＋(20＋21＋22＋…＋2n－1)的值D．计算[1＋2＋3＋…＋(n－1)]＋(20＋21＋22＋…＋2n)的值解析：选C初始值k＝1，S＝0，第1次进入循环体时，S＝1＋20，k＝2；当第2次进入循环体时，S＝1＋20＋2＋21，k＝3，…；给定正整数n，当k＝n时，最后一次进入循环体，则有S＝1＋20＋2＋21＋…＋n＋2n－1，k＝n＋1，终止循环体，输出S＝(1＋2＋3＋…＋n)＋(20＋21＋22＋…＋2n－1)，故选C．[悟技法]与循环结构有关问题的常见类型及解题策略(1)已知程序框图，求输出的结果，可按程序框图的流程依次执行，最后得出结果．(2)完善程序框图问题，结合初始条件和输出结果，分析控制循环的变量应满足的条件或累加、累乘的变量的表达式．(3)对于辨析程序框图功能问题，可将程序执行几次，即可根据结果作出判断．[刷好题]1．秦九韶是我国南宋时期的数学家，普州(现四川省安岳县)人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例，若输入n，x的值分别为3,2，则输出v的值为()A．35B．20C．18D．9解析：选C按照图中的程序计算，当i＝2时，得v＝4；当i＝1时，得v＝2×4＋1＝9；当i＝0时，得v＝2×9＋0＝18；当i＝－1时，直接输出v＝18，即输出的v值为18.2．(2017·全国卷Ⅱ)执行如图所示的程序框图，如果输入的a＝－1，则输出的S＝()A．2B．3C．4D．5解析：选B当K＝1时，S＝0＋(－1)×1＝－1，a＝1，执行K＝K＋1后，K＝2；当K＝2时，S＝－1＋1×2＝1，a＝－1，执行K＝K＋1后，K＝3；当K＝3时，S＝1＋(－1)×3＝－2，a＝1，执行K＝K＋1后，K＝4；当K＝4时，S＝－2＋1×4＝2，a＝－1，执行K＝K＋1后，K＝5；当K＝5时，S＝2＋(－1)×5＝－3，a＝1，执行K＝K＋1后，K＝6；当K＝6时，S＝－3＋1×6＝3，执行K＝K＋1后，K＝7＞6，输出S＝3，结束循环．故选B．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一步 投票 第二步 统计票数，如果有一座城市的得票数 超过总票数的一半，那么该城市就获得举办权； 否则将得票数最少的城市淘汰，并转而执行第一步
第三步 输出举办城市
算法步骤 第一步：投票 第二步 统计票数 第三步 输出举办城市
开始 投票
有一座城市的得票数 超过总票数的一半
是
输出该城市为举办城市
P42例5
新课引入
算法是由一系列明确和有限的步骤组成，我们可以用自然语言表示一 个算法，但往往过程复杂，缺乏简洁性，因此必须引入一种使算法表达 的更直观，更准确的方法，这就是今天我们要学习的程序框图。
程序框图基本概念：
程序框图又称流程图，是一种用规定的框、带箭头的线（也称为流程 线或指向线）及文字说明来准确、直观地表示算法的图形。
（2）确切性 算法中的每一个步骤都是确切的，能有效的执行且能得到确定的结果，不能模 棱两可，不存在歧义 （3）可行性（或有效性） 算法的每一个步骤都是可执行的操作，即每一步都可以在有限的时间内完成。 （4）有0个、1个、或多个输入，用于刻画运算对象的初始情况。 （5）有1个或多个输出，用以反映对输入数据加工后的结果，没有输出的算法 是毫无意义的。
结束
将得票数最少 的城市淘汰 否
二、算法的三种基本逻辑结构：
开始 输入n
i=2
①顺序结构 求n除以i的余数r i的值增加1，仍用i表示
③循环结构
i>n-1或r=0?
否
是
是
r=0?
否否
N不是质数
N是质数
②条件结构
结束
算法千差万别，但都是由这 三种基本逻辑结构构成的.
输入n
i=2
求n除以i的余数r
i的值增加1，仍用i表示
有农夫看管，则狼要吃羊，羊要吃白菜。但是船很小，只够农夫带 一样东西过河。问农夫该如何解此难题？
解决步骤： 1、带羊到对岸，返回；
2、带菜到对岸，并把羊带回；
3、带狼到对岸，返回；
4、带羊到对岸。
算法的概念
算法（algorithm）：
算法是指用来解决问题的一系列明确而有效的步骤， 是解决问题的清新的指令。
步骤A
步骤B
例3 已知一个三角形的三边分别为a、b、c，
利用海伦公式设计一个算法，求出它的面积，并画出算法的程序框图。
算法步骤：（自然语言）
第一步,输入三角形三条边的边长a,b,c.
第二步,计算 p＝
a+b+c 2
第三步,计算S＝ p(p - a)(p - b)(p - c).
第四步，输出S.
算法步骤：（自然语言）
开始 i=0,s=0
输入x
S=s+x
i=i+1
i≥40
否
是
a=s/40
输入s,a
结束
（3）循环结构
循环结构指的是按照一定的条件反复执行的某些算法步骤. 反复执行的步骤称为循环体.
循环体
满足条件？ 否 是
执行一次循环体后，对条件进行 判断，如果条件不满足，就继续执行 循环体，直到条件满足时终止循环.
条件结构可用程序框图表示.
满足条件？ 否
是
步骤A
步骤B
当条件成立时，执行A步骤， 不成立时执行B步骤
例5设计一个求任意实数的绝对值的算法，并画出程序框图.
开始
解：第一步 输入x
第二步 如果x≥0,则输出x,否
输入x
则输出-x
x≥0
否
是
输出x
输出-x
结束
例6.某班有40名 学生，依次输入 这40名学生的数 学考试成绩，输 入全班学生的数 学总分和平均分。 请画出解决这个 问题的算法的程 序框图
（2）确切性 算法中的每一个步骤都是确切的，能有效的执行且能得到确定的结果，不能模 棱两可，不存在歧义 （3）可行性（或有效性） 算法的每一个步骤都是可执行的操作，即每一步都可以在有限的时间内完成。 （4）有0个、1个、或多个输入，用于刻画运算对象的初始情况。 （5）有1个或多个输出，用以反映对输入数据加工后的结果，没有输出的算 法是毫无意义的。
广义的算法：完成某项工作的方法和步骤。
• 菜谱是做菜的算法； • 歌谱是一首歌曲的算法； • 空调说明书是空调使用的算法等
算法的概念
例1：设计一个算法，求出1+2+3+…+10的值
解：第一步算1+2=3； 第二步3+3=6；、、、第九步45+10=55
例2：现有一杯开水和一杯茶，你能设计一个算法，将两个杯子中的开水和茶对调 吗？
如何计算选手最后得分？ 第一步：100+20=120 第二步： 120+30=150 第三步：150-15=135 第四步：135+50=185
如果引入变量S S=100； S=S+20； S=S+30； S=S-15; S=S+50 输出S
可使算法的表示非常简洁。
算法的概念
问题1：结合实际过程，应当如何理解“x=x+20”这样的式子？ 问题2：左右两边的x的意义或取值是否一样？能不能消去？
开始
空杯子是C杯，将A 中的开水倒入C杯中记
作A→C
第一步:找一个大小与A相同的空杯子C;
第二步:将A 中的开水倒入C杯中;
第三步:将B杯中的茶倒入A杯中;
A→C C→B B→A
结束
第四步:将C杯中的开水倒入B杯中。
2、条件结构
在一个算法中，经常会遇到一些条件的判断，算法的流程根据条件是
否成立有不同的流向.条件结构就是处理这种过程的结构. 分类是算法中经常发生的事情，条件结构的主要作用就是表示分类.
练习：
A 1、下列关于程序框图的说法正确的是 （ ）
A、程序框图是描述算法的语言
B、程序框图可以没有输出框，但必须要有输入框给变量赋值
C、程序框图可以描述算法，但不如自然语言描述算法直观
D、程序框图和流程图不是一个概念
例1.写出求任意两个数的平均数的算法，并
画出程序框图
程序框图
解：算法 第一步：输入两个数a,b；
第一步,输入三角形三条 边的边长a,b,c.
第二步,计算p=. 第三步,计算S= 第四步，输出S.
开始 输入a,b,c
p＝
a+b+c 2
S＝
p(p - a)(p - b)(p - c).
输出S 结束
例4 现有一杯开水和一杯茶，你能设计一个算法，将 两个杯子中开水和茶对调吗，并画出程序框图
解 设原来装开水的是A杯，裝茶的是B杯，
第12章 算法与程序框图
本章目录
12.1 算法的概念 12.2 程序框图 12.3 算法与程序框图应用举例
12.1 算法的概念
算法的概念
引入
什么是算法？
问题1：计算 6+5×(4-2)的顺序？
先算括号里的
再算乘法
后算加法
算法的概念
引入
什么是算法？
问题2：有一个农夫带一条狼、一只羊和一筐白菜过河。如果没
变量定义：在研究问题的过程中可以取不同的值的量. 变量的表示：一般由一个或几个英文字母组成，或字母加数字 表示.如 a、s、a1等. 赋值的定义：依次给予变量不同的值叫做给变量赋值.
算法的概念
大家在看娱乐类电视节目时有没有听过类似这样的话“总分再加20分”？ 知识竞赛开始时，1号选手的起始分数为100. 第一环节结束，主持人报：“1号选手得分加20.” 第二环节结束，主持人报：“1号选手得分加30.” 第三环节结束，主持人报：“1号选手得分减15.” 第四环节结束，主持人报：“1号选手得分加50.”
12.2 程序框图
复习
1、算法的概念
算法是指用来解决问题的一系列明确而有效的步骤，是解决问题 的清新的指令。
2、变量赋值
给变量赋值一般格式为： “变量名＝表达式”
算法的特征
（1）有穷性 算法应由有限步组 成，必须能在执行有限个步骤之后终止，也就是说，算
法的步骤不能是无限的。
有人对歌德巴赫猜想“任何大于4的偶数都能写成两个奇质数之和”设计了如下操 作步骤： 第1步：检验 6＝3＋3 第2步：检验 8＝3＋5 第3步：检验 10＝5＋5 …… 利用计算机无穷的进行下去！ 请问，利用这种程序能够证明猜想的正确性吗？这是一个算法吗？
第一步：将茶水倒入空杯中；第二步将开水倒入茶水杯中；第三步将茶水倒入开 水杯中
算法的概念
练习：
（1）给出求 1×2×…×10的一个算法 （2）设计一个算法 从12、3、-1、2、6、9、18、5、-3、17中搜 出5.
算法的概念
变量与赋值
我们发现在设计算法的过程中，解决问题 的思想方法并不难，但描 述的时候却很繁琐，为解决这一问题我们引入变量和赋值的概念。
算法的概念
例.仔细阅读下列算法： 第一步 A＝1，B＝2，C＝3； 第二步 A＝A＋B，B＝A＋1； 第三步 A＝A＋B＋C； 第四步 输出A，B，C． 问：最后输出的A，B，C值各为多少？
可以先后给一个变量赋多个不同的值，但变量的取值只与最后一次赋值有关 .
练习： 仔细阅读下列算法：
第一步 n＝1，S＝1； 第二步 n＝n＋1，S＝S×n； 第三步 n＝n＋1，S＝S×n； 第四步 输出n，S． 问：最后输出的n，S值各为多少？
开始 输入a,b,
第二步：计算c=a+b；
C=a+b
第三步：计算x=c/2；
x=c/2
输出x
第四步：输出x
Байду номын сангаас
结束
例2.2008年中国北京成功举行了第29届夏季奥林匹克运动会，在申报奥运会 的最后时刻，国际奥委会对5作申办的候选城市进行表决，其程序是：每位委 员每轮只能投1座城市，新进行第一轮投票，如果有一座城市的得票数超过总 票数的一半，那么该城市就获得举办权；如果所有城市的得票数都不超过总票 数的一半，将得票数最少的城市淘汰，然后重复上述过程，知道选出一座举办 城市为止，写出该程序的算法，并画出程序框图。