[经管营销]计量经济学第七章
计量经济学 第7章

ˆ 的经济含义为GNP对货币供应量M2的
弹性。
解释:货币供应量每增加1个百分点,GNP增加0.988个百分点。
ˆ ˆ gnpt c ln m2t et 2.半对数模型:
解释:货币供应量每增加1个百分点,GNP增加2584.785个单位(10亿美元)
7.2 虚拟变量回归
注意:区分两种类别,只需要一个虚拟变 量。一般来说,如果一个定性变量有n个 类别,则只需要引入n-1个虚拟变量就可 以了。 从变量的特征进行分类,如果变量有n个 特征,若没有截距项,则需要n个虚拟变 量 若有截距项,则只需要n-1个虚拟变量。 虚拟变量的数量与样本容量的大小无关。
WAGE
估算倒数模型: Wage c ( ˆ ˆ
1 ˆ )u Unemployment
估算出来的菲利普斯曲线
Wage 6 4 2 Unemployment
2
4
6
8
例5:货币供给增长率对GNP的影响(半对数模型 与对数模型)。
理论背景,货币供给的增加对GDP有乘数作用(货币政策效果,货币 政策的支出乘数)。 以1973-1987美国的数据为例(单位:10亿美元)
yi 0 1D1 ui
其中: yi 为工资水平, Di 为虚拟变量:
Di 1, 如果某人为男性 Di 0, 如果某人为女性
如果影响工资的其他因素保持不变,由上 述模型很容易得到: E ( yi Di 0) 0 女性的平均工资水平: E ( yi Di 1) 0 1 男性的平均工资水平: 斜率反映了男性与女性的平均工资差别。
yi 1 2 Di xi ui
其中:xi 为工作年限,为一个普通变量。
《计量经济学》第七章课后答案(李子奈编第四版)

《计量经济学》第七章课后答案(李子奈编第四版)回复关键词:计量经济学即可获取其他章节答案第七章:计量经济学应用模型1.分析教材例7.1.1中的问题,回答:为什么按照(1). (2)、(3)的方法建立的农户借贷因素分析模型都是不正确的?答:例题中农户借贷需求调查共采集了5100家农户的数据,其中,在一年中发生借贷行为的农户占55.3%(包括向亲友借贷),为2820户,其余2280户没有发生借贷。
为了对农户借货行为进行因素分析,建立了农户借贷因素分析模型。
以农户借贷额为被解释变量,各种影响因素包括家庭总收入、总支出、总收入中农业生产经营收入所占比例、总支出中生产性支出所占的比例、户主受教育程度、户主健康状况、家庭人口数等为解释变量。
按照(1)的方法,仅利用2820户发生借贷的农户为样本,即以他们的借贷额为被解释变量,各种影响因素为解释变量,建立经典的回归模型,是不正确的。
首先,既然采集了5100家农户的数据,而只利用2820户的数据,损失了大量的样本信息。
其次,如果只利用2820户的数据建立模型,那么显然是“选择性样本”,应该建立“选择性样本”模型,而不是经典回归模型,属于模型类型选择错误。
按照(2)的方法,利用5100农户为样本,建立经典的回归模型,也是不正确的。
有大约45%的样本被解释变量观测值为0,这样的样本仍然属于“选择性样本”,只是与(1) 具有不同的“选择性”而已。
仍然应该建立“选择性样本”模型,而不是经典回归模型,属于模型类型选择错误。
按照(3)的方法,考虑样本的选择性,发现不应该将没有发生借贷的农户的借贷额统统视为0,而应该视为小于等于0 (s0),于是利用5100农户为样本,建立归并数据模型(Tobit 模型)。
从模型类型选择的角度,是正确的。
问题在于,对没有发生借贷的农户进行更进- - 步分析发现,不应该将他们的借贷额统统视为小于等于0,因为其中一部分农户有借贷需求,只是因为各种原因( 例如提出借贷被拒绝,担心借不到而不敢提出借贷要求)而没有发生实际借贷。
计量经济学第07章

36
★ D· W检验
Step3:判断 0<D· dl W< dl <D· du W< 4<D· W<4- du 4-du <D· W<4-dl 4- dl <D· <4 W
存在正自相关 不能确定 无自相关 不能确定 存在正自相关
37
不能检验
正自相关
无自相关
负自相关
dL
dU
2
4-dU
4-dL
1 Var i
13
⑧同理可得
1 i xi 2 i yi i xi i xi yi
1 Var i xi 2
14
例3 上周练习题
已知模型
y i xi i
Y XB U , 其中 E (U ) 0, E (UU )
' 2 u
42
例7 假设 已知,考虑模型
yt t
t t 1 t
该模型满足其它基本条件, 试用OLS和GLS分别估计未知参数 及其方差的 估计量。
43
因为
yt t
H ki 2 i 2 1 ( ki ) 2 ( ki xi 1)
10
⑤对参数求偏导数可得
2ki 2 i 2 1 2 xi 0 i 1, 2,, n
k =0
i
k x
记
i i
1
i
1
i
2
, = i i xi
2
4
对未知参数求偏导数可得
2
2
k z 0 k 1
计量经济学07

由于最小二乘估计量拥有一个“好”的估计量 所应具备的小样本特性,它自然也拥有大样本特性。
现考察b1的一致性。
P lim b1 P lim B1 kiui
P
lim
B1
P
lim
xi ui xi2
P lim B1 P lim
xiui / n xi2 / n
Cov X , u
B1
Q
B1
对于博彩的例子,其方差和标准误分别是:
见教材表7-1(P126)
蒙特卡洛试验
如何操作?——P127 X=12rnd()-6
OLS估计量的抽样分布(概率分布)及随机干 扰项方差的估计
1、参数估计量b0和b1的概率分布 普通最小二乘估计量b0 、 b1分别是Yi的线性组 合,因此, b0和b1的概率分布取决于Y的分布特 征。
Yi=B1+B2Xi+ui 假设2. 解释变量X与扰动误差项u不相关。
Cov(X, u)=0
线性回归模型的基本假设
假设3. 给定Xi,扰动项的期望或均值为零,即:
E(u|Xi)=0;
PRF : E(Y|Xi)=B1+B2Xi
扰动项ui的条件分布
线性回归模型的基本假设
假设4. ui的方差为常数,即同方差假定:
一、参数的置信区间
回归分析希望通过样本所估计出的参数b1来代 替总体的参数B1
假设检验可以通过一次抽样的结果检验总体参 数可能的假设值的范围(如是否为零),但它 并没有指出在一次抽样中样本参数值到底离总 体参数的真值有多“近”。
要判断样本参数的估计值在多大程度上可以 “近似”地替代总体参数的真值,往往需要通 过构造一个以样本参数的估计值为中心的“区 间”,来考察它以多大的可能性(概率)包含 着真实的参数值。这种方法就是参数检验的置 信区间估计。
计量经济学第七章练习题及参考答案
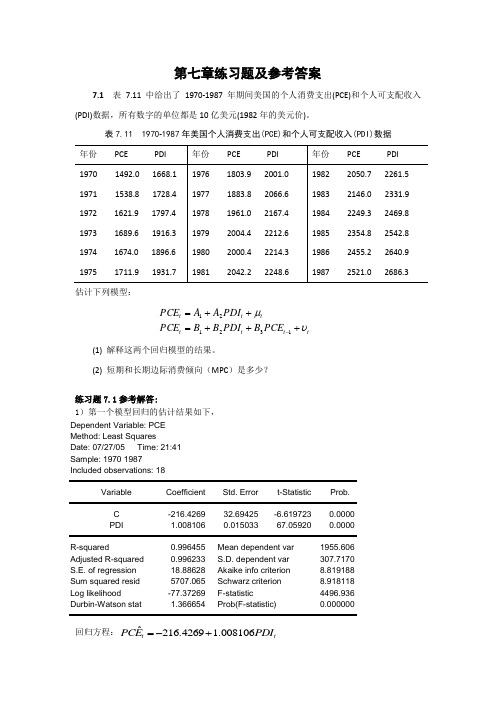
第七章练习题及参考答案7.1 表7.11中给出了1970-1987年期间美国的个人消费支出(PCE)和个人可支配收入(PDI)数据,所有数字的单位都是10亿美元(1982年的美元价)。
表7.11 1970-1987年美国个人消费支出(PCE)和个人可支配收入(PDI)数据估计下列模型:tt t t tt t PCE B PDI B B PCE PDI A A PCE υμ+++=++=-132121(1) 解释这两个回归模型的结果。
(2) 短期和长期边际消费倾向(MPC )是多少?练习题7.1参考解答:1)第一个模型回归的估计结果如下,Dependent Variable: PCEMethod: Least Squares Date: 07/27/05 Time: 21:41 Sample: 1970 1987 Included observations: 18Variable Coefficient Std. Error t-StatisticProb. C -216.4269 32.69425 -6.619723 0.0000 PDI 1.008106 0.015033 67.05920 0.0000 R-squared 0.996455 Mean dependent var1955.606 Adjusted R-squared 0.996233 S.D. dependent var 307.7170 S.E. of regression 18.88628 Akaike info criterion 8.819188 Sum squared resid 5707.065 Schwarz criterion 8.918118 Log likelihood -77.37269 F-statistic 4496.936 Durbin-Watson stat 1.366654 Prob(F-statistic)0.000000回归方程:ˆ216.4269 1.008106t tPCE PDI =-+(32.69425) (0.015033) t =(-6.619723) (67.05920) 2R =0.996455 F=4496.936 第二个模型回归的估计结果如下,Dependent Variable: PCEMethod: Least Squares Date: 07/27/05 Time: 21:51 Sample (adjusted): 1971 1987 Included observations: 17 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.C -233.2736 45.55736 -5.120436 0.0002 PDI 0.982382 0.140928 6.970817 0.0000 PCE(-1) 0.037158 0.144026 0.2579970.8002R-squared 0.996542 Mean dependent var 1982.876 Adjusted R-squared 0.996048 S.D. dependent var 293.9125 S.E. of regression 18.47783 Akaike info criterion 8.829805 Sum squared resid 4780.022 Schwarz criterion 8.976843 Log likelihood -72.05335 F-statistic 2017.064 Durbin-Watson stat 1.570195 Prob(F-statistic)0.000000回归方程:1ˆ233.27360.98240.0372t t t PCE PDI PCE -=-+- (45.557) (0.1409) (0.1440)t = (-5.120) (6.9708) (0.258) 2R =0.9965 F=2017.0642)从模型一得到MPC=1.008;从模型二得到,短期MPC=0.9824,由于模型二为自回归模型,要先转换为分布滞后模型才能得到长期边际消费倾向,我们可以从库伊克变换倒推得到长期MPC=0.9824/(1+0.0372)=0.9472。
计量经济学课件第7章

7
在实际经济活动中,经济变量的关系是复杂的,直 接表现为线性关系的情况并不多见。
如著名的恩格尔曲线(Engle curves)表现为 幂函数曲线形式、宏观经济学中的菲利普斯曲线 (Pillips cuves)表现为双曲线形式等。 但是,大部分非线性关系又可以通过一些简 单的数学处理,使之化为数学上的线性关系,从 而可以运用线性回归的方法进行计量经济学方面 的处理。
31
若区别男女两类的不同,引入两个虚拟变量, 则会导致完全共线性。
Yi Yi . ln X 1i X 1i / X 1i
给出了当X 2保持不变时,X 1i 变化 1%时Y的绝对变化量, Y的绝对变化量Yi 1 * X 1i / X 1i),即Y的绝对变化量为 0.01* 1。 ( P120,图 7 3,右边
17
例:牛肉需求方程
P120-121
t t 1
PF 为t年的农场劳动价格。
t
注意解释经济意义:保 持今年农场劳动价格不 变,
度量了去年棉花价格增 加一单位所引起的
1
今年棉花产量的平均单 位增加量。
27
7.4 虚拟变量的应用
一、虚拟变量模型 虚拟变量(dummy variable):在实际建模过程 中,被解释变量不但受定量变量影响,同时还受定 性变量影响。例如性别、民族、不同历史时期、季 节差异、企业所有制性质不同等因素的影响。这些 因素也应该包括在模型中。 由于定性变量通常表示的是某种特征的有和无, 所以量化方法可采用取值为1或0。这种变量称作虚 拟变量,用D表示。虚拟变量应用于模型中,对其 回归系数的估计与检验方法与定量变量相同。
28
加法模型:
1.包含一个虚拟变量的模型
i 0 1 i 2 i i
计量经济学第七章答案详解

练习题7.1参考解答(1)先用第一个模型回归,结果如下:22216.4269 1.008106 t=(-6.619723) (67.0592)R 0.996455 R 0.996233 DW=1.366654 F=4496.936PCE PDI =-+==利用第二个模型进行回归,结果如下:122233.27360.9823820.037158 t=(-5.120436) (6.970817) (0.257997)R 0.996542 R 0.996048 DW=1.570195 F=2017.064t t t PCE PDI PCE -=-++==(2)从模型一得到MPC=1.008106;从模型二得到,短期MPC=0.982382,长期MPC= 0.982382+(0.037158)=1.01954 练习题7.2参考答案(1)在局部调整假定下,先估计如下形式的一阶自回归模型:*1*1*0*t t t t u Y X Y +++=-ββα 估计结果如下:122ˆ15.104030.6292730.271676 se=(4.72945) (0.097819) (0.114858)t= (-3.193613) (6.433031) (2.365315)R =0.987125 R =0.985695 F=690.0561 DW=1.518595t t t Y X Y -=-++根据局部调整模型的参数关系,有****11 ttu u αδαβδββδδ===-=将上述估计结果代入得到: *1110.2716760.728324δβ=-=-=*20.738064ααδ==-*0.864001ββδ==故局部调整模型估计结果为:*ˆ20.7380640.864001ttYX =-+ 经济意义解释:该地区销售额每增加1亿元,未来预期最佳新增固定资产投资为0.864001亿元。
运用德宾h 检验一阶自相关:(121(1 1.34022d h =-=-⨯=在显著性水平05.0=α上,查标准正态分布表得临界值21.96h α=,由于21.3402 1.96h h α=<=,则接收原假设0=ρ,说明自回归模型不存在一阶自相关。
计量经济学(数字教材版)教案第七章
教学环节
教学内容与教学设计
导入主题
教学内容:
先简要回顾OLS回归的基本假定,再问题式导入主题——如何对时间序列时间建模分析。
经济增长的时间序列数据、人口增长的时间序列数据、工资增长的时间序列数据等问题表明时间序列数据从普遍性。问题:如何对时间序列数据建模找出经济规律?
教学设计:
采用真实的数据进行演示,通过现实问题,引导学生感受到所学思考内生性问题的本质,从而产生好奇心,激起学习新知的欲望。适时设疑,启发学生思考,调动学生学习的积极性。
巩固加深
教学内容:
向量自回归模型的软件实现。教材7.6给出了工具变量法的应用案例。
教学设计:
1实际问题引导学生思考:影响中美贸易量的因素是什么?人民币汇率是决定因素吗?引导学生学应用计量模型分析实际问题。
2软件实现数据平稳性检验,训练学生动手能力。
3软件实习方差分解和脉冲响应分析,让学生对软件得出的结果进行分析,进一步激发学习兴趣和树立为国家繁荣富强而奋斗的志向。
(3)合理设计板书:重点凸显DF检验和ADF检验的推导公式。
(4)请两个小组各派一个同学对DF检验与ADF检验作个小结,教师打分。
深入研讨
教学内容:
知识点:协整与误差修正模型。
具体如下:
(1)由协整的定义引出误差修正模型。
(2)推导误差修正模型,着重讲解模型的应用。
教学设计:
(1)通过协整的定义,问题式导入误差修正模型,让学生感受所学知识在计量经济学体系中的定位,激发其学习热情与探究欲望。
总结提高
在小结之前,及时设疑,设置思考题,启发学生。要想更深入地思考,要更好地估计模型,还需本课程的后续知识,让学生对课程充满期待,激发自主探究欲。学生完成随堂测验,并借习题练习对数据序列数据建模的能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
36个投保人年龄的数据
23 35 39 27 36 44
36 42 46 43 31 33
+1.96x
90%的样本
95% 的样本
99% 的样本 h
x
17
评价估计量的标准
无偏性 有效性 一致性
h
18
总体均值的区间估计
正态总体、方差已知,或非正态总体、大样本
z
x
N(0,1)
n
x z 2
n
h
19
总体均值的区间估计(例题分析)
【 例 】一家食品生产企业以生产袋装食品为主,为对产量
h
11
置信区间
(confidence interval)
1. 由样本统计量所构造的总体参数的估计区间称为 置信区间
2. 统计学家在某种程度上确信这个区间会包含真正 的总体参数,所以给它取名为置信区间
3. 用一个具体的样本所构造的区间是一个特定的区 间,我们无法知道这个样本所产生的区间是否包 含总体参数的真值
第七章 参数估计
参数估计的一般问题 抽样估计的基本方法 样本容量的确定
h
1
抽样估计的过程
总体
样 本
h
样本统计量 例如:样本均 值、比例
2
参数估计的一般问题
参数估计:用样本统计量估计去估计参数
估计量:用来估计总体参数的统计量。 估计值:根据样本计算出来的估计量的数值。
h
3
参数估计的方法
点估计: 区间估计:
我们只能是希望这个区间是大量包含总体参数真值的 区间中的一个,但它也可能是少数几个不包含参数真 值的区间中的一个
h
12
置信水平
(confidence level)
1. 将构造置信区间的步骤重复很多次,置信 区间包含总体参数真值的次数所占的比例 称为置信水平
2. 表示为 (1 - 为是总体参数未在区间内的比例
h
4
点估计 (point estimate)
1、用样本的估计量直接作为总体参数的估计值
▪ 例如:用样本均值直接作为总体均值的估计 ▪ 例如:用样本的方差直接作为总体方差的估计
2、没有给出估计值接近总体参数程度的信息
h
5
点估计
可以估计的总体参数
平均
μ
比例
π
样本值 (点估计)
x
p
h
6
区间估计 (interval estimate)
102.6 107.5 95.0 108.8 115.6
100.0 123.5 102.0 101.6 102.2
116.6
95.4
97.8 108.6 105.0
136.8 102.8 101.5 98.4 93.3
h
20
总体均值的区间估计(例题分析)
已知:X~N(,102),n=25, 1- = 95%,z/2=1.96。根
P{55xi 6}516.67%33.34%16.67%66.68%
P{55Xxi X65X}16.67%33.34%16.67%66.68%
P{5xi X5}16.67%33.34%16.67%66.68%
P{xi X5}16.67%33.34%16.67%66.68%
h
10
总体平均数的置信区间
3. 常用的置信水平值有 99%, 95%, 90%
相应的 为0.01,0.05,0.10
h
13
抽样极限误差 E
抽样极限误差:在一定概率条件下,样本统计量和总体 参数之间误差的可能范围。
Pˆ E 1
如:样本均值的抽样极限误差
P{xXE}1
h
14
根据中心极限定理:
总体均值 X = E(x) 设总体的标准差为
预先给定的概率(1)称为置信水平。
可信区间通常由两个数值即可信限/置信限 (confidence limit, CL)构成。其中较小的值 称可信下限(lower limit, L),较大的值称可 信上限(upper limit, U),一般表示为LU。
h
8
样本均值的抽样分布
1. 样本均值的数学期望(无偏性)
E(x)
2. 重复抽样
样本均值的抽样方差
2 x
2
n
样本均值的抽样标准差
x
2
n
h
9
统计量与总体参数接近程度的概率度量
不重复:样本平均数的抽样分布
样本平均数 xi
样本平均数个数(个) 概率(频率)(%)
45
55
60
65
75 合计
2
2
4
2
2 12
16.67 16.67 33.34 16.67 16.67 100
质量进行监测,企业质检部门经常要进行抽检,以分析 每袋重量是否符合要求。现从某天生产的一批食品中随 机抽取了25袋,测得每袋重量如下表所示。已知产品重 量的分布服从正态分布,且总体标准差为10g。试估计该 批产品平均重量的置信区间,置信水平为95%
25袋食品的重量
112.5 101.0 103.0 102.0 100.5
据样本数据计算得:
总体均值在1-置信水平下的置信区间为
x z 2
105.361.96
n
1.44,109.28
该食品平均重量的置信区间为101.44g~109.28g
h
21
总体均值的区间估计(例题分析)
【例】一家保险公司收集到由36投保个人组成的随机样 本,得到每个投保人的年龄(周岁)数据如下表。试建 立投保人年龄90%的置信区间
x 由中心极限定理得 服从正态分布
x~
2
N(X, )
n
h
15
由中心极限定理 (xX) ~ N(0,1)
/ n
xX
P(
z) 1
/ n
P(xXz/ n)1
xX z/ n 得到极限误差
Ex z/ n
h
16
区间估计的图示
xz2x
x
- 2.58x
-1.65 x
+1.65x
+2.58x
-1.96 x
P{55 xi 65}16.67%33.34%16.67% 66.68% P{xi X 5}16.67%33.34%16.67% 66.68%
P{5 xi X 5}16.67%33.34%16.67% 66.68% P{xi 5 X xi 5}16.67%33.34%16.67% 66.68%
1. 在点估计的基础上,给出总体参数估计的一个区间范围,该 区间由样本统计量加减抽样极限误差而得到的
2. 根据样本统计量的抽样分布能够对样本统计量与总体参数的 接近程度给出一个概率度量
比如,某班级平均分数在75~85之间,置信水平是95%
置信区间
样本统计量 (点估计)
置信下限
置信上限
h
7
区间估计是按预先给定的概率(1)所确定的 包含未知总体参数的一个范围。该范围称为 参数的可信区间或置信区间(confidence interval, CI);
