高数第一章答案
高等数学课后习题答案--第一章
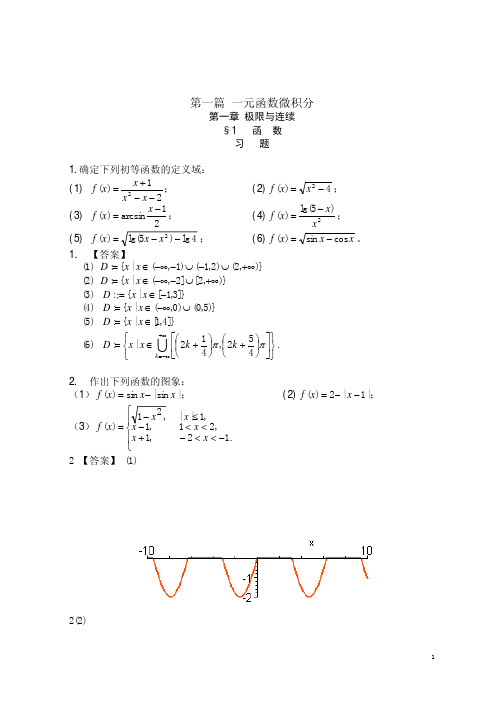
《高等数学》习题参考资料第一篇 一元函数微积分第一章 极限与连续§1 函 数习 题1.确定下列初等函数的定义域:(1) 21)(2−−+=x x x x f ;(2)4)(2−=x x f ;(3) 21arcsin )(−=x x f ;(4)2)5lg()(x x x f −=;(5) 4lg )5lg()(2−−=x x x f ;(6)x x x f cos sin )(−=。
1. 【答案】(1) )},2()2,1()1,(|{:+∞∪−∪−−∞∈=x x D (2) )},2[]2,(|{:+∞∪−−∞∈=x x D (3) ]}3,1[|{:;−∈=x x D (4) )}5,0()0,(|{:∪−∞∈=x x D (5) ]}4,1[|{:∈=x x D (6)+ +∈=+∞−∞=U k k k x x D ππ452,412|:.2. 作出下列函数的图象:(1)|sin |sin )(x x x f −=;(2)|1|2)(−−=x x f ;(3)+−−=,1,1,21)(x x x x f .12,21,1||−<<−<<≤x x x 2 【答案】 (1)2(2)2 (3)3.判断下列函数的奇偶性:(1)x x x f ++−=11)(;(2)xxx f x x +−+−=11lg110110)(;(3)x x a a x f x x sin )(++=−;(4))1lg()(2x x x f ++=。
3. 【答案】 (1) 偶函数; (2) 偶函数; (3) 偶函数; (4) 奇函数 .4.证明:两个奇函数的乘积是偶函数;一个奇函数与一个偶函数的乘积是奇函数。
4. 【答案】 设)(x f ,)(x h 是奇函数, )(x g 是偶函数,)()()(x h x f x f =,)()()(x g x f x G =, 于是)()()(x h x f x F −−=−))())(((x h x f −−=)()()(x F x h x f ==, 因此)(x F 是偶函数.)()()(x g x f x G −−=−)()(x g x f −=)(x G −=, 因此)(x G 是奇函数.5.设函数f 满足:D (f )关于原点对称,且()xc x bf x af =+1)(,其中a ,b ,c 都是常数,||||b a ≠,试证明f 是奇函数。
高等数学第一章课后习题答案

高等数学(本)第一章 函数与极限1. 设 ⎪⎩⎪⎨⎧≥<=3||,03|||,sin |)(ππϕx x x x , 求).2(446ϕπϕπϕπϕ、、、⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛6sin )6(ππϕ=21=224sin )4(==ππϕ ()0222)4sin()4(==-=-ϕππϕ2. 设()x f 的定义域为[]1,0,问:⑴()2x f ; ⑵()x f sin ; ⑶()()0>+a a x f ; ⑷()()a x f a x f -++ ()0>a 的定义域是什么?(1)][;,-的定义域为所以知-11)(,111022x f x x ≤≤≤≤[]ππππ)12(,2)(sin ),()12(21sin 0)2(+∈+≤≤≤≤k k x f Z k k x k x 的定义域为所以知由][a a a x f ax a a x -+-≤≤≤+≤1,)(110)3(-的定义域为所以知-由][φ时,定义域为当时,定义域为当从而得-知由211,210111010)4(>-≤<⎩⎨⎧+≤≤-≤≤⎩⎨⎧≤-≤≤+≤a a a a a x a ax a a x a x班级 姓名 学号3. 设()⎪⎩⎪⎨⎧>-=<=111011x x x x f ,()x e x g =,求()[]x g f 和()[]x f g ,并做出这两个函数的图形。
⎪⎪⎩⎪⎪⎨⎧>=<==⎪⎩⎪⎨⎧>-=<=⎪⎩⎪⎨⎧>-=<=-1,1,11,)]([.)20,10,00,1)]([1)(,11)(,01)(,1)]([.)11)(x e x x e e x f g x x x x g f x g x g x g x g f x f 从而得4. 设数列{}n x 有界, 又,0lim =∞→n n y 证明: .0lim =∞→n n n y x{}结论成立。
高等数学讲义答案第一章

第一章 极限与连续第一节 函 数【例1】研究函数)1ln()(2x x x f ++=的奇偶性,并求其反函数. 【分析】()f x 定义域为R ,()ln(ln(()f x x x f x -=-==-+=-故()f x 为奇函数.由)1ln()(2x x x f ++=得,y e x =yex -=-+两式相减得.2y ye e x --=【例2】设0,0()1,0x f x x <⎧=⎨≥⎩, 22,1()||2,1x x g x x x ⎧-<⎪=⎨-≥⎪⎩, 试求[()],[()]f g x g f x .【分析】0,12[()]1,12x f g x x x ⎧≤<⎪=⎨<≥⎪⎩或,2,0[()]=1,0x g f x x <⎧⎨-≥⎩.【例3】设函数2||sin(2)()(1)(2)x x f x x x x -=--在下列哪个区间内有界( ).()()A 1,0- ()()B 0,1 ()()C 1,2 ()()D 2,3【分析】()1,0x ∈-,2||sin(2)11()(1)(2)144x x f x x x x -=≤=--⨯,故有界,选(A ) 2111||sin(2)sin(2)lim ()lim lim (1)(2)(1)x x x x x x f x x x x x ---→→→--===+∞--- 111sin(2)sin(2)lim ()lim lim (1)(1)x x x x x f x x x +++→→→--===-∞-- 222222sin(2)(2)1lim ()lim lim lim (2)(2)2x x x x x x f x x x x ++++→→→→--====+∞--- 故BCD 均不正确.第二节 极 限【例1】讨论11012lim12x x x→-+.【分析】1111001212lim 1,lim 11212x x x x xx+-→→--=-=++,故此极限不存在.【例2】讨论1121lim ()xx x x e e+→-. 【分析】111111221122lim ()lim ,lim ()limttttt t xx xx t t x x e e e ex e e x e e t t +-++++→+∞→-∞→→---==+∞-==故此极限不存在.【例3】110|sin |lim 21x x x x e x e →⎛⎫⎪- ⎪ ⎪+⎝⎭. 【分析】1111000|sin |sin lim 2lim 2lim 12111x xx x x x x x e x e x x e e +++→→→⎛⎫ ⎪-=-=-=- ⎪ ⎪++⎝⎭1111000|sin |sin lim 2lim 2lim 10111x xx x x x x x e x e x x e e --+→→→⎛⎫- ⎪-=-=--=- ⎪ ⎪++⎝⎭,故110|sin |lim 2 1.1x x x x e x e →⎛⎫⎪-=- ⎪ ⎪+⎝⎭【例1】)0,0,0()(lim 1>>>++∞→c b a c b a nnnn n【分析】不妨设0a b c ≥≥>,由3n n n nna abc a ≤++≤得11()3n nn n na abc a ≤++≤ 又因为1lim lim3nn n a a a →∞→∞==,由三明治定理得1lim().nnn nn a b c a →∞++=故()1lim()max ,,.nnn nn a b c a b c →∞++=【例2】)2211(lim 222n n nn n n +++++∞→【分析】由2221i i i n n n i n ≤≤+++得2221111n n n i i i i i in n n i n ===≤≤+++∑∑∑又因为22111lim lim 12nn n n i i i i n n n →∞→∞====++∑∑,由三明治定理得211lim .2nn i i n i→∞==+∑题型一 极限概念与性质【例1】设数列{}n x 与{}n y 满足lim 0n n n x y →∞=, 则下面断言正确的是 ( ).(A)若{}n x 发散,则{}n y 必发散 (B)若{}n x 无界,则{}n y 必有界 (C)若{}n x 有界, 则{}n y 必为无穷小 (D)若1{}nx 为无穷小,则{}n y 必为无穷小 【分析】令,0n n x n y ==,(A)不正确;令0,n n x y n ==,(C)不正确;令,1,3,50,1,3,5,0,2,4,6,2,4,6n n n n n x y n n n ==⎧⎧==⎨⎨==⎩⎩(B)不正确;选(D). 事实上,lim lim01nn n n n ny x y x →∞→∞==,分母趋于0,分子趋于0,(D)正确. 【例2】{},{},{}n n n a b c 均为非负数列, 且lim 0n n a →∞=,lim 1n n b →∞=,lim n n c →∞=∞, 则 ( ). (A),n n a b n <∀ (B),n n b c n <∀ (C)lim n n n a c →∞不存在 (D)lim n n n b c →∞不存在【分析】对n ∀,(A) (B)肯定不正确,lim n n n a c →∞可能存在可能不存在,选(D).【例3】设函数()f x 在(),-∞+∞内单调有界, {}n x 为数列, 下面命题正确的是 ( ). (A)若{}n x 收敛,则{()}n f x 必收敛 (B)若{}n x 单调,则{()}n f x 必收敛 (C)若{()}n f x 收敛, 则{}n x 收敛 (D)若{()}n f x 单调, 则{}n x 收敛【分析】{}n x 单调,由于()f x 单调,则{()}n f x 单调,又因为其有界,故由单调有界定理,(B)正确.题型二 不定式求极限【例1】(1) 0x0011233lim .3x x xx o x o x x (2) )cos 1(sin 1tan 1limx x xx x -+-+→()30002tan 1cos 1tan sin 1lim lim .1222x x x x x x xx x x →→→--===⨯(3) limxlimlimlim1.x x x ===(4) 3012cos lim 13x x x x32200012cos 12cos 1cos 11lim 1lim ln lim .3336x x x x x x x xx x(5) sin 30limx xx e e x →-()sin sin 3330001sin 1lim lim lim .6x x x x x x x x e e e e x x x x x -→→→---===-(6) 211lim (arctan arctan )1x x x x →∞-+()222220011arctan arctan 11111lim (arctan arctan )lim lim 12x t t t t t t t t x x x t t →∞→→--++++-==+()()222011lim1.2t t t t t→++-+==(7) ()()4sin sin sin sin limx x x x x →-()()()34330001sin sin sin sin sin sin sin sin 16lim lim lim .6x x x x x x x x x x x x →→→--=== (8)()()()401cos ln 1tan limsin x x x x x→--+()()()()()42220001cos ln 1tan ln 1tan tan ln 1tan 11tan limlim lim sin 22x x x x x x x x x x x x xx x x →→→--+-+-+⎛⎫-==+ ⎪⎝⎭2201tan 112lim .24x xx →==【例2】 (1) 22211lim sin cos x x x x →⎛⎫- ⎪⎝⎭()()2222222224000cos sin cos sin 11cos sin lim lim lim sin cos cos sin x x x x x x x x x x x x x x x x x x x →→→+--⎛⎫-== ⎪⎝⎭30cos sin 22lim.3x x x x x →-==-(2)()12lim x x x x e →+∞⎛- ⎝ ()()()121222011lim lim 1.txx t t e t x x e t +→+∞→--+⎛-==- ⎝【例3】(1) 310sin 1tan 1lim x x x x ⎪⎭⎫ ⎝⎛++→()333000tan 1cos 11tan 1tan sin 1limln lim lim .1sin 1sin 2x x x x x x x x x x x x x →→→-+-⎛⎫⎛⎫=== ⎪ ⎪++⎝⎭⎝⎭ 311201tan lim .1sin x x x e x →+⎛⎫= ⎪+⎝⎭(2) 21coslim x x x ⎪⎭⎫ ⎝⎛∞→ 222211111lim ln cos lim cos 1lim .22x x x x x x x x x →∞→∞→∞⎛⎫⎛⎫⎛⎫=-=-⋅=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2121lim cos .x x e x -→∞⎛⎫= ⎪⎝⎭ (3) ()110ln 1lim xe x x x -→+⎛⎫ ⎪⎝⎭()()()2000ln 1ln 1ln 1111lim ln lim 1lim .12x x x x x x x x e x x x x →→→+++-⎛⎫⎛⎫=-==- ⎪ ⎪-⎝⎭⎝⎭()11120ln 1lim .xe x x e x --→+⎛⎫= ⎪⎝⎭(4)()()2lim xx xx a x b →∞⎡⎤⎢⎥-+⎣⎦()()()()()()22lim ln lim .x x x x a x b x x x a b x a x b x a x b →∞→∞⎡⎤--+==-⎢⎥-+-+⎣⎦()()2lim .xa b x x e x a x b -→∞⎡⎤=⎢⎥-+⎣⎦(5) 11ln lim 1xxx x →+∞⎛⎫- ⎪⎝⎭()1112111ln 1ln 1ln 11ln lim ln 1lim lim lim 1.ln 111xx x x x x x x x x x x x x x x x x x x x x x x e →+∞→+∞→+∞→+∞-⎛⎫ ⎪⎛⎫--⎝⎭-=⋅===- ⎪⎛⎫⎛⎫⎝⎭--- ⎪ ⎪⎝⎭⎝⎭ 11ln 1lim 1.xxx x e -→+∞⎛⎫-= ⎪⎝⎭(6) lim nn →∞⎣⎦()02ln ln 1lim ln lim 1lim ln 22222t t x x t a b a b x x ab t +→+∞→+∞→⎤+-+=-===⎢⎢⎥⎣⎦⎣⎦lim lim n xn x →∞→+∞==⎣⎦⎣⎦【例4】 (1) 若30sin 6()lim0x x xf x x →+=, 求206()lim .x f x x →+233300006()sin 6()6sin 6sin 6()6sin 6limlim lim lim 36.x x x x f x x xf x x x x xf x x xx x x x →→→→+++-+-==+=(2)设0ln(1()sin 5)lim 121x x f x x →+=-, 求0lim ().x f x →000ln(1()sin 5)()sin 55()lim lim lim 1.21ln 2ln 2x x x x f x x f x x f x x →→→+===-0ln 2lim ().5x f x →= 题型三 连加或连乘求极限【例1】(1) ()11lim ()nn i l N i i l +→∞=∈+∑(2)231lim nn i i n →∞=∑ (3) n n x x x 2cos 4cos 2cos lim ∞→ 11111111111,11,lim 1.()22311()nnn i i l i i l n n n i i l →∞====-+-++-=-=++++∑∑1111111111112,11,()232422212ni l i i l n n n n =⎛⎫⎛⎫==-+-++-=+-- ⎪ ⎪++++⎝⎭⎝⎭∑1111lim 1.()22nn i i i l →∞=⎛⎫=+ ⎪+⎝⎭∑同理,得()11111lim1.()2nn i l N i i l l l +→∞=⎛⎫∈=+++ ⎪+⎝⎭∑ (2)231lim nn i i n →∞=∑ ()()2331111lim lim 121.63nn n i i n n n nn →∞→∞==⨯++=∑ (3) n n xx x 2cos 4cos 2coslim ∞→cos cos cos 2sin sin sin 2422lim cos cos cos limlim .2422sin 2sin 22n n nn n n n n n n nx x x xx x x x x x x x →∞→∞→∞⋅===【例2】 (1))212654321(lim nn n -⋅⋅∞→()()()()()22222212+11352113355711()=24622462+12+12n n n n n n n --⨯⨯⨯⋅⋅⋅⋅⋅≤ 因为1lim=02+1n n →∞,由三明治定理得213521lim()=02462n n n →∞-⋅⋅, 故13521lim()=0.2462n n n→∞-⋅⋅ (2)⎰∞→xx dt t x 0sin 1lim()()()10sin sin 11,sin 1n n xt dtt dt n x n t dt n x n ππππππ+≤<+≤≤+⎰⎰⎰即()()02121sin 1xn n t dt n x n ππ+≤≤+⎰ ()()2122lim lim 1x x n n n n πππ→∞→∞+==+,由三明治定理得012lim sin .x x t dt x π→∞=⎰(3))0,0i n p a >>设()12max ,,p M a a a =M ≤≤lim n n M M →∞==,由三明治定理得()1max ,,.p n M a a == 【例3】(1)1limn n i →∞=11011limlnln 1112lim lim .nn i in nxdxn n n n i n e e e n n n →∞=-→∞→∞=∑⎛⎫⎰=⋅⋅⋅=== ⎪⎝⎭(2)lim n11013lim 112lim .n n i i xdxn n n e e e →∞=⎛⎫+ ⎪+⎝⎭∑⎰===【例4】(1) 1limn i →∞=111nnni i i ===≤≤11lim lim 1.nnn n i i →∞→∞====由三明治定理,得1lim 1.nn i →∞==(2)1limnn i →∞=((11111lim lim ln ln 1.nnn n i i x n →∞→∞======+⎰(3)1limnn i →∞=)10111lim lim 21.nn n n i i n →∞→∞======⎰(4)21limnn i →∞=222111nn ni i i ===≤≤22111lim lim .3n n n n i i →∞→∞====故211lim.3nn i →∞==(5)11limnn i n i →∞=+∑()1100111111lim lim ln 1ln 2.11nn n n i i dx x i n i n x n→∞→∞=====+=+++∑∑⎰(6)21limn i nn i →∞=++∑2221111nn ni i i i i in n n n n i n n ===≤≤++++++∑∑∑ 22111lim lim .12nnn n i i i i n n n n n →∞→∞====++++∑∑ 故211lim.2nn i i n n i →∞==++∑ (7) 221limnn i n n i →∞=+∑ 1102222011111lim lim arctan .141nnn n i i n dx x n i n x i n π→∞→∞======++⎛⎫+ ⎪⎝⎭∑∑⎰(8) 221lim1nn i n n i →∞=++∑()22222211111nnni i i nn nn i n i ni ===≤≤+++++∑∑∑()1222220111lim lim .141nnn n i i nn dx n i x n i π→∞→∞=====++++∑∑⎰【例5】(1)2sin sin sin lim 1112n n n n n n n n n πππ→∞⎛⎫ ⎪+++ ⎪+ ⎪++⎝⎭222sin sin sin sin sin sin sin sin sin 1111112n n n n n n n n n n n n n n n n nn n n n n πππππππππ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪+++≤+++≤+++ ⎪ ⎪ ⎪++++ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭1022sin sin sin sin sin sin 2lim lim sin .111n n n n n n n n n n xdx n n n n n n ππππππππ→∞→∞⎛⎫⎛⎫ ⎪ ⎪+++=+++== ⎪ ⎪+++ ⎪ ⎪⎝⎭⎝⎭⎰2sin sin sin 2lim .1112n n n n n n n n n ππππ→∞⎛⎫⎪+++=⎪+ ⎪++⎝⎭(2)21tanlim nn i i n n n i →∞=+∑222111tann tan tan 1n n ni i i i i in n n n n n n n i n ===≤≤+++∑∑∑1100222111tantan tanlim lim lim tan ln cos lncos1.1n n n n n n i i i i i in n n n n n xdx x n n n n →∞→∞→∞=======-=-++∑∑∑⎰【例6】(1)1lim 1nn i →∞=⎫⎪⎪⎭∑111lim 1lim .4nn n n i i →∞→∞==⎫==⎪⎪⎭∑ (2)()1222411lim n n n i n i n →∞=+∏()()()12222421011limln 2ln 12242arctan 2411lim25.n n n i n i nn nx dx n i niee e n →∞=⎡⎤+⎢⎥+⎢⎥-+⎣⎦→∞=∏⎰+===∏题型四 数列极限的存在性【例1】(1)设111,0n a a +=+=,证明数列{}n a 收敛,并求lim n n a →∞.121,0a a ==设1k k a a +≤,则≤21k k a a ++≤由数学归纳法得{}n a 递减下面证明n a ≥显然112a ≥-设12k a +≥-则12+≥-,即112k a +≥-由数学归纳法得n a ≥由单调有界必收敛得{}n a 收敛.设lim ,n n a A →∞=两边取极限得0A =,即A =(2) 123a a a === ,证明数列{}n a 收敛,并求lim n n a →∞.lim 2.n n a →∞=(3) 设1111,2n n n a a a a a a +⎛⎫=>=+ ⎪⎝⎭,证明数列{}n a 收敛,并求lim n n a →∞. lim n n a →∞=(4) 设1103,n a a +<<={}n a 收敛,并求lim n n a →∞.3lim .2n n a →∞= 【例2】设)(x f 是区间[)0,+∞上单调减少且非负的连续函数,()()()11,1,2,nnn k a f k f x dx n ==-=∑⎰…证明数列{}n a 的极限存在.()()()()1111110n n n n nna a f n f x dx f n f n dx +++-=+-≤+-+=⎰⎰,即{}n a 递减.()()()()()()23112112nn n k a f k f x dx f f x dx f f x dx ==-=-+-+∑⎰⎰⎰()()()()110.nn f n f x dx f n f n -+--+≥≥⎰故{}n a 有下界.由单调有界定理,{}n a 的极限存在.题型五 含参数的极限【例1】确定,,a b c 值,使()()3sin lim0ln 1x x bax xc c t dtt→-=≠+⎰. 【分析】分式极限不为0,分子趋于0,则分母趋于0,故0.b =()()()233000sin cos cos limlimlim 0ln 1ln 1x x x x ax xa x a xc c x t x dttx→→→---===≠++⎰故11,.2a c ==【例2】()()22ln 1lim2x x ax bx x →+-+=,求,a b .【分析】()()()()222222001ln 12lim lim 2x x x x o x ax bx x ax bx x x →→-+-++-+==故51,.2a b ==-题型六 含变积分限的极限【例1】设()(),g f x x 连续,且()()()g 0f x x x → ,又lim ()0x ax ϕ→=,证明:()()()()()0x x f t dt g t dt x a ϕϕ→⎰⎰.【例2】设)(x f 是[)0,+∞上的连续函数,且满足()2lim 1x f x x →+∞=,求()()220limxx t x e e f t dtf x -→+∞⎰.【分析】()()()()()222222222limlimlimxxxxttt xxx x x ee f t dte f t dte f t dt xf x x e f x x e -→+∞→+∞→+∞=⋅=⎰⎰⎰()()()2222221limlim .22222xxx x f x e f x x x x x xx e →+∞→+∞==⋅=++题型七 函数的连续与间断【例1】设()()()f x x ϕ-∞+∞和在内有定义,()f x 为连续函数,且()()0,f x x ϕ≠有间断点,则 ( ). (A)()f x ϕ⎡⎤⎣⎦必有间断点(B)()2f x ϕ⎡⎤⎣⎦必有间断点(C)()f x ϕ⎡⎤⎣⎦必有间断点 (D)()()x f x ϕ必有间断点【分析】(D) 【例2】设函数nn x xx f 211lim)(++=∞→,讨论函数)(x f 的连续性与间断点.【分析】0,11,11()1,10,1x x x f x x x ≤-⎧⎪+-<<⎪=⎨=⎪⎪>⎩()f x 在1x =处是跳跃间断点,在其他区域均连续.【例3】求()sin sin sin lim sin x t xt x t f x x -→⎛⎫=⎪⎝⎭的间断点,并判别其类型.【分析】()sin sin sin sin lim .sin xx t xxt x t f x e x -→⎛⎫== ⎪⎝⎭其中,,0x k k Z k π=∈≠且为第二类间断点,0x =为可去间断点.。
高等数学第一章总习题及答案

7. 已知 lim
x →0
f ( x) ) sin x = 3 , 求 lim f ( x) . x →0 x 2 2x − 1
解
因为 lim(2 − 1) = 0 , lim
x →0
x
ln(1 +
x →0
f ( x) ) sin x = 3 , 故必有 lim ln(1 + f ( x) ) = 0 , x →0 sin x 2x − 1
2
2
x
1 1 . = ( )2 = 2 2
1
(4) (5) (6)
lim
x →0
1 x sin x 1 = lim 2 2 = . x →0 2 x
1
x
lim(1 + 3tan 2 x)cot
x →0
= [lim(1 + 3tan 2 x) 3tan x ]3 = e3 .
2
x →0
设 k 为任一个大于 2c 的自然数, 则当 n > k 时,
0 < x ≤ e, 在 x = e 处, lim+ f ( x) = ln e = 1 , lim− f ( x) = 1 , x →e x →e x > e,
故 f ( x) 在 x = e 处连续, 故函数连续区间为 (0, + ∞) .
9.
⎧ cos x , x ≥ 0, ⎪ ⎪x + 2 设 f ( x) = ⎨ 要使 f ( x) 在 (−∞, + ∞) 内连续, 应如何选择 ⎪ a − a − x , x < 0, ⎪ x ⎩
n →∞ n →∞
(B) 无界数列必定发散; (D) 单调数列必有极限.
yn . xn
大学高数高数第一章(终)课后参考答案及知识总结

第一章函数、极限与连续内容概要课后习题全解习题1-1★1.求下列函数的定义域:知识点:自然定义域指实数范围内使函数表达式有意义的自变量x 的取值的集合; 思路:常见的表达式有 ① a log □,( □0>) ② /N □, ( □0≠) ③(0)≥W④ arcsin W (W[]1,1-∈)等解:(1)[)(]1,00,11100101122⋃-∈⇒⎩⎨⎧≤≤-≠⇒⎩⎨⎧≥-≠⇒--=x x x x x x x y ;(2)31121121arcsin≤≤-⇒≤-≤-⇒-=x x x y ; (3)()()3,00,030031arctan 3⋃∞-∈⇒⎩⎨⎧≠≤⇒⎩⎨⎧≠≥-⇒+-=x x x x x x x y ;(4)()()3,11,1,,1310301lg 3⋃-∞-∈⇒⎩⎨⎧-<<<⇒⎩⎨⎧-<-<⇒-=-x x or x x x x x y x;(5)()()4,22,11601110)16(log 221⋃∈⇒⎪⎩⎪⎨⎧-<-≠-<⇒-=-x x x x x y x ; ★ 2.下列各题中,函数是否相同?为什么?(1)2lg )(x x f =与x x g lg 2)(=;(2)12+=x y 与12+=y x知识点:函数相等的条件;思路:函数的两个要素是f (作用法则)及定义域D (作用范围),当两个函数作用法则f 相同(化简后代数表达式相同)且定义域相同时,两函数相同;解:(1)2lg )(x x f =的定义域D={}R x x x ∈≠,0,x x g lg )(=的定义域{},0R x x x D ∈>=,虽然作用法则相同x x lg 2lg 2=,但显然两者定义域不同,故不是同一函数;(2)12+=x y ,以x 为自变量,显然定义域为实数R ;12+=y x ,以x 为自变量,显然定义域也为实数R ;两者作用法则相同“2□1+”与自变量用何记号表示无关,故两者为同一函数;★ 3.设⎪⎪⎩⎪⎪⎨⎧≥<=3,03,sin )(ππϕx x x x ,求)2()4()4()6(--ϕπϕπϕπϕ,,,,并做出函数)(x y ϕ=的图形知识点:分段函数;思路:注意自变量的不同范围; 解:216sin)6(==ππϕ,224sin 4==⎪⎭⎫⎝⎛ππϕ,224sin 4=⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛-ππϕ()02=-ϕ;如图:★ 4.试证下列各函数在指定区间内的单调性 :(1)()1,1∞--=xxy (2)x x y ln 2+=,()+∞,0 知识点:单调性定义。
高数练习册答案

第一章 函数与极限部分习题答案§1 映射与函数一、填空题:1、224>-<<-x x 或2、)01(1ln>>-=x x x y 3、奇函数 4、41 §2 数列的极限一、填空题:1、不存在 2、必要 3、1二、计算题:1、0 2、1 3、21§3 函数的极限一、填空题:1、 充要 2、1 3、1;不存在 二、计算题:1、 6 2、21 3、62- 4、(1):1;(2):-1;(3):不存在§4 无穷小和无穷大二、计算题:1、0 2、1 3、2§5 极限的运算法则一、计算题:1、-11 2、32 3、214、-15、236、17、528、1二、计算:a=2; b=-8 三、计算;a=1; b=-1§6 极限存在准则 两个重要极限一、填空题:1、0;1;1;0 2、1-e ;2e ;3e ;2e ;二、计算题:1、0; 2、2; 3、2; 4、2e ; 5、 3-e ; 6、6-e ;三、计算:1§7无穷小的比较一、 计算题:1、2; 2、32; 3、0; 4、1 二、 计算题;3=α§8函数的连续性与间断点一、 填空题:1、充要; 2、可去;二、不连续,跳跃间断点 三、跳跃间断点 四、41=a §9连续函数的运算与初等函数的连续性一、计算题;∞,21,31;二、1、2ln π2、1;3、0;4、1三、计算a=1; b=-1第一章自测题一、填空题:1、0≠x,1,-1; 2、0; 3、0; 4、2; 5、21三、计算题:1、2 x ; 2、1; 3、1; 4、3e ; 5、; 6、41; 7、1; 8、1四、计算;a=1; 23-=b§ 2.1 二、 )(a φ;三、 4311;33x ---;四、460;470x y x y --=++=;五、连续且可导。
§2.2 二、2,e e ππ--; 三、(1; (2);(3)1tan 221111(cos sin sec )x e x x x x-+;(4)22sin 2[(sin )(cos )]x f x f x -。
《高等数学一》第一章-函数--课后习题(含答案解析)
第一章函数历年试题模拟试题课后习题(含答案解析)[单选题]1、设函数,则f(x)=()A、x(x+1)B、x(x-1)C、(x+1)(x-2)D、(x-1)(x+2)【正确答案】B【答案解析】本题考察函数解析式求解.,故[单选题]2、已知函数f(x)的定义域为[0,4],函数g(x)=f(x+1)+f(x-1)的定义域是().A、[1,3]B、[-1,5]C、[-1,3]D、[1,5]【正确答案】A【答案解析】x是函数g(x)中的定义域中的点,当且仅当x满足0≤x+1≤4且0≤x-1≤4即-1≤x≤3且1≤x≤5也即1≤x≤3,由此可知函数g(x)的定义域D(g)={x|1≤x≤3}=[1,3]. [单选题]3、设函数f(x)的定义域为[0,4],则函数f(x2)的定义域为().A、[0,2]B、[0,16]C、[-16,16]D、[-2,2]【正确答案】D【答案解析】根据f(x)的定义域,可知中应该满足:[单选题]4、函数的定义域为().A、[-1,1]B、[-1,3]C、(-1,1)D、(-1,3)【正确答案】B【答案解析】根据根号函数的性质,应该满足:即[单选题]5、写出函数的定义域及函数值(). A、B、C、D、【正确答案】C【答案解析】分段函数的定义域为各个分段区间定义域的并集,故D=(-∞,-1]∪(-1,+∞).[单选题]6、设函数,则对所有的x,则f(-x)=().A、B、C、D、【正确答案】A【答案解析】本题考察三角函数公式。
.[单选题]7、设则=().A、B、C、D、【正确答案】B【答案解析】令则,故[单选题]8、则().A、B、C、D、【正确答案】D【答案解析】[单选题]9、在R上,下列函数中为有界函数的是().xA、eB、1+sin xC、ln xD、tan x【正确答案】B【答案解析】由函数图像不难看出在R上e x,lnx,tanx都是无界的,只有1+sinx可能有界,由于|sinx|≤1,|1+sinx|≤1+|sinx|≤2所以有界.[单选题]10、不等式的解集为().A、B、C、D、【正确答案】D【答案解析】[单选题]11、().A、B、C、D、【正确答案】A【答案解析】根据二角和公式,[单选题]12、函数的反函数是().A、B、C、D、【正确答案】A【答案解析】由所以,故.[单选题]13、已知则().A、B、C、D、【正确答案】C【答案解析】[单选题]14、已知为等差数列,,则().A、-2B、1C、3D、7【正确答案】A【答案解析】因为同理可得:故d=a4-a3=-2.[单选题]15、计算().A、B、C、D、【正确答案】A【答案解析】根据偶次根式函数的意义,可知,故[单选题]16、计算().A、0B、1C、2D、4【正确答案】C【答案解析】原式=[单选题]17、将函数|表示为分段函数时,=().A、B、C、D、【正确答案】B【答案解析】由条件[单选题]18、函数f(x)=是().A、奇函数B、偶函数C、有界函数D、周期函数【正确答案】C【答案解析】易知不是周期函数,,即不等于,也不等于,故为非奇、非偶函数.,故为有界函数.[单选题]19、函数,则的定义域为().A、[1,5]B、(1,5]C、(1,5]D、[1,5)由反正切函数的定义域知:,故定义域为[1,5].[单选题]20、下列等式成立的是()A、B、C、D、【正确答案】B【答案解析】A中(e x)2=,C中,D中[单选题]21、下列函数为偶函数的是()A、y=xsinxB、y=xcosxC、y=sinx+cosxD、y=x(sinx+cosx)【正确答案】A【答案解析】sinx是奇函数,cosx是偶函数。
高数第一章参考答案
第一章:第1节: 1A 。
2D 。
3A 。
4x y =。
5.21)(nxx x f n +=。
6.当2/10<<a 时,定义域为]1,[a a -;当2/1>a 时,定义域为空集;当2/1=a 时,定义域2/1=x 。
7.)1ln()(x x -=ϕ,定义域为}0|{≤x x 。
第2节: 1D 。
2C 。
3B 。
4.证明:由定义知0>∀ε,N N ∈∃,使得当n N >时,有||n u a ε-<成立。
注意到a u a u n n -≤-。
因此当n N >时,有ε<-≤-a u a u n n 。
即||||lim a u n n =∞→。
反过来若1||lim =∞→n n u ,则n n u ∞→lim 不一定存在。
比如(1),n n u =-则n n u ∞→lim 不存在,但1||lim =∞→n n u 。
若0||lim =→∞n n u ,则由00-=-n n u u 知0lim =∞→n n u 。
第3节:1A 。
2B 。
3D 。
4C 。
5C 。
第4节: 1D 。
2D 。
3D 。
4C 。
5D 。
6.证:假设函数xx y 1sin 1=在区间]1,0(上有界,则0,M ∃>使得函数11sin y M x x =≤。
若取2/)1]([21ππ++=M x ,则有M M y >++=2/)1]([2ππ矛盾。
所以在区间]1,0(上无界,但也不是+→0x 时的无穷大。
因为若取πk x 21=(N k ∈),则当+∞→k 时,+→0x ,而此时0≡y 不是无穷大。
第5节: 1A 。
2C 。
3B 。
4B 。
5.1。
6.21。
7。
a 21-。
8.1。
9.2。
10.21。
11.6。
12.1,1-==b a 第6节: 1C 。
2D 。
3B 。
4.3。
5.3/5。
6.0 。
7.由于()nnn n11333213⋅<++<,所以由夹逼定理可得()3321lim 1=++∞→nn nn 。
高等数学一上册教材答案
高等数学一上册教材答案第一章:函数与极限1.1 函数的概念与性质函数的概念函数是一种特殊的关系,它将一个集合中的每个元素对应到另一个集合中的唯一元素。
用数学符号表示为:y = f(x),其中 x 是自变量,y 是因变量,f(x) 是函数关系。
函数的性质(1)定义域和值域定义域是自变量可能的取值范围,值域是因变量对应的所有可能取值的范围。
(2)奇偶性如果对任意 x,有 f(-x) = f(x),则函数为偶函数;如果对任意 x,有f(-x) = -f(x),则函数为奇函数。
(3)单调性如果对任意 x1、x2,当 x1 < x2 时有f(x1) ≤ f(x2),则函数为增函数;如果对任意 x1、x2,当 x1 < x2 时有f(x1) ≥ f(x2),则函数为减函数。
1.2 一次函数与二次函数一次函数一次函数的标准式表示为 y = kx + b,其中 k 是斜率,b 是 y 轴截距。
一次函数的图像是一条直线,它的性质包括:与 y 轴平行的直线的斜率为零,与 x 轴平行的直线的斜率为无穷大。
例题:已知函数 f(x) = 3x + 2,求 f(2) 的值。
解:将 x 替换为 2,得到 f(2) = 3(2) + 2 = 8。
二次函数二次函数的标准式表示为 y = ax^2 + bx + c,其中a ≠ 0。
二次函数的图像是一个抛物线,它的性质包括:抛物线开口向上(a > 0)或向下(a < 0),顶点的横坐标为 -b/2a。
例题:已知函数 f(x) = x^2 + 2x - 1,求 f(-1) 的值。
解:将 x 替换为 -1,得到 f(-1) = (-1)^2 + 2(-1) - 1 = -2。
1.3 幂函数与指数函数幂函数幂函数的定义形式为 y = x^p,其中 p 是常数。
幂函数的图像随着 p 的取值不同,可能是增函数、减函数或常数函数。
例题:已知函数 f(x) = x^3,求 f(2) 的值。
高等数学课后习题及参考答案(第一章)
高等数学课后习题及参考答案(第一章)习题1-11. 设A =(-∞, -5)⋃(5, +∞), B =[-10, 3), 写出A ⋃B , A ⋂B , A \B 及A \(A \B )的表达式.解 A ⋃B =(-∞, 3)⋃(5, +∞),A ⋂B =[-10, -5),A \B =(-∞, -10)⋃(5, +∞),A \(A \B )=[-10, -5).2. 设A 、B 是任意两个集合, 证明对偶律: (A ⋂B )C =A C ⋃B C .证明 因为x ∈(A ⋂B )C ⇔x ∉A ⋂B ⇔ x ∉A 或x ∉B ⇔ x ∈A C 或x ∈B C ⇔ x ∈A C ⋃B C , 所以 (A ⋂B )C =A C ⋃B C .3. 设映射f : X →Y , A ⊂X , B ⊂X . 证明(1)f (A ⋃B )=f (A )⋃f (B );(2)f (A ⋂B )⊂f (A )⋂f (B ).证明 因为y ∈f (A ⋃B )⇔∃x ∈A ⋃B , 使f (x )=y⇔(因为x ∈A 或x ∈B ) y ∈f (A )或y ∈f (B )⇔ y ∈f (A )⋃f (B ),所以 f (A ⋃B )=f (A )⋃f (B ).(2)因为y ∈f (A ⋂B )⇒∃x ∈A ⋂B , 使f (x )=y ⇔(因为x ∈A 且x ∈B ) y ∈f (A )且y ∈f (B )⇒ y ∈ f (A )⋂f (B ),所以 f (A ⋂B )⊂f (A )⋂f (B ).4. 设映射f : X →Y , 若存在一个映射g : Y →X , 使X I f g = , Y I g f = , 其中I X 、I Y 分别是X 、Y 上的恒等映射, 即对于每一个x ∈X , 有I X x =x ; 对于每一个y ∈Y , 有I Y y =y . 证明: f 是双射, 且g 是f 的逆映射: g =f -1.证明 因为对于任意的y ∈Y , 有x =g (y )∈X , 且f (x )=f [g (y )]=I y y =y , 即Y 中任意元素都是X 中某元素的像, 所以f 为X 到Y 的满射.又因为对于任意的x 1≠x 2, 必有f (x 1)≠f (x 2), 否则若f (x 1)=f (x 2)⇒g [ f (x 1)]=g [f (x 2)] ⇒ x 1=x 2.因此f 既是单射, 又是满射, 即f 是双射.对于映射g : Y →X , 因为对每个y ∈Y , 有g (y )=x ∈X , 且满足f (x )=f [g (y )]=I y y =y , 按逆映射的定义, g 是f 的逆映射.5. 设映射f : X →Y , A ⊂X . 证明:(1)f -1(f (A ))⊃A ;(2)当f 是单射时, 有f -1(f (A ))=A .证明 (1)因为x ∈A ⇒ f (x )=y ∈f (A ) ⇒ f -1(y )=x ∈f -1(f (A )),所以 f -1(f (A ))⊃A .(2)由(1)知f -1(f (A ))⊃A .另一方面, 对于任意的x ∈f -1(f (A ))⇒存在y ∈f (A ), 使f -1(y )=x ⇒f (x )=y . 因为y ∈f (A )且f 是单射, 所以x ∈A . 这就证明了f -1(f (A ))⊂A . 因此f -1(f (A ))=A . 6. 求下列函数的自然定义域:(1)23+=x y ;解 由3x +2≥0得32->x . 函数的定义域为) ,32[∞+-. (2)211xy -=; 解 由1-x 2≠0得x ≠±1. 函数的定义域为(-∞, -1)⋃(-1, 1)⋃(1, +∞).(3)211x xy --=; 解 由x ≠0且1-x 2≥0得函数的定义域D =[-1, 0)⋃(0, 1].(4)241x y -=; 解 由4-x 2>0得 |x |<2. 函数的定义域为(-2, 2).(5)x y sin =;解 由x ≥0得函数的定义D =[0, +∞).(6) y =tan(x +1);解 由21π≠+x (k =0, ±1, ±2, ⋅ ⋅ ⋅)得函数的定义域为 12-+≠ππk x (k =0, ±1, ±2, ⋅ ⋅ ⋅).(7) y =arcsin(x -3);解 由|x -3|≤1得函数的定义域D =[2, 4].(8)xx y 1arctan 3+-=; 解 由3-x ≥0且x ≠0得函数的定义域D =(-∞, 0)⋃(0, 3).(9) y =ln(x +1);解 由x +1>0得函数的定义域D =(-1, +∞).(10)x e y 1=.解 由x ≠0得函数的定义域D =(-∞, 0)⋃(0, +∞).7. 下列各题中, 函数f (x )和g (x )是否相同?为什么?(1)f (x )=lg x 2, g (x )=2lg x ;(2) f (x )=x , g (x )=2x ;(3)334)(x x x f -=,31)(-=x x x g .(4)f (x )=1, g (x )=sec 2x -tan 2x .解 (1)不同. 因为定义域不同.(2)不同. 因为对应法则不同, x <0时, g (x )=-x .(3)相同. 因为定义域、对应法则均相相同.(4)不同. 因为定义域不同.8. 设⎪⎩⎪⎨⎧≥<=3|| 03|| |sin |)(ππϕx x x x , 求)6(πϕ, )4(πϕ, )4(πϕ-, ϕ(-2), 并作出函数y =ϕ(x )的图形.解 21|6sin |)6(==ππϕ, 22|4sin |)4(==ππϕ, 22|)4sin(|)4(=-=-ππϕ, 0)2(=-ϕ. 9. 试证下列函数在指定区间内的单调性:(1)xx y -=1, (-∞, 1); (2)y =x +ln x , (0, +∞).证明 (1)对于任意的x 1, x 2∈(-∞, 1), 有1-x 1>0, 1-x 2>0. 因为当x 1<x 2时, 0)1)(1(112121221121<---=---=-x x x x x x x x y y ,所以函数xx y -=1在区间(-∞, 1)内是单调增加的. (2)对于任意的x 1, x 2∈(0, +∞), 当x 1<x 2时, 有0ln )()ln ()ln (2121221121<+-=+-+=-x x x x x x x x y y , 所以函数y =x +ln x 在区间(0, +∞)内是单调增加的.10. 设 f (x )为定义在(-l , l )内的奇函数, 若f (x )在(0, l )内单调增加, 证明f (x )在(-l , 0)内也单调增加.证明 对于∀x 1, x 2∈(-l , 0)且x 1<x 2, 有-x 1, -x 2∈(0, l )且-x 1>-x 2.因为f (x )在(0, l )内单调增加且为奇函数, 所以f (-x 2)<f (-x 1), -f (x 2)<-f (x 1), f (x 2)>f (x 1),这就证明了对于∀x 1, x 2∈(-l , 0), 有f (x 1)< f (x 2), 所以f (x )在(-l , 0)内也单调增加. 11. 设下面所考虑的函数都是定义在对称区间(-l , l )上的, 证明:(1)两个偶函数的和是偶函数, 两个奇函数的和是奇函数;(2)两个偶函数的乘积是偶函数, 两个奇函数的乘积是偶函数, 偶函数与奇函数的乘积是奇函数.证明 (1)设F (x )=f (x )+g (x ). 如果f (x )和g (x )都是偶函数, 则F (-x )=f (-x )+g (-x )=f (x )+g (x )=F (x ),所以F (x )为偶函数, 即两个偶函数的和是偶函数.如果f (x )和g (x )都是奇函数, 则F (-x )=f (-x )+g (-x )=-f (x )-g (x )=-F (x ),所以F (x )为奇函数, 即两个奇函数的和是奇函数.(2)设F (x )=f (x )⋅g (x ). 如果f (x )和g (x )都是偶函数, 则F (-x )=f (-x )⋅g (-x )=f (x )⋅g (x )=F (x ),所以F (x )为偶函数, 即两个偶函数的积是偶函数.如果f (x )和g (x )都是奇函数, 则F (-x )=f (-x )⋅g (-x )=[-f (x )][-g (x )]=f (x )⋅g (x )=F (x ),所以F (x )为偶函数, 即两个奇函数的积是偶函数.如果f (x )是偶函数, 而g (x )是奇函数, 则F (-x )=f (-x )⋅g (-x )=f (x )[-g (x )]=-f (x )⋅g (x )=-F (x ),所以F (x )为奇函数, 即偶函数与奇函数的积是奇函数.12. 下列函数中哪些是偶函数, 哪些是奇函数, 哪些既非奇函数又非偶函数?(1)y =x 2(1-x 2);(2)y =3x 2-x 3;(3)2211x x y +-=; (4)y =x (x -1)(x +1);(5)y =sin x -cos x +1;(6)2x x a a y -+=. 解 (1)因为f (-x )=(-x )2[1-(-x )2]=x 2(1-x 2)=f (x ), 所以f (x )是偶函数.(2)由f (-x )=3(-x )2-(-x )3=3x 2+x 3可见f (x )既非奇函数又非偶函数.(3)因为())(111)(1)(2222x f x x x x x f =+-=-+--=-, 所以f (x )是偶函数. (4)因为f (-x )=(-x )(-x -1)(-x +1)=-x (x +1)(x -1)=-f (x ), 所以f (x )是奇函数.(5)由f (-x )=sin(-x )-cos(-x )+1=-sin x -cos x +1可见f (x )既非奇函数又非偶函数.(6)因为)(22)()()(x f a a a a x f x x x x =+=+=-----, 所以f (x )是偶函数. 13. 下列各函数中哪些是周期函数?对于周期函数, 指出其周期:(1)y =cos(x -2);解 是周期函数, 周期为l =2π.(2)y =cos 4x ;解 是周期函数, 周期为2π=l . (3)y =1+sin πx ;解 是周期函数, 周期为l =2.(4)y =x cos x ;解 不是周期函数.(5)y =sin 2x .解 是周期函数, 周期为l =π.14. 求下列函数的反函数:(1)31+=x y ;解 由31+=x y 得x =y 3-1, 所以31+=x y 的反函数为y =x 3-1.(2)xx y +-=11; 解 由x x y +-=11得y y x +-=11, 所以x x y +-=11的反函数为xx y +-=11. (3)dcx b ax y ++=(ad -bc ≠0); 解 由d cx b ax y ++=得a cy b dy x -+-=, 所以d cx b ax y ++=的反函数为acx b dx y -+-=. (4) y =2sin3x ;解 由y =2sin 3x 得2arcsin 31y x =, 所以y =2sin3x 的反函数为2arcsin 31x y =. (5) y =1+ln(x +2);解 由y =1+ln(x +2)得x =e y -1-2, 所以y =1+ln(x +2)的反函数为y =e x -1-2.(6)122+=x x y . 解 由122+=x x y 得y y x -=1log 2, 所以122+=x x y 的反函数为x x y -=1log 2. 15. 设函数f (x )在数集X 上有定义, 试证: 函数f (x )在X 上有界的充分必要条件是它在X 上既有上界又有下界.证明 先证必要性. 设函数f (x )在X 上有界, 则存在正数M , 使|f (x )|≤M , 即-M ≤f (x )≤M . 这就证明了f (x )在X 上有下界-M 和上界M .再证充分性. 设函数f (x )在X 上有下界K 1和上界K 2, 即K 1≤f (x )≤ K 2 . 取M =max{|K 1|, |K 2|}, 则 -M ≤ K 1≤f (x )≤ K 2≤M ,即 |f (x )|≤M .这就证明了f (x )在X 上有界.16. 在下列各题中, 求由所给函数复合而成的函数, 并求这函数分别对应于给定自变量值x 1和x 2的函数值:(1) y =u 2, u =sin x , 61π=x , 32π=x ; 解 y =sin 2x , 41)21(6sin 221===πy ,43)23(3sin 222===πy . (2) y =sin u , u =2x , 81π=x ,42π=x ; 解 y =sin2x , 224sin )82sin(1==⋅=ππy ,12sin )42sin(2==⋅=ππy .(3)u y =, u =1+x 2, x 1=1, x 2= 2;解 21x y +=, 21121=+=y , 52122=+=y .(4) y =e u , u =x 2, x 1 =0, x 2=1;解 2x e y =, 1201==e y , e e y ==212.(5) y =u 2 , u =e x , x 1=1, x 2=-1.解 y =e 2x , y 1=e 2⋅1=e 2, y 2=e 2⋅(-1)=e -2.17. 设f (x )的定义域D =[0, 1], 求下列各函数的定义域:(1) f (x 2);解 由0≤x 2≤1得|x |≤1, 所以函数f (x 2)的定义域为[-1, 1].(2) f (sin x );解 由0≤sin x ≤1得2n π≤x ≤(2n +1)π (n =0, ±1, ±2⋅ ⋅ ⋅), 所以函数f (sin x )的定义域为[2n π, (2n +1)π] (n =0, ±1, ±2⋅ ⋅ ⋅) .(3) f (x +a )(a >0);解 由0≤x +a ≤1得-a ≤x ≤1-a , 所以函数f (x +a )的定义域为[-a , 1-a ].(4) f (x +a )+f (x -a )(a >0).解 由0≤x +a ≤1且0≤x -a ≤1得: 当210≤<a 时, a ≤x ≤1-a ; 当21>a 时, 无解. 因此当210≤<a 时函数的定义域为[a , 1-a ], 当21>a 时函数无意义. 18. 设⎪⎩⎪⎨⎧>-=<=1|| 11||01|| 1)(x x x x f , g (x )=e x , 求f [g (x )]和g [f (x )], 并作出这两个函数的图形.解 ⎪⎩⎪⎨⎧>-=<=1|| 11||01|| 1)]([x x x e e e x g f , 即⎪⎩⎪⎨⎧>-=<=0 10 00 1)]([x x x x g f . ⎪⎩⎪⎨⎧>=<==-1|| 1||e 1|| )]([101)(x e x x e e xfg x f , 即⎪⎩⎪⎨⎧>=<=-1|| 1|| 11|| )]([1x e x x e x f g .19. 已知水渠的横断面为等腰梯形, 斜角ϕ=40︒(图1-37). 当过水断面ABCD 的面积为定值S 0时, 求湿周L (L =AB +BC +CD )与水深h 之间的函数关系式, 并指明其定义域.图1-37解 40sin h DC AB ==, 又从0)]40cot 2([21S h BC BC h =⋅++ 得h hS BC ⋅-= 40cot 0, 所以 h h S L40sin 40cos 20-+=. 自变量h 的取值范围应由不等式组h >0, 040cot 0>⋅-h hS 确定, 定义域为40cot 00S h <<.20. 收敛音机每台售价为90元, 成本为60元. 厂方为鼓励销售商大量采购, 决定凡是订购量超过100台以上的, 每多订购1台, 售价就降低1分, 但最低价为每台75元.(1)将每台的实际售价p 表示为订购量x 的函数;(2)将厂方所获的利润P 表示成订购量x 的函数;(3)某一商行订购了1000台, 厂方可获利润多少?解 (1)当0≤x ≤100时, p =90.令0.01(x 0-100)=90-75, 得x 0=1600. 因此当x ≥1600时, p =75.当100<x <1600时,p =90-(x -100)⨯0.01=91-0. 01x .综合上述结果得到⎪⎩⎪⎨⎧≥<<-≤≤=1600 75160010001.0911000 90x x x x p . (2)⎪⎩⎪⎨⎧≥<<-≤≤=-=1600 151600100 01.0311000 30)60(2x x x x x x x x p P .(3) P =31⨯1000-0.01⨯10002=21000(元).习题1-21. 观察一般项x n 如下的数列{x n }的变化趋势, 写出它们的极限:(1)nn x 21=; 解 当n →∞时, nn x 21=→0, 021lim =∞→n n . (2)nx n n 1)1(-=; 解 当n →∞时, n x n n 1)1(-=→0, 01)1(lim =-∞→nn n . (3)212nx n +=; 解 当n →∞时, 212n x n +=→2, 2)12(lim 2=+∞→nn . (4)11+-=n n x n ; 解 当n →∞时, 12111+-=+-=n n n x n →0, 111lim =+-∞→n n n . (5) x n =n (-1)n .解 当n →∞时, x n =n (-1)n 没有极限.2. 设数列{x n }的一般项nn x n 2cos π=. 问n n x ∞→lim =? 求出N , 使当n >N 时, x n 与其极限之差的绝对值小于正数ε , 当ε =0.001时, 求出数N .解 0lim =∞→n n x . n n n x n 1|2cos ||0|≤=-π. ∀ε >0, 要使|x n -0|<ε , 只要ε<n 1, 也就是ε1>n . 取]1[ε=N , 则∀n >N , 有|x n -0|<ε .当ε =0.001时, ]1[ε=N =1000. 3. 根据数列极限的定义证明:(1)01lim 2=∞→n n ;分析 要使ε<=-221|01|n n , 只须ε12>n , 即ε1>n . 证明 因为∀ε>0, ∃]1[ε=N , 当n >N 时, 有ε<-|01|2n , 所以01lim 2=∞→n n . (2)231213lim =++∞→n n n ; 分析 要使ε<<+=-++n n n n 41)12(21|231213|, 只须ε<n41, 即ε41>n . 证明 因为∀ε>0, ∃]41[ε=N , 当n >N 时, 有ε<-++|231213|n n , 所以231213lim =++∞→n n n . (3)1lim 22=+∞→na n n ; 分析 要使ε<<++=-+=-+na n a n n a n n a n n a n 22222222)(|1|, 只须ε2a n >. 证明 因为∀ε>0, ∃][2εa N =, 当∀n >N 时, 有ε<-+|1|22n a n , 所以1lim 22=+∞→na n n . (4)19 999.0lim =⋅⋅⋅∞→个n n . 分析 要使|0.99 ⋅ ⋅ ⋅ 9-1|ε<=-1101n , 只须1101-n <ε , 即ε1lg 1+>n . 证明 因为∀ε>0, ∃]1lg 1[ε+=N , 当∀n >N 时, 有|0.99 ⋅ ⋅ ⋅ 9-1|<ε , 所以19 999.0lim =⋅⋅⋅∞→个n n . 4. a u n n =∞→lim , 证明||||lim a u n n =∞→. 并举例说明: 如果数列{|x n |}有极限, 但数列{x n }未必有极限.证明 因为a u n n =∞→lim , 所以∀ε>0, ∃N ∈N , 当n >N 时, 有ε<-||a u n , 从而 ||u n |-|a ||≤|u n -a |<ε .这就证明了||||lim a u n n =∞→.数列{|x n |}有极限, 但数列{x n }未必有极限. 例如1|)1(|lim =-∞→n n , 但n n )1(lim -∞→不存在.5. 设数列{x n }有界, 又0lim =∞→n n y , 证明: 0lim =∞→n n n y x .证明 因为数列{x n }有界, 所以存在M , 使∀n ∈Z , 有|x n |≤M .又0lim =∞→n n y , 所以∀ε>0, ∃N ∈N , 当n >N 时, 有M y n ε<||. 从而当n >N 时, 有εε=⋅<≤=-M M y M y x y x n n n n n |||||0|,所以0lim =∞→n n n y x .6. 对于数列{x n }, 若x 2k -1→a (k →∞), x 2k →a (k →∞), 证明: x n →a (n →∞).证明 因为x 2k -1→a (k →∞), x 2k →a (k →∞), 所以∀ε>0, ∃K 1, 当2k -1>2K 1-1时, 有| x 2k -1-a |<ε ; ∃K 2, 当2k >2K 2时, 有|x 2k -a |<ε .取N =max{2K 1-1, 2K 2}, 只要n >N , 就有|x n -a |<ε . 因此x n →a (n →∞).习题1-31. 根据函数极限的定义证明: (1)8)13(lim 3=-→x x ;分析 因为|(3x -1)-8|=|3x -9|=3|x -3|, 所以要使|(3x -1)-8|<ε , 只须ε31|3|<-x .证明 因为∀ε>0, ∃εδ31=, 当0<|x -3|<δ时, 有|(3x -1)-8|<ε , 所以8)13(lim 3=-→x x .(2)12)25(lim 2=+→x x ;分析 因为|(5x +2)-12|=|5x -10|=5|x -2|, 所以要使|(5x +2)-12|<ε , 只须ε51|2|<-x .证明 因为∀ε >0, ∃εδ51=, 当0<|x -2|<δ时, 有 |(5x +2)-12|<ε , 所以12)25(lim 2=+→x x .(3)424lim 22-=+--→x x x ;分析 因为|)2(||2|244)4(2422--=+=+++=--+-x x x x x x x , 所以要使ε<--+-)4(242x x , 只须ε<--|)2(|x . 证明 因为∀ε >0, ∃εδ=, 当0<|x -(-2)|<δ时, 有ε<--+-)4(242x x , 所以424lim22-=+--→x x x .(4)21241lim 321=+--→x x x . 分析 因为|)21(|2|221|212413--=--=-+-x x x x , 所以要使ε<-+-212413x x , 只须ε21|)21(|<--x .证明 因为∀ε >0, ∃εδ21=, 当δ<--<|)21(|0x 时, 有ε<-+-212413x x , 所以21241lim 321=+--→x x x . 2. 根据函数极限的定义证明:(1)2121lim 33=+∞→x x x ; 分析 因为333333||21212121x x x x x x =-+=-+, 所以要使ε<-+212133x x , 只须ε<3||21x , 即321||ε>x . 证明 因为∀ε >0, ∃321ε=X , 当|x |>X 时, 有ε<-+212133x x , 所以2121lim 33=+∞→x x x . (2)0sin lim =+∞→xx x .分析 因为xx x x x 1|sin |0sin ≤=-. 所以要使ε<-0sin x x , 只须ε<x1, 即21ε>x .证明 因为∀ε>0, ∃21ε=X , 当x >X 时, 有ε<-0sin xx ,所以0sin lim =+∞→xx x .3. 当x →2时, y =x 2→4. 问δ等于多少, 使当|x -2|<δ时, |y -4|<0.001? 解 由于当x →2时, |x -2|→0, 故可设|x -2|<1, 即1<x <3. 要使|x 2-4|=|x +2||x -2|<5|x -2|<0.001, 只要0002.05001.0|2|=<-x .取δ=0.0002, 则当0<|x -2|<δ时, 就有|x 2-4|<0. 001.4. 当x →∞时, 13122→+-=x x y , 问X 等于多少, 使当|x |>X 时, |y -1|<0.01?解 要使01.034131222<+=-+-x x x , 只要397301.04||=->x , 故397=X .5. 证明函数f (x )=|x |当x →0时极限为零.证明 因为|f (x )-0|=||x |-0|=|x |=|x -0|, 所以要使|f (x )-0|<ε, 只须|x |<ε.因为对∀ε>0, ∃δ=ε, 使当0<|x -0|<δ, 时有 |f (x )-0|=||x |-0|<ε, 所以0||lim 0=→x x .6. 求,)(xx x f = x x x ||)(=ϕ当x →0时的左﹑右极限, 并说明它们在x →0时的极限是否存在. 证明 因为11lim lim )(lim 000===---→→→x x x x x x f ,11lim lim )(lim 000===+++→→→x x x x x x f ,)(lim )(lim 0x f x f x x +→→=-,所以极限)(lim 0x f x →存在.因为1lim ||lim )(lim 000-=-==---→→→xx x x x x x x ϕ,1lim ||lim )(lim 000===+++→→→x x x x x x x x ϕ,)(lim )(lim 0x x x x ϕϕ+→→≠-,所以极限)(lim 0x x ϕ→不存在.7. 证明: 若x →+∞及x →-∞时, 函数f (x )的极限都存在且都等于A , 则A x f x =∞→)(lim .证明 因为A x f x =-∞→)(lim , A x f x =+∞→)(lim , 所以∀ε>0, ∃X 1>0, 使当x <-X 1时, 有|f (x )-A |<ε ;∃X 2>0, 使当x >X 2时, 有|f (x )-A |<ε .取X =max{X 1, X 2}, 则当|x |>X 时, 有|f (x )-A |<ε , 即A x f x =∞→)(lim .8. 根据极限的定义证明: 函数f (x )当x →x 0 时极限存在的充分必要条件是左极限、右极限各自存在并且相等.证明 先证明必要性. 设f (x )→A (x →x 0), 则∀ε>0, ∃δ>0, 使当0<|x -x 0|<δ 时, 有|f (x )-A |<ε .因此当x 0-δ<x <x 0和x 0<x <x 0+δ 时都有 |f (x )-A |<ε .这说明f (x )当x →x 0时左右极限都存在并且都等于A . 再证明充分性. 设f (x 0-0)=f (x 0+0)=A , 则∀ε>0, ∃δ1>0, 使当x 0-δ1<x <x 0时, 有| f (x )-A <ε ; ∃δ2>0, 使当x 0<x <x 0+δ2时, 有| f (x )-A |<ε .取δ=min{δ1, δ2}, 则当0<|x -x 0|<δ 时, 有x 0-δ1<x <x 0及x 0<x <x 0+δ2 , 从而有 | f (x )-A |<ε ,即f (x )→A (x →x 0).9. 试给出x →∞时函数极限的局部有界性的定理, 并加以证明.解 x →∞时函数极限的局部有界性的定理: 如果f (x )当x →∞时的极限存在, 则存在X >0及M >0, 使当|x |>X 时, |f (x )|<M .证明 设f (x )→A (x →∞), 则对于ε =1, ∃X >0, 当|x |>X 时, 有|f (x )-A |<ε =1. 所以 |f (x )|=|f (x )-A +A |≤|f (x )-A |+|A |<1+|A |.这就是说存在X >0及M >0, 使当|x |>X 时, |f (x )|<M , 其中M =1+|A |. 习题1-41. 两个无穷小的商是否一定是无穷小?举例说明之. 解 不一定.例如, 当x →0时, α(x )=2x , β(x )=3x 都是无穷小, 但32)()(lim0=→x x x βα, )()(x x βα不是无穷小.2. 根据定义证明:(1)392+-=x x y 当x →3时为无穷小; (2)xx y 1sin =当x →0时为无穷小.证明 (1)当x ≠3时|3|39||2-=+-=x x x y . 因为∀ε>0, ∃δ=ε , 当0<|x -3|<δ时, 有εδ=<-=+-=|3|39||2x x x y ,所以当x →3时392+-=x x y 为无穷小. (2)当x ≠0时|0||1sin |||||-≤=x xx y . 因为∀ε>0, ∃δ=ε , 当0<|x -0|<δ时, 有εδ=<-≤=|0||1sin |||||x xx y ,所以当x →0时xx y 1sin =为无穷小.3. 根据定义证明: 函数xx y 21+=为当x →0时的无穷大. 问x 应满足什么条件,能使|y |>104?证明 分析2||11221||-≥+=+=x x x x y , 要使|y |>M , 只须M x >-2||1, 即21||+<M x .证明 因为∀M >0, ∃21+=M δ, 使当0<|x -0|<δ时, 有M x x >+21,所以当x →0时, 函数xx y 21+=是无穷大.取M =104, 则21014+=δ. 当2101|0|04+<-<x 时, |y |>104. 4. 求下列极限并说明理由: (1)xx x 12lim +∞→;(2)xx x --→11lim 20.解 (1)因为xx x 1212+=+, 而当x →∞ 时x 1是无穷小, 所以212lim =+∞→x x x .(2)因为x xx +=--1112(x ≠1), 而当x →0时x 为无穷小, 所以111lim 20=--→x x x .6. 函数y =x cos x 在(-∞, +∞)内是否有界?这个函数是否为当x →+∞ 时的无穷大?为什么?解 函数y =x cos x 在(-∞, +∞)内无界.这是因为∀M >0, 在(-∞, +∞)内总能找到这样的x , 使得|y (x )|>M . 例如y (2k π)=2k π cos2k π=2k π (k =0, 1, 2, ⋅ ⋅ ⋅),当k 充分大时, 就有| y (2k π)|>M .当x →+∞ 时, 函数y =x cos x 不是无穷大.这是因为∀M >0, 找不到这样一个时刻N , 使对一切大于N 的x , 都有|y (x )|>M . 例如0)22cos()22()22(=++=+ππππππk k k y (k =0, 1, 2, ⋅ ⋅ ⋅),对任何大的N , 当k 充分大时, 总有N k x >+=22ππ, 但|y (x )|=0<M .7. 证明: 函数xx y 1sin 1=在区间(0, 1]上无界, 但这函数不是当x →0+时的无穷大.证明 函数xx y 1sin 1=在区间(0, 1]上无界. 这是因为∀M >0, 在(0, 1]中总可以找到点x k , 使y (x k )>M . 例如当221ππ+=k x k (k =0, 1, 2, ⋅ ⋅ ⋅)时, 有22)(ππ+=k x y k ,当k 充分大时, y (x k )>M .当x →0+ 时, 函数xx y 1sin 1=不是无穷大. 这是因为∀M >0, 对所有的δ>0, 总可以找到这样的点x k , 使0<x k <δ, 但y (x k )<M . 例如可取πk x k 21=(k =0, 1, 2, ⋅ ⋅ ⋅),当k 充分大时, x k <δ, 但y (x k )=2k πsin2k π=0<M .习题1-51. 计算下列极限:(1)35lim 22-+→x x x ; 解 9325235lim 222-=-+=-+→x x x .(2)13lim 223+-→x x x ; 解 01)3(3)3(13lim 22223=+-=+-→x x x . (3)112lim 221-+-→x x x x ;解 02011lim )1)(1()1(lim 112lim 121221==+-=+--=-+-→→→x x x x x x x x x x x . (4)xx x x x x 2324lim2230++-→; 解 2123124lim 2324lim 202230=++-=++-→→x x x x x x x x x x . (5)hx h x h 220)(lim -+→;解 x h x hx h hx x h x h x h h h 2)2(lim 2lim )(lim 02220220=+=-++=-+→→→. (6))112(lim 2xx x +-∞→; 解 21lim 1lim2)112(lim 22=+-=+-∞→∞→∞→x x x x x x x . (7)121lim 22---∞→x x x x ; 解 2111211lim 121lim 2222=---=---∞→∞→xx x x x xx x . (8)13lim 242--+∞→x x x x x ; 解 013lim 242=--+∞→x x x x x (分子次数低于分母次数, 极限为零). 或 012111lim 13lim 4232242=--+=--+∞→∞→x x x x x x x x x x . (9)4586lim 224+-+-→x x x x x ; 解 32142412lim )4)(1()4)(2(lim 4586lim 44224=--=--=----=+-+-→→→x x x x x x x x x x x x x .(10))12)(11(lim 2x x x -+∞→;解 221)12(lim )11(lim )12)(11(lim 22=⨯=-⋅+=-+∞→∞→∞→x x x x x x x . (11))21 41211(lim n n +⋅⋅⋅+++∞→;解 2211)21(1lim )21 41211(lim 1=--=+⋅⋅⋅++++∞→∞→n n n n . (12)2)1( 321limnn n -+⋅⋅⋅+++∞→; 解 211lim 212)1(lim )1( 321lim 22=-=-=-+⋅⋅⋅+++∞→∞→∞→n n n nn n n n n n . (13)35)3)(2)(1(limn n n n n +++∞→;解 515)3)(2)(1(lim 3=+++∞→nn n n n (分子与分母的次数相同, 极限为 最高次项系数之比).或 51)31)(21)(11(lim 515)3)(2)(1(lim 3=+++=+++∞→∞→n n n n n n n n n . (14))1311(lim 31x x x ---→;解 )1)(1()2)(1(lim )1)(1(31lim )1311(lim 2122131x x x x x x x x x x x x x x x ++-+--=++--++=---→→→ 112lim21-=+++-=→x x x x . 2. 计算下列极限: (1)2232)2(2lim -+→x x x x ; 解 因为01602)2(lim 2322==+-→x x x x , 所以∞=-+→2232)2(2lim x x x x . (2)12lim 2+∞→x x x ;解 ∞=+∞→12lim 2x x x (因为分子次数高于分母次数).(3))12(lim 3+-∞→x x x .解 ∞=+-∞→)12(lim 3x x x (因为分子次数高于分母次数).3. 计算下列极限: (1)xx x 1sin lim 20→;解 01sin lim 20=→xx x (当x →0时, x 2是无穷小, 而x 1sin 是有界变量).(2)xx x arctan lim ∞→.解 0arctan 1lim arctan lim =⋅=∞→∞→x x xx x x (当x →∞时, x 1是无穷小,而arctan x 是有界变量).4. 证明本节定理3中的(2).习题1-61. 计算下列极限: (1)xx x ωsin lim 0→;解 ωωωωω==→→x x xx x x sin lim sin lim 00.(2)xx x 3tan lim 0→;解 33cos 133sin lim 33tan lim 00=⋅=→→xx x x x x x .(3)xx x 5sin 2sin lim 0→;解 52525sin 522sin lim 5sin 2sin lim 00=⋅⋅=→→x x x x x x x x .(4)x x x cot lim 0→;解 1cos lim sin lim cos sin lim cot lim 0000=⋅=⋅=→→→→x x x x x x x x x x x x .(5)xx x x sin 2cos 1lim 0-→;解 2)sin (lim 2sin 2lim 2cos 1lim sin 2cos 1lim 20220200===-=-→→→→x x x x x x x x x x x x x . 或 2sin lim 2sin sin 2lim sin 2cos 1lim 0200===-→→→xx x x x x x x x x x . (6)n n n x 2sin 2lim ∞→(x 为不等于零的常数). 解 x x xx x nn n n nn =⋅=∞→∞→22sin lim2sin 2lim . 2. 计算下列极限:(1)x x x 1)1(lim -→; 解 11)(1)1()(101})](1[lim {)](1[lim )1(lim ---→--→→=-+=-+=-e x x x x x x x x x .(2)x x x 1)21(lim +→;解 2221221010])21(lim [)21(lim )21(lim e x x x x x x x x x =+=+=+→⋅→→.(3)x x xx 2)1(lim +∞→; 解 222])11(lim [)1(lim e xx x x x x x =+=+∞→∞→.(4)kx x x)11(lim -∞→(k 为正整数).解 k k x x kx x e xx ---∞→∞→=-+=-))(()11(lim )11(lim .3. 根据函数极限的定义, 证明极限存在的准则I '. 证明 仅对x →x 0的情形加以证明.设ε为任一给定的正数, 由于A x g x x =→)(lim 0, 故由定义知, 对ε>0, 存在δ1>0, 使得当0<|x -x 0|<δ1时, 恒有|g (x )-A |<ε, 即A -ε<g (x )<A +ε.由于A x h x x =→)(lim 0, 故由定义知, 对ε>0, 存在δ2>0, 使得当0<|x -x 0|<δ2时, 恒有|h (x )-A |<ε, 即A -ε<h (x )<A +ε.取δ=min{δ1, δ2}, 则当0<|x -x 0|<δ时, A -ε<g (x )<A +ε与A -ε<h (x )<A +ε 同时成立, 又因为g (x )≤f (x )≤h (x ), 所以 A -ε<f (x )<A +ε, 即 |f (x )-A |<ε, 因此A x f x x =→)(lim 0.证明 仅对x →x 0的情形加以证明. 因为A x g x x =→)(lim 0, A x h x x =→)(lim 0,所以对任一给定的ε>0, 存在δ>0, 使得当0<|x -x 0|<δ时, 恒有 |g (x )-A |<ε及|h (x )-A |<ε,即 A -ε<g (x )<A +ε及A -ε<h (x )<A +ε.又因为 g (x )≤f (x )≤h (x ), 所以 A -ε<f (x )<A +ε, 即 |f (x )-A |<ε, 因此A x f x x =→)(lim 0.4. 利用极限存在准则证明: (1)111lim =+∞→nn ;证明 因为n n 11111+<+<,而 11lim =∞→n 且1)11(lim =+∞→n n ,由极限存在准则I , 111lim =+∞→nn .(2)1)1 211(lim 222=++⋅⋅⋅++++∞→πππn n n n n n ;证明 因为πππππ+<++⋅⋅⋅++++<+2222222)1 211(n n n n n n n n n n , 而 1lim 22=+∞→πn n n n , 1lim 22=+∞→πn n n , 所以 1)1 211(lim 222=++⋅⋅⋅++++∞→πππn n n n n n .(3)数列2,22+, 222++, ⋅ ⋅ ⋅ 的极限存在;证明 21=x , n n x x +=+21(n =1, 2, 3, ⋅ ⋅ ⋅). 先证明数列{x n }有界.当n =1时221<=x , 假定n =k 时x k <2, 则当n =k +1时, 22221=+<+=+k k x x , 所以x n <2(n =1, 2, 3, ⋅ ⋅ ⋅), 即数列{x n }有界.再证明数列单调增. 因为nn n n n n n n n n n n x x x x x x x x x x x x +++--=++-+=-+=-+2)1)(2(22221, 而x n -2<0, x n +1>0, 所以x n +1-x n >0, 即数列{x n }单调增.因为数列{x n }单调增加有上界, 所以此数列是有极限的. (4)11lim 0=+→n x x ;证明 当|x |≤1时, 则有 1+x ≤1+|x |≤(1+|x |)n , 1+x ≥1-|x |≥(1-|x |)n , 从而有 ||11||1x x x n +≤+≤-. 因为 1|)|1(lim |)|1(lim 0=+=-→→x x x x ,根据夹逼准则, 有 11lim 0=+→n x x .(5)1]1[lim 0=+→xx x .证明 因为x x x 1]1[11≤<-, 所以1]1[1≤<-xx x .又因为11lim )1(lim 00==-++→→x x x , 根据夹逼准则, 有1]1[lim 0=+→xx x .习题 1-71. 当x →0时, 2x -x 2 与x 2-x 3相比, 哪一个是高阶无穷小?解 因为02lim 2lim 202320=--=--→→xx x x x x x x x ,所以当x →0时, x 2-x 3是高阶无穷小, 即x 2-x 3=o (2x -x 2).2. 当x →1时, 无穷小1-x 和(1)1-x 3, (2))1(212x -是否同阶?是否等价?解 (1)因为3)1(lim 1)1)(1(lim 11lim 212131=++=-++-=--→→→x x xx x x x x x x x , 所以当x →1时, 1-x 和1-x 3是同阶的无穷小, 但不是等价无穷小.(2)因为1)1(lim 211)1(21lim 121=+=--→→x x x x x , 所以当x →1时, 1-x 和)1(212x -是同阶的无穷小, 而且是等价无穷小.3. 证明: 当x →0时, 有: (1) arctan x ~x ;(2)2~1sec 2x x -. 证明 (1)因为1tan limarctan lim 00==→→y yxx y x (提示: 令y =arctan x , 则当x →0时, y →0),所以当x →0时, arctan x ~x .(2)因为1)22sin 2(lim 22sin 2lim cos cos 1lim 2211sec lim 202202020===-=-→→→→x xx x x x x xx x x x x , 所以当x →0时, 2~1sec 2x x -. 4. 利用等价无穷小的性质, 求下列极限: (1)xx x 23tan lim 0→;(2)mn x x x )(sin )sin(lim 0→(n , m 为正整数);(3)x x x x 30sin sin tan lim -→; (4))1sin 1)(11(tan sin lim320-+-+-→x x x x x .解 (1)2323lim 23tan lim 00==→→x x x x x x .(2)⎪⎩⎪⎨⎧<∞>===→→mn m n m n x x x x mn x m n x 0 1lim )(sin )sin(lim00. (3)21cos 21lim sin cos cos 1lim sin )1cos 1(sin lim sin sin tan lim 220203030==-=-=-→→→→x x x x x x xx x x x x x x x x . (4)因为32221)2(2~2sin tan 2)1(cos tan tan sin x x x x x x x x x -=⋅--=-=-(x →0),23232223231~11)1(11x x x x x ++++=-+(x →0), x x x x x ~sin ~1sin 1sin 1sin 1++=-+(x →0), 所以 33121lim )1sin 1)(11(tan sin lim 230320-=⋅-=-+-+-→→x x x x x x x x x .5. 证明无穷小的等价关系具有下列性质: (1) α ~α (自反性);(2) 若α ~β, 则β~α(对称性); (3)若α ~β, β~γ, 则α~γ(传递性). 证明 (1)1lim =αα, 所以α ~α ;(2) 若α ~β, 则1lim =βα, 从而1lim=αβ. 因此β~α ;(3) 若α ~β, β~γ, 1lim limlim =⋅=βαγβγα. 因此α~γ. 习题1-81. 研究下列函数的连续性, 并画出函数的图形:(1)⎩⎨⎧≤<-≤≤=21 210 )(2x x x x x f ;解 已知多项式函数是连续函数, 所以函数f (x )在[0, 1)和(1, 2]内是连续的. 在x =1处, 因为f (1)=1, 并且1lim )(lim 211==--→→x x f x x , 1)2(lim )(lim 11=-=++→→x x f x x .所以1)(lim 1=→x f x , 从而函数f (x )在x =1处是连续的.综上所述,函数f (x )在[0, 2]上是连续函数.(2)⎩⎨⎧>≤≤-=1|| 111 )(x x x x f .解 只需考察函数在x =-1和x =1处的连续性. 在x =-1处, 因为f (-1)=-1, 并且)1(11lim )(lim 11-≠==---→-→f x f x x ,)1(1lim )(lim 11-=-==++-→-→f x x f x x ,所以函数在x =-1处间断, 但右连续. 在x =1处, 因为f (1)=1, 并且1lim )(lim 11==--→→x x f x x =f (1), 11lim )(lim 11==++→→x x x f =f (1),所以函数在x =1处连续.综合上述讨论, 函数在(-∞, -1)和(-1, +∞)内连续, 在x =-1处间断, 但右连续. 2. 下列函数在指出的点处间断, 说明这些间断点属于哪一类, 如果是可去间断点, 则补充或改变函数的定义使它连续:(1)23122+--=x x x y , x =1, x =2;解 )1)(2()1)(1(23122---+=+--=x x x x x x x y . 因为函数在x =2和x =1处无定义, 所以x =2和x =1是函数的间断点.因为∞=+--=→→231lim lim 2222x x x y x x , 所以x =2是函数的第二类间断点;因为2)2()1(limlim 11-=-+=→→x x y x x , 所以x =1是函数的第一类间断点, 并且是可去间断点. 在x =1处, 令y =-2, 则函数在x =1处成为连续的. (2)x x y tan =, x =k , 2ππ+=k x (k =0, ±1, ±2, ⋅ ⋅ ⋅);解 函数在点x =k π(k ∈Z)和2ππ+=k x (k ∈Z)处无定义, 因而这些点都是函数的间断点.因∞=→x x k x tan lim π(k ≠0), 故x =k π(k ≠0)是第二类间断点;因为1tan lim0=→xx x , 0tan lim2=+→x x k x ππ(k ∈Z), 所以x =0和2ππ+=k x (k ∈Z) 是第一类间断点且是可去间断点.令y |x =0=1, 则函数在x =0处成为连续的;令2 ππ+=k x 时, y =0, 则函数在2ππ+=k x 处成为连续的.(3)xy 1cos 2=, x =0;解 因为函数x y 1cos 2=在x =0处无定义, 所以x =0是函数xy 1cos 2=的间断点.又因为xx 1cos lim 20→不存在, 所以x =0是函数的第二类间断点.(4)⎩⎨⎧>-≤-=1 311x x x x y , x =1.解 因为0)1(lim )(lim 11=-=--→→x x f x x 2)3(lim )(lim 11=-=++→→x x f x x , 所以x =1是函数的第一类不可去间断点.3. 讨论函数x x x x f nnn 2211lim )(+-=∞→的连续性, 若有间断点, 判别其类型. 解 ⎪⎩⎪⎨⎧<=>-=+-=∞→1||1|| 01|| 11lim)(22x x x x x x x x x f nn n .在分段点x =-1处, 因为1)(lim )(lim 11=-=---→-→x x f x x , 1lim )(lim 11-==++-→-→x x f x x , 所以x =-1为函数的第一类不可去间断点.在分段点x =1处, 因为1lim )(lim 11==--→→x x f x x , 1)(lim )(lim 11-=-=++→→x x f x x , 所以x =1为函数的第一类不可去间断点.4. 证明: 若函数f (x )在点x 0连续且f (x 0)≠0, 则存在x 0的某一邻域U (x 0), 当x ∈U (x 0)时, f (x )≠0.证明 不妨设f (x 0)>0. 因为f (x )在x 0连续, 所以0)()(lim 00>=→x f x f x x , 由极限的局部保号性定理, 存在x 0的某一去心邻域)(0x U , 使当x ∈)(0x U时f (x )>0, 从而当x ∈U (x 0)时, f (x )>0. 这就是说, 则存在x 0的某一邻域U (x 0), 当x ∈U (x 0)时, f (x )≠0. 5. 试分别举出具有以下性质的函数f (x )的例子:(1)x =0, ±1, ±2, 21±, ⋅ ⋅ ⋅, ±n , n1±, ⋅ ⋅ ⋅是f (x )的所有间断点, 且它们都是无穷间断点;解 函数x x x f ππcsc )csc()(+=在点x =0, ±1, ±2, 21±, ⋅ ⋅ ⋅, ±n , n1±, ⋅ ⋅ ⋅处是间断的且这些点是函数的无穷间断点.(2)f (x )在R 上处处不连续, 但|f (x )|在R 上处处连续;解 函数⎩⎨⎧∉∈-=QQx x x f 1 1)(在R 上处处不连续, 但|f (x )|=1在R 上处处连续.(3)f (x )在R 上处处有定义, 但仅在一点连续.解 函数⎩⎨⎧∉-∈=Q Qx x x x x f )(在R 上处处有定义, 它只在x =0处连续.习题1-91. 求函数633)(223-+--+=x x x x x x f 的连续区间, 并求极限)(lim 0x f x →, )(lim 3x f x -→及)(lim 2x f x →.解 )2)(3()1)(1)(3(633)(223-++-+=-+--+=x x x x x x x x x x x f , 函数在(-∞, +∞)内除点x =2和x =-3外是连续的, 所以函数f (x )的连续区间为(-∞, -3)、(-3, 2)、(2, +∞). 在函数的连续点x =0处, 21)0()(lim 0==→f x f x .在函数的间断点x =2和x =-3处, ∞=-++-+=→→)2)(3()1)(1)(3(lim)(lim 22x x x x x x f x x , 582)1)(1(lim )(lim 33-=-+-=-→-→x x x x f x x .2. 设函数f (x )与g (x )在点x 0连续, 证明函数ϕ(x )=max{f (x ), g (x )}, ψ(x )=min{f (x ), g (x )} 在点x 0也连续.证明 已知)()(lim 00x f x f x x =→, )()(lim 00x g x g x x =→.可以验证] |)()(|)()([21)(x g x f x g x f x -++=ϕ,] |)()(|)()([21)(x g x f x g x f x --+=ψ.因此 ] |)()(|)()([21)(00000x g x f x g x f x -++=ϕ,] |)()(|)()([21)(00000x g x f x g x f x --+=ψ.因为] |)()(|)()([21lim )(lim 00x g x f x g x f x x x x x -++=→→ϕ] |)(lim )(lim |)(lim )(lim [210000x g x f x g x f x x x x x x x x →→→→-++=] |)()(|)()([210000x g x f x g x f -++==ϕ(x 0),所以ϕ(x )在点x 0也连续.同理可证明ψ(x )在点x 0也连续.3. 求下列极限: (1)52lim 20+-→x x x ;(2)34)2(sin lim x x π→;(3))2cos 2ln(lim 6x x π→;(4)xx x 11lim 0-+→;(5)145lim 1---→x x x x ;(6)a x a x a x --→sin sin lim ;(7))(lim 22x x x x x --++∞→.解 (1)因为函数52)(2+-=x x x f 是初等函数, f (x )在点x =0有定义, 所以 55020)0(52lim 220=+⋅-==+-→f x x x .(2)因为函数f (x )=(sin 2x )3是初等函数, f (x )在点4π=x 有定义, 所以1)42(sin )4()2(sin lim 334=⋅==→πππf x x .(3)因为函数f (x )=ln(2cos2x )是初等函数, f (x )在点6π=x 有定义, 所以0)62cos 2ln()6()2cos 2ln(lim 6=⋅==→πππf x x .(4))11(lim)11()11)(11(lim 11lim 000++=++++-+=-+→→→x x x x x x x x x x x x 211101111lim=++=++=→x x .(5))45)(1()45)(45(lim 145lim 11x x x x x x x x x x x x +--+---=---→→)45)(1(44lim 1x x x x x +---=→214154454lim 1=+-⋅=+-=→x x x .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 函数,极限与连续
第一节 函数
一、集合与区间
1.集合
一般地说,所谓集合(或简称集)是指具有特定性质的一些事物的总体,组成这个集合的事物称为该集合的元素。
由有限个元素组成的集合称为有限集。
由无穷多个元素组成的集合称为无限集。
不含任何元素的集合称为空集。
数集合也可以称为(数轴上的)点集。
区间是用得较多的一类数集。
设a,b 为实数,且a<b
数集{x|a<x<b}称为开区间,记作(a,b),即(a,b)= {x|a<x<b}。
数集}|{b x a x ≤≤称为闭区间,记作[a,b],即[a,b]= }|{b x a x ≤≤。
类似地,[a,b),(a,b]称为半开区间,即[a,b)=}|{b x a x <≤,(a,b]=}|{b x a x ≤< 以上这些区间都称为有限区间,此外还有无限区间,引进记号∞及-∞,则可类似表示
}|{),(},|{),(},|{),[+∞<<-∞=∞-∞<=-∞≤=+∞x x b x x b x a x a 还有一类可变开区间,我们称其为邻域。
设δ与a 是两个实数,且δ>0。
开区间),(δδδ+-a a 称为点a 的δ邻域,记作),(δa U ,即}|{),(δδδ+<<-=a x a x a U 。
其中a 叫作这个邻域的中心,δ称为这个邻域的半径。
在点a 的领域中去掉中心后,称为点a 的去心邻域,记作),(),(}||0|{),(),,(0
0δδδδδ+⋃-=<-<=a a a a a x x a U a U 即 二、函数概念
定义:设x 和y 是两个变量,若对于x 的每一个可能的取值,按照某个法则f 都有一个确定的y 的值与之对应,我们称变量y 是变量x 的函数,记为y =)(x f .这里称x 为自变量,y 为因变量。
自变量x 的所以可能取值的集合称为定义域,记为D(f);因变量y 的相
应的值的集合称为值域,记为R(f)。
这里D(f)与R(f)都是数集,且R(f)={)(x f |x ∈D(f)}。
三、函数的几种特性
1.函数的有界性
设函数)(x f 在D 上有定义,如果存在正数M ,使得对于任何的x ∈D 都满|)(x f |≤M ,则称函数)(x f 在D 上有界,或称)(x f 是D 上的有界函数。
若这样的正数M 不存在,则称)(x f 是D 上无界函数。
2.函数的单调性
设函数)(x f 的定义域为D ,区间D I ⊆,若对于任意的I x x ∈21,,当1x <2x 时总有
f (1x )<f (2x ),
则称)(x f 是区间I 上的单调增加函数;若对于任意的I x x ∈21,,当1x <2x 时总有f (1x )>f (2x ),则称)(x f 是区间I 上的单调减少函数。
单调增加或单调减少的函数均称为单调函数。
若在某个区间上,函数)(x f 为单调函数,则称该区间为函数)(x f 的单调区间。
3.函数的奇偶性
设函数)(x f 的定义域D 关于原点对称,即若x ∈D ,则必x -∈D 。
若对于任意的x ∈D 总有)(x f -=)(x f ,则称)(x f 是偶函数;若对于任意的x ∈D 总有)(x f -=)(x f -,则称)(x f 是奇函数。
4.函数的周期性
设函数)(x f 的定义域为D ,若存在不为零的数T ,使得对于任一x ∈D 有D T x ∈±)(, 且f )(T x ±=)(x f 总成立,则称)(x f 是周期函数,T 称为周期函数)(x f 的周期。
由定义容易得出,若T 为)(x f 的周期,则2T ,3T ,…,nT ,…都是)(x f 的周期。
如果在周期中存在最小的正值,我们把它称为最小正周期,通常我们说周期函数的周期均指最小正周期。
四.反函数
设函数)(x f y =的定义域为D ,值域为R 。
若对于任意的R y ∈只有唯一D x ∈与之。
