磁通定理(磁场中的高斯定理)
磁场高斯定理 知乎

磁场高斯定理
磁场的高斯定理是磁场理论中的一个重要定律,它表述为:磁场中通过任一封闭曲面的磁通量一定为零。
这里,磁通量表示的是通过某个曲面的磁感线的数量,磁感线是用来表示磁场分布的线。
高斯定理告诉我们,不论磁场如何分布,无论曲面如何取向,只要它是封闭的,通过这个曲面的磁通量总是为零。
这个定理反映了磁场的无源性质。
在磁场中,没有类似于电荷这样的源,磁场线是闭合的,从一处出发的磁场线会形成闭合回路,不会像电场线那样从一个正电荷出发终止于一个负电荷。
因此,磁场线不会从一个地方出发而终止于另一处,这就意味着磁场线不会穿越一个封闭的曲面,导致磁通量恒为零。
与静电场的高斯定理相比,磁场的高斯定理体现了磁场的本质差异。
在静电场中,由于电荷的存在,电场线会从正电荷出发终止于负电荷,因此,通过一个封闭曲面的电通量可以不为零。
而磁场的高斯定理表明磁场是无源的,不存在孤立的磁荷,磁场线总是闭合的。
这个定理在磁场的实际应用中具有重要意义,例如在电磁感应、磁场的能量传递等方面都是基于磁场的高斯定理的原理。
通过理解和应用磁场的高斯定理,我们可以更好地理解和预测磁场的行为和作用。
1。
大学物理-7-3 磁通量 磁场的高斯定理

B
磁通量:通过某一曲面 的磁感线数为通过此曲面 的磁通量.
Φ BS cosBS
Φ B S B enS dΦ B dS
B dΦ BdS cos
s
Φ s BdS
单位 1Wb 1T 1m2
B dS1
1 B1
S
B2
2
dS2
dΦ1 B1 dS1 0 dΦ2 B2 dS2 0
SB cosdS 0
S B d S 0
3a
2a 5a
l
Φ s BdS = 0
I
磁场高斯定理
S B d S 0
物理意义:通过任意闭合曲面的磁通量必等于零。
(故磁场是无源的.)
求磁通量(1)用磁通量的定义求(2)用高斯定理求
例1 如图载流长直导线的电流为
积的磁通量.
解 先求
,试I 求 通过矩形面 ,B对变磁场给出
B
后积B 分dΦ求0I
2π x
Φ
B // S
I
l
d1 d2
dΦ BdS 0I ldx
Φ
S
B
dS
2π x
0Il
2π
d2
d1
dx x
o
x Φ 0Il ln d2
2π d1
例2 一半径为a的无限长直载流导线,沿轴向均
匀地流有电流I,若作一个半径为 R= 5a,高为l
的柱形曲面,已知此柱形曲面的轴与载流导线的 轴平行且相距3a(如图),则在圆柱侧面S上的 磁通量=?
第三节 磁场的高斯定理
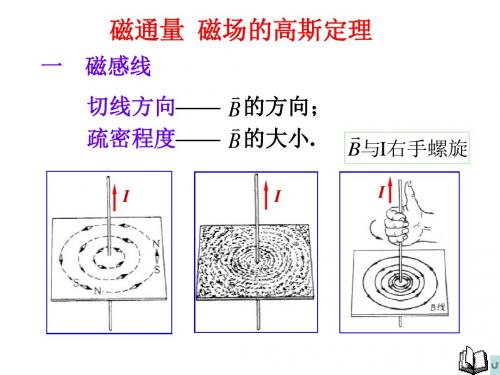
一 磁感线
规定:曲线上每一点的切线方向就是该点的磁感
强度 B 的方向,曲线的疏密程度表示该点的磁感强 度 B 的大小.
I
5磁通量 磁场的高斯定理
4
一般情况 dΦ B dS
dS 2
B
2 S
dS1
1
B2
B1
dΦ 1B 1 dS1 0 dΦ2 B2 dS2 0
B cos dS 0
S
磁场高斯定理
S B d S 0
物理意义:通过任意闭合曲面的为零 ——磁场是无源场。 静电场高斯定理
a
r2
o
r1
dr
r
7
解:在距离左边导线r处取面积元ds=adr,两长直 导线在该处产生的磁感应强度之和为:
0 I 1 1 B ( ) 2 r r r1 r2
通过这个面积元的磁通量为:
为正方向
0 I 1 1 d Bds ( )adr 2 r r r1 r2
2
S2
S
磁场高斯定律 B ds 0
2 B ds B ds (ai bj ck ) dsk s s
2 1
S1
B ds B ds 0
S2
s1
cds S1c R c s
面积元d s取和B相同方向
8
则通过导线框的磁通量为:
d
r1 b
r1
0 I 1 1 ( )adx 2 x x r1 r2
0 Ia (r1 b)(r2 b) ln 2 r1r2
9
例3两根平行无限长直导线相距为d,载有大小相 等方向相反的电流I,一个边长为d的正方形线圈 位于导线平面内与一根导线相距d,如图示。求通 过矩形面积的磁通量. 。
08磁场高斯环路定理

0 Ii 0
i 1
n
d
螺绕环:
B外 0
B内
R
n B dl 0 Ii l i 1
0 NI
2πR
20
7-7带电粒子在磁场中的运动 一.带电粒子在磁场中受力:
Fm qV B
q>0,F 沿 V B 方向;
q<0, 沿V B 反方向。 F
qB
mv
Fm q
B
v 0
(回旋)频率f:
f
qB 2 m
23
3.一般情况:
v v sin
Fm qvB sin qv B
Fm qV B
v// v cos
Fm 0
v
dF
B
Idl
※安培力是作用在整个载流导线上,而不是集中作用于一个点上。
26
均匀磁场中载流导线所受安培力
(1)载流直导线 取电流元 受力大小
Idl
F
dF Idl B
I
Idl B
L
Idl
×
dF
B
B
dF BIdl sin
方向
乘以该闭合路径所包围的各电流的代数和.
7
任意回路
由 环 路 内 电 流 决 定
n B dl 0 I i l i 1
环路上的 磁感应强 度(环路 内、外电 流产生的B 的叠加)
环路所包围电流的代 数和(若电流方向与 环路绕行方向满足右 手定则电流取正,反 之取负).
1、说明磁场是有旋场(非保守场). 2、利用安培环流定理可以求某些具有特殊 对称性的电流分布的磁场
6. 2 磁场中的高斯定理

I
d S B
二.磁通量 (1) 匀强磁场中
——通过磁场中某个曲面的磁感线数。
B
n
S
n
dS
B
S
B B
m =BS
(2) 非均匀场中
m =BS =BScos B S
穿过dS 的元磁通量
d Φ m B d S =Bcos dS
一.磁场的形象描述 ——磁感线 ( B 线)
§6. 2
磁场中的高斯定理
B
闭合曲线
(1) 磁感线上任一点的切线方向表示该点的磁场方向。 规定:
电流的流向与磁感线回转方向满足右手螺旋关系
I I S N
(2) 通过磁场中某点处垂直 B 矢量的单位面积的磁感线数等于该 B 点 B的量值。 P172 dΦ m B ——磁通密度 d SB
B dx
l d2
I
x d1
解:先求 B , 再求d m , 后积分出m 。 0 I B B // d S 2 x 0 I ldx d Φ m B dS 2 x
0 Il m B dS S 2
d2
d1
O 4a a 2a
S
B B
单位: 韦伯(wb) 对闭合曲面: 取曲面外法向为正向
B 线穿出m >0,B 线穿入m <0 。 (6-9) S B d S =0
S
N
——磁场的高斯定理 物理意义:通过磁场中任一闭合曲面的磁通量为零。 磁场是 无源 场。
例:如图示载流长直导线的电流为 I , 试求通过矩形面积的磁 通量。
大学物理-7-5磁通量磁场的高斯定理

第七章 恒定磁场
6
物理学
第五版
选择进入下一节:
本章目录
7-4 毕奥-萨伐尔定律 7-5 磁通量 磁场的高斯定理
7-6 安培环路定理
7-7 带电粒子在电场和磁场中的运动 7-8 载流导线在磁场中所受的力 7-9 磁场中的磁介质
第七章 恒定磁场
7
量必等于零(故磁场是无源的).
第七章 恒定磁场
5
物理学
第五版
7-5 磁通量 磁场的高斯定理
例 如图载流长直导线的电流为 I,试求
通过矩形面积的磁通量.
解 B 0I
B
2π x
dx
dΦBdS0I ldx
I
l
d1 d2
2πx
ΦSB dS20πIldd12dxx
ox
x Φ 0Il ln d2
磁通场过中的某磁点感处 线垂 数直 目等B 矢于量该的点单B 的位数面值积.上
第七章 恒定磁场
3
物理学
第五版
7-5 磁通量 磁场的高斯定理
B
磁通量:通过
en
某曲面的磁感线数
s
s
B
B dS
B
匀强磁场中,通 过面曲面S的磁通量:
Φ B SB enS
ΦBcSo sBS
物理学
第五版
7-5 磁通量 磁场的高斯定理
一 磁感线
切线方向—— 疏密程度——
B B的 的方 大向 小.;
I
I
I
第七章 恒定磁场
1
物理学
第五版
7-5 磁通量 磁场的高斯定理
I
S
I
S
毕奥-萨伐尔定律 磁通量 磁场的高斯定理
解:(1)判断电流元产生 每个电流元产生磁场同方向
磁场的方向是否一致
z
D
2
z r 0 cot
dz
I
z
1
r
r0
x
C
o
r0 dz d 2 sin dB r0 又r * y P sin 0 Idl sin (1) 大小 dB 2 4 r
B
0 I
2πr
I
B
I
X
B
电流与磁感强度成右手螺旋关系
2013-7-5
10
[例14-2] 圆电流轴线上的磁场。
0 Idl 解: dB sin 90 2 4 r 0 Idl B dB sin 90 2 4 r
x 因为圆线圈上各个电流元在P点产生的磁感应强度 的方向是不同的,所以只能用它的矢量表示:
第五版
四.运动电荷的磁场
7-4
毕奥-萨伐尔定律
考虑一段导体,其截面积为S,其 中载流子的密度为n,载流子带电 q,以漂移速度 v 运动。
毕奥—萨伐尔定律:
0 Idl r dB 4 π r3 0 nSdlqv r dB 3 4π r
P r dB Idl j Sdl nSdlqv
z
o
r
Idl
y
R
0 I dl sin x 2 2 2 r2 r R z 4 2 2 R 0 IR 0 I sin dl 3 2 0 2 2 4 r 2( R z ) 2
B
0 IR
2
2 2 32
2( R z )
磁通量 磁场的高斯定理
B
B
0 I
dl
(5)多电流情况
I1
I2
I3
B B1 B2 B3 B d l 0 ( I 2 I 3 )
l
l
以上结果对任意形状 的闭合电流(伸向无限远 的电流)均成立.
n B dl 0 Ii i 1
安培环路定理
B
0 I
B
dB
I
.
dI
B
B
的方向与 I 成右螺旋
0 r R,
r R,
I
2π R 0 I B 2π r
B
0 Ir
2
0 I
2π R
B
R
o R
r
rR
0 I B 2r
区域:
rR
0 Ir B 2R 2
区域:
I
思考:具有一圆柱形空腔的无限长载流 圆柱,求空腔内的磁场?
B dl B (d l d l// )
L L
(4) 如果闭合曲线不在垂直 于导线的平面内:
B cos 90 dl B cos dl//
L L
I
0 Br d
L
dl
dl
dl
2
0
0 I r d 2 r
结果一样!
I
L 成右螺旋时,
二 安培环路定理的证明 (1)载流长直导线的情况
0 I l B dl 2π Rdl 0 I l B dl 2π R l dl B dl 0 I
l
0 I B 2πR
I
o
B
R
磁场的高斯定理
一 磁感线 规定:曲线上每一点的切线方向就是该点的磁感 规定:曲线上每一点的切线方向就是该点的磁感 切线方向 的方向,曲线的疏密程度 疏密程度表示该点的磁感强度 强度 B 的方向,曲线的疏密程度表示该点的磁感强度 B 的大小 的大小.
I I I
磁通量(Magnetic flux)v • 磁通量
单位 1Wb = 1T × 1m
2
v B
S
I
v B
v B
由电流与磁场的关系可知电流元的磁力线都是 圆心在电流元轴线上的同心圆。 圆心在电流元轴线上的同心圆。磁力线是无头无尾 的闭合曲线。 的闭合曲线。 r v v dB⋅ dS = 0 dB 是电流元的磁场
∫∫
S
载流导线的磁场
r r r r B = dB1 + dB2 + L + dBn + L
µ0 I
x
s⊥
θ
s
v B
θ v B
v dS
v en
B
磁通量: 磁通量:通过某一曲 面的磁感线数为通过此曲 面的磁通量. 面的磁通量
v θ B
s
Φ = BS cosθ = BS⊥ v v v v Φ = B ⋅ S = B ⋅ enS v v dΦ = B ⋅ dS dΦ = BdS cosθ v v Φ = ∫s B ⋅ dS
大学物理学》 《基础物理学》路果编著p345 《大学物理学》卢德馨编著线起始于正电荷,终止于负电荷。 电场线起始于正电荷,终止于负电荷。 磁感应线为无头无尾的闭合线。 磁感应线为无头无尾的闭合线。 原因: 原因:正、负电荷可单独存在,而磁单 负电荷可单独存在, 极子却不可单独存在 磁场是一种涡旋场
磁场中的高斯定理
磁场中的高斯定理
高斯定理是电磁学中常用的重要定理之一。
在磁场中,我们也可以使用高斯定理来描述磁场的性质。
首先,我们需要了解磁场的基本概念。
磁场是由带电粒子运动所产生的一种物理现象。
磁场的强度和方向可以用磁感应强度B来描述。
磁场中,有一个重要的物理量叫做磁通量,通常用Φ表示。
磁通量表示通过一个面积S的磁场线的总量。
接下来,我们来介绍高斯定理。
高斯定理是指,在一个封闭曲面的内部,如果存在电荷或电流,那么通过该曲面的电场通量等于该曲面内部的电荷或电流的代数和。
在磁场中,我们也可以使用高斯定理来描述磁通量的性质。
在磁场中,高斯定理可以表述为:在一个封闭曲面的内部,如果存在磁荷或磁流,那么通过该曲面的磁通量等于该曲面内部的磁荷或磁流的代数和。
这个定理的本质是描述了磁场的源与汇。
高斯定理对于磁场的研究非常重要,它可以用来计算磁通量,进而计算磁场强度。
同时,高斯定理也可以用来解释磁场中的许多现象,比如磁荷的存在和运动等。
总之,高斯定理在磁场中的应用非常广泛,它是研究磁场性质的基础之一。
通过对高斯定理的理解和运用,我们可以更深入地了解磁场的本质和特性,为磁场应用提供更加可靠的理论基础。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
磁通定理(磁场中的高斯定理)
如果在磁场中任取一闭合面,规定外法线为正,则穿出闭合面的磁通量为正,穿入闭合面的磁通量为负。
由于磁感应线是无头无尾的闭合线,有几根磁感应线穿入闭合面,一定有同样数目的磁感应线穿出闭合面。
所以,通过任意闭合面的磁通量恒等于零。
这就是磁通定理,其数学表达式为
磁通定理与静电场的高斯定理在数学表达式上相似,但它们在本质上不同,分别反映磁场和静电场(从磁感应线和电力线)在本质上的不同。
上式可以从毕 - 萨定律出发加以严格证明。
