梁的剪力方程和弯矩方程常用弯矩图
快速绘制梁的剪力图和弯矩图

CB段: F
3、依方程而作图
简支梁受集中力偶作用,如图示,试画梁的剪力图和 弯矩图。 解:1.求约束反力
2.列剪应力方程和弯矩方程 AC段: V
CB段:V
3、依方程而作图
荷载图、剪力图、弯矩图的规律
从左往右做图
在无荷载作用的梁段:剪力图为水平线,弯矩图为斜直线, 斜率的大小等于对应梁段上剪力的大小。V>0时向右下方斜斜, V<0时向右上方倾斜,V=0时为水平线。 在均布荷载作用的梁段上:剪力图为斜直线,斜率等于荷载 集度,q<0( )向右下方倾斜,反之,向右上方倾斜。 弯矩图为二次抛物线,q<0,向下凸起;q>0( )向上凸。 遇到集中荷载:剪力图突变,突变方向与集中荷载方向相同, 突变大小等于集中荷载的大小。弯矩图出现转折,转折方向与 集中力的方向相反。 遇到集中力偶:剪力图不变,弯矩图突变,突变方向由力偶的 转向决定,逆上顺下。突变大小等于力偶矩的大小。 极值弯矩:集中力作用截面、集中力偶截面或弯矩为零的截面。
画剪力图和弯矩图时,一定要将梁正确分段, 分段建立方程,依方程而作图
简支梁受均布荷载作用,如图示, 作此梁的剪力图和弯矩图。
解:1.求约束反力 由对称关系,可得:
2、建立内力方程
Fs
RA
qx
1 2
ql
qx
(0<x<l)
3、依方程作剪力图和弯矩图
载作用,如图示, 作此梁的剪力图和弯矩图。 1.求约束反 力
vv vv
vv v v
v
利用上述规律:
1、可以检查剪力图和弯矩图是否正确。 2、可以快速的绘制剪力图和弯矩图,步骤如下: (1)将梁正确分段 (2)根据各段梁上的荷载情况,判断剪力图和弯矩图的 形状
剪力、弯矩方程与剪力、弯矩图

截面位置对剪力和弯矩的影响
总结词
截面位置对剪力和弯矩具有显著影响。不同的截面位置会导致剪力和弯矩的大小和方向发生变化。
详细描述
在结构分析中,截面位置是影响剪力和弯矩的重要因素之一。不同的截面位置会导致剪力和弯矩的大小和方向发 生变化,从而影响结构的整体受力性能。例如,在梁中选取不同的截面位置进行支撑或固定,会对梁的剪力和弯 矩产生显著影响。
05 剪力、弯矩与材料力学性 能的关系
材料弹性对剪力和弯矩的影响
弹性材料在剪力和弯矩作用下会发生弹性变形,变形量与外力成正比,当外力去 除后,材料能够恢复原状。
弹性材料的剪切模量和弯曲刚度决定了剪力和弯矩的大小,剪切模量越大,材料 抵抗剪切变形的能力越强;弯曲刚度越大,材料抵抗弯曲变形的能力越强。
根据绕顺时针方向观察确定,使上侧 纤维受拉时为正。
02 剪力方程与弯矩方程
剪力图与弯矩图的绘制
1
剪力图和弯矩图是表示梁上剪力和弯矩随截面位 置变化的图形。
2
这些图的绘制基于剪力方程和弯矩方程的计算结 果,通过将计算得到的剪力和弯矩值标在图中相 应的位置上,并连接成线。
3
剪力图和弯矩图的绘制有助于直观地了解梁在不 同截面位置的受力状态和应力分布情况。
弯矩
在梁或结构中,由于弯曲而产生 的力矩,表示弯曲变形的大小。
剪力与弯矩在力学中的作用
剪力
主要影响结构的剪切变形,对梁的剪切承载能力有重要影响 。
弯矩
主要影响结构的弯曲变形,对梁的弯曲承载能力有重要影响 。
剪力与弯矩的符号规定
剪力正方向
根据右手定则确定,从杆件的受压一 侧指向受拉一侧。
弯矩正方向
02
材料强度越高,抵抗剪力和弯矩等外力的能力越强, 所能承受的剪力和弯矩越大。
梁的剪力方程和弯矩方程常用弯矩图

梁的剪力方程和弯矩方程常用弯矩图Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】5-7.试列出下列梁的剪力方程和弯矩方程,并画出剪力图和弯矩图。
解:首先求出支座反力。
考虑梁的整体平衡 由 0,0=+⋅=∑e RA B M l F M 得lM F eRA -= 由 0,0=-⋅=∑e RB A M l F M 得 lM F eRB= 则距左端为x 的任一横截面上的剪力和剪力图 弯矩表达式为:()l M F x F eRA S -== ()x lM x F x M eRA ⋅-=⋅= 剪力方程为常数,表明剪图应是一条平行梁轴线的直线;弯矩方程是x 的一次函数,表明弯矩图是一条斜直线。
(如图) 解:首先求出支座反力。
考虑梁的平衡由 0452,0=⋅⋅-⋅=∑l l q l F M RB c得 ql F RB 85=由 021,02=+⋅=∑ql l F M RC B得 ql F RC 21-=则相应的剪力方程和弯矩方程为:AB 段:(201l x ≤≤) 剪力BC段:(2322lxl≤≤)AB段剪力方程为x1的一次函数,弯矩方程为x1的二次函数,因此AB段的剪力图为斜直线,弯矩图为二次抛物线;BC段剪力方程为常数,弯矩方程为x2的一次函数,所以BC 段剪力图为平行梁轴线的水平线段,弯矩图为斜直线。
(如图)5-9 用简便方法画下列各梁的剪力图和弯矩图。
解:由梁的平衡求出支座反力:AB段作用有均布荷载,所以AB段的剪力图为下倾直线,弯矩图为下凹二次抛物线;BC段没有荷载作用,所以BC段的剪力图为平行梁轴线的水平线段,弯矩图为直线。
在B支座处,剪力图有突变,突变值大小等于集中力(支座反力F RB)的大小;弯矩图有转折,转折方向与集中力方向一致。
(如图)(5)解:由梁的平衡求出支座反力:KNFKNFRBRA5.6,5.3==AB 与BC 段没有外载作用,所以AB 、BC 段的剪力图为平行梁轴线的水平线段,弯矩图为直线;CD 段作用均布荷载,所以CD 段的剪力图为下倾直线,弯矩图为下凹二次抛物线。
梁的剪力和弯矩.剪力图和弯矩图
突变,顺下逆上,大小与M 同,FS图不发生变化。
例题
4.9
作图示梁的内力图
3kN 4.5kN m
2kN m
D
A
C
B
FA 10kN
1m 2m
2m
7
3
x 1.56 2
3
2
2.44 2
E FB 2kN 1m
kN
kNm
例题
4.10
4kN m
6kN
1m
1m
4.5
kN
FL
0 xL 0x L
kNm
例题 4.6
图示外伸梁,,试作剪力图和弯矩图.
20kN 40kN m
X1 A 1m 35kN
15
20
kN
20
10kN m
4m
2.5
FS x1 20kN
X2
B
0 x1 1
25kN
M x1 20x1
0 x1 1
FS x2 25 10x2
2Fl
lC
l
FCs
l
C MC
2Fl
FCs
MC
C
l
F
B D
FCs F FCs F
MC Fl MC Fl
MC 2Fl Fl 0
F
B
D
FDs
MD
F
DB
FDs F MD 0
截开后取左边为示力对象:
❖向上的外力引起正剪力,向下的外力引起负剪力; ❖向上的外力引起正弯矩,向下的外力引起负弯矩; ❖顺时针引起正弯矩,逆时针引起负弯矩。
剪力图是斜直线. 弯矩图是二次抛物线.
梁的剪力弯矩方程和剪力弯矩图

5.4.1 梁的剪力、弯矩方程和剪力、弯矩图梁在外力作用下,各个截面上的剪力和弯矩一般是不相等的。
若以横坐标表示横截面沿梁轴线的位置,则剪力Q 和弯矩M 可以表示为坐标的函数,即它们分别称为梁的剪力方程和弯矩方程。
与绘制轴力图或扭矩图一样,可用图线表明梁的各截面上剪力和弯矩沿梁轴线的变化情况。
作图时,取平行于梁轴线的直线为横坐标轴,值表示各截面的位置;以纵坐标表示相应截面上的剪力、弯矩的大小及其正负,这种表示梁在各截面上剪力和弯矩的图形,称为剪力图和弯矩图。
例5-1 简支梁AB 承受承受均布荷载作用,如图 5 - 10a 所示。
试列出剪力方程和弯矩方程,并绘制剪力图和弯矩图。
图5-10解:(1) 计算支反力以整梁为研究对象,利用平衡条件计算支反力。
由于简支梁上的载荷对于跨度中央截面是对称的,所以 A 、 B 两端的支反力应相等,即(1)方向如图。
(2) 建立剪力、弯矩方程以梁左端A 为的坐标原点,取坐标为的任意横截面的左侧梁段为研究对象。
设截面上的剪力Q () 、弯矩M () 皆为正,如图5-10b 所示。
由平衡方程将(1) 式代入上面两式,解得( 2 )( 3 )(2) 、(3) 两式分别为剪力方程和弯矩方程。
(3) 绘制剪力图、弯矩图由式(2) 可知,剪力图为一直线。
只需算出任意两个截面的剪力值,如A 、B 两截面的剪力,即可作出剪力图,如图5 - 10c 所示。
由式(3) 可知,弯矩图为一抛物线,需要算出多个截面的弯矩值,才能作出曲线。
例如计算下列五个截面的弯矩值:当时, M =0 ;当时,;当时,。
由此作出的弯矩图,如图5-10d 所示。
由剪力图和弯矩图可知,在靠近A 、B 支座的横截面上剪力的绝对值最大,其值为在梁的中央截面上,剪力Q =0 ,弯矩为最大,其值为例5-2 简支梁AB 承受集中力偶M0作用,如图 5 - 11a 所示。
试作梁的剪力图、弯矩图。
图5-11解:(1) 计算支反力由平衡方程分别算得支反力为反力R A的方向如图,R B为负值,表示其方向与图 5 - 11a 中假设的方向相反。
剪力、弯矩方程与剪力、弯矩图
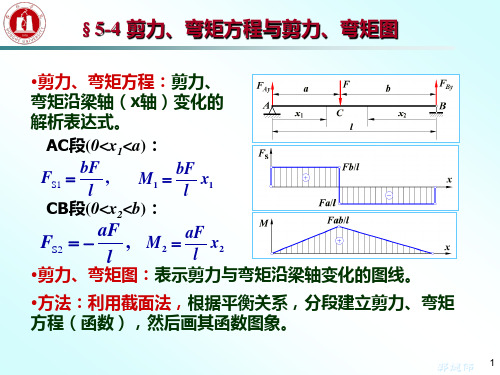
(0 x 1m)
(1m x 2m) (1m x 2m)
FS3 1 2x (2m x 4m)
M3 x2 x 10 (2m x 4m)
22
DE段:
FS4 2kN (4m x 5m)
M4 2x 10 (4m x 5m)
例:试建立图示梁的剪力、弯矩方程,并画剪力、弯矩图。
F1=10kN
q=2kN/m
AB FA
C M0=4kN.m
F2=2kN
DE FD
解: (1) 求支反力,
由梁的平衡: FA=7kN
FD=9kN
1m 1m
2m
1m (2) 建立剪力方程和弯矩
方程(由载荷形式将梁分
AB段:
成四个区域)
M1
FA FS1 0 FS1 FA 7kN
F[(4
x)
A
1]
M3 x FS3
0
q
M
FD
3
F2 D
x2
E
x
10
FS3 1 2x (2m x 4m) M3 x2 x 10 (2m x 4m)
郭德伟 6
§5-4 剪力、弯矩方程与剪力、弯矩图
F1=10kN
q
AB FA
1m
C
M0=4kN.m
1m
7
| FS |max 7kN
(kN.m)
| M |max 8kN m
2
郭德伟 8
§5-4 剪力、弯矩方程与剪力、弯矩图
•剪力、弯矩方程:剪力、 弯矩沿梁轴(x轴)变化的
解析表达式。
AC段(0<x1<a):
《材料力学》课件4-2梁的剪力和弯矩.剪力图和弯矩图

实例1
实例2
实例3
03
剪力图和弯矩图的解读
剪力图和弯矩图的解读方法
截面法
通过在梁上选择若干个截面,分别计算出每个截面的剪力 和弯矩值,然后以这些值为纵坐标,以截面位置为横坐标, 绘制出剪力图和弯矩图。
微分关系法
利用剪力和弯矩的微分关系,通过积分求解出剪力图和弯 矩图。
叠加法
对于分段常数的情况,将每一段的剪力和弯矩分别叠加, 得到整体的剪力图和弯矩图。
在机械工程中,梁的剪力和弯矩分析用于设计和优化各种机 械设备,如起重机、输送机和机床等,以提高设备的性能和 可靠性。
梁的剪力和弯矩在科研中的应用
在科研领域,梁的剪力和弯矩分析也是重要的研究内容之 一。通过深入研究梁的剪力和弯矩的分布规律和影响因素 ,可以揭示材料的力学性能和结构行为的本质。
科研人员利用先进的实验技术和数值模拟方法,对梁的剪 力和弯矩进行深入探索,为材料科学、固体力学和结构工 程等领域的发展提供理论支持和实践指导。
选择截面位置
在梁上选择若干个具有代表性的截面,用于 计算剪力和弯矩。
计算剪力和弯矩
对每个截面进行受力分析,计算出剪力和弯 矩的大小。
绘制剪力图和弯矩图
根据计算结果,绘制出相应的剪力图和弯矩 图。
剪力图和弯矩图的绘制实例
悬臂梁在集中力作用下的 剪力和弯矩图
简支梁在均布载荷作用下 的剪力和弯矩图
简支梁在集中力作用下的 剪力和弯矩图
感谢您的观看
THANKS
截面法
通过在梁上选择若干个截面,计算每个截面的剪 力和弯矩,然后绘制相应的图形。
微元法
将梁分成若干个微元段,对每个微元段进行受力 分析,计算剪力和弯矩,然后绘制图形。
解析法
梁的内力 剪力弯矩方程 剪力弯矩图

(3)若某截面处FS=0
dF S dx
q(x)
dM dx
FS
d M dx
2
2
q(x)
则该截面上M取极值:当q>0, M取到极小值 当q<0, M取到极大值 (4)集中力F作用处,FS突变,跳跃值为F,M有尖点; q>0 q<0
集中力偶M作用处,M突变,跳跃值为M, FS不受影响。 F M
例题
例 题 2
2qa
A
§9 变形体静力学概述 及一般杆件内力分析
qa2 q
B C
解: 1.求约束力
FB q 2 a a 2 qa 3 a qa 2a 7 2 qa ( )
2
D
a
3 2 qa
FB a
a
a 2
FD
F D 4 qa
7 2
qa
1 2
qa ( )
D
FD
FD
F Ax 1 2 2 ( kN )( )
A
FAx
FAy
2m
F Ay 5 3 2 kN ( )
例题
例 题 4
5kN B
§9 变形体静力学概述 及一般杆件内力分析
4kN· m C
2.作内力图 D 3kN 轴力图: AB段 F N 2 kN
1m
1m
(F S )
1 qa
2
2.作内力图
1 2 qa
M
7 2
1 4 qa
2
B
2 qa
2
2qa (M)
qa
8
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5-7.试列出下列梁的画力方程和弯拒方程,并ntuw 力图和弯拒图。
解:首先求出支座反力。
考虑梁的整休平何由 £M fi =0, Fg/ + M<,=o由工M 「0, F 加/-M 严0则距左端为X 的任一横截面上的剪力和 弯葩表达式为:两力方程为常数,表明囲图应是一条平行梁轴线的直线;弯矩方程是X 的一次函 数,表明弯矩图是一条斜直线。
(如图)解:首先求岀支座反力。
考虑梁的平衡由工瓯=0,你小-“£心0 得F RB =討由》%=0,甩./ + *厂=0 得 F RC = - * qi则相应的画力方程和弯犯方程为:©M./1兀⑴=F RA = --—•X剪力图0」25g/8KN.M6.4KN.M弯矩图解:由梁的平求出支座反力:梯=8KN, F42KNAB段作用有均布荷裁,所以AB I?的剪力图为下颐直线,弯矩图为下凹二次I!物线;BC段没有荷教作用,所以BCI3的卿力图为平行梁轴线的水平线段,弯矩图为直线。
在B支座处,卿力图有突变,AB段:心是)心(“)=一处BC段:(*弓)集(小¥-如qiTAB段剪力方程为冷的一次函数,弯矩方程为冷的二次函数,因lit ABH的卿力图为斜直线,弯矩图为二次枢物线;BC段卿力方程为常数,弯拒方程为X2的一次函数,所以BC段勢力图为平行梁轴线的水平线fL弯葩图为斜直线。
(如图)5-9用简便方法画下列各梁的卿力图和弯葩图。
A/ (x2) = -q ・—・ x2(2 ) g=5KN/m Mr =8KN.mF RA4m F RB 2m解:由梁的平求岀支座反力:匚=3.5KN, F KB = 6.5KNAB 与BC 段没有外载作用,所 以AB 、BCB 的勇力图为平行 梁轴线的水平线段,弯矩图为 直线;CD 段作用均布荷载, 所以CD 段的卿力图为下颐直 线,弯拒图为下凹二次拋物 线。
在B 处,剪力图有突变,突变5)反力F RB )的大小;弯矩图有 转折,转折方向习集中力方向 一致。
(如图)F=2K Ng = 4 kN / m值大小等于集中力F的大小;弯矩图有转折,转折方向习集中力方向一致。
(如图)解:ABK作用有均布荷教(方向向下),所KABg的剪力图为下Mi 直线,弯葩图为下凹二次拋物线;BC 段作用有均布荷载(方向向上),所以BC段的剪力图为上偵貞线,弯葩图为5.14试用叠加法画下列各梁的弯拒图。
上(J直Mo( SO图)(1)F=10KN3m 3m 6KN.m(4)F 二0・25ql弯矩图F 二0・25ql0.51 0.51 0.51-< -------- < ------------ ►■<------- ►0.51,°・5/ .「0 51 .^0.125ql20.0625qP弯矩图題里:计尊題題目:试作图所示悬胃梁AB的可力图和弯拒图。
[爾]1、列阿力方程和弯拒方程皿坐廉原点与梁左竭点A对应。
选取血梁左竭虑A为*的什一0(而,如图(a)所示,以该啟面左障梁段上的外力,写良截面上的冏力和弯呃表il it,即可福到梁AB的西力方椁和弯拒方棺为列工)二-P(0 <x<l)Mg 二-& (OH)上而两it后的牯号,表明方程适用围。
由干戲面A,B?t有集中力作用,也具可力为不定讀,第一It的适用围为(° <X<1\由干啟面B有集中力岡作用,叫其弯拒也片不定憤,弟二贰的诚用国(0<x</)关于这个间題,待后而作进一步说明。
2、作啤力图和弯矩图9?力方棺表明,梁各截面上的科力M相等,因lit坍力图陋是一条平打干廉轴的育线。
取肓角坐标系x—兔,同出梁的鸭力图片一水平盲鼓。
S 各HI散面的何力力负値,故画在磺轴下面,血图(b ) Bi示。
弯距方棺表明,弯拒M是*的一次因数,困此弯距图应是一条倾斜直毀。
可以确定其上两点,S = 0 it , M = 0;在nL处(应理舗为*略爪干L处),M = PL O取言怖坐廉系0涮,表示弯拒的级坐标从陶卞刃正,冋出梁的弯拒图,eu @ (C )«示。
由图可见,最大弯拒发牛在固定端B#j|g左的横啟而上,其値片當见冋題體2題里:廿耳起題目:试作图(a)所示筒支梁AB的艸力图和弯矩图。
9【瞬]1、求支用反力由梁的平葡方棺,可求傅支A.B两处的反力为R A=R B=醫2、列舅力疗程和弯拒冇棺取坐廉黒虑与梁左端点A対国。
列出梁AB的坍力方相和弯拒方程为响二"牡二”_旷(0<2)M⑴二R A X-存2 二号x-新(0 g °3、ft舅力图和弯拒图9?力方椁表明,剪力耳是X的一次因散,坍力图应是一条做斜肓找。
S lit ,只更确定其上两点,即可绘出孩梁的卯力图。
在兀二。
处(应理辭片真=-ql巧二--ql尤昭大干0), 2 ;兀二/处(应理餡片*略小干/ ), 2 。
冋岀梁的何力图,血图(b)两示。
由阴力因可见,,该梁负大剪力发生在支疥fl 的柜截而上,其値为弯距方棺表明,弯拒M 是*的二次函数,弯矩图应是一条他物找。
Q 此,只要确定其上三f 点,即可绘111垓梁的弯矩图。
在^ = °5b , M = 0; K X=1x = —I51: , M = o ; fi 2 处,见,垓梁罠大弯拒发生在梁的跨中截面处,s ot a 而上可力为專。
阳见冋體體3 題里:汁第超題目:试作图G)所示商支梁AB 的列力图和弯拒图。
汽3AAA、 、【解]1、求支疥瓦力 由梁的"力平新方程, ^=T^=T2、列9?力方f?和弯矩当作用在梁上的外力不连续时,通阳不能的一个方程描述全梁的聊力(I M = -qlxL--q _ 2 2 2⑵2=v8画出弯拒图, m 图6-1 2(c)障示。
由弯迪图可可求借支ff A,B 两处的反力为或弯矩,必须分段研究。
S 15 M 8中,集中力P 把梁分AC 和CB 两目, 这两段粱的何力方程栩弯矩方椁分别为AC 段:pb巧(心)二匕二丁(0 5 ―)M (xJ 二出x 二丁心(0G]")CB 段:巧亿)二-鸟二・¥@5乙)M (X?)二去B f 1 勺)二—C 1 兀2 ) (@ 兰工2 乞 2)3、作9?力图和弯距图两段粱的科力方棺表明,两段梁的科力图均片水平肓线。
画出梁的卿 力图,规图(b )Bi 示。
由何力图可见,在集中力P 作用的C 处,與左右两剧Pb Pa■ "■ ■横啟面上啣力的数値分别为)和 】,9?力图发生突变■其夷变値等干集中力P 的大爪。
由lit 可福,住集中力作用处列力图发生突变,具突变値 等于孩集中力的大爪。
规果b > a , W M 大剪力发生在AC 段梁的任一啟面上, 其値为两段梁的弯柜方棺表明,两段梁的弯拒图沟力倾斜肓线。
两出梁的弯 粗图,则图(C )两示。
由弯拒图可见,AC 和CB 两段梁的弯畢图两肓线斜率 不同,在C 处附域向卞凸的“尖角”,而坍力图在此处枚变了正、负号。
晟大弯柜发生在集中力P 作用的啟面上,其値为忘 —Pb_ 丁血果a = b, QH 最大弯拒的値为& — PI皿创_ 丁曲见冋朝固4型目 題題3 :or 示 a /\ 图 卄 图矩 和 图 力 B : 的 B 梁支 简pW_L¥【幣]仁求支用反力由梁的弱力平画方程,可求需支A.B两处的反力片心=-怎=牛2、列9?力方f?和弯拒方相集中力IS Me把梁分成AC和CB两段,这两段梁的珂力方程和弯矩方材AC 15 :巧(心)"盯牛(0兰可0)MOJ *严牛*0詁J)CB段:巧亿)"严学</))二_ 乳2 )二Y Q _ 兀2)(a U 花 N)3、ft舅力图和弯柜图在集中力凰作用处的左、右梁段上,剪力方程相同,全梁冏力图为一水平言线。
冋出梁的9?力图,如图(b)除示示。
由坍力图可见,在集中力IS 作用处,冏力图并不发生突变,即集中力偶不剧咱坍力图。
两段梁的弯距方程表明,两段梁的弯拒图沟力顷制直线。
画出梁的弯矩图,ai图(C)障示。
由弯矩图可见,在集中力偶八作用曲C5H 其左右两M€a - M e bn R a面上弯拒的数is分制片i和i,弯拒图发生突变,其突变闻等于集中力IS Me的大小。
由lit可福,在集中力偶作用处弯拒图发生突变,其突变值等干孩集中力偶的大丿h。
如果b>a,则最大弯矩发生在集中力僻八作用处右剧横啟面上,其值为題里:计其題題目:试作图示笛支梁的可力图和弯拒图。
【解]1 求支用反力由梁的"力平働方程可知,支A.B的反力为R A = 29KN R£ =-\5KN2、列9?力方f?相弯拒方困当粱上商我不连镇,9?力或弯拒不能用一个坏一的函数式表必时,必须什段列出何力方程和弯拒方棺。
通阳分段是以集中力、集中力偶和分布荷我的起虑与终点分界。
因此,孩简支梁应分为AC,CD ft DB E段,什制列岀坍力方相和寺拒方程。
AC段:巴(xj二R A -阿二29-12X](0 <Xj < 3)M(X])==尺卫& - = 29兀](On】< 3)CD段:F s亿)二匕一3g 二29_ 36 二-7.07(3<x2 <4.5)M(小 3 - 知见-1.5)=29J2-3X12(X2 -1.5)=-7X2+54 (3<X2 <4.5)DB段:爲(心)二-Rg 二-乃疋N(4 为<JC3 <6)"(心)二&(6_x3) = 15X(6-J3)=90-15X3(4.5 <x5 <6)3、作舅力图fll弯柜图按上述阴力方棺和弯砸方杓,画出剪力图和弯犯图,如图(b)、(c)两不0在画AC段弯拒因时,由干弯距方椁是二次函散,弯拒图应是一条他期线,至少侖熨确定其上三个戍,才可绘出孩梁的弯拒图。
g = ° 5t ,M = 0;在x= 3m处,M = 33kN. m。
在坍力凤为零处*=2.4m,该虑处弯矩^=29x2.4-6x2.42= 35KH m o用光滑曲线连接逹三f虑即可用AC目的弯距M图。
5图(c )示。
