北邮研究生矩阵论课后题作业标准答案
研究生矩阵理论课后答案4,5章习题
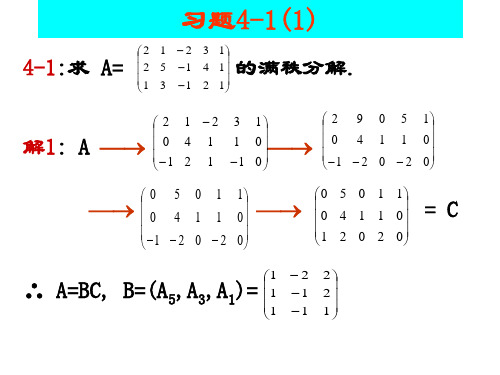
2 1 − 2 3 1 0 4 1 1 0 −1 2 1 −1 0
0 5 0 1 1 0 4 1 1 0 −1 −2 0 −2 0
→
1 1 1 −2 −1 −1
0 5 0 1 1 0 4 1 1 0 1 2 0 2 0
同一向量的三种范数之间的大小关系 习题#5-4:对n维线性空间的任意向量x成 习题#5维线性空间的任意向量x #5
‖x‖∞ ≤‖x‖2 ≤‖x‖1 ≤ n‖x‖∞ ≤ n‖x‖2 ≤ n‖x‖1 ≤ n2‖x‖∞ ≤ …
立
证: |,…,|x ‖x‖∞= max{|x1|, ,|xn|} ≤(Σi=1n|xi|2)1/2 = ‖x‖2 |+…+|x ≤((|x1|+ +|xn|)2)1/2 = ‖x‖1 |,…,|x ≤ n max{|x1|, ,|xn|} = n‖x‖∞
习题#5是正定矩阵,x ,x∈ 习题#5-6A∈Cn×n是正定矩阵,x∈Cn #5
是向量范数. •证明:‖x‖=(x*Ax)1/2 是向量范数. 证明:‖x‖=(x
解1:因A是正定Hermite矩阵A,故存在可逆矩阵B 是正定Hermite矩阵A,故存在可逆矩阵B Hermite矩阵A,故存在可逆矩阵 使得A=B B.则 的上述表示式可写为: 使得A=B*B.则x的上述表示式可写为: (Bx)) ‖x‖=(x*Ax)1/2 =((Bx)*(Bx))1/2 =‖Bx‖2 其中‖‖ 是向量2 范数.再注意可逆矩阵B 其中‖‖2 是向量2-范数.再注意可逆矩阵B的性 Bx=0,即可直接推出非负性 即可直接推出非负性. 质:x=0 ⇔ Bx=0,即可直接推出非负性. ‖kx‖=‖B(kx)‖2=|k|‖Bx‖2=|k|‖x‖ 推出齐次性;三角不等式则由下式推出: 推出齐次性;三角不等式则由下式推出: ‖x+y‖=‖B(x+y)‖2≤‖Bx‖2+‖By‖2
矩阵论课后题答案(研究生用书)改

⎞ ⎠
⎠
A
P
⎞ ⎠
⎠ ⎞
P
⎠
− 1
A
⎠
A
J
P
P
A P
J
A f f A f E E A A A A
⎞ ⎠
A
A
A
A
E
A
E
⎞
A
A A E
A
⎠
f A
A
A
A
A
A
E
A
E
E
A A
⎠
⎞
A A A
A
A
E
2
f
E
A
f A
⎞ ⎠
A
A A A E A
A
E
A
A
⎠ ⎞
E
A
E
⎠
⎞
⎞ ⎠
f A E
E
⎞
A
A
E
⎞ ⎠
f A E E E
0 0
x
x
x
A A
E
E E A A A A A E
⎞ ⎠
j
E
E A A A A
A
E E
A E
E A
A
A
E A
A
A
F
j
F
j
j
A
E
A
A
A A E A g A E A E A E A g A A E A E E A A A E
A
A
A
F
A
A
H
A
A A A A
F
A
H
A
A
A
A
A
A
F
北京邮电大学《矩阵论》2015-2016-1-期末试卷及答案精选全文

可编辑修改精选全文完整版北京邮电大学2015——2016学年第一学期《矩阵论》期末考试试题评分参考标准一、(10分)设 x 1,x 2 是线性空间 V 的一组基,线性变换 T 在这组基下的矩阵为 A =[21−10] 。
y 1,y 2 是另一组基,且 (y 1,y 2)=(x 1,x 2) [1−1−12] 。
(1)求 T 在 y 1,y 2 下的矩阵 B ;(2) 计算 A 100 。
解:(1)B =[1−1−12]−1A [1−1−12]=[1101]。
(5分) (2)A 100=[1−1−12]B 100[1−1−12]−1A =[101100−100−99]。
(5分)二、(10分)计算 ln A ,其中 A =[e1e 1e 1e ] 。
解:ln A =[11/e −1/2e 21/3e 311/e −1/2e 211/e 1]。
(10分)三、(15分) 设 x =[512] 。
(1)计算Givens 变换 G 1 使得 G 1x =[a 0] ; (2)计算Givens 变换 G 2 使得 G 2x =b [11] 。
解:(1)G 1=[5/1312/13−12/135/13],a =13,或G 1=[−5/13−12/1312/13−5/13],a =−13。
(7分) (2)G 2=[17/13√27/13√2−7/13√217/13√2],b =13√2/2,或G 2=[−17/13√2−7/13√27/13√2−17/13√2],b =−13√2/2。
(8分)四、(10分)设 A =[−1−600−630000 00344−3] ,计算 ‖A ‖1,‖A ‖2,‖A ‖∞,‖A ‖F 。
解:‖A ‖1=9,‖A ‖2=1+2√10,‖A ‖∞=9,‖A ‖F =2√33。
(10分)五、(10分)设矩阵A ∈R n×n 满足 A 3=A ,证明存在非奇异矩阵 X 使得 X −1AX =[I r −I s0t ]。
研究生矩阵理论课后答案第6-7章

求矩阵的Jordan标准形与变换矩阵 求矩阵的Jordan标准形与变换矩阵 Jordan
由行列式因子定不变因子和初等因子:( :(参看 ①由行列式因子定不变因子和初等因子:(参看 0 λ − 2 0 第二章有关定义及结果). ).如 第二章有关定义及结果).如 λE-A= −1 λ −1 −1 )=λ行列式因子:D 行列式因子:D1(λ)=1; D2(λ)=λ-2;
第六章 矩阵函数
•矩阵函数一般定义:矩阵函数是从Cm×n到Cu×v的一 矩阵函数一般定义:矩阵函数是从C 个对应规则f:C 使对每个x 个对应规则f:Cm×n→Cu×v,使对每个x∈Cm×n,都 对应于唯一 f(x)∈ 唯一的 对应于唯一的f(x)∈Cu×v. 例如:det:C ,det(A)∈ 例如:det:Cn×n→C1×1,∀A∈Cn×n,det(A)∈C1×1; ,f(A)=2Af:Cn×n→Cn×n,∀A∈Cn×n,f(A)=2A-E∈Cn×n. 矩阵函数的概念十分广泛, •矩阵函数的概念十分广泛,其应用也相应地十分 广泛. 广泛. 我们仅限于讨论从C •我们仅限于讨论从Cn×n到自身的函数 f:Cn×n→Cn×n. 特别更限于最简单的矩阵多项式函数和由矩阵 矩阵多项式函数和由 特别更限于最简单的矩阵多项式函数和由矩阵 幂级数定义的矩阵函数. 幂级数定义的矩阵函数.
0 1 1 1 0 0 1 0 −1
. P -1=
0 1 0 1 −1 1 0 1 − 1
2 0 0 2 0 0 0 A − 2E = 1 1 1 − 2 = 1 −1 1 1 −1 3 2 1 −1 1 0 0 x = 1 , ( A − 2E)x = 1 1 1 1 0 z = 0 , ( A − 2E)z = 1 −1 1 0 00 −1 1 1 = 0 −1 1 1 0 0 1 −1 1 0 = 0 −1 1 −1
研究生矩阵论课后习题答案(全)习题一

i =1 j =1 n n
成的线性空间的一组基,该线性空间的维数是
n(n + 1) . 2
② 令 Gij = Eij − E ji (i < j ) , 则 Gij 是 反 对 称 矩 阵 , 易 证
解
(1)设 Eij 是第 i 行第 j 列的元素为 1 而其余元素全为 0 的 n 阶方阵.
①令 Fij = ⎨
⎧ Eii , i = j , 则 Fij 是对称矩阵, 易证 F11 ,L , F1n , F22 , L , F2 n , ⎩ Eij + E ji , i ≠ j
L , Fnn 线 性 无 关 , 且 对 任 意 n 阶 对 称 矩 阵 A = (aij ) n×n , 其 中 aij = a ji , 有
1(1 − 1) 2 a ) = ( a, b) 2
= k o ( a, b) + l o ( a, b) = k o α + +l o α ;
⑧ k o (α ⊕ β ) = k o (a + c, b + d + ac)
k (k − 1) (a + c) 2 ) 2 k (k − 1) 2 k (k − 1) 2 = (ka + kb, (kb + a ) + (kd + c ) + (ka)(kc)) 2 2 k (k − 1) 2 k (k − 1) 2 = (ka, kb + a ) ⊕ (kc, kd + c ) 2 2 = (k (a + b), k (b + d + ac) +
矩阵论课后参考答案-第一章.doc

其基为竺12个心〃阶的矩阵, 2_1 0 0 00 0 0 00 10 010 0 0J.八八 / 1、 / c\ \ (〃一 1)((〃 一 1) +I) 〃(〃一1)2其基为些12个〃x 〃阶的矩阵,故基可写为矩阵论课后参考答案:习题1.12(1)解:由定义知dim(C'g) = 〃5故可知其基为5个〃冰〃阶矩阵,简单基记为在矩阵上的某一元素位置上为1,其他元素为0 ,如下1 0 0 0' 0 0 0 00 0 0 0' 0 10 0(2)解:对约束A ,= A 分析可知,其为一个上下对称的矩阵(对称阵),则其维数为dim(V) = n + (/? -1) H -- 1 =°故基可写为 (3)解:同上理,对AW"分析可知其为一个上下成负对称的矩阵,且对角元全为0,则其维数为2k、— kf — 2/| - /9= 0 2k] — k~> + " +,= 0 k、—加—3/] = 0 k2-l~-7l2=0k、——,故有h2=4Z2 I】=—3/2解:由题可得+ VK = span(^, , /?2)不难看出其秩为3,则dim(W|+W2)= 3设工即",则存在"以有x— A]。
】+ = I、。
、+1、即尤=切]+ k2a2 = l2(4a2一%) =,2(-5,2,3,4)所以dim(W%) = l(先补充定理:定理:设n元齐次线性方程组的系数矩阵A的秩r(A) = r<n,则齐次线性方程组的基础解析存在,并且基础解系所含线性无关的解向量的个数等于〃-「)证:1)对任意的B E %""则有AB = O且(A-/)B = O成立,故B = 0所以X"={0} O2)明显明㊉岭uF〃3)对于%来说,X为A的一个基础解系,不妨设dim(A) = r ,则有dim(%) = n-尸式 1 而由约束条件f=A知3故有5A (A-I ) = O其中A -/为A 的一个基础解系,则有dim (A-/) = n-/*故岭的秩为dim (岭)= n-dim (A-/) = r 式2故由式 1 及式 2 可知:dim (V ;) + dim (K ) = n = dim (F ,?) 综上则有P l =V }®V 2证毕习题1.2解:由题可知0,%,%与〃]刀2,〃3时空间瑚3)的两组基,则存在一个过渡矩阵c 使得引入£(尸)的一组简单基 环再2,耳3-------------------------- 2(“I ,%,%)=(芯11, 芯12' E 【3)G = (%,%,%)《[G8 -16 91 3 2-6 7 -3 ,C 2-2 -1 1 7-13 71 2 2/(。
研究生 矩阵论 课后答案
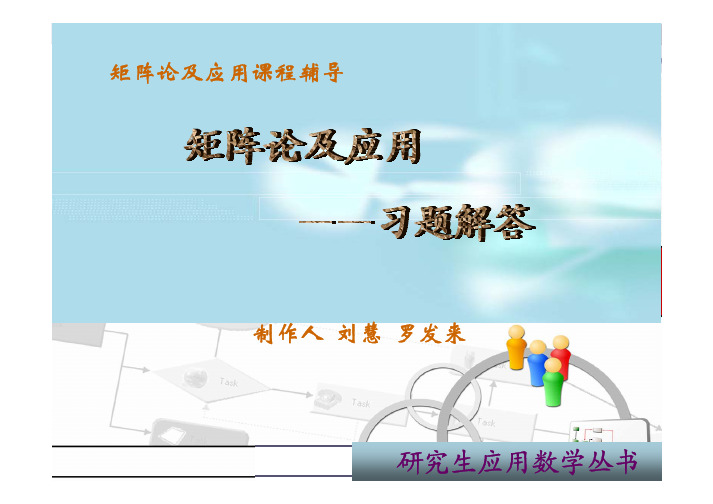
|
xk
|2
)
1 2
是范数.
k =1
(2)证明函数 || x ||∞ = max{| x1 |,| x2 |,...,| xn |}是范数.
2.设
x∈R2,
A=
⎛4 ⎜⎝1
1⎞ 4⎟⎠
,请画出由不等式||
x
||
A
≤
1决定的x的全
体所对应的几何图形.
3.在平面 R2中将一个棍子的一端放在原点,另一端放
生成子空间V,求V的正交补空间V ⊥.
15.(MATLAB)将以下向量组正交化.
(1) x1 = (1,1,1)T , x2 = (1,1, 0)T , x3 = (1, −1, 2);T
(2) f (t) = 1, g(t) = t, h(t) = t2是[0,1]上的多项式空间
的基,并且定义(
f
9.把下面矩阵A对应的λ -矩阵化为Smith标准形,并且写
出与A相似的Jordan标准形.
⎛1 −1 2 ⎞
(1)
⎜ ⎜
3
−3
6
⎟ ⎟
⎜⎝ 2 − 2 4⎟⎠
⎛ −4 2 10⎞
(2)
⎜ ⎜⎜⎝
−4 −3
3 1
7 7
⎟ ⎟⎟⎠
⎧ dx1
⎪ ⎪
dt
=
3x1
+ 8x3
10.(MATLAB)求解微分方程:
α3 = (0,1,1)T 的矩阵为: ⎡ 1
A=⎢ 1 ⎢⎣−1
0 1⎤ 1 0⎥ 2 1⎥⎦
求在基e1 = (1,0,0)T ,e2 = (0,1,0)T ,e3 = (0,0,1)T下的矩阵.
10.设S = {ε1,ε2 ,ε3,ε4}是四维线性空间V的一个基,已知
矩阵论课后习题答案

第一章 线性空间与线性映射 习题一 (43-45)1、(1)对于V y x ∈∀,,x y x y x y x y y x y x y x y x +=⎪⎪⎭⎫⎝⎛+++=⎪⎪⎭⎫ ⎝⎛+++=+112211112211;(2)对于V z y x ∈∀,,,⎪⎪⎭⎫ ⎝⎛+++++++=⎪⎪⎭⎫⎝⎛+++++++=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+++=++))()(1111112221111112112211121112211z y z x y x z y x z y x y x z z y x y x z y x z z y x y x y x z y x ,⎪⎪⎭⎫ ⎝⎛+++++++=⎪⎪⎭⎫⎝⎛+++++++=⎪⎪⎭⎫ ⎝⎛++++⎪⎪⎭⎫ ⎝⎛=++))()(1111112221111111122211111221121z y z x y x z y x z y x z y x z y z y x z y x z y z y z y x x z y x ,即)()(z y x z y x ++=++。
(3)对于⎪⎪⎭⎫⎝⎛=00θ和V x ∈∀,显然x x x x x x x =⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛+++=+21121000θ; (4)对于V x ∈∀,令⎪⎪⎭⎫⎝⎛--=2211x x x y , 则θ=⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛--+-=⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎭⎫ ⎝⎛=+0021221211221121x x x x x x x x x x x y x ,即x y -=。
(5)对于R ∈∀μλ,和V x ∈∀,有x x x x x x x x x x x x x x x x x x x x x x x )()()]()[(21)()()2(21)()()]1()1([21)1(21)1(2121212212122212121221121212121μλμλμλμλμλμλμλμλμλμλμλλμμμλλμλμλμμμμλλλλμλ+=⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎪⎭⎫⎝⎛+-++++=⎪⎪⎪⎭⎫ ⎝⎛--+++++=⎪⎪⎪⎭⎫ ⎝⎛+-+-+++=⎪⎪⎪⎭⎫⎝⎛-++⎪⎪⎪⎭⎫ ⎝⎛-+=+(6)对于R ∈∀λ和V y x ∈∀,,有⎪⎪⎪⎭⎫⎝⎛+-++++=⎪⎪⎭⎫ ⎝⎛+++=+211112211112211))(1(21)()()(y x y x y x y x y x y x y x y x λλλλλλ, ⎪⎪⎪⎭⎫ ⎝⎛+-++++=⎪⎪⎪⎭⎫ ⎝⎛-+-++-++++=⎪⎪⎪⎭⎫ ⎝⎛+-++-++=⎪⎪⎪⎭⎫⎝⎛-++⎪⎪⎪⎭⎫ ⎝⎛-+=+211112211112212211122111122122121121212121))(1(21)()()1(21)1(21)()1(21)1(21)1(21)1(21y x y x y x y x y x y y x y x y x y x y x y y x x y x y y y x x x y x λλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλ,即y x y x λλλ+=+)(。
