复合命题及其推理文档
合集下载
第五章 复合命题及其推理1-3

例如:“矛盾既有同一性,又有斗争性。” “生活是美好的,同时也是艰辛的。”
第二节 联言命题
2、联言命题的结构 联言支、联结项
联言支可以是两个或两个以上,联结项一般应化 归为“并且” 例如:“矛盾既有同一性,又有斗争性”化归后为 联结项 “矛盾有同一性并且矛盾有斗争性” 联言支
第二节 联言命题
3、联言命题的公式
(2)不相容选言命题的真值表
p 1 1 0 0
q 1 0 1 0
· p∨q 0 1 1 0
第四章 复合命题
第三节 选言命题 四、选言命题方面的逻辑错误 1、遗漏选言支
例如:“一个人的血型要么是A,要么是B, 要么是O型。”
2、选言支重叠
例如:“可以预料,他这次考察要么不了了之,要么半 途而废。” “报考大学时,考生或者选择艺术类、或者选择 理工类、或者选择文史类,或者选择电子类。”
例如:“从外表看,这群人或者是教师或者是干部” 在这群人既不是“教师”也不是“干部”的情况 下,判断为假。
第四章 复合命题
第三节 选言命题 二、相容选言命题 5、相容选言命题的逻辑值
(2)相容选言命题的真值表
p 1 1 0 0
q 1 0 1 0
p∨q 1 1 1 0
第四章 复合命题
第三节 选言命题 三、不相容选言命题 1、不相容选言命题的定义 不相容选言命题是断定若干事物情 况至少并且只能有一个存在的选言命题
F T T
F T F F F T F F F
F
元素表
p T T F F q T F T F判断表p∧q TF F F第四章 复合命题
第二节 联言命题 一、联言命题概述 二、联言命题的逻辑值 三、联言命题方面的逻辑错误
第四章 复合命题
第二节 联言命题
2、联言命题的结构 联言支、联结项
联言支可以是两个或两个以上,联结项一般应化 归为“并且” 例如:“矛盾既有同一性,又有斗争性”化归后为 联结项 “矛盾有同一性并且矛盾有斗争性” 联言支
第二节 联言命题
3、联言命题的公式
(2)不相容选言命题的真值表
p 1 1 0 0
q 1 0 1 0
· p∨q 0 1 1 0
第四章 复合命题
第三节 选言命题 四、选言命题方面的逻辑错误 1、遗漏选言支
例如:“一个人的血型要么是A,要么是B, 要么是O型。”
2、选言支重叠
例如:“可以预料,他这次考察要么不了了之,要么半 途而废。” “报考大学时,考生或者选择艺术类、或者选择 理工类、或者选择文史类,或者选择电子类。”
例如:“从外表看,这群人或者是教师或者是干部” 在这群人既不是“教师”也不是“干部”的情况 下,判断为假。
第四章 复合命题
第三节 选言命题 二、相容选言命题 5、相容选言命题的逻辑值
(2)相容选言命题的真值表
p 1 1 0 0
q 1 0 1 0
p∨q 1 1 1 0
第四章 复合命题
第三节 选言命题 三、不相容选言命题 1、不相容选言命题的定义 不相容选言命题是断定若干事物情 况至少并且只能有一个存在的选言命题
F T T
F T F F F T F F F
F
元素表
p T T F F q T F T F判断表p∧q TF F F第四章 复合命题
第二节 联言命题 一、联言命题概述 二、联言命题的逻辑值 三、联言命题方面的逻辑错误
第四章 复合命题
第六讲 复合命题及其推理(分析“命题”文档)共118张PPT

• 三 复合判断的基本类型
• 根据联结词,分为四种基本类型:联言判断、选言判 断(相容的、不相容的)、假言判断(充分条件的、 必要条件的和充分必要条件的)和负判断。
• 四 复合判断的推理及其种类
• 前提或结论中有复合判断并且是根据复合判断的 逻辑性质进行推演的演绎推理就是复合判断的推 理。复合推理基本类型有联言推理、选言推理、 假言推理和负判断推理。另外,还有一些包含几 种复合判断的比较复杂的推理,如假言选言推理 (二难推理)、假言联言推理等。
∨ 表示。
• 4,“如果……那么……”,如果p,那么q,用蕴涵符号
“→”表示。 • 5“只有……才……”,只有p才q,用逆蕴涵符号“←”表示。
• 6,“……当且仅当……”,q当且仅当p,用等值符号“←→”
表示。
• 7,“并非”,并非p,用否定符号“¬”表示。
• 其中,∧、∨、→、←→、¬是基本命题联结词。
• 人生要么奋力拼搏,要么激流勇退。
• 他在赛场上的失误或者是因为准备不够充分,或者是因为太 紧张。
• 支命题称为选言支。
• 用p、q、r、s等字母表示。至少包括两选言 支。
• 表示几种可能的事物情况有一种存在的关联词叫
选言联结词,选言联结词有“或者……或者”、
“要么……要么”两种。
• 分为相容选言命题和不相容选言命题。
• 第二,肯定一个选言支,就要否定其它的选言支。 两个有效推理式,即“否定肯定式”和“肯定否定 式”。
• 这幅字要么是蔡襄的作品,要么是米芾的作品
•
这幅字不是米芾的作品
• 所以,这幅字是蔡襄的作品
• 这些人要么是便衣警察,要么是商场工作人员
•
这些人是便衣警察
•
第五章 复合命题及其推理

“只有努力学习,才能取得好成绩。”可转换为 “只有没有取得好成绩,才没有努力学习。”
要领 否定式:调换否定前后件,不换联结词。
四、充分条件、必要条件假言命题和选言命题 间的转换
联言命题一般用并列、递进、转折、顺承 关系的复句表达,有时也用单句。 郭沫若是历史学家和文学家。 苏步青和华罗庚都是数学家。 和平和发展是中印两国人民的共同愿望。
2、构成
①联言支:即构成联言命题的支命题。 ②联言联项:即联结联言肢的联结词 二肢联言命题的逻辑形式:p并且q或 p∧q 联项有时可以省略
2、构成 ①选言支:即构成选言命题的支命题。 ②选言联项:即联结选言支并确定选言支之 间关系的联结词。 一个人的死,或重于泰山,或轻于鸿毛。 不是鱼死,就是网破。 他也许是数学家,也许是哲学家。
(二)选言命题的种类
1、相容选言命题 ①什么是相容选言命题 是反映若干可能的对象情况中至少有一种 存在的复合命题。 这场球赛失败的原因或者是队员技术水 平不高,或者是队员之间配合不好。 这场战争的失败或因兵力弱,或因指挥 失误。
二、假言命题的种类
(一)充分条件假言命题 1、什么是充分条件和充分条件假言命题 ①什么是充分条件 在情况p和q之间,有p必有q;无p未 必无q,这时p是q的充分条件。 A、p:摩擦 q:生热 B、p:x等于2 q:x的平方等于4 ◆“有之必然,无之未必不然”的条 件。
②什么是充分条件假言命题
就是反映一事物情况存在是另一事物 情况存在的充分条件的假言命题。
(二)复合命题推理的种类 联言推理、选言推理、假言推理和负 命题等值关系推理四种基本类型。
第二节
联言命题和选言命题
一、联言命题 (一)联言命题及其构成 1、什么是联言命题 是反映若干事物情况同时存在的复合 命题。
第五章 复合命题及其推理(上)

第三步,判定∶①与②是矛盾关系;①与③是不可同假但可同 真关系;②与③是蕴涵关系。
B.用真值表确定若干命题是否一致。 例如∶用真值表确定是否存在一种方案使①②③④ 同时能成立,①如果王强出国,那么李明出国;②如 果李明不出国,那么王强出国;③王强或者李明不出 国;④要么王强要么李明出国。
解题∶设王强出国为p,李明出国为q。则①为p→q, ②为﹁q→p,③为﹁ p∨﹁q,④为p∨·q。列表如下∶ p q ﹁p ﹁q p→q ﹁q→p ﹁ p∨﹁q p∨·q T T F F T F T F F F T T F T F T T F T T T T T F F T T Tp←q)↔(q→p); (p←q)↔(﹁p→﹁q); (p→q)↔(q←p)。
(2)间接的纯假言推理 如∶(1)如果要实现四个现代化,那么就要有大批科技人才;
如果就要有大批科技人才,那就必须发展高等教育; 如果要实现四个现代化,那就必须发展高等教育。 (2)只有确立远大志向,才能不畏艰难险阻; 只有不畏艰难险阻,才能不断攀登科学高峰; 如果不能确立远大志向,就不能不断攀登科学高峰。
三、复合命题的判定方法—真值表方法 复合命题的判定方法
1.真值形式
真值联结词是指只反映复合命题与肢命题之间真假关系的逻 真值联结词 辑联结词,通常有五个:﹁(否定)∧(合取)∨(析取)→ 否定) 合取) 析取) 蕴涵) 等值)。 (蕴涵)↔(等值)。 真值表就是包含命题变项和真值联结词,准确地定义、直观 真值表 地刻画真值联结词所包含的真假关系的图表。命题逻辑的五个 基本的真值联结词可用真值表作如下定义:
间接纯假言推理的有效式有如下几种:
p→q p→q p←q p←q q→r q←r q←r q→r p→r ﹁r→﹁p ﹁p→﹁r r→p (p→q)∧(q→r)→(p→r); (p→q)∧(q→r)→(﹁r→﹁p) ; (p←q)∧(q←r)→(﹁p→﹁r); (p←q)∧(q←r)→(r→p) 。
逻辑学·第5章 复合命题及其推理

在日常语言中,表达联言判断的语句也常采用
合并或省略形式。
例如:“你我都是可怜人。” “他分不清是非。” “我起了床,叠了被。”
三、联言命题的逻辑值
1、联言命题的逻辑性质(共存性)
一个联言命题真,当且仅当其联言支都真;
如果联言支有假,则联言命题为假。
例如:“矛盾既有同一性,又有斗争性”
如果并且只有“同一性”和“斗争性”都存 在着,这一判断才是真的。
定义:充分条件假言命题是断定一事物情况存在,
另一事物情况就存在的假言判断。 (前件是后件的充分条件)
例如:“如果发生摩擦,物体就会生热”
“如果天下雨,那么路面湿”
联结词的语言表达: 在日常语言中,应当化归为“如果…那么…” 的语言形式有: “假使…就…” “倘若…则…” “只要…就…” “要是…就…” “当…便…” 等
例如:“他又肥胖又消瘦” “他的作品既是长篇小说又是短篇小说”
第三节 选言命题及其推理
一、选言命题概述
1、选言命题的定义
选言命题是反映若干对象情况至少有一种情况 存在或只能有一个情况存在的命题。 “析取关系”
例如:“小张学习成绩差或者因为不够努力或者因 为方法不对。”
选言命题的构成:
支命题 联结词
第二节 联言命题及其推理
一、联言命题的定义 联言命题是反映若干对象情况共同存在命题。
联言命题的基本特性在于对象情况的共存性。
例如:“矛盾既有同一性,又有斗争性”
联言命题的结构: 联言支、联结项 联言支可以是两个或两个以上, 联结项一般应化归为“并且”
例如:“矛盾既有同一性,又有斗争性”化归后为 联结项 “矛盾有同一性并且矛盾有斗争性” 联言支
联言命题的公式: p并且q 或 p∧q
复合命题及其推理
第二联 言肢q
现代逻辑刻画的形式
p
∧
q
以“并且”作为联言联结词的代表 ∧是合取词,读作“并且” 。 p ∧
q 称为合取式。
真值
[1]事物是普遍联系的 (真) 不断发展的 。(真) 、 [2]事物是普遍联系的 (真) 静止不变的 。 、 (假) (假) 不断发展的。(真) [3]事物是彼此孤立的 、 [4]事物是彼此孤立的 、 (假) 静止不变的。 (假) 联言命题的真值可概括为:肢命题都真才真 现代逻辑合取式真值表为: p T F F q F T F p ∧ q T F F F 真 假 假 假
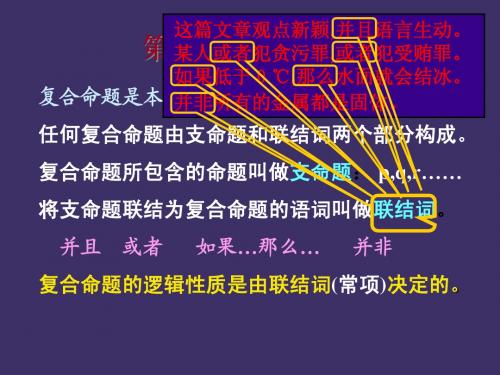
这篇文章观点新颖,并且语言生动。 第四章 命题逻辑 某人或者犯贪污罪,或者犯受贿罪。 如果低于0℃,那么水面就会结冰。 复合命题是本身包含其他命题的命题。 并非所有的金属都是固体。
任何复合命题由支命题和联结词两个部分构成。 复合命题所包含的命题叫做支命题: p,q,r…… 将支命题联结为复合命题的语词叫做联结词。 并且 或者 如果…那么… 并非
··
·
·
p
T T T T F F
q
T T F F T T
r
T F T F T F
p∨q
F F T T T T
·
(p ∨ q) ∨ r
T F F T F T
· ·
p∨q∨r
F F F T F T
··
F
F
F
F
T
F
F
F
T
F
T
F
选言推理
这里的选言推理指选言直言推理,即大前提是选言命 题,小前提是对选言肢的肯定或否定(直言命题),并 根据选言联结词的逻辑性质进行推导的推理。 例 一个演绎推理不正确,或者是前提虚假,或者是形式 无效,这个不正确的演绎推理前提不是虚假的,所以,它的 形式是无效的。 相容选言推理 选言 推理 不相容选言推理 选言 推理 肯定否定式选言推理
复合命题及其推理

“如果我有一千万,我就能买一栋房子。
万吗?没有。
然没有房子。
翅膀,我就能飞。
吗?没有。
没办法飞。
个太平洋的水倒出,也浇不熄我对你爱情的火。
洋的水全部倒得出吗?不行。
不爱你。”
“如果我还有一天寿命,那天我要做你女友。
一天的命吗?……没有。
很可惜。我今生仍然不是你的女友。
有翅膀,我要从天堂飞下来看你。
P
q
P q
T
T
T
T
F
T
F
T
F
F
F
T
真值:前(件)假而后(件)真,则 假 前(件)真,或后(件)假,则 真
充分必要条件假言命题的概念
定义:反映一事物情况是另一事物情况的存在的充分且必要条件命题 有p必有q,无p必无q(P等值于q)
充分必要条件假言命题的公式表示
结构:如果p,那么q,并且只有p,才q 或 当且仅当p才q p q “ 等值” 自然语句:当且仅当;如果,则;如果不,则不
4 充分条件假言命题 ¬(p q) (p∧¬q )
¬(p q) ( ¬p∧q )
必要条件假言命题
1
¬(¬ p) p
负命题的负命题推理
3
充要条件假言命题负命题推理
¬(p q)(p∧¬ q )∨(¬p∧q )
2
三、负命题的等值命题
前提为负命题,结论为其等值命题 选言可以转化为假言:p∨q=﹁p→q;p→q=﹁p∨q
(p q) (q p )
通过变换前提中假言命题前后件的位置,推出一个假言命题作结论的推理。
三、假言易位推理
四、假言联锁推理
两个以上假言命题作前提 特点:前提中,前一个假言命题的后件和后一个假言命题的前件相同,由几个假言命题的联结而推出结论 (一)充分条件假言联锁推理 肯定式(p q )∧(q r )(p r) 否定式(p q)∧(q r )(¬ r ¬ p) (二)必要条件假言联锁推理 肯定式(p q)∧(q r )(r p) 否定式(p q)∧(q r)(¬ p ¬ r)
复合命题及其推理上

第二节 联言命题及其有效推理
在现代逻辑中,通常用真值表来 定义命题联结词的逻辑含义。
真值表:用来显示复合命题在其 变项的各种真假组合下的真假情 况的图表。其中,用“T(true)” 代表真,“F(false)”代表假; 也可以用“1”代表真,“0”代 表假。在真值表中,有n个不同的 命题变项,就会有2n组真假搭配 的组合,故要列出2n行真假组合。
第一节 复合命题和命题联结词
支命题:复合命题所包含的其他命题。 命题联结词:将支命题连接成为复合命题的语词。 复合命题的支命题可以是简单命题,也可以是复合命题。 如果合同有效,那么甲方和乙方就应遵守合同。 复合命题的基本形式不止一种。不同种类的复合命题逻辑特性不同,由其组
成的有效的推理形式也不一样。
从逻辑的角度看,语言联结词主要存在着两个问题: 首先,不精确。
4. 明天或者刮风或者下雨。 5. 德国队或者小组出线,或者不能小组出线。
识别上述语言联结词(或者……或者……)表达的两种情况究竟是相容 的还是不相容的,需要相关背景知识,超出了逻辑学的范围。
第一节 复合命题和命题联结词
其次,负载了许多非逻辑的内容。
第五章 复合命题及其推理(上)
击此处添加文本具体内容,简明扼要地阐述你的观点
第一节 复合命题和命题联结词
一.复合命题的逻辑性质 复合命题:包含其他命题的命题。
1. 所有金属都是固体。 2. “所有金属都是固体”不合乎事实。
① 复合命题——命题变项——“所有金属都是固体” ② 简单命题——词项(概念)变项——“金属”、“固体”
三.▪ 否定肯定式
○p q
● p
或
○q
pq q
p
第三节 选言命题及其有效推理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
必要条件假言命题的逻辑性质是:只有当其前件假而后件真时,该假言命题是假的;在其余情况下,它都是真的。
Truth Table
3、充要条件假言命题
充分必要条件假言命题是指前件是后件的充分必要条件的假言命题。
充分必要条件(Sufficient and necessary condition)就是同时具有充分条件和必要条件的含义,即:
不相容选言命题的逻辑性质
不相容选言命题的逻辑性质是:当选言肢仅有一真时,它是真的;当选言肢都真或都假时,它是假的。
■正确运用选言命题
⒈关于选言肢应当穷尽的问题
选言肢穷尽的选言命题必真,选言肢不穷尽的可能假。
⒉关于区分两种选言命题的问题
肢命题之间的关系逻辑涵义不同,选择适当的逻辑联结词。
⒊关于区分相容选言命题与联言命题的问题
三、一般复合命题及其真值形式
•真值联结词和真值形式
•一般复合命题及其真值形式
•真值形式的判断:真值表方法
(一)真值联结词和真值形式
第二章第一节命题和推理概述
一、命题与判断、语句
命题是通过语句来反映事物情况的思维形式。(proposition)
命题的主要特征是有真假。命题总是或真(true)或假的(false)。
逻辑学把命题的真和假称为命题的真值(Truth),真命题有真的真值,假命题有假的真值。真值简称为值。
“李白是唐代诗人。”
充分条件假言命题负命题的等值命题是一个形如“p并且非q”的联言命题,用符号表示则为:(p→q)←→p∧q
㈤必要条件假言命题的负命题
及其对应的等值命题
充分条件假言命题的负命题的逻辑形式是:并非(只有p,才q)
必要条件假言命题负命题的等值命题是一个形如“非p并且q”的联言命题,用符号表示则为:(p←q)←→p∧q
在战略上藐视敌人,在战术上重视敌人。
坚冰已经打破,航线已经开通,道路已经指明。
我们不能轻信口供,要尊重事实。
合取式
构成联言命题的联结词“并且”,可用符号“∧”表示(“∧”读作“合取”),因此“p并且q”又可表示为:
p∧q
此公式读作“p合取q”,称为合取式。
联言命题的逻辑性质
联言命题的逻辑性质是:当联言肢(Conjunct)都真时,联言命题为真;但联言肢不都真时,联言命题为假。
科学和真理都不是从天上掉下来的,也不是人们头脑里固有的。
我们不但要改造世界,并且还要认识世界。
(二)选言命题
选言命题是反映几种可能的事物情况至少有一种存在的命题。
根据选言命题的肢命题(选言肢<Disjunct>)是否相容,选言命题分为两种:相容选言命题和不相容选言命题。
1、相容(Compatible)选言命题
简言之:“无之必不然,有之未必然”。
逆蕴涵
必要条件假言命题的联结词用“只有,才”来表示。其命题形式为:
只有p,才q
符号表示为“p←q”(“←”读作“逆蕴涵”)
根据必要条件假言命题的含义,“只有p,才q”等于说“如果非p,那么非q”,因此,必要条件假言命题的形式又可换以充分条件假言命题的形式:
p→q
必要条件假言命题的逻辑性质
(p∨q)←→p∧q
㈢不相容选言命题的负命题
及其对应的等值命题
不相容选言命题的负命题的逻辑形式是:
“并非(要么p要么q)”。
不相容选言命题负命题的等值命题是形如“(p并且q)或者(非p并且非q)”的命题。
用符号表示为:
(p∨q)←→(p∧q)∨(p∧q)
㈣充分条件假言命题的负命题及其对应的等值命题
充分条件假言命题的负命题的逻辑形式是:并非(如果p,那么q)
此公式读作“p等值q”,称为等值式。
“p等值q”是指p和q之间相互蕴涵,即p蕴涵q,q也蕴涵p。
充要条件假言命题的逻辑性质
充分必要条件假言命题的逻辑性质是:只有当其前、后件具有逻辑上的等值关系(即同真同假)时,该命题才是真的;反之,该命题便是假的。
有关假言命题应注意的问题
一个假言命题的真假,取决于其前后件之间的关系,而不取决于其前后件单独抽出来看它是真的,还是假的。
可用符号“”来表示,因此,“并非p”又可表示为:“p”。(读作“非p”)
负命题的逻辑性质
负命题的逻辑性质是:肢命题真,则负命题假;肢命题假,则负命题真。
二、负复合命题的等值命题
每个负复合命题都有与其对应的等值命题。所谓两个命题等值,就是指两个命题的逻辑值完全相同,即同真且同假。
㈠联言命题的负命题(此处在笔记)
真值表(Trut合谓项联言命题
2.复合主项联言命题
3.复合主谓项联言命题
注意!在现代逻辑中,p∧q与q∧p是等值的,被称作“合取交换律”,合取与次序无关。但在传统逻辑中,p且q有时不能改变次序,否则会影响原命题的意义。
我们要承认困难,分析困难,向困难作斗争。
辱骂和恐吓决不是战斗。
第二节复合命题
■联言命题、选言命题、假言命题和负命题是四种基本的复合命题。
■负复合命题的等值命题。
■一般命题的真值形式。
一、几种基本的复合命题
㈠联言命题
联言命题是陈述若干事物情况同时存在的命题。
构成联言命题的联结词用“并且”表示。具有两个联言肢的联言命题,其命题形式为:
p并且q
我们不但要认识世界,而且要改造世界。
1、充分条件假言命题
充分条件假言命题是指前件是后件的充分条件的假言命题。
充分条件(Sufficient condition)是指:前件(p)存在,后件(q)必存在,即有p必有q。
需要注意:充分条件只是陈述了前件存在,后件就存在的意思,它并没有陈述前件不存在,后件也不存在的意思。
简言之:“有之必然,无之未必不然”。
㈥充分必要条件假言命题的
负命题及其对应的等值命题
充分充分条件假言命题的负命题的逻辑形式是:并非(p当且仅当q)
充分必要条件假言命题负命题的等值命题是一个形如“(p并且非q)或者(非p并且q)”的命题,用符号表示则为:
(p←→q)←→(p∧q)∨(p∧q)
㈦负命题的负命题
及其等值命题
对负命题也可以加以否定,实际上这是一种双重否定。如果用“非p”表示负命题,那么负命题的否定就是“并非(非p)”。“并非(非p)”等值于“p”,其等值式为:¬ ¬p←→p
两种命题不同的逻辑涵义;共存关系与选择关系。
(三)假言命题
假言命题是陈述某一事物情况是另一事物情况的条件的命题,因而又称为条件命题假言命题由两个肢命题组成,其中位于前面表示条件的肢命题叫作前件(p),位于后面表示依赖条件而成立的肢命题叫作后件(q)。
根据假言命题所表达的条件性质的不同,假言命题分为充分条件假言命题、必要条件假言命题和充分必要条件假言命题三种。
相容选言命题是陈述选言肢中至少有一真的选言命题。相容的意思是不排斥选言肢同时为真。
相容选言命题的联结词通常用“或者”表示。具有两个选言肢的相容选言命题,其命题形式为:
p或者q
析取式
相容选言命题的联结词“或者”可用符号“∨”(读作“析取”)表示,因此“p或者q”又可表示为:
p∨q
此公式读作“p析取q”,称之为析取式。
相容选言命题的逻辑性质
相容选言命题的逻辑性质是:只要有一个选言肢为真,它就是真的;当选言肢没有一个真时,它是假的。
Truth Table
2、不相容选言命题
不相容选言命题是陈述选言肢中有而且仅有一真的选言命题。不相容的意思是选言肢不能同时为真。
具有两个选言肢的不相容选言命题,其命题形式为:
要么p,要么q
前件(p)存在,后件(q)必存在;前件(p)不存在,后件(q)必不存在。
简言之:“有之必然,无之必不然”。
等值式(Equivalence)
充分必要条件假言命题的联结词用“当且仅当”来表示。其命题形式为:
p当且仅当q
其联结词“当且仅当”,可用符号“←→”表示。因此,“p当且仅当q”又可表示为:
p←→q
及其对应的等值命题
联言命题的负命题的逻辑形式是:
并非(p并且q)
联言命题负命题的等值命题是形如“非p或者非q”的选言命题。可表示为:
(p∧q)←→p∨q
㈡相容选言命题的负命题
及其对应的等值命题
相容选言命题的负命题的逻辑形式是:
并非(p或者q)
相容选言命题负命题的等值命题是形如“非p并且非q”的联言命题,可表示为:
每一个推理都由前提(Premise)、结论(Conclusion)和推理形式(逻辑联系)组成,它们被称为推理三要素。
推理的前提和结论都是命题。推理就是从作为前提的命题得出作为结论的命题。在现代逻辑中,推理就是演算(Calculus)。
推理要合乎逻辑
任何一个推理,要推出正确的结论,必须具备两个条件,即前提真实,形式正确。
命题总是一种语句,但只有表达一种要么真要么假的思想的语句才是命题。
同一个命题可以用不同的语句来表达;同一个语句还可以表达不同的命题。
人总是要死的。
没有人是不死的。
不死的人是没有的。
难道有不死的人吗?
他翻身了。
那是白头翁。
小王在火车上画画。
二、命题形式及其种类
任何命题都有内容和形式两个方面。命题内容是指命题所反映的事物情况,命题形式(propositional form)是指命题内容的联系方式,即命题的逻辑形式。
不相容析取(exclusive disjunction)
“要么p,要么q”的逻辑联结词可用符号“∨”表示,读作“不相容析取”。
“要么p,要么q”的含义是:或者p真,或者q真,但不能p和q都真。据此,不相容选言命题又可表示为:
或者p或者q,但并非(p并且q)
用符号表示为:
(p∨q)∧(p∧q)
(其中的“”,读作“并非”)
命题内容不同,却可以有共同的逻辑形式。
Truth Table
3、充要条件假言命题
充分必要条件假言命题是指前件是后件的充分必要条件的假言命题。
充分必要条件(Sufficient and necessary condition)就是同时具有充分条件和必要条件的含义,即:
不相容选言命题的逻辑性质
不相容选言命题的逻辑性质是:当选言肢仅有一真时,它是真的;当选言肢都真或都假时,它是假的。
■正确运用选言命题
⒈关于选言肢应当穷尽的问题
选言肢穷尽的选言命题必真,选言肢不穷尽的可能假。
⒉关于区分两种选言命题的问题
肢命题之间的关系逻辑涵义不同,选择适当的逻辑联结词。
⒊关于区分相容选言命题与联言命题的问题
三、一般复合命题及其真值形式
•真值联结词和真值形式
•一般复合命题及其真值形式
•真值形式的判断:真值表方法
(一)真值联结词和真值形式
第二章第一节命题和推理概述
一、命题与判断、语句
命题是通过语句来反映事物情况的思维形式。(proposition)
命题的主要特征是有真假。命题总是或真(true)或假的(false)。
逻辑学把命题的真和假称为命题的真值(Truth),真命题有真的真值,假命题有假的真值。真值简称为值。
“李白是唐代诗人。”
充分条件假言命题负命题的等值命题是一个形如“p并且非q”的联言命题,用符号表示则为:(p→q)←→p∧q
㈤必要条件假言命题的负命题
及其对应的等值命题
充分条件假言命题的负命题的逻辑形式是:并非(只有p,才q)
必要条件假言命题负命题的等值命题是一个形如“非p并且q”的联言命题,用符号表示则为:(p←q)←→p∧q
在战略上藐视敌人,在战术上重视敌人。
坚冰已经打破,航线已经开通,道路已经指明。
我们不能轻信口供,要尊重事实。
合取式
构成联言命题的联结词“并且”,可用符号“∧”表示(“∧”读作“合取”),因此“p并且q”又可表示为:
p∧q
此公式读作“p合取q”,称为合取式。
联言命题的逻辑性质
联言命题的逻辑性质是:当联言肢(Conjunct)都真时,联言命题为真;但联言肢不都真时,联言命题为假。
科学和真理都不是从天上掉下来的,也不是人们头脑里固有的。
我们不但要改造世界,并且还要认识世界。
(二)选言命题
选言命题是反映几种可能的事物情况至少有一种存在的命题。
根据选言命题的肢命题(选言肢<Disjunct>)是否相容,选言命题分为两种:相容选言命题和不相容选言命题。
1、相容(Compatible)选言命题
简言之:“无之必不然,有之未必然”。
逆蕴涵
必要条件假言命题的联结词用“只有,才”来表示。其命题形式为:
只有p,才q
符号表示为“p←q”(“←”读作“逆蕴涵”)
根据必要条件假言命题的含义,“只有p,才q”等于说“如果非p,那么非q”,因此,必要条件假言命题的形式又可换以充分条件假言命题的形式:
p→q
必要条件假言命题的逻辑性质
(p∨q)←→p∧q
㈢不相容选言命题的负命题
及其对应的等值命题
不相容选言命题的负命题的逻辑形式是:
“并非(要么p要么q)”。
不相容选言命题负命题的等值命题是形如“(p并且q)或者(非p并且非q)”的命题。
用符号表示为:
(p∨q)←→(p∧q)∨(p∧q)
㈣充分条件假言命题的负命题及其对应的等值命题
充分条件假言命题的负命题的逻辑形式是:并非(如果p,那么q)
此公式读作“p等值q”,称为等值式。
“p等值q”是指p和q之间相互蕴涵,即p蕴涵q,q也蕴涵p。
充要条件假言命题的逻辑性质
充分必要条件假言命题的逻辑性质是:只有当其前、后件具有逻辑上的等值关系(即同真同假)时,该命题才是真的;反之,该命题便是假的。
有关假言命题应注意的问题
一个假言命题的真假,取决于其前后件之间的关系,而不取决于其前后件单独抽出来看它是真的,还是假的。
可用符号“”来表示,因此,“并非p”又可表示为:“p”。(读作“非p”)
负命题的逻辑性质
负命题的逻辑性质是:肢命题真,则负命题假;肢命题假,则负命题真。
二、负复合命题的等值命题
每个负复合命题都有与其对应的等值命题。所谓两个命题等值,就是指两个命题的逻辑值完全相同,即同真且同假。
㈠联言命题的负命题(此处在笔记)
真值表(Trut合谓项联言命题
2.复合主项联言命题
3.复合主谓项联言命题
注意!在现代逻辑中,p∧q与q∧p是等值的,被称作“合取交换律”,合取与次序无关。但在传统逻辑中,p且q有时不能改变次序,否则会影响原命题的意义。
我们要承认困难,分析困难,向困难作斗争。
辱骂和恐吓决不是战斗。
第二节复合命题
■联言命题、选言命题、假言命题和负命题是四种基本的复合命题。
■负复合命题的等值命题。
■一般命题的真值形式。
一、几种基本的复合命题
㈠联言命题
联言命题是陈述若干事物情况同时存在的命题。
构成联言命题的联结词用“并且”表示。具有两个联言肢的联言命题,其命题形式为:
p并且q
我们不但要认识世界,而且要改造世界。
1、充分条件假言命题
充分条件假言命题是指前件是后件的充分条件的假言命题。
充分条件(Sufficient condition)是指:前件(p)存在,后件(q)必存在,即有p必有q。
需要注意:充分条件只是陈述了前件存在,后件就存在的意思,它并没有陈述前件不存在,后件也不存在的意思。
简言之:“有之必然,无之未必不然”。
㈥充分必要条件假言命题的
负命题及其对应的等值命题
充分充分条件假言命题的负命题的逻辑形式是:并非(p当且仅当q)
充分必要条件假言命题负命题的等值命题是一个形如“(p并且非q)或者(非p并且q)”的命题,用符号表示则为:
(p←→q)←→(p∧q)∨(p∧q)
㈦负命题的负命题
及其等值命题
对负命题也可以加以否定,实际上这是一种双重否定。如果用“非p”表示负命题,那么负命题的否定就是“并非(非p)”。“并非(非p)”等值于“p”,其等值式为:¬ ¬p←→p
两种命题不同的逻辑涵义;共存关系与选择关系。
(三)假言命题
假言命题是陈述某一事物情况是另一事物情况的条件的命题,因而又称为条件命题假言命题由两个肢命题组成,其中位于前面表示条件的肢命题叫作前件(p),位于后面表示依赖条件而成立的肢命题叫作后件(q)。
根据假言命题所表达的条件性质的不同,假言命题分为充分条件假言命题、必要条件假言命题和充分必要条件假言命题三种。
相容选言命题是陈述选言肢中至少有一真的选言命题。相容的意思是不排斥选言肢同时为真。
相容选言命题的联结词通常用“或者”表示。具有两个选言肢的相容选言命题,其命题形式为:
p或者q
析取式
相容选言命题的联结词“或者”可用符号“∨”(读作“析取”)表示,因此“p或者q”又可表示为:
p∨q
此公式读作“p析取q”,称之为析取式。
相容选言命题的逻辑性质
相容选言命题的逻辑性质是:只要有一个选言肢为真,它就是真的;当选言肢没有一个真时,它是假的。
Truth Table
2、不相容选言命题
不相容选言命题是陈述选言肢中有而且仅有一真的选言命题。不相容的意思是选言肢不能同时为真。
具有两个选言肢的不相容选言命题,其命题形式为:
要么p,要么q
前件(p)存在,后件(q)必存在;前件(p)不存在,后件(q)必不存在。
简言之:“有之必然,无之必不然”。
等值式(Equivalence)
充分必要条件假言命题的联结词用“当且仅当”来表示。其命题形式为:
p当且仅当q
其联结词“当且仅当”,可用符号“←→”表示。因此,“p当且仅当q”又可表示为:
p←→q
及其对应的等值命题
联言命题的负命题的逻辑形式是:
并非(p并且q)
联言命题负命题的等值命题是形如“非p或者非q”的选言命题。可表示为:
(p∧q)←→p∨q
㈡相容选言命题的负命题
及其对应的等值命题
相容选言命题的负命题的逻辑形式是:
并非(p或者q)
相容选言命题负命题的等值命题是形如“非p并且非q”的联言命题,可表示为:
每一个推理都由前提(Premise)、结论(Conclusion)和推理形式(逻辑联系)组成,它们被称为推理三要素。
推理的前提和结论都是命题。推理就是从作为前提的命题得出作为结论的命题。在现代逻辑中,推理就是演算(Calculus)。
推理要合乎逻辑
任何一个推理,要推出正确的结论,必须具备两个条件,即前提真实,形式正确。
命题总是一种语句,但只有表达一种要么真要么假的思想的语句才是命题。
同一个命题可以用不同的语句来表达;同一个语句还可以表达不同的命题。
人总是要死的。
没有人是不死的。
不死的人是没有的。
难道有不死的人吗?
他翻身了。
那是白头翁。
小王在火车上画画。
二、命题形式及其种类
任何命题都有内容和形式两个方面。命题内容是指命题所反映的事物情况,命题形式(propositional form)是指命题内容的联系方式,即命题的逻辑形式。
不相容析取(exclusive disjunction)
“要么p,要么q”的逻辑联结词可用符号“∨”表示,读作“不相容析取”。
“要么p,要么q”的含义是:或者p真,或者q真,但不能p和q都真。据此,不相容选言命题又可表示为:
或者p或者q,但并非(p并且q)
用符号表示为:
(p∨q)∧(p∧q)
(其中的“”,读作“并非”)
命题内容不同,却可以有共同的逻辑形式。
