薛定谔方程应用举例共25页文档
18.0 薛定谔方程及其应用
一维运动粒子的含时薛定谔方程
Ψ ( x , t ) = ψ ( x )φ (t ) = ψ 0 ( x ) e
2 2
− i 2 π Et / h
在势场中一维运动粒子的定态薛定谔方程 势场中一维运动粒子的定态薛定谔方程 运动粒子的定态
d ψ 8π m + ( E − E p )ψ ( x ) = 0 2 2 dx h
一. 物质波的波函数
微观粒子 具有波动性
1925年薛定谔 年薛定谔
用物质波波函数描述 微观粒子的概率波
轴正方向运动，由于其能量、动量为常量， 例如 自由粒子沿 x 轴正方向运动，由于其能量、动量为常量， 不随时间变化，其物质波是单色平面波， 所以 v 、 λ 不随时间变化，其物质波是单色平面波，波 函数为
r 2 r * r dW =|Ψ(r,t)| dV =Ψ(r,t)Ψ (r,t)dV
2. 归一化条件 (粒子在整个空间出现的概率为 粒子在整个空间出现的概率为1) 粒子在整个空间出现的概率为
r 2 ∫∫∫|Ψ(r,t)| dxdydz =1
3. 波函数必须单值、有限、连续 波函数必须单值、有限、 概率密度在任一处都是唯一、有限的 概率密度在任一处都是唯一、有限的, 并在整个空间内连续
2
归一化条件 归一化条件
2 a A sin 2 0
∫−∞ ψ
∞
2
dx = ∫ ψψ dx = 1
* 0
a
∫
nπ xd x = 1 a
2 A= a
ψ ( x) =
2 nπ sin x , (0 ≤ x ≤ a ) a a
d ψ 8π mE + ψ = 0 ∞ Ep ∞ 波动方程 2 2 dx h
2 2
薛定谔方程及其简单应用
75.5neV
当n>>1时，能量相对间隔
En En
21 nn
当
n 时
E E 量子化不显著。
n
n
经典物理可看成是
n 时量子物理的特殊情况。
H
26
a =102 m时：
E
n 2h 2 8ma 2
8n29(.61.61301310314)024
3.7 810 1n 52ev
显然电子在宏观尺度上运动时其能级差是很小的。
H
24
经典理论中，处于无限深方势阱中粒子
的能量为连续值，粒子在阱内运动不受限制， 各处概率相等。
| |2
n4
随着能级的升高，几率密度的峰值增多，
当
时，粒子在势阱内各处出现的概率
n 相等，量子力学的结果过渡到经典力学的情
况。
n3 n2
0
a/2
n1 a
从以上分析可知：对于无限深势阱来说，粒子只能在势阱U=0的区域能运 动。。
2 m 2d2d 32 (x x)E 3(x), xa
aa
n 很大时，相邻波腹靠得很近，接近经典 力学各处概率相同。
H
3x
E3
2x
E2
1x E 1
o
n+1个
x a节点
稳定的驻波能级23
一维无限深方势阱中粒子的能级、波函数和几率密度
n4
| |2
4
16E1
3
n3
9E1
n2
n1 0
a/2
2
1 a0
a/2
4E1 E1 a Ep 0
对于不同的量子数，在阱内某一特定的点，粒子出现的几率是不同的。
粒 r 处 子 的 在 2 （ 几 r ,t) （ *r ,t 率 )
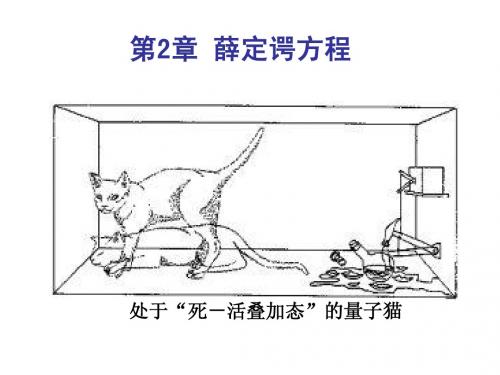
薛定谔方程及其应用
x
y ( x, t ) Re[ Ae
]
1
2、量子力学波函数（复函数） 自由粒子是不受外力作用的粒子，它在运动 过程中作匀速直线运动（设沿X轴），其能量和 动量保持不变。 E h , 对应的德布罗意波的频率和波长： h P 结论：自由粒子的物质波是单色平面波。
波函数为：
对三维空间，沿矢径 r 方向传播的自由粒子的
粒子在0到a/2区域内出现的概率
8
二、薛定谔方程
9
经典力学中，已知力 F 及 x0、 υ 0，可由牛顿方 程求质点任意时刻状态。 在量子力学中，微观粒子的运动状态由波函数来 描写；状态随时间的变化遵循着一定的规律。
当微观粒子在某一时刻的状态为已知时，以后 时刻粒子所处的状态也要薛定谔方程来决定。
2
方程（1）的解为： f ( t ) ce
i Et
Et
（c为任一常数） 将 f ( t ) ce 代入 ( r , t ) ( r ) f ( t ) ， 并把常数包含在 ( r ) 中，这样 就得到薛定谔方程的特解为：
定态薛定谔方程
( r , t ) ( r )e
0 (0 x a ) U ( x) ( x 0 , x a )
U ( x )
d U E 2 2m dx
2 2
2 d 2 E 2 2m dx
须有
U(x)
0
( x) 0
0 a
边界条件：
(0) (a ) 0
13
若粒子不是在一维空间而是在三维空间的势场 中运动，则其薛定谔方程为：
2 2 2 2 ( r , t ) ( r , t ) ( r , t ) ( r , t ) i [ ] 2 2 2 t 2m x y z U ( r , t ) ( r , t ) ⑥
B11_薛定谔方程
U ( r , t )
2 2
引入拉普拉斯算符 引入哈密顿算符
(Hamiltonian operator)
2
2 2
2
x
y
2 2
薛定谔方程：
i t ˆ H
z
ˆ H
2 U (r , t )
2m
4、关于薛定谔方程的说明 是量子力学的一个基本原理；是量子力学的基本方程， 描述非相对论性粒子波函数的演化规律。 是线性齐次微分方程，解满足态叠加原理 若 1 和 2 是方程的解，则它们的线性组合 （C11＋C22）也一定是方程的解。 方程中含有虚数 i 它的解 是复函数，复数不能直接测量。 而 的模方代表概率密度，可测量。 2 薛定谔方程关于时间是一阶的，这 2 2 u 2 不同于经典波动方程（时间二阶） t
U ( r , t )
若势函数U不显含t，为求解薛定谔方程，分离变量 (r , t ) (r ) T (t )
ˆ 代入薛定谔方程，得 i d T ( t ) ( r ) [ H ( r )]T ( t ) dt
dT(t ) 除以 ( r ) T ( t ) ，得 i
( x ) A sin kx ） 待定常数A、 由 应满足的物理条件决定。 （
以上的解已自然满足单值，有限的条件。 连续条件： 由于边界外 = 0，所以有：
x a 2 a , 0 A sin ( ka 2 ) 0
ka 2
l1
2 l1 l 2 ) l （ l
x
, 0 A sin (
薛定谔方程可以解释的生活中的问题
薛定谔方程（Schrödinger equation）是量子力学中的基本方程之一，它描述了微观粒子的运动和行为。
虽然其理论极其复杂，但薛定谔方程却可以被用来解释生活中许多奇妙的现象和问题。
本文将围绕薛定谔方程可以解释的生活中的问题展开讨论，以帮助读者更好地理解这一基础物理理论在日常生活中的应用。
一、量子隧穿效应薛定谔方程首次揭示了量子隧穿效应（quantum tunneling effect），即微观粒子可以在经典力学下无法穿越的势垒的情况下通过反常的方式穿越而无需克服这一势垒。
这一效应在生活中有很多应用，例如：1. 在隧道二极管中，量子隧穿效应使电子得以“穿越”势垒，从而帮助二极管正常工作；2. 核聚变反应中，负电子穿越核力垒，帮助实现核聚变；3. 化学反应中的“反常”速率，有时是由于量子隧穿效应引起的。
二、量子纠缠薛定谔方程还描述了量子纠缠现象，即使两个空间分隔较远的粒子，它们的状态仍然会同时发生变化，这种现象被爱因斯坦称为“一种鬼魅的行为”。
量子纠缠的出现在生活中也有许多实际应用：1. 量子计算机中，利用量子纠缠可以实现超越经典计算机的运算速度和处理能力；2. 量子密钥分发技术中的安全传输，依赖于量子纠缠的特性来保证信息的安全传输；3. 量子纠缠还被应用于实现远距离的量子通信，实现了远距离的量子纠缠态转移。
三、量子力学与生活除了上面提到的具体现象外，薛定谔方程的一些概念和原理也对我们日常生活产生了深远的影响：1. 不确定性原理：薛定谔方程提出了不确定性原理，即无法同时准确地确定微观粒子的位置和动量，这一概念改变了人们对于现实世界的理解，并且在科学研究和生活中也有很多应用；2. 双缝实验：薛定谔方程对光子和电子的双缝干涉实验提出了解释，这一实验揭示了微粒子的波粒二象性，为光学技术和电子技术的发展做出了重要贡献；3. 量子力学的数学形式和基本原理也为信息技术、纳米技术、光学技术等领域的发展提供了理论基础。
固体物理学 1-5-薛定谔方程应用举例II
薛定谔方程应用举例II---原子系统¾ 氢原子 ¾ 电子自旋 ¾ 多电子原子1氢原子的定态薛定谔方程•原子由一个原子核和核外电子构成，属于多粒子体系。
多粒 子体系的总能量等于每一个粒子的能量与粒子间相互作用能量 之和。
•氢原子包括一个原子核和电子，库仑场是各向同性的，哈密 顿量可记作（绝热近似）：Hˆ=−h2 2me∇2+qeU(r)me为电子质量，qe是电子电荷。
U(r)为原子核静电场中的库 仑势，记作：U(r) = − Zqe = − Z h24πε0r a1meqerZ为核的电荷数，a1 = 4πε0ħ2/(meqe2) = 0.529Å，为氢原子的第一波尔轨道半径。
2⎡⎢− ⎣h2 2me∇2−Zh 2 a1meqer⎥⎤ψ⎦(r)=E⋅ψ(r)中心力场问题，采用球坐标，薛定谔方程为：⎡ ⎢− ⎢⎣h2 2me⋅⎝⎛⎜⎜1 r2∂ ∂rr2∂ ∂r−Lˆ2 r2⎟⎟⎠⎞ −Zh2⎤⎥ψ (r,ϕ,θ ) =a1mer ⎥⎦E ⋅ψ (r,ϕ,θ )用分离变量法求解，令：ψ (r,θ ,φ) = R(r) ⋅Y (ϕ,θ )分别求解径向波函数R(r)和角向波函数Y(ϕ,θ)。
3氢原子电子能级•能量本征值： En=−Z2h2 2me a12 n2n=1, 2, 3,……，称为主量子数•电子能级量子化（仅通过数学求解薛定谔方程即可获得）。
•基态能量用E1表示，记作：E1=−Z2h2 2me a12氢原子的电离能Ei = −E1 = 13.6 eV，也称里德伯常 数。
•氢原子电子能级仅与主量子数n有关，多电子原子则不然。
4氢原子电子的径向密度分布函数•径向波函数：Rn,l(r)=N n,l(2Z na1r)l−eZ na0rL ( 2l+1 n−l −12Z na1r)l = 0, 1, 2, …, n−1，共n个取值，称为角量子数。
（n、l确定径向波 函数。
薛定谔方程一维情况
E只能取一系列分离值 2 E1 n
π2 2 式中 E1 2m a2
O 粒子不可能静止不动，满足不确定关系
n=4 n=3 n=2 n=1
最小能量E1即零点能,
a
x
第9页 共30页
大学物理
由
k 22 n 2 π 2 2 E n 2 E1 (n 1,2,3,) 2m 2m a2
O
a
x
1 ( 0) 2 ( 0) d 1 d 2
dx dx 2 (a ) 3 (a ) ( 0)
可解得
( 0)
A2 , A3 B1 , B2
第20页 共30页
d 2 d 3 (a ) (a ) dx dx
大学物理
U
入射波+反射波
U0
透射波
O 经典
E U0
解：
1 2 5 | | dx c x ( L x) dx 30 c L 1 0 0
2 2 2 2
L
L
得
30 c 5 L
L 3 2
30 5 x( L x ) L
L 3
30 2 17 2 P | | dx 5 x ( L x ) dx 0.21 L 81 0 0
d 2 2m 2 E 0 (0 x a ) 2 dx
O
a
x
d 2 2m 2 E 0 ( x 0, x a ) 2 dx
第5页 共30页
2. 求解波函数 d 2 2m 2 E 0 (0 x a ) 2 dx
d 2 2m 2 E 0 ( x 0, x a ) 2 dx
2
15 量子物理学的诞生 薛定谔方程及应用
一维自由粒子的 含时薛定谔方程
2、一维势场 U ( x , t ) 中运动粒子薛定谔方程
P E Ek U U 2m Ψ i EΨ t 2Ψ P2 2 Ψ 2 x
2
Ψ i P2 [ U ( x , t )]Ψ t 2m
Ψ ( x, t ) Ψ oe
x
E p0
A B
2 一维无限深势阱
0
0
a x
U (x)
0 0< x < a
x 0, x a
U 与t 无关，写出定态定谔方程
1
1= 0
d Φ UΦ EΦ 2 2m dx
2 2
0 2
3
3 = 0
1 势阱外
dΦ Φ EΦ 2 2m dx
2 2
x
0
a
x
讨论
1.能量只能取分立值 是解薛定谔方程自然而然得到的结论。 按经典理论……粒子的“能量连续”； 但量子力学……束缚态能量只能取分立值（能级）
2.当 m 很大（宏观粒子）时，能量连续， 量子 经典。 3.最低能量不为零（称零点能） 2 2 E1 0 2 ———符合不确定关系。 2 ma
2 2 Φ UΦ EΦ 2m
定态薛定薛方程 一维定态薛定谔方程
2m Φ 2 ( E U )Φ 0
2
d 2Φ( x ) 2m 2 (E U)Φ( x ) 0 2 dx
势阱中的粒子 势垒 谐振子
一、 一维无限深势阱
1 势阱
U (x)
金属表面
金属中自 由电子的 势能曲线
推广到三维情况， 2 2Ψ Ψ U ( x , t )Ψ i 薛定谔方程可写为： 2
薛定谔方程及的应用
1 f (t ) 1 2 2 i [ (r ) V (r ) (r )] f (t ) t (r ) 2m
很明显，上式右边只是 矢径 的函数，而左边只 是时间t的函数，为了使上式成立，必须两边恒等于 某一个常数，设以E表示，则有： 11
r
f (t ) i Ef (t ) （ 1） t 2 2 (r ) V (r ) (r ) E (r ) （2） 2m
p E V ( x, t ) 2m
将上式作用于波函数上，此时的薛定谔方程为：
2
( x, t ) ( x, t ) i V ( x, t ) ( x, t ) 2 t 2m x
2 2
⑤
8
由此可知，粒子能量E和动量P与下列作用在波 函数上的算符相当：
E i , t
方程（1）的解为： f 将 f (t ) ce 入 并把常数包含在 程的特解为：
( x, t ) i E0e t
上式两边都乘以
i ( Et px )
i E ( x, t ) ①
( x, t ) i E ( x, t ) t
对 x 求二阶偏导
i
得：
( x, t ) i i p0e p ( x, t ) x i 2 2 ( Et px ) ( x, t ) ip 2 p ( ) e 2 ( x, t ) 0 2 x 2
i ( Et px )
②
6
上式两边都乘以
2m
得：
2 2 ( x, t ) p 2 ( x, t ) 2 2m x 2m
把对t 求导的式子写在下面
波函数与薜定谔方程,薜定谔方程应用举例
5
例：限制在一维空间运动的粒子，其状态波函数可 表示为：
0
(
x,
t
)
A
cos(
x
a
)
e
iE
t
(x a / 2, x a / 2) (a / 2 x a / 2)
其中A 为待定常数；E 、a为确定常数。
求：1.归一化的波函数； 2.概率密度。
解：由归一化条件得
| |2 dx a/2 | |2 dx 1
2 sin2 a
n
a
x
E2 E1
2 1
x
0
a
16
讨论 1.粒子的能量
●量子化
最小值
E1
2 2
2ma2
基态能（零点能）不为零，这 是与经典理论的一个重大区别。 各能量本征值：
En n2E1 n 1, 2,3,
n>1:激发态能
基态能
E
E4
16E1
E3
9E1
E2
4E1
E1 0
x a
17
2.粒子在势阱中的概率分布
P
| 2 (a) |2 | 2 (0) |2
T T
exp(2k1a) exp(2k10)
U 隧道效应
U0
exp 2a
2m(U0
E)
I II III
oa x
当 U0 E 5eV 、势垒的宽度为50nm 以上时，贯穿
系数会小于10-6以上，隧道效应已无实际意义。从量 子化概念过渡到经典问题。
28
第二十六章
概率波
●在量子力学中，描述微观粒子运动状态的基本物 理量是波函数，反映微观粒子运动的基本方程是薜 定谔方程。 1924－1926年间，经德布罗意、薜定谔、海森伯、 玻恩、狄拉克等人的工作，建立了反映微观粒子属 性和运动规律的量子力学。
薛定谔方程在化学中的应用
薛定谔方程是一个重要的物理学理论，它描述了原子和分子中电子的运动。
在化学中，薛定谔方程可用于解释许多化学现象，包括：1 原子吸收光谱：原子吸收光谱是利用薛定谔方程来研究原子的结构和性质的一种方法。
原子吸收光谱是通过向原子送入电磁辐射，然后观察原子是否吸收光谱中的某些波长的光来研究原子结构的。
2 化学反应速率：薛定谔方程可用于解释化学反应速率的变化。
例如，当反应物分子的能级较高时，反应速率较快，因为电子越容易被转移到产物分子中。
3 化学平衡：薛定谔方程可用于解释化学平衡的原理。
在平衡反应中，反应物和产物的能级相差较小，因此反应物和产物之间的转化速率相差较小。
4 化学结构：薛定谔方程可以用来解释化学分子的结构，例如，它可以解释为什么某些分子的电子密度分布的方式是如此的不同。
总的来说，薛定谔方程是化学研究中的一个重要理论工具，它对于更多的化学研究和应用，薛定谔方程还可以用于：5 化学结合能：薛定谔方程可用于研究原子之间的化学结合能，即相邻原子之间的能量差。
这有助于解释为什么某些原子更容易形成化合物，而其他原子不容易。
6 电子转移反应：薛定谔方程可用于研究电子转移反应，即原子或分子之间电子的转移。
这对于研究催化剂的作用至关重要，因为催化剂能够促进电子转移反应的发生。
7 电子结构：薛定谔方程可用于研究分子的电子结构，包括电子密度分布、电子云形状以及分子的极性。
这些信息对于研究分子的化学性质非常重要。
8 光解反应：薛定谔方程可用于研究光解反应，即分子在受到光照射时分解的过程。
这是一种常见的化学反应，可以用来制造许多有用的化学物质。
总的来说，薛定谔方程是一个非常强大的化学工具，它能够帮助我们理解许多化学现象，并为我们提供重要的研究和应用信息。
§16.3 一维定态薛定谔方程的建立和求解举例
§16.3 一维定态薛定谔方程的建立和求解举例（一）一维运动自由粒子的薛定谔方程波函数随时间和空间而变化的基本方程，是薛定谔于1926年提出的，称为薛定谔波动方程，简称波动方程或薛定谔方程，它成为量子力学的基本方程．将（16.2.14）式分别对t 和x 求导，然后从这两式消去E 、p 、和ψ，便可得到一维运动自由粒子的薛定谔方程：ψ-=∂ψ∂)/iE (t 即ψ=∂ψ∂E t i （16.3.1）ψ=∂ψ∂22)/ip (x 2ψ=ψ∂-2222p⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡<<的薛定谔方程自由粒子轴运动的沿)c x (v方程（16.3.3）中不含有能量E 和动量p ，表明此方程是不受E 和p 的数值限制的普遍方程．请同学们自己试一试，如果上述波函数不用复数表式（16.2.14），改用类似于（16.2.1）式的余弦函数或正弦函数表式，就不会得到合乎要求的薛定谔方程（16.3.3）式❶．这薛定谔方程不是根据直接实验结果归纳而得，也不是由经典波动理论或其他理论推导出来的，它是在物质波假设的基础上，参照经典波动方程而建立起来的．薛定谔方程在微观领域中得到广泛的应用，它推导出来的结果，都与相关实验结果符合得很好，这才是薛定谔方程正确反映微观领域客观规律的最有力的证明．（二）一维运动自由粒子的定态薛定谔方程❶❷上述薛定谔方程（16.3.3）是偏微分方程，从此方程可解出波函数ψ（x ，t ）．在量子力学中最重要的解，是可把波函数ψ（x,t ）分离成空间部分u （x ）和时间部分f （t ）两函数的乘积的特解，即〔一维运动自由粒子的定态波函数〕 ψ（x,t ）=u （x ）f （t ）（16.3.4）将此式代入（16.3.3）式得：222dx u d )t (f )m 2/(dt df )x (u i -=两边除以ψ=uf 得：222dx u d u 1)m 2/(dt df f 1i -=此式左边是时间t 的函数，右边是坐标x 的函数．已知t 与x 是互相独立的自变量，左右两边相等，必须是两边都等于同一常量E ，即❶ 郭敦仁《量子力学初步》16—17页，人民教育出版社1978年版.❶ 郭敦仁《量子力学初步》21—22页，人民教育出版社1978年版.❷ 周世勋编《量子力学》32—33页，上海科学技术出版社1961年版.（16.3.8） （16.3.9） (图16.3a )一维矩形深势阱E dt df f 1i = E dx u d u 1)m 2/(222=- （16.3.5）因此，一个偏微分方程（16.3.3）可分解成两个常微分方程（16.3.5）以求解．如〔附录16C 〕所示，（16.3.5）式的E 就是粒子的能量E ．上述两个常微分方程的解分别为：〔时间波函数f （t ）〕 /iEt Ce )t (f -= （16.3.6）〔空间波函数u （x ）〕 （16.3.7）将上式的待定常量C 合并到A 和B 中，便可得到下式：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡<<函数和几率密度的定态波子一维运动自由粒)c (v从此式可知，特解ψ=uf 使得几率密度|ψ|2与时间t 无关，这是粒子的几率分布与时间无关的恒定状态，因此称为定态．ψ=uf 称为定态波函数，其中空间部分u （x ）可称空间波函数，时间部分f （t ）可称时间波函数．如（16.3.9）式所示，定态的几率密度|ψ|2决定于空间波函数u ，与时间波函数f 无关．（16.3.5）式中空间波函数u 满足的方程，称为定态薛定谔方程，此方程重写如下： ⎥⎦⎤⎢⎣⎡<<的定态薛定谔方程一维运动自由粒子)c (v （16.3.10） （16.3.7）式表明，空间波函数u （x ）的表式中有三个待定常量A 、B 、α，它们要由实际例子中的边界条件和归一化条件来确定．下面就要介绍确定常量A 、B 、α的一个实际例子．（三）一维矩形深势阱中，自由粒子的薛定谔方程定态解（1）金属中自由电子的运动金属中自由电子的运动，假设可简化为自由粒子的一维运动．在外界条件不变的情况下，可设想自由电子的几率分布是恒定的，不随时间而变．这就是上述定态的一维运动自由粒子的一个例子．上述（16.3.3）至（16.3.10）诸式均可应用于此例子．上述待定常量A 、B 、α，可按此例的边界条件和归一化条件确定之．（2）边界条件确定常量B 与α上述自由电子只能在金属中运动，可设定它的运动范围为0＜x ＜b ．在此范围内，设它的势能为零，即E p =0，E=E k ．在此范围外，它的势能必须达到无限大，即E p →∞，E →∞．所谓E p →∞，就是用势能条件表示自由电子不能越出金属之外，也就是说，这些自由电子被限制在矩形无限深势阱中运动，如（图16.3a ）所示．按几率来说，在金属表面以外没有自由电子，就是说，在x≤0和x ≥b 的范围中，这些电子的几率密度|ψ|2=0．因此，在此范围中，波函数ψ=0，u=0．这就是边界条件，或称边值条件．/mE 2x cos B x sin A )x (u =+=ααα222/iEt |u |x cos B x sin A e )x cos B x sin A ()t (f )x (u )t ,x (=+=ψ+===ψ-αααα ()0Eu /m 2dx u d 222=+（16.3.16） （16.3.17） (图16.3b)一维矩形深势阱中、自由粒子的几率密度与能级将此边值条件代入（16.3.7）式便可确定B 与α的数值，计算如下：在x=0处：u （0）=Asin0°+Bcos0°=B=0 （16.3.11）∴u （x ）=Asin αx （16.3.12）在x=b 处：u （b ）=Asin αb=0，αb=n π即α=n π/b ， n=1,2,3,…… （16.3.13）∴ψ（x,t ）=Asin （n πx/b ） /iEt e - （16.3.14）在（16.3.13）式中，u （b ）=0不选用A=0的答案．这因为A=0，则u （x ）=0，|ψ|2=0．这是x 等于任何数值，都使|ψ|2=0的不合理答案．在（16.3.13）式，不选用n=0的答案．因为n=0则α=0、u （x ）=0、|ψ|2=0，这也是处处都没有电子的不合理答案．在（16.3.13）式，如果选用n=－1,－2,－3，……所得ψ值，与选用n=1,2,3,……求得的ψ值，绝对值相等、正负号相反．因此，在计算|ψ|2时，不必要保留n 的负值．（3）归一化条件确定常量A将波函数表式（16.3.14）代入归一化条件式（16.2.11），按上述一维情况进行积分，并考虑到自由电子只在0＜x ＜b 范围内运动，可得结论如下：1dx x sin A dx dx 2b 0 2b 0 2 ==ψ=ψ⎰⎰⎰∞∞-α即()()[]=-=-=⎰b 022b0 2x 2sin )4A (2b A dx x 2cos 12A 1ααα()[]2b A )b x n 2sin(n 4b A 2b A 2b 0 22=ππ-=． b /2A 2=∴， b /2A = （16.3.15）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡<<ψ的定态波函数自由粒子中一维无限深矩形势阱)c (v ,（四）一维矩形无限深势阱中、自由粒子的几率分布从（16.3.17）式可得上述自由粒子的几率密度|ψ|2的表式：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡<<的几率密度自由粒子中一维矩形深势阱)c (v , （16.3.18）上述空间波函数u 和几率密度|ψ|2的图线，如（图16.3b ）所示．自由粒子的运动范围限制在0＜x ＜b ，因此（16.3.18）式的角度αx=n πx/b 的变化范围为0＜αx ＜n π．当量子数n=1时，u 1（x ）=)b /x sin(b /2π；,3,2,1n ,b x 0),b /x n sin(b /2)x (u ,e )b /x n sin(b /2)t ,x (/iEt =<<π=π=ψ- b x 0 ,,3,2,1n )b /x n sin()b /2(u 222<<=π==ψ21ψ=(2/b)sin 2(πx/b)．如（图16.3b ）所示，曲线u 1和21ψ的最高点都在πx/b=π/2，即x=b/2处．这就是说，当n=1时，在势阱中x=b/2处，粒子的几率密度最大．这与经典理论所说自由粒子应是均匀分布的结论不同．经典理论不能说明微观粒子的情况．当n=2时， )b /x 2(sin )b /2(),b /x 2sin(b /2)x (u 2222π=ψπ=．角度的变化范围是0＜αx ＜2π．曲线u 2的最高点在2πx/b=π/2，即x=b/4处．曲线u 2的最低点在2πx/b=3π/2，即x=3b/4处．曲线u 2还有一个零点在2πx/b=π，即x=b/2处，如图所示．当n=2时，几率密度22ψ的曲线应有两个最高点，在x=b/4和x=3b/4处，有一个零点在x=b/2处．当n=3和n=4时的曲线图，由同学们在习题中计算分析．（图16.3b ）所示曲线形状，与两端固定的弦线中，形成驻波的形状相似．虽然粒子的物质波与弦线中机械波的驻波，在本质上是不同的现象．但是人们仍然喜欢引用驻波中的熟悉名词描写微观粒子的几率分布，把2ψ=0的位置叫做波节或节点，把|ψ|2的最大位置叫做波腹或腹点．（五）一维矩形无限深势阱中、自由粒子的能级从（16.3.7）与（16.3.13）式可得到能量E 的表式： ⎢⎢⎢⎣⎡<<n E )c (的能级自由粒子中一维矩形深势阱v ,E n 是能量E 的本征值．粒子的能量E 只能具有这一系列分立的数值E n ，也就是说，能量E 是量子化的．上述的n 值相当于玻尔理论中的量子数．虽然能级E n 和量子数n 都是玻尔先提出的，但他只作为一种假设提出．而在量子力学中，从薛定谔方程解出波函数ψ的过程，很自然地得出E n 和n ，不必求助于人为的假设．最低的能级E 1是为基态能级，相当于n=1的E 1值．其他各级能量E n =n 2E 1，如（图16.3b ）所示．粒子的能量不能小于E 1．但经典理论原以为，粒子的最小能量为零，所以最小能量E 1也被称为零点能．〔例题16.3A 〕已知原子核的线度为b=10－14米的数量级，质子的静质量为m=1.67×10－27千克．假设质子在原子核内作线性自由运动．求：（1）此质子的能量E 和速率v ．（2）它的动量p 和物质波波长λ．（3）它的总能ε和频率ν．（4）它的空间波函数u(x)和几率密度|ψ|2．〔解〕（1）把此质子看做是在线度为b 的无限深矩形势阱中，作线性自由运动．应用（16.3.20）式可求得它的能量E （即动能E k ）：E=n 2（h 2/8mb 2）=n 2×6.632×10－68/8×1.67×10－27×10－28= =n 2×3.29×10－13焦． E=E k =m v 2/2， v 2=2E/m=2n 2×3.29×10－13/1.67×10－27=n 2×3.94×1014，v =n ×1.98×107米/秒．当v <<c 时，可应用上述计算和下面的计算．（2）p=m v =1.67×10－27×n ×1.98×107=n ×3.31×10－20千克·米/秒．λ=h/p=6.63×10－34/n ×3.31×10－20=(1/n)×2.00×10－14米．（3）ε=E k +mc 2=n 2×3.29×10－13+1.67×10－27×9×1016= =n 2×3.29×10－13＋1.50×10－10=1.50×10－10焦．ν=ε/h=1.50×10－10/6.63×10－34=2.26×1023赫，或ν=c 2/v λ=9×1016/n ×1.98×107×(1/n)×2×10－14=2.27×1023赫． （4）按（16.3.17）式可求得此质子的空间波函数u(x)和几率密度|ψ|2的表式，其图解如（图16.3b ）所示． u(x)=)b /x n sin(b /2π=1.41×107sin （n πx ×1014）米－1/2.|ψ|2=|u|2=2×1014sin 2（n πx ×1014）米－1．〔说明〕请注意德布罗意波长λ=(1/n)×2b ，即势阱宽度b=n （λ/2）．还请注意，本题讨论自由粒子的一维运动，它的|ψ|2与|u|2的单位决定于b 的单位．。
15-2 薛定谔方程及其应用
七、薛定谔方程的应用三
氢原子的量子理论
七、薛定谔方程的应用三
2. 解方程得到的主要结论 4 1 me （1）能量量子化 En 2 n 2 8 o h 2
氢原子的量子理论
n 1,2,
（主量子数）
（2）（轨道）角动量（大小）量子化
h L l (l 1) 2
l 0,1,2, (n 1)
E1 e E m B Lz B 2m
七、薛定谔方程的应用三 补充说明：
氢原子的量子理论
（1）氢原子中电子的稳定状态，可以用一组量子数 （n, l, ml）表示，其定态波函数为 nlml (r , , )
nlml 2
（2）根据求得的氢原子电子定态波函数 nlml (r , , ) 2 就可求得电子出现在原子核周围的概率密度 (r , , )
Pdr Rnl r dr Θ sin d
2 2 0
π
2
2π
0
Φ d
2
由归一化条件，对于基态（n=1, l=0）：
玻尔半径 2 0h
a0 π me
在 r r dr内， Rnl (r ) r 2 P
2
5.29 10
11
m
4 3e a0
2r a0
r2
x i 2 (t )
2. 波函数的物理意义
复函数 （自由粒子在空间各点等概率）
Ψ 0e
i
2 ( Et px ) h
t 时刻粒子在空间某点附近体积元 dV 中出现的 概率与该处波函数绝对值的平方成正比。即
2 * dW Ψ (r , t ) dV Ψ (r , t )Ψ (r , t )dV
第3章薛定谔方程及应用简例
n
1 2 3
En
π2 2 E1 2ma 2
n
2 π 1 sin x a a
P n
2 2πx P sin 1 a a
分子束缚 在箱子内
三维方势肼
方势阱
25
3.势垒
U( x)
U( x)
梯形势 散射问题
势垒 隧道贯穿
U( x)
U( x)
26
4.其他形式
超晶格
谐振子
27
一、一维无限深方形势阱
U=U0 U(x) 功函数 U=U0 极 U→∞ U(x) U→∞
E
U=0
金属
E
a 0 x 无限深方势阱 （ potential well ） U=0
为了方便将波函数脚标去掉
•令 将方程写成 •通解
k2
2mE 2
( x) k 2 ( x) 0
( x) A coskx B sinkx
式中 A 和 B 是待定常数
33
5.由波函数标准条件和边界条件定特解
通解是
( x) A coskx B sinkx
(1)解的形式
2
同学可以将波函数代入验证该方程
可以与经典的波动方程比较形式的不同
4
2. 写薛定谔方程的简单路径 自由粒子波函数 ( x,t )
i ( Px x E t) Ae
微分
( x,t) i － E ( x,t) t
注意到
i E t
( x,t) i P ( x,t) x x
利用
2 2 2 2 2 2 2 x y z
2 写为 i (r , t ) [ 2 U (r , t )] (r, t) t 2m
薛定谔方程——精选推荐
生足够强的电流了.
金属 E
真空 无场时的势能 E
有场时的势能
(2)超导体电子的隧道贯穿: 电子绝缘层穿过.
约瑟夫逊效应 两块或两片超导体之间存在的 势垒层（10～20埃）或弱连接形成超导结时， 超导电子对通过这些结而呈现的一系列电学、 磁学和辐射方面的特性、统称为约瑟夫逊效应 或超导电子隧道效应。
时间部分满足: 空间部分满足:
ih
∂ ∂t
f
(t)
=
Ef (t)
− h2 ∇2ϕ(r) +V (r)ϕ(r) = Eϕ(r)
2m
§25-3 一维无限深势阱
在这个问题里薛定谔方程为
−
h2 2m
dψ (x)
dx2
+
V
(
x)ψ
(
x)
=
Eψ
(
x)
其中势能为
V
(
x)
=
⎧ 0, ⎩⎨∞,
0< x<a x ≤ 0, x ≥ a
ξ=x α
薛定谔方程变为
d 2ψ dξ 2
+ (λ
− ξ 2 )ψ
=0
令
ψ = e−ξ 2 / 2u
考虑到
(e−ξ 2 / 2u)''= [u''−2ξu'+(ξ 2 −1)u]e−ξ 2 / 2
得到 u''−2ξu'+(λ −1)u = 0
u''−2ξu'+(λ −1)u = 0
这个方程的解称为厄米多项式. 在这里它要满足的边界条件为:
02 薛定谔方程及其应用
df = Edt ♦ 一个是变量为t 的方程 ih f 可以把它先解出来： 可以把它先解出来：
其解为
f = Ae
i t − E h
……（★） （
是待定复常数； 有能量量纲, （A 是待定复常数； E 有能量量纲,以后可知是 粒子的能量： 势能， 包括静能） 粒子的能量：动能 + 势能，不包括静能） 一个是变量为x ♦ 一个是变量为 的方程
∂2 ∂2 ∂2 ∇2 = 2 + 2 + 2 ∂x ∂y ∂z
奥地利物理学家 薛定谔 （Schrodinger 1887-1961） ）
1933年薛定谔获 年薛定谔获 诺贝尔物理奖。 诺贝尔物理奖。
说明： 说明： （1）它是一个复数偏微分方程； 它是一个复数偏微分方程； 复数偏微分方程 r 复函数。 其解波函数 Ψr, t) 是一个复函数。 ( 是一个复函数 （2）它的解满足态的叠加原理 r r 是薛定谔方程的解， 若 Ψ ( r , t )和 Ψ ( r , t ) 是薛定谔方程的解， 1 2 因为薛定谔方程是线性偏微分方程。 因为薛定谔方程是线性偏微分方程。 线性偏微分方程 （3）它并非推导所得，最初是假设，后来通过实验 它并非推导所得，最初是假设， 检验了它的正确性，地位相当“牛顿定律” 检验了它的正确性，地位相当“牛顿定律”。 （4）它是非相对论形式的方程。 它是非相对论形式的方程。
于是对每一个
n
值，波函数的空间部分为
2 nπ sin x, n = 2,4,6,L ψon = a a 2 nπ cos x, n =1,3,5,L ψen = a a ψn = 0,
这些波函数也称为能量本征函数。 这些波函数也称为能量本征函数。 能量本征函数
｝
a x≤ 2