薛定谔方程及其简单应用共37页文档
合集下载
18.0 薛定谔方程及其应用
一维运动粒子的含时薛定谔方程
Ψ ( x , t ) = ψ ( x )φ (t ) = ψ 0 ( x ) e
2 2
− i 2 π Et / h
在势场中一维运动粒子的定态薛定谔方程 势场中一维运动粒子的定态薛定谔方程 运动粒子的定态
d ψ 8π m + ( E − E p )ψ ( x ) = 0 2 2 dx h
一. 物质波的波函数
微观粒子 具有波动性
1925年薛定谔 年薛定谔
用物质波波函数描述 微观粒子的概率波
轴正方向运动，由于其能量、动量为常量， 例如 自由粒子沿 x 轴正方向运动，由于其能量、动量为常量， 不随时间变化，其物质波是单色平面波， 所以 v 、 λ 不随时间变化，其物质波是单色平面波，波 函数为
r 2 r * r dW =|Ψ(r,t)| dV =Ψ(r,t)Ψ (r,t)dV
2. 归一化条件 (粒子在整个空间出现的概率为 粒子在整个空间出现的概率为1) 粒子在整个空间出现的概率为
r 2 ∫∫∫|Ψ(r,t)| dxdydz =1
3. 波函数必须单值、有限、连续 波函数必须单值、有限、 概率密度在任一处都是唯一、有限的 概率密度在任一处都是唯一、有限的, 并在整个空间内连续
2
归一化条件 归一化条件
2 a A sin 2 0
∫−∞ ψ
∞
2
dx = ∫ ψψ dx = 1
* 0
a
∫
nπ xd x = 1 a
2 A= a
ψ ( x) =
2 nπ sin x , (0 ≤ x ≤ a ) a a
d ψ 8π mE + ψ = 0 ∞ Ep ∞ 波动方程 2 2 dx h
2 2
薛定谔方程及其简单应用
75.5neV
当n>>1时，能量相对间隔
En En
21 nn
当
n 时
E E 量子化不显著。
n
n
经典物理可看成是
n 时量子物理的特殊情况。
H
26
a =102 m时：
E
n 2h 2 8ma 2
8n29(.61.61301310314)024
3.7 810 1n 52ev
显然电子在宏观尺度上运动时其能级差是很小的。
H
24
经典理论中，处于无限深方势阱中粒子
的能量为连续值，粒子在阱内运动不受限制， 各处概率相等。
| |2
n4
随着能级的升高，几率密度的峰值增多，
当
时，粒子在势阱内各处出现的概率
n 相等，量子力学的结果过渡到经典力学的情
况。
n3 n2
0
a/2
n1 a
从以上分析可知：对于无限深势阱来说，粒子只能在势阱U=0的区域能运 动。。
2 m 2d2d 32 (x x)E 3(x), xa
aa
n 很大时，相邻波腹靠得很近，接近经典 力学各处概率相同。
H
3x
E3
2x
E2
1x E 1
o
n+1个
x a节点
稳定的驻波能级23
一维无限深方势阱中粒子的能级、波函数和几率密度
n4
| |2
4
16E1
3
n3
9E1
n2
n1 0
a/2
2
1 a0
a/2
4E1 E1 a Ep 0
对于不同的量子数，在阱内某一特定的点，粒子出现的几率是不同的。
粒 r 处 子 的 在 2 （ 几 r ,t) （ *r ,t 率 )
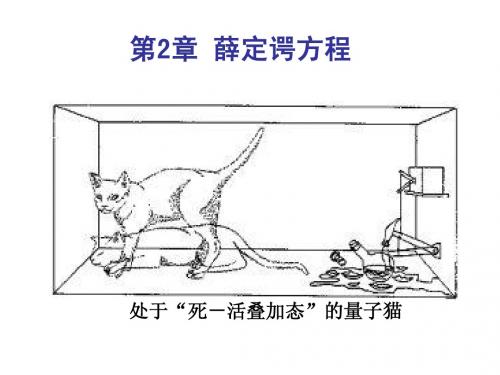
《薛定谔方程》课件
波函数需要满足归一化条件，即 ∫Ψ*(r,t)Ψ(r,t)dV=1，以确保粒 子存在于有限空间内。
时间演化算符
时间演化算符定义
时间演化算符描述波函数的演化过程，通常表示为 U(t)，其中t是时间。
时间演化算符的性质
时间演化算符是幺正算符，即U(t)U*(t)=I，其中I是 单位算符。
时间演化算符的作用
时间演化算符可以将初始时刻的波函数演化到任意时 刻的波函数。
能量算符
能量算符定义
能量算符描述微观粒子的能 量，通常表示为H。
能量算符的性质
能量算符是厄米特算符，即 H=H*。
能量算符的作用
能量算符可以将波函数投影 到能量本征态上，得到粒子 的能量。
边界条件和初始条件
边界条件
描述波函数在边界上的行为，如周期 边界、反射边界等。
原理
通过选取适当的变分函数，将薛定谔方程的 求解问题转化为求变分极值的问题。
步骤
选取合适的变分函数，将薛定谔方程转化为变分问 题，然后利用变分法的基本原理求解该问题。
应用范围
适用于具有某些特殊性质的薛定谔方程，如 具有对称性、周期性等性质的问题。
04
薛定谔方程的经典实例
一维无限深势阱
描述
一维无限深势阱是一个理想化的模型，用于描述粒子在一维空间中的 运动，其中势能只在有限区域内存在。
在生物学中，它可以用来描述生物分子的结构和性质， 如蛋白质的结构和功能等。
02
薛定谔方程的基本概念
波函数
01
波函数定义
波函数是描述微观粒子状态的函 数，通常表示为Ψ(rห้องสมุดไป่ตู้t)，其中r是 位置向量，t是时间。
02
波函数的性质
B11_薛定谔方程
U ( r , t )
2 2
引入拉普拉斯算符 引入哈密顿算符
(Hamiltonian operator)
2
2 2
2
x
y
2 2
薛定谔方程：
i t ˆ H
z
ˆ H
2 U (r , t )
2m
4、关于薛定谔方程的说明 是量子力学的一个基本原理；是量子力学的基本方程， 描述非相对论性粒子波函数的演化规律。 是线性齐次微分方程，解满足态叠加原理 若 1 和 2 是方程的解，则它们的线性组合 （C11＋C22）也一定是方程的解。 方程中含有虚数 i 它的解 是复函数，复数不能直接测量。 而 的模方代表概率密度，可测量。 2 薛定谔方程关于时间是一阶的，这 2 2 u 2 不同于经典波动方程（时间二阶） t
U ( r , t )
若势函数U不显含t，为求解薛定谔方程，分离变量 (r , t ) (r ) T (t )
ˆ 代入薛定谔方程，得 i d T ( t ) ( r ) [ H ( r )]T ( t ) dt
dT(t ) 除以 ( r ) T ( t ) ，得 i
( x ) A sin kx ） 待定常数A、 由 应满足的物理条件决定。 （
以上的解已自然满足单值，有限的条件。 连续条件： 由于边界外 = 0，所以有：
x a 2 a , 0 A sin ( ka 2 ) 0
ka 2
l1
2 l1 l 2 ) l （ l
x
, 0 A sin (
15 量子物理学的诞生 薛定谔方程及应用
2 2
一维自由粒子的 含时薛定谔方程
2、一维势场 U ( x , t ) 中运动粒子薛定谔方程
P E Ek U U 2m Ψ i EΨ t 2Ψ P2 2 Ψ 2 x
2
Ψ i P2 [ U ( x , t )]Ψ t 2m
Ψ ( x, t ) Ψ oe
x
E p0
A B
2 一维无限深势阱
0
0
a x
U (x)
0 0< x < a
x 0, x a
U 与t 无关，写出定态定谔方程
1
1= 0
d Φ UΦ EΦ 2 2m dx
2 2
0 2
3
3 = 0
1 势阱外
dΦ Φ EΦ 2 2m dx
2 2
x
0
a
x
讨论
1.能量只能取分立值 是解薛定谔方程自然而然得到的结论。 按经典理论……粒子的“能量连续”； 但量子力学……束缚态能量只能取分立值（能级）
2.当 m 很大（宏观粒子）时，能量连续， 量子 经典。 3.最低能量不为零（称零点能） 2 2 E1 0 2 ———符合不确定关系。 2 ma
2 2 Φ UΦ EΦ 2m
定态薛定薛方程 一维定态薛定谔方程
2m Φ 2 ( E U )Φ 0
2
d 2Φ( x ) 2m 2 (E U)Φ( x ) 0 2 dx
势阱中的粒子 势垒 谐振子
一、 一维无限深势阱
1 势阱
U (x)
金属表面
金属中自 由电子的 势能曲线
推广到三维情况， 2 2Ψ Ψ U ( x , t )Ψ i 薛定谔方程可写为： 2
一维自由粒子的 含时薛定谔方程
2、一维势场 U ( x , t ) 中运动粒子薛定谔方程
P E Ek U U 2m Ψ i EΨ t 2Ψ P2 2 Ψ 2 x
2
Ψ i P2 [ U ( x , t )]Ψ t 2m
Ψ ( x, t ) Ψ oe
x
E p0
A B
2 一维无限深势阱
0
0
a x
U (x)
0 0< x < a
x 0, x a
U 与t 无关，写出定态定谔方程
1
1= 0
d Φ UΦ EΦ 2 2m dx
2 2
0 2
3
3 = 0
1 势阱外
dΦ Φ EΦ 2 2m dx
2 2
x
0
a
x
讨论
1.能量只能取分立值 是解薛定谔方程自然而然得到的结论。 按经典理论……粒子的“能量连续”； 但量子力学……束缚态能量只能取分立值（能级）
2.当 m 很大（宏观粒子）时，能量连续， 量子 经典。 3.最低能量不为零（称零点能） 2 2 E1 0 2 ———符合不确定关系。 2 ma
2 2 Φ UΦ EΦ 2m
定态薛定薛方程 一维定态薛定谔方程
2m Φ 2 ( E U )Φ 0
2
d 2Φ( x ) 2m 2 (E U)Φ( x ) 0 2 dx
势阱中的粒子 势垒 谐振子
一、 一维无限深势阱
1 势阱
U (x)
金属表面
金属中自 由电子的 势能曲线
推广到三维情况， 2 2Ψ Ψ U ( x , t )Ψ i 薛定谔方程可写为： 2
第二十七章薛定谔方程ppt课件
粒子在x距离内的动量不确定度为
p 2x
2m(U0 E)
粒子进入该区域的速度为
xpx 2
v v p 2(U0 E)
m
m
则粒子进入的时间不确定度为
x
m
t
v 2 2m(U0 E) 2(U0 E) 4(U0 E)
根据能量-时间的不确定关系，粒子能量的不确定度为
E 2t 2(U0 E)
En
pn2 2m
,
k
n
a
x0 a 2
16E1
9E1 4E1 E1
ax
粒子的德布罗意波长
k n
n
h pn
2a n
2
k
a
, n 1, 2,...
波长也是量子化的，为势阱宽度2倍的整数分之一
n与两端固定弦的驻波波 长形式相同（见P158式n=2L/n）
n
n (x) 2
En
L
4 a 2
1 2L 1 2
2.无限深方势阱中粒子的波函数
一维定态薛定谔方程
2
2m
2
x2
U x
E
势阱外：x<0，x>a区域(边界条件)，U=∞，不会有粒子
存在，则
0 , x 0, x a
势阱内：0≤x≤a区域，U=0，则有方程
2
x2
2mE
2
0
令
k2
2mE
2
k
2mE
2
x2
k 2
0
2
x2
k 2
0
与简谐运动方程
d2x dt 2
用波函数来描述微观粒子的运动
经典波的波函数:
机械波 y(x,t) Acos 2π( t x )
p 2x
2m(U0 E)
粒子进入该区域的速度为
xpx 2
v v p 2(U0 E)
m
m
则粒子进入的时间不确定度为
x
m
t
v 2 2m(U0 E) 2(U0 E) 4(U0 E)
根据能量-时间的不确定关系，粒子能量的不确定度为
E 2t 2(U0 E)
En
pn2 2m
,
k
n
a
x0 a 2
16E1
9E1 4E1 E1
ax
粒子的德布罗意波长
k n
n
h pn
2a n
2
k
a
, n 1, 2,...
波长也是量子化的，为势阱宽度2倍的整数分之一
n与两端固定弦的驻波波 长形式相同（见P158式n=2L/n）
n
n (x) 2
En
L
4 a 2
1 2L 1 2
2.无限深方势阱中粒子的波函数
一维定态薛定谔方程
2
2m
2
x2
U x
E
势阱外：x<0，x>a区域(边界条件)，U=∞，不会有粒子
存在，则
0 , x 0, x a
势阱内：0≤x≤a区域，U=0，则有方程
2
x2
2mE
2
0
令
k2
2mE
2
k
2mE
2
x2
k 2
0
2
x2
k 2
0
与简谐运动方程
d2x dt 2
用波函数来描述微观粒子的运动
经典波的波函数:
机械波 y(x,t) Acos 2π( t x )
薛定谔方程及其应用
薛定谔方程及其应用薛定谔方程是量子力学的基础方程之一，描述了微观粒子的行为和性质。
它由奥地利物理学家薛定谔于1925年提出，被广泛应用于原子物理、分子物理、凝聚态物理等领域。
本文将介绍薛定谔方程的基本原理以及其在量子力学研究和实际应用中的重要性。
薛定谔方程是描述量子力学体系中粒子的波动性质的基本方程。
它的一般形式为：iħ∂Ψ/∂t = ĤΨ其中，i是虚数单位，ħ是约化普朗克常数，Ψ是波函数，t是时间，Ĥ是哈密顿算符。
薛定谔方程是一个偏微分方程，描述了波函数随时间的演化规律。
通过求解薛定谔方程，可以得到粒子的波函数，从而计算出粒子的能量、动量、位置等物理量。
薛定谔方程的解可以用波函数表示，波函数的模的平方表示了粒子存在于不同位置的概率。
波函数的具体形式取决于体系的边界条件和势能场。
对于自由粒子，波函数可以用平面波表示；对于束缚态，波函数则由边界条件和势能场决定。
薛定谔方程的解可以通过数值计算或近似方法求得。
薛定谔方程在量子力学的研究中起着重要的作用。
它可以用来描述原子和分子的电子结构，解释化学反应的机理，预测材料的性质等。
在原子物理中，薛定谔方程被用来计算原子的能级和光谱线；在分子物理中，薛定谔方程可以用来研究分子的振动和转动；在凝聚态物理中，薛定谔方程被用来描述电子在晶体中的行为和导电性质。
除了用于研究基本粒子和物质的性质，薛定谔方程还被应用于量子计算和量子通信等领域。
量子计算是一种基于量子力学原理的新型计算方法，利用量子叠加和量子纠缠的特性，可以在某些情况下比传统计算方法更高效。
薛定谔方程提供了描述量子比特（qubit）行为的数学工具，为量子计算的实现提供了理论基础。
此外，薛定谔方程还被应用于量子力学中的一些基本现象的研究，如量子隧穿效应、量子干涉和量子纠缠等。
这些现象在实验室中已经得到了验证，并且在量子信息科学和量子技术的发展中发挥着重要作用。
总之，薛定谔方程是量子力学的基本方程之一，描述了微观粒子的波动性质。
张丹海《简明大学物理》11-7 薛定谔方程
得
f (t ) 2 i (r ) f (t )( V ) (r ) t 2m
2
两边同除以 Ψ ( r , t ) Ψ ( r ) f ( t ) 得
i f (t ) f (t ) t 1 2 (r ) V ( r ) 2m
上页
下页
返回
帮助
11-7 薛定谔方程
第十一章 量子物理基础
扫描遂穿显微镜 ( STM )原理图
上页
下页
返回
帮助
11-7 薛定谔方程
第十一章 量子物理基础
扫描隧道显微镜中的原子形象
量子围栏照片
上页
下页
返回
帮助
0 xa
2
d (x) dx
2m E
2
E ( x )
2m
令 k
d
2
dx
2
k 0
2
上式的通解为
( x ) A sin kx B cos kx
上页 下页 返回 帮助
11-7 薛定谔方程
第十一章 量子物理基础
( x ) A sin kx B cos kx
粒子的能量虽不足以超越 势垒 , 但在势垒中似乎有一个 隧道, 入 能使少量粒子穿过而进 的区域 , 所以人
(x)
1
2
3
x a
o
a
x
们形象地称之为隧道效应。
隧道效应的本质：来源于微观粒子的波粒二相。
上页
下页
返回
帮助
11-7 薛定谔方程
应用
第十一章 量子物理基础
1981年宾尼希和罗雷尔利用电子的隧道效应制成了扫描遂 穿显微镜 ( STM ), 可观测固体表面原子排列的状况。1986年 宾尼希又研制了原子力显微镜。
薛定谔方程及其应用
21.5 波函数 薛定谔方程 一 、波函数 1、经典的波与波函数 、 机械波
y ( x , t ) = A cos 2π (ν t −
x
λ
)
电磁波
E ( x , t ) = E 0 cos 2π (νt − )
x
λ
经典波为实 经典波为实函数
H ( x , t ) = H 0 cos 2π (ν t − )
7
例：作一维运动的粒子被束缚在0<x<a 作一维运动的粒子被束缚在 的范围内，已知其波函数为： 的范围内，已知其波函数为：
Ψ ( x ) = A sin
πx
a
求：(1)常数 ；(2)粒子在 到a/2区域内出现的概率；(3)粒子在何 常数A； 粒子在0到 区域内出现的概率； 粒子在何 常数 粒子在 区域内出现的概率 处出现的概率最大？ 处出现的概率最大？ 解：(1)由归一化条件 由归一化条件
求二阶偏导： 对 x 求二阶偏导：
i − ( Et − px ) ℏ
i = − EΨ ( x , t ) ① ℏ
Ψ ( x , t ) = Ae
i − ( Et − px ) ℏ
i ∂Ψ ( x , t ) i = pΨ0 e = pΨ( x , t ) ℏ ℏ ∂x i 2 2 − ( Et − px ) ∂ Ψ ( x , t ) ip 2 p ℏ = ( ) Ψ 0e = − 2 Ψ( x , t ) ② 2 ∂x ℏ ℏ
1 ∂f ( t ) 1 ℏ2 2 iℏ [− = ∇ ϕ ( r ) + U ( r )ϕ ( r )] = E ϕ ( r ) 2m f ( t ) ∂t
d 2π 2πx 2 sin Ψ = =0 dx a a 即当 2πx = kπ , k = 0,±1,±2, ⋯ a
y ( x , t ) = A cos 2π (ν t −
x
λ
)
电磁波
E ( x , t ) = E 0 cos 2π (νt − )
x
λ
经典波为实 经典波为实函数
H ( x , t ) = H 0 cos 2π (ν t − )
7
例：作一维运动的粒子被束缚在0<x<a 作一维运动的粒子被束缚在 的范围内，已知其波函数为： 的范围内，已知其波函数为：
Ψ ( x ) = A sin
πx
a
求：(1)常数 ；(2)粒子在 到a/2区域内出现的概率；(3)粒子在何 常数A； 粒子在0到 区域内出现的概率； 粒子在何 常数 粒子在 区域内出现的概率 处出现的概率最大？ 处出现的概率最大？ 解：(1)由归一化条件 由归一化条件
求二阶偏导： 对 x 求二阶偏导：
i − ( Et − px ) ℏ
i = − EΨ ( x , t ) ① ℏ
Ψ ( x , t ) = Ae
i − ( Et − px ) ℏ
i ∂Ψ ( x , t ) i = pΨ0 e = pΨ( x , t ) ℏ ℏ ∂x i 2 2 − ( Et − px ) ∂ Ψ ( x , t ) ip 2 p ℏ = ( ) Ψ 0e = − 2 Ψ( x , t ) ② 2 ∂x ℏ ℏ
1 ∂f ( t ) 1 ℏ2 2 iℏ [− = ∇ ϕ ( r ) + U ( r )ϕ ( r )] = E ϕ ( r ) 2m f ( t ) ∂t
d 2π 2πx 2 sin Ψ = =0 dx a a 即当 2πx = kπ , k = 0,±1,±2, ⋯ a
第一章薛定谔方程
相等, 即:ρ=*=A*A=常数,因
此 x的位置完全不确定。
三、势阱中的粒子
1.一维无限势阱
在区间I和III, Schroedinger方程为:
d 2
dx2
2m 2
(E
)
0
即:
d 2
dx2
,
1
d 2
dx2
0
因此, I 0, III 0.
在区间II, Schroedinger方程为:
0
l
l
1
2 l 3x
mx
sin( )sin(
l0
l
l
)dx
3m
量子力学中的隧道效应问题:
在经典力学中, 若势阱中粒子的总能量E
小于势阱的高度 V=c, 这时粒子不可能跑到
势阱外面。
但在量子力学中, 由于粒子具有波动性,
通过理论计算可以证明, 粒子可以出现在势
阱外。
≠0 V=c
V(x) V=0 E<c
dx2
2mE ( 2
mk x2 2
)
0. 令 :
2mE 2
,
mk 2
得:
d 2
dx2
(
x2 )
0
(1.8)
方程(1.8)可通过幂级数法求解(Powerseries solution) ,得到一维谐振子体系的解:
n
(
x)
Nn
exp(
1 2
z2
)Hn
h2
8 2m
(
2 x 2
2 y2
2 z 2
此 x的位置完全不确定。
三、势阱中的粒子
1.一维无限势阱
在区间I和III, Schroedinger方程为:
d 2
dx2
2m 2
(E
)
0
即:
d 2
dx2
,
1
d 2
dx2
0
因此, I 0, III 0.
在区间II, Schroedinger方程为:
0
l
l
1
2 l 3x
mx
sin( )sin(
l0
l
l
)dx
3m
量子力学中的隧道效应问题:
在经典力学中, 若势阱中粒子的总能量E
小于势阱的高度 V=c, 这时粒子不可能跑到
势阱外面。
但在量子力学中, 由于粒子具有波动性,
通过理论计算可以证明, 粒子可以出现在势
阱外。
≠0 V=c
V(x) V=0 E<c
dx2
2mE ( 2
mk x2 2
)
0. 令 :
2mE 2
,
mk 2
得:
d 2
dx2
(
x2 )
0
(1.8)
方程(1.8)可通过幂级数法求解(Powerseries solution) ,得到一维谐振子体系的解:
n
(
x)
Nn
exp(
1 2
z2
)Hn
h2
8 2m
(
2 x 2
2 y2
2 z 2
15-2 薛定谔方程及其应用
七、薛定谔方程的应用三
氢原子的量子理论
七、薛定谔方程的应用三
2. 解方程得到的主要结论 4 1 me （1）能量量子化 En 2 n 2 8 o h 2
氢原子的量子理论
n 1,2,
（主量子数）
（2）（轨道）角动量（大小）量子化
h L l (l 1) 2
l 0,1,2, (n 1)
E1 e E m B Lz B 2m
七、薛定谔方程的应用三 补充说明：
氢原子的量子理论
（1）氢原子中电子的稳定状态，可以用一组量子数 （n, l, ml）表示，其定态波函数为 nlml (r , , )
nlml 2
（2）根据求得的氢原子电子定态波函数 nlml (r , , ) 2 就可求得电子出现在原子核周围的概率密度 (r , , )
Pdr Rnl r dr Θ sin d
2 2 0
π
2
2π
0
Φ d
2
由归一化条件，对于基态（n=1, l=0）：
玻尔半径 2 0h
a0 π me
在 r r dr内， Rnl (r ) r 2 P
2
5.29 10
11
m
4 3e a0
2r a0
r2
x i 2 (t )
2. 波函数的物理意义
复函数 （自由粒子在空间各点等概率）
Ψ 0e
i
2 ( Et px ) h
t 时刻粒子在空间某点附近体积元 dV 中出现的 概率与该处波函数绝对值的平方成正比。即
2 * dW Ψ (r , t ) dV Ψ (r , t )Ψ (r , t )dV
第3章薛定谔方程及应用简例
n
1 2 3
En
π2 2 E1 2ma 2
n
2 π 1 sin x a a
P n
2 2πx P sin 1 a a
分子束缚 在箱子内
三维方势肼
方势阱
25
3.势垒
U( x)
U( x)
梯形势 散射问题
势垒 隧道贯穿
U( x)
U( x)
26
4.其他形式
超晶格
谐振子
27
一、一维无限深方形势阱
U=U0 U(x) 功函数 U=U0 极 U→∞ U(x) U→∞
E
U=0
金属
E
a 0 x 无限深方势阱 （ potential well ） U=0
为了方便将波函数脚标去掉
•令 将方程写成 •通解
k2
2mE 2
( x) k 2 ( x) 0
( x) A coskx B sinkx
式中 A 和 B 是待定常数
33
5.由波函数标准条件和边界条件定特解
通解是
( x) A coskx B sinkx
(1)解的形式
2
同学可以将波函数代入验证该方程
可以与经典的波动方程比较形式的不同
4
2. 写薛定谔方程的简单路径 自由粒子波函数 ( x,t )
i ( Px x E t) Ae
微分
( x,t) i － E ( x,t) t
注意到
i E t
( x,t) i P ( x,t) x x
利用
2 2 2 2 2 2 2 x y z
2 写为 i (r , t ) [ 2 U (r , t )] (r, t) t 2m
薛定谔方程及简单应用
i Et
(x) ei Et
由d2 (x)
dx 2
p2 2
(x)
和
p2 E
2m
振幅函数
得
d2 (x) 2mE (x) 0
dx 2
2
自由粒子的振幅方程
（二）定态薛定谔方程
粒子在力场中运动，且势能不随时间变化
E
Ek
Ep
p2 2m
U ；p2
2m(E
U)
代入
d 2 ( x)
dx 2
p 2
2
( x)
U(x) =
x 0, x a
o
ax
代入一维定态薛定谔方程
d2
d x2
2m 2
(
E
U )
0
得本问题中的薛定谔方程: 0<x<a
U
d2
d x2
2m 2
E
0
x 0, x a
o
a
x
d2
d x2
2m 2
E
0
0 （粒子不能逸出势阱）
2. 求解波函数
由
d2
dx 2
2mE 2
0
0 x a
令
k
2
最小能量E1即零点能,
o
n= 4
n= 3
n= 2
n= 1
a
x
粒子不可能静止不动， 满足不确定关系
由
E
k 22 2m
n2 22
2ma 2
n2E1
E
En1
En
2n
1
22
2ma 2
n E
(n 1,2,3,...)
E n= 4
a E
Schrodinger方程及应用
Schrodinger方程及应用薛定谔方程是量子力学中的基本方程之一，描述了微观粒子的运动和行为。
本文将介绍薛定谔方程的基本原理和应用，并探讨其在物理、化学和工程领域的重要性。
薛定谔方程由奥地利物理学家艾尔温·薛定谔于1925年提出。
这个方程揭示了微观粒子（如电子和原子等）的双重性质，即既可以表现为粒子，又可以表现为波动。
薛定谔方程的形式如下：iħ∂Ψ/∂t = ĤΨ其中，ħ是普朗克常量的约化形式，Ψ是波函数，t是时间，Ĥ是哈密顿算符。
薛定谔方程可以用来描述系统的演化，并预测粒子的位置、动量和能量等物理量的概率分布。
薛定谔方程的解是波函数，用于描述粒子在空间中的分布。
波函数的模的平方给出了粒子在不同位置上被观测到的概率。
这种概率性描述在传统物理理论中是无法解释的，但在量子力学中得到了很好的解释。
薛定谔方程在量子力学的许多应用中起到了关键作用。
首先，它可以用来计算和预测原子和分子的能级和光谱。
通过求解薛定谔方程，我们可以得到包括电子在内的粒子在各种势场中的能量。
这为解释和预测原子和分子的化学行为提供了理论基础。
其次，薛定谔方程也被广泛应用于材料科学和纳米技术领域。
通过求解薛定谔方程，研究者可以了解材料的电子结构和载流子行为，从而设计出具有特定性能和功能的新材料。
例如，在半导体器件的设计中，通过计算材料的能带结构和载流子的输运性质，可以优化器件的性能。
另外，薛定谔方程还被广泛运用于量子力学系统的模拟和计算。
利用计算机数值求解薛定谔方程，可以模拟和研究各种量子系统，如原子核、凝聚态物质和量子计算机等。
这为研究人员提供了一个重要的工具，帮助他们理解和探索微观世界的奥秘。
除了物理和化学领域，薛定谔方程还在工程应用中发挥着重要作用。
例如，在量子信息技术中，薛定谔方程被用于描述和处理量子比特（qubit）的演化和相互作用。
这对于实现量子计算和量子通信等新一代技术具有重要意义。
总结而言，薛定谔方程是量子力学的基本方程之一，描述了微观粒子的波动性和运动行为。
02 薛定谔方程及其应用
df = Edt ♦ 一个是变量为t 的方程 ih f 可以把它先解出来： 可以把它先解出来：
其解为
f = Ae
i t − E h
……（★） （
是待定复常数； 有能量量纲, （A 是待定复常数； E 有能量量纲,以后可知是 粒子的能量： 势能， 包括静能） 粒子的能量：动能 + 势能，不包括静能） 一个是变量为x ♦ 一个是变量为 的方程
∂2 ∂2 ∂2 ∇2 = 2 + 2 + 2 ∂x ∂y ∂z
奥地利物理学家 薛定谔 （Schrodinger 1887-1961） ）
1933年薛定谔获 年薛定谔获 诺贝尔物理奖。 诺贝尔物理奖。
说明： 说明： （1）它是一个复数偏微分方程； 它是一个复数偏微分方程； 复数偏微分方程 r 复函数。 其解波函数 Ψr, t) 是一个复函数。 ( 是一个复函数 （2）它的解满足态的叠加原理 r r 是薛定谔方程的解， 若 Ψ ( r , t )和 Ψ ( r , t ) 是薛定谔方程的解， 1 2 因为薛定谔方程是线性偏微分方程。 因为薛定谔方程是线性偏微分方程。 线性偏微分方程 （3）它并非推导所得，最初是假设，后来通过实验 它并非推导所得，最初是假设， 检验了它的正确性，地位相当“牛顿定律” 检验了它的正确性，地位相当“牛顿定律”。 （4）它是非相对论形式的方程。 它是非相对论形式的方程。
于是对每一个
n
值，波函数的空间部分为
2 nπ sin x, n = 2,4,6,L ψon = a a 2 nπ cos x, n =1,3,5,L ψen = a a ψn = 0,
这些波函数也称为能量本征函数。 这些波函数也称为能量本征函数。 能量本征函数
｝
a x≤ 2
薛定谔方程的应用
例：n=8
0
a
（4）当 n，粒子在各处出现的几率相同 ——量子化消失 （ En En能级连成一片）
二. 势垒穿透和隧道效应
m
U0 E
U
3
x
U 0 0 x a U ( x) 0 x 0, x a
薛定谔方程：
2mE 2 1( x ) 0 (1) x 0, x a 2 x 2 2 ( x ) 2 m( E U 0 ) 2( x ) 0 0 x a 2 2 x
(r , t ) (r )e
i Et
能量本征方程 动量本征方程
一维无限深势阱 1 一维无限深势阱中粒子的运动
（1） 求解. 设粒子处在势阱U(x)中
解:显然在
x 0, x a 的区域内 ( x) 0 (0) 0 (a) 0
U ( x) 0 0 x a （定态问题） U ( x) x 0, x a
i E t 2 n sin xe , 0 xa n ( x, t ) a a 0, x 0, x a
n
例题2 证明无限深方势阱中，不同能级的粒子波函数 具有下面的性质
d 0
* 1 2
这种性质称为正交性，即不同能级的波函数是互相正交的。 解将m能级的波函数 m 取其复共轭 m ，与n能级的波函数
x 0,U ( 0) , ( 0) 0
代入： ( x)
x a,U ( a ) , ( a ) 0
Asin kx B cos kx
得:
0 Asin 0 B cos0 0 Asin ka B coska
0 Asin 0 B cos0 0 Asin ka B coska
0
a
（4）当 n，粒子在各处出现的几率相同 ——量子化消失 （ En En能级连成一片）
二. 势垒穿透和隧道效应
m
U0 E
U
3
x
U 0 0 x a U ( x) 0 x 0, x a
薛定谔方程：
2mE 2 1( x ) 0 (1) x 0, x a 2 x 2 2 ( x ) 2 m( E U 0 ) 2( x ) 0 0 x a 2 2 x
(r , t ) (r )e
i Et
能量本征方程 动量本征方程
一维无限深势阱 1 一维无限深势阱中粒子的运动
（1） 求解. 设粒子处在势阱U(x)中
解:显然在
x 0, x a 的区域内 ( x) 0 (0) 0 (a) 0
U ( x) 0 0 x a （定态问题） U ( x) x 0, x a
i E t 2 n sin xe , 0 xa n ( x, t ) a a 0, x 0, x a
n
例题2 证明无限深方势阱中，不同能级的粒子波函数 具有下面的性质
d 0
* 1 2
这种性质称为正交性，即不同能级的波函数是互相正交的。 解将m能级的波函数 m 取其复共轭 m ，与n能级的波函数
x 0,U ( 0) , ( 0) 0
代入： ( x)
x a,U ( a ) , ( a ) 0
Asin kx B cos kx
得:
0 Asin 0 B cos0 0 Asin ka B coska
0 Asin 0 B cos0 0 Asin ka B coska