正式稿二分法求方程的根演示文稿
二分法求解方程PPT优秀课件

算法的特点
有穷性 确定性 可行性
算法的描述
一般有下列三种描述方法 1)自然语言 2)框图语言——流程图 3)程序语言
基本语句
输入输出语句 赋值语句 条件语句 循环语句
算法学习的意义
有利于培养学生的思维能力 有利于培养学生理性精神和实践能力 有利于学生理解构造性数学
ab 2
循环语句
repeat If f (a b) 0
2
then 跳出repeat 循环; else if f(a) f (a b) 0
2
then b:= a b
2
else a:=
ab 2
until b-a < ε ;
说明
选择一个适当的语言实现上述步骤, 标准并未对这一点进行要求。
ab
输出 2
.
输入、输出语句
输入ε ;
输出 a b . 2
a:=-1; b:=5;
赋值语句
条件语句
If
f (a b) 0 2
then 跳出repeat 循环; else if f(a) f (a b) 0
2
then b:= a b
2
else a:=
循环结构的算法
输出1000以内所有能被 3和5整除的正整数。
循环结构的三个要素 1)循环变量 2)循环体 3)循环终止条件
循环结构的算法
循环结构比较困难的是,决定循环结束 的条件,我们通常都是用变量表示循环 结束的条件,一般有两种情况:
一是,用循环变量表示循环的次数; 二是,用循环变量表示精度或其他的量。
――[阿萨·赫尔帕斯爵士] 115.旅行的精神在于其自由,完全能够随心所欲地去思考.去感觉.去行动的自由。――[威廉·海兹利特]
用二分法求方程的根

⽤⼆分法求⽅程的根总时间限制: 1000ms 内存限制: 65536kB题⽬链接:/function1/4/描述⽤⼆分法求下⾯⽅程在(-10, 10)之间的⼀个根。
2x3- 4x2+ 3x- 6 = 0输⼊⼀个⼩于1的⾮负实数e,它的值表⽰所能允许的误差输出⼀个实数,其值为求得的⼀个根,要求精确到⼩数点后8位。
若该区间上没有根,则输出“No Solution”样例输⼊样例输出2.00000000提⽰对于⼀个连续函数f(x),若f(a)*f(b) <= 0,则f(x)在区间[a, b]内⾄少有⼀个根。
特别的,对于⼀个单调的连续函数,上述定理得逆定理也成⽴若[a, b]上有根,则可进⼀步考察根是否在 [a, (a+b)/2]内,或者在[(a+b)/2, b]内。
若b-a <= e 则可终⽌迭代,并认为(a+b)/2是⼀个近似解,将它输出请使⽤double类型!1 #include<stdio.h>2 #include<math.h>3double f(double x);4double fun(double a,double b,double e);5int main()6 {7double e,x1,x2,x;8 x1=-10;x2=10;9 scanf("%lf",&e);10 x=fun(x1,x2,e);11 printf("%.8lf\n",x);12return0;13 }14double f(double x)15 {16double y;17 y=2*x*x*x-4*x*x+3*x-6;18return y;19 }20double fun(double a,double b,double e)21 {22double fa,fb,fc,c;23 fa=f(a);24 fb=f(b);25 c=(a+b)/2;26while(fabs(b-a)>e)27 {28 fc=f(c);29if(fc==0)30 {31break;32 }33else if(fc*fa<0)34 {35 b=c;36 fb=fc;37 }38else39 {40 a=c;41 fa=fc;42 }43 c=(a+b)/2;44 }45return c;46 }这个题⽬要⽤while语句实现才可以通过。
实验7二分法求方程的根

实验7二分法求方程的根实验7 二分法求方程的根一、问题:求324100x x +-=于区间[1,2]内的一个实根,且要求精确到0.001 二、算法:第一步:计算);(),(21b f y a f y ←←第二步:计算)(),(5.0000x f y b a x ←+←,若00ε<="" ,则输出0x="">否则转第三步; 第三步:若010<="" ,则置;,020y="">第四步; 第四步:若1ε>-a b 则转第二步;否则,输出0x 结束.三、练习编写程序或函数实现上以上区间的近似解,要求记录迭代次数。
函数或程序为:结果为:迭代次数为:四、逐步搜索法求方程根的存在区间在给定的区间[,]a b上判定根的大致分布,从区间左端点a出发,按某个预定的步长h一步一步地向右跨,每跨一步进行一次根的搜索,并记录所有的根的存在区间。
用你编写的程序搜索问题中[0,5]的根的存在区间,步长要求为0.1 h函数为:根的存在区间为:五、综合练习(选做)用逐步搜索法找到根的存在区间,并用二分法求出在该区间上方程根的近似解。
附:分组名单星期二下午5-6节第1组组长:陈絮莹缪妃何贵堂刘钰马倩第2组组长:李杰玉黎筱惠雷霞肖娴林碧珍朱元正第3组组长:陈静苏小丽李郑何淑楠田冬秀曾敬军第4组组长:杨欣王雪梅徐莉萍石小芳雷敏唐嘉第5组组长:杨佳悦郭滢李媛媛何可陈思露第6组组长:王钰琪寇玠杨丹熊晨曦周丹第7组组长:姚瑶高倩倩金杨周海宁杨琴第8组组长:雷芳陈艳王玉娇余非张雪王海燕星期三下午5-6节第9组组长:刘超慧王玉利秦佳丽张青梅廖婷程思远第10组组长:杨琴冯康欣黄宜纯田晓东郑美艳第11组组长:黄倩肖雪梅舒玉秀杨阳黄倩宋亚超第12组组长:乔欢曹人月万袁源刘学勤师小诚沈金勇第13组组长:张全兴程德超冯啸魏丹李茜罗凤菊第14组组长:张洋何婷婷刘云丹彭英萍马静第15组组长:杨丽王书琪袁杰宋慧玲杨璐萍李琳玲星期三下午7-8节第16组组长:李欢蒋书丽康斯梦王菊花李芝琴第17组组长:杨梅郑雨来李维刘玉兰羊玲第18组组长:左艳君古月黄文凤杨娟胡洲黄川第19组组长:吴星谭婷张欢向巧钱强陈虹弟第20组组长:曾大超胡敏马树述罗玉婷第21组组长:石章波拉吉石明岳榆川金小刚张泽松第22组组长:贾孙鹏袁鹏颜冬芹陈诚张博第23组组长:李自强黄金辉彭琦岳琪李宾李闯第24组组长:王文媛林小渝刘燕严英何思敏穆芦芸。
二分法求方程的根

【例5.21】二分法求方程的根。
求方程x3+4x2+x+1=0在[-5,5]之间的近似根,误差为10-4。
若函数有实根,则函数的曲线应和x轴有交点,在根附近的左右区间内,函数的值的符号应当相反。
利用这一原理,逐步缩小区间的范围,保持在区间的两个端点处函数值的符号相反,就可以逐步逼近函数的根。
设f (x)在[a, b]上连续,且f (a) f (b)<0, 找使f (x)=0的点。
如图5-7-2所示。
图5-7-2 二分法示意图二分法的步骤如下:①取区间[a, b]中点x=(a+b)/2。
②若f (x)=0, 即(a+b)/2为方程的根。
③否则,若f (x)与f (a)同号,则变区间为[x,b];异号,则变区间为[a,x]。
④重复①~③各步,直到取到近似根为止。
#include "stdio.h"#include "math.h"main(){ float a,b,x;float fa,fb,fx;a=-5;b=5;fa=a*a*a+4*a*a+a+1;fb=b*b*b+4*b*b+b+1;do{ x=(a+b)/2;fx=x*x*x+4*x*x+x+1;if(fa*fx<0){ b=x;fb=b*b*b+4*b*b+b+1;}else{ a=x;fa=a*a*a+4*a*a+a+1;}}while(fabs(fa-fb)>1e-4);printf("x=%f\n",(a+b)/2);printf("f(%f)=%f",(a+b)/2,fa);}运行结果:x=-3.806303f(-3.806303)=-0.000059经过多次迭代,当x= -3.806 303时,f(x)的结果为-0.000 059已经接近0,误差小于10- 4数量级。
读者可进行简单的改写,输出每一次的迭代结果。
二分法求方程的实根

二分法求方程的实根一:实验目的 通过编程实现二分法,并利用所编程序求函数x e x y --=3在(0,1)的近似解,然后比较和计算器所求的结果,从理性和实践上认识两种计算方法。
二:基本原理连续函数的零点定理1、假定f(x)在区间(x ,y )上连续 , 先找到a 、b 属于区间(x ,y ),使f(a),f(b)异号,说明在区间(a,b)内一定有零点,然后求f[(a+b)/2]。
2、假设f(a)<0,f(b)>0,a<b①令a a =1,()11121,b a x b b +==,如果f(x)=0,该点就是零点。
如果0)()(1<x f a f ,则新的有根区间为[][]x a b a ,,122=;否则[][]122,,b x b a =。
此时有[][]2211,,b a b a ⊃,且()112221a b a b -=-。
对区间[]22,b a 重复上述做法多步有[][][][] n n b a b a b a b a ,,,,332211⊃⊃⊃且()a b a b n n n -=--121(式1)记*x 为0)(=x f 的根,我们有[]n n b a x ,*∈,即),3,2,1(* =≤≤n b x a n n 由(式1)及夹逼定理有:*lim lim x b a n n n n ==∞→∞→,实际计算时,当ε<-)(n n a b 时,取)(21*n n b a x +≈作为所求根近似值。
三:实验步骤1:建立如下函数文件f.m :Function f=f(x)f=x e x --32:通过如下框图编写二分法程序:erfen.m开始输入f,a,b,delta计算fa,fb,fa*fbfa*fb>0计算最多二分次数max1计算c=(a+b)/2, fcfc=0fb*fc>0b=c,a=a a=c,b=b|a-b|<=0.0005结束是否是否是否是否(3)、在Matlab 命令窗口键入:[c,err,yc]=bisect(‘f ’,0,1,0.005)(4)、得出结果,并与计算器所得结果比较分析误差。
高校工程数学二分法求方程根教学课件

x0的右侧;这时令a1=x0,b1=b;
否则x*必在x0的左侧,这时 取a1=a,b1=x0;这样得到新
的有根区间(a1,b1),其长度
仅为(a,b)的一半(见图)。
二分法原理/步骤
对压缩了的有根区间(a1,b1)又可施行同样的手续,即 用中点x1=(a1+b1)/2将区间(a1,b1)再分为两半,然后通 过根的扫描判定所求的根在x1的哪一侧,从而又确定 一个新的有根区间(a2,b2),其长度是(a1,b1)的一半。 如此反复二分下去,便可得到一系列有根区间: (a,b),(a1,b1),(a2,b2),…,(ak,bk),… 其中每个区间都是前一个区间的一半, 因此区间(ak,bk)的长度
误差 分析:
因为:
1 1 x xk bk ak k 1 b a 2 2
*
所以实际计算时,只要二分足够多次,便有 里,ε为预定精度。
x * x k 。这
对于给定的精度 ,可估计二分法所需的步数 k :
ba ε k 1 2 k
l gb a l g ε 1
bk–ak=(b–a)/2k
二分法原理
显然,如果二分过程无限地继续下去,这些区间 最终必收缩于一点x*,该点x*就是所求的根。
每次二分后,设取有根区间(ak,bk)的中点
xk=(ak+bk)/2 作为所求根的近似值,在二分过程中可以获得一 个近似根的序列 x0, x1, x2, …, xk, … 该序列必以根x*为极限。
§2.2 二分法求方程根
思路:二分法的基本思想 就是逐步对分区间,经过对 根的搜索,将有根区间的长度缩小到充分小,从而求出 满足精度的根 的近似值。
二分法步骤
二分法求方程的根
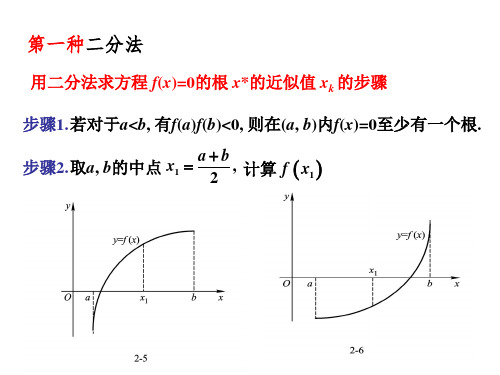
用二分法求方程 f(x)=0的根 x*的近似值 xk 的步骤
步骤1.若对于a<b, 有f(a)f(b)<0, 则在(a, b)内f(x)=0至少有一个根.
步骤2. 取a,
b的中点
x1
a
2
b
,
计算
f
x1
步骤3. 若f x1 0,则x1是f(x)=0的根, 停止计算,
运行后输出结果x*=x1.
若f a f x1 0,则在(a, x1 )内f(x)=0至少有一个根. 取a1=a, b1=x1; 若f a f x1 0, 则取a1=x1, b1=b;
用二分法求方程 f(x)=0的根 x*的近似值 xk 的步骤
步骤1.若对于a<b, 有f(a)f(b)<0, 则在(a, b)内f(x)=0至少有一个根.
for k=1: max1+1 a;ya=fun(a); b;yb=fun(b); x=(a+b)/2; yx=fun(x); wuca=abs(b-a)/2; k=k-1; [k,a,b,x,wuca,ya,yb,yx] if yx==0 a=x; b=x; elseif yb*yx>0 b=x;yb=yx; else a=x; ya=yx; end if b-a< abtol , return, end end k=max1; x; wuca; yx=fun(x);
步骤2.取a, b的中点
x1
ab, 2
计算
f
x1
步骤3. 若 f x1 0, 则x1是f(x)=0的根, 停止计算,
运行后输出结果x*=x1.
若 f a f x1 0, 则在(a, x1 )内f(x)=0至少有一个根. 取a1=a, b1=x1;
用二分法求方程课件

二分法的基本思想
二分法的基本思想是通过不断将搜索区间一分为二,并根据 函数值在左右端点的符号来判断根所在的子区间,从而逐步 逼近根的近似值。
在每次迭代过程中,选取当前搜索区间的中点,并根据函数 值在该点的正负来判断根所在的子区间,然后舍弃非根所在 的子区间,继续在剩余的子区间上重复该过程,直到达到预 设的精度要求。
定的鲁棒性。
缺点
收敛速度慢
二分法的收敛速度取决于初始区间的 大小和方程的性质,对于一些复杂的 方程,可能需要多次迭代才能得到精 确解。
需要判断根的存在性
对初始区间选择敏感
二分法的收敛速度和精度与初始区间 的选择密切相关,如果初始区间选择 不当,可能会影响最终的求解结果。
在使用二分法之前,需要先判断方程 是否在给定的区间内有根,否则可能 无法收敛。
复杂的非线性方程时具有一定的优势。
END
THANKS
感谢观看
KEEP VIEW
计算中点
在初始区间内选择一个中点,通常是区间的中点。 中点的计算是二分法求解方程的关键步骤之一,需要精确计算中点的坐标。
判断中点处的函数值
判断中点处的函数值是二分法求解方程的重要步骤,根据 函数值的不同情况,可以决定下一步的行动。
如果函数值异号,说明解在区间内,继续进行下一步;如 果函数值同号,说明解不在区间内,需要重新选择初始区 间或调整中点位置。
PART 05
二分法的改进和变种
变种方法一:插值二分法
总结词
通过插值多项式来逼近方程的根,从而提高二分法的收敛速度。
详细描述
插值二分法是在二分法的基础上,利用插值多项式来逼近方程的根。通过构造插值多项式,可以更精 确地估计方程的根的位置,从而加快二分法的收敛速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
区间长度: ba
0.5
2 2.75
0.512
(22..55 , 22.7.755 )
0.25
Hale Waihona Puke 3 2.6250.215
(2.5, 2.625)
0.125
4 2.5625
0.066
由于|2.5625-2.5|=0.0625<0.1
所以方程的近似解为:
(2.5, 2.5625)
0.0625
f (x) ln x 2x 6
f (1.375) 0, f (1.5) 0 x0 (1.375,1.5), f (1.375) 0, f (1.4375) 0 x0 (1.375,1.4375),
|1.375 1.4375 | 0.0625 0.1, x 1.4375
练习
1.用二分法求方程log3 x x 3的近似根时,
新知探究
零点存在定理 如果函数f(x)在区间[a,b]上
的图象是连续不断的一条曲线,并且f(a)·f(b)<0,那 么,函数y=f(x)在区间(a,b) 内有零点,即存在 c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根。
函数f(x)=lnx+2x-6=0在区间(2,3) 内有一个零点
想一想?
二分法的理论依据是什么? 把区间一分为二,那零点在哪一半呢 零点存在定理
问题4:
次数
1
给定精确度 0.1,求f x ln x 2x 6零点在2,3
近似值初. 始区间(2,3)且 f (2) 0, f (3) 0
ab 2
2.5
f (a b) 2
-0.084
取a
取b
(22.5.5,33)
f (x) ln x 2x 6
给这种
方法起
个名字
吧
2
2.5
2.625 2.75
3
二分法
啥叫二分法?
概念形成
二分法的定义:
对于在区间a,b上连续不断且f (a) f (b) 0的函数
y f (x), 通过不断的把函数f (x)的零点所在区间
一分为二,使区间的两个端点逐步逼近零点
,进而得到零点近似值的方法叫做二分法.
y
y 7 3x
y 2x
f (0) 0, f (2) 0 x0 (0, 2) f (1) 0, f (2) 0 x0 (1, 2) f (1) 0, f (1.5) 0 x0 (1,1.5),
02
x
f (1.25) 0, f (1.5) 0 x0 (1.25,1.5)
问题:如何找出这个零点?
新知探究
我们先来看一张照片
我怎么能 得到呢
你说规定 多少次?
游戏规则: 给出一件商品,请你猜出它的准确价格,我们给的
提示只有“高了”和“低了”。给出的商品价格在 (0,100)之间的整数,如果你能在规定的次数之内猜中 价格,这件商品就是你的了。
新知探究 问题1
例题:函数f(x)=lnx+2x-6=0 在区间(2,3)内有一个零点 如何找出这个零点?
这个游戏能提供求函数零点的思路吗?
思路:用区间两个端点的中点, 将区间一分为二……
新知探究
函数f(x)=lnx+2x-6=0在区间 (2,3)内有一个零点,怎样求?
如果能够将零点的范围尽量缩小, 那么在一定精确度的要求下,我们 可以得到零点的近似值.
我要说
我要问
新知探究
二分法
问题3:你有进一步缩小函数零点的范围的方法吗? 思路:用区间两个端点的中点,将区间一分为二……
x 2.5625或2.5
2.5
2 2.562
2.75 3 2.65
探究归纳
给定精确度,用二分法求函数零点近似值的步骤如下:
1.确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
2.求区间(a,b)的中点c; 定区间,找中点, 3.计算f(c);中值计算两边看;零点落在异号间, (1)若f(c)=0,则c就是函数的零点;区间长度缩一半;
§ 3.1.2 用二分法求 方程的近似解
知识回顾
零点概念:
对于函数y=f(x),我们把使f(x)=0的实 数x叫做函数y=f(x)的零点.
等价关系:
方程f(x)=0有实数根
函数y=f(x) 的图象与x轴有交点
函数y=f(x)有零点
零点存在定理:
如果函数y=f(x)在区间[a,b]上的 图象是连续不断的一条曲线,并 且f(a)·f(b)<0,那么,函数 y=f(x)在区间(a,b) 内有零点, 即存在c∈(a,b),使得f(c)=0,
先确定零点的范围;再用二分法去求方程的近似解
列表
x
0
1 23 45 6
7
8
f x 2x 3x 7 -6 -2 3 10 21 40 75 142
273
概实念拓践展探实究践探究
例2、利用计算器,求方程 2x 3x 7 0 的近似解
(精确度 0.1)
解: 记函数 f (x) 2x 3x 7
正式稿二分法求方程的根演示文稿
优选正式稿二分法求方程的根
练习:
上节回忆
函数 f (x) x3 x 1在下列哪个区间内
有零点?
( C)
A.(1,0) B.(1,2) C.(0,1) D.(2,3)
思考:如何得到一个更小的区间,使得零 点还在里面,从而得到零点的近似值, 如何缩小零点所在的区间?
口诀
定区间,找中点, 中值计算两边看; 零点落在异号间, 区间长度缩一半; 周而复始怎么办? 精确度上来判断.
概念拓展 实践探究
例题11.下:列函数的图像中,其中不能用二分法求解其零点的
是( C )
y
y
y
y
0
x
0
x
0
A
B
c
x
0
x
D
注意:二分法仅对函数的变号零点适用,对函数的 不变号零点不适用.
例题2:借助计算器或计算机用二分法求方 程2x+3x=7的近似解(精确度0.1).
(2)若f(a)·f(c)<0,则令b= c(此时零点x0∈(a, c) );
(3)若f(c)·f(b)<0,则令a= c(此时零点x0∈( c, b) ). 4.判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值a(或b); 否则重复步骤2~4.
周而复始怎么办? 精确度上来判断.
反思小结 体会收获
可以取的初始区间是:
( D)
A.-1,0 B.0,1C.1,2 D.2,3
2: 下列函数的图象与x轴均有交点,其中不 能用二分法求其零点的是
(C)
y
y
y
y
x
x
x
x
0
0
0
0
A
B
C
D
四大数学思想:等价转化,函数与方程,数形结合,分类讨论
练习2:
下列函数的图象与x轴均有交点,其中不能
