2011-2012学年广东省广州市中大附中八年级(下)期中数学试卷

广东省中山大学附属中学2011-2012学年下学期初中八年级

广东省中山大学附属中学2011-2012 学年下学期初中八年级期末考试语文试卷考生注意事项：本试卷共8 页，分三部分，共22 小题，满分150 分。

考试用时120 分钟。

请用黑色钢笔、签字笔在答题卷上作答。

第一部分积累与运用( 共 35 分)一、（6 小题， 20 分）1．下列词语中，加点字的读音全．都．正．确．的一组是 ( ) (3 分)A．淳．( ch ún ) 朴招徕．( l ái ) 馈．( ku ì ) 赠炽．（chì）热藏污纳垢．(g òu)B．蜿．( w ān ) 蜒禁锢．( g ù ) 吞噬．( sh ì ) 稽．（j ī）首众目睽睽．( k úi )C．缄．(ji ān ) 默狩．( sh ǒu ) 猎发怵．(ch ù) 黝．（yó u）黑龙吟凤哕．( h ùi)D．媲．(p ǐ) 美笃．( d ú ) 信干涸．(g ù ) 湖泊．（pō）相形见绌．(zhu ó )２．下列词语中没．有．错．别．字．的一项是 ( ) （3 分）A. 矫健葱笼园满成功难以置信B．憔悴凛洌重峦叠嶂谈笑风声C．晒笑殉职杳无消息莫忠一是D．门楣执拗痛心疾首顾名思义3．下列句子中，加点词语运用不．恰．当．的一项是 ( ) （3 分）A．央视 2012 年春晚，来自山东省菏泽市的“大衣哥”朱之文的成功演出成为许多观众茶余饭后津津乐．道．．．的话题。

B．2011 年 11 月 22 日至 28 日，第九届广州车展在中国进出口商品交易会展馆举行。

靓车、明星、美女汇聚，场面蔚．为．壮．观．。

C．杭州司机吴斌高速公路遭遇意外，在生命的最后时刻能够沉着处置车辆，救下一车乘客。

他的事迹，一经新闻媒体报道，就被传得满城．风．雨．．，感动了无数市民。

D．2012 年“31.5 ”晚会曝光了欺诈消费者的现象，令人不可思．议．．．的是，麦当劳、家乐福等一批国际大品牌也有如此侵犯消费者权益的虚假欺诈行为。

2019-2020学年广东省广州市中山大学附中八年级(下)期中数学试卷

2019-2020学年广东省广州市中山大学附中八年级（下）期中数学试卷一、选择题（每题3分，共30分）1．（3分）二次根式中，x的取值范围是（）A．x≤3B．x＝3C．x≠3D．x＜32．（3分）下列二次根式中，是最简二次根式的是（）A．B．C．2D．3．（3分）下列各组数据中能作为直角三角形的三边长的是（）A．1，2，2B．1，1，C．4，5，6D．1，，2 4．（3分）下列命题的逆命题是假命题的是（）A．两直线平行，同位角相等B．全等三角形的对应角相等C．等边三角形三个角相等D．直角三角形中，斜边的平方等于两直角边的平方和5．（3分）某学校组织学生进行速算知识竞赛，进入决赛的共有10名学生，他们的决赛成绩如表所示：决赛成绩/分95908580人数2341那么10名学生决赛成绩的众数和中位数分别是（）A．85，90B．85，87.5C．90，85D．95，906．（3分）已知y＝，则的值为（）A．B．﹣C．D．﹣7．（3分）一次函数y＝﹣mx+n的图象经过第二、三、四象限，则化简所得的结果是（）A．m B．﹣m C．2m﹣n D．m﹣2n8．（3分）王老师在讲“实数”时画了一个图（如图），即“以数轴的单位长度的线段为边作一个正方形，然后以表示﹣1的点为圆心，正方形的对角线长为半径画弧交数轴于点A”．则数轴上点A所表示的数是（）A．﹣1B．﹣+1C．D．﹣9．（3分）如图，将一个边长分别为4、8的矩形纸片ABCD折叠，使点C与点A重合（AB ＝4，BC＝8），则折痕EF的长度为（）A．B．2C．D．210．（3分）在一条笔直的公路上有A，B两地，甲骑自行车从A地到B地；乙骑自行车从B 地到A地，到达A地后立即按原路返回B地．如图是甲、乙两人离B地的距离y（km）与行驶时间x（h）之间的函数图象．下列说法中正确的个数为（）①A，B两地距离是30千米；②甲的速度为15千米/时；③点M的坐标为（，20）；④当甲、乙两人相距10千米时，他们的行驶时间是小时或小时．A．1个B．2个C．3个D．4个二、填空题（每题3分，共18分）11．（3分）把函数y＝2x的图象沿着y轴向下平移3个单位，得到的直线的解析式为．12．（3分）已知a，b，c为三角形的三边，且满足a2c2﹣b2c2＝a4﹣b4，那么它的形状是．13．（3分）若的整数部分为x，小数部分为y，则（x+）y的值是．14．（3分）已知直角三角形的两边a，b满足a2+＝10a﹣25，则第三边长为．15．（3分）如图，四边形ABCD中，∠A＝∠C＝90°，∠ABC＝135°，CD＝6，AB＝2，则四边形ABCD的面积为．16．（3分）如图，直线y＝﹣x+m与y＝nx+4n（n≠0）的交点的横坐标为﹣2．则下列结论：①m＜0，n＞0；②直线y＝nx+4n一定经过点（﹣4，0）；③m与n满足m＝2n﹣2；④当x＞﹣2时，nx+4n＞﹣x+m，其中正确结论的个数是个．三、解答题（共8题，72分）17．（8分）计算（1）3+﹣4；（2）9÷×（﹣）．18．（8分）先化简，再求值：（﹣）÷，其中a＝+，b＝﹣．19．（8分）如图，在7×7网格中，每个小正方形边长都为1．建立适当的平面直角坐标系，使点A（3，4）、C（4，2）．（1）判断△ABC的形状，并求图中格点△ABC的面积；（2）在x轴上有一点P，使得P A+PC最小，则P A+PC的最小值为．20．（8分）小青在本学期的数学成绩如下表所示（成绩均取整数）：测验平时期中期末类别测验1测验2测验3课题考试考试练习成绩8870968685X （1）计算小青本学期的平时平均成绩；（2）如果学期的总评成绩是根据图所示的权重计算，那么本学期小青的期末考试成绩x 至少为多少分才能保证达到总评成绩90分的最低目标？21．（8分）如图，折叠长方形纸片ABCD，先折出折痕（对角线）BD，再折叠使AD边与BD重合，得折痕DG，若AB＝4，BC＝3，求AG的长．22．（10分）已知O为坐标原点，过点A（1，2）的直线y＝kx+b与x轴交于点B，且S△ABO ＝4，求k的值．23．（10分）某工厂新开发生产一种机器，每台机器成本y（万元）与生产数量x（台）之间满足一次函数关系（其中10≤x≤70，且为整数），函数y与自变量x的部分对应值如表：x（单位：台）102030y（单位：万元/台）605550（1）求y与x之间的函数关系式；（2）市场调查发现，这种机器每月销售量z（台）与售价a（万元/台）之间满足如图所示的函数关系．则当该厂第一个月生产的这种机器40台都按同一售价全部售出，请求出该厂第一个月销售这种机器的总利润．（注：利润＝售价﹣成本）24．（12分）如图1，直线AB：y＝﹣x﹣b分别与x、y轴交于A（6，0）、B两点，过点B 的直线交x轴负半轴于点C，且OB：OC＝3：1．（1）求直线BC的解析式；（2）如图2，P为A点右侧x轴上的一动点，以P为直角顶点，BP为腰在第一象限内作等腰直角△BPQ，连接QA并延长交y轴于点K，当P点运动时，K点的位置是否发现变化？若不变，请求出它的坐标；如果变化，请说明理由．2019-2020学年广东省广州市中山大学附中八年级（下）期中数学试卷参考答案与试题解析一、选择题（每题3分，共30分）1．（3分）二次根式中，x的取值范围是（）A．x≤3B．x＝3C．x≠3D．x＜3【解答】解：根据题意，得3﹣x≥0，解得x≤3．故选：A．2．（3分）下列二次根式中，是最简二次根式的是（）A．B．C．2D．【解答】解：A、＝，被开方数含分母，不是最简二次根式；B、＝，被开方数含分母，不是最简二次根式；C，2，是最简二次根式；D、＝|x|，含能开得尽方的因式，不是最简二次根式；故选：C．3．（3分）下列各组数据中能作为直角三角形的三边长的是（）A．1，2，2B．1，1，C．4，5，6D．1，，2【解答】解：A、∵12+22＝5≠22，∴此组数据不能作为直角三角形的三边长，故本选项错误；B、∵12+12＝2≠（）2，∴此组数据不能作为直角三角形的三边长，故本选项错误；C、∵42+52＝41≠62，∴此组数据不能作为直角三角形的三边长，故本选项错误；D、∵12+（）2＝4＝22，∴此组数据能作为直角三角形的三边长，故本选项正确．故选：D．4．（3分）下列命题的逆命题是假命题的是（）A．两直线平行，同位角相等B．全等三角形的对应角相等C．等边三角形三个角相等D．直角三角形中，斜边的平方等于两直角边的平方和【解答】解：A、两直线平行，同位角相等的逆命题为同位角相等，两直线平行，此逆命题为真命题；B、全等三角形的对应角相等的逆命题为对应角相等的两三角形全等，此逆命题为假命题；C、等边三角形三个角相等的逆命题为三个角相等的三角形为等边三角形，此逆命题为真命题；D、直角三角形中，斜边的平方等于两直角边的平方和的逆命题为如果一个三角形的一边的平方等于另外两边的平方和，那么这个三角形为直角三角形，此逆命题为真命题．故选：B．5．（3分）某学校组织学生进行速算知识竞赛，进入决赛的共有10名学生，他们的决赛成绩如表所示：决赛成绩/分95908580人数2341那么10名学生决赛成绩的众数和中位数分别是（）A．85，90B．85，87.5C．90，85D．95，90【解答】解：85分的有4人，人数最多，故众数为85分；10个数据从大到小依次排列，处于中间位置的数为第5、6两个数，分别为90分，85分，所以中位数为87.5分．故选：B．6．（3分）已知y＝，则的值为（）A．B．﹣C．D．﹣【解答】解：由题意得，4﹣x≥0，x﹣4≥0，解得x＝4，则y＝3，则＝，故选：C．7．（3分）一次函数y＝﹣mx+n的图象经过第二、三、四象限，则化简所得的结果是（）A．m B．﹣m C．2m﹣n D．m﹣2n【解答】解：∵一次函数y＝﹣mx+n的图象经过第二、三、四象限，∴﹣m＜0，n＜0，即m＞0，n＜0，∴＝|m﹣n|+|n|＝m﹣n﹣n＝m﹣2n．故选：D．8．（3分）王老师在讲“实数”时画了一个图（如图），即“以数轴的单位长度的线段为边作一个正方形，然后以表示﹣1的点为圆心，正方形的对角线长为半径画弧交数轴于点A”．则数轴上点A所表示的数是（）A．﹣1B．﹣+1C．D．﹣【解答】解：由勾股定理得，正方形的对角线的长＝＝，∴数轴上点A所表示的数﹣1，故选：A．9．（3分）如图，将一个边长分别为4、8的矩形纸片ABCD折叠，使点C与点A重合（AB ＝4，BC＝8），则折痕EF的长度为（）A．B．2C．D．2【解答】解：过点F作FM⊥BC于GM，∵EF是直角梯形AECD的折痕∴AE＝CE，∠AEF＝∠CEF．又∵AD∥BC，∴∠AFE＝∠FEM，根据翻折不变性，∠AEF＝∠FEM，∴∠AFE＝∠AEF，∴AE＝AF．在Rt△ABE中，设BE＝x，AB＝4，AE＝CE＝8﹣x．x2+42＝（8﹣x）2解得x＝3．在Rt△FEM中，EM＝BM﹣BE＝AF﹣BE＝AE﹣BE＝5﹣3＝2，FM＝4，∴EF＝＝2．故选：D．10．（3分）在一条笔直的公路上有A，B两地，甲骑自行车从A地到B地；乙骑自行车从B 地到A地，到达A地后立即按原路返回B地．如图是甲、乙两人离B地的距离y（km）与行驶时间x（h）之间的函数图象．下列说法中正确的个数为（）①A，B两地距离是30千米；②甲的速度为15千米/时；③点M的坐标为（，20）；④当甲、乙两人相距10千米时，他们的行驶时间是小时或小时．A．1个B．2个C．3个D．4个【解答】解：根据题意可以列出甲、乙两人离B地的距离y（km）与行驶时间x（h）之间的函数关系得y甲＝﹣15x+30y乙＝由此可知，①②正确．当﹣15x+30＝30x时，解得x＝则M坐标为（，20），故③正确．当两人相遇前相距10km时，30x+15x＝30﹣10x＝，当两人相遇后，相距10km时，30x+15x＝30+10，解得x＝15x﹣（30x﹣30）＝10解得x＝∴④错误．故选：C．二、填空题（每题3分，共18分）11．（3分）把函数y＝2x的图象沿着y轴向下平移3个单位，得到的直线的解析式为y＝2x﹣3．【解答】解：由“上加下减”的原则可知，将直线y＝2x沿着y轴向下平移3个单位得到直线解析式为：y＝2x﹣3．故答案为：y＝2x﹣3．12．（3分）已知a，b，c为三角形的三边，且满足a2c2﹣b2c2＝a4﹣b4，那么它的形状是等腰三角形或直角三角形．【解答】解：∵a2c2﹣b2c2＝a4﹣b4，∴c2（a2﹣b2）＝（a2+b2）（a2﹣b2），∴a2﹣b2＝0或c2＝a2+b2，当a2﹣b2＝0时，a＝b；当c2＝a2+b2时，∠C＝90°，∴△ABC是等腰三角形或直角三角形．故答案为：等腰三角形或直角三角形．13．（3分）若的整数部分为x，小数部分为y，则（x+）y的值是4．【解答】解：∵9＜13＜16，∴3＜＜4，∴的整数部分为x＝3，小数部分为y＝﹣3，∴（x+）y＝（3）（﹣3）＝4．故答案为：4．14．（3分）已知直角三角形的两边a，b满足a2+＝10a﹣25，则第三边长为4或．【解答】解：由a2+＝10a﹣25，得（a﹣5）2+＝0．所以a＝5，b＝3．①当a＝5是斜边时，第三边的长度为：＝4．②当a＝5是直角边时，第三边的长度为：＝．综上所述，第三边的长度为4或．故答案是：4或．15．（3分）如图，四边形ABCD中，∠A＝∠C＝90°，∠ABC＝135°，CD＝6，AB＝2，则四边形ABCD的面积为16．【解答】解：延长AB和DC，两线交于O，∵∠C＝90°，∠ABC＝135°，∴∠OBC＝45°，∠BCO＝90°，∴∠O＝45°，∵∠A＝90°，则OB＝BC，OD＝OA，OA＝AD，BC＝OC，设BC＝OC＝x，则BO＝x，∵CD＝6，AB＝2，∴6+x＝（x+2），解得：x＝6﹣2，∴OB＝x＝6﹣4，BC＝OC＝6﹣2，OA＝AD＝2+6﹣4＝6﹣2，∴四边形ABCD的面积S＝S△OAD﹣S△OBC＝×OA×AD﹣＝×（6﹣2）×﹣＝16，故答案为：16．16．（3分）如图，直线y＝﹣x+m与y＝nx+4n（n≠0）的交点的横坐标为﹣2．则下列结论：①m＜0，n＞0；②直线y＝nx+4n一定经过点（﹣4，0）；③m与n满足m＝2n﹣2；④当x＞﹣2时，nx+4n＞﹣x+m，其中正确结论的个数是4个．【解答】解：①∵直线y＝﹣x+m与y轴交于负半轴，∴m＜0；∵y＝nx+4n（n≠0）的图象从左往右逐渐上升，∴n＞0，故结论①正确；②将x＝﹣4代入y＝nx+4n，得y＝﹣4n+4n＝0，∴直线y＝nx+4n一定经过点（﹣4，0）．故结论②正确；③∵直线y＝﹣x+m与y＝nx+4n（n≠0）的交点的横坐标为﹣2，∴当x＝﹣2时，y＝2+m＝﹣2n+4n，故结论③正确；④∵当x＞﹣2时，直线y＝nx+4n在直线y＝﹣x+m的上方，∴当x＞﹣2时，nx+4n＞﹣x+m，故结论④正确．故正确结论的个数是4个，故答案为4．三、解答题（共8题，72分）17．（8分）计算（1）3+﹣4；（2）9÷×（﹣）．【解答】解：（1）原式＝9+﹣2＝8；（2）原式＝9××（﹣）×＝﹣．18．（8分）先化简，再求值：（﹣）÷，其中a＝+，b＝﹣．【解答】解：（﹣）÷＝＝＝＝，当a＝+，b＝﹣时，原式＝＝＝．19．（8分）如图，在7×7网格中，每个小正方形边长都为1．建立适当的平面直角坐标系，使点A（3，4）、C（4，2）．（1）判断△ABC的形状，并求图中格点△ABC的面积；（2）在x轴上有一点P，使得P A+PC最小，则P A+PC 的最小值为．【解答】解：（1）△ABC是直角三角形，理由：∵AC2+BC2＝25，AB2＝25，∴AC2+BC2＝AB2，∴△ABC 是直角三角形；△ABC的面积＝××＝5；（2）如图所示，作点C关于x轴的对称点C'，连接AC'交x轴于P，连接CP，则CP＝C'P，∴P A+PC 的最小值为AC '的长，∵AC'＝＝，∴P A+PC的最小值为，故答案为：．20．（8分）小青在本学期的数学成绩如下表所示（成绩均取整数）：测验类别平时期中考试期末考试测验1测验2测验3课题练习成绩8870968685X （1）计算小青本学期的平时平均成绩；（2）如果学期的总评成绩是根据图所示的权重计算，那么本学期小青的期末考试成绩x至少为多少分才能保证达到总评成绩90分的最低目标？【解答】解：（1）小青该学期的平时平均成绩为：（88+70+96+86）÷4＝85；（2）按照如图所示的权重，小青该学期的总评成绩为：85×10%+85×30%+60%x，依题意得：85×10%+85×30%+60%x＝90解得：x＝93.33．答：小青期末考试成绩至少需要94分．21．（8分）如图，折叠长方形纸片ABCD，先折出折痕（对角线）BD，再折叠使AD边与BD重合，得折痕DG，若AB＝4，BC＝3，求AG的长．【解答】解：过点G作GE⊥BD于E，根据题意可得：∠GDA＝∠GDB，AD＝ED，∵四边形ABCD是矩形，∴∠A＝90°，AD＝BC＝3，∴AG＝EG，ED＝3，∵AB＝4，BC＝3，∠A＝90°，∴BD＝5，设AG＝x，则GE＝x，BE＝BD﹣DE＝5﹣3＝2，BG＝AB﹣AG＝4﹣x，在Rt△BEG中，EG2+BE2＝BG2，即：x2+4＝（4﹣x）2，解得：x＝，故AG＝．22．（10分）已知O为坐标原点，过点A（1，2）的直线y＝kx+b与x轴交于点B，且S△ABO ＝4，求k的值．【解答】解：∵S△ABO＝4，∴OB•y A＝4，即×2OB＝4，∴OB＝4，∴点B的坐标为（4，0）或（﹣4，0）．当点B的坐标为（4，0）时，将A（1，2），B（4，0）代入y＝kx+b，得：，解得：；当点B的坐标为（﹣4，0）时，将A（1，2），B（﹣4，0）代入y＝kx+b，得：，解得：．∴k的值为﹣或．23．（10分）某工厂新开发生产一种机器，每台机器成本y（万元）与生产数量x（台）之间满足一次函数关系（其中10≤x≤70，且为整数），函数y与自变量x的部分对应值如表：x（单位：台）102030y（单位：万元/台）605550（1）求y与x之间的函数关系式；（2）市场调查发现，这种机器每月销售量z（台）与售价a（万元/台）之间满足如图所示的函数关系．则当该厂第一个月生产的这种机器40台都按同一售价全部售出，请求出该厂第一个月销售这种机器的总利润．（注：利润＝售价﹣成本）【解答】解：（1）设每台机器成本y（万元）与生产数量x（台）之间函数关系为y＝kx+b，，解得，，即y与x之间的函数关系式为y＝﹣0.5x+65；（2）当x＝40时，y＝﹣0.5×40+65＝45，设z与a之间的函数关系式为z＝ma+n，，解得，，即z与a之间的函数关系式为z＝﹣a+90，当z＝40时，40＝﹣a+90，解得，a＝50，（50﹣45）×40＝5×40＝200（万元），答：该厂第一个月销售这种机器的总利润是200万元．24．（12分）如图1，直线AB：y＝﹣x﹣b分别与x、y轴交于A（6，0）、B两点，过点B 的直线交x轴负半轴于点C，且OB：OC＝3：1．（1）求直线BC的解析式；（2）如图2，P为A点右侧x轴上的一动点，以P为直角顶点，BP为腰在第一象限内作等腰直角△BPQ，连接QA并延长交y轴于点K，当P点运动时，K点的位置是否发现变化？若不变，请求出它的坐标；如果变化，请说明理由．【解答】解：（1）直线AB：y＝﹣x﹣b分别与x，y轴交于A（6，0）、B两点，∴0＝﹣6﹣b，∴b＝﹣6，∴直线AB的解析式为：y＝﹣x+6，∴B（0，6），∴OB＝6，∵OB：OC＝3：1，∴OC＝OB＝2，∴C（﹣2，0），设BC的解析式是y＝ax+c，∴，∴，∴直线BC的解析式是：y＝3x+6；（2）K点的位置不发生变化，K（0，﹣6）．理由如下：如图2，过Q作QH⊥x轴于H，∵△BPQ是等腰直角三角形，∴∠BPQ＝90°，PB＝PQ，∵∠BOA＝∠QHA＝90°，∴∠BPO＝∠PQH，在△BOP与△PHQ中，，∴△BOP≌△PHQ（AAS），∴PH＝BO，OP＝QH，∴PH+PO＝BO+QH，即OA+AH＝BO+QH，又∵OA＝OB，∴AH＝QH，∴△AHQ是等腰直角三角形，∴∠QAH＝45°，∴∠OAK＝45°，∴△AOK为等腰直角三角形，∴OK＝OA＝6，∴K（0，﹣6）．。

广东省中大附中、三水实验学校2011-2012学年八年级上学期期中考试数学试题(无答案)

中大附中三水实验学校2011-2012学年上学期期中考试八年级数学试卷（命题人：潘火军审核人：刘佛新）说明：本次考试时间100分钟，满分120分。

[来源:学*科*网]一、选择题(本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的)．1.化简16的值为 ( )A.4B. 4C. －4D. 162.下列运动属于平移的是（）A.冷水加热过程中小气泡上升成大气泡B.打开教室门，门的移动C.上升的电梯D.随风飘动的风筝在空中运动3.如图，在平行四边形ABCD 中，若∠B=100°，那么∠A 、∠D 的度数分别是（）度A.80、100B.100、80C.80、80D.100、1004.已知平行四边形ABCD ，下列判断正确的是（）A.若∠A=90°，则四边形ABCD 是矩形B.AC=BDC.AB=CD ，则ABCD 是菱形D.若AC 丄BD ，则四边形ABCD 为正方形5.四个角都相等，且邻边相等的四边形是（）A. 平行四边形B.菱形C. 矩形D. 正方形6.在下列长度的各组线段中，能组成直角三角形的是（）A.5，6，7B.1，4，9C.5，12，13D.5，11，127. 下列各式中，正确的是( ).A.3355-=-B.6.06.3-=- C.13)13(2-=- D.636=8.下列说法中正确的是（）A.一组对边平行，另一组对边相等的四边形是平行四边形；B.对角线相等的四边形是矩形；C.对角线相等的菱形是正方形；D.对角线互相垂直的四边形是菱形9.已知正方形的边长为4cm, 则其对角线长( )A. 8cmB. 16cmC. 32cm D 42cm.10. 若a a =-2)3(-3，则a 的取值范围是( ).A. a ＞3B. a ≥3C. a＜3D. a≤3第Ⅱ卷（非选择题共90分）二、填空题(本大题共5小题，每小题3分，共15分．)11.请你任意写出一组勾股数 .12.若x的立方根是—1，则x＝___________．13.平方根等于它本身的数是．14.在ABCD中，若满足，则四边形ABCD为矩形.15.已知菱形的两条对角线长为6cm和8cm，则菱形的周长是.三、解答题(写出必要的解题步骤．16～20题每小题6分，21～23题每小题8分，24题10分，25题11分，共75分)．16.化简: 31217.化简861221.如图，在平行四边形ABCD中，E、F是对角线AC上的点，且AE=CF，则四边形EBFD是平行四边形吗?说说你的理由．[来源:学.科.网Z.X.X.K]B22.工人师傅做铝合金窗框分下面三个步骤进行:先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;(2)摆放成如图②的四边形,则这时窗框的形状是形,根据数学道理是: 。

广州八年级下期中数学试卷(有答案)

广东省广州八年级（下）期中数学试卷、选择题（共10小题，每小题3分，共30 分）对角线互相平分的四边形（3分）已知三角形的三边长之比为 1:1:二，则此三角形一定是（（3分）如图，把矩形ABCD 沿EF 对折后使两部分重合，若/ 仁50°则/ AEF=（）£A. 4cmB. 6cmC. 8cmD. 10cm1. （3分）下列根式中，不是最简二次根式的是（ A . 二 B . 一 C .2. （3分）下列各组数中，以a, b , c 为边的三角形不是直角三角形的是（ A . a=1.5, b=2, c=3 B . a=7, b=24, c=25 C. a=6, b=8, c=10 D. a=3, b=4, c=53. （3分）根据下列条件，不能判定四边形是平行四边形的是（ A . 一组对边平行且相等的四边形 B. 两组对边分别相等的四边形 C. 对角线相等的四边形D . 4. A . 锐角三角形B .钝角三角形 C. 等边三角形D .等腰直角三角形A . 110°. 115°C . 120°D. 130° 6 . （3分）实数a 、b在数轴上对应的位置如图，则“hr 讥•「」‘=（）A . b - a B. 2— a - b C. a - b D . 2+a — b20cm 的?ABCD 中，AB M AD ,对角线AC BD 相交于点O , OE 丄BD5. C7. （3分）如图，在周长为一条到达底部的直吸管在罐内部分 a 的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是A .①③④B.①②⑤C .③④⑤D .①③⑤、填空题（共6小题，每小题3分，共18 分） 11. （3分）计算V 的结果是 _________5<a < 12D . 5<a < 139. （3分）如图，在直角坐标系中, 将矩形OABC 沿OB 对折，使点A 落在A i 处，已知OA= _，■1yAiCJ> %/JBOAXA . （［•匚）B .（』：）C.(-D.(-10. （3分）已知：如图，在正方形交DE 于点P.若AE=AP=1 PBVE .下列结论: ABCD 外取一点 E,连接 AE 、BE 、DE A 作AE 的垂线① 厶 APH A AEB② 点B 到直线AE 的距离为二; ③ E B 丄ED; ④ S A APD +S A APE F 1+ "；⑤ S其中正确结论的序号是（）B . 12< a < 15 C. AB=1,13. _______________________________________________________________ （3分）直角二角形两直角边长分别为5和12,则它斜边上的咼为 _________________________ .14. （3 分）如图，在？ABCD中，AB=7, AD=11, DE平分/ ADC,贝U BE ____15. （3分）如图，ABCD是对角线互相垂直的四边形，且OB=OD,请你添加一个适当的条件______ ，使ABCD成为菱形（只需添加一个即可）16. （3分）如图，在直角坐标系中，已知点A （- 3, 0）、B （0, 4）,对厶OAB连续作旋转变换，依次得到△?、△ 3、厶4…，则厶2013的直角顶点的坐标为______ .、计算题（共9小题，共20 分）17. （20分）（1）计算「+|「- 1| - n+ （.：）18. （8分）如图，在边长为1的小正方形组成的网格中，△ ABC的三个顶点均在格点上，请按要求完成下列各题：（1）画线段AD// BC且使AD=BC连接CD;（2）线段AC的长为_____ , CD的长为_______ , AD的长为_______ ;（3）△ ACD为___ 三角形，四边形ABCD的面积为________ .12. （3分）要使式子有意义，则a的取值范围为19. （8 分）如图，在△ ABC中，/ A=30°, / ACB=105, CD丄AB 于D, BC=2cm 求AC和AB的长.（结果保留二次根式）20. （8分）有一只喜鹊在一棵3m高的小树上觅食，它的巢筑在距离该树24m远的一棵大树上，大树高14m，且巢离树顶部1m，当它听到巢中幼鸟的叫声，立即赶过去，如果它飞行的速度为5m/s，那它至少需要多少时间才能赶回巢中？（画出符合题意的几何图形，并求解）O是对角线AC和BD的交点，OE± AD于E, OF丄BC于F.求22. （12分）如图，在四边形ABCD中，AB=BC对角线BD平分/ABC, P是BD上一点，过点P作PM丄AD，PN丄CD,垂足分别为M， N.（1 ）求证：/ ADB=Z CDB；（2）若/ ADC=90，求证：四边形MPND是正方形.证：OE=OF23. （12 分）如图，在△ ABC中，/ ACB=90，/ B>Z A,点D 为边AB的中点，DE// BC交AC團1 图2于点E, CF// AB 交DE 的延长线于点F. (1) 求证：DE=EF(2) 连结CD,过点D 作DC 的垂线交CF 的延长线于点 G,求证：/ B= / A+Z DGC24. ( 12分)先观察下列等式，再回答下列问题:(1) 请你根据上面三个等式提供的信息，猜想• .'[—‘—J 的结果，并验证； (2) 请你按照上面各等式反映的规律，试写出用含 n 的式子表示的等式(n 为正整数). 25. (14分)如图1,在厶ABC 中，AB=BC P 为AB 边上一点，连接 CP,以PA PC 为邻边作 ?APCD AC 与 PD 相交于点 E ,已知Z ABC=Z AEP a (0°v a 90°. (1) 求证：Z EAP=/ EPA(2) ?APCD 是否为矩形？请说明理由；(3) 如图2, F 为BC 中点，连接FP,将Z AEP 绕点E 顺时针旋转适当的角度，得到Z MEN (点 M 、N 分别是Z MEN 的两边与BA 、FP 延长线的交点).猜想线段EM 与EN 之间的数量关系，并证明你的结论.参考答案与试题解析一、选择题（共10小题，每小题3分，共30分） 1. （3分）下列根式中，不是最简二次根式的是（）A •匚B .二C . 【解答】解：C 、： •••它不是最简二次根式. 故选：C.2.（3分）下列各组数中，以a, b , c 为边的三角形不是直角三角形的是（）A. a=1.5, b=2， c=3 B . a=7， b=24，c=25 C. a=6， b=8， c=10 D. a=3， b=4， c=5【解答】解：A 、T 1.52+22工32，A 该三角形不是直角三角形，“故A 选项符合题意;B 、 t 72+242=252，A 该三角形是直角三角形，故 B 选项不符合题意； C. v 62+82=10"，^该三角形是直角三角形，故C 选项不符合题意；D 、 t 32+42=52，A 该三角形不是直角三角形，故 D 选项不符合题意. 故选：A .3. （3分）根据下列条件，不能判定四边形是平行四边形的是（）A. —组对边平行且相等的四边形B. 两组对边分别相等的四边形C. 对角线相等的四边形D. 对角线互相平分的四边形【解答】解: A 、t AD=BC AD// BC,•四边形ABCD 是平行四边形，故本选项正确；B 、T AD =BC AB =CD•四边形ABCD 是平行四边形，故本选项正确；C 由AC=BD 不能推出四边形ABCD 是平行四边形，故本选项错误;.V2DD、t OA=OC OD=OB,•四边形ABCD是平行四边形，故本选项正确；故选：c.4. （3分）已知三角形的三边长之比为1：1：坏；，贝U此三角形一定是（A.锐角三角形B.钝角三角形C.等边三角形D.等腰直角三角形【解答】解：由题意设三边长分别为：x, x, ；xx2+x2= （「x）2，二三角形一定为直角三角形，并且是等腰三角形.故选：D.5. （3分）如图，把矩形ABCD沿EF对折后使两部分重合，若/ 1=50°A. 110°B. 115°C. 120°D. 130°【解答】解：根据题意得：/ 2=7 3,vZ 1+72+7 3=180°,•••7 2= (180°- 50° - 2=65°,v四边形ABCD是矩形，•AD// BC,•7 AEF+Z 2=180°,•7 AEF=180 - 65°=1150.故选：B.6 . （3分）实数a、b在数轴上对应的位置如图，则：|.-j ---------------- ■——-——*--------- ・a nb iA. b- aB. 2- a- bC. a- bD. 2+a- bB则7AEF=( )则「..-=|b - 1| - |a- 1|=1 - b - 1+a =a- b故选：C.7. （3分）如图，在周长为20cm的？ABCD中，AB M AD,对角线AC BD相交于点O, 0E丄BD 交AD于匕则厶ABE的周长为（）A. 4cmB. 6cmC. 8cmD. 10cm【解答】解：根据平行四边形的性质得：OB=OD••• EO丄BD,••• EO为BD的垂直平分线，根据线段的垂直平分线上的点到两个端点的距离相等得：BE=DE•••△ ABE 的周长=ABAE+DE=AB+AD= X 20=10cm.故选：D.8. （3分）如图是一个圆柱形饮料罐，底面半径是5,高是12,上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是( )A. 12< a< 13B. 12< a< 15C. 5< a< 12D. 5< a< 13【解答】解：a的最小长度显然是圆柱的高12,最大长度根据勾股定理，得：「：=13.即a的取值范围是12<a< 13.故选：A.9. （3分）如图，在直角坐标系中，将矩形OABC沿OB对折，使点A落在A1处，已知OA= 一 ,而 Rt A AOB ^ Rt A A 1OB ,•••/ A i OB=Z AOB=30.作A i D 丄OA,垂足为D ,如图所示.在 Rt A A i OD 中，OA i =OA= 一，/ A i OD=60 , A,D••• sin / A i OD= ,0 Aj • A i D=OA?sin / A i OD=/^ OD又 cos / A i OD=「一,• OD=OA?cos / A i OD pX 寻專.£ £ •••点A i 的坐标是 i0. （3分）已知：如调，在正方形ABCD 外取一点E,连接AE 、BE 、DE 过点A 作AE 的垂线交DE 于点P.若AE=AP=I PBVE .下列结论： ① 厶 APD ^A AEB ； ② 点B 到直线AE 的距离为-;1 C1yAi / J ’JBO AX【解答】解：在Rt A AOB 中,C (一 J D.(-tan / AOB=-二 -, OA V33 'Cy才t *BA TXAB=1,则点A i 的坐标是（A . (一)B .A. 故选:③EB丄ED;④S A APD+S A APB=1+ I：；⑤S 正方形ABCD=4+VE .其中正确结论的序号是（）A.①③④B.①②⑤C.③④⑤D.①③⑤【解答】解：①•••/ EAB^Z BAP=90 , / PAD F Z BAP=90,•••/ EAB=Z PAD,又••• AE=AP, AB二AD,•••△ APD^A AEB（故①正确）;③•••△ APD^A AEB,•••Z APD=Z AEB,又VZ AEB=/ AEP^Z BEP Z APD=Z AEF+Z PAE•Z BEP=/ PAE=90 ,•EB丄ED （故③正确）;②过B作BF丄AE,交AE的延长线于F ,V AE=AP Z EAP=90 ,•Z AEP=/ APE=45 ,又V③中EB丄ED, BF丄AF,•Z FEB=/ FBE=45 ,又V BE=「「. =71；二■,•BF=EF=（故②不正确）;④如图，连接BD,在Rt A AEP中，V AE=AP=I•EP=「,又V PB= 7 ,•BE=-,13•••△ APHA AEB ••• PD=BE= =,S ^ABP +Sx ADF =S\ABD — S\BDF = S 正方形 ABCD~ X DP X 22④ 不正确）.⑤ ••• EF=BF= , AE=1,2•••在 Rt X ABF 中,AB 2= (AE+EF ) 2+BF 2=4+ 7, --S 正方形ABCt = A^=4+ -(故⑤正确)；二、填空题（共6小题，每小题3分，共18 分） ii. （3分）计算心-心的结果是3【解答】解：原式=（5 -— 2 "）- T =3. 故答案为：3.12. （3分）要使式子有意义，则a 的取值范围为 a 》-2且a ^ 0a【解答】解：根据题意得：a+2> 0且a M 0, 解得：a > — 2且a M 0. 故答案为：a > — 2且a M 0.13. （3分）直角二角形两直角边长分别为 5和12,则它斜边上的咼为【解答】解：由勾股定理可得：斜边长2=52+122, 则斜边长=13, 直角，三角形面积S= X 5X 12= X 13 X 斜边的高, 可得：斜边的高< . 6014. （3 分）如图，在？ABCD 中，AB=7, AD=11, DE 平分/ ADC,贝U BE= 460故答案为:故选：D .A D【解答】解：：DE平分/ ADC,•••/ ADE=Z CDE••• ?ABCD中AD// BC,•••/ ADE=Z CED•••/ CDE=/ CED,来源••• CE=CD•••在?ABCD中, AB=7, AD=11 ,••• CD=AB=7 , BC=AD=11••• BE=BC- CE=11- 7=4.故答案为：4.15. (3分)如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件OA=OC ,使ABCD成为菱形(只需添加一个即可)【解答】解：OA=OC•••OB=OD, OA=OC•••四边形ABCD是平行四边形,••• AC丄BD,•••平行四边形ABCD是菱形,故答案为：OA=OC16. (3分)如图，在直角坐标系中，已知点A (- 3 , 0)、B (0 , 4),对厶OAB连续作旋转变换,依次得到厶?、△ 3、厶4…，则厶2013的直角顶点的坐标为(8052, 0).二AB= | i =5,由图可知，每三个三角形为一个循环组依次循环，一个循环组前进的长度为:••• 2013-3=671,•••△2013的直角顶点是第671个循环组的最后一个三角形的直角顶点，••• 671 X 12=8052,2013的直角顶点的坐标为（8052, 0）.故答案为：（8052, 0）.三、计算题（共9小题，共20 分）17. (20分)(1)计算「+| 7- 1| -⑶先化简，后计算：,+；+_：,其中a「, b=「【解答】解：（1）原式=2二+二-1 - 1+2=3二3 ? a 2a（3）当a=「，b=「时,1 1=.+ I4+5+3=12,0 -1n+c.);(2) J-：：」J (a> 0);(2)原式=3 . +】=718. （8分）如图，在边长为1的小正方形组成的网格中，△ ABC的三个顶点均在格点上，请按要求完成下列各题：（1）画线段AD// BC且使AD=BC连接CD;（2）线段AC的长为2「, CD的长为「，AD的长为5（3）△ ACD为直角三角形，四边形ABCD的面积为10 .【解答】解：（1）如图所示:(2) AC= ：=2 匚;CD=U+T=!;AD= ； . , =5；(3)：( 2 三)2+ (三)2=52，•••△ ACD是直角三角形，S四边形ABCD=4X 6 —2X 1 —= X 4X 3 —= X 2X 1 - —X 3X 4=10.故答案为：2 "，"，5;直角，10.19. （8 分）如图，在△ ABC中，/ A=30°，/ ACB=105，CD丄AB 于D，BC=2cm 求AC和AB的长.（结果保留二次根式）【解答】解：•••在△ ABC 中，/ A=30°, / ACB=105, CD 丄AB 于 D ,ADC 中，/ ADC=90，/ ACD=60••• AC=2CD在厶 BDC 中，/ BDC=90,Z BCD=Z DBC=45••• CD=BD由勾股定理可得，BD 2+CD 2=4 二 CD=BD=三， --AC=2*，/ cm ; 在厶ADC 中，AD=AC?si n60° =2?萼=乙 AB=AD+BD= (-；；) cm .20. （8分）有一只喜鹊在一棵3m 高的小树上觅食，它的巢筑在距离该树 24m 远的一棵大树上，大树高14m ，且巢离树顶部1m ，当它听到巢中幼鸟的叫声，立即赶过去，如果它飞行的速度为5m/s ，那它至少需要多少时间才能赶回巢中？（画出符合题意的几何图形，并求解）【解答】解：如图，由题意知 AB=3m, CD=14-仁13 (m )，BD=24m 过 A 作 AE 丄 CD 于 E .贝U CE=13- 3=10 (m )，AE=24m, 在 Rt A AEC 中, AC 2=CE 2+AE ?=102+242. 故 AC=26m , 则 26- 5=5.2 (s ),n B21. （8分）如图，在?ABCD中，O是对角线AC和BD的交点，OE±AD于E, OF丄BC于F.求证：OE=OF【解答】证明：•••四边形ABCD是平行四边形,•••OA=OC AD// BC,:丄 EAO=Z FCQ•••OE丄AD, OF丄BC,•••/ AEO=/ CFO=90,在厶AEO和△ CFO中，'ZEA0=ZFC0Z 期gZCFO,PARC•••△ AEO^A CFO( AAS,•••OE=OF22. (12分)如图，在四边形ABCD中，AB=BC对角线BD平•:分/ABC, P是BD上一点，过点P 作PM丄AD, PN丄CD,垂足分别为M, N.(1 )求证：/ ADB=/ CDB；(2)若/ ADC=90,求证：四边形MPND是正方形.【解答】证明：(1 )•对角线BD平分/ ABC,•••/ ABD=/ CBD,在厶ABD和厶CBD中，f AB=CB■ ZABD^ZCBD,SD=BD•••△ ABD^A CBD( SAS, •••/ ADB=/ CDB(2 PM 丄AD, PN丄CD,•••/ PMD=Z PND=90 ,vZ ADC=90,•••四边形MPND是矩形，vZ ADB=Z CDB•••Z ADB=45••• PM=MD,23. （12 分）如图，在△ ABC中，Z ACB=90, Z B>Z A,点D 为边AB的中点，DE/ BC交AC于占-J八、、连结CD,过点D作DC的垂线，交CF的延长线于点G,求证：Z B=Z A+Z DGC• DF=BCv D为边AB的中点，DE/ BC,• DE= BC,• EF=D R DE=BO -CB= CBE, CF// AB交DE的延长线于点F.(1) 求证：DE=EF(2)•四边形MPND是正方形.•四边形DBCF为平行四边形:,CF/AB,••• DE=EF(2 )：DB// CF,•••/ ADG=Z G,vZ ACB=90, D为边AB的中点,••• CD=DB=AD•••Z B=Z DCB Z A=Z DCAv DG丄DC,•Z DCA+Z 1= 90°°vZ DCB^Z DCA=90 ,•Z 1 = Z DCB=/ B ,vZ A+Z ADG=Z 1,•Z A+Z G=Z B.24. (12分)先观察下列等式,再回答下列问题:(1)请你根据上面三个等式提供的信息，猜想.i 的结果，并验证;(2)请你按照上面各等式反映的规律，试写出用含n的式子表示的等式(n为正整数). 【解答】解:(1)25. (14分)如图1,在厶ABC中，AB=BC P为AB边上一点，连接CP,以PA PC为邻边作?APCD AC与PD相交于点E,已知/ ABC=Z AEP a (0°v a 90°.(1 )求证：/ EAP=/ EPA(2)?APCD是否为矩形？请说明理由；(3)如图2, F为BC中点，连接FP,将/ AEP绕点E顺时针旋■转适当的角度，得到/ MEN (点M、N分别是/ MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系，并证明你的结论.【解答】（1）证明：在厶ABC和厶AEP中,•••/ ABC=/ AEP, / BACK EAP,•••/ ACB=/ APE 在厶ABC中, AB=BC•••/ ACB=/ BAC,•••/ EPA=/ EAR（2）解：?APCD是矩形.理由如下:•••四边形APCD是平行四边形，••• AC=2EA PD=2EP•••由（1）知/ EPA/ EAF,••• EA=EP贝U AC=PD••• ?APCD是矩形.(2) !：匚「二(n为正整数).(3)解：EM=EN证明：••• EA=EP•— EPA=「「呵=_ - =90°- ' a,2 2 2•••/ EAM=180 -Z EPA=180-( 90°-寺a) =90召a,由(2)知/ CPB=90, F是BC的中点，••• FP=FB•••Z FPB=Z ABC=a,•••Z EPN=/ EPA+Z APN=Z EPA+Z FPB=90 -寺a+ a =90° a,•Z EAM=Z EPN,•••Z AEP绕点E顺时针旋转适当的角度，得到Z MEN,•Z AEP=Z MEN,•Z AEP-Z AEN=Z MEN -Z AEN，即Z MEA=Z NEP,在厶EAM和A EPN中，'Z EAM-Z EPN(EArEP,ZMEA-ZNEP•••△EAM^A EPN (ASA , • EM=EN.。

2012年八年级(下)期中考试数学试卷(含答案)

xyO图1xO yP 4题图八年级 (下) 期中数学试题（友情提醒：全卷满分120分，答卷时间100分钟，请你掌握好时间．）题号一二三四总分得分一、选择题（每小题3分，共30分）（请将正确答案序号填入以下表格相应的题号下，否则不得分）题号 1 2 3 4 5 6 7 8 9 10 答案1．代数式42,1,3,31nm b a b a ，x -++π中，分式有（ ☆ ） A ．1个； B ．2个； C ．3个； D ．4个。

2．若分式方程33x x -++1=m 有增根，则这个增根的值为（ ☆ ）A ．1B ．3C ．－3D ．3或－33．（2011广西来宾）计算11x x y--的结果是（ ☆ ） A.()y x x y -- B.2()x y x x y -+ C.2()x y x x y -- D.()yx x y -4．如图，点P （3a ，a ）是反比例函y ＝kx（k ＞0）与⊙O 的一个交点，图中阴影部分的面积为10π，则反比例函数的解析式为（ ☆ ） A ．y ＝3x B ．y ＝5x C ．y ＝10x D ．y ＝12x5．反比例函数1y x=（x ＞0）的图象如图1所示，随着x 值的增大，y 值（ ☆ ）． A ．减小 B ．增大 C ．不变 D ．先减小后不变 6．已知反比例函数1y x-=，下列结论不正确．．．的是（ ☆ ） A ．图象经过点（－1，1） B ．图象在第二、四象限C ．当1x >时，10y -<<D ．当0x <时，y 随着x 的增大而减小 7．若反比例函数ky x=的图象经过点（－3，2），则k 的值为（ ☆ ）． A ．－6 B ．6 C ．－5 D ．5 8．在△ABC 中，AB =6，AC =8，BC =10，则该三角形为（ ☆ ）图4S 2S 3S 1C BA12-3-210-13A 9．如图所示：数轴上点A 所表示的数为a ，则a 的值是（ ☆ ） A ．5+1B ．-5+1C ．5-1D ．510．如图2是一张直角三角形的纸片，两直角边AC ＝6 cm 、BC ＝8 cm ，现将△ABC 折叠，使点B 与点A 重合，折痕为DE ，则BE 的长为（ ☆ ） A ．4 cm B ．5 cm C ．6 cm D ．10 cm 二、填空题（每小题3分，共30分）11．若方程0414=----xxx m 有增根，则m 的值是． 12．计算：x 2x y － xy =_______13．当x= 时，分式31x x +-的值等于2 14．已知反比例函数1m y x-=的图象如图3，则m 的取值范围是．15．观察下面一列有规律的数:31，82，153，244，355，486，……，根据其规律可知第n 个数应是 (n 为整数)．16．若点（－2，－1）在反比例函数xky =的图象上，则该函数的图象位于第象限． 17．有两块面积相同的果园，分别收获苹果900kg 和1500kg ．已知第一块试验田每亩收获苹果比第二块少300kg ，求第一块试验田每亩收获苹果多少千克．设第一块试验田每亩收获苹果x kg ，根据题意，可得方程。

广东省中大附中2012-2013学年八年级上学期期中考试数学试题

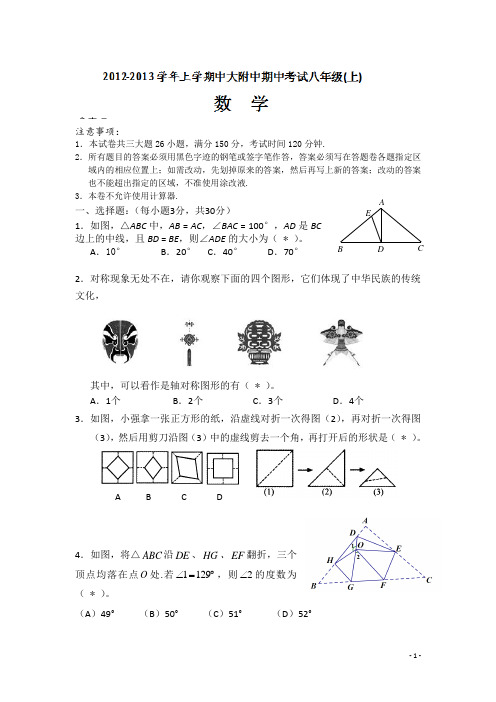
注意事项：1．本试卷共三大题26小题，满分150分，考试时间120分钟.2．所有题目的答案必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卷各题指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；改动的答案也不能超出指定的区域，不准使用涂改液. 3．本卷不允许使用计算器.一、选择题：（每小题3分，共30分） 1．如图，△ABC 中，AB = AC ，∠BAC = 100°，AD 是BC 边上的中线，且BD = BE ，则∠ADE 的大小为（ * ）。

A ．10°B ．20°C ．40°D ．70°2．对称现象无处不在，请你观察下面的四个图形，它们体现了中华民族的传统文化，其中，可以看作是轴对称图形的有（ * ）。

A ．1个 B ．2个 C ．3个D ．4个3．如图，小强拿一张正方形的纸，沿虚线对折一次得图（2），再对折一次得图（3），然后用剪刀沿图（3）中的虚线剪去一个角，再打开后的形状是（ * ）。

A B C D4．如图，将△ABC 沿DE 、HG 、EF 翻折，三个顶点均落在点O 处.若1129∠=︒，则2∠的度数为（ * ）。

（A ）49° （B ）50° （C ）51° （D ）52°D EC B A5．估算24+3的值（ * ）。

A ．在5和6之间B ．在6和7之间C ．在7和8之间D ．在8和9之间6．下列可使两个直角三角形全等的条件是（ * ）。

A ．一条边对应相等B ．斜边和一直角边对应相等C ．一个锐角对应相等D ．两个锐角对应相等 7．如图，△ABC 的三边AB 、BC 、AC 的长分别为20、 30、40，其三条角平分线将△ABC 分成三个三角形，则=∆∆∆OAC OBC OAB S S S ::（ * ）。

A ．1:1:1B. 6:4:3C. 2:3:4D. 4:3:28．如图所示，一位同学书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（ * ）。

广东省广州市各地八年级下学期期中数学试卷精选汇编

广东省广州市各地八年级下学期期中数学试卷精选汇编（考试时间：90分钟，满分：100分）一、选择题（每题2分，共30分）1. 若一个正方形的对角线长为10cm，则其面积为多少平方厘米？A. 50B. 100C. 200D. 50√22. 下列哪个数是9的平方根？A. 3B. 3C. 9D. 93. 已知函数y=2x+3，当x=4时，y的值为多少？A. 11B. 12C. 13D. 144. 若|a|=5，则a的值为多少？A. 5B. 5C. 25D. 255. 在直角坐标系中，点A(2,3)关于y轴的对称点坐标为多少？A. (2,3)B. (2,3)C. (2,3)D. (2,3)二、判断题（每题1分，共20分）6. 两个负数相乘，其结果为正数。

（）7. 任何数的平方都是非负数。

（）8. 两个正数相除，其结果为负数。

（）9. 一次函数的图像是一条直线。

（）10. 互为相反数的两个数绝对值相等。

（）三、填空题（每空1分，共10分）11. 若一个数的平方为9，则这个数为______。

12. 已知一组数据2，3，5，7，10，则这组数据的平均数为______。

13. 若一个等腰三角形的底边长为8cm，腰长为10cm，则这个三角形的周长为______cm。

14. 若一个圆的半径为5cm，则这个圆的直径为______cm。

15. 若|a|=3，则a的值为______。

四、简答题（每题10分，共10分）16. 简述勾股定理及其应用。

17. 简述一次函数的性质及其图像。

五、综合题（1和2两题7分，3和4两题8分，共30分）18. 已知一个等差数列的前三项分别为2，5，8，求该数列的通项公式及第10项的值。

19. 解方程组：\[\begin{cases}2x+3y=12 \\x2y=5\end{cases}\]20. 已知一个正方形的对角线长为10cm，求该正方形的面积。

21. 已知函数y=2x+3，求当x=4时，y的值。

广州八年级下期中数学试卷(有答案)

广东省广州八年级（下）期中数学试卷、选择题（共10小题，每小题3分，共30 分）对角线互相平分的四边形（3分）已知三角形的三边长之比为 1:1:二，则此三角形一定是（（3分）如图，把矩形ABCD 沿EF 对折后使两部分重合，若/ 仁50°则/ AEF=（）£A. 4cmB. 6cmC. 8cmD. 10cm1. （3分）下列根式中，不是最简二次根式的是（ A . 二 B . 一 C .2. （3分）下列各组数中，以a, b , c 为边的三角形不是直角三角形的是（ A . a=1.5, b=2, c=3 B . a=7, b=24, c=25 C. a=6, b=8, c=10 D. a=3, b=4, c=53. （3分）根据下列条件，不能判定四边形是平行四边形的是（ A . 一组对边平行且相等的四边形 B. 两组对边分别相等的四边形 C. 对角线相等的四边形D . 4. A . 锐角三角形B .钝角三角形 C. 等边三角形D .等腰直角三角形A . 110°. 115°C . 120°D. 130° 6 . （3分）实数a 、b在数轴上对应的位置如图，则“hr 讥•「」‘=（）A . b - a B. 2— a - b C. a - b D . 2+a — b20cm 的?ABCD 中，AB M AD ,对角线AC BD 相交于点O , OE 丄BD5. C7. （3分）如图，在周长为一条到达底部的直吸管在罐内部分 a 的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是A .①③④B.①②⑤C .③④⑤D .①③⑤、填空题（共6小题，每小题3分，共18 分） 11. （3分）计算V 的结果是 _________5<a < 12D . 5<a < 139. （3分）如图，在直角坐标系中, 将矩形OABC 沿OB 对折，使点A 落在A i 处，已知OA= _，■1yAiCJ> %/JBOAXA . （［•匚）B .（』：）C.(-D.(-10. （3分）已知：如图，在正方形交DE 于点P.若AE=AP=1 PBVE .下列结论: ABCD 外取一点 E,连接 AE 、BE 、DE A 作AE 的垂线① 厶 APH A AEB② 点B 到直线AE 的距离为二; ③ E B 丄ED; ④ S A APD +S A APE F 1+ "；⑤ S其中正确结论的序号是（）B . 12< a < 15 C. AB=1,13. _______________________________________________________________ （3分）直角二角形两直角边长分别为5和12,则它斜边上的咼为 _________________________ .14. （3 分）如图，在？ABCD中，AB=7, AD=11, DE平分/ ADC,贝U BE ____15. （3分）如图，ABCD是对角线互相垂直的四边形，且OB=OD,请你添加一个适当的条件______ ，使ABCD成为菱形（只需添加一个即可）16. （3分）如图，在直角坐标系中，已知点A （- 3, 0）、B （0, 4）,对厶OAB连续作旋转变换，依次得到△?、△ 3、厶4…，则厶2013的直角顶点的坐标为______ .、计算题（共9小题，共20 分）17. （20分）（1）计算「+|「- 1| - n+ （.：）18. （8分）如图，在边长为1的小正方形组成的网格中，△ ABC的三个顶点均在格点上，请按要求完成下列各题：（1）画线段AD// BC且使AD=BC连接CD;（2）线段AC的长为_____ , CD的长为_______ , AD的长为_______ ;（3）△ ACD为___ 三角形，四边形ABCD的面积为________ .12. （3分）要使式子有意义，则a的取值范围为19. （8 分）如图，在△ ABC中，/ A=30°, / ACB=105, CD丄AB 于D, BC=2cm 求AC和AB的长.（结果保留二次根式）20. （8分）有一只喜鹊在一棵3m高的小树上觅食，它的巢筑在距离该树24m远的一棵大树上，大树高14m，且巢离树顶部1m，当它听到巢中幼鸟的叫声，立即赶过去，如果它飞行的速度为5m/s，那它至少需要多少时间才能赶回巢中？（画出符合题意的几何图形，并求解）O是对角线AC和BD的交点，OE± AD于E, OF丄BC于F.求22. （12分）如图，在四边形ABCD中，AB=BC对角线BD平分/ABC, P是BD上一点，过点P作PM丄AD，PN丄CD,垂足分别为M， N.（1 ）求证：/ ADB=Z CDB；（2）若/ ADC=90，求证：四边形MPND是正方形.证：OE=OF23. （12 分）如图，在△ ABC中，/ ACB=90，/ B>Z A,点D 为边AB的中点，DE// BC交AC團1 图2于点E, CF// AB 交DE 的延长线于点F. (1) 求证：DE=EF(2) 连结CD,过点D 作DC 的垂线交CF 的延长线于点 G,求证：/ B= / A+Z DGC24. ( 12分)先观察下列等式，再回答下列问题:(1) 请你根据上面三个等式提供的信息，猜想• .'[—‘—J 的结果，并验证； (2) 请你按照上面各等式反映的规律，试写出用含 n 的式子表示的等式(n 为正整数). 25. (14分)如图1,在厶ABC 中，AB=BC P 为AB 边上一点，连接 CP,以PA PC 为邻边作 ?APCD AC 与 PD 相交于点 E ,已知Z ABC=Z AEP a (0°v a 90°. (1) 求证：Z EAP=/ EPA(2) ?APCD 是否为矩形？请说明理由；(3) 如图2, F 为BC 中点，连接FP,将Z AEP 绕点E 顺时针旋转适当的角度，得到Z MEN (点 M 、N 分别是Z MEN 的两边与BA 、FP 延长线的交点).猜想线段EM 与EN 之间的数量关系，并证明你的结论.参考答案与试题解析一、选择题（共10小题，每小题3分，共30分） 1. （3分）下列根式中，不是最简二次根式的是（）A •匚B .二C . 【解答】解：C 、： •••它不是最简二次根式. 故选：C.2.（3分）下列各组数中，以a, b , c 为边的三角形不是直角三角形的是（）A. a=1.5, b=2， c=3 B . a=7， b=24，c=25 C. a=6， b=8， c=10 D. a=3， b=4， c=5【解答】解：A 、T 1.52+22工32，A 该三角形不是直角三角形，“故A 选项符合题意;B 、 t 72+242=252，A 该三角形是直角三角形，故 B 选项不符合题意； C. v 62+82=10"，^该三角形是直角三角形，故C 选项不符合题意；D 、 t 32+42=52，A 该三角形不是直角三角形，故 D 选项不符合题意. 故选：A .3. （3分）根据下列条件，不能判定四边形是平行四边形的是（）A. —组对边平行且相等的四边形B. 两组对边分别相等的四边形C. 对角线相等的四边形D. 对角线互相平分的四边形【解答】解: A 、t AD=BC AD// BC,•四边形ABCD 是平行四边形，故本选项正确；B 、T AD =BC AB =CD•四边形ABCD 是平行四边形，故本选项正确；C 由AC=BD 不能推出四边形ABCD 是平行四边形，故本选项错误;.V2DD、t OA=OC OD=OB,•四边形ABCD是平行四边形，故本选项正确；故选：c.4. （3分）已知三角形的三边长之比为1：1：坏；，贝U此三角形一定是（A.锐角三角形B.钝角三角形C.等边三角形D.等腰直角三角形【解答】解：由题意设三边长分别为：x, x, ；xx2+x2= （「x）2，二三角形一定为直角三角形，并且是等腰三角形.故选：D.5. （3分）如图，把矩形ABCD沿EF对折后使两部分重合，若/ 1=50°A. 110°B. 115°C. 120°D. 130°【解答】解：根据题意得：/ 2=7 3,vZ 1+72+7 3=180°,•••7 2= (180°- 50° - 2=65°,v四边形ABCD是矩形，•AD// BC,•7 AEF+Z 2=180°,•7 AEF=180 - 65°=1150.故选：B.6 . （3分）实数a、b在数轴上对应的位置如图，则：|.-j ---------------- ■——-——*--------- ・a nb iA. b- aB. 2- a- bC. a- bD. 2+a- bB则7AEF=( )则「..-=|b - 1| - |a- 1|=1 - b - 1+a =a- b故选：C.7. （3分）如图，在周长为20cm的？ABCD中，AB M AD,对角线AC BD相交于点O, 0E丄BD 交AD于匕则厶ABE的周长为（）A. 4cmB. 6cmC. 8cmD. 10cm【解答】解：根据平行四边形的性质得：OB=OD••• EO丄BD,••• EO为BD的垂直平分线，根据线段的垂直平分线上的点到两个端点的距离相等得：BE=DE•••△ ABE 的周长=ABAE+DE=AB+AD= X 20=10cm.故选：D.8. （3分）如图是一个圆柱形饮料罐，底面半径是5,高是12,上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是( )A. 12< a< 13B. 12< a< 15C. 5< a< 12D. 5< a< 13【解答】解：a的最小长度显然是圆柱的高12,最大长度根据勾股定理，得：「：=13.即a的取值范围是12<a< 13.故选：A.9. （3分）如图，在直角坐标系中，将矩形OABC沿OB对折，使点A落在A1处，已知OA= 一 ,而 Rt A AOB ^ Rt A A 1OB ,•••/ A i OB=Z AOB=30.作A i D 丄OA,垂足为D ,如图所示.在 Rt A A i OD 中，OA i =OA= 一，/ A i OD=60 , A,D••• sin / A i OD= ,0 Aj • A i D=OA?sin / A i OD=/^ OD又 cos / A i OD=「一,• OD=OA?cos / A i OD pX 寻專.£ £ •••点A i 的坐标是 i0. （3分）已知：如调，在正方形ABCD 外取一点E,连接AE 、BE 、DE 过点A 作AE 的垂线交DE 于点P.若AE=AP=I PBVE .下列结论： ① 厶 APD ^A AEB ； ② 点B 到直线AE 的距离为-;1 C1yAi / J ’JBO AX【解答】解：在Rt A AOB 中,C (一 J D.(-tan / AOB=-二 -, OA V33 'Cy才t *BA TXAB=1,则点A i 的坐标是（A . (一)B .A. 故选:③EB丄ED;④S A APD+S A APB=1+ I：；⑤S 正方形ABCD=4+VE .其中正确结论的序号是（）A.①③④B.①②⑤C.③④⑤D.①③⑤【解答】解：①•••/ EAB^Z BAP=90 , / PAD F Z BAP=90,•••/ EAB=Z PAD,又••• AE=AP, AB二AD,•••△ APD^A AEB（故①正确）;③•••△ APD^A AEB,•••Z APD=Z AEB,又VZ AEB=/ AEP^Z BEP Z APD=Z AEF+Z PAE•Z BEP=/ PAE=90 ,•EB丄ED （故③正确）;②过B作BF丄AE,交AE的延长线于F ,V AE=AP Z EAP=90 ,•Z AEP=/ APE=45 ,又V③中EB丄ED, BF丄AF,•Z FEB=/ FBE=45 ,又V BE=「「. =71；二■,•BF=EF=（故②不正确）;④如图，连接BD,在Rt A AEP中，V AE=AP=I•EP=「,又V PB= 7 ,•BE=-,13•••△ APHA AEB ••• PD=BE= =,S ^ABP +Sx ADF =S\ABD — S\BDF = S 正方形 ABCD~ X DP X 22④ 不正确）.⑤ ••• EF=BF= , AE=1,2•••在 Rt X ABF 中,AB 2= (AE+EF ) 2+BF 2=4+ 7, --S 正方形ABCt = A^=4+ -(故⑤正确)；二、填空题（共6小题，每小题3分，共18 分） ii. （3分）计算心-心的结果是3【解答】解：原式=（5 -— 2 "）- T =3. 故答案为：3.12. （3分）要使式子有意义，则a 的取值范围为 a 》-2且a ^ 0a【解答】解：根据题意得：a+2> 0且a M 0, 解得：a > — 2且a M 0. 故答案为：a > — 2且a M 0.13. （3分）直角二角形两直角边长分别为 5和12,则它斜边上的咼为【解答】解：由勾股定理可得：斜边长2=52+122, 则斜边长=13, 直角，三角形面积S= X 5X 12= X 13 X 斜边的高, 可得：斜边的高< . 6014. （3 分）如图，在？ABCD 中，AB=7, AD=11, DE 平分/ ADC,贝U BE= 460故答案为:故选：D .A D【解答】解：：DE平分/ ADC,•••/ ADE=Z CDE••• ?ABCD中AD// BC,•••/ ADE=Z CED•••/ CDE=/ CED,来源••• CE=CD•••在?ABCD中, AB=7, AD=11 ,••• CD=AB=7 , BC=AD=11••• BE=BC- CE=11- 7=4.故答案为：4.15. (3分)如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件OA=OC ,使ABCD成为菱形(只需添加一个即可)【解答】解：OA=OC•••OB=OD, OA=OC•••四边形ABCD是平行四边形,••• AC丄BD,•••平行四边形ABCD是菱形,故答案为：OA=OC16. (3分)如图，在直角坐标系中，已知点A (- 3 , 0)、B (0 , 4),对厶OAB连续作旋转变换,依次得到厶?、△ 3、厶4…，则厶2013的直角顶点的坐标为(8052, 0).二AB= | i =5,由图可知，每三个三角形为一个循环组依次循环，一个循环组前进的长度为:••• 2013-3=671,•••△2013的直角顶点是第671个循环组的最后一个三角形的直角顶点，••• 671 X 12=8052,2013的直角顶点的坐标为（8052, 0）.故答案为：（8052, 0）.三、计算题（共9小题，共20 分）17. (20分)(1)计算「+| 7- 1| -⑶先化简，后计算：,+；+_：,其中a「, b=「【解答】解：（1）原式=2二+二-1 - 1+2=3二3 ? a 2a（3）当a=「，b=「时,1 1=.+ I4+5+3=12,0 -1n+c.);(2) J-：：」J (a> 0);(2)原式=3 . +】=718. （8分）如图，在边长为1的小正方形组成的网格中，△ ABC的三个顶点均在格点上，请按要求完成下列各题：（1）画线段AD// BC且使AD=BC连接CD;（2）线段AC的长为2「, CD的长为「，AD的长为5（3）△ ACD为直角三角形，四边形ABCD的面积为10 .【解答】解：（1）如图所示:(2) AC= ：=2 匚;CD=U+T=!;AD= ； . , =5；(3)：( 2 三)2+ (三)2=52，•••△ ACD是直角三角形，S四边形ABCD=4X 6 —2X 1 —= X 4X 3 —= X 2X 1 - —X 3X 4=10.故答案为：2 "，"，5;直角，10.19. （8 分）如图，在△ ABC中，/ A=30°，/ ACB=105，CD丄AB 于D，BC=2cm 求AC和AB的长.（结果保留二次根式）【解答】解：•••在△ ABC 中，/ A=30°, / ACB=105, CD 丄AB 于 D ,ADC 中，/ ADC=90，/ ACD=60••• AC=2CD在厶 BDC 中，/ BDC=90,Z BCD=Z DBC=45••• CD=BD由勾股定理可得，BD 2+CD 2=4 二 CD=BD=三， --AC=2*，/ cm ; 在厶ADC 中，AD=AC?si n60° =2?萼=乙 AB=AD+BD= (-；；) cm .20. （8分）有一只喜鹊在一棵3m 高的小树上觅食，它的巢筑在距离该树 24m 远的一棵大树上，大树高14m ，且巢离树顶部1m ，当它听到巢中幼鸟的叫声，立即赶过去，如果它飞行的速度为5m/s ，那它至少需要多少时间才能赶回巢中？（画出符合题意的几何图形，并求解）【解答】解：如图，由题意知 AB=3m, CD=14-仁13 (m )，BD=24m 过 A 作 AE 丄 CD 于 E .贝U CE=13- 3=10 (m )，AE=24m, 在 Rt A AEC 中, AC 2=CE 2+AE ?=102+242. 故 AC=26m , 则 26- 5=5.2 (s ),n B21. （8分）如图，在?ABCD中，O是对角线AC和BD的交点，OE±AD于E, OF丄BC于F.求证：OE=OF【解答】证明：•••四边形ABCD是平行四边形,•••OA=OC AD// BC,:丄 EAO=Z FCQ•••OE丄AD, OF丄BC,•••/ AEO=/ CFO=90,在厶AEO和△ CFO中，'ZEA0=ZFC0Z 期gZCFO,PARC•••△ AEO^A CFO( AAS,•••OE=OF22. (12分)如图，在四边形ABCD中，AB=BC对角线BD平•:分/ABC, P是BD上一点，过点P 作PM丄AD, PN丄CD,垂足分别为M, N.(1 )求证：/ ADB=/ CDB；(2)若/ ADC=90,求证：四边形MPND是正方形.【解答】证明：(1 )•对角线BD平分/ ABC,•••/ ABD=/ CBD,在厶ABD和厶CBD中，f AB=CB■ ZABD^ZCBD,SD=BD•••△ ABD^A CBD( SAS, •••/ ADB=/ CDB(2 PM 丄AD, PN丄CD,•••/ PMD=Z PND=90 ,vZ ADC=90,•••四边形MPND是矩形，vZ ADB=Z CDB•••Z ADB=45••• PM=MD,23. （12 分）如图，在△ ABC中，Z ACB=90, Z B>Z A,点D 为边AB的中点，DE/ BC交AC于占-J八、、连结CD,过点D作DC的垂线，交CF的延长线于点G,求证：Z B=Z A+Z DGC• DF=BCv D为边AB的中点，DE/ BC,• DE= BC,• EF=D R DE=BO -CB= CBE, CF// AB交DE的延长线于点F.(1) 求证：DE=EF(2)•四边形MPND是正方形.•四边形DBCF为平行四边形:,CF/AB,••• DE=EF(2 )：DB// CF,•••/ ADG=Z G,vZ ACB=90, D为边AB的中点,••• CD=DB=AD•••Z B=Z DCB Z A=Z DCAv DG丄DC,•Z DCA+Z 1= 90°°vZ DCB^Z DCA=90 ,•Z 1 = Z DCB=/ B ,vZ A+Z ADG=Z 1,•Z A+Z G=Z B.24. (12分)先观察下列等式,再回答下列问题:(1)请你根据上面三个等式提供的信息，猜想.i 的结果，并验证;(2)请你按照上面各等式反映的规律，试写出用含n的式子表示的等式(n为正整数). 【解答】解:(1)25. (14分)如图1,在厶ABC中，AB=BC P为AB边上一点，连接CP,以PA PC为邻边作?APCD AC与PD相交于点E,已知/ ABC=Z AEP a (0°v a 90°.(1 )求证：/ EAP=/ EPA(2)?APCD是否为矩形？请说明理由；(3)如图2, F为BC中点，连接FP,将/ AEP绕点E顺时针旋■转适当的角度，得到/ MEN (点M、N分别是/ MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系，并证明你的结论.【解答】（1）证明：在厶ABC和厶AEP中,•••/ ABC=/ AEP, / BACK EAP,•••/ ACB=/ APE 在厶ABC中, AB=BC•••/ ACB=/ BAC,•••/ EPA=/ EAR（2）解：?APCD是矩形.理由如下:•••四边形APCD是平行四边形，••• AC=2EA PD=2EP•••由（1）知/ EPA/ EAF,••• EA=EP贝U AC=PD••• ?APCD是矩形.(2) !：匚「二(n为正整数).(3)解：EM=EN证明：••• EA=EP•— EPA=「「呵=_ - =90°- ' a,2 2 2•••/ EAM=180 -Z EPA=180-( 90°-寺a) =90召a,由(2)知/ CPB=90, F是BC的中点，••• FP=FB•••Z FPB=Z ABC=a,•••Z EPN=/ EPA+Z APN=Z EPA+Z FPB=90 -寺a+ a =90° a,•Z EAM=Z EPN,•••Z AEP绕点E顺时针旋转适当的角度，得到Z MEN,•Z AEP=Z MEN,•Z AEP-Z AEN=Z MEN -Z AEN，即Z MEA=Z NEP,在厶EAM和A EPN中，'Z EAM-Z EPN(EArEP,ZMEA-ZNEP•••△EAM^A EPN (ASA , • EM=EN.。

广东省中大附中2011-2012学年八年级语文下学期期中考试试题

某某省中大附中2011-2012学年八年级语文下学期期中考试试题第一部分积累与运用（34分）一、（本大题共 6小题，共19分．）1．下列词语中加点的字注音全都正确．．的一项是（）（3分）A、炽．热（chì）栖．息(qī) 粗糙． (cāo) 广袤无垠．(yíng)B、稽．首(qǐ) 朔．方(suò) 禁锢． (gù) 藏污纳垢．(gòu)C、纤．细 (xiān) 解剖．(pōu) 馈．赠 (guì) 长吁．短叹(xū)D、污秽．(huì) 脊．背(jǐ)驿．站 (yì) 恍．然大悟(huǎng)2．下列各句中加点的词语运用错误．．的一项是（）（3分）A、福泰隆超市以其优质的服务和合理的价格吸引远近的顾客，超市生意葱茏．．．．。

B、随着社会经济的发展，汽车越来越多地进入了平常百姓家庭，由此而引起的道路交通事故也越来越多，其中酒后驾驶又是交通事故的罪魁祸首．．．．。

C、3月15日，央视在节目中曝光，双汇集团济源分公司以“瘦肉精”喂养生猪，“瘦肉精”事件在社会上引起了轩然大波．．．．。

D、今天高呼“卡扎菲已丧失一切统治法理”的萨科齐，3年前还令人瞠目结舌．．．．地当众宣布“我个人认为卡扎菲不是什么独裁者”。

3．下列各句中，没有．．语病的一项是（）（3分）A、某某首次发现超大稀土矿，估价超700亿左右，数家上市公司有意开发。

B、日方宣称福岛第一核电站附近海水中所测得的放射性碘含量持续不断上升，已超过法定限度的4385倍。

C、国务院常务会议通过决议，中国设立国家旅游日，时间确定为5月19日。

D、同学们要厉行节约，杜绝不浪费水电等不良行为，积极推行绿色的生活方式。

4．下列语序排列正确．．的一项是（）（3分）雪远去了，迟迟不见归来。

时间长了，盼雪的心愿总成为泡影。

无奈之余，我只好用心捧读咏雪的诗篇，____________，_____________，____________，____________。

中大附中2011-2012学年度初二下学期期中考试

中山大学附属中学2011-2012学年度下学期期中考试初二英语试卷二、语言知识及运用（共两节，满分25）第一节单项选择(共15小题，每小题1分，满分15分）16. -- When will your mother leave for Beijing?-- She will go there _______ one week’s time.A. forB. afterC. inD. on17. I’ve spent _______ reading the novel.A. one day and twoB. one day or twoC. a day or twoD. a day and two18. The villagers _______ for the lost child at this time last night.A. searchedB. are searchingC. will searchD. were searching19. Shoes of this kind ________ very well.A. sellB. sellsC. are soldD. is sold20. ---- It’s careless _______ you to make so many mistakes in the exam.A. forB. ofC. toD. by21. I prefer _______ basketball rather than _______.A. play; to swimB. to play; swimmingC. playing; swimmingD. to play; swim22. _______ sometimes I disagree with Mary, _______ we get on well with each other.A. Though; butB. Because; soC. Though; /D. /; so23. ---- How many of you have been to Africa?---- _______.A. NoneB. No oneC. NobodyD. Neither24. ---- What did Tracy say on the phone?---- She asked _______.A. when I saw the filmB. when did I see the filmC. when do I see the filmD. when will I see the film25. We found ______ very useful to know the customs of foreign countries.A. thatB. thisC. /D. it26. Dad _______ newspaper in the armchair while Mum _______ in the kitchen when I got home.A. read; cookedB. was reading; cookedC. read; was cookingD. was reading; was cooking27. There are lots of trees on _______ side of the road.A. bothB. eitherC. neitherD. any28. It’s _______ cold outside and there is _______ snow on the playground.A. much too; too muchB. too much; much tooC. much too; too manyD. many too; too much29. -- How long have you _______ this new TV set?-- For two months. I _______ it in Parking Supermarket.A. bought; boughtB. bought; hadC. had; hadD. had; bought30. Our summer holiday is coming. Two _______ the students in our school will go to England.A. hundredB. hundredsC. hundred ofD. hundreds of第二节语法选择(共10小题，每小题1分，满分10分）If you have failed in the past to try to make big changes in life, try again now, one small step at a time.Every year it’s the same. As December __31__ to the end, you think about the new year and all the ways you want to improve your life. But as you start to write down your hope for the new year, you think about the last year. You ___32____ write down all the changes you are going to make, but by the end of January those idea get ___33____ in your busy life.Here’s the suggestion: Forget the too big, hard-to-achieve goals and just think about the small ones. “We often think that we must do everything in big steps, ___34____ it’s so hard for us to reach,” said Robert Maurer, ____35___ recently wrote the book One Small Step Can Change Your Life. “What we try to do is to begin with ___36____ small step that we can’t find any excuse__37_____ it.”During ___38____, American factory managers were able to increase productivity (提高生产率) ___39____ trying small, continuous (持续的) improvements instead of sudden changes. After the war, the idea __40____ to a rebuilding Japan. It made Japan strong quickly. The Japanese called it “Kaizen”, which means “improvement.”( ) 31. A. come B. came C. comes D. coming( ) 32. A. excite B. excited C. exciting D. excitedly( ) 33. A. loses B. lost C. lose D. to lose( ) 34. A. but B. / C. because D. if( ) 35. A. which B. that C. whom D. who( ) 36. A. such a B. such C. so D. so a( ) 37. A. don’t do B. doesn’t do C. not to do D. not do( ) 38. A. world war two B. World War ⅡC. the World War TwoD. Second World War( ) 39. A. for B. from C. by D. with( ) 40. A. brought B. bring C. is brought D. was brought三、完型填空(共10小题,每小题1分，满分10分）Harry saw ___41____ ad in a window. It said, “Wanted. The Best Salesman in the World. Top Pay.”“I’m a great salesman,” Harry told ___42____. “I can sell anything. I’ll ask for that job.” He went into the building and spoke to the manager.“I’m the best salesman in the world,” he said. “Give me the job.”“You ___43____ prove you’re the best,” the manager said.“___44____,” Harry said. “Good.” The manager took a box of candy out of his desk. “Last week, I bought a thousand boxes of this candy. ___45____ you can sell them all before the end of the week, you can have the job.”“That’s easy,” Harry said. Every day, he tried to sell boxes of candy ___46____ shop to shop. But he couldn’t sell one. The candy was so bad that he couldn’t even give it away. ___47____ of the week he went back to the manager.“I’m sorry, sir,”he said. “I was wrong about myself. I’m not the best salesman in theworld.___48____I know ____49___ is.”“Oh,”said the manager, “Who?”“The guy who ___50____ you a thousand boxes of this candy,” Harry said.( ) 41. A. a B. an C. the D. /( ) 42. A. himself B. his C. him D. he( ) 43. A. can B. may C. could D. must( ) 44. A. You’re welcome B. That’s all right C. No problem D. You wait to see( ) 45. A. When B. If C. While D. Though( ) 46. A. between B. among C. from D. up( ) 47. A. By the end B. In the end C. To the end D. At the end( ) 48. A. and B. or C. but D. then( ) 49. A. who B. where C. which D. what( ) 50. A. sells B. sold C. am selling D. will sell四、阅读理解（共20小题，每小题2分，满分40分）（A）I received a letter from my Aunt Lorraine a while age. It was a handwritten letter thanking me for some Shanghai cookies I’d sent her. Aunt Lorraine is ninety-one years old and she has wonderful manners, which is why she sent me the “thank you”letter. She also has wonderful handwriting. Her penmanship is smooth and flowing with each individual letter and word perfectly formed. She is a pleasure to read.Aunt Lorraine was educated at a time when penmanship was considered an important skill. Today, in this age of e-mail and text messaging, few people have the time or incline to write letters or practice their penmanship. This is unfortunate, but good penmanship is still important, especially in school. If you want to get good grades on your essays, neatness counts. Your essay might be full of good ideas but messy handwriting can turn an A into a B. And illegible handwriting can get you a D.Good penmanship has other benefits, too. Since it’s a skill, it trains your brain and develops your learning abilities. It also helps you to organize your thoughts and ideas. And, believe it or not, that slow process of pushing a pen long paper improves your reading, spelling and even your pronunciation of English.Apart from (除了) all these educational benefits, good penmanship also has personal benefits.A neatly written letter to a friend is something they will treasure forever. A letter that looks as if a chicken had danced across the paper will be quickly tossed. I’ve kept the letter from my Aunt Lorraine, it’s a treasure!( )51. Aunt Lorraine thanked me because I sent her _______.A. Shanghai cookiesB. Shanghai giftsC. the map of ShanghaiD. a flower( )52. Aunt Lorraine wrote the thanking letter ________.A. by computerB. by typewriterC. by handD. by asking others for help( )53. The writer thinks the neatness can bring you _______.A. moneyB. good gradesC. wishesD. something to eat( )54. The word “penmanship” in the passage means _______.A. skills or style in handwritingB. an articleC. a letterD. a piece of paper( )55. The passage is mainly about _______.A. the importance of handwritingB. Aunt Lorraine’s letterC. the writer’s Shanghai cookiesD. the writer’s grades（B）Spider-Man 3 (《蜘蛛侠3》) got $29.15 million on the very first day in 16 overseas markets and beat the first two Spider-Man movies.“The movie had the best opening day ever in some countries on Tuesday, including France, Italy and South Korea.” A man from Sony Pictures said.“Spider-Man 3 will open during the next few days in many other countries, including the United States on Friday. We certainly hope the same thing will happen in North America,” said Jeff Blake, Sony vice chairman, on Wednesday.2002’s Spider-Man opened with $114.8 million in its first weekend, a debut record that stood until Pirates of the Caribbean: Dead Man’s Chest broke it last year with $135.6 million a weekend.Spider-Man2 opened on a Wednesday before the fourth weekend of July in 2004, and set a record of $180.1 million in its first six days.In France, Spider-Man 3 took in $6.8 million on the opening day, more than the first days for Spider-Man and Spider-Man 2 combined.It earned $4.6 million in Germany, $4 million in Italy, $3.7 million in Japan, $3.4 million in South Korea, $1.1 million in the Philippines and $1 million each in Hong Kong and Thailand. ( )56. Spider-Man 3 _______ when it was shown on the first day.A. was not very popularB. was enjoyed by the people in CanadaC. earned more money than Spider-Man 2D. got $29.15 million in America( )57. Jeff Blake hopes that _______.A. more and more people can see the movieB. Spider-Man 3 will be enjoyed by childrenC. Spider-Man 3will make as much money as the first two moviesD. Spider-Man 3 will be as popular in North America as it was in other places( )58. In which country did Spider-Man 3 earn the most money?A. GermanyB. ItalyC. South KoreaD. America( )59. The main idea of the passage is that _______.A. people expect to see Spider-Man 4 soonB. Spider-Man 3 is more popular in South Korea than in GermanyC. Spider-Man 3 cost lots of moneyD. Spider-Man 3 is very popular all over the world( )60. You should probably read this passage from ________.A. a talk showB. a movie magazineC. an adD. a notice（C）Did you ever wonder why your favorite foods taste so good? Well, you should thank yourtaste buds (味蕾) for letting you enjoy the saltiness and the sweetness.Taste buds are sensory organs (感觉器官) that are found on your tongue and allow you to experience tastes that are sweet, salty, sour and bitter. The average person has about 10,000 taste buds and they’re replaced (替换) every 2 weeks or so. But as a person grows older, some of those taste buds don’t get replaced. An older person may only have 5,000 working taste buds. That’s why certain foods may have a stronger taste for children than they do for adults. Smoking can also reduce the number of taste buds a person has.But before you give taste buds all the thanks for your favorite flavors (滋味), it’s important to thank your nose too. The upper part of your nose can receive the chemicals that make your brain create the sensation (感觉) of flavor. If you hold your nose while eating, your taste buds are able to tell your brain something about what you’re eating —that it’s sweet, for instance—but you won’t able to pick out the exact flavor until you let go of your nose.So next time you enjoy an apple or some soup, thank your tongue and your nose! Without them, life wouldn’t have any flavors.( )61. How many working taste buds may an old man have?A. 10,000B. 5,000C. 2,000D. 8,000( )62. What does the underlined word “reduce” mean in Chinese?A. 减少B. 增加C. 改变D.失去( )63. What can we learn from the passage?A. The same food has a stronger taste for children than for adultsB. Adults can enjoy some foods more easilyC. A person can’t smell things that are sweet, salty, sour, and bitterD. People’s taste buds will not work when they hold their noses( )64. What will happen if you catch a bad cold and your nose is stuffy?A. You can’t taste anything at allB. Things will taste the sameC. You won’t be able to tell the exact flavorD. Your brain will create a stronger flavor( )65. What does the second paragraph mainly tell us?A. How to enjoy delicious foodB. What are taste budsC. How do taste buds workD. We should thank our noses（D）Here are some tips on how to talk with your parents.Try to start your talk with something fun. This will make talking easier. For example, ask your parents questions about their day. They love this!Make it clear what you want to tell your parents. If they have an opinion, let them finish and don’t disturb. Ask them to do the same for you.Show them respect by listening to them carefully. Look at their eyes sincerely.Be honest. Honesty builds trust (信任). Life is good when your parents trust you.If your parents don’t understand, that’s OK. It doesn’t mean they don’t love you or they’re not trying. Sometimes you have to explain things to them again or in a different way.When you finish the talk, thank them for listening. Say something like, “thanks! Thathelped.” It will let them know this is important to you, and make them want to do more often.If you feel there are still things to talk about, set up a time with them to talk about it another day.( )66. What’s the main idea of this passage?A. We should show respect to our parentsB. I t’s important to trust our parentsC. We should be thankful to our parentsD. There are some ways to talk with our parents( )67. What should we do when our parents have some opinion?A. Ask them to stopB. Argue with them and then said sorryC. Let them listen to youD. Let them finish and don’t disturb( )68. Why should we look at their eyes when listening?A. Because they make us do thatB. Because this shows we agree with what they sayC. Because this makes them feel respectedD. Because this shows we understand them( )69. When we finish the talk, we should tell our parents that we _______ what they have done for us. This will let them know talking is important to us.A. are careful ofB. are satisfied withC. are angry aboutD. are thankful for( )70. Which is the best title of this passage?A. Some Tips How to Talk with ParentsB. Parents Are Very ImportantC. Try to Talk with ParentsD. Respect Parents五、写作（共三节，满分40分）第一节单词拼写(共10小题，每小题1分，满分10分）71. Lin Shuhao showed a great i_______ in playing basketball when he was young.72. Men and women should be e_______ to get jobs according to the law.73. Jerry, our English teacher is very kind but s_______ with us in our study.74. The news about the earthquake spread t_______ the world.75. I w _______ if he will come here on time.76. Don’t force your o_______ upon others.77. Thieves always get t_______ with the police.78. The students were e_______ to take part in all kinds of activities during the 9th Art Festival last term.79. She took p_______ in winning the first prize in the English speech competition.80. There are 46 students in our class, three Japanese i_______.第二节完成句子(共5小题，每空一个词，每空1分，满分15分）81. 我非常感激他给予我很多帮助。

广东省广州大学附中八年级(下)期中数学试卷

八年级（下）期中数学试卷题号一二三总分得分一、选择题（本大题共10小题，共30.0分）1.当a是怎样的实数时，在实数范围内有意义（）A. a≤3B. a≥3C. a≤-3D. a≥-32.下列二次根式中，与能合并的是（）A. B. C. D.3.下列计算中，正确的是（）A.÷= B. （4）2=8C.=2 D. 2×2=24.在Rt△ABC中，∠C=90°，∠B=45°，c=10，则a的长为（）A.5 B. C. 5 D.5.下列关于平行四边形ABCD的叙述，一定正确的是（）A. 若AB=AD，则平行四边形ABCD是矩形B. 若AC=BD，则平行四边形ABCD是矩形C. 若AB⊥BC，则平行四边形ABCD是菱形D. 若AC⊥BD，则平行四边形ABCD是矩形6.小明想知道学校旗杆的高度，他发现旗杆上的绳子垂到地面还多1米，当他把绳子的下端拉开5米后，发现下端刚好接触地面，则旗杆的高是（）A. 8米B. 10米C. 12米D. 14米7.如图，在菱形ABCD中，对角线AC，BD相交于点O，AB=5，AC=6，则菱形ABCD的面积是（）A. 24B. 26C. 30D. 488.△ABC中∠A、∠B、∠C的对边分别是a、b、c，下列命题中的假命题是（）A. 如果∠C-∠B=∠A，则△ABC是直角三角形B. 如果a：b：c=5：12：13，则△ABC是直角三角形C. 如果（c+a）（c-a）=b2，则△ABC是直角三角形D. 如果∠A：∠B：∠C=3：4：5，则△ABC是直角三角形9.如图，Rt△AMC中，∠C=90°，∠AMC=30°，N，B分别是MC，AC的中点，CN=2cm，则AM的长度为（）A. 4cmB. 8cmC. 9cmD. 6cm10.下列命题：如图，正方形ABCD中，E、F分别为AB、AD上的点，，CE、BF交于H，BF交AC于M，O为AC的中点，OB交CE于N，连下列结论中：；；；其中正确的命题有A.只有 B. 只有 C. 只有 D.二、填空题（本大题共6小题，共18.0分）11.若最简二次根式与是同类二次根式，则a=______．12.等式成立的条件是______．13.若一个等腰三角形的腰长为10，底边长为12，则其底边上的高为______．14.已知a、b、c是三角形的三边长，如果满足（a-6）2++|c-10|=0，则该三角形的面积为：______．15.已知：如图，在四边形ABCD中，∠BAD=∠BCD=90°，M，N分别是BD，AC的中点，且AC=8，BD=10，则MN=______．16.如图，将两张一样（长为8cm，宽为2cm）的矩形纸条交叉叠放，重合部分为四边形；则四边形的周长的最大值是______cm．三、解答题（本大题共7小题，共72.0分）17.计算愿（1）（2-3）×（2）+6-2x（x＞0）18.如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．（1）在图1中以格点为顶点画一个面积为10的正方形；（2）在图2中以格点为顶点画一个三角形，使三角形三边长分别为2、、；（3）如图3，点A、B、C是小正方形的顶点，求∠ABC的度数．19.一个长方体的塑料容器中装满水，该塑料容器的底面是长为4cm，宽为3cm的长方形，现将塑料容器内的一部分水倒入一个底面半径2cm的圆柱形玻璃容器中，玻璃容器水面高度上升了3cm，求长方形塑料容器中的水下降的高度．（注意：π取3）．20.如图，在△ABC中；AD⊥BC，AB=20，AC=15，CD=9（1）求BD的长；（2）求∠BAC的度数．21.如图，在平行四边形ABCD中，∠BAD和∠DCB的平分线AE，CF分别交BC，AD于点E，F，点M，N分别是AE，CF的中点，连接FM，EN（1）求证：BE=DF；（2）求证：四边形FMEN是平行四边形．22.如图1，在矩形纸片ABCD中，AB=3，AD=5，折叠纸片使点B落在AD上的点E处，折痕为PQ，过点E作EF∥AB交P于点BF．（1）求证：四边形BFED为菱形．（2）当折痕PQ的点Q与点C重合时（如图2），求菱形BFEP的边长．23.已知边长为2的正方形ABCD中，P是对角线AC上的一个动点（与点A、C不重合），过点P作PE⊥PB，PE交射线DC于点E，过点E作EF⊥AC，垂足为点F．（1）求证：PB=PE；（2）在点P的运动过程中，PF的长度是否发生变化？若不变，试求出这个不变的值，写出解答过程；若变化，试说明理由；（3）在点P的运动过程中，△PEC能否为等腰三角形？如果能，直接写出此时AP 的长；如果不能，试说明理由．答案和解析1.【答案】A【解析】解：由题意得，3-a≥0，解得a≤3．故选：A．根据被开方数大于等于0列不等式求解即可．本题考查了二次根式有意义的条件，二次根式中的被开方数必须是非负数，否则二次根式无意义．2.【答案】D【解析】解：A、与不能合并，故本选项不符合题意；B、=2与不能合并，故本选项不符合题意；C、=4与不能合并，故本选项不符合题意；D、=与能合并，故本选项符合题意；故选：D．先化简，再根据同类二次根式的定义判断即可．本题考查了同类二次根式的定义，能熟记同类二次根式的定义是解此题的关键．3.【答案】C【解析】解：A、原式===3，不符合题意；B、原式=32，不符合题意；C、原式=|-2|=2，符合题意；D、原式=4，不符合题意；故选：C．各项计算得到结果，即可作出判断．本题考查了二次根式的性质和化简，二次根式的乘除，熟练掌握法则是解题的关键．4.【答案】C【解析】解：如图，∵在Rt△ABC中，∠C=90°，∠B=45°，∴∠B=∠A=45°，∴a=b，∵c2=a2+b2，c=10，∴2a2=100解得a=5．故选：C．根据已知条件易推知Rt△ABC是等腰直角三角形，则a=b，所以根据勾股定理来求线段a的长度即可．本题考查了等腰直角三角形的判定与性质．解题时，也可以通过解直角三角形来求线段BC的长度．5.【答案】B【解析】解：A、错误．若AB=AD，则平行四边形ABCD是菱形；B、正确．C、错误．若AB⊥BC，则平行四边形ABCD是矩形；D、错误．若AC⊥BD，则平行四边形ABCD是菱形；故选：B．根据菱形、矩形、正方形的判定方法即可判断；本题考查正方形的判定、菱形的判定、矩形的判定等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．6.【答案】C【解析】【分析】此题考查了勾股定理在实际问题中的应用，能够正确理解题意，继而构造直角三角形是解决本题的关键，难度一般．根据题意设旗杆的高AB为x米，则绳子AC的长为（x+1）米，再利用勾股定理即可求得AB的长，即旗杆的高．【解答】解：画出示意图如下所示：设旗杆的高AB为xm，则绳子AC的长为（x+1）m，在Rt△ABC中，AB2+BC2=AC2，∴x2+52=（x+1）2，解得：x=12，∴AB=12m，即旗杆的高是12m．故选：C．7.【答案】A【解析】解：∵四边形ABCD是菱形，∴OA=OC=3，OB=OD，AC⊥BD，在Rt△AOB中，∠AOB=90°，根据勾股定理，得：OB=，=，=4，∴BD=2OB=8，∴S菱形ABCD=×AC×BD=×6×8=24．故选：A．根据菱形的对角线互相垂直，利用勾股定理列式求出OB，再根据菱形的对角线互相平分求出AC、BD，然后利用菱形的面积等于对角线乘积的一半列式进行计算即可得解．本题考查了菱形的周长公式，菱形的对角线互相垂直平分线的性质，勾股定理的应用，比较简单，熟记性质是解题的关键．8.【答案】D【解析】解：A、如果∠C-∠B=∠A，则△ABC是直角三角形，是真命题；B、如果a：b：c=5：12：13，则△ABC是直角三角形，是真命题；C、如果（c+a）（c-a）=b2，则△ABC是直角三角形，是真命题；D、如果∠A：∠B：∠C=3：4：5，则△ABC不是直角三角形，是假命题；故选：D．直角三角形的判定方法有：①求得一个角为90°，②利用勾股定理的逆定理．考查了命题与定理的知识，解题的关键是了解直角三角形的判定方法，难度不大．9.【答案】B【解析】解：∵CN=2cm，N，B分别是MC，AC的中点，∴CM=2CN=4，∵∠C=90°，∠AMC=30°，∴CM=AM，4=AM，∴AM=8，故选：B．根据含30°的直角三角形的性质和平行线分线段成比例进行解答即可．此题考查平行线分线段成比例，关键是根据含30°的直角三角形的性质和平行线分线段成比例解答．10.【答案】B【解析】解：∵AF=BE，AB=BC，∠ABC=∠BAD=90°，∴△ABF≌△BEC，∴∠BCE=∠ABF，∠BFA=∠BEC，∴△BEH∽△ABF，∴∠BAF=∠BHE=90°，即BF⊥EC，①正确；∵四边形是正方形，∴BO⊥AC，BO=OC，由题意正方形中∠ABO=∠BCO，在上面所证∠BCE=∠ABF，∴∠ECO=∠FBO，∴△OBM≌△ONC，∴ON=OM，即②正确；③∵△OBM≌△ONC，∴BM=CN，∵∠BOM=90°，∴当H为BM中点时，OH=BM=CN（直角三角形斜边中线等于斜边的一半），因此只有当H为BM的中点时，，故③错误；④过O点作OG垂直于OH，OG交CH与G点，在△OGC与△OHB中，，故△OGC≌△OHB，∵OH⊥OG，∴△OHG是等腰直角三角形，按照前述作辅助线之后，OHG是等腰直角三角形，OH乘以根2之后等于HG，则在证明证明三角形OGC与三角形OHB全等之后，CG=BH，所以④式成立．综上所述，①②④正确．故选：B．①可证△ABF≌△BEC到△BEH∽△ABF，所以∠BAF=∠BHE=90°得证．②由题意正方形中∠ABO=∠BCO，在上面所证∠BCE=∠ABF，由△OBM≌△ONC得到ON=OM即得证．③利用AAS证明三角形OCN全等于三角形OBM，所以BM=CN，只有H是BM的中点时，OH等于BM（CN）的一半，所以（3）错误．过O点作OG垂直于OH，OG交CH于G点，由题意可证得三角形OGC与三角形OHB 全等．按照前述作辅助线之后，OHG是等腰直角三角形，OH乘以根2之后等于HG，则在证明证明三角形OGC与三角形OHB全等之后，CG=BH，所以④式成立．本题考查了正方形的性质，全等三角形的证明以及直角三角形斜边中线的性质，比较综合，有一定难度．11.【答案】1【解析】解：∵最简二次根式与是同类二次根式，∴2a+1=3，解得，a=1，故答案为：1．根据同类二次根式的定义列出方程，解方程即可．本题考查的是同类二次根式的定义，一般地，把几个二次根式化为最简二次根式后，如果它们的被开方数相同，就把这几个二次根式叫做同类二次根式．12.【答案】a≥3【解析】解：由题意得，，解得：a≥3．故答案为：a≥3．根据二次根式有意义的条件求解即可．本题考查了二次根式有意义的条件，解答本题的关键是掌握二次根式有意义：被开方数为非负数．13.【答案】8【解析】解：如图：BC=12．AB=AC=10，在△ABC中，AB=AC，AD⊥BC；则BD=DC=BC=6；Rt△ABD中，AB=10，BD=6；由勾股定理，得：AD==8．故答案是：8．在等腰三角形的腰和底边高线所构成的直角三角形中，根据勾股定理即可求得等腰底边上的高．本题主要考查了等腰三角形的性质以及勾股定理的应用．等腰三角形的高也是等腰三角形的中线．14.【答案】24【解析】解：∵（a-6）2++|c-10|=0，∴a-6=0，b-8=0，c-10=0，∴a=6，b=8，c=10，∵62+82=102，∴该三角形是直角三角形，∴该三角形的面积为=×6×8=24．故答案为：24．首先根据非负数的性质可得a、b、c的值，再利用勾股定理逆定理证明△ABC是直角三角形，然后根据三角形的面积公式计算即可．此题考查了非负数的性质，勾股定理逆定理以及三角形的面积，关键是掌握如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．15.【答案】3【解析】解：连接AM、CM．∵∠BAD=∠BCD=90°，M是BD的中点，∴AM=BD，CM=BD，∴AM=CM=，∵N分别是AC的中点，∴MN⊥AC，AN=CN=AC=，∴在Rt△CMN中，由勾股定理得，MN===3．故答案为3．连接AM、CM．根据∠BAD=∠BCD=90°，M是BD的中点，AM=CM，三角形AMC为等腰三角形，又N是AC的中点，根据等腰三角形三线合一的性质，可知MN⊥AC，AN=CN ，最后由勾股定理求出MN．本题考查了勾股定理的应用，熟练运用直角三角形和等腰三角形的性质是解题的关键．16.【答案】17【解析】解：如图所示，此时菱形的周长最大，∵四边形AECF是菱形∴AE=CF=EC=AF，在Rt△ABE中，AE2=AB2+BE2，∴AE2=22+（8-AE）2，∴AE=，∴菱形AECF的周长=×4=17；故答案为：17．由矩形和菱形的性质可得AE=EC，∠B=90°，由勾股定理可求AE的长，即可求四边形AECF的周长．本题考查了旋转的性质，菱形的性质，矩形的性质，勾股定理，熟练运用勾股定理求线段的长度是本题的关键．17.【答案】解：（1）原式=（4-）×=3×=9；（2）原式=2+3-2=3．【解析】（1）先把二次根式化为最简二次根式，然后合并后进行二次根式的乘法运算；（2）先把二次根式化为最简二次根式，然后合并即可．本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后合并同类二次根式即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．18.【答案】解：（1）如图1的正方形的边长是，面积是10；（2）如图2的三角形的边长分别为2，，；（3）如图3，连接AC，CD，则AD=BD=CD==，∴∠ACB=90°，由勾股定理得：AC=BC==，∴∠ABC=∠BAC=45°．【解析】本题考查了勾股定理，三角形的面积，直角三角形的判定的应用，主要考查学生的计算能力和动手操作能力．（1）根据勾股定理画出边长为的正方形即可；（2）根据勾股定理和已知画出符合条件的三角形即可；（3）连接AC、CD，求出△ACB是等腰直角三角形即可．19.【答案】解：设长方形塑料容器中水下降的高度为h，根据题意得：4×3h=3×（2）2×3，解得：h=2，所以长方形塑料容器中的水下降2cm．【解析】根据倒出的水的体积不变列式计算即可．本题考查了二次根式的应用，能够正确的列出算式是解答本题的关键，难度不大．20.【答案】解：（1）∵AD⊥BC，∴∠ADB=∠ADC=90°，∴AD===12，∴BD===16；（2）由（1）得：BD=16，∴BC=BD+CD=16+9=25，∵AB=20，AC=15，∴AB2+AC2=202+152=625，BC2=625，∴AB2+AC2=BC2，∴△ABC是直角三角形，∠BAC=90°．【解析】（1）由垂直的定义得出∠ADB=∠ADC=90°，由勾股定理得出AD==12，中由勾股定理得出BD==16；（2）由（1）得：BD=16，得出BC=BD+CD=25，证出AB2+AC2=BC2，由勾股定理的逆定理即可得出△ABC是直角三角形，∠BAC=90°．本题考查了勾股定理的逆定理和勾股定理的应用，熟练掌握勾股定理是解题的关键．21.【答案】（1）证明；∵四边形ABCD是平行四边形，∴AD∥BC，AB=CD，∠BAD=∠DCB，∠B=∠D，∠DAE=∠AEB，∠DFC=∠BCF，∵∠BAD和∠DCB的平分线AE、CF分别交BC、AD于点E、F，∴∠BAE=∠DAE=∠BAD，∠BCF=∠DCF=∠DCB，∴∠BAE=∠DCF，在△BAE和△DCF中，，∴△BAE≌△DCF（ASA），∴BE=DF；（2）证明：∵△BAE≌△DCF，∴AE=CF，∠AEB=∠DFC，∴∠AEB=∠BCF，∴AE∥CF，∵点M、N分别为AE、CF的中点，∴ME∥FN，ME=FN，∴四边形FMEN是平行四边形．【解析】（1）由平行四边形的性质得出AD∥BC，AB=CD，∠BAD=∠DCB，∠B=∠D，证出∠BAE=∠DCF，由ASA证明△BAE≌△DCF，即可得出结论；（2）由全等三角形的性质得出得出AE=CF，∠AEB=∠DFC，证出AE∥CF，由已知得出ME∥FN，ME=FN，即可证出四边形MENF是平行四边形．本题考查了平行四边形的判定与性质、全等三角形的判定与性质、平行线的判定与性质；熟练掌握平行四边形的性质与判定，证明三角形全等是解决问题的关键．22.【答案】（1）证明：∵折叠纸片使B点落在边AD上的E处，折痕为PQ，∴点B与点E关于PQ对称，∴PB=PE，BF=EF，∠BPF=∠EPF，又∵EF∥AB，∴∠BPF=∠EFP，∴∠EPF=∠EFP，∴EP=EF，∴BP=BF=EF=EP，∴四边形BFEP为菱形；（2）解：∵四边形ABCD是矩形，∴BC=AD=5cm，CD=AB=3cm，∠A=∠D=90°，∵点B与点E关于PQ对称，∴CE=BC=5cm，在Rt△CDE中，DE==4cm，∴AE=AD-DE=5cm-4cm=1cm；在Rt△APE中，AE=1，AP=3-PB=3-PE，∴EP2=12+（3-EP）2，解得：EP=cm，∴菱形BFEP的边长为cm．【解析】（1）由折叠的性质得出PB=PE，BF=EF，∠BPF=∠EPF，由平行线的性质得出∠BPF=∠EFP，证出∠EPF=∠EFP，得出EP=EF，因此BP=BF=EF=EP，即可得出结论；（2）由矩形的性质得出BC=AD=5cm，CD=AB=3cm，∠A=∠D=90°，由对称的性质得出CE=BC=5cm，在Rt△CDE中，由勾股定理求出DE=4cm，得出AE=AD-DE=1cm；在Rt△APE中，由勾股定理得出方程，解方程得出EP即可．本题考查了矩形的性质、折叠变换的性质、菱形的判定与性质、平行线的性质、勾股定理等知识；熟练掌握矩形的性质和折叠变换的性质是解题的关键．23.【答案】（1）证明：过点P作PG⊥BC于G，过点P作PH⊥DC于H，如图1．∵四边形ABCD是正方形，PG⊥BC，PH⊥DC，∴∠GPC=∠ACB=∠ACD=∠HPC=45°．∴PG=PH，∠GPH=∠PGB=∠PHE=90°．∵PE⊥PB即∠BPE=90°，∴∠BPG=90°-∠GPE=∠EPH．在△PGB和△PHE中，．∴△PGB≌△PHE（ASA），∴PB=PE．（2）解：连接BD，如图2．∵四边形ABCD是正方形，∴∠BOP=90°．∵PE⊥PB即∠BPE=90°，∴∠PBO=90°-∠BPO=∠EPF．∵EF⊥PC即∠PFE=90°，∴∠BOP=∠PFE．在△BOP和△PFE中，，∴△BOP≌△PFE（AAS），∴BO=PF．∵四边形ABCD是正方形，∴OB=OC，∠BOC=90°，∴BC=OB．∵BC=2，∴OB=，∴PF=OB=．∴点PP在运动过程中，PF的长度不变，值为．（3）①若点E在线段DC上，如图1．∵∠BPE=∠BCE=90°，∴∠PBC+∠PEC=180°．∵∠PBC＜90°，∴∠PEC＞90°．若△PEC为等腰三角形，则EP=EC．∴∠EPC=∠ECP=45°，∴∠PEC=90°，与∠PEC＞90°矛盾，∴当点E在线段DC上时，△PEC不可能是等腰三角形．②若点E在线段DC的延长线上，如图4．若△PEC是等腰三角形，∵∠PCE=135°，∴CP=CE，∴∠CPE=∠CEP=22.5°．∴∠APB=180°-90°-22.5°=67.5°．∵∠PRC=90°+∠PBR=90°+∠CER，∴∠PBR=∠CER=22.5°，∴∠ABP=67.5°，∴∠ABP=∠APB．∴AP=AB=2．∴AP的长为2．【解析】（1）过点P作PG⊥BC于G，过点P作PH⊥DC于H，如图1．要证PB=PE，只需证到△PGB≌△PHE即可；（2）连接BD，如图2．易证△BOP≌△PFE，则有BO=PF，只需求出BO的长即可；（3）可分点E在线段DC上和点E在线段DC的延长线上两种情况讨论，通过计算就可求出符合要求的AP的长；本题主要考查了正方形的性质、等腰三角形的性质、全等三角形的判定与性质、角平分线的性质、勾股定理、四边形的内角和定理、三角形的内角和定理及外角性质等知识，有一定的综合性，而通过添加辅助线证明三角形全等是解决本题的关键．。

广东省下学期初中八年级期中考试数学试卷(含答案解析)

广东省下学期初中八年级期中考试数学试卷（考试时间：90分钟，满分：120分）一、选择题（每小题3分，共30分）1、下列图形中，是中心对称图形的是（）A． B． C． D．2、不等式1＋x＜0的解集在数轴上表示正确的是（）A． B．C． D．3、有一直角三角板，30°角所对直角边长是6㎝，则斜边的长是（）A．3㎝ B. 6㎝ C. 10㎝ D. 12㎝4、下列各式由左边到右边的变形中，是分解因式的为（）A．x2﹣4x+4=x（x﹣4）+4 B．a（x+y）=ax+ayC．x2﹣16+3x=（x﹣4）（x+4）+3x D．10x2﹣5x=5x（2x﹣1）5、如图1所示，OA是∠BAC的平分线，OM⊥AC于M，ON⊥AB于N，若ON=5cm，则OM长为（）A．4cm B．5cm C．8cm D．不能确定6、在直角坐标系中，点P（2，-3）向上平移3个单位长度后的坐标为（）A．（5，-3） B.（-1，-3） C.（2，0） D.（2，-6）7、下列说法中，正确的有（）①等腰三角形的两腰相等；②等腰三角形底边上的中线与底边上的高相等；③等腰三角形的两底角相等；④等腰三角形两底角的平分线相等．A．1个 B．2个 C．3个 D．4个8、不等式3x+1＞7最小整数解是 ( )图1A ．4B ．3C ．2D ．1 9、若a ＜b ，则下列各式中不成立的是（）A ．a+2＜b+2B ．﹣3a ＜﹣3bC ．2﹣a ＞2﹣bD ．3a ＜3b10、如图2，在△ABC 中，∠C=90°，点E 是AC 上的点，且∠1=∠2，DE 垂直平分AB ，垂足是D ，如果EC=3cm ，则AE 等于（）A ．3cmB ．4cmC ．6cmD ．9cm 二、填空题（每小题4分，共24分） 11、分解因式x 2-8x+16= .12、如图3，在△ABC 中，AB=AC ，∠A=36°，AB 的垂直平分线交AC 于点E ，垂足为点D ，连接BE ，则∠EBC的度数为．13、若m+n=10，m ﹣n=2，则m 2﹣n 2= ．14、已知一元一次方程1213-=+-x m x 的根是正数，那么m 的取值范围是。

广东省中大附中八年级数学下学期期中考试试题(无答案)

B考生注意事项：⒈本试卷分第Ⅰ卷和第Ⅱ卷，第Ⅱ卷用黑色钢笔、签字笔在答题卷上作答； ⒉考试时间 120分钟，全卷满分150分；第Ⅰ卷选择题（30分）一、选择题：本大题共10小题，每小题3分，共30分．1、医学研究发现一种新病毒的直径约为0.000043毫米，•则这个数用科学记数法表示为（）A ．0.43×10-4B ．0.43×104C ．4.3×10-5D ．0.43×1052、在式子1a 、2xy π、2334a b c、109x y +、78x y +、xx 2中，分式的个数有（）A 、2个B 、3个C 、4个D 、5个 3、下列各式中正确的是（）A 、1x y x y -+=--B 、22y y x x= C 、a 2÷a -3=a -1 D 、11x y x y =--+-4、在xy 1=的图象中，阴影部分面积不为1的是（）．5、直角三角形中一直角边的长为9，另两边为连续自然数，则直角三角形的周长为（）A ．90B ．120C ．121D ．不能确定6、一个四边形，对于下列条件：①一组对边平行，一组对角相等；②一组对边平行，一条对角线被另一条对角线平分；③一组对边相等，一条对角线被另一条对角线平分；④两组对角的平分线分别平行，不能判定为平行四边形的是（）A ．①B ．②C ．③D ．④7、已知()111,P x y 、()222,P x y 、()333,P x y 是反比例函数2y x=的图象上的三点，且1230x x x <<<，则1y 、2y 、3y 的大小关系是…………………（）A 、321y y y <<B 、123y y y <<C 、213y y y <<D 、231y y y << 8、如图4，在ABC ∆中，6,5===BC AC AB ，点M 为BC 中点，AC MN ⊥于点N ，则MN 等于（）A.65 B. 95 C. 125 D. 1659、有一长、宽、高分别是5㎝、4㎝、3㎝的长方体木块，一只蚂蚁要从长方体的一个顶点A 处沿长方体的表面爬到长方体上和A 相对的顶点B第8题图ABCP 第14题图处，则需要爬行的最短路径长为（）A 、cm 25 B、cm 74 C 、cm 54 D 、cm 103 10、如图：等腰直角三角形ABC 位于第一象限，AB=AC=2，直角顶点A 在直线y =x 上，其中A 点的横坐标为1，且两条直角边AB 、AC 分别平行于x 轴、y 轴，若双曲线ky x=(k ≠0)与ABC ∆有交点，则k 的取值范围是（）A 、12k <<B 、13k ≤≤C 、14k ≤≤D 、14k <≤第Ⅱ卷非选择题（分）一、细心填一填（本大题共6小题，每小题3分，共18分．直接把答案填在题中的横线上） 11、当x 时，分式22-+x x 有意义。

2023-2024学年广东省广州大学附中八年级(下)期中数学试卷+答案解析

2023-2024学年广东省广州大学附中八年级（下）期中数学试卷一、选择题：本题共10小题，每小题3分，共30分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.若二次根式有意义，则a的取值范围为()A. B. C. D.2.下列一次函数中，y随x增大而增大的有()①；②；③；④；⑤A.①②③B.①②⑤C.①③⑤D.①④⑤3.平行四边形ABCD中，：：：的值可以是()A.4：3：3：4B.7：5：5：7C.4：3：2：1D.7：5：7：54.下列命题中，正确的命题的是()A.有两边相等的平行四边形是菱形B.有一个角是直角的四边形是矩形C.四个角相等的菱形是正方形D.两条对角线相等的四边形是矩形5.如图，一次函数的图象与x轴交于点，则不等式的解为()A.B.C.D.6.已知化简的结果是一个整数，则正整数a的最小值是()A.1B.2C.3D.57.要从的图象得到直线，就要将直线()A.向上平移个单位B.向下平移个单位C.向上平移2个单位D.向下平移2个单位8.如图有一块菜地，经人工测得菜地的四周分别为，，，，，则这块菜地的面积为()A.24B.30C.32D.369.如图：顺次连接矩形四边的中点得到四边形，再顺次连接四边形四边的中点得四边形，…，按此规律得到四边形若矩形的面积为24，那么四边形的面积为()A.B.C.D.10.如图，菱形ABCD中，，，E是边AD上一动点，将沿CE折叠，得到，则面积的最大值是()A.8B.C.16D.二、填空题：本题共6小题，每小题3分，共18分。

11.化简______.12.如图，矩形ABCD的对角线AC与BD相交于O，，，则BC的长是______.13.若关于x、y的二元一次方程组的解是，则直线与的交点坐标是______.14.一次函数的图象不经过的象限是______.15.如图，在的正方形网格中，每个小正方形的边长都为1，的三个顶点均在格点上，则AB边上的高为______.16.如图，在中，，，以其三边为边分别向外作正方形，连接DH，EG，EG交AC于点P，连接BP，当时，则BP的长为______.三、解答题：本题共9小题，共72分。

广州市八年级下学期数学期中考试试卷

广州市八年级下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分）下列图形中，是轴对称图形而不是中心对称图形的是（）A . 圆B . 正方形C . 矩形D . 正三角形2. （2分）下列抽样方法是随机抽样的是（）A . 为了解刚生产的零件的质量情况，从每一个包装箱内抽5个加以检查B . 为了解全市学生的身高情况，以一、三中的学生为代表进行考察C . 为了解小学生的视力情况，选中六年级20名学生进行调查D . 为了解某地区的车流量，记录某一红绿灯处早上8：00至9：00的车流量3. （2分）下列式子没有意义的是（）A .B .C .D .4. （2分）下列式子中，属于最简二次根式的是（）A .B .C .D .5. （2分）下列各式中，正确的是（）A . =B . =C . =D . =-6. （2分）如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3， H 是AF的中点，那么CH的长是（）A . 2.5B .C .D . 27. （2分）如图所示，在▱ABCD中，对角线AC、BD相交于点O，且AB≠AD，则下列式子不正确的是（）A . AC⊥BDB . AB＝CDC . BO＝ODD . ∠BAD＝∠BCD8. （2分）分式方程=1的解为（）A . 1B . 2C .D . 09. （2分）若顺次连接四边形ABCD四边的中点，得到一个四边形，则此四边形一定是（）A . 平行四边形B . 矩形C . 菱形D . 正方形10. （2分） (2019八上·榆林期末) 如图，将一副三角板如图放置，，，，若，则A .B .C .D .二、填空题 (共7题；共7分)11. （1分） (2016八下·平武月考) 若3，m，5为三角形三边，则-=________．12. （1分）如图，将△ABC绕点A按顺时针方向旋转60°得△ADE，则∠BAD=________ 度．13. （1分） (2020九上·镇平期末) 如图，矩形纸片ABCD中，AB=3，AD=5，点P是边BC上的动点，现将纸片折叠使点A与点P重合，折痕与矩形边的交点分别为E，F，要使折痕始终与边AB，AD有交点，BP的取值范围是________.14. （1分） (2017九下·盐城期中) 在菱形ABCD中，DE⊥AB，cosA= ，BE=2，则tan∠DBE的值是________．15. （1分）方程的根为________.16. （1分）(2020·灯塔模拟) 如图在坐标系中放置一菱形OABC，已知∠ABC=60°，OA=1.先将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2016次，点B的落点依次为B1 ， B2 ， B3 ，…，则B2016的坐标为________.17. （1分）如图，已知菱形OABC，点C在x轴上，直线y=x经过点A，菱形OABC面积是，若反比例函数图象经过点B，则此反比例函数表达式为________三、解答题 (共10题；共118分)18. （10分）计算：（1）（3 ﹣）（﹣3 ﹣）；（2） + × ÷ ．19. （8分）(2020·南开模拟) 解不等式组请结合题意填空，完成本题的解答．（1）解不等式①，得________；（2）解不等式②，得________；（3）把不等式①和②的解集在数轴上表示出来：（4）原不等式维的解集为________．20. （15分）如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A(0，1)，B(﹣1，1)，C(﹣1，3).（1）画出△ABC关于x轴对称的△A1B1C1 ，并写出点C1的坐标；（2）画出△ABC绕原点O顺时针方向旋转90°后得到的△A2B2C2 ，并写出点C2的坐标；（3）将△A2B2C2平移得到△A3B3C3 ，使点A2的对应点是A3 ，点B2的对应点是B3 ，点C2的对应点是C3(4，﹣1)，在坐标系中画出△A3B3C3 ，并写出点A3 ， B3的坐标.21. （10分）如图，在平行四边形中，点是对角线的中点，点是上一点，且，连接并延长交于点，过点作的垂线，垂足为，交于点 .（1）若，，求的面积；（2）若，求证： .22. （15分）为了了解全校1800名学生对学校设置的体操、球类、跑步、踢毽子等等课外体育活动项目的喜爱情况，在全校范围内随机抽取了若干名学生．对他们最喜爱的体育项目（每人只选一项）进行了问卷调查，将数据进行了统计并绘制成了如图所示的频数分布直方图和扇形统计图（均不完整）．（1）在这次问卷调查中，一共抽查了多少名学生？（2）补全频数分布直方图；（3）估计该校1800名学生中有多少人最喜爱球类活动？23. （5分）(2017·乌鲁木齐模拟) 乌苏市某生态示范园，计划种植一批苹果梨，原计划总产量达36万千克，为了满足市场需求，现决定改良苹果梨品种，改良后平均每亩产量是原计划的1.5倍，总产量比原计划增加了9万千克，种植亩数减少了20亩，则原计划和改良后平均每亩产量各多少万千克？24. （10分）(2017·鹤壁模拟) 如图，已知BC是⊙O的直径，AC切⊙O于点C，AB交⊙O于点D，E为AC 的中点，连结DE．（1）若AD=DB，OC=5，求切线AC的长；（2）求证：ED是⊙O的切线．25. （15分）(2018·绍兴) 小敏思考解决如下问题：原题：如图1，点P，Q分别在菱形ABCD的边BC，CD上，∠PAQ=∠B，求证AP=AQ。