初二上几何证明题 题专题训练 好题汇编
初二上几何证明题100题专题训练-

初二上几何证明题100题专题训练-八年级上册几何题专题训练1000题1、已知:在⊿ABC中,A=900,AB=AC,在BC上任取一点P,作PQ∥AB交AC于Q,作PR∥CA交BA 于R,D是BC的中点,求证:⊿RDQ是等腰直角三角形。
RQDCABP2、已知:在⊿ABC中,A=900,AB=AC,D是AC的中点,AEBD,AE延长线交BC于F,求证:ADB=FDC。
EFDCAB3、已知:在⊿ABC中BD、CE是高,在BD、CE或其延长线上分别截取BM=AC、CN=AB,求证:MANA。
4、已知:如图(1),在△ABC中,BP、CP分别平分ABC和ACB,DE过点P交AB于D,交AC于E,且DE∥BC.求证:DE-DB=EC.MNDEBCAABCDEP 图⑴5、在Rt△ABC中,AB=AC,BAC=90,O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系(不要求证明);(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。
6、如图,△ABC为等边三角形,延长BC到D,延长BA到E,AE=BD,连结EC、ED,求证:CE=DE7、如图,等腰三角形ABC中,AB=AC,A =90,BD平分ABC,DEBC且BC=10,求△DCE的周长。
8.如图,已知△EAB≌△DCE,AB,EC分别是两个三角形的最长边,A =C=35,CDE=100,DEB=10,求AEC的度数.ABCOMN9.如图,点E、A、B、F在同一条直线上,AD与BC交于点O,已知CAE=DBF,AC=BD.求证:C=D10.如图,OP平分AOB,且OA=OB.(1)写出图中三对你认为全等的三角形(注:不添加任何辅助线);(2)从(1)中任选一个结论进行证明.11.已知:如图,AB=AC,DB=DC,AD的延长线交BC于点E,求证:BE=EC。
12.如图,在△ABC中,AB=AD=DC,BAD=28,求B和C的度数。
八年级几何证明题集锦及解答值得收藏

For personal use only in study and research; not for commercial use八年级几何全等证明题归纳1.如图,梯形ABCD中,AD∥BC,∠DCB=45°,BD⊥CD.过点C作CE⊥AB 于E,交对角线BD于F,点G为BC中点,连接EG、AF.求证:CF=AB+AF.证明:在线段CF上截取CH=BA,连接DH,∵BD⊥CD,BE⊥CE,∴∠EBF+∠EFB=90°,∠DFC+∠DCF=90°,∵∠EFB=∠DFC,∴∠EBF=∠DCF,∵DB=CD,BA=CH,∴△ABD≌△HCD,∴AD=DH,∠ADB=∠HDC,∵AD∥BC,∴∠ADB=∠DBC=45°,∴∠HDC=45°,∴∠HDB=∠BDC—∠HDC=45°,∴∠ADB=∠HDB,∵AD=HD,DF=DF,∴△ADF≌△HDF,∴AF=HF,∴CF=CH+HF=AB+AF,∴CF=AB+AF.2.如图,ABCD为正方形,E为BC边上一点,且AE=DE,AE与对角线BD交于点F,连接CF,交ED于点G.判断CF与ED的位置关系,并说明理由.解:垂直.理由:∵四边形ABCD为正方形,∴∠ABD=∠CBD,AB=BC,∵BF=BF,∴△ABF≌△CBF,∴∠BAF=∠BCF,∵在RT△ABE和△DCE中,AE=DE,AB=DC,∴RT△ABE≌△DCE,∴∠BAE=∠CDE ,∴∠BCF=∠CDE ,∵∠CDE+∠DEC=90°,∴∠BCF+∠DEC=90°,∴DE ⊥CF .3.如图,在直角梯形ABCD 中,AD ∥BC ,∠A =90º,AB =AD ,DE ⊥CD 交AB 于E ,DF 平分∠CDE 交BC 于F ,连接EF .证明:CF =EF解:过D 作DG ⊥BC 于G .由已知可得四边形ABGD 为正方形, ∵DE ⊥DC∴∠ADE+∠EDG=90°=∠GDC+∠EDG ,∴∠ADE=∠GDC .又∵∠A=∠DGC 且AD=GD ,∴△ADE ≌△GDC ,∴DE=DC 且AE=GC .在△EDF 和△CDF 中∠EDF=∠CDF ,DE=DC ,DF 为公共边,∴△EDF≌△CDF ,∴EF=CF4.已知:在⊿ABC 中,∠A=900,A EB F CDAB=AC,D是AC的中点,AE⊥BD,AE延长线交BC于F,求证:∠ADB=∠FDC。
初二上几何证明题100题专题训练

M N DEB CA八年级上册几何题专题训练100题之五兆芳芳创作1、 已知:在⊿ABC 中,∠A=900,AB=AC ,在BC 上任取一点P ,作PQ ∥AB 交AC 于Q ,作PR ∥CA 交BA 于R ,D 是BC 的中点,求证:⊿RDQ 是等腰直角三角形.2、 已知:在⊿ABC 中,∠A=900,AB=AC ,D 是AC 的中点,AE ⊥BD ,AE 延长线交BC 于F ,求证:∠ADB=∠FDC.3、 已知:在⊿ABC 中BD 、CE 是高,在BD 、CE 或其延长线上辨别截取BM=AC 、CN=AB ,求证:MA ⊥NA. 4、已知:如图(1),在△ABC 中,BP 、CP 辨别平分∠ABC 和∠ACB ,DE 过点P 交AB 于D ,交AC 于E ,且DE ∥BC .求证:DE -DB=EC . 5、在Rt △ABC 中,AB =AC ,∠BAC=90°,O 为BC 的中点.(1)写出点O 到△ABC 的三个顶点A 、B 、C 的距离的大小关系(不要求证明);(2)如果点M 、N 辨别在线段AB 、AC 上移动,在移动中保持AN =BM ,请判断△OMN 的形状,并证明你的结论.6、如图,△ABC 为等边三角形,延长BC 到D ,延长BA 到E ,AE=BD , 连结EC 、ED ,求证:CE=DE7、如图,等腰三角形ABC 中,AB =AC ,∠A =90°,BD 平分∠ABC ,DE ⊥BC 且BC =10,求△DCE 的周长.8. 如图,已知△EAB ≌△DCE ,AB ,EC 辨别是两个三角形的最长边,∠A =∠C =35°,∠CDE =100°,∠DEB =10°,求∠AEC 的度数.9. 如图,点E 、A 、B 、F 在同一条直线上,AD 与BC 交于点O,A BCO M N已知∠CAE=∠DBF,AC=BD.求证:∠C=∠D10.如图,OP平分∠AOB,且OA=OB.(1)写出图中三对你认为全等的三角形(注:不添加任何帮助线);(2)从(1)中任选一个结论进行证明.11. 已知:如图,AB=AC,DB=DC,AD的延长线交BC于点E,求证:BE=EC.12. 如图,在△ABC中,AB=AD=DC,∠BAD=28°,求∠B和∠C的度数.13. 如图,B、D、C、E在同一直线上,AB=AC,AD=AE,求证:BD=CE.14. 写出下列命题的逆命题,并判断逆命题的真假.如果是真命题,请赐与证明;•如果是假命题,请举反例说明.命题:有两边上的高相等的三角形是等腰三角形.15. 如图,在△ABC中,∠ACB=90º,D是AC上的一点,且AD=BC,DE AC 于D,∠EAB=90º.求证:AB=AE.16. 如图,等边△ABC中,点P在△ABC内,点Q在△ABC外,B,P,Q 三点在一条直线上,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试证明你的结论.17. 如图,△ABC中,∠C=90°,AB的中垂线DE交AB于E,交BC于D,若AB=13,AC=5,则△ACD的周长为多少?18.如图所示,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足辨别是E,F,求证:CE=DF.19. 如图,已知△ABC 中,∠ACB =90°,AC =BC ,BE ⊥CE ,垂足为E ,AD ⊥CE ,垂足为D.(1)判断直线BE 与AD 的位置关系是____;BE 与AD 之间的距离是线段____的长;(2)若AD =6 cm ,BE =2 cm ,求BE 与AD 之间的距离及AB 的长.20. 如图,已知 △ABC 、△ADE 均为等边三角形,点D 是BC 延长线上一点,连结CE ,求证:BD=CE 21. 如图,△ABC 中,AB=AC ,∠BAC=120°,AD ⊥AC 交BC•于点D ,求证:•BC=3AD.22. 如图,四边形ABCD 中,∠DAB=∠BCD=90°,M 为BD 中点,N 为AC中点,求证:MN ⊥AC .23、已知:如图所示,在△ABC 中,∠ABC=45°,CD ⊥AB 于点D ,BE 平分∠ABC ,且BE ⊥AC 于点E ,与CD 相交于点F ,H 是BC 边的中点,连接DH 与BE 相交于点G .(1)求证:BF=AC ; (2)求证:DG=DF .24. 如图,点B ,D 在射线AM 上,点C ,E 在射线AN 上,且AB=BC=CD=DE ,已知∠EDM=84°,求∠A 的度数.25. 如图所示,在△ABC 中,AB=AC ,BD ⊥AC 于点D ,CE ⊥AB 于点E ,BD ,CE 相交于F.求证:AF 平分∠BAC.26. 如图所示,△ABC ≌△ADE ,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求 ∠DFB 和∠DGB 的度数.27. 已知:如图,在△ABC 中,AB=AC ,点D 在边BC 上,DE ⊥AB ,DF ⊥AC ,且DE=DF ,求证:△ABD ≌△ACDB AED C28. 如图,一张直角三角形的纸片ABC ,两直角边AC=6cm ,BC=8cm .现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,且AC 与AE 重合,求CD 的长.29. 已知:如图,在△ABC 中,AB=AC ,BD 平分∠ABC ,E 是底边BC 的延长线上的一点且CD=CE.(1)求证:△BDE 是等腰三角形(2)若 ∠A=36°,求∠ADE 的度数. 30. 如图,在△ABC 中,AB=CB ,∠ABC=90°,D 为AB 延长线上一点,点E 在BC 边上且BE=BD ,连结AE 、DE 、DC .(1)求证:AE=CD ;(2)若∠CAE=30°,求∠BDC 的度数.31. 如图,在ABC ∆中,点D 在AC 边上,DB=BC ,点E 是CD 的中点,点F 是AB 的中点,则可以得到结论:12EF AB =,请说明理由. 32. 已知:如图,在ABC ∆中,C ABC ∠=∠,点D 为边AC 上的一个动点,延长AB 至E ,使BE=CD ,连结DE ,交BC 于点P.(1)DP 与PE 相等吗?请说明理由.(2)若60C ∠=︒,AB=12,当DC=_________时,BEP ∆是等腰三角形.(不必说明理由)33. 如图,C 为线段BD 上一点(不与点B ,D 重合),在BD 同侧辨别作正三角形ABC 和正三角形CDE ,AD 与BE 交于一点F ,AD 与CE 交于点H ,BE 与AC 交于点G .(1)求证:BE=AD ;(2)求∠AFG 的度数;A B C D E(3)求证:CG=CH34. 已知:如图,在△ABC 中,CD ⊥AB ,CD=BD ,BF 平分∠DBC ,与CD ,AC 辨别交与点E 、点F ,且DA=DE ,H 是BC 边的中点,连结DH 与BE 相交于点G .(1)求证:△EBD ≌△ACD ;(2)求证:点G 在∠DCB 的平分线上(3)试探索CF 、GF 和BG 之间的等量关系,并证明你的结论.35. 如图,在在△ABC 中,AB=CB ,∠ABC=90°,F 为AB 延长线上一单,点E 在BC 上,且AE=CF.(1)求证:CBF Rt ABE Rt ∆≅∆(2)若∠CAE=30°,求∠ACF 的度数36. 如图,△ACD 和△BCE 都是等腰直角三角形,∠ACD =∠BCE =90°,AE 交DC 于F ,BD 辨别交CE ,AE 于点G 、H. 试猜测线段AE 和BD 数量关系,并说明理由.37. 如图,在△ABC 中,AB =AC ,AD 和BE 是高,它们相交于点H ,且AE =BE .求证:AH =2BD .38. 如图,在ABC ∆中,32B ︒∠=,48C ︒∠=AE 平分BAC ∠交BC 于点E ,DF AE ⊥于点F ,求ADF ∠39. 如图所示,在△ABC 中,已知点D ,E ,,CE 的中点,AAM EG F D CB A 且ABC S ∆ =4,则BEF S ∆ 的值为多少.40. 如图,ABC ∆中,90ACB ∠=,CD BA ⊥于D ,AE 平分BAC ∠交CD 于F ,交BC 于E ,求证:CEF ∆是等腰三角形.41. 如图,在四边形ABCD 中,DC ∥AB , BD 平分∠ADC , ∠ADC=60°,过点B 作BE ⊥DC ,过点A 作AF ⊥BD ,垂足辨别为E 、F ,连接EF.判断△BEF 的形状,并说明理由.42. 如图,已知Rt △ABC ≌Rt △ADE ,∠ABC =∠ADE =90°,BC 与DE 相交于点F ,连接CD ,EB.(1)图中还有几对全等三角形,请你一一列举;(不必证明)(2)求证:CF =EF.43. 在ABC ∆中,BO 平分ABC ∠,点P 为直线AC 上一动点,PO BO ⊥于点O .(1)如图1,当40ABC ︒∠=,60BAC ︒∠=,点P 与点C 重应时,求APO ∠的度数;(2)如图2,当点P 在AC 延长线时,求证:()12APO ACB BAC ∠=∠-∠; (3)如图3,当点P 在边AC 所示位置时,请直接写出APO ∠与ACB∠,BAC ∠之间的数量关系式.44. 如图,在ABC ∆中,BAD DAC ∠=∠,DF AB ⊥,DM AC ⊥,AF=10cm , AC=14cm ,动点E 以2cm/s 的速度从A 点向F 点运动,动点G 以1cm/s 的速度从C 点向A 点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t .(1) 求证:在运动进程中,不管取何值,都有2AED DGC S S ∆∆=; (2) 当取何值时,DFE ∆与DMG ∆全等.45. 如图,在Rt △ABC 中,∠B=90°,AB=3, D CBC=4,将△ABC折叠,使点B恰好落在边AC上,与点'B重合,AE为折痕,求'EB的长度46. 如图,已知ΔABC是等腰直角三角形,∠C=90°.(1)操纵并不雅察,如图,将三角板的45°角的顶点与点C重合,使这个角落在∠ACB的内部,两边辨别与斜边AB交于E、F两点,然后将这个角绕着点C在∠ACB的内部旋转,不雅察在点E、F的位置产生变更时,AE、EF、FB中最长线段是否始终是EF?写出不雅察结果.(2)探索:AE、EF、FB这三条线段能否组成以EF为斜边的直角三角形?如果能,试加以证明.47. 已知BD,CE是△ABC的两条高,M、N辨别为BC、DE的中点.(1)请写出线段MN与DE的位置有什么关系?请说明理由.(2)当∠A=45°时,请判断1△EMD为何种三角形,并说明理由48. 如图(1),已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且点B,C在AE的两侧,BD⊥AE于点D,CE⊥AE于点E.(1)求证:BD=DE+CE;(2)若直线AE绕点A旋转到如图(2)的位置(BD<CE)时,其余条件不变,问BD与DE,CE的关系如何?请赐与证明;(3)若直线AE绕点A旋转到如图(3)的位置(BD>CE)时,其余条件不变,问BD与DE,CE的关系如何?请直接写出结果,不需证明.49. 如图1,两个不全等的等腰直角三角形OAB和等腰直角三角形OCD叠放在一起,并且有公共的直角顶点O.(1)在图1中,你发明线段AC ,BD 的数量关系是________________ , 直线AC ,BD 相交成_________度角.(2)将图1中的△OAB 绕点O 顺时针旋转90°角,这时(1)中的两个结论是否成立?请做出判断并说明理由(3)将图1中的△OAB 绕点O 顺时针旋转一个锐角,得到图3,这时(1)中的两个结论是否成立?请作出判断并说明理由.50.△BEC 是等腰直角三ABCD 的面积. 51. △O ,过点O 辨别作OD AB OE BC OF CA ⊥⊥⊥、、,垂足辨别为点D E F 、、. (1)如图1,若点O 是等边ABC △的三条高线的交点,请辨别说明下列两个结论成立的理由. 结论1.2OD OE OF ++=;结论2.32AD BE CF a ++=; (2)如图2,若点O 是等边ABC △内任意一点,则上述结论12、是否仍然成立?(写出说理进程).52. 已知两个共一个顶点的等腰Rt △ABC ,Rt △CEF ,∠ABC=∠CEF=90°,连接AF ,M 是AF 的中点,连接MB 、ME .(1)如图1,当CB 与CE 在同一直线上时,求证:MB ∥CF ;(2)如图1,若CB=a ,CE=2a ,求BM ,ME 的长;(3)如图2,当∠BCE=45°时,求证:BM=ME .53. 如图,已知ABC △中,∠B=∠C ,AB=AC=8厘米,BC=6厘米,点D 为AB 的中点.如果点P 在线段BC 上以每秒2厘米的速度由B 点向C 点运动,同时,点Q 在线段CA 上以每秒a 厘米的速度由C 点向A 点运动,设运动时间为t (秒).(1)用含t 的代数式暗示线段PC 的长度;O 图1 图2 图B(2)若点P 、Q 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由;(3)若点P 、Q 的运动速度不相等,当点Q 的运动速度a为多少时,能够使BPD △与CQP △全等?(4)若点Q 以(3)中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都顺时针沿ABC △三边运动,求经过量长时间点P 与点Q 第一次在ABC △的哪条边上相遇?54. 如图,在ABC ∆中,BAD DAC ∠=∠,DF AB ⊥,DM AC ⊥,AF=10cm ,AC=14cm ,动点E 以2cm/s 的速度从A 点向F 点运动,动点G 以1cm/s 的速度从C 点向A 点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t .(1)求证:在运动进程中,不管t 取何值,都有2AED DGC S S ∆∆=;(2)当t 取何值时,DFE ∆与DMG ∆全等求(3)在(2)的前提下,若119126BD DC =,228AED S cm ∆=,BFD S ∆55. 已知等边△ABC 和点P ,设点P 到△ABC3边的AB 、AC 、BC•的距离辨别是h1,h2,h3,△ABC 的高为h ,若点P 在一边BC 上(图1),此时h=0,可得结论h1+h2+h3=h ,请你探索以下问题:当点P 在△ABC 内(图2)和点P 在△ABC 外(图3)这两种情况时,h1、h2、h3与h•之间有怎样的关系,请写出你的猜测,并扼要说明理由.(1) (2) (3)56.如图,△ABC 中,∠C=Rt ∠,AC=8cm ,BC=6cm ,若动点P 从点C 开始,按CABC 的路径运动,且速度为每秒2㎝,设运动的时间为t 秒.(1)求t为何值时,CP把△ABC的周长分红相等的两部分;(2)求t为何值时,CP把△ABC的面积分红相等的两部分;并求此时CP 的长;(3)求t为何值时,△BCP为等腰三角形?57. 已知,△ABC是边长3cm的等边三角形.动点P以1cm/s的速度从点A 出发,沿线段AB向点B运动.(1)如图1,设点P的运动时间为t(s),那么t=(s)时,△PBC是直角三角形;(2)如图2,若另一动点Q从点B出发,沿线段BC向点C运动,如果动点P、Q都以1cm/s的速度同时出发.设运动时间为t(s),那么t为何值时,△PBQ是直角三角形?(3)如图3,若另一动点Q从点C出发,沿射线BC标的目的运动.连接PQ交AC于D.如果动点P、Q都以1cm/s的速度同时出发.设运动时间为t(s),那么t为何值时,△DCQ是等腰三角形?(4)如图4,若另一动点Q从点C出发,沿射线BC标的目的运动.连接PQ交AC于D,连接PC.如果动点P、Q都以1cm/s的速度同时出发.请你猜测:在点P、Q的运动进程中,△PCD和△QCD的面积有什么关系?并说明理由.58.如图所示,已知AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于点F,交AD于点E,连接AF,求证:∠B=∠CAF.59.如图所示,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足辨别为E,F,连接EF,EF与AD交于点G,求证:AD垂直平分EF.60.已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为_________.15.如图所示,已知点D是等边三角形ABC的边BC延长线上的一点,∠EBC=∠DAC ,CE ∥AB.求证:△CDE 是等边三角形.61.如图所示,在△ABC 中,AB=AC ,在AB 边上取点D ,在AC 的延长线上取点E ,使得BD=CE ,连接DE 交BC 于点G ,求证:DG=GE.62.一艘轮船以15海里/时的速度由南向北飞行,如图,在A 处望小岛P ,测得∠PAN=15°,两小时后,轮船到达B 处,测得∠PBN=30°,在小岛P 周围18海里的规模内有暗礁,若轮船持续向北飞行,有无触礁危险? 63.如图,公园内两条小河MO 、NO 在O处会合,两河形成的半岛上有一处奇迹P.现筹划在两条小河上各建一座小桥Q 和R ,并在半岛上修三段小路,连通两座小桥和奇迹.这两座小桥应建在何处,才干使修路费最少? 64. 三角形ABC 中,AB=AC ,∠BAC=120°,AB 的垂直平分线EF 交AB 于E ,交BC 于F .若FC=3cm ,则求BF 长度65. 在Rt △ABC 中,∠是斜边上的高.(1)请说明△的长.668cm ,•长BC•为10cm 痕为AE ).想一想,此时EC 67、如图一块四边形草坪求这块草坪的面积.68. 如图,A 、B 两个小集镇在河道CD 的同侧,辨别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河滨建一自来水厂,向A 、BN BA AB两镇供水,铺设水管的用度为每千米3万,请你在河道CD上选择水厂的位置M,使铺设水管的用度最节省,并求出总用度是多少?69.如图,A市气象站测得台风中心在A市正东标的目的300千米的B处,以107千米/时的速度向北偏西60°的BF标的目的移动,距台风中心200•千米规模内是受台风影响的区域.(1)A市是否会受到台风的影响?写出你的结论并赐与说明;(2)如果A市受这次台风影响,那么受台风影响的时间有多长?70、如图:在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B,试说明AB=AC+CD71、如图,AD是∠BAC的角平分线,DE⊥AB垂足为E,DF⊥AC,垂足为点F,且BD=CD 求证:BE=CF72、如图,点B和点C辨别为∠MAN两边上的点,AB=AC.(1)按下列语句画出图形:①AD⊥BC,垂足为D;②∠BCN的平分线CE与AD的延长线交于点E;③连结BE;(2)在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形:____≌____,____≌____;(3)并选择其中的一对全等三角形予以证明.73、已知:AB=AC,AD⊥BC,CE平分∠BCN,求证:△ADB≌△ADC;△BDE≌△CDE.AB D CM NE74、如图,PB、PC辨别是△ABC的外角平分线且相交于点P.求证:点P在∠A的平分线上AB CP75、如图,△ABC中,p是角平分线AD,BE的交点. 求证:点p在∠C的平分线上76、下列说法中,错误的是()A.三角形任意两个角的平分线的交点在三角形的内部B.三角形两个角的平分线的交点到三边的距离相等C.三角形两个角的平分线的交点在第三个角的平分线上D.三角形任意两个角的平分线的交点到三个顶点的距离相等77、如图在三角形ABC中BM=MC∠ABM=∠ACM求证AM平分∠BAC78、如图,AP、CP辨别是△ABC外角∠MAC与∠NCA的平分线,它们相交于点P,PD⊥BM于点D,PF⊥BN于点F.求证:BP为∠MBN的平分线.79、如图,在∠AOB的两边OA,OB上辨别取OM=ON,OD=OE,DN和EM相交于点C.求证:点C在∠AOB的平分线上.80、如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.(1)若连接AM,则AM是否平分∠BAD?请你证明你的结论;(2)线段DM与AM有怎样的位置关系?请说明理由.81、八(1)班同学上数学勾当课,利用角尺平分一个角(如图所示).设计了如下筹划:(Ⅰ)∠AOB是一个任意角,将角尺的直角顶点P介于射线OA、OB之间,移动角尺使角尺两边相同的刻度与M、N重合,即PM=PN,过角尺顶点P的射线OP 就是∠AOB 的平分线.(Ⅱ)∠AOB 是一个任意角,在边OA 、OB 上辨别取OM=ON ,将角尺的直角顶点P 介于射线OA 、OB 之间,移动角尺使角尺两边相同的刻度与M 、N 重合,即PM=PN ,过角尺顶点P 的射线OP 就是∠AOB 的平分线.(1)筹划(Ⅰ)、筹划(Ⅱ)是否可行?若可行,请证明;若不成行,请说明理由;(2)在筹划(Ⅰ)PM=PN 的情况下,持续移动角尺,同时使PM ⊥OA ,PN ⊥OB .此筹划是否可行?请说明理由.内的一点,PE ⊥AB ,PF ⊥AC ,垂足辨别为点E ,F ,AE=AF.求证:(1)PE=PF ;(2)点P 在∠BAC 的角平分线上.83、如图,点D 、B 辨别在∠A 的两边上,C 是∠A 内一点,AB=AD ,BC=CD ,CE ⊥AD 于E ,CF ⊥AF 于F.求证:CE=CF84、已知三角形三边长为a ,b ,c ,且丨a+b+c 丨+丨a-b-c 丨=10,求b 的值.85、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC86、如图,△ABC 和△ADE 都是等腰直角三角形,CE与BD 相交于点M,BD 交AC 于点N ,证明:(1)BD=CE.(2)BD ⊥CE.87、如图,已知AD ∥BC ,∠PAB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD+BC=AB88、如图,△ABC 中BA=BC ,点D 是AB 延长线上一点,DF ⊥AC 于F 交B A C D F 2 1 EBC于E,求证:△DBE是等腰三角形.89、如图,在△ABC中,AC=BC,∠ACB=90°,D是AC上一点,AE⊥BD1BD.求证:BD是∠ABC的角平分线.交BD的延长线于E,且AE=290、如图,∠BAD=∠CAD,AD⊥BC,垂足为点D,BD=CD可知哪些线段是哪个三角形的角平分线、中线、高?91、如图所示,在△ABC中,已知AC=8,BC=6,AD⊥BC于D,AD=5,BE⊥AC于E,求BE的长92、如图,AD是△ABC的角平分线,DE∥AB,DF∥AC,EF交AD于点O.请问:DO是△DEF的角平分线吗?请说明理由.(2)若将结论与AD是∠CAB的角平分线、DE∥AB、DF∥AC中的任一条件互换,所得命题正确吗?93、如图,△ABC中,∠ABC与∠ACB的平分线交于点I,按照下列条件,求∠BIC的度数.(1)若∠ABC=70°,∠ACB=50°,则∠BIC=°(2)若∠ABC+∠ACB=120°,则∠BIC=°(3)若∠A=90°,则∠BIC=°;(4)若∠A=n°则∠BIC=°(5)从上述计较中,我们能发明∠BIC与∠A的关系吗?AIB C94、如图,求证∠A+∠B+∠C+∠D+∠E=180°95、如图,不法则的五角星图案,求证:∠A+∠B+∠C+∠D+∠E=180°96、D为△ABC的边AB上一点,且∠ADC=∠ACD.求证:∠ACB>∠B97、如图,D是BC延长线上的一点,∠ABC.∠ACD的平分线交于点E,求证:∠E=1/2∠A98、如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的角平分线.(1)试求∠F与∠B,∠D的关系;(2)若∠B:∠D:∠F=2:4:x 求X的值99、如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=度.100.如图,在Rt△ABC中,已知∠ACB=90°,AC=BC,D为DC的中点,CE⊥AD于E,BF∥AC交CE的延长线于点F.求证:AB垂直平分DF.。
八年级几何证明题集锦及解答值得收藏
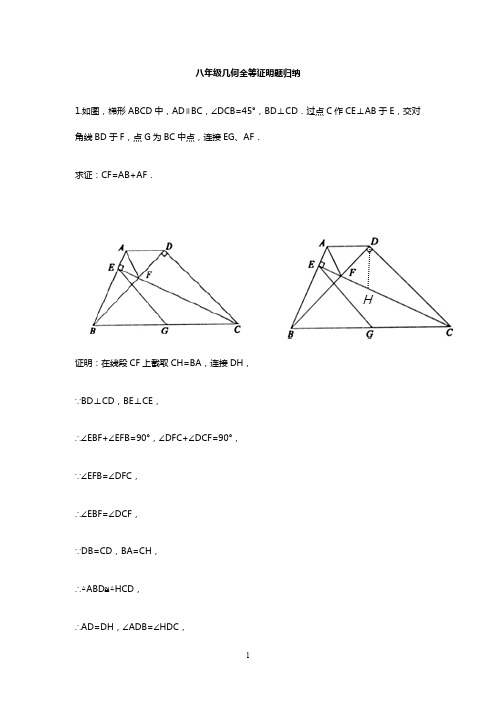
八年级几何全等证明题归纳1.如图,梯形ABCD中,AD∥BC,∠DCB=45°,BD⊥CD.过点C作CE⊥AB于E,交对角线BD于F,点G为BC中点,连接EG、AF.求证:CF=AB+AF.证明:在线段CF上截取CH=BA,连接DH,∵BD⊥CD,BE⊥CE,∴∠EBF+∠EFB=90°,∠DFC+∠DCF=90°,∵∠EFB=∠DFC,∴∠EBF=∠DCF,∵DB=CD,BA=CH,∴△ABD≌△HCD,∴AD=DH,∠ADB=∠HDC,∵AD∥BC,∴∠ADB=∠DBC=45°,∴∠HDC=45°,∴∠HDB=∠BDC—∠HDC=45°,∴∠ADB=∠HDB,∵AD=HD,DF=DF,∴△ADF≌△HDF,∴AF=HF,∴CF=CH+HF=AB+AF,∴CF=AB+AF.2.如图,ABCD为正方形,E为BC边上一点,且AE=DE,AE与对角线BD交于点F,连接CF,交ED于点G.判断CF与ED的位置关系,并说明理由.解:垂直.∴∠ADE+∠EDG=90°=∠GDC+∠EDG,∴∠ADE=∠GDC.又∵∠A=∠DGC且AD=GD,∴△ADE≌△GDC,∴DE=DC且AE=GC.在△EDF和△CDF中∠EDF=∠CDF,DE=DC,DF为公共边,∴△EDF≌△CDF,∴EF=CF4.已知:在⊿ABC中,∠A=900,AB=AC,D是AC的中点,AE⊥BD,AE延长线交BC 于F,求证:∠ADB=∠FDC。
证明:过点C作CG⊥CA交AF延长线于G∴∠G+∠GAC=90°…………①又∵AE⊥BD∴∠BDA+∠GAC=90°…………②综合①②,∠G=∠BDA在△BDA与△AGC中,∵∠G=∠BDA∠BAD=∠ACG=90°BA=CA∴△BDA≌△AGC∴DA=GC∵D是AC中点,∴DA=CD∴GC=CD由∠1=45°,∠ACG=90°,故∠2=45°=∠1在△GCF与△DCF中,∵GC=CD∠2=45°=∠1CF=CF∴△GCF≌△DCF∴∠G=∠FDC,又∠G=∠BDA∴∠ADB=∠FDC5.如图,梯形ABCD中,AD∥BC,CD⊥BC,BC=CD,O是BD的中点,E是CD延长线上一点,作OF⊥OE交DA的延长线于F,OE交AD于H,OF交AB于G,FO的延长线交CD于K,求证:OE=OF提示:由条件知△BCD为等腰Rt△,连接OC,可证△OCK≌△ODH(AAS),得OK=OH,再证△FOH ≌△EOK(AAS),得OE=OF∴△OCM≌△OBN.∴OM=ON,∠COM=∠BON,而∠COM+∠MOB=90°,∴∠BON+∠MOB=90°.∴∠MON=90°.∴OM与ON之间的关系是OM=ON;OM⊥ON.7.如图,正方形CGEF的对角线CE在正方形ABCD的边BC的延长线上(CG>BC),M 是线段AE的中点,DM的延长线交CE于N.探究:线段MD、MF的关系,并加以证明.证明:根据题意,知AD∥BC.∴∠EAD=∠AEN(内错角相等),∵∠DMA=∠NME(对顶角相等),又∵M是线段AE的中点,∴AM=ME.∴△ADM≌△ENM(ASA).∴AD=NE,DM=MN.(对应边相等).连接线段DF,线段FN,线段CE是正方形的对角线,∠DCF=∠NEF=45°,根据上题可知线段AD=NE,又∵四边形CGEF是正方形,∴线段FC等于FE.∴△DCF≌△NEF(SAS).∴线段FD=FN.∴△FDN是等腰三角形.∴线段MD⊥线段MF.8.如图,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角∠NDM,角的两边分别交AB、AC边于M、N两点,连接MN.试探究BM、MN、CN之间的数量关系,并加以证明.证明:BM+CN=NM延长AC至E,使CE=BM,连接DE,∵△BDC是顶角∠BDC=120°的等腰三角形,△ABC是等边三角形,∴∠BCD=30°,∴∠ABD=∠ACD=90°,∵DB=DC,CE=BM,∴△DCE≌△BMD,∵∠MDN=∠NDE=60°∴DM=DE(上面已经全等)∴DN=ND(公共边)∴△DMN≌△DEN∴BM+CN=NM9.如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°.E为AD延长线上的一点,且CE=CA,求证:AD+CD=DE;证明:∵AC=BC,∠ACB=90°,∴∠CAB=∠ABC=45°.∵∠CAD=∠CBD=15°,∴∠BAD=∠ABD=30°.∴AD=BD.在DE上截取DM=DC,连接CM,∵AD=BD,AC=BC,DC=DC,∴△ACD≌△BCD.∴∠ACD=∠BCD=45°.∵∠CAD=15°,∴∠EDC=60°.∵DM=DC,∴△CMD是等边三角形.∴∠CDA=∠CME=120°.∵CE=CA,∴∠E=∠CAD.∴△CAD≌△CEM.∴ME=AD.∴DA+DC=ME+MD=DE.即AD+CD=DE.10.如图,在正方形ABCD中,F是CD的中点,E是BC边上的一点,且AF平分∠DAE,求证:AE=EC+CD.证明:∵AF平分∠DAE,∠D=90°,FH⊥AE,∴∠DAF=∠EAF,FH=FD,在△AHF与△ADF中,∵AF为公共边,∠DAF=∠EAF,FH=FD(角平分线上的到角的两边距离相等),∴△AHF≌△ADF(HL).∴AH=AD,HF=DF.又∵DF=FC=FH,FE为公共边,∴△FHE≌△FCE.∴HE=CE.∵AE=AH+HE,AH=AD=CD,HE=CE,∴AE=EC+CD.11.已知梯形ABCD中,AB∥CD,BD⊥AC于E,AD=BC,AC=AB,DF⊥AB于F,AC、DF 相交于DF的中点O.求证:AB+CD=2BE.证明:过D作DM∥AC交BA的延长线于M.∵梯形ABCS中,AD=BC,∴BD=AC.又∵CD∥AM,DM∥AC,∴四边形CDMA为平行四边形.∴DM=AC,CD=AM.∵MD∥AC,又AC⊥BD,且AC=BD,∴DM⊥BD,DM=BD,∴△DMB为等腰直角三角形.又∵DF⊥BM,∴DF=BF.∴BM=2DF=2BF∴AM+AB=2BF.∵CD=AM,∴AB+CD=2BF.∵AC=BD=AB,∴在△BEA和△BFD中,△BEA≌△BFD.∴BE=BF.∵AB+CD=2BF,∴AB+CD=2BE.12.已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.求证:AD=DE.证明:(1)∵CF平分∠BCD,∴∠BCF=∠DCF.在△BFC和△DFC中,∴△BFC≌△DFC.∴BF=DF,∴∠FBD=∠FDB.连接BD.∵DF∥AB,∴∠ABD=∠FDB.∴∠ABD=∠FBD.∵AD∥BC,∴∠BDA=∠DBC.∵BC=DC,∴∠DBC=∠BDC.∴∠BDA=∠BDC.又BD是公共边,∴△BAD≌△BED.∴AD=DE.13.如图,在直角梯形ABCD中,AD⊥DC,AB∥DC,AB=BC,AD与BC延长线交于点F,G是DC延长线上一点,AG⊥BC于E.求证:CF=CG;证明:连接AC,∵DC∥AB,AB=BC,∴∠1=∠CAB,∠CAB=∠2,∴∠1=∠2;∵∠ADC=∠AEC=90°,AC=AC,∴△ADC≌△AEC,∴CD=CE;∵∠FDC=∠GEC=90°,∠3=∠4,∴△FDC≌△GEC,∴CF=CG.14.如图,已知P为∠AOB的平分线OP上一点,PC⊥OA于C,PA=PB,求证AO+BO=2CO证明:过点P作PQ⊥OB于Q,则∠PQB=90°∵OP平分∠AOB,且PC⊥OA,PQ⊥OB∴PC=PQ在Rt△POC与Rt△POQ中,∵PC=PQPO=PO∴Rt△POC≌Rt△POQ(HL)∴OC=OQ∴2OC=OC+OQ=OC+OB+BQ在Rt△PCA与Rt△PQB中,∵PC=PQPA=PB∴Rt△PCA≌Rt△PQB(HL)∴CA=QB又2OC=OC+OB+BQ∴2OC=OC+OB+CA=OA+OB15.已知:如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且AE=AC.求证:BG=FG;证明:∵∠ABC=90°,DE⊥AC于点F,∴∠ABC=∠AFE.∵AC=AE,∠EAF=∠CAB,∴△ABC≌△AFE∴AB=AF.连接AG,∵AG=AG,AB=AF,∴Rt△ABG≌Rt△AFG.∴BG=FG16.如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,连接CE、CF,求证:①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边△解:∵△ABE、△ADF是等边三角形∴FD=AD,BE=AB∵AD=BC,AB=DC∴FD=BC,BE=DC∵∠B=∠D,∠FDA=∠ABE∴∠CDF=∠EBC∴△CDF≌△EBC,∵AF=FD,AE=DC,EF=CF∴△EAF≌△CDF∴∠CDF=∠EAF,∵∠AFC=∠AFE+∠EFD+∠DFC,∠AFE+∠EFD=60°∴∠AFC-∠DFC=60°∴∠AFE=∠DFC∴∠EFC=60°同理,∠FEC=60°∵CF=CE∴△ECF是等边三角形17.已知正方形ABCD中,F为对角线BD上一点,过F点作EF⊥BA于E,G为DF中点,连接EG,CG.求证:EG=CG;证明:延长CG至M,使MG=CG,连接MF,ME,EC,在△DCG与△FMG中,∵FG=DG,∠MGF=∠CGD,MG=CG,∴△DCG≌△FMG.∴MF=CD,∠FMG=∠DCG,∴MF∥CD∥AB,∴EF⊥MF.在Rt△MFE与Rt△CBE中,∵MF=CB,EF=BE,∴△MFE≌△CBE∴∠MEF=∠CEB.∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°,∴△MEC为直角三角形.∵MG=CG,∴EG= MC,∴EG=CG.18.如图,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,求证:AC=AE+CD.解:在AC上取AF=AE,连接OF,则△AEO≌△AFO(SAS),∴∠AOE=∠AOF;∵AD、CE分别平分∠BAC、∠ACB,∴∠ECA+∠DAC= (180°-∠B)=60°则∠AOC=180°-∠ECA-∠DAC=120°;∴∠AOC=∠DOE=120°,∠AOE=∠COD=∠AOF=60°,则∠COF=60°,∴∠COD=∠COF,又∵∠FCO=∠DCO,CO=CO,∴△FOC≌△DOC(ASA),∴DC=FC,∵AC=AF+FC,∴AC=AE+CD.19.已知:如图,AD∥BC,AE平分∠BAD,AE⊥BE;说明:AD+BC=AB.解:如图,在AB上截取AF=AD,∴AE平分∠BAD,∴∠DAE=∠FAE,∵AF=AD,AE=AE,∴△DAE≌△FAE,∴∠D=∠AFE,∠DEA=∠FEA,∵AD∥BC,∴∠DAB+∠CBA=180°,∵AE⊥BE,∴∠BAE+∠ABE=90°,∴∠DAE+∠CBE=90°,∴∠ABE=∠CBE,同理,∠FEB=∠CEB,∵BE=BE,∴△BEF≌△BEC,∴BF=BC,∴AB=AF+FB=AD+BC.20.如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.求证:CF=EF.证明:∵Rt△ABC≌Rt△ADE,∴AC=AE,AD=AB,∠CAB=∠EAD,∴∠CAB-∠DAB=∠EAD-∠DAB.即∠CAD=∠EAB.∴△CAD≌△EAB,∴CD=EB,∠ADC=∠ABE.又∵∠ADE=∠ABC,∴∠CDF=∠EBF.又∵∠DFC=∠BFE,∴△CDF≌△EBF.∴CF=EF.21.将两个全等的直角三角形ABC和DBE如图方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.求证:AF+EF=DE证明:连接BF∵△ABC≌△DBE,∴BC=BE,AC=DE.∵∠ACB=∠DEB=90°,∴∠BCF=∠BEF=90°.∵BF=BF,∴Rt△BFC≌Rt△BFE.∴CF=EF.又∵AF+CF=AC,∴AF+EF=DE.21。
八年级几何证明题集锦及解答值得收藏

八年级几何全等证明题归纳1.如图,梯形ABCD中,AD∥BC,∠DCB= 45°,BD⊥CD.过点C作CE⊥AB于E,交对角线BD于F,点G为BC中点,连接EG、AF.求证:CF= AB+AF.证明:在线段CF上截取CH= BA,连接DH,∵BD⊥CD,BE⊥CE,∴∠EBF+∠EFB= 90°,∠DFC+∠DCF= 90°,∵∠EFB= ∠DFC,∴∠EBF= ∠DCF,∵DB= CD,BA= CH,∴△ABD≌△HCD,∴AD= DH,∠ADB= ∠HDC,∵AD∥BC,∴∠ADB= ∠DBC= 45°,∴∠HDC= 45°,∴∠HDB= ∠BDC—∠HDC= 45°,∴∠ADB= ∠HDB,∵AD= HD,DF= DF,∴△ADF≌△HDF,∴AF= HF,∴CF= CH+HF= AB+AF,∴CF= AB+AF.2.如图,ABCD为正方形,E为BC边上一点,且AE= DE,AE与对角线BD交于点F,连接CF,交ED于点G.判断CF与ED的位置关系,并说明理由.解:垂直.理由:∵四边形ABCD为正方形,∴∠ABD= ∠CBD,AB= BC,∵BF= BF,∴△ABF≌△CBF,∴∠BAF= ∠BCF,∵在RT△ABE和△DCE中,AE= DE,AB= DC,∴RT△ABE≌△DCE,∴∠BAE= ∠CDE,∴∠BCF= ∠CDE,∵∠CDE+∠DEC= 90°,∴∠BCF+∠DEC= 90°,∴DE⊥CF.3.如图,在直角梯形ABCD中,AD∥BC,∠A=90º,AB=AD,DE⊥CD交AB于E,DF平分∠CDE交BC于F,连接EF.证DA明:CF=EF解:EB F C过D作DG⊥BC于G.由已知可得四边形ABGD为正方形,∵DE⊥DC∴∠ADE+∠EDG= 90°= ∠GDC+∠EDG,∴∠ADE= ∠GDC.又∵∠A= ∠DGC且AD= GD,∴△ADE≌△GDC,∴DE= DC且AE= GC.在△EDF和△CDF中∠EDF= ∠CDF,DE= DC,DF为公共边,∴△EDF ≌△CDF,∴EF= CF4.已知:在⊿ABC中,∠A= 900,AB= AC,D是AC的中点,AE⊥BD,AE延长线交BC于F,求证:∠ADB= ∠FDC。
八年级上数学几何证明练习题(17题)

C A B C DE P 图 ⑴八年级数学(上)几何证明练习题1、 已知:在⊿ABC 中,∠A=900,AB=AC ,在BC 上任取一点P ,作PQ ∥AB 交AC 于Q ,作PR∥CA 交BA 于R ,D 是BC 的中点,求证:⊿RDQ 是等腰直角三角形。
B2、 已知:在⊿ABC 中,∠A=900,AB=AC ,D 是AC 的中点,AE ⊥BD ,AE 延长线交BC 于F ,求证:∠ADB=∠FDC 。
3、 已知:在⊿ABC 中BD 、CE 是高,在BD 、CE 或其延长线上分别截取BM=AC 、CN=AB ,求证:MA ⊥NA 。
4、已知:如图(1),在△ABC 中,BP 、CP 分别平分∠ABC 和∠ACB ,DE 过点P 交AB 于D ,交AC 于E ,且DE ∥BC .求证:DE -DB=EC .5、在Rt △ABC 中,AB =AC ,∠BAC =90°,O 为BC 的中点。
(1)写出点O 到△ABC 的三个顶点A 、B 、C 的距离的大小关系(不要求证明);(2)如果点M 、N 分别在线段AB 、AC 上移动,在移动中保持AN =BM ,请判断△OMN 的形状,并证明你的结论。
6、如图,△ABC 为等边三角形,延长BC 到D ,延长BA 到E ,AE=BD , 连结EC 、ED ,求证:CE=DE7、如图,等腰三角形ABC 中,AB =AC ,∠A =90°,BD 平分∠ABC ,DE ⊥BC 且BC =10,求△DCE 的周长。
8.如图所示,已知AD 是∠BAC 的平分线,EF 垂直平分AD 交BC 的延长线于点F ,交AD 于点E ,连接AF ,求证:∠B=∠CAF 。
A B COM N9.如图所示,AD 是∠BAC 的平分线,DE ⊥AB ,DF ⊥AC ,垂足分别为E ,F ,连接EF ,EF 与AD 交于点G ,求证:AD 垂直平分EF 。
C10.如图所示,已知点D 是等边三角形ABC 的边BC 延长线上的一点,∠EBC=∠DAC ,CE ∥AB 。
2024年数学八年级几何证明专项练习题1(含答案)

2024年数学八年级几何证明专项练习题1(含答案)试题部分一、选择题:1. 在三角形ABC中,若∠A = 90°,AB = 6cm,BC = 8cm,则AC 的长度为()。
A. 2cmB. 10cmC. 4cmD. 5cm2. 下列哪个条件不能判定两个三角形全等?()A. SASB. ASAC. AASD. AAA3. 在直角坐标系中,点A(2,3)关于原点对称的点是()。
A. (2,3)B. (2,3)C. (2,3)D. (3,2)4. 下列哪个比例式是正确的?()A. 若a∥b,则∠1 = ∠2B. 若a∥b,则∠1 + ∠2 = 180°C. 若a⊥b,则∠1 = 90°D. 若a⊥b,则∠1 + ∠2 = 180°5. 在等腰三角形ABC中,若AB = AC,∠B = 70°,则∠C的度数为()。
A. 70°B. 40°C. 55°D. 110°6. 下列哪个条件可以判定两个角相等?()A. 对顶角B. 邻补角C. 内错角D. 同位角7. 在平行四边形ABCD中,若AD = 8cm,AB = 6cm,则对角线AC 的长度()。
A. 10cmB. 14cmC. 12cmD. 15cm8. 下列哪个图形是轴对称图形?()A. 等腰三角形B. 等边三角形C. 矩形D. 梯形9. 在三角形ABC中,若a = 8cm,b = 10cm,c = 12cm,则三角形ABC是()。
A. 锐角三角形B. 钝角三角形C. 直角三角形D. 不能确定10. 下列哪个条件不能判定两个直线平行?()A. 内错角相等B. 同位角相等C. 同旁内角互补D. 两直线垂直二、判断题:1. 若两个三角形的两边和夹角分别相等,则这两个三角形全等。
()2. 在等腰三角形中,底角相等。
()3. 平行线的同位角相等,内错角相等。
()4. 若两个角的和为180°,则这两个角互为补角。
完整初二上几何证明题50题专题训练好题汇编推荐文档

八年级上册几何题专题训练50题1.如图,已知△ EAB^A DCE AB, EC分别是两个三角形的最长边,/ A=Z C= 35°, / CDE= 100°, / DEB= 10求/ AEC的度数.2.如图,点E、A、B F在同一条直线上,AD与BC交于点O,已知/ CAE=Z DBF,AC=BD求证:/ C=Z D4. 已知:如图,AB= AC, DB= DC, AD的延长线交BC于点E,求证:BE= EG5. 如图,在△ ABC中,AB=AD=DC / BAD=28,求/ B和/ C 的度数。
3.如图,OP平分/ AOB且OA=OB(1)写出图中三对你认为全等的三角形(注:不添加任何辅助线)6. 如图,B D 、C 、E 在同一直线上, AB=AC AD=AE 求证:BD=CE9.如图,等边△ ABC 中,点P 在厶ABC 内,点0在厶ABC 外,B, P, Q 三点在一条直线上,且/ABF =Z ACQ BP=CQ 问厶APC 是什么形状的三角形?试证明你的结论.10. 如图,△ ABC 中,/ C=90°, AB 的中垂线 DE 交AB 于E ,交BC 于 D,若AB=13, AC=5则厶ACD 的周长为多少?7.写出下列命题的逆命题,并判断逆命题的真假•如果是真命题,请给予证明; 命题:有两边上的高相等的三角形是等腰三角形.?如果是假命题,请举反例说明.8.如图,在△ABC 中,/ ACB=90o D 是AC 上的一点,且 AD=BC, DE AC 于D , / EAB=90o.求证:AB=AE15. 如图,四边形 ABCD 中,/ DAB=Z BCD=90 °, M 为 BD 中点,N为AC 中点,求证:MN 丄AC.11.如图所示,AC 丄BC, AD 丄BD,AD= BC, CEL AB, DF 丄AB,垂足分别是 E , F ,求证:CB DF.12. 如图,已知△ ABC 中,/ ACB= 90°, AC = BC BE L CE 垂足为 E , AD L CE 垂足为 D. (1) ________________________________ 判断直线BE 与AD 的位置关系是 _________________________________ ; BE与AD 之间的距离是线段⑵cm cm的长;B13. 如图,已知 △ ABC △ ADE 均为等边三角形,点求证:BD=CE14.如图,△ ABC 中, ABAC / BAC 120°, AD L AC 交 BC ?于点 D,求证:7BO 3ADD 是BC 延长线上一点,连结 CE[来源:16、已知:如图所示,在厶ABC中,/ ABC=45 ° , CD丄AB于点D, BE平分/ ABC,且BE丄AC于点E, 与CD相交于点F, H是BC边的中点,连接DH与BE相交于点G.(1 )求证:BF=AC;(2)求证:DG=DF.A17. 如图,点B, D在射线AM上,点C, E在射线AN上,且AB=BC=CD=DE已知/ EDM=84,求/ A的度数.18. 如图所示,在△ABC中,AB=AC BD丄AC于点D, CE! AB于点E, B D, CE相交于F.求证:AF平分/ BAC.19. 如图所示,△ ABC^A ADE 且/ CAD=10,/ B=Z D=25°,Z EAB=120,求/ DFB和/ DGB的度数.20. 已知:如图,在△ ABC中,AB=AC点D在边BC上,DEL AB, DF丄AC,且DE=DF 求证:△ ABD^A ACD21. 如图,一张直角三角形的纸片ABC两直角边AC=6cm BC=8cm现将直角边AC沿直线AD折叠,使它落在斜边AB上,且AC与AE重合,求CD的长.22. 已知:如图,在△ ABC中,AB=AC BD平分/ ABC E是底边BC的延长线上的一点且CD=CE.(1) 求证:△ BDE是等腰三角形(2) 若 / A=36°,求/ ADE的度数.23. 如图,在△ ABC中,AB=CB / ABC=90 , D为AB延长线上一点,点E在BC边上且BE=BD连结AE DE DC(1) 求证:AE=CD(2) 若/ CAE=30,求/ BDC的度数.24. 如图,在 ABC 中,点D 在AC 边上,DB=BC 点E 是CD 的中点,点F 是AB 的中点,则可以得到结论:EF 1AB , 2请说明理由ABC ,点D 为边AC 上的一个动点,延长 AB 至E ,使BE=CD 连结DE 交时,BEP 是等腰三角形•(不必说明理由)26. 如图,C 为线段BD 上一点(不与点 B ,D 重合),在BD 同侧分别作正三角形 ABC 和正三角形 CDE AD 与BE 交 于一点F ,AD 与CE 交于点H, BE 与AC 交于点 G(1) 求证:BE=AD (2) 求/ AFG 的度数; (3) 求证:CG=CH27. 已知:如图,在△ ABC 中,CDL AB, CD=BD BF 平分/ DBC 与 CD AC 分别交与点 E 、点F ,且 DA=DE H 是BC 边的中点,连结 DH 与BE 相交于点 G(1) 求证:△ EBD^A ACD(2) 求证:点 G 在/ DCB 的平分线上 (3) 试探索CF 、GF 和BG 之间的等量关系,并证明你的结论.25.已知:如图,在 ABC 中, C BC 于点P.(1)DP 与PE 相等吗?请说明理由.28. 如图,在在△ ABC 中,AB=CB, / ABC=90 ° , F为AB延长线上一单,点E在BC上,且AE=CF。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级上册几何题专题训练50题1. 如图,已知△EAB ≌△DCE ,AB ,EC 分别是两个三角形的最长边,∠A =∠C =35°,∠CDE =100°,∠DEB =10°,求∠AEC 的度数.2. 如图,点E 、A 、B 、F 在同一条直线上,AD 与BC 交于点O, 已知∠CAE=∠DBF,AC=BD.求证:∠C=∠D3.如图,OP 平分∠AOB ,且OA=OB .(1)写出图中三对你认为全等的三角形(注:不添加任何辅助线);(2)从(1)中任选一个结论进行证明.4. 已知:如图,AB =AC ,DB =DC ,AD 的延长线交BC 于点E ,求证:BE =EC 。
5. 如图,在△ABC 中,AB=AD=DC ,∠BAD=28°,求∠B 和∠C 的度数。
7. 写出下列命题的逆命题,并判断逆命题的真假.如果是真命题,请给予证明;•如果是假命题,请举反例说明.命题:有两边上的高相等的三角形是等腰三角形.8. 如图,在△ABC 中,∠ACB=90o , D 是AC 上的一点,且AD=BC ,DE AC 于D , ∠EAB=90o .求证:AB=AE .9. 如图,等边△ABC 中,点P 在△ABC 内,点Q 在△ABC 外,B ,P ,Q 三点在一条直线上,且∠ABP =∠ACQ ,BP =CQ ,问△APQ 是什么形状的三角形试证明你的结论.10. 如图,△ABC 中,∠C=90°,AB 的中垂线DE 交AB 于E ,交BC 于D ,若AB=13,AC=5,则△ACD 的周长为多少11. 如图所示,AC ⊥BC ,AD ⊥BD ,AD =BC ,CE ⊥AB ,DF ⊥AB ,垂足分别是E ,F ,求证:CE =DF.12. 如图,已知△ABC 中,∠ACB =90°,AC =BC ,BE ⊥CE ,垂足为E ,AD ⊥CE ,垂足为D.(1)判断直线BE 与AD 的位置关系是____;BE 与AD 之间的距离是线段____的长;(2)若AD =6 cm ,BE =2 cm ,求BE 与AD 之间的距离及AB 的长.13. 如图,已知 △ABC 、△ADE 均为等边三角形,点D 是BC 延长线上一点,连结CE ,求证:BD=CE 14. 如图,△ABC 中,AB =AC ,∠BAC =120°,AD ⊥AC 交BC •于点D ,求证:•BC =3AD . 15. 如图,四边形ABCD 中,∠DAB=∠BCD=90°,M 为BD 中点,N 为AC 中点,求证:MN⊥AC .16、已知:如图所示,在△ABC 中,∠ABC=45°,CD ⊥AB 于点D ,BE 平分∠ABC ,且BE⊥AC 于点E ,与CD 相交于点F ,H 是BC 边的中点,连接DH 与BE 相交于点G .(1)求证:BF=A C ;? (2)求证:DG=DF .6. 如图,B 、D 、C 、E 在同一直线上,AB=AC ,AD=AE ,求证:BD=CE 。
B A E D C17. 如图,点B ,D 在射线AM 上,点C ,E 在射线AN 上,且AB=BC=CD=DE ,已知∠EDM=84°,求∠A的度数.18. 如图所示,在△ABC 中,AB=AC ,BD ⊥AC 于点D ,CE ⊥AB 于点E ,BD ,CE 相交于F.求证:AF 平分∠BAC.19. 如图所示,△ABC ≌△ADE ,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求 ∠DFB 和∠DGB 的度数.20. 已知:如图,在△ABC 中,AB=AC ,点D 在边BC 上,DE ⊥AB ,DF ⊥AC ,且DE=DF ,求证:△ABD ≌△ACD21. 如图,一张直角三角形的纸片ABC ,两直角边AC=6cm ,BC=8cm .现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,且AC 与AE 重合,求CD 的长.22. 已知:如图,在△ABC 中,AB=AC ,BD 平分∠ABC ,E 是底边BC 的延长线上的一点且CD=CE. (1)求证:△BDE 是等腰三角形(2)若 ∠A=36°,求∠ADE 的度数.23. 如图,在△ABC 中,AB=CB ,∠ABC=90°,D 为AB 延长线上一点,点E 在BC 边上且BE=BD ,连结AE 、DE 、DC .(1)求证:AE=CD ; (2)若∠CAE=30°,求∠BDC 的度数.24. 如图,在ABC ∆中,点D 在AC 边上,DB=BC ,点E 是CD 的中点,点F 是AB 的中点,则可以得到结论:12EF AB =,请说明理由. 25. 已知:如图,在ABC ∆中,C ABC ∠=∠,点D 为边AC 上的一个动点,延长AB 至E ,使BE=CD ,连结DE ,交BC 于点P.(1)DP 与PE 相等吗请说明理由.(2)若60C ∠=︒,AB=12,当DC=_________时,BEP ∆是等腰三角形.(不必说明理由)26. 如图,C 为线段BD 上一点(不与点B ,D 重合),在BD 同侧分别作正三角形ABC 和正三角形CDE ,AD 与BE 交于一点F ,AD 与CE 交于点H ,BE 与AC 交于点G 。
(1)求证:BE=AD ;(2)求∠AFG 的度数;(3)求证:CG=CH27. 已知:如图,在△ABC 中,CD ⊥AB ,CD=BD ,BF 平分∠DBC ,与CD ,AC 分别交与点E 、点F ,且DA=DE ,H 是BC 边的中点,连结DH 与BE 相交于点G 。
(1)求证:△EBD ≌△ACD ;(2)求证:点G 在∠DCB 的平分线上(3)试探索CF 、GF 和BG 之间的等量关系,并证明你的结论.28. 如图,在在△ABC 中,AB=CB ,∠ABC=90°,F 为AB 延长线上一单,点E 在BC 上,且AE=CF 。
(1)求证:CBF Rt ABE Rt ∆≅∆(2)若∠CAE=30°,求∠ACF 的度数29. 如图,△ACD 和△BCE 都是等腰直角三角形,∠ACD =∠BCE =90°,AE 交DC 于F ,BD 分别交CE ,AE 于点G 、H . 试猜测线段AE 和BD 数量关系,并说明理由.A B C DEM E G F D CB A30. 如图,在△ABC 中,AB =AC ,AD 和BE 是高,它们相交于点H ,且AE =BE .求证:AH =2BD . 31. 如图,在ABC ∆中,32B ︒∠=,48C ︒∠=,AD BC ⊥于点D ,AE 平分BAC ∠ 交BC 于点E ,DF AE ⊥于点F ,求ADF ∠的度数. 32. 如图所示,在△ABC 中,已知点D ,E ,F 分别是BC ,AD ,CE 的中点,且ABC S ∆ =4,则BEF S ∆ 的值为多少。
33. 如图,ABC ∆中,90ACB ∠=o ,CD BA ⊥于D ,AE 平分BAC ∠交CD 于F ,交BC 于E ,求证:CEF ∆是等腰三角形.34. 如图,在四边形ABCD 中,DC ∥AB , BD 平分∠ADC , ∠ADC=60°,过点B 作BE ⊥DC ,过点A 作AF ⊥BD ,垂足分别为E 、F ,连接EF.判断△BEF 的形状,并说明理由.35. 如图,已知Rt △ABC ≌Rt △ADE ,∠ABC =∠ADE =90°,BC 与DE 相交于点F ,连接CD ,EB .(1)图中还有几对全等三角形,请你一一列举;(不必证明)(2)求证:CF =EF .36. 在ABC ∆中,BO 平分ABC ∠,点P 为直线AC 上一动点,PO BO ⊥于点O .(1)如图1,当40ABC ︒∠=,60BAC ︒∠=,点P 与点C 重合时,求APO ∠的度数;(2)如图2,当点P 在AC 延长线时,求证:()12APO ACB BAC ∠=∠-∠; (3)如图3,当点P 在边AC 所示位置时,请直接写出APO ∠与ACB ∠,BAC ∠之间的数量关系式.37. 如图,在ABC ∆中,BAD DAC ∠=∠,DF AB ⊥,DM AC ⊥,AF =10cm , AC =14cm ,动点E 以2cm /s 的速度从A 点向F 点运动,动点G 以1cm /s 的速度从C 点向A 点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t . (1) 求证:在运动过程中,不管取何值,都有2AED DGC S S ∆∆=;EDACF G HAE HB DC D C(2) 当取何值时,DFE ∆与DMG ∆全等.38. 如图,在Rt △ABC 中,∠B=90°,AB=3,BC=4,将△ABC 折叠,使点B 恰好落在边AC上,与点'B 重合,AE 为折痕,求'EB 的长度39. 如图,已知ΔABC 是等腰直角三角形,∠C =90°.(1)操作并观察,如图,将三角板的45°角的顶点与点C 重合,使这个角落在∠ACB 的内部,两边分别与斜边AB 交于E 、F 两点,然后将这个角绕着点C 在∠ACB 的内部旋转,观察在点E 、F 的位置发生变化时,AE 、EF 、FB 中最长线段是否始终是EF 写出观察结果.(2)探索:AE 、EF 、FB 这三条线段能否组成以EF 为斜边的直角三角形如果能,试加以证明.40. 已知BD ,CE 是△ABC 的两条高,M 、N 分别为BC 、DE 的中点。
(1)请写出线段MN 与DE 的位置有什么关系请说明理由。
(2)当∠A=45°时,请判断1△EMD 为何种三角形,并说明理由41. 如图(1),已知△ABC 中,∠BAC =90°,AB =AC ,AE 是过点A 的一条直线,且点B ,C 在AE 的两侧,BD ⊥AE 于点D ,CE ⊥AE 于点E.(1)求证:BD =DE +CE ;(2)若直线AE 绕点A 旋转到如图(2)的位置(BD <CE)时,其余条件不变,问BD 与DE ,CE 的关系如何请给予证明;(3)若直线AE 绕点A 旋转到如图(3)的位置(BD >CE)时,其余条件不变,问BD 与DE ,CE 的关系如何请直接写出结果,不需证明.42. 如图1,两个不全等的等腰直角三角形OAB 和等腰直角三角形OCD 叠放在一起,并且有公共的直角顶点O .(1)在图1中,你发现线段AC ,BD 的数量关系是________________ , 直线AC ,BD 相交成_________度角.(2)将图1中的△OAB 绕点O 顺时针旋转90°角,这时(1)中的两个结论是否成立请做出判断并说明理由(3)将图1中的△OAB 绕点O 顺时针旋转一个锐角,得到图3,这时(1)中的两个结论是否成立请作出判断并说明理由.43. 如图,AB ∥DC A=90°,AE=DC 。
