数字信号处理_吴镇扬_第二版_第一章习题答案
数字信号处理_吴镇扬_习题解答 第二版

1. 解丗由题意可知 N=5
则周期为丗其中为整数丆且满足使N为最小整数。
2. •i1•j解丗由题意可知 N=14
则周期为丗
•i2•j解丗由题意可知 N= 8
则
则所求周期 N=14
最小公倍数丆即为丗56
3.19 (1)周期卷积的主值序列为丗f(n)R(n) ={6,3, 6,10,14,12,9};
(2)循环卷积f (n) ={6,3, 6,10,14,12,9};
•i3•j线性卷积为f(n) ={1,3, 6,10,14,12,9,5, 0, 0, 0, 0}
2.21 •i 第二种方法乯按频率抽取算法丗输入顺
序丆
输出倒序(0,8,4,12,2,10,6,14,1,9,5,13,3,11,7, 15);
4
共有4(16=2*2*2*2 )节
第一节丗数据点间距、蝶形类型均是8•C
0 1 2 3 4 5 6 7
所乘因子丗W ,W ,W ,W ,W ,W ,
W ,W ;
N N N N N N N N N
第二节丗数据点间距、蝶形类型均是4 •C
0 2 4 6
所乘因子丗W ,W ,W ,W ;
N N N N
0 4
第三节丗数据点间距、蝶形类型均是2 •C所乘因
子丗W ,W ;
N N
第四节丗数据点间距、蝶形类型均是1 •C所乘因
子丗W ;
N。
数字信号处理课后答案

k = n0
∑
n
x[ k ]
(B) T {x[n]} =
∑
x[k ]
(C) T {x[ n]} = 0.5
x[ n ]
(D) T {x[n]} = x[− n]
1-5 有一系统输入为 x[n] ,输出为 y[n] ,满足关系 y[n] = ( x[n] ∗ u[n + 2])u[n] ,则系统是(A) (A)线性的 (B)时不变的 (C)因果的 (D)稳定的 解:
(a) T { x[ n ]} = h[ n] + x[ n ], (c) T {x[ n]} = ∑ x[ n − k ]
δ [n] + aδ [n − n0 ] ,单位阶跃响应 s[n] = u[n] + au[n − n0 ] 。
1-15 线性常系数差分方程为 y[n] − y[n − 1] +
y[n] = 0 , n < 0 , 则 y[3] = 0.5 。 解: y[0] = y[ −1] − 0.25 y[ −2] + x[0] = 1 y[1] = y[0] − 0.25 y[ −1] + x[1] = 1 y[2] = y[1] − 0.25 y[0] + x[2] = 0.75 y[3] = y[2] − 0.25 y[1] + x[3] = 0.5
∞ ∞ k =−∞ n '=−∞
解: (a)
n =−∞
∑ y[n] = ∑ ∑ x[k ]h[n − k ] = ∑ x[k ] ∑ h[n − k ] = ∑ x[k ] ∑ h[n ']
n =−∞ k =−∞ k =−∞ n =−∞
∞
∞
∞
数字信号处理(吴镇扬)第一章习题解答
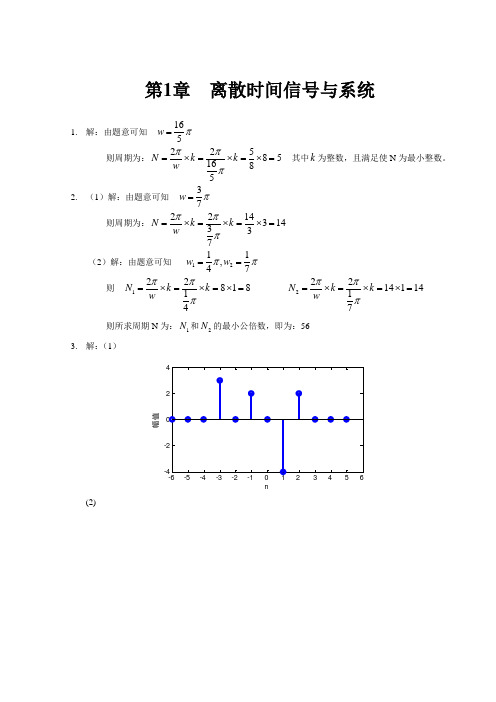
(3)解:
1.18y(n)=1,n=0
y(n)=3*2-n,n≥1
解:
1.19
(1)解:
无论 还是 ,右边序列的围线C内包含 两个极点。
当 时
当 时
因此
思考:1、为何讨论当 时的情况;2、为何不用讨论 的情况
解答过程如下:
(2)解:
右边序列的围线C内包含 一个极点。故
当 时
因此,
思考:1、为何只讨论当 时的情况
(2)解:
该系统不是线性系统;
该系统是时不变系统。
(3)解:
令 ,则
而
该系统是线性系统时不变系统。
注:
令 ,则
而
该系统是线性时不变系统。
(4)解:
该系统是线性系统时不变系统。
(5)解:
该系统是线性系统时变系统。
1.14解:
(1)
(2)
(3)
1.16
(1)解:因果、稳定。
(2)当n0<0时,系统非因果,不稳定。
(2)解:
所求序列为双边序列,采用留数法求解。
当n>=1时,围线C内只有一个极点 ,
则:
当n<1时,围线外只有一个极点 ,利用辅助留数定理,则:
因此
(4)解:
1.12
(1)解:定理:
(3)解:直接法
帕氏定理:
1.13
(1)解:
该系统不是线性系统;
该系统是时不变系统。
第1章
1.解:由题意可知
则周期为: 其中 为整数,且满足使N为最小整数。
2.(1)解:由题意可知
则周期为:
(2)解:由题意可知
则
则所求周期N为: 和 的最小公倍数,即为:56
数字信号处理课后习题答案(全)1-7章

1
4
(2m 5) (n m) 6 (n m)
m4
m0
第 1 章 时域离散信号和时域离散系统
(3) x1(n)的波形是x(n)的波形右移2位, 再乘以2, 画出图形如题2解图 (二)所示。
(4) x2(n)的波形是x(n)的波形左移2位, 再乘以2, 画出图形如题2解图(三) 所示。
因此系统是非线性系统。
第 1 章 时域离散信号和时域离散系统
(6) y(n)=x(n2)
令输入为
输出为
x(n-n0)
y′(n)=x((n-n0)2) y(n-n0)=x((n-n0)2)=y′(n) 故系统是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n2)+bx2(n2) =aT[x1(n)]+bT[x2(n)]
0≤m≤3
-4≤m≤n
非零区间如下:
第 1 章求解: ① n<0时, y(n)=0
② 0≤n≤3时, y(n)= ③ 4≤n≤7时, y(n)= ④ n>7时, y(n)=0
1=n+1
n
1=8-m n0
3
mn4
第 1 章 时域离散信号和时域离散系统
x(m)h(n-m)
m
第 1 章 时域离散信号和时域离散系统
题7图
第 1 章 时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
第 1 章 时域离散信号和时域离散系统
解法(二) 采用解析法。 按照题7图写出x(n)和h(n)的表达式分别为
吴镇扬数字信号处理课后习题答案

jw0 n
u (n)] e jw0n z n
n 0
1 1 (e jw0 z 1 )
(1) 解:令 y (n) RN (n)
由题意可知,所求序列等效为 x (n 1) y (n) y (n) 。
Z [ y (n)] z n
n 0
N 1
1 zN z N 1 , 1 z 1 z N 1 ( z 1)
1
A B 1 2 1 1 1 1 z 1 2z 1 z 1 2 z 1 B 1 | 1 2 1 z 1 z 1 2
1 | 1 1 1 2 z 1 z 1
x(n) u (n) 2 2 n u ( n 1) u (n) 2 n 1u ( n 1)
n0
若n0 0时,收敛域为:0 z ;
(2) 解: Z [0.5 u (n)]
n
若n0 0 时,收敛域为: z 0 z 0.5
0.5
n 0
n
z n
1
1 , 1 0.5 z 1
n
(3) 解: Z [ 0.5 u ( n 1)]
n
n
j j 1 1 (3) X (e 2 ) X ( e 2 ) 2 2 j
(2) e
j n0
X (e j ) (移位特性)
2
数字信号处理习题指导
G ( z ) ZT [ x (2n)] G( z)
n
g ( n )e
jwn
令n' 2n, 则
n ' 取偶数
( z 5) z n |z 0.5 (1 0.5 z)
数字信号处理(吴镇扬)第一章习题解答

提示:与理想采样信号的频谱进行比较。上述过程是物理采样后的频谱。
1.6解:
(1) (性质1)
(2) (性质4)
(3)
(4)1.7(1)Fra bibliotek:(2)解:
(3)解:
(4)解:
(5)解:
1.8 (1)解:令
由题意可知,所求序列等效为 。
而
故:
(2)解:
因为:
所以,
1.10 (1)解:
,为双边序列
本小题采用部分分式法求逆Z变换,可以使用“留数法”…..
所以
(3)解:
1.18y(n)=1,n=0
y(n)=3*2-n,n≥1
解:
1.19
(1)解:
无论 还是 ,右边序列的围线C内包含 两个极点。
当 时
当 时
因此
思考:1、为何讨论当 时的情况;2、为何不用讨论 的情况
解答过程如下:
(2)解:
右边序列的围线C内包含 一个极点。故
当 时
因此,
思考:1、为何只讨论当 时的情况
(3) 当n0>0时,该系统是因果系统;当n0<0时,该系统是非因果系统;系统稳定。
(4)因果、稳定。
(5)因果、稳定。
(6)因果、稳定。
(7)因果,但由于 。
(8) 在 时刻有值,故非因果。由于 的值都在 的时刻内,那么 ,故系统稳定。
1.17解:由图可知:
所以
(1)解:
(2)解:
通解
特解
带入方程得:
(3)解:
当 时,右边序列的围线C内包含 两个极点。故
因此
第1章
1.解:由题意可知
则周期为: 其中 为整数,且满足使N为最小整数。
数字信号处理-第1章习题答案
解:
2 i 14i i 3 , N min 14 (1) N 0 3 / 7 3 (2) i 7, j 4, N min 56 2 j 2 j 14 j N2 0 / 7 2 i 8i N1 0 / 4 2 i
0
20
40
60 n
80
100
120
1 3 绘出如下序列的波形。 1.3
(1) x(n) 3 (n 3) 2 (n 1) 4 (n 1) 2 (n 2) (2) x(n) 0.5n R5 (n)
解 (1)
3
2
1
0 x(n n) -1 -2 2 -3 -4 -4
因此,T[.]为线性系统;
T x( n n1 ) nx ( n n1 ) T x( n n1 ) y ( n n1 ) y ( n n1 ) ( n n1 ) x ( n n1 )
因此 T[.]为时变系统。 因此, 为时变系统
1 16 确定下列系统的因果性与稳定性。 1.16
(2) 收敛区域为|z|>a,即圆|z|=a的外部。
1 0.8 0.6 0.4 Imagina ary Part 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 -1 -0.5 0 Real Part 0.5 1 1.5
j 1 1 2 e a c 1 2 a cos a 1 j (3) H (e ) j 2 e a d a 1 2a cos a
2 i
3 x(n) cos n 4 7
1 0.8 0.6 04 0.4 0.2 x(n) 0 -0.2 -0.4 -0 0.6 6 -0.8 -1
数字信号处理(吴镇扬)课后习题答案(比较详细的解答过程)chap6
x ( m) x1 (m) = 0
或
m = 0,± M ,±2M ,⋯
其它
∞
(6.2a)
(6.2b .2b) x1 (m) = x(m) p(m) = x(m) ∑ δ (m − Mi) (6.2b)
i =−∞
是一脉冲串序列, 式中 p(m) 是一脉冲串序列, 它在 M 的整数倍处的值 其余皆为零。 表示将采样率减少 为 1,其余皆为零。令 ↓M 表示将采样率减少 M 倍 的抽取, 6.1.1) 6.1.2 式的含意如图 6.1.1 (6.1.1 和 .2) 6.1. 的抽取, 6.1.1) (6.1.2) ( 所示, M=3。 所示,图中 M=3。
1 p( n ) = M 数展开。 数展开。
M −1 k =0
e j 2πnk / M 为周期序列 p(n) 的付里叶级 p(n)的付里叶级 ∑
所以
1 M −1 j (ω − 2πk ) / M ′(e ) = X ) (6.4) .4) ∑ X (e M k =0
jω
′(e jω ) , X (e jω ) 分 别 是 x ′(n) 和 x (n) 的 式中 X DTFT。这样, DTFT。这样, X ′(e jω ) 是原信号频谱 X (e jω ) 先作 的移位叠加 位叠加, M 倍的扩展再在 ω 轴上每隔 2π / M 的移位叠加,
而 X 1 (e ) =
jω n = −∞
∞
∑ x ( n ) p ( n)e
− jωn
1 M −1 j 2πnk / M − jωn = ∑ [ x ( n) ]e ∑e n = −∞ M k =0 1 M −1 = X (e j (ω − 2πk / M ) ) (6.3b (6.3b) ∑ M k =0
数字信号处理作业答案(参考版-第一章)
1-2习题1-2图所示为一个理想采样—恢复系统,采样频率Ωs =8π,采样后经过理想低通G jΩ 还原。
解:(1)根据余弦函数傅里叶变换知:)]2()2([)]2[cos(πδπδππ-Ω++Ω=t F ,)]6()6([)]6[cos(πδπδππ-Ω++Ω=t F 。
又根据抽样后频谱公式:∑∞-∞=∧Ω-Ω=Ωk s a a jk j X T j X )(1)(,得到14T= ∑∞-∞=∧--Ω+-+Ω=Ωk a k k j X )]82()82([4)(1ππδππδπ∑∞-∞=∧--Ω+-+Ω=Ωk a k k j X )]86()86([4)(2ππδππδπ所以,)(1t x a ∧频谱如下所示)(2t x a ∧频谱如下所示(2))(1t y a 是由)(1t x a ∧经过理想低通滤波器)(Ωj G 得到,)]2()2([)()()]([11πδπδπ-Ω++Ω=ΩΩ=∧j G j X t y F a a ,故)2cos()(1t t y a π=(4π) (4π) (4π)(4π)(4π) (4π) Ω-6π-10π-2π 2π0 6π10π)(1Ω∧j X a Ω10π-10π -6π-2π 0 2π6π-14π 14π(4π)(4π) (4π)(4π) (4π) (4π)(4π) (4π))(2Ω∧j X a同理,)]2()2([)()()]([22πδπδπ-Ω++Ω=ΩΩ=∧j G j X t y F a a 故)2cos()(2t t y a π=(3)由题(2)可知,无失真,有失真。
原因是根据采样定理,采样频率满足信号)(1t x a 的采样率,而不满足)(2t x a 的,发生了频谱混叠。
1-3判断下列序列是否为周期序列,对周期序列确定其周期。
(1)()5cos 86x n A ππ⎛⎫=+ ⎪⎝⎭(2)()8n j x n eπ⎛⎫- ⎪⎝⎭=(3)()3sin 43x n A ππ⎛⎫=+ ⎪⎝⎭解:(1)85πω=,5162=ωπ为有理数,是周期序列,.16=N (2)πωπω162,81==,为无理数,是非周期序列; (3)382,43==ωππω,为有理数,是周期序列,8=N 。
数字信号处理习题及答案解析
==============================绪论==============================1. A/D 8bit 5V 00000000 0V 00000001 20mV 00000010 40mV 00011101 29mV==================第一章 时域离散时间信号与系统==================1.①写出图示序列的表达式答:3)1.5δ(n 2)2δ(n 1)δ(n 2δ(n)1)δ(n x(n)-+---+++= ②用δ(n) 表示y (n )={2,7,19,28,29,15}2. ①求下列周期)54sin()8sin()4()51cos()3()54sin()2()8sin()1(n n n n n ππππ-②判断下面的序列是否是周期的; 若是周期的, 确定其周期。
(1)A是常数 8ππn 73Acos x(n)⎪⎪⎭⎫ ⎝⎛-= (2))81(j e )(π-=n n x 解: (1) 因为ω=73π, 所以314π2=ω, 这是有理数, 因此是周期序列, 周期T =14。
(2) 因为ω=81, 所以ωπ2=16π, 这是无理数, 因此是非周期序列。
③序列)Acos(nw x(n)0ϕ+=是周期序列的条件是是有理数2π/w 0。
3.加法乘法序列{2,3,2,1}与序列{2,3,5,2,1}相加为__{4,6,7,3,1}__,相乘为___{4,9,10,2} 。
移位翻转:①已知x(n)波形,画出x(-n)的波形图。
②尺度变换:已知x(n)波形,画出x(2n)及x(n/2)波形图。
卷积和:①h(n)*求x(n),其他02n 0n 3,h(n)其他03n 0n/2设x(n) 例、⎩⎨⎧≤≤-=⎩⎨⎧≤≤= }23,4,7,4,23{0,h(n)*答案:x(n)=②已知x (n )={1,2,4,3},h (n )={2,3,5}, 求y (n )=x (n )*h (n )x (m )={1,2,4,3},h (m )={2,3,5},则h (-m )={5,3,2}(Step1:翻转)解得y (n )={2,7,19,28,29,15}③(n)x *(n)x 3),求x(n)u(n u(n)x 2),2δ(n 1)3δ(n δ(n)2、已知x 2121=--=-+-+=}{1,4,6,5,2答案:x(n)=4.如果输入信号为,求下述系统的输出信号。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.12(1) y(n) = 4δ (n + 1) + 4δ (n −1) + δ (n − 3) − 2δ (n − 5) − δ (n − 7)
⎧ 2 − 0 .5 n 0≤n≤4 (2) y ( n ) = ⎨ n − 4 0 .5 ( 2 − 0 .5 4 ) n≥5 ⎩
(3) y ( n) = δ (n) + 2δ (n − 1) + 3δ ( n − 2) + 6δ ( n − 3) − 4δ (n − 4) − 8δ ( n − 5) 1.14 (1) 因果、稳定。 (2)系统是因果,不稳定 (n → ∞ )
∑
y ( n) z
−n
=
n =−∞
∑
x( −n) z
−n
=
m=−∞
∑
x( m)( z −1 ) − m
1 1 < z< Rx + Rx −
1 , 1.10 (1) 1 − ab
ab < 1
(2) 1
n0 a n0 (3)
1.11(1) (2) (3) (4) (5)
该系统不是线性系统;该系统是时不变系统。 该系统不是线性系统;该系统是时不变系统。 线性系统时不变系统。 线性系统时不变系统。 线性系统时变系统
∞ n − jωn (4)G (e jω ) = ∑ x( ) e = ∑ x( m) e − jω 2 m = X ( e j 2ω ) n =−∞ ( 偶数) 2 m =−∞
∞
1.5 (1) (3)
z
− n0
1 (2) 1 − 0.5 z −1 ,
| z |> 0.5
1 , −1 1 − 0.5z
= − 1;
z =1
d X ( z) 1 d −1 2 B= [ × ( z − 1) ] × = = −1; dz z 1! z =1 dz ( z − 2) z =1
−1 −1 1 所以X ( z) = + + 2 ( z − 1) ( z −1) ( z − 2)
x(n ) = −nu (n ) − u (n ) + 2 n u (n ) x(n ) = −nu (n ) − u (n ) − 2n u (−n − 1)
n −2 (2) f (n ) = a u (n − 2)
1 − a n+1 (3) f ( n) = 1− a
0 ≤ n ≤ N − 1; f (n ) = a
− ( N −1) + n
1− aN 1− a
n ≥ N;
g ( n) = ( n − 3)2 3n−3 f ( n − 3) + (n − 3)3n−3 f (n − 3) 1.18 1.20 (1) a < 1;
所以系统为全通系统。
| z |< 0.5
(4)
1 − (0.5 z −1 )10 , −1 1 − 0.5 z
| z |> 0
1− z− N 2 ) , z > 0; 1.6 (1) X ( z) = z −1 ( −1 1− z dX ( z ) z (2)利用性质Z [nx (n)] = − Z ; 其中X ( z) = Z [ a nu( n)] = dz z −a d z az 所以Z [nx (n)] = − Z [ ]= z >a 2 dz z − a ( z − a )
(2)零点z = a −1 , 极点z = a , 收敛域 z > a
(3)
H (e jω ) =
1 a
jIm(z) jIm(z)
A
ABO∽△ACO
B
∴
AB OB = = a −1 AC OA
(为常数)
O
C
Re(z ) Re(z)
H (e jω ) = H ( z) z =e jω
e jω − a −1 AB = jω = = a−1 e −a AC
k =−∞(偶数)
∑
x( n)z +
−k
k =−∞(奇数)
∑
x( n)z−k
= ∑ x(n)z
n=−∞
+ ∑ x(n)z −2 n+1 = X ( z2 ) + X ( z2 ) z−1 = (1 + z−1 ) X( z2 )
n =−∞
∞
∞
∞
(4)Y ( z ) = = X (z )
−1
n =−∞
(3) 当n0>0时,该系统是因果系统, 当n0<0时,该系统是非因果系统;
∵ h( n) = δ (n − n0 )∴系统稳定。
(4)因果、稳定。 (5)因果、稳定。 (6)因果、稳定。 (7)因果、不稳定。 (8)非因果、稳定。
1 1.15(1)差分方程 y ( n) = x( n − 1) + y ( n − 1) 3
− jω n
=
∞
n =−∞
∞ − jω n
∑
x( m) e− jω ( m+ n ) = e− jω n X ( e jω )
0 0
(3)G (e jω ) =
∞
n =−∞
∑ g (n )e
− jω n
=
n =−∞
∑ x (2n )e
=
m =−∞( 偶数)
∑
x (m )e
− jω
m 2
m m m − jω − jω − jω 1 1 ∞ 1 ∞ = ∑ [ x (m ) + ( −1) m x (m )]e 2 = ∑ x (m )e 2 + ∑ x (m )e jπ me 2 2 m= −∞ 2 m= −∞ m=−∞ 2 ω ω ω ω j j ( −π ) j j 1 1 1 1 = X ( e 2 ) + X ( e 2 ) = X ( e 2 ) + X ( −e 2 ) 2 2 2 2
z > a;
(3)
az −1 + a 2 z −1 X ( z) = , −1 3 (1 − az )
z >a
X ( z) 1 A B C 1.7 解: = = + + z ( z − 1) 2 ( z − 2) ( z −1) 2 ( z −1) ( z − 2) C= X ( z) X ( z) × ( z − 2) = 1;A = × ( z − 1)2 z z z =2
1.1周期序列,最小周期长度为5。 1.2 (1) 周期序列,最小周期长度为14。 (2) 周期序列,最小周期长度为56。
∞ ∞ − jω n
1.4(1)
∞
n =−∞
∑ kx (n )e
=kቤተ መጻሕፍቲ ባይዱ
n =−∞
∑ x (n )e
∞
− jω n
= kX (e jω )
(2)
n =−∞
∞
∑
x( n − n0 )e
具有线性特性 ; 而 y (n − n0 ) = (n − n0 ) x(n − n0 )
(5)解:T [ax1 (n) + bx2 (n)] = n[ax1 (n) + bx2 (n)] = ay1 (n) + by2 ( n)
T[ x(n − n0 )] = nx(n − n0 ),
所以T [ x(n − n0 )] ≠ y(n − n0 ),具有使不变性;因此,是线性时变系统。
则零状态响应:Yzs ( z ) = H (Z ) X (z ) = 3 1 ∴ yzs ( n) = [1 − ( ) n ]u( n) 2 3 ∴
z 3 z 1 = [ − ] 1 z −1 2 z −1 1 z− z− 3 3
1 i
3 1 1 y ( n) = yzi ( n) + yzs (n) = [ − ( ) n ]u (n) 2 2 3
y(n)=1,n=0 y(n)=4*3-n ,n≥1 y(n)=1, =0;y(n)=4 y(n)=4*
1 (2)差分方程为:y (n) = x( n − 1) + y( n − 1) 3 1 设零输入响应为:y zi = A( ) n u (n),∵ y (0) = 1,∴ y (−1) = 3 y (0) − x( −1) = 3 3 1 由起始条件y (−1) = 3可解得A = 1, y zi = ( ) n u( n) ∴ 3 z −1 1 由差分方程可得系统函数为: ( z) = H = 1 1 1 − z −1 z − 3 3
z > 2;
1 < z < 2;
x(n ) = nu ( −n − 1) + u ( −n − 1) − 2 n u ( −n − 1)
z <1
1.8(1)
− u (n) − 2n +1 u (−n − 1)
n n (2) − 6(0.5) u ( n) − 4 ⋅ 2 u (− n − 1) 1 + cos ω0 (cos nω0 + sin nω0 )u (n) (3) sin ω0 −1 −n (4) − aδ ( n) + ( a − a ) a u ( n)
3 1 1 n 3 1 n−5 (3) y ( n) = [ − ⋅ ( ) ]u ( n) + [1 − ( ) ]u (n − 5) 2 2 3 2 3
1 1.16 y(n)=1, n=0 y(n)=3*2-n , n≥1 =0; y(n)=3*
1 [a n +1 − (b) n +1 ]u ( n) 1.17(1) f ( n) = a−b
X ( c −1 z ) 1.9(1)
∞ k −k (2)Y ( z) = ∑ y( k) z = ∑ x( )z = ∑ x( n)z−2n = X ( z 2 ) k =−∞ k =−∞(偶数) 2 n =−∞ −k ∞ ∞
