数字信号处理吴镇扬第一章答案
合集下载
数字信号处理第一章课后答案
故系统是线性系统。
第 1 章 时域离散信号和时域离散系统
n
（7） y(n)= x(m) 令输入为m0
x(n－n0)
输出为
n
y′(n)= =0[DD)]x(m-n0)
m0
nn0
y(n－n0)= x(m)≠y′(n) m0
故系统是时变系统。 由于
n
T［ax1(n)+bx2(n)］=
［ax1(m)+bx2(m)
第 1 章 时域离散信号和时域离散系统
解：
x(n)=δ(n+4)+2δ(n+2)－δ(n+1)+2δ(n)+δ(n－1)
+2δ(n－2)+4δ(n－3)+0.5δ(n－4)+2δ(n－6)
2． 给定信号：
2n+5
－4≤n≤－1
(x(n)= 6 0
0≤n≤4 其它
(1) 画出x(n)序列的波形， 标上各序列值；
（2） y(n)=x(n)+x(n+1)
n n0
（3） y(n)= x(k) k nn0
（4） y(n)=x(n－n0) （5） y(n)=ex(n)
第 1 章 时域离散信号和时域离散系统
解：（1）只要N≥1， 该系统就是因果系统， 因为输出 只与n时刻的和n时刻以前的输入有关。
如果|x(n)|≤M， 则|y(n)|≤M， （2） 该系统是非因果系统， 因为n时间的输出还和n时间以 后（（n+1）时间）的输入有关。如果|x(n)|≤M, 则 |y(n)|≤|x(n)|+|x(n+1)|≤2M,
第 1 章 时域离散信号和时域离散系统 题2解图（四）
第 1 章 时域离散信号和时域离散系统
n
（7） y(n)= x(m) 令输入为m0
x(n－n0)
输出为
n
y′(n)= =0[DD)]x(m-n0)
m0
nn0
y(n－n0)= x(m)≠y′(n) m0
故系统是时变系统。 由于
n
T［ax1(n)+bx2(n)］=
［ax1(m)+bx2(m)
第 1 章 时域离散信号和时域离散系统
解：
x(n)=δ(n+4)+2δ(n+2)－δ(n+1)+2δ(n)+δ(n－1)
+2δ(n－2)+4δ(n－3)+0.5δ(n－4)+2δ(n－6)
2． 给定信号：
2n+5
－4≤n≤－1
(x(n)= 6 0
0≤n≤4 其它
(1) 画出x(n)序列的波形， 标上各序列值；
（2） y(n)=x(n)+x(n+1)
n n0
（3） y(n)= x(k) k nn0
（4） y(n)=x(n－n0) （5） y(n)=ex(n)
第 1 章 时域离散信号和时域离散系统
解：（1）只要N≥1， 该系统就是因果系统， 因为输出 只与n时刻的和n时刻以前的输入有关。
如果|x(n)|≤M， 则|y(n)|≤M， （2） 该系统是非因果系统， 因为n时间的输出还和n时间以 后（（n+1）时间）的输入有关。如果|x(n)|≤M, 则 |y(n)|≤|x(n)|+|x(n+1)|≤2M,
第 1 章 时域离散信号和时域离散系统 题2解图（四）
数字信号处理课后答案
k = n0
∑
n
x[ k ]
（B） T {x[n]} =
∑
x[k ]
（C） T {x[ n]} = 0.5
x[ n ]
（D） T {x[n]} = x[− n]
1-5 有一系统输入为 x[n] ，输出为 y[n] ，满足关系 y[n] = ( x[n] ∗ u[n + 2])u[n] ，则系统是（A） （A）线性的 （B）时不变的 （C）因果的 （D）稳定的 解：
（a） T { x[ n ]} = h[ n] + x[ n ], （c） T {x[ n]} = ∑ x[ n − k ]
δ [n] + aδ [n − n0 ] ，单位阶跃响应 s[n] = u[n] + au[n − n0 ] 。
1-15 线性常系数差分方程为 y[n] − y[n − 1] +
y[n] = 0 ， n < 0 ， 则 y[3] = 0.5 。 解： y[0] = y[ −1] − 0.25 y[ −2] + x[0] = 1 y[1] = y[0] − 0.25 y[ −1] + x[1] = 1 y[2] = y[1] − 0.25 y[0] + x[2] = 0.75 y[3] = y[2] − 0.25 y[1] + x[3] = 0.5
∞ ∞ k =−∞ n '=−∞
解： （a）
n =−∞
∑ y[n] = ∑ ∑ x[k ]h[n − k ] = ∑ x[k ] ∑ h[n − k ] = ∑ x[k ] ∑ h[n ']
n =−∞ k =−∞ k =−∞ n =−∞
∞
∞
∞
数字信号处理(吴镇扬)第一章习题解答
所以
（3）解：
1.18y(n)=1,n=0
y(n)=3*2-n,n≥1
解：
1.19
（1）解：
无论 还是 ，右边序列的围线C内包含 两个极点。
当 时
当 时
因此
思考：1、为何讨论当 时的情况；2、为何不用讨论 的情况
解答过程如下：
（2）解：
右边序列的围线C内包含 一个极点。故
当 时
因此，
思考：1、为何只讨论当 时的情况
（2）解：
该系统不是线性系统；
该系统是时不变系统。
（3）解：
令 ，则
而
该系统是线性系统时不变系统。
注：
令 ，则
而
该系统是线性时不变系统。
（4）解：
该系统是线性系统时不变系统。
（5）解：
该系统是线性系统时变系统。
1.14解：
(1)
(2)
(3)
1.16
（1）解：因果、稳定。
(2)当n0<0时，系统非因果,不稳定。
（2）解：
所求序列为双边序列，采用留数法求解。
当n>=1时，围线C内只有一个极点 ，
则：
当n<1时，围线外只有一个极点 ，利用辅助留数定理，则：
因此
（4）解：
1.12
(1)解：定理：
（3）解：直接法
帕氏定理：
1.13
(1)解：
该系统不是线性系统；
该系统是时不变系统。
第1章
1.解：由题意可知
则周期为： 其中 为整数，且满足使N为最小整数。
2.（1）解：由题意可知
则周期为：
（2）解：由题意可知
则
则所求周期N为： 和 的最小公倍数，即为：56
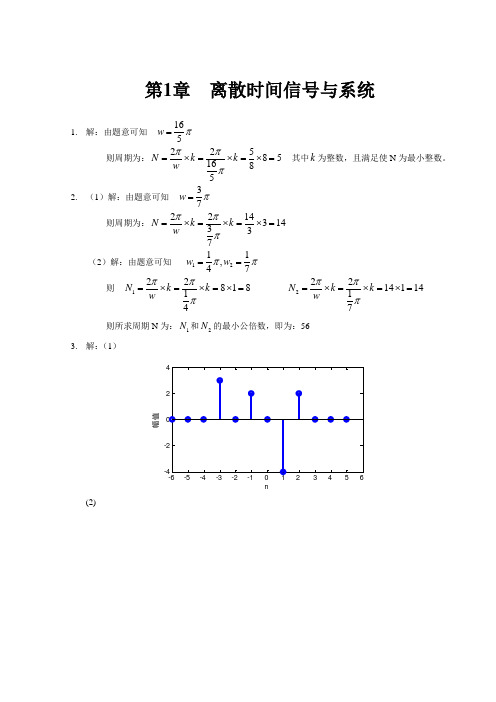
（3）解：
1.18y(n)=1,n=0
y(n)=3*2-n,n≥1
解：
1.19
（1）解：
无论 还是 ，右边序列的围线C内包含 两个极点。
当 时
当 时
因此
思考：1、为何讨论当 时的情况；2、为何不用讨论 的情况
解答过程如下：
（2）解：
右边序列的围线C内包含 一个极点。故
当 时
因此，
思考：1、为何只讨论当 时的情况
（2）解：
该系统不是线性系统；
该系统是时不变系统。
（3）解：
令 ，则
而
该系统是线性系统时不变系统。
注：
令 ，则
而
该系统是线性时不变系统。
（4）解：
该系统是线性系统时不变系统。
（5）解：
该系统是线性系统时变系统。
1.14解：
(1)
(2)
(3)
1.16
（1）解：因果、稳定。
(2)当n0<0时，系统非因果,不稳定。
（2）解：
所求序列为双边序列，采用留数法求解。
当n>=1时，围线C内只有一个极点 ，
则：
当n<1时，围线外只有一个极点 ，利用辅助留数定理，则：
因此
（4）解：
1.12
(1)解：定理：
（3）解：直接法
帕氏定理：
1.13
(1)解：
该系统不是线性系统；
该系统是时不变系统。
第1章
1.解：由题意可知
则周期为： 其中 为整数，且满足使N为最小整数。
2.（1）解：由题意可知
则周期为：
（2）解：由题意可知
则
则所求周期N为： 和 的最小公倍数，即为：56
吴镇扬数字信号处理课后习题答案
jw0 n
u (n)] e jw0n z n
n 0
1 1 (e jw0 z 1 )
(1) 解：令 y (n) RN (n)
由题意可知，所求序列等效为 x (n 1) y (n) y (n) 。
Z [ y (n)] z n
n 0
N 1
1 zN z N 1 , 1 z 1 z N 1 ( z 1)
1
A B 1 2 1 1 1 1 z 1 2z 1 z 1 2 z 1 B 1 | 1 2 1 z 1 z 1 2
1 | 1 1 1 2 z 1 z 1
x(n) u (n) 2 2 n u ( n 1) u (n) 2 n 1u ( n 1)
n0
若n0 0时，收敛域为：0 z ;
(2) 解： Z [0.5 u (n)]
n
若n0 0 时，收敛域为： z 0 z 0.5
0.5
n 0
n
z n
1
1 , 1 0.5 z 1
n
(3) 解： Z [ 0.5 u ( n 1)]
n
n
j j 1 1 (3) X (e 2 ) X ( e 2 ) 2 2 j
(2) e
j n0
X (e j ) （移位特性）
2
数字信号处理习题指导
G ( z ) ZT [ x (2n)] G( z)
n
g ( n )e
jwn
令n' 2n, 则
n ' 取偶数
( z 5) z n |z 0.5 (1 0.5 z)
数字信号处理(吴镇扬)第一章习题解答
傅立叶系数
提示：与理想采样信号的频谱进行比较。上述过程是物理采样后的频谱。
1.6解：
(1) （性质1）
(2) （性质4）
(3)
(4)1.7（1）Fra bibliotek：(2)解：
(3)解：
(4)解：
（5）解:
1.8 (1)解：令
由题意可知，所求序列等效为 。
而
故：
（2）解：
因为：
所以,
1.10 (1)解：
，为双边序列
本小题采用部分分式法求逆Z变换，可以使用“留数法”…..
所以
（3）解：
1.18y(n)=1,n=0
y(n)=3*2-n,n≥1
解：
1.19
（1）解：
无论 还是 ，右边序列的围线C内包含 两个极点。
当 时
当 时
因此
思考：1、为何讨论当 时的情况；2、为何不用讨论 的情况
解答过程如下：
（2）解：
右边序列的围线C内包含 一个极点。故
当 时
因此，
思考：1、为何只讨论当 时的情况
(3) 当n0＞0时，该系统是因果系统；当n0＜0时，该系统是非因果系统；系统稳定。
（4）因果、稳定。
（5）因果、稳定。
（6）因果、稳定。
（7）因果，但由于 。
（8） 在 时刻有值，故非因果。由于 的值都在 的时刻内，那么 ，故系统稳定。
1.17解：由图可知：
所以
（1）解：
（2）解：
通解
特解
带入方程得：
（3）解：
当 时，右边序列的围线C内包含 两个极点。故
因此
第1章
1.解：由题意可知
则周期为： 其中 为整数，且满足使N为最小整数。
提示：与理想采样信号的频谱进行比较。上述过程是物理采样后的频谱。
1.6解：
(1) （性质1）
(2) （性质4）
(3)
(4)1.7（1）Fra bibliotek：(2)解：
(3)解：
(4)解：
（5）解:
1.8 (1)解：令
由题意可知，所求序列等效为 。
而
故：
（2）解：
因为：
所以,
1.10 (1)解：
，为双边序列
本小题采用部分分式法求逆Z变换，可以使用“留数法”…..
所以
（3）解：
1.18y(n)=1,n=0
y(n)=3*2-n,n≥1
解：
1.19
（1）解：
无论 还是 ，右边序列的围线C内包含 两个极点。
当 时
当 时
因此
思考：1、为何讨论当 时的情况；2、为何不用讨论 的情况
解答过程如下：
（2）解：
右边序列的围线C内包含 一个极点。故
当 时
因此，
思考：1、为何只讨论当 时的情况
(3) 当n0＞0时，该系统是因果系统；当n0＜0时，该系统是非因果系统；系统稳定。
（4）因果、稳定。
（5）因果、稳定。
（6）因果、稳定。
（7）因果，但由于 。
（8） 在 时刻有值，故非因果。由于 的值都在 的时刻内，那么 ，故系统稳定。
1.17解：由图可知：
所以
（1）解：
（2）解：
通解
特解
带入方程得：
（3）解：
当 时，右边序列的围线C内包含 两个极点。故
因此
第1章
1.解：由题意可知
则周期为： 其中 为整数，且满足使N为最小整数。
数字信号处理-第1章习题答案
解：
2 i 14i i 3 , N min 14 (1) N 0 3 / 7 3 (2) i 7, j 4, N min 56 2 j 2 j 14 j N2 0 / 7 2 i 8i N1 0 / 4 2 i
0
20
40
60 n
80
100
120
1 3 绘出如下序列的波形。 1.3
(1) x(n) 3 (n 3) 2 (n 1) 4 (n 1) 2 (n 2) (2) x(n) 0.5n R5 (n)
解 (1)
3
2
1
0 x(n n) -1 -2 2 -3 -4 -4
因此，T[.]为线性系统；
T x( n n1 ) nx ( n n1 ) T x( n n1 ) y ( n n1 ) y ( n n1 ) ( n n1 ) x ( n n1 )
因此 T[.]为时变系统。 因此， 为时变系统
1 16 确定下列系统的因果性与稳定性。 1.16
(2) 收敛区域为|z|>a，即圆|z|=a的外部。
1 0.8 0.6 0.4 Imagina ary Part 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 -1 -0.5 0 Real Part 0.5 1 1.5
j 1 1 2 e a c 1 2 a cos a 1 j (3) H (e ) j 2 e a d a 1 2a cos a
2 i
3 x(n) cos n 4 7
1 0.8 0.6 04 0.4 0.2 x(n) 0 -0.2 -0.4 -0 0.6 6 -0.8 -1
数字信号处理作业答案（参考版-第一章）
1-2习题1-2图所示为一个理想采样—恢复系统，采样频率Ωs =8π,采样后经过理想低通G jΩ 还原。
解：(1)根据余弦函数傅里叶变换知：)]2()2([)]2[cos(πδπδππ-Ω++Ω=t F ，)]6()6([)]6[cos(πδπδππ-Ω++Ω=t F 。
又根据抽样后频谱公式：∑∞-∞=∧Ω-Ω=Ωk s a a jk j X T j X )(1)(，得到14T= ∑∞-∞=∧--Ω+-+Ω=Ωk a k k j X )]82()82([4)(1ππδππδπ∑∞-∞=∧--Ω+-+Ω=Ωk a k k j X )]86()86([4)(2ππδππδπ所以，)(1t x a ∧频谱如下所示)(2t x a ∧频谱如下所示（2）)(1t y a 是由)(1t x a ∧经过理想低通滤波器)(Ωj G 得到，)]2()2([)()()]([11πδπδπ-Ω++Ω=ΩΩ=∧j G j X t y F a a ，故)2cos()(1t t y a π=(4π) (4π) (4π)(4π)(4π) (4π) Ω-6π-10π-2π 2π0 6π10π)(1Ω∧j X a Ω10π-10π -6π-2π 0 2π6π-14π 14π(4π)(4π) (4π)(4π) (4π) (4π)(4π) (4π))(2Ω∧j X a同理，)]2()2([)()()]([22πδπδπ-Ω++Ω=ΩΩ=∧j G j X t y F a a 故)2cos()(2t t y a π=（3）由题（2）可知，无失真，有失真。
原因是根据采样定理，采样频率满足信号)(1t x a 的采样率，而不满足)(2t x a 的，发生了频谱混叠。
1-3判断下列序列是否为周期序列，对周期序列确定其周期。
（1）()5cos 86x n A ππ⎛⎫=+ ⎪⎝⎭（2）()8n j x n eπ⎛⎫- ⎪⎝⎭=（3）()3sin 43x n A ππ⎛⎫=+ ⎪⎝⎭解：（1）85πω=，5162=ωπ为有理数，是周期序列，.16=N （2）πωπω162,81==，为无理数，是非周期序列； （3）382,43==ωππω，为有理数，是周期序列，8=N 。
数字信号处理(第三版)第1章习题答案
－m≤3， 或写成n－3≤m≤n， 这样y(n)的非零区间要求m同时满足下
面两个不等式：
0≤m≤3
m－3≤m≤n
上面公式表明m的取值和n的取值有关， 需要将n作分段的假设。 按 照上式， 当n变化时， m应该按下式取值：
第九页，共105页。
max{0, n－3}≤m≤min{3, n}
当0≤n≤3时， 下限应该是0， 上限应该是n； 当4≤n≤6时， 下限应该是
y(n)=
n 1 y(n) 7 n
0
0≤n≤3
4≤n≤6
其它
第十一页，共105页。
在封闭式求解过程中， 有时候决定求和的上下限有些麻烦， 可借助于 非零值区间的示意图确定求和限。 在该例题中， 非零值区间的示意图如图
1.2.1所示。 在图1.2.1(b)中， 当n<0时， 图形向左移动， 图形不可能 和图1.2.1(a)的图形有重叠部分， 因此y(n)=0。 当图形向右移动时， 0≤n≤3， 图形如图1.2.1(c)所示， 对照图1.2.1(a)， 重叠部分的上下限自 然是0≤m≤n。 当图形再向右移动时， 4≤n≤6， 如图1.2.1(d)所示， 重 叠部分的上下限是n－3≤m≤3。 当图形再向右移动时, 7≤n， 图形不可能和
(1) x(n) Acos 3 πn A是常数
第二十二页，共105页。
图1.3.2
第二十三页，共105页。
［例1.3.5］已知x1(n)=δ(n)+3δ(n－1)+2δ(n－2)，x2(n)=u(n)－u(n－3)，
试求信号x(n)， 它满足x(n)=x1(n)*x2(n), 并画出x(n)的波形。
解： 这是一个简单的计算线性卷积的题目。
x(n)=x1(n)*x2(n) =［δ(n)+3δ(n－1)+2δ(n－2)］*［u(n)－u(n－3)
面两个不等式：
0≤m≤3
m－3≤m≤n
上面公式表明m的取值和n的取值有关， 需要将n作分段的假设。 按 照上式， 当n变化时， m应该按下式取值：
第九页，共105页。
max{0, n－3}≤m≤min{3, n}
当0≤n≤3时， 下限应该是0， 上限应该是n； 当4≤n≤6时， 下限应该是
y(n)=
n 1 y(n) 7 n
0
0≤n≤3
4≤n≤6
其它
第十一页，共105页。
在封闭式求解过程中， 有时候决定求和的上下限有些麻烦， 可借助于 非零值区间的示意图确定求和限。 在该例题中， 非零值区间的示意图如图
1.2.1所示。 在图1.2.1(b)中， 当n<0时， 图形向左移动， 图形不可能 和图1.2.1(a)的图形有重叠部分， 因此y(n)=0。 当图形向右移动时， 0≤n≤3， 图形如图1.2.1(c)所示， 对照图1.2.1(a)， 重叠部分的上下限自 然是0≤m≤n。 当图形再向右移动时， 4≤n≤6， 如图1.2.1(d)所示， 重 叠部分的上下限是n－3≤m≤3。 当图形再向右移动时, 7≤n， 图形不可能和
(1) x(n) Acos 3 πn A是常数
第二十二页，共105页。
图1.3.2
第二十三页，共105页。
［例1.3.5］已知x1(n)=δ(n)+3δ(n－1)+2δ(n－2)，x2(n)=u(n)－u(n－3)，
试求信号x(n)， 它满足x(n)=x1(n)*x2(n), 并画出x(n)的波形。
解： 这是一个简单的计算线性卷积的题目。
x(n)=x1(n)*x2(n) =［δ(n)+3δ(n－1)+2δ(n－2)］*［u(n)－u(n－3)