弧长及扇形面积的计算习题
弧长扇形面积的计算

1、已知扇形的圆心角为120°,半径为6,则扇形的弧长是.
2、一个扇形的圆心角为120°,面积为3πcm2,这个扇形的半径
是.
3、已知扇形的弧长为20cm,面积为16cm2,那么扇形的半径
为 .
4、扇形的半径是6cm,圆心角为10°,则这个扇形的面积是______ cm2.
5、扇形的面积是5πcm2 ,圆心角为72°,则这个扇形的半径是__ _ cm.
6、已知扇形的圆心角为120°,弧长等于半径为5cm的圆周长,则扇形
的面积为()
A.75 cm2
B.75πcm2
C.150cm2
D.150πcm2
7、如图所示,实线部分是半径为9m的两条等弧组成的游泳池,若每条弧所在的圆都经过另一个圆的圆心,则游泳池的周长为()
A.12πm B.18πm
C.20πm D.24πm
8、如图3所示,OA=30B,则的长是的长的倍.
9、如图,两个同心圆被两条半径截得的的长为6πcm,的长为10πcm,又AC=12cm,求阴影部分ABDC的面积。
弧长与扇形面积经典习题(有难度)

弧长与扇形面积练习题1. 一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是()A.5πB. 4πC.3πD.2π2. 如图,如果从半径为9cm的圆形纸片剪去13圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为()A.6cmB.35cm C.8cm D.53cm3.如图,是一圆锥的主视图,则此圆锥的侧面展开图的圆心角的度数是()A.60° B.90° C.120° D.180°12cm 6cm7.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B’,则图中阴影部分的面积是().A. 3πB. 6πC. 5πD. 4π8.如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC= 6cm,点P是母线BC上一点,且PC=23 BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是()A.(64π+)cm B.5cm C.35cm D.7cm9.如图,半径为1的小圆在半径为 9 的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为()A . 17πB . 32πC . 49πD . 80π10. 如图,AB切⊙O于点B,OA=23,AB=3,弦BC∥OA,则劣弧⌒BC的弧长为().A.33πB.32πC.πD.32π11. 在半径为4π的圆中,45°的圆心角所对的弧长等于.12. 已知一个半圆形工件,未搬动前如图所示,直径平行于地面放置,搬动时为了保护圆弧部分不受损伤,先将半圆作如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面平移50m,半圆的直径为4m,则圆心O所经过的路线长是 m。
(结果用π表示)13.如图,圆锥的底面半径OB为10cm,它的展开图扇形的半径AB为30cm,则这个扇形的圆心角a的度数为____________.14. 如图,点A、B、C在直径为32的⊙O上,∠BAC=45º,则图中阴影的面积等于______________,(结果中保留π).2、如果一条弧长等于l,它的半径等于R,这条弧所对的圆心角增加1o,则它的弧长增加()A.lnB.180RπC.180lRπD.360l3、已知圆锥的母线长为6cm,底面圆的半径为3cm,则此圆锥侧面展开图的面积为()A、18πcm2B、36πcm2C、12πcm2D、9πcm24、圆的半径增加一倍,那么圆的面积增加到()A、1倍B、2倍C、3倍D、4倍5、一个点到圆的最小距离为6cm,最大距离为9cm,则该圆的半径是()A、1.5cmB、7.5cmC、1.5cm或7.5cmD、3cm或15cm8、扇形的周长为16,圆心角为360πo,则扇形的面积是()A.16 B.32 C.64 D.16π10、如图,AC是⊙O的直径,BD是⊙O的弦,EC∥AB交⊙O于E,则图中与12∠BOC相等的角共有()A、2个B、3个C、4个D、5个15、如图,将三角尺ABC(其中∠B=60°,∠C=90°,AB=6)绕点B按顺时针转动一个角度到A1BC1的位置,使得点A、B、C1在同一条直线上,点A所经过的路程是()A、2πB、4πC、8πD、12π16、如图,圆锥的轴截面是边长为6cm 的正三角形ABC ,P 是母线AC 的中点.则在圆锥的侧面上从B 点到P 点的最短路线的长为( )13、如图,扇形OAB 的圆心角为90o,且半径为R ,分别以OA ,OB 为直径在扇形内作半圆,P 和Q 分别表示两个阴影部分的面积,那么P 和Q 的大小关系是()A.P Q = B.P Q > C.P Q <D.无法确定17、如图,在足球比赛场上,甲、乙两名队员互相配合向对方球门MN 进攻,当甲带球冲到A 点时,乙已跟随冲到B 点。
弧长和扇形面积练习题

长为30cm ,制作这个纸帽至少需要纸板的面积至少为 cm 2
.(结果保留π)
4.如图已知扇形AOB 的半径为6cm ,圆心角的度数为120°,若将此扇形围成一个圆锥,如图,将一个含有旋转,当点A 的对应点'
A 落在A
B 边的起始位置上时即停止转动,则B 点转过的路径长为 .
9.已知扇形的圆心角为150°,它所对应的弧长cm π20,则此扇形的半径是
cm ________,面积是2________cm 。
第6题
10.若扇形面积为3π,半径为3,则弧长为_______,圆心角是________.
11.已知一个圆锥形的零件的母线长为3cm,底面半径为2cm,则这个圆锥形的零件的侧面积为 cm2.(用π表示).
12.有一段弯道是圆弧形的,如图1,道长是12m,弧所对的圆心角是81°,•求这段弧的半径R为________.
(1) (2) (3)
13.如图2,正△ABC的边长AB=2,以A为圆心的圆切BC于点D,交AB于点E,交AC•于点F,则弧EF的长=_________.
15.如图3所示,三个圆是同心圆,图中阴影部分的面积为______.
16.如图,一块边长为10cm的正方形木板ABCD,在水平桌面上绕点D按顺时针方向旋转到A′B′C′D′的位置时,顶点B从开始到结束所经过的路程长为()
A.20πcm B.πcm C.10πcm D.πcm
17.已知圆柱的底面半径为2cm,高为5cm,则圆柱的侧面积是 ( )
A.20 cm2 B.20π cm2 C.10πcm2 D.5πcm2。
初三数学扇形和弧长练习题

初三数学扇形和弧长练习题1. 计算扇形的面积问题:一个半径为5cm的圆的一个扇形的圆心角为60度,求该扇形的面积。
解析:扇形的面积等于圆的面积乘以扇形的圆心角度数除以360度。
已知半径为5cm,圆心角为60度,代入公式可得:扇形面积 = 圆的面积 ×圆心角度数 / 360= π × 5^2 × 60 / 360= π × 25 × 60 / 360= π × 25 / 6≈ 13.09cm^2所以该扇形的面积约为13.09cm^2。
2. 计算弧长问题:一个圆的周长为10π cm,求圆的一段弧长。
解析:弧长等于圆的周长乘以弧所占圆周的比例。
已知圆的周长为10π cm,我们可以设所求弧长为x cm,代入公式可得:x / (10π) = 所求弧所占圆周的比例 = 弧长 / 圆的周长解得 x = 弧长= (10π) × 弧长 / 圆的周长= (10π) × 1 / 4π= 10 / 4= 2.5 cm所以该圆的一段弧长为2.5 cm。
3. 综合计算问题:一个半径为8cm的圆的两个扇形的圆心角分别为120度和60度,求这两个扇形的面积之和。
解析:根据第一题的解析,我们可以计算出两个扇形的面积,然后相加即可。
已知半径为8cm,圆心角分别为120度和60度,代入公式可得:第一个扇形的面积= π × 8^2 × 120 / 360= π × 64 × 120 / 360= π × 8 × 40= 320π cm^2第二个扇形的面积= π × 8^2 × 60 / 360= π × 64 × 60 / 360= π × 8 × 10= 80π cm^2两个扇形的面积之和 = 第一个扇形的面积 + 第二个扇形的面积= 320π + 80π= 400π cm^2所以这两个扇形的面积之和为400π cm^2。
圆的弧长与扇形面积综合练习题

圆的弧长与扇形面积综合练习题题1:已知一个半径为3cm的圆的弧长为12πcm,求扇形的面积。
题解:求扇形的面积时,需要知道扇形的圆心角和半径。
已知圆的弧长是12πcm,可以计算出圆心角的大小。
因为弧长等于半径乘以圆心角的弧度,所以可以得到12π = 3cm × 圆心角。
解方程可以得到圆心角为4π/3弧度。
扇形的面积等于圆心角占据的比例乘以整个圆的面积,所以扇形的面积为(4π/3)(π(3)^2) = 12π平方cm。
题2:若一个圆的半径是5cm,那么它的弧长和扇形面积各是多少?题解:已知圆的半径是5cm,它的弧长可以计算得出。
弧长等于半径乘以圆心角的弧度,所以弧长等于5cm ×圆心角。
圆心角的弧度可以通过圆弧长除以半径得到。
假设圆心角为θ弧度,则弧长为5θ。
要求扇形的面积,也需要知道圆心角的大小。
同样,我们可以利用扇形的面积公式,并确认圆心角的弧度为θ。
扇形的面积等于圆心角占据的比例乘以整个圆的面积。
所以扇形的面积为θ(π(5)^2) = 25θπ平方cm。
题3:已知一个扇形的半径是8m,扇形的面积是12π平方m,求圆心角和弧长各是多少?题解:已知扇形的半径是8m,扇形的面积是12π平方m。
要求圆心角的大小,可以利用扇形面积的公式,并确认圆心角的弧度为θ。
扇形的面积等于圆心角占据的比例乘以整个圆的面积,所以12π平方m = θ(π(8)^2)。
解方程可以得到θ = 3π/4。
要求弧长的大小,同样可以利用扇形的面积公式,但是需要先计算出圆心角的弧度。
扇形的面积等于圆心角占据的比例乘以整个圆的面积,所以12π平方m = (3π/4)(π(8)^2)。
解方程可以得到弧长为6πm。
题4:一个扇形的圆心角是π/2,弧长是4,求扇形的面积。
题解:已知扇形的圆心角是π/2,弧长是4。
要求扇形的面积,需要用到圆心角和半径的关系。
圆心角所占的比例乘以整个圆的面积就是扇形的面积。
所以扇形的面积等于(π/2)(πr^2),其中r表示圆的半径。
(完整版)弧长和扇形面积练习题

24.4 弧长和扇形面积习题一、 选择题1.已知扇形的圆心角为120°,半径为6,则扇形的弧长是( ).A .3πB .4πC .5πD .6π2.如图1所示,把边长为2的正方形ABCD 的一边放在定直线L 上,按顺时针方向绕点D 旋转到如图的位置,则点B 运动到点B ′所经过的路线长度为( )A .1B .πC .2D .2π(1) (2) (3)3.如图2所示,实数部分是半径为9m 的两条等弧组成的游泳池,若每条弧所在的圆都经过另一个圆的圆心,则游泳池的周长为( )A .12πmB .18πmC .20πmD .24πm4.圆锥的母线长为13cm ,底面半径为5cm ,则此圆锥的高线为( )A .6cmB .8cmC .10cmD .12cm 5.在半径为50cm 的圆形铁皮上剪去一块扇形铁皮,•用剩余部分制作成一个底面直径为80cm ,母线长为50cm 的圆锥形烟囱帽,则剪去的扇形的圆心角度数为( )A .228°B .144°C .72°D .36°6.如图所示,圆锥的母线长是3,底面半径是1,A 是底面圆周上一点,•从点A 出发绕侧面一周,再回到点A 的最短的路线长是( )A .3B .332 C .3 D .3 二、填空题1.如果一条弧长等于4πR ,它的半径是R ,那么这条弧所对的圆心角度数为______,• 当圆心角增加30°时,这条弧长增加________.2.如图3所示,OA=30B ,则AD 的长是BC 的长的_____倍.3.母线长为L ,底面半径为r 的圆锥的表面积=_______.4.矩形ABCD 的边AB=5cm ,AD=8cm ,以直线AD 为轴旋转一周,•所得圆柱体的表面积是__________(用含π的代数式表示)5.粮仓顶部是一个圆锥形,其底面周长为36m ,母线长为8m ,为防雨需在粮仓顶部铺上油毡,如果按用料的10%计接头的重合部分,那么这座粮仓实际需用________m 2的油毡.三、综合提高题1.如图所示,AB 所在圆的半径为R ,AB 的长为3πR ,⊙O ′和OA 、OB 分别相切于点C 、E ,且与⊙O 内切于点D ,求⊙O ′的周长.2.如图,若⊙O 的周长为20πcm ,⊙A 、⊙B 的周长都是4πcm ,⊙A 在⊙O•内沿⊙O 滚动,⊙B 在⊙O 外沿⊙O 滚动,⊙B 转动6周回到原来的位置,而⊙A 只需转动4周即可,你能说出其中的道理吗?3.如图所示,在计算机白色屏幕上,有一矩形着色画刷ABCD ,AB=1,AD=3,将画刷以B 为中心,按顺时针转动A ′B ′C ′D ′位置(A ′点转在对角线BD 上),求屏幕被着色的面积.4.一个圆锥形和烟囱帽的底面直径是40cm ,母线长是120cm ,需要加工这样的一个烟囱帽,请你画一画:(1)至少需要多少厘米铁皮(不计接头)(2)如果用一张圆形铁皮作为材料来制作这个烟囱帽,那么这个圆形铁皮的半径至少应是多少?_ . . . _B_A_O5.如图所示,已知圆锥的母线长AB=8cm,轴截面的顶角为60°,求圆锥全面积.6.如图所示,一个几何体是从高为4m,底面半径为3cm的圆柱中挖掉一个圆锥后得到的,圆锥的底面就是圆柱的上底面,圆锥的顶点在圆柱下底面的圆心上,求这个几何体的表面积.。
专题 弧长及扇形面积的计算(学生版)

专题41弧长及扇形面积的计算题型一弧长的计算1.如图,已知O 的直径6AB =,点C 、D 是圆上两点,且30BDC ∠=︒,则劣弧BC 的长为()A .πB .2πC .32πD .2π2.如图,正六边形ABCDEF 内接于O ,O 的半径为1,则AB 的长为()A .6πB .3πC .2πD .π3.如图,扇形纸扇完全打开后,外侧两竹条AB ,AC 的夹角为150︒,AB 的长为30cm ,BD 的长为15cm ,则DE 的长为()A .254πcm B .252πcm C .25πcm D .50πcm4.如图,在44⨯的正方形网格中,每个小正方形的边长都为1,AOB ∆的三个顶点都在格点上,现将AOB ∆绕点O 逆时针旋转90︒后得到对应的COD ∆,则点A 经过的路径弧AC 的长为()A .32πB .πC .2πD .3π5.如图,PA、PB是O的切线,切点分别为A、B,若2OA=,60P∠=︒,则AB的长为()A.23πB.πC.43πD.53π6.如图,ABCD中,70B∠=︒,6BC=,以AD为直径的O交CD于点E,则DE的长为()A.13πB.23πC.76πD.43π7.如图,“凸轮”的外围是由以正三角形的顶点为圆心,正三角形的边长为半径的三段等弧组成.已知正三角形的边长为a,则“凸轮”的周长等于()A.aπB.2aπC.12aπD.13aπ8.如图,以O为圆心的圆与直线3y x=-+交于A、B两点,若OAB∆恰为等边三角形,则弧AB的长度为()A.23πB.πC2D.13π9.如图,半圆O的直径4AB=,P,Q是半圆O上的点,弦PQ的长为2,则AP与QB的长度之和为.10.如图,花园边墙上有一宽为1m 的矩形门ABCD ,量得门框对角线AC 的长为2m ,现准备打掉部分墙体,使其变成以AC 为直径的圆弧形门,则打掉墙体后,弧形门洞的周长(含线段)BC 为.题型二扇形面积的计算11.如图,边长为2的正方形ABCD 内接于O ,则阴影部分的面积为()A .12π+B .12π-C .14π+D .14π-12.如图,以AB 为直径,点O 为圆心的半圆经过点C ,若2AC BC ==,则图中阴影部分的面积是()A .4πB .124π+C .2πD .122π+13.如图,在扇形AOB 中90AOB ∠=︒,正方形CDEF 的顶点C 是AB 的中点,点D 在OB 上,点E 在OB 的延长线上,当正方形CDEF 的边长为22时,则阴影部分的面积为()A .24π-B .48π-C .28π-D .44π-14.如图,在Rt ABC ∆中,90ACB ∠=︒,5AB =,2BC =,以点A 为圆心,AC 的长为半径画弧,交AB 于点D ,交AC 于点C ,以点B 为圆心,AC 的长为半径画弧,交AB 于点E ,交BC 于点F ,则图中阴影部分的面积为()A .8π-B .4π-C .24π-D .14π-15.如图,正三角形ABC 的边长为4cm ,D ,E ,F 分别为BC ,AC ,AB 的中点,以A ,B ,C 三点为圆心,2cm 长为半径作圆.则图中阴影部分的面积为()A .2(23)cm π-B .2(3)cm π-C .2(432)cm π-D .2(223)cm π-16.如图,在Rt ABC ∆中,90ACB ∠=︒,30A ∠=︒,2BC =,以点B 为圆心,BC 的长为半径作弧,交AB 于点D ,则阴影部分的面积是()A .2233π-B .2433-C .4233π-D .23π17.如图所示的图案(阴影部分)是这样设计的:在ABC ∆中,2AB AC cm ==,30ABC ∠=︒,以A 为圆心,以AB 为半径作弧BEC ,以BC 为直径作半圆BFC ,则图案(阴影部分)的面积是.(结果保留)π18.如图,在扇形OAB 中,90AOB ∠=︒,半径2OA =.将扇形OAB 沿过点B 的直线折叠.点O 恰好落在弧AB 上点D 处,折痕交OA 于点C ,则整个阴影部分的面积为.19.如图,在ABC ∆中,90C ∠=︒,AC BC =,斜边42AB =,O 是AB 的中点,以O 为圆心,线段OC 的长为半径画圆心角为90︒的扇形OEF ,EF 经过点C ,则图中阴影部分的面积为()A .24π-B .4π-C .2π-D .48π-20.如图,在平行四边形ABCD 中,6BC =,BC 边上高为4,120B ∠=︒,M 为B C 中点,若分别以B 、C 为圆心,BM 长为半径画弧,交A B ,CD 于E ,F 两点,则图中阴影部分面积是()A .243π-B .123π-C .9242π-D .3242π-21.如图,在ABC ∆中,AB AC =,以AB 为直径的O 分别与BC ,AC 交于点D ,E ,过点D 作DF AC ⊥,垂足为点F ,若O 的半径为43,15CDF ∠=︒,则阴影部分的面积为()A .16123π-B .16243π-C .20123π-D .20243π-22.如图,在菱形ABCD 中,60D ∠=︒,2AB =,以B 为圆心、BC 长为半径画AC ,点P 为菱形内一点,连接PA ,PB ,PC .当BPC ∆为等腰直角三角形时,图中阴影部分的面积为()A .23132π+-B .23132π--C .2πD .3122π--23.如图,正方形ABCD 的边长为2,O 为对角线的交点,点E ,F 分别为BC ,AD 的中点.以C 为圆心,2为半径作圆弧BD ,再分别以E ,F 为圆心,1为半径作圆弧BO ,OD ,则图中阴影部分的面积为()A .1π-B .3π-C .2π-D .4π-24.如图,在菱形ABCD 中,60B ∠=︒,2AB =,把菱形ABCD 绕BC 的中点E 顺时针旋转60︒得到菱形A B C D '''',其中点D 的运动路径为DD ',则图中阴影部分的面积为.25.如图,在矩形ABCD 中,23AB =,4BC =,以点A 为圆心,AD 长为半径画弧交BC 于点E ,连接AE ,则阴影部分的面积为()A .833π-B .2433π-C .2633π-D .8663π26.如图,在菱形ABCD 中,以AB 为直径画弧分别交BC 于点F ,交对角线AC 于点E ,若4AB =,F 为BC 的中点,则图中阴影部分的面积为()A .2233π-B .23C .4333π-D .23π题型三圆锥27.已知圆锥底面半径为4cm ,侧面积为232cm π,设圆锥的母线与高的夹角为θ,如图,则tan θ的值()A .33B 3C .12D .1428.若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为.29.圆柱体内挖去一个与它不等高的圆锥,如其实物图和其剖面图所示.锥顶O 到AD 的距离为1,30OCD ∠=︒,4OC =,则挖去后该物体的表面积是.30.如图,圆锥的轴截面ABC ∆是一个以圆锥的底面直径为底边,圆锥的母线为腰的等腰三角形,若圆锥的底面直径4BC cm =,母线6AB cm =,则由点B 出发,经过圆锥的侧面到达母线AC 的最短路程是.31.底面半径为3,母线长为4的圆锥的侧面积为.(结果保留)π32.已知圆锥的底面周长是2π分米,母线长为1分米,则圆锥的侧面积是平方分米.33.如图,从一块半径为1m 的圆形铁皮上剪出一个圆周角为120︒的扇形ABC ,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为m .34.用一个半径为4,圆心角度数为120︒的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径为.35.如图,圆锥的底面半径6r =,高8h =,则圆锥的侧面积是()A .15πB .30πC .45πD .60π36.用一个圆心角为180︒,半径为6的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径是.37.如图,从一块直径是4m 的圆形铁皮上剪出一个圆心角为60︒的扇形,如果剪出来的扇形围成一个圆锥,那么围成的圆锥的高是()A .3mB 23C 105D 43。
初中数学扇形面积弧长计算练习题(附答案)
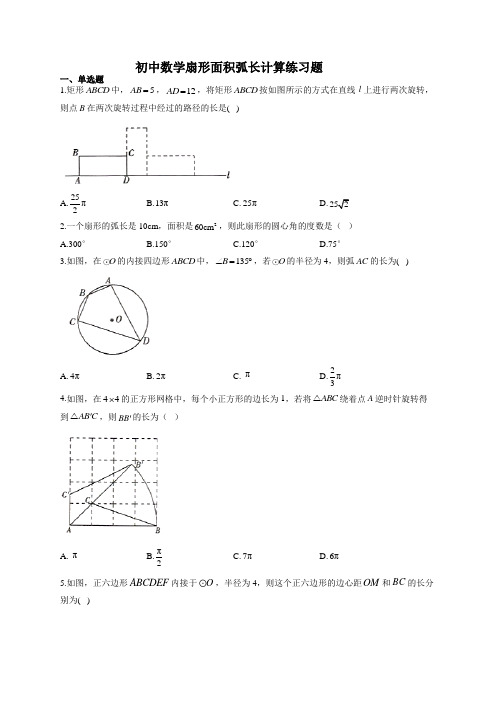
初中数学扇形面积弧长计算练习题一、单选题1.矩形ABCD中,5AB=,12AD=,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,则点B在两次旋转过程中经过的路径的长是( )A.25π2B.13πC.25πD.2522.一个扇形的弧长是10cm,面积是260cm,则此扇形的圆心角的度数是()A.300°B.150°C.120°D.75°3.如图,在O的内接四边形ABCD中,135B∠=︒,若O的半径为4,则弧AC的长为( )A.4πB.2πC.πD.2π34.如图,在44⨯的正方形网格中,每个小正方形的边长为1,若将ABC△绕着点A逆时针旋转得到AB C'△,则BB'的长为()A.πB.π2C.7πD.6π5.如图,正六边形ABCDEF内接于O,半径为4,则这个正六边形的边心距OM和BC的长分别为( )A.π2,3B.π2π3 D.4π36.如图,矩形ABCD 的边1,AB BE =平分ABC ∠交AD 于点E .若点E 是AD 的中点,以点B 为圆心,BE 长为半径画弧,交BC 于点F ,则图中阴影部分的面积是( )A.π24-B.3π24-C.π28-D.3π28- 7.如图,AB 是O 的直径,CD 是弦,30,2BCD OA ∠==°,则阴影部分的面积是( )A.π3B.2π3C.πD.2π 8.如图.从一块直径为2 m 的圆形铁皮上剪出一个圆心角为90︒的扇形,则此扇形的面积为( )A.2πm 2 2m C.2πm D.22πm9.如图,点,,A B C 在O 上,若45,2BAC OB ∠==则图中阴影部分的面积为( )A. π4-B. 2π13- C. π2- D. 2π23- 二、解答题10.如图,已知在Rt ABC △中,30,90B ACB ∠=︒∠=︒.延长CA 到,O 使AO AC =,以点O 为圆心,OA 为半径作O 交BA 的延长线于点,D 连接CD .(1)求证:CD 是O 的切线;(2)若4AB =,求图中阴影部分的面积.三、填空题11.一个扇形的弧长是11πcm ,半径是18cm ,则此扇形的圆心角是 度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弧长及扇形面积的计算
习题
集团企业公司编码:(LL3698-KKI1269-TM2483-LUI12689-ITT289-
《弧长及扇形面积的计算》习题一、基础过关
1.如图,正方形ABCD的边AB=1,和都是以1为半径的圆弧,则无阴影两部
分的面积之差是()
A.B.1﹣C.﹣1 D.1﹣
2.一个圆锥的侧面展开图形是半径为8cm,圆心角为120°的扇形,则此圆锥的底面
半径为()
A.cm B.cm C.3cm D.cm
3.圆心角为120°,弧长为12π的扇形半径为()
A.6 B.9 C.18 D.36
4.在半径为2的圆中,弦AB的长为2,则的长等于()
A.B.C.D.
5.一个扇形的半径为8cm,弧长为cm,则扇形的圆心角为
()
A.60°B.120°C.150°D.180°
6.已知一个扇形的半径为12,圆心角为150°,则此扇形的弧长是()
A.5πB.6πC.8πD.10π
7.已知扇形半径是3cm,弧长为2πcm,则扇形的圆心角为°.(结果保留π)
8.若扇形的圆心角为60°,弧长为2π,则扇形的半径为.9.半径为4cm,圆心角为60°的扇形的面积为πcm2.
10.如图,在△ABC中,AB=BC=2,∠ABC=90°,则图中阴影部分的面积是.
二、综合训练
1.如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,
AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
2.如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,OC=2,求阴影部分图形的面积(结果保留π).
三、拓展应用
1.如图,在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点
E,交AD的延长线于点F,设DA=2.
(1)求线段EC的长;
(2)求图中阴影部分的面积.
参考答案
一、基础过关
1.解:A
2.解:A
3.解:C
4.解:C
5.解:B
6.解:D
7.解:120
8.解:6
9.解:π
10.解:π﹣2
二、综合训练
1.(1)证明:连接OC.
∵AC=CD,∠ACD=120°,∴∠A=∠D=30°.
∵OA=OC,∴∠2=∠A=30°.
∴∠OCD=180°﹣∠A﹣∠D﹣∠2=90°.
∴CD是⊙O的切线.
(2)解:∵∠A=30°,∴∠1=2∠A=60°.
=.
∴S
扇形BOC
在Rt△OCD中,
∵,∴.
∴.
∴图中阴影部分的面积为:.
2.解:∵AB是⊙O的直径,弦CD⊥AB于点E,
∴CE=DE ,∠CEO=∠DEB=90°.
∵∠CDB=30°,∴∠COB=60°,∠OCE=∠CDB , 在△OCE 和△BDE 中, ∵,
∴△OCE ≌△BDE ,
∴S 阴影=S 扇形OCB =
=π. 三、拓展应用 1.解:(1)∵在矩形ABCD 中,AB=2DA ,DA=2, ∴AB=AE=4,
∴DE==2,
∴EC=CD ﹣DE=4﹣2;
(2)∵sin ∠DEA==,∴∠DEA=30°, ∴∠EAB=30°,∴图中阴影部分的面积为: S 扇形FAB ﹣S △DAE ﹣S 扇形EAB
=
﹣×2×2﹣
=﹣2.。
