八年级数学阅读理解题专项练习
1_2022初二上代数阅读题

燕山26.阅读下列材料:利用完全平方公式,可以把多项式2++x bx c 变形为2()++x m n 的形式.例如,243x x -+=24443x x -+-+=2(2)1x --.观察上式可以发现,当2-x 取任意一对互为相反数的值时,多项式243x x -+的值是相等的.例如,当2-x =±1,即x =3或1时,243x x -+的值均为0;当2-x =±2,即x =4或0时,243x x -+的值均为3.我们给出如下定义:对于关于x 的多项式,若当+x m 取任意一对互为相反数的值时,该多项式的值相等,则称该多项式关于x =-m 对称,称x =-m 是它的对称轴.例如,243x x -+关于x =2对称,x =2是它的对称轴.请根据上述材料解决下列问题:(1) 将多项式265-+x x 变形为2()++x m n 的形式,并求出它的对称轴;(2) 若关于x 的多项式221+-x ax 关于x =-5对称,则a = ; (3) 代数式22(21)(816)++-+x x x x 的对称轴是x = .西城23. (本题10分)(1)如果2(3)(2)++x x x mx n -+=,那么m 的值是 ,n 的值是 ; (2)如果21()()2+2x a x b x x ++=-, ①求(2)(2)a b --的值;②求22111a b++的值.25.(本题4分)观察下列等式: ①1111212--=-⨯;②1111 23434 --=-⨯;③1111 35656 --=-⨯;④1111 47878 --=-⨯;……根据上述规律回答下列问题:(1)第⑤个等式是;(2)第n个等式是(用含n的式子表示,n为正整数).通州石景山26.小石根据学习“数与式”积累的经验,想通过“由特殊到一般”的方法探究下面二次根式的运算规律.下面是小石的探究过程,请补充完整:(1)具体运算,发现规律.特例1特例2=,特例3,特例4特例5= (填写运算结果). (2)观察、归纳,得出猜想.如果n 为正整数,用含n 的式子表示上述的运算规律为: . (3)证明你的猜想. (4)应用运算规律.= ;=(a ,b 均为正整数),则a b +的值为 .平谷28. 我们已经学过()()()2---,x a x b x a b x ab =++如果关于x 的分式方程满足abx a b x+=+(a ,b 分别为非零整数),且方程的两个跟分别为12=,x a x b =. 我们称这样的方程为“十字方程”.例如:2=3x x +可化为1212=3x x⨯+=+ ∴12=1,2x x = 再如:6=-5x x+ 可化为()()-2-3-2-3=-5x x ⨯+= ∴12=-2,-3x x = 应用上面的结论解答下列问题:(1)“十字方程”8-6x x +=,则12= , x x =; (2)“十字方程”2--1x x =的两个解分别为12,x a x b ==,求11a b+的值;(3)关于x 的 “十字方程”2243n nx n x ++=+-的两个解分别为1212,()x x x x <, 求211xx +的值.密云26.阅读下面材料: 将形如cx dax b++的分式表示成一个整式与一个分式和(或差)的形式,可以先观察分母的特征,设法用含有分母的代数式表示分子再变形解决问题. 例如21111111x x x x x +++==++++ ,212(1)2132111x x x x x -+--==-+++. 解决问题:(1)已知3122x mx x +=+--,则m =______. (2)已知211mx nm x x +=+++,用含m 的代数式表示n . (3)已知m >0,x >1,直接写出21mx mx --与2m 的大小关系.门头沟26.阅读理解:材料:小华在学习分式运算时,通过具体运算:111122=-⨯,1112323=-⨯,1113434=-⨯,1114545=-⨯,…, 发现规律:()11111n n n n =-⨯++(n 为正整数),并证明了此规律成立. 应用规律,快速计算:111111111111911122334910223349101010++++=-+-+-++-=-=⨯⨯⨯⨯.根据材料,回答问题:在学习二次根式运算时,小华根据分式学习积累的活动经验,类比探究二次根式的运算规律,并解决问题.请将下面的探究过程,补充完整. (1)具体运算:特例111111122+=+-⨯,特例2111112323+=+-⨯,特例3111113434+=+-⨯,特例4: (填写一个符合上述运算特征的例子).……(2=________________________(n 为正整数),并证明了此规律成立.(3)应用规律:222222222211111111111111112233489910+++++++++++ ()()()22222222111111111111151223211n nn n n +++++++++----, 那么n = .怀柔25.我们知道,假分数可以化为整数与真分数的和的形式.例如:54=1+14. 在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,称之为“假分式”;当分子的次数小于分母的次数时,称之为“真分式”.例如:像52x x ++,21x x -,…,这样的分式是假分式;像34x -,21xx -,…,这样的分式是真分式.类似的,假分式也可以化为整式与真分式的和的形式.例如:()23531222x x =x x x +++=++++; ()()211111111x x x x x x x +-+==++---. 解决下列问题:(1)写出一个假分式为: ; (2)将分式13x x +-化为整式与真分式的和的形式为: ;(直接写出结果即可)(3)如果分式22x xx --的值为整数,求x 的整数值.海淀27.在分式中,若 M ,N 为整式,分母 M 的次数为 a ,分子 N 的次数为b (当 N 为常数时,b = 0 ),则称分式 为(a - b ) 次分式. 例如, 为三次分式.(1)请写出一个只含有字母 x 的二次分式 ;(2) 已知 (其中 m ,n 为常数).① 若 m = 0 , n = -5 ,则 A ⋅ B , A + B , A - B , A 2 中,化简后是二次分式的为;② 若 A 与 B 的和化简后是一次分式,且分母的次数为 1,求2m + n 的值.丰台26.在“整式乘法与因式分解”这一章的学习过程中,我们常采用构造几何图形的方法对代数式的变形加以说明.例如,利用图1中边长分别为a ,b 的正方形,以及长为a ,宽为b 的长方形卡片若干张拼成图2(卡片间不重叠、无缝隙),可以用来解释完全平方公式: .请你解答下面的问题:(1)利用图1中的三种卡片若干张拼成图3,可以解释等式:_________________; (2)利用图1中三种卡片若干张拼出一个面积为22252a ab b ++的长方形ABCD ,请你分析这个长方形的长和宽.图1222()2a b a ab b +=++图3图2a ab b a b a b a b a a b ab大兴朝阳24.阅读材料:对于两个实数a ,b 大小的比较,有如下规律:若a -b >0,则a >b ;若a -b =0,则a =b ;若a -b <0,则a <b . 反过来也成立. 解决问题:(1)已知实数x ,则()()37x x ++ ()()46x x ++(填“<”,“=”或“>”); (2)甲、乙二人同时从A 地出发去B 地,甲用一半时间以每小时x km 的速度行走,另一半时间以每小时y km 的速度行走;乙以每小时x km 的速度行走一半路程,另一半路程以每小时y km 的速度行走. 若x ≠y ,判断谁先到达B 地,并说明理由.下面是小明参考上面的规律解决问题的过程,请补充完整:(1)()()37x x ++ ()()46x x ++(填“<”,“=”或“>”);(2)先到达B 地的是 .说明:设甲从A 地到B 地用2t h ,则A ,B 两地的路程为(x +y )t km ,乙从A 地到B 地用)22x y x yt x y+++(h.昌平27. 是无理数,而无理数是无限不循环小数. 的小数部分1的小数部分. 理由是:对于正无理数,用本身减去其整数部分,差就是其小数部分. 的整数部分为11.参考小燕同学的做法,解答下列问题:(1________;(2)已知77的小数部分分别为a和b,求a2+2ab+b2的值;(3)39=x y,其中x是整数,0 < y < 1,那么325x y=________;(4(m为正整数)的整数部分为n,那么m m的小数部分为________(用含m,n的式子表示).。
八年级数学阅读理解题集

八年级数学阅读理解题集题目1:小明和小红共有20块糖果,小明的糖果数是小红的两倍。
问小明有多少块糖果?解析:设小红有x块糖果,则小明有2x块糖果。
根据题意得到方程2x + x = 20,解方程可得x = 5,所以小明有10块糖果。
题目2:某商店折扣价售卖一款原价为200元的电脑,打折后降价为原价的80%。
小明购买了这款电脑,他需要支付多少钱?解析:原价为200元,打折后为200 * 80% = 160元。
所以小明需要支付160元。
题目3:一个边长为3cm的正方形,内部有一条延长线,将该正方形分成一大角和三小角。
大角的度数是小角度数的两倍,求小角的度数。
解析:设小角的度数为x度,则大角的度数为2x度。
根据正方形内角和为360度,得到方程2x + 3x = 360,解方程可得x = 60,所以小角的度数为60度。
题目4:甲、乙两个人同时从两个不同的地点出发,相向而行,两人相距100km。
甲的速度是乙的两倍,乙每小时行驶的距离是多少?解析:设乙每小时行驶的距离为x km,则甲每小时行驶的距离为2x km。
根据题意得到方程x + 2x = 100,解方程可得x = 25,所以乙每小时行驶25km。
题目5:一个数乘以4再减去5等于17,这个数是多少?解析:设这个数为x,则根据题意得到方程4x - 5 = 17,解方程可得x = 6,所以这个数是6。
题目6:某书店有300本书,其中3/5是数学书,其余是故事书。
故事书的数量是数学书的几分之一?解析:数学书的数量为3/5 * 300 = 180本。
故事书的数量为300 - 180 = 120本。
所以故事书的数量是数学书的1/180。
通过以上题目的解析,我们可以发现在数学中,应用数学知识解决问题是非常重要的。
希望大家能够掌握数学的基础知识,提高自己的数学能力。
初二数学经典阅读理解题

阅读理解题型训练1.阅读下面材料:小明遇到这样一个问题:如图1,△ABO 和△CDO 均为等腰直角三角形, ∠AOB =∠COD=90︒.若△BOC 的面积为1, 试求以AD 、BC 、OC+OD 的长度为三边长的三角形的面积.图1 图2小明是这样思考的:要解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他利用图形变换解决了这个问题,其解题思路是延长CO 到E , 使得OE =CO , 连接BE , 可证△OBE ≌△OAD , 从而得到的△BCE 即是以AD 、BC 、OC+OD 的长度为三边长的三角形(如图2).请你回答:图2中△BCE 的面积等于 .2.如图所示,圆圈内分别标有1,2,…,12,这12个数字,电子跳蚤每跳一步,可以从一个圆圈逆时针跳到相邻的圆圈,若电子跳蚤所在圆圈的数字为n ,则电子跳蚤连续跳(2-3n )步作为一次跳跃,例如:电子跳蚤从标有数字1的圆圈需跳12-13=⨯步到标有数字2的圆圈内,完成一次跳跃,第二次则要连续跳42-23=⨯步到达标有数字6的圆圈,…依此规律,若电子跳蚤从①开始,那么第3次能跳到的圆圈内所标的数字为 ;第2012次电子跳蚤能跳到的圆圈内所标的数字为 .3.请阅读下列材料:已知:如图(1)在Rt △ABC 中,∠BAC =90°,AB = AC ,点D 、E 分别为线段BC 上两动点,若∠DAE =45°.探究线段BD 、DE 、EC 三条线段之间的数量关系. 小明的思路是:把△AEC 绕点A 顺时针旋转90°,得到△ABE′,连结E′D , 使问题得到解决.请你参考小明的思路探究并解决下列问题:(1)猜想BD 、DE 、EC 三条线段之间存在的数量关系式,并对你的猜想给予证明; 图(1)ADCOBBOCDA111210987654321图2图1A'A ABCBC(2)当动点E 在线段BC 上,动点D 运动在线段CB 延长线上时,如图(2),其它条件 不变,(1)中探究的结论是否发生改变? 请说明你的猜想并给予证明.4.阅读下面材料:小伟遇到这样一个问题:如图1,在△ABC (其中∠BAC 是一个可以变化的角)中,AB=2,AC=4,以BC 为边在BC 的下方作等边△PBC ,求AP 的最大值。
初二数学阅读试题及答案

初二数学阅读试题及答案一、选择题1. 已知一个数的平方是49,那么这个数可能是()。
A. 7B. -7C. 7或-7D. 以上都不对答案:C解析:一个数的平方是49,那么这个数可以是7或者-7,因为7的平方是49,-7的平方也是49。
2. 一个等腰三角形的底边长为6,腰长为5,那么这个三角形的周长是()。
A. 16B. 21C. 26D. 以上都不对答案:B解析:等腰三角形的两腰相等,所以周长为底边长加上两倍的腰长,即6+5+5=16。
3. 一个数的绝对值是5,那么这个数可能是()。
A. 5B. -5C. 5或-5D. 以上都不对答案:C解析:一个数的绝对值是5,那么这个数可以是5或者-5,因为5的绝对值是5,-5的绝对值也是5。
二、填空题4. 已知一个直角三角形的两个直角边长分别为3和4,那么这个三角形的斜边长为______。
答案:5解析:根据勾股定理,直角三角形的斜边长等于两直角边长的平方和的平方根,即√(3²+4²)=√(9+16)=√25=5。
5. 一个数的立方是-8,那么这个数是______。
答案:-2解析:一个数的立方是-8,那么这个数是-2,因为(-2)³=-8。
三、解答题6. 已知一个二次函数y=ax²+bx+c的图像经过点(1,2)和(2,3),且对称轴为x=1,求这个二次函数的解析式。
答案:y=x²-2x+1解析:首先,由于对称轴为x=1,我们可以设二次函数的顶点式为y=a(x-1)²+k。
将点(1,2)代入得2=a(1-1)²+k,即k=2。
再将点(2,3)代入得3=a(2-1)²+2,即a=1。
所以二次函数的解析式为y=(x-1)²+2=x²-2x+1。
7. 一个等腰三角形的底边长为8,腰长为10,求这个三角形的面积。
答案:24解析:首先,我们可以从底边的两个端点向腰作垂线,将等腰三角形分为两个直角三角形。
【英语】八年级数学上册阅读理解专项练习

【英语】八年级数学上册阅读理解专项练
习
一、阅读下面的数学题并回答问题。
1.若ab=0,则a= __ 或b= __ 。
答:a=0或b=0。
2.当x>0 时,(-2x+6)÷(x-3) 的值的范围是 __ 。
答:(-∞,-2)∪(3,+∞)。
3.已知k是1到9之间的整数,下列k的取值中,使下列不等式成立的是( __ ).
2×3^k < 81
答:k=3或k<3。
4.把大于0,小于10的数字排成一个五位数,使千位百位还有个位上的数字之和等于十位和数字,其五位数是( __ ).
答:。
5.已知正整数n,且100≤n<1000,将n的个、十、百位上数字分别用a、b、c表示。
若n=a^b+c,请问n最小是多少?
答:当a=2、b=2、c=4时,n最小,即264=2^2+4。
二、阅读下面的文学作品,回答问题。
甲乙丙丁四名运动员参加了100米比赛,裁判员按照比赛成绩,前四名分别是甲、乙、丙、丁。
下面是他们的论述:
甲:我得了第一。
乙:我不是倒数第一。
丙:我得了第三,不是第一和第二。
丁:我不是第一,我是倒数第二。
请问甲、乙、丙、丁四个人中,哪个人拿到了比赛的冠军。
答:甲。
因为乙是倒数第二,那么丁比他倒数第一,而丙不是第一和第二,所以,他只能是第三,那么剩下的甲就是第一。
七八年级下期及九上专项训练-阅读理解

专项训练-阅读理解
25.若正整数k 满足个位数字为1,其他数位上的数字均不为1且十位与百位上的数字相等,
我们称这样的数k 为“言唯一数”,交换其首位与个位的数字得到一个新数'k ,并记
()''11127
k k k k F k +-=-+. (1)最大的四位“言唯一数”是 ,最小的三位“言唯一数”是 ;
(2)证明:对于任意的四位“言唯一数”m ,'m m +能被11整除;
(3)设四位“言唯一数”1000100101n x y y =+++(29x ≤≤,09y ≤≤且1y ≠,
x 、y 均为整数),若()F n 仍然为“言唯一数”,求所有满足条件的四位“言
唯一数”n .
25.已知一个三位自然数,若满足百位数字等于十位数字与个位数字的和,则称这个数为“和数”,若满
足百位数字等于十位数字与个位数字的平方差,则称这个数为“谐数”.如果一个数即是“和数”,又是“谐数”,则称这个数为“和谐数”.例如321,123+=,∴321是“和数”,221-23=,∴321是“谐数”,∴321是“和谐数”.
(1)最小的和谐数是 ,最大的和谐数是 ;
(2)证明:任意“谐数”的各个数位上的数字之和一定是偶数;
(3)已知178301++=c b m (4170≤≤≤≤c b ,,且c b ,均为整数)是一个“和数”,请求出所有m .。
八年级数学阅读理解题专项练习
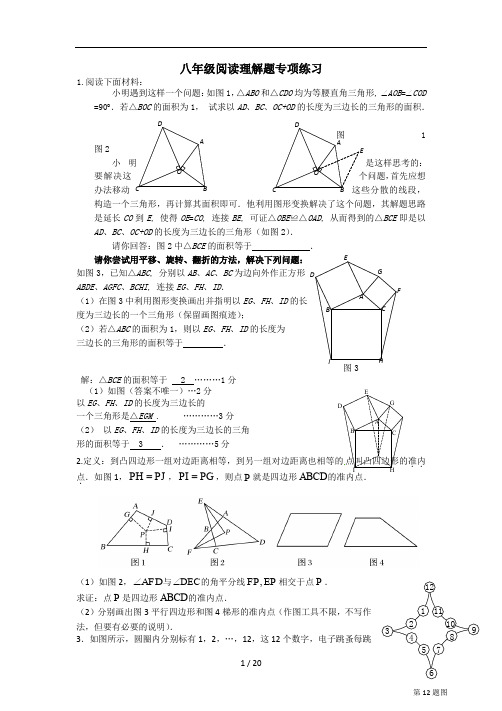
八年级阅读理解题专项练习1.阅读下面材料:小明遇到这样一个问题:如图1,△ABO 和△CDO 均为等腰直角三角形, ∠AOB =∠COD=90︒.若△BOC 的面积为1, 试求以AD 、BC 、OC+OD 的长度为三边长的三角形的面积.1图2小明是这样思考的:要解决这首先应想办法移动构造一个三角形,再计算其面积即可.他利用图形变换解决了这个问题,其解题思路是延长CO 到E , 使得OE =CO , 连接BE , 可证△OBE ≌△OAD , 从而得到的△BCE 即是以AD 、BC 、OC+OD 的长度为三边长的三角形(如图2).请你回答:图2中△BCE 的面积等于 .请你尝试用平移、旋转、翻折的方法,解决下列问题: 如图3,已知△ABC , 分别以AB 、AC 、BC 为边向外作正方形 ABDE 、AGFC 、BCHI , 连接EG 、FH 、ID .(1)在图3中利用图形变换画出并指明以EG 、FH 、ID 的长 度为三边长的一个三角形(保留画图痕迹); (2)若△ABC 的面积为1,则以EG 、FH 、ID 的长度为 三边长的三角形的面积等于 .图3解:△BCE 的面积等于 2 ………1分 (1)如图(答案不唯一)…2分 以EG 、FH 、ID 的长度为三边长的 一个三角形是△EGM . …………3分 (2) 以EG 、FH 、ID 的长度为三边长的三角 形的面积等于 3 . …………5分2.定义:到凸四边形一组对边距离相等,到另一组对边距离也相等的点叫凸四边形的准内..点..如图1,PH PJ =,PI PG =,则点P 就是四边形ABCD 的准内点.(1)如图2,AFD ∠与DEC ∠的角平分线,FP EP 相交于点P . 求证:点P 是四边形ABCD 的准内点.(2)分别画出图3平行四边形和图4梯形的准内点(作图工具不限,不写作法,但要有必要的说明).3.如图所示,圆圈内分别标有1,2,…,12,这12个数字,电子跳蚤每跳BOCDAIHG FABCDEEDCBAG 11121098754321一步,可以从一个圆圈逆时针跳到相邻的圆圈,若电子跳蚤所在圆圈的数字为n ,则电子跳蚤连续跳(2-3n )步作为一次跳跃,例如:电子跳蚤从标有数字1的圆圈需跳12-13=⨯步到标有数字2的圆圈内,完成一次跳跃,第二次则要连续跳42-23=⨯步到达标有数字6的圆圈,…依此规律,若电子跳蚤从①开始,那么第3次能跳到的圆圈内所标的数字为 ;第2012次电子跳蚤能跳到的圆圈内所标的数字为 .4.△A B C 是等边三角形,P 为平面内的一个动点,B P =B A , 若0︒<∠PBC <180°,且∠PBC 平分线上的一点D 满足DB=DA ,(1)当BP 与BA 重合时(如图1),∠BPD= °; (2)当BP 在∠ABC 的内部时(如图2),求∠BPD 的度数;(3)当BP 在∠ABC 的外部时,请你直接写出∠BPD 的度数,并画出相应的图形.5.请阅读下列材料: 已知:如图(1)在Rt △ABC中,∠BAC =90°,AB = AC ,点D 、E 分别为线段BC 上两动点,若∠DAE =45°.探究线段BD 、DE 、EC 三条线段之间的数量关系.小明的思路是:把△AEC 绕点A 顺时针旋转90°,得到△ABE′,连结E′D , 使问题得到解决.请你参考小明的思路探究并解决下列问题:(1)猜想BD 、DE 、EC 三条线段之间存在的数量关系式,并对你的猜想给予证明;图(1)(2)当动点E 在线段BC 上,动点D 运动在线段CB 延长线上时,如图(2),其它条件 不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明. 图(2)6.(石景山二)25.(1)如图1,四边形ABCD 中,CB AB =,︒=∠60ABC ,︒=∠120ADC ,请你 猜想线段DA 、DC 之和与线段BD 的数量关系,并证明你的结论;(2)如图2,四边形ABCD 中,BC AB =,︒=∠60ABC ,若点P 为四边形ABCD 内一点,且︒=∠120APD ,请你猜想线段PA 、PD 、PC 之和与线段BD 的 数量关系,并证明你的结论.7.问题:如图1,P 为正方形ABCD 内一点,且PA ∶PB ∶PC =1∶2∶3,求∠APB 的度数.小娜同学的想法是:不妨设PA=1, PB=2,PC=3,设法把PA 、PB 、PC 相对集中,于是他将△BCP 绕点B 顺时针旋转90°得到△BAE (如图2),然后连结PE ,问题得以解决.请你回答:图2中∠APB 的度数为 .请你参考小娜同学的思路,解决下列问题:图2图1图2图1A'B如图3,P 是等边三角形ABC 内一点,已知∠APB=115°,∠BPC=125°.(1)在图3中画出并指明以PA 、PB 、PC 的长度为三边长的一个三角形(保留画图痕迹);(2)求出以PA 、PB 、PC 的长度为三边长的三角形的各内角的度数分别等于 .EDDPPPCCCBBBAAA图1 图2 图38.阅读下面材料:小伟遇到这样一个问题:如图1,在△ABC (其中∠BAC 是一个可以变化的角)中,AB=2,AC=4,以BC 为边在BC 的下方作等边△PBC ,求AP 的最大值。
人教版八下数学18 新定义与阅读理解题(第01期)(解析版)

专题18 新定义与阅读理解题1.(2019•湘西州)阅读材料:设a r=(x 1,y 1),b r=(x 2,y 2),如果a r∥b r,则x 1•y 2=x 2•y 1,根据该材料填空,已知a r=(4,3),b r=(8,m ),且a r∥b r,则m =__________. 【答案】6【解析】∵a r=(4,3),b r=(8,m ),且a r∥b r,∴4m =3×8,∴m =6;故答案为:6. 【名师点睛】本题考查新定义,点的坐标;理解阅读材料的内容,转化为所学知识求解是关键. 2.(2019•白银)定义:等腰三角形的顶角与其一个底角的度数的比值k 称为这个等腰三角形的“特征值”.若等腰△ABC 中,∠A =80°,则它的特征值k =__________. 【答案】85或14【解析】①当∠A 为顶角时,等腰三角形两底角的度数为:218080︒-︒=50°, ∴特征值k =808505︒=︒; ②当∠A 为底角时,顶角的度数为:180°–80°–80°=20°,∴特征值k =208014︒=︒; 综上所述,特征值k 为85或14;故答案为85或14.【名师点睛】本题主要考查等腰三角形的性质,熟记等腰三角形的性质是解题的关键,要注意到本题中,已知∠A 的底数,要进行判断是底角或顶角,以免造成答案的遗漏.3.(2019•河北)如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.示例:即4+3=7.则(1)用含x 的式子表示m =__________; (2)当y =–2时,n 的值为__________.【答案】(1)3x;(2)1.【解析】(1)根据约定的方法可得:m=x+2x=3x;故答案为:3x;(2)根据约定的方法即可得x+2x+2x+3=m+n=y.当y=–2时,5x+3=–2.解得x=–1.∴n=2x+3=–2+3=1.故答案为:1.【名师点睛】本题考查了列代数式和代数式求值,解题的关键是掌握列代数式的约定方法.4.(2019•枣庄)对于实数a、b,定义关于“⊗”的一种运算:a⊗b=2a+b,例如3⊗4=2×3+4=10.(1)求4⊗(–3)的值;(2)若x⊗(–y)=2,(2y)⊗x=–1,求x+y的值.【答案】(1)5;(2)1 3 .【解析】(1)根据题中的新定义得:原式=8–3=5;(2)根据题中的新定义化简得:2241x yx y-=⎨+=-⎧⎩①②,①+②得:3x+3y=1,则x+y=13.【名师点睛】此题考查了解二元一次方程组,以及实数的运算,熟练掌握运算法则是解本题的关键.5.(2019•济宁)阅读下面的材料:如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1,x2,(1)若x1<x2,都有f(x1)<f(x2),则称f(x)是增函数;(2)若x1<x2,都有f(x1)>f(x2),则称f(x)是减函数.例题:证明函数f(x)=6x(x>0)是减函数.证明:设0<x1<x2,f(x1)–f(x2)=()212112121266666x xx xx x x x x x---==.∵0<x1<x2,∴x2–x1>0,x1x2>0.∴()21126x xx x->0.即f(x1)–f(x2)>0.∴f (x 1)>f (x 2),∴函数f (x )═6x(x >0)是减函数. 根据以上材料,解答下面的问题: 已知函数f (x )=21x+x (x <0), f (–1)=21(1)-+(–1)=0,f (–2)=21(2)-+(–2)=–74. (1)计算:f (–3)=__________,f (–4)=__________; (2)猜想:函数f (x )=21x+x (x <0)是__________函数(填“增”或“减”); (3)请仿照例题证明你的猜想.【答案】(1)–269,–6316;(2)增;(3)见解析. 【解析】(1)∵f (x )=21x+x (x <0),∴f (–3)=21(3)-–3=–269,f (–4)=21(4)-–4=–6316,故答案为:–269,–6316; (2)∵–4<–3,f (–4)>f (–3), ∴函数f (x )=21x+x (x <0)是增函数, 故答案为:增; (3)设x 1<x 2<0, ∵f (x 1)–f (x 2)=12221211x x x x +--=(x 1–x 2)(1–122212x x x x +)∵x 1<x 2<0,∴x 1–x 2<0,x 1+x 2<0,∴f (x 1)–f (x 2)<0,∴f (x 1)<f (x 2), ∴函数f (x )=21x+x (x <0)是增函数. 【名师点睛】本题考查反比例函数图象上的坐标特征、反比例函数的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用反比例函数的性质解答.6.(2019•随州)若一个两位数十位、个位上的数字分别为m ,n ,我们可将这个两位数记为mn ,易知mn =10m +n ;同理,一个三位数、四位数等均可以用此记法,如abc =100a +10b +c .【基础训练】(1)解方程填空:①若2x+3x=45,则x=__________;②若7y–8y=26,则y=__________;③若93t+58t=131t,则t=__________;【能力提升】(2)交换任意一个两位数mn的个位数字与十位数字,可得到一个新数nm,则mn+nm一定能被__________整除,mn–nm一定能被__________整除,mn•nm–mn一定能被__________整除;(请从大于5的整数中选择合适的数填空)【探索发现】(3)北京时间2019年4月10日21时,人类拍摄的首张黑洞照片问世,黑洞是一种引力极大的天体,连光都逃脱不了它的束缚.数学中也存在有趣的黑洞现象:任选一个三位数,要求个、十、百位的数字各不相同,把这个三位数的三个数字按大小重新排列,得出一个最大的数和一个最小的数,用得出的最大的数减去最小的数得到一个新数(例如若选的数为325,则用532–235=297),再将这个新数按上述方式重新排列,再相减,像这样运算若干次后一定会得到同一个重复出现的数,这个数称为“卡普雷卡尔黑洞数”.①该“卡普雷卡尔黑洞数”为__________;②设任选的三位数为abc(不妨设a>b>c),试说明其均可产生该黑洞数.【答案】(1)①2.②4.③7.(2)11;9;10.【解析】(1)①∵mn=10m+n,∴若2x+3x=45,则10×2+x+10x+3=45,∴x=2,故答案为:2.②若7y–8y=26,则10×7+y–(10y+8)=26,解得y=4,故答案为:4.③由abc=100a+10b+c,及四位数的类似公式得若93t+58t=131t,则100t+10×9+3+100×5+10t+8=1000×1+100×3+10t+1,∴100t=700,∴t=7,故答案为:7.(2)∵mn+nm=10m+n+10n+m=11m+11n=11(m+n),∴则mn+nm一定能被11整除,∵mn–nm=10m+n–(10n+m)=9m–9n=9(m–n),∴mn–nm一定能被9整除.∵mn•nm–mn=(10m+n)(10n+m)–mn=100mn+10m2+10n2+mn–mn=10(10mn+m2+n2)∴mn•nm–mn一定能被10整除.故答案为:11;9;10.(3)①若选的数为325,则用532–235=297,以下按照上述规则继续计算,972–279=693,963–369=594,954–459=495,954–459=495,…故答案为:495.②当任选的三位数为abc时,第一次运算后得:100a+10b+c–(100c+10b+a)=99(a–c),结果为99的倍数,由于a>b>c,故a≥b+1≥c+2,∴a–c≥2,又9≥a>c≥0,∴a–c≤9,∴a–c=2,3,4,5,6,7,8,9,∴第一次运算后可能得到:198,297,396,495,594,693,792,891,再让这些数字经过运算,分别可以得到:981–189=792,972–279=693,963–369=594,954–459–495,954–459=495…,故都可以得到该黑洞数495.【名师点睛】本题是较为复杂的新定义试题,题目设置的问题较多,但解答方法大同小异,总体中等难度略大.7.(2019•自贡)阅读下列材料:小明为了计算1+2+22+…+22017+22018的值,采用以下方法:设S=1+2+22+…+22017+22018①,则2S=2+22+…+22018+22019②,②–①得2S–S=S=22019–1,∴S=1+2+22+…+22017+22018=22019–1.请仿照小明的方法解决以下问题:(1)1+2+22+…+29=__________;(2)3+32+…+310=__________;(3)求1+a+a2+…+a n的和(a>0,n是正整数),请写出计算过程.【答案】(1)210–1;(2)11312-;(3)a=1时,S=n+1;a≠1时,S=111naa+--.【解析】(1)设S=1+2+22+…+29①,则2S=2+22+…+210②,②–①得2S–S=S=210–1,∴S=1+2+22+…+29=210–1;故答案为:210–1;(2)设S=3+3+32+33+34+…+310①,则3S=32+33+34+35+…+311②,②–①得2S=311–1,所以S=1131 2-,即3+32+33+34+ (310)1131 2-;故答案为:1131 2-;(3)设S=1+a+a2+a3+a4+…+a n①,则aS =a +a 2+a 3+a 4+…+a n +a n +1②, ②–①得:(a –1)S =a n +1–1,a =1时,不能直接除以a –1,此时原式等于n +1;a ≠1时,a –1才能做分母,所以S =111n a a +--,即1+a +a 2+a 3+a 4+…+a n=111n a a +--. 【名师点睛】根据题目给出的信息,提炼解题方法.认真观察、仔细思考,善用联想,利用类比的方法是解决这类问题的方法. 8.(2019·江西)特例感知(1)如图1,对于抛物线211y x x =--+,2221y x x =--+,2331y x x =--+,下列结论正确的序号是_________;①抛物线1y ,2y ,3y 都经过点(0,1)C ;②抛物线2y ,3y 的对称轴由抛物线1y 的对称轴依次向左平移12个单位得到; ③抛物线1y ,2y ,3y 与直线1y =的交点中,相邻两点之间的距离相等. 形成概念(2)把满足21n y x nx =--+(n 为正整数)的抛物线称为“系列平移抛物线”.知识应用在(2)中,如图2.①“系列平移抛物线”的顶点依次为1P ,2P ,3P ,…,n P ,用含n 的代数式表示顶点n P 的坐标,并写出该顶点纵坐标y 与横坐标x 之间的关系式;②“系列平移抛物线”存在“系列整数点(横、纵坐标均为整数的点)”:1C ,2C ,3C ,…,n C ,其横坐标分别为:1k --,2k --,3k --,…,k n --(k 为正整数),判断相邻两点之间的距离是否都相等,若相等,直接写出相邻两点之间的距离;若不相等,说明理由.③在②中,直线1y =分别交“系列平移抛物线”于点1A ,2A ,3A ,…,n A ,连接n n C A ,11n n C A --,判断n n C A ,11n n C A --是否平行?并说明理由.【答案】(1)①②③(2)①2,124n n n P ⎛⎫-+ ⎪⎝⎭,21y x =+.③不平行,直线n n C A 的斜率(比例系数)为k n +,与n 取值有关(若两直线平行,则斜率会相等). 【解析】(1)①当x =0,1231y y y ===,所以正确;②123,,y y y 的对称轴分别是直线112x =-,21x =-,332x =-,所以正确;③123,,y y y 与1y =交点(除了点C )横坐标分别为–1,–2,–3,所以距离为1,都相等,正确.(2)①2224124n n n y x nx x +⎛⎫=--+=-++ ⎪⎝⎭,所以顶点24,24n n n P ⎛⎫+- ⎪⎝⎭,令顶点n P 横坐标2n x =-,纵坐标244n y +=,22241142n n y x +⎛⎫==-+=+ ⎪⎝⎭, 即:n P 顶点满足关系式21y x =+.②相邻两点之间的距离相等.理由:根据题意得;()2,1n C k n k nk ----+,()211,1n C k n k nk k ---+--++, ∴C n C n –1两点之间的铅直高度=()2211k nk k k nk k --++---+=. C n C n –1两点之间的水平距离=1()1k n k n --+---=. ∴由勾股定理得C n C n –12=k 2+1,∴C n C n –1③n n C A 与11n n C A --不平行. 理由:根据题意得:()2,1n C k n k nk ----+,()211,1n C k n k nk k ---+--++,(),1n A n -,()11,1n A n --+.过C n ,C n –1分别作直线y =1的垂线,垂足为D ,E ,所以D (–k –n ,1),E (–k –n +1,1). 在Rt △DA n C n 中,tan ∠DA n C n =()2211()n n k nk C D k nkk n A D n k n k---++===+----,在Rt △EA n –1C n –1中,tan ∠EA n –1C n –1=()22111111(1)n n k nk k C E k nk kk n A E n k n k-----+++-===+--+---+,∵1k n +-≠k n +,∴tan ∠DA n C n ≠tan ∠EA n –1C n –1, ∴n n C A 与11n n C A --不平行.9.(2019·甘肃白银)阅读下面的例题及点拨,并解决问题:例题:如图①,在等边△ABC 中,M 是BC 边上一点(不含端点B ,C ),N 是△ABC 的外角∠ACH 的平分线上一点,且AM =MN .求证:∠AMN =60°.点拨:如图②,作∠CBE =60°,BE 与NC 的延长线相交于点E ,得等边△BEC ,连接EM .易证:△ABM ≌△EBM (SAS ),可得AM =EM ,∠1=∠2;又AM =MN ,则EM =MN ,可得∠3=∠4;由∠3+∠1=∠4+∠5=60°,进一步可得∠1=∠2=∠5,又因为∠2+∠6=120°,所以∠5+∠6=120°,即:∠AMN =60°. 问题:如图③,在正方形A 1B 1C 1D 1中,M 1是B 1C 1边上一点(不含端点B 1,C 1),N 1是正方形A 1B 1C 1D 1的外角∠D 1C 1H 1的平分线上一点,且A 1M 1=M 1N 1.求证:∠A 1M 1N 1=90°.【答案】见解析.【解析】延长A 1B 1至E ,使EB 1=A 1B 1,连接EM 1、EC 1, 如图所示:则EB 1=B 1C 1,∠EB 1M 1=90°=∠A 1B 1M 1, ∴△EB 1C 1是等腰直角三角形, ∴∠B 1EC 1=∠B 1C 1E =45°,∵N 1是正方形A 1B 1C 1D 1的外角∠D 1C 1H 1的平分线上一点, ∴∠M 1C 1N 1=90°+45°=135°, ∴∠B 1C 1E +∠M 1C 1N 1=180°, ∴E 、C 1、N 1三点共线,在△A 1B 1M 1和△EB 1M 1中,111111111111A B EB A B M EB MM B M B =⎧⎪∠=∠⎨⎪=⎩,∴△A 1B 1M 1≌△EB 1M 1(SAS ), ∴A 1M 1=EM 1,∠1=∠2,∵A1M1=M1N1,∴EM1=M1N1,∴∠3=∠4,∵∠2+∠3=45°,∠4+∠5=45°,∴∠1=∠2=∠5,∵∠1+∠6=90°,∴∠5+∠6=90°,∴∠A1M1N1=180°﹣90°=90°.【名师点睛】此题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、等腰三角形的判定与性质、三角形的外角性质等知识;本题综合性强,熟练掌握正方形的性质,通过作辅助线构造三角形全等是解本题的关键.10.(2019·甘肃天水)如图1,对角线互相垂直的四边形叫做垂美四边形.(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;(2)性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.试证明:AB2+CD2=AD2+BC2;(3)解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE.已知AC=4,AB=5,求GE的长.【答案】(1)四边形ABCD是垂美四边形.理由见解析.(2)见解析.(3)GE【解析】(1)四边形ABCD是垂美四边形.理由如下:∵AB=AD,∴点A在线段BD的垂直平分线上,∵CB=CD,∴点C在线段BD的垂直平分线上,∴直线AC是线段BD的垂直平分线,∴AC⊥BD,即四边形ABCD是垂美四边形;(2)如图1,∵AC⊥BD,∴∠AOD=∠AOB=∠BOC=∠COD=90°,由勾股定理得,AB2+CD2=AO2+BO2+DO2+CO2=AD2+BC2,∴AD2+BC2=AB2+CD2;(3)连接CG 、BE ,∵∠CAG =∠BAE =90°,∴∠CAG +∠BAC =∠BAE +∠BAC ,即∠GAB =∠CAE ,在△GAB 和△CAE 中,AG AC GAB CAE AB AE =⎧⎪∠=∠⎨⎪=⎩,∴△GAB ≌△CAE (SAS ),∴∠ABG =∠AEC ,又∠AEC +∠AME =90°,∴∠ABG +∠AME =90°,即CE ⊥BG ,∴四边形CGEB 是垂美四边形,由(2)得,CG 2+BE 2=CB 2+GE 2,∵AC =4,AB =5,∴BC =3,CG,BE∴GE 2=CG 2+BE 2-CB 2=73,∴GE【名师点睛】(1)根据垂直平分线的判定定理证明即可;(2)根据垂直的定义和勾股定理解答即可; (3)根据垂美四边形的性质、勾股定理、结合(2)的结论计算.本题考查的是正方形的性质、全等三角形的判定和性质、垂直的定义、勾股定理的应用,正确理解垂美四边形的定义、灵活运用勾股定理是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级阅读理解题专项练习1•阅读下面材料:小明遇到这样一个问题: 如图1, △ ABOFH A CD%为等腰直角三角形,ZAOBZCOD =90 •若△ BOC 勺面积为1,试求以AD BC OC+O 的长度为三边长的三角形的面积.1AEGF CHDC点叫凸四PI £li图2图图412不写作2图3ID 的长度为夕的准内PG ,则点P 就是四边形 ABCD 的准内点2•定义:到凸四边形一组对边距离相等,到另一组对边距离也相等的 EG FH ID 的长 (1)如图2, . AFD 与.DEC 的角平分线FP,EP 相交于点P 求证:点P 是四边形ABCD 的准内点.(2)分别画出图3平行四边形和图4梯形的准内点(作图工具不限 法,但要有必要的说明)•3•如图所示,圆圈内分别标有 1, 2点.如图1 , PH = PJ12,这12个数字,电子跳蚤每跳 图2 小明 要解决这 办法移动构造一个三角形,再计算其面积即可•他利用图形变换解决了这个问题是延长CO 到 E ,使得OECO 连接BE 可证△ OBE^A OAD 从而得到的△ BCE 即是以 ADBC OC+O 的长度为三边长的三角形(如图 2).请你回答:图2中厶BCE 的面积等于 ______________ .请你尝试用平移、旋转、翻折的方法,解决下列问题: 如图3,已知△ ABC 分别以AB ACBC 为边向外作正方形 DABDE AGFC BCH ,连接 EG FH ID .(1) 在图3中利用图形变换画出并指明以 度为三边长的一个三角形(保留画图痕迹)(2) 若厶ABC 的面积为1,则以EG FH 三边长的三角形的面积等于 ___________ .解:△ BCE 的面积等于 2_ ............... 1分(1)如图(答案不唯一)… 2分 以EG FH ID 的长度为三边长的 一个三角形是△ EGM ............................................ 3分 (2)以EG FH ID 的长度为三边长的三角 形的面积等于 3............. 5分图AE、/ 是这样思考的: 个问题,首先应想这些分散的线段,其解题思路E乂GDD一步,可以从一个圆圈逆时针跳到相邻的圆圈,若电子跳蚤所在圆圈的数字为 n ,则电子跳蚤连续跳(3n-2)步作为一次跳跃,例如:电子跳蚤从标有数字 1的圆圈需跳3 1-2=1步到标有数字 2的圆圈内,完成一次跳跃,第二次则要连续跳3 2-2=4步到达标有数字 6的圆圈,…依此规律,若电子跳蚤从①开始,那么第3次能跳到的圆圈内所标的 数字为 ________ ;第2012次电子跳蚤能跳到的圆圈内所标的 数字为 _______ .4 . △ ABC 是等边三角形,P 为平面内的一个动点,BP = BA , 若0 °<Z PBC < 180° 且/ PBC 平分线上的一点 D 满足DB=DA,(1) __________________________________________ 当BP 与BA 重合时(如图 1) , / BPD° ;(2) 当BP 在/ ABC 的内部时(如图 2),求/ BPD 的度数;(3) 当BP 在/ ABC 的外部时,请你直接写出/ BPD 的度数,并画出相应的图形.下列材料: 知:如图(1 ) ABC 中,/AB = AC,点 DE 分别为线段 BC 上两动点,若/ DAE=45 °探究线段BD 、DE 、EC 三条线段之间的数量关小明的思路是:把△ AEC 绕点A 顺时针旋转90°得到△ ABE ,连结E', 吕 使问题得到解决•请你参考小明的思路探究并解决下列问题: (1)猜想BD 、DE 、EC 三条线段之间存在的数 量关系式,并对你的猜想给予证明;■图(1)(2)当动点E 在线段BC 上,动点D 运动在线 段CB 延长线上时,如图(2),其它条件 不变,(1 )中探究的结论是否发生改变? 请说明你的猜想并给予证明•6.(石景山二)25.( 1)如图 1,四边形 ABCD 中,AB =CB , ABC =60 , ADC = 120 , 请你 猜想线段DA 、DC 之和与线段BD 的数量关系,并证明你的结论;(2)如图2,四边形ABCD 中,AB =BC , • ABC = 60,若点P 为四边形 ABCD 内一点,且• APD -120,请你猜想线段 PA 、PD 、PC 之和与线段BD 的 数量关系,并证明你的结论.1/7•问题:如霜1 , P 为PA=1 , PB5.请阅读已 在 Rt △BAC=90 A田2APA::2 : 3,求/ APB 的度数. PA 、PB PC 相对集中,形ABCD 内一点 C=3,设A丁想法是:不妨设W B顺时针旋转90得到△ BAE(如图2),然后连结PE,问题得以解决.閱c 图2于是他将△图1请你回答:图2中/ APB的度数为______________ .请你参考小娜同学的思路,解决下列问题:如图3, P是等边三角形ABC内一点,已知/ APB=115 °,/ BPC=I25 ° .(1 )在图3中画出并指明以PA、PB PC的长度为三边长的一个三角形(保留画图痕迹);(2)求出以PA、PB、PC的长度为三边长的三角形的各内角的度数分别等A小伟遇到这样一个问题:如图1,在A ABC (其中/BAC是一个可以变化的角)中,AB=2, AC=4,以BC为边在BC的下方作等边△ PBC,求AP的最大值。
m个点,共(m+n)个点为顶点,可把原n边形分割成多少个互不重叠的小三角形?问题探究:为了解决上面的问题,我们将采取一般问题特殊化的策略,先从简单和具体的情形入手:探究一:以△ ABC 的三个顶点和它内部的一个点 P ,共4个点为顶点,可把△ ABC 分割成 多少个互不重叠的小三角形?如图①,显然,此时可把△ ABC 分割成3个互不重叠的小三角形.探究二:以△ ABC 的三个顶点和它内部的 2个点P 、Q ,共5个点为顶点,可把△ ABC 分 割成多少个互不重叠的小三角形?在探究一的基础上,我们可看作在图①△ ABC 的内部,再添加1个点Q ,那么点Q 的位置会有两种情况:一种情况,点Q 在图①分割成的某个小三角形内部, 不妨假设点Q 在厶PAC 内部,如图②;占 八A'A羊思考的:利用变换和等边三角形将边的位置重新此题可解(如图 请你回答:P 的最大值是问题的方法,解决下列问题:如图3,等腰严ABC •边AB =4,P 为ABC 内部一点, 则AP+BP+CP 的最小值是.(结果可以不化简)9.如图,在△ ABC 中,.C =90",M 是AB 的中点,动点 P 从点 动到终点C ,动点Q 从点C 出发,沿CB 方向匀速运动到终点 并同时到达终点,连结 MP ,MQ ,PQ 。
在整个运动过程中,△ 发,沿AC 方向匀速运 知P , Q 两点同时出发, 小变化情况是 ( A. 一直增大 C.先减小后增大10.(2012山东省青岛B.—直减小 D.先增大后减少23 , 10) (10分)问题提出:n 边形的n 个顶点和它内部的 寸针旋转60 °得到2).参考小伟同学思 A小伟是 旋转中心将△ ABP 逆 合.他的方法是以' '连接A A ,当AC 上时,)图2MPQ'的面图3AB o P另一种情况,点Q在图①分割成的小三角形的某条公共边上,不妨假设点Q在PA上,如图③;显然,不管哪种情况,都可把厶ABC分割成5个互不重叠的小三角形.探究三:以△ ABC的三个顶点和它内部的3个点P、Q、R,共6个点为顶点可把厶ABC分割成___________ 个互不重叠的小三角形,并在图④画出一种分割示意图④探究四:以△ ABC的三个顶点和它内部的m个点,共(m+3)个顶点可把△ ABC分割成4+2 ( m-1 )或 2m+2 n+2(m-1)或 2m+n-2把n=8,m=2012代入上述代数式, 本题考查规律型中的图形变化问题,解题关键是结合图形,探寻其规律,发现规 律才能顺利解题,体现特殊到一般的数学思想. 11.在由mx n (mx n > 1 )个小正方形组成的矩形网格中,研究它的一条对角线所穿过的小 正方形个数f ,(1 )当m 、n 互质(m 、n 除1外无其他公因数)时,观察下列图形并完成下表:猜想:当m 、n 互质时,在mx n 的矩形网格中,一条对角线所穿过的小正方形的个数f 与m 、n 的关系式是 ___________________________________ (不需要证明); 解:(2)当m 、n 不互质时,请画图验证你猜想的关系式是否依然成立, 17:解析:(1)通过题中所给网格图形,先计算出 2X 5, 3x 4,对角线所穿过的小正方形个数f ,再对照表中数值归纳 f 与m 、n 的关系式.(2)根据题意,画出当 m 、n 不互质时,结论不成立的反例即可 . 解:(1)如表:_________ 互不重叠的小三角形。
探究拓展:以四边形的 4个顶点和它内部的 成 ____________ 个互不重叠的小三角形。
问题解决:以n 边形的n 个顶点和它内部的 成 ______________ 个互不重叠的小三角形。
实际应用:以八边形的 8个顶点和它内部的 多少个互不重叠的小三角形?(要求列式计算) 23.【解析】观察图形发现:内部每多一个点, 或2m+n-2.根据根据规律逐一解答• 【答案】探究三:7 分割示意图•(答案不唯一)•m 个点,共(m+4)个顶点,可把四边形分割m 个点,共(m+n )个顶点,可把△ ABC 分割 2012个点,共2020个点,可把八边形分割成 则多2个三角形,从而得到一般规律为n+2(m-1)探究拓展 问题解决 实际应用 【点评】得 2m+n-2=2 x 2012+8-2=4024+8-2=4030. 1X2 1X3—72X5m n m+n f 1 2 3 2 1 3 4 3 23 5 424 7 357点评:本题是操作探究题,根据操作规则得出数据,并归纳总结其中规律,对于错误结论 的证明,只要举出反例即可 •12.操作与探究:4(1)对数轴上的点P 进行如下操作:先把点 P 表示的数乘以-,再把所得数对应的点3 向右平移1个单位,得到点 P 的对应点P •点A , B 在数轴上,对线段AB 上的每个点进行上述操作后得到线段A B ,其中点A ,B 的对应点分别为 A ; B •如图1,若点A 表示的数是-3,则点A 表示的数 是 ________ ;若点B 表示的数是2,则点B 表示的数是 ____________ ;已知线段AB 上 的点E 经过上述操作后得到的对应点 E •与点E 重合,则点E 表示的数是 __________ ;AB f 0]23 A~»图(2)如图2,在平面直角坐标系 xOy 中,对正方形ABCD 及其内部的每DDC*个点进行如下操作:把每个点的横、纵坐标都乘以同一种实数 a ,将得到的点先向右平移 m 个单位,再向上平移 n 个单位(m=0, n=0),得到正方形ABCD ,及其内部的点,其中点A , B "卜1丁 3F的对应点分别为 A , B '。
