【恒心】【好卷速递】山东省泰安市2012届高三第一次模拟考试_数学(理)
山东省泰安市高三理数第一次统测数学试卷

山东省泰安市高三理数第一次统测数学试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共12分)1. (1分) (2016高二上·衡水期中) 已知集合A={﹣1,0,1},B={x|x=|a﹣1|,a∈A},则A∪B中的元素的个数为()A . 2B . 4C . 6D . 82. (1分)已知是虚数单位,则满足的复数为()A .B .C .D .3. (1分)已知=(5,-3),C(-1,3),=2,则点D的坐标为()A . (11,9)B . (4,0)C . (9, 3)D . (9,-3)4. (1分)已知复数,则的最大值为()A .B .C .D . 35. (1分)具有线性相关关系的变量x、y的一组数据如表所示.若y与x0123y﹣11m6x的回归直线方程为 =3x﹣,则m的值是()A . 4B .C . 5.5D . 66. (1分) (2019高三上·双流期中) 已知实数,满足不等式组,则的最大值为()A . 3B . 9C . 22D . 257. (1分) (2018高三上·云南期末) 程序框图如图所示,若输入a的值是虚数单位i ,则输出的结果是()A .B .C . 0D .8. (1分)设,是两个非零向量,则“•<0”是“,夹角为钝角”的()A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件9. (1分)(2016·黄山模拟) 如图为三棱锥S﹣ABC的三视图,其表面积为()A . 16B . 8 +6C . 16D . 16+610. (1分)(2017·衡阳模拟) 下面是关于公差d>0的等差数列{an}的四个命题:p1:数列{an}是递增数列;p2:数列{an}的前n项和Sn是递增数列;p3:数列{ }是递增数列;p4:数列{an+nd}是递增数列.其中的真命题为()A . p1 , p2B . p3 , p4C . p2 , p3D . p1 , p411. (1分) (2018高二下·龙岩期中) 某天某校的校园卫生清扫轮到高二(5)班,该班劳动委员把班级同学分为5个劳动小组,该校共有A、B、C、D四个区域要清扫,其中A、B、C三个区域各安排一个小组,D区域安排2个小组,则不同的安排方法共有()A . 240种B . 150种C . 120种D . 60种12. (1分) (2016高三上·怀化期中) 已知一几何体的正视图、俯视图为直角三角形,侧视图为矩形,则该几何体的体积为()A . 6B . 12C . 18D . 36二、填空题 (共4题;共4分)13. (1分) (2017高二下·临淄期末) 已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)=________.14. (1分)二项式的展开式中,前三项的系数依次成等差数列,则此展开式中有理项有________项.15. (1分)小明通过英语四级测试的概率为,他连续测试3次,那么其中恰有一次获得通过的概率________16. (1分)(2017·南通模拟) 如图,在平面四边形中,为的中点,且OA=3,OC=5.若,则的值是________三、解答题 (共7题;共9分)17. (2分)如图,设长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=2,Q是AA1的中点,点P在线段B1D1上;(1)试在线段B1D1上确定点P的位置,使得异面直线QB与DP所成角为60°,并请说明你的理由;(2)在满足(1)的条件下,求四棱锥Q﹣DBB1P的体积.18. (2分)(2017·内江模拟) 某工厂为了解用电量y与气温x℃之间的关系,随机统计了5天的用电量与当天气温,得到如下统计表:8月18日8月25日曰期8月1曰8月7日8月14日平均气温(℃)3330323025用电量(万度)3835413630xiyi=5446, xi2=4538, = , = ﹣(1)请根据表中的数据,求出y关于x的线性回归方程.据气象預报9月3日的平均气温是23℃,请预测9月3日的用电量;(结果保留整数)(2)请从表中任选两天,记用电量(万度)超过35的天数为ξ,求ξ的概率分布列,并求其数学期望和方差.19. (1分) (2016高一下·新化期中) 如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC= ,O,M分别为AB,VA的中点.(1)求证:VB∥平面MOC;(2)求证:平面MOC⊥平面VAB(3)求三棱锥V﹣ABC的体积.20. (1分)(2017·广西模拟) 某校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题获得学分2分,便可通过考察.已知6道备选题中考生甲有4题能正确完成:考生乙每题正确完成的概率都是,且每题正确完成与否互不影响.求:(Ⅰ)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;(Ⅱ)请你判断两考生的实验操作学科能力,比较他们能通过本次考查的可能性大小.21. (1分) (2019高三上·吉林月考) 如图,三棱柱的侧棱垂直于底面,且,,,,是棱的中点.(1)证明:;(2)求二面角的余弦值.22. (1分)将圆x2+y2=1 每一点的,横坐标保持不变,纵坐标变为原来的2倍,得到曲线C.(1)写出C的参数方程;(2)设直线l:2x+y-2=0 与C的交点为P1,P2 ,以坐标原点为极点, x 轴的正半轴为极轴建立极坐标系,求线段 P1P2 的中点且与 l 垂直的直线的极坐标方程.23. (1分)(2018·南充模拟) 选修4-5:不等式选讲已知函数 .(Ⅰ)解不等式;(Ⅱ)若,且,证明: .参考答案一、单选题 (共12题;共12分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题;共9分) 17-1、17-2、18-1、18-2、19-1、19-2、19-3、21-1、21-2、22-1、22-2、23-1、。
【恒心】【好卷速递】山东省日照市2012届高三第一次模拟考试试题_数学理

绝密★启用前 试卷类型:A山东省日照市2012届高三第一次模拟考试理 科 数 学2012.03本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
第I 卷1至2页,第II 卷3至4页。
满分150分。
考试用时120分钟。
考试结束后,将本试卷和答题卡一并交回。
第I 卷(共60分)注意事项:1、答第I 卷前,考生务必用0.5毫米黑色签字笔将姓名、座号、准考证号填写在答题卡和试卷规定的位置。
2、第I 卷共2页。
答题时,考生须用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案。
在试卷上作答无效。
参考公式:圆柱的侧面公式:,2Rl s π=圆锥侧面其中R 为圆柱的底面半径,l 为圆柱的母线。
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合{}}{Z n n x x N x x M ∈+==<-=,12,042,则集合N M ⋂等于( )(A ){-1,1} (B ){-1,0,1} (C ){0,1} (D ){-1,0} (2)某学校有教师150人,其中高级教师15人,中级教师45人,初级教师90人,现按职称分层抽样选出30名教师参加教职工代表大会,则选出的高、中、初级教师人数分别为 (A )3,9,18 (B )5,10,15 (C )3,10,17 (D )5,9,16 (3)已知定义在复数信C 上的函数)(x f 满足{)1( )(1 )1(i fx f Rx x R x x i +=∈+∉-则等于(A )2+i (B )-2 (C )0 (D )2 (4)已知数列{}n a 为等差数列,且a 1=2,a 2+a 3=13,那么a 4+a 5+a 6等于 (A )40 (B )42 (C )43 (D )45 (5)如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置可能性相等),恰有40粒落入半径为1的圆 内,则该多边形的面积约为(A )4π (B )5π(C )6π (D )7π (6)函数xx og y 21=的图象大致是(7)已知程序框图如右,则输出的=i (A )7(B )8 (C )9 (D )10 (8)设y a 、、β为平面,m 、n 、l 为直线, 则β⊥m 的一个充分条件是(A )l m a a ⊥=⋂⊥,1,ββ (B )y y a m y a ⊥⊥=⋂β,, (C )a m y r a ⊥⊥⊥,,β (D )a m n a n ⊥⊥⊥,,β(9)已知点p(x,y)的坐标满足条件⎪⎩⎪⎨⎧≥+-≥≥032,,1y x x y x 那么点P 到直线3x-4y-9=0的距离的最小值为 (A )514 (B )56 (C )2 (D )1(10)若(113)2(x x +的二项展开式中有n 个有理项,则=⎰dx x n1(A )31 (B )21 (C )1 (D )2(11)已知又曲线12222=-by ax (a>0,b>0)的离心率为2,一个焦点与抛物线y 2=16x 的焦点相同,则双曲线的渐近线方程为 (A )y=±x 23 (B)y=±x 23 (C)y=±x 33 (D)y=±x 3(12)已知定义在R 上奇函数)(x f 满足①对任意x ,都有)()3(x f x f =+成立;②当]23,0[∈x 时x x f 22323)(--=,则xx f 1)(=在[-4,4]上根的个数是(A )4 (B )5 (C )6 (D )7第II 卷(共90分)注意事项:第II 卷共2页。
山东省泰安市高三理综第一次高考模拟(泰安一模)

山东省泰安市2012届高三第一次模拟考试理科综合试题2012.03 本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共16页,满分240分,考生用时150分钟。
考试结束后,将本试卷、答题卡和答题纸一并交回。
答卷前,考生务必将自己的姓名、准考证号、考试科目填涂在答题卡和答题纸规定的地方。
第I卷(必做题,共87分)注意事项:1.每小题选出答案后,用2B铅笔把答题卡上对应的答案标号涂黑,如需改动,用橡皮擦干净以后,再涂写其他答案标号。
不涂答题卡,只答在试卷上不得分。
2.第I卷共20小题,1~13题,每小题4分;14~20题,每小题5分,共87分。
可能用到的相对原子质量:H l C 12 N 14 O 16 Na 23 Fe 56 Cu 64 Ba 137一、选择题(本题包括1 3小题。
每小题只有一个选项符合题意)1.端粒存在于真核生物染色体的末端,是由DNA序列及其相关的蛋白质所组成的复合体。
端粒酶是一种逆转录酶,由蛋白质和RNA构成。
由此可知,属于核膜、端粒和端粒酶共同点的是A.都存在于所有生物细胞中 B.都含有C、H、O、N、P等化学元素C.都与遗传信息的传递无关 D.都含有遗传物质2.右图是物质进出细胞方式的概念图。
下列分析正确的是A.①方式表示协助扩散B.⑤、⑥两种方式的共同特点是都需要载体C.③、④两种方式都与细胞膜的流动性有关D.质壁分离实验中蔗糖进入细胞的方式为④3.下列关于植物激素的说法正确的是A.单侧光照使植物弯曲生长时,背光侧生长素浓度比向光侧低B.探究不同浓度生长素类似物对插条生根影响时.应选不同种的植物材料C.用赤霉素多次喷洒水稻植株后,将导致产量降低D.种子在浸泡过程中,用适量的乙烯处理可解除休眠而萌发4.动物细胞中的一类基因是维持基本生命活动的。
在各种细胞中都处于活动状态。
另一类基因是选择性表达的基因。
右图是能产生A抗体的细胞。
关于该细胞中三个基因的开闭状态,下列说法正确的是A.其中有一个处于活动状态。
山东省泰安市2012届高三第二次模拟考试数学(理)试题

山东省泰安市2012届高三第二次模拟考试数学试题(理)2012.5一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.对于实数a 、b 、c ,“a >b ”是“2ac >2bc ”的 A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.已知复数z 满足()i i z -=+11(i 为虚数单位),则z 等于A.iB.i -C.i -2D.i +23.某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了解该单位职工的健康情况,用分层抽样的方法从中抽取样本,若样本中的青年职工为7人,则样本容量为 A.35 B.25 C.15 D.74.下列命题中的真命题是 A.23cos sin ,=+∈∃x x R x B.()x x sin ,,0π∈∀>x cos C.()x x 2,0,∞-∈∃<x3D.()x e x ,,0+∞∈∀>1+x5.对于平面α和直线m 、n ,下列命题是真命题的是 A.若n m ,与α所成的角相等,则m//n B.若,//,//ααn m 则m//n C.若n m m ⊥⊥,α,则α//nD. 若αα⊥⊥n m ,,则n m // 6. 如图给出的是计算20121614121+⋅⋅⋅+++的值的程序框图,其中判断框内应填入的是 A.2012≤iB.i >2012C.1006≤iD.i >10067.若点()n m ,在直线01034=-+y x 上,则22n m +的最小值是A.2B.22C.4D. 328.如图曲线2x y =和直线41,1,0===y x x 所围成的图形(阴影部分)的面积为A.32 B.31 C.21 D.41 9.在ABC ∆中,60=∠BAC °,,E,F ,AC AB 12==为边BC 的三等分点,则⋅等于A.35 B.45 C.910D.815 10.用数字0,1,2,3,4,5可以组成没有重复数字,并且比20000大的五位偶数共有 A.288个 B.240个 [来源:学科网ZXXK] C.144个 D.126个 11.已知A ,B ,C ,D ,E 是函数()ϕω+=x y sin (ω>0,0<ϕ<⎪⎭⎫2π一个周期内的图像上的五个点,如图所示,⎪⎭⎫⎝⎛-0,6πA ,B 为y 轴上的点,C 为图像上的最低点,E 为该函数图像的一个对称中心,B 与D 关于点E 对称,CD 在x 轴上的投影为12π,则ϕω,的值为[来源:] A.6,2πϕω== B.3,2πϕω==C.3,21πϕω==D.12,21πϕω==12.已知()x x f x3log 21-⎪⎭⎫⎝⎛=,实数a 、b 、c 满足()()()c f b f a f <0,且0<a <b <c ,若实数0x 是函数()x f 的一个零点,那么下列不等式中,不可能...成立的是 A.0x <aB.0x >bC.0x <cD.0x >c[来源:学.科.网Z.X.X.K]二、填空题:本大题共4个小题,每小题4分,共16分.请把答案填在答题纸的相应位置. 13.设()x f 是周期为2的奇函数,当10≤≤x 时,()()x x x f -=12,则=⎪⎭⎫⎝⎛-25f ▲ . 14.在三棱柱ABC-A 1B 1C 1中,各侧面均为正方形,侧面AA 1C 1C 的对角线相交于点A ,则BM 与平面AA 1C 1C 所成角的大小是 ▲ .15.已知实数y x ,满足不等式组⎪⎩⎪⎨⎧≥≤+≤,0,2,y y x x y 那么目标函数y x z 3+=的最大值是 ▲ .16.给出下列四个命题:①若直线l 过抛物线22x y =的焦点,且与这条抛物线交于A 、B两点,则AB 的最小值为2;②双曲线1916:22-=-y x C 的离心率为35;③若⊙,02:221=++x y x C ⊙012:222=-++y y x C ,则这两圆恰有2条公切线;④若直线06:21=+-y x a l 与直线()0934:2=+--y a x l 互相垂直,则.1-=a 其中正确命题的序号是 ▲ .(把你认为正确命题的序号都填上)三、解答题:本大题共6个小题,满分74分.解答应写出必要的文字说明、证明过程或演算步骤.请将解答过程写在答题纸的相应位置. 17.(本小题满分12分)已知等差数列{}n a 的公差0≠d ,它的前n 项和为n S ,若,355=S 且2272,,a a a 成等比数列.(I )求数列{}n a 的通项公式;(II )设数列⎭⎬⎫⎩⎨⎧n S 1的前n 项和为T n ,求T n .[来源:]18.(本小题满分12分)已知函数().2sin 22cos 2sin 22x x x x f -⎪⎭⎫ ⎝⎛+=(I )若()332=x f ,求sin2x 的值; (II )求函数()()()()x f x f x f x F 2+-⋅=的最大值与单调递增区间. [来源:学科网ZXXK] 19.(本小题满分12分)如图,四棱锥P —ABCD 中,底面ABCD 为矩形,PA ⊥平面ABCD ,1,2===AD AB PA ,点E 是棱PB 的中点.(I )求证:平面ECD ⊥平面PAD ;(II )求二面角A —EC —D 的平面角的余弦值.20.(本小题满分12分)形状如图所示的三个游戏盘中(图(1)是正方形,M 、N 分别是所在边中点,图(2)是半径分别为2和4的两个同心圆,O 为圆心,图(3)是正六边形,点P 为其中心)各有一个玻璃小球,依次水平摇动三个游戏盘,当小球静止后,就完成了一局游戏。
山东省泰安一模数学试题及答案(理)

山东省泰安一模数学试题及答案(理) 高三第一轮复质量检测数学试题(理科)第I卷一、选择题:本大题共12小题,每小题5分。
共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={-10.-9.…。
2},集合B={y | y=2x-3.x∈A},则A∩B等于()。
A。
{-10.-9.…。
-1}B。
{-1}C。
{-1.0 (2)D。
{0 (2)2.若(1-2i)z=5i,则z的值为()。
A。
3B。
5C。
3+2iD。
5+2i3.在各项均为正数的等比数列{an}中,a6=3,则a4+a8()。
A。
有最小值6B。
有最大值6C。
有最大值9D。
有最小值34.下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x与相应的生产能耗y的几组对应数据:x | 1 | 2 | 3 | 4 | 5 |y | 18.5 | 28.9 | 38.3 | 47.7 | 57.1 |根据上表可得回归方程y=9.4x+9.1,则表中m的值为()。
A。
27.9B。
25.5C。
26.9D。
265.阅读右侧程序框图,运行相应程序,则输出i的值为()。
i = 0while i < 5:if i % 3 == 0:i += 2elif i % 3 == 1:i += 3else:i += 1print(i)A。
3B。
4C。
5D。
66.将函数f(x)=sin(2x+π/3)的图像向右平移π/6个单位,得到函数g(x)的图像,则下列说法不正确的是()。
A。
g(x)的周期为πB。
g(π/3)=f(0)C。
x=π/6是g(x)的一条对称轴D。
g(x)为奇函数7.以F(0.2√2)为焦点的抛物线C的准线与双曲线x-y=2相交于M、N两点,若△MNF为正三角形,则抛物线C的标准方程为()。
A。
y2=26xB。
y2=46xC。
x2=46yD。
x2=26y8.a=∫2(-cosx)dx,则ax+2ax2的展开式中项的系数为()。
【恒心】【好卷速递】2012年高三模拟理综【3月好题】【教师专版】
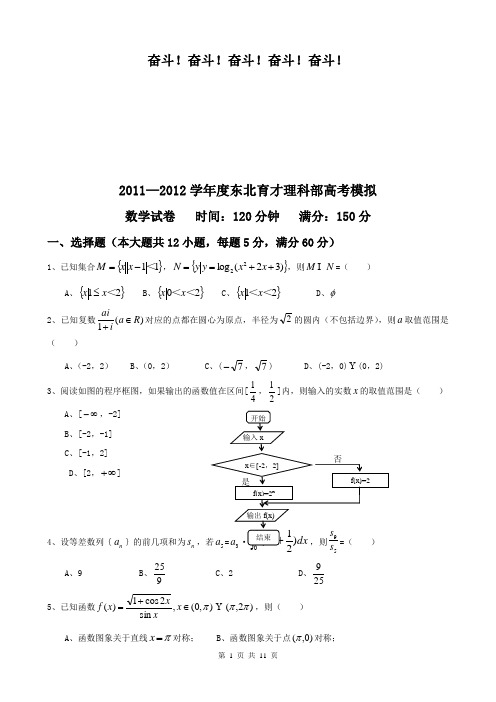
奋斗!奋斗!奋斗!奋斗!奋斗!2011—2012学年度东北育才理科部高考模拟数学试卷 时间:120分钟 满分:150分一、选择题(本大题共12小题,每题5分,满分60分)1、已知集合{}11<-=x x M ,{})32(log 22++==x x y y N ,则N M =( ) A 、{}21<x x ≤ B 、{}20<<x x C 、{}21<<x x D 、φ 2、已知复数)(1R a iai∈+对应的点都在圆心为原点,半径为2的圆内(不包括边界),则a 取值范围是( )A 、(-2,2)B 、(0,2)C 、(7-,7)D 、(-2,0) (0,2) 3、阅读如图的程序框图,如果输出的函数值在区间[41,21]内,则输入的实数x 的取值范围是( ) A 、[∞-,-2] B 、[-2,-1] C 、[-1,2] D 、[2,∞+]4、设等差数列{n a }的前几项和为n s ,若5a =3a ·⎰+2)212(dx x,则59s s =( )A 、9B 、925 C 、2 D 、2595、已知函数),0(,sin 2cos 1)(π∈+=x xxx f )2,(ππ,则( )A 、函数图象关于直线π=x 对称;B 、函数图象关于点)0,(π对称;是OCOB OA )21()1()1(λλλ++-+-OCOB OA )21()1()1(λλλ++-+-开始x ∈[-2,2]f(x)=2x结束 f(x)=2输入x输出f(x) 否OC OB OA )21()1()1(λλλ++-+-OCOB OA )21()1()1(λλλ++-+-C 、函数在区间),2(ππ上递减; D 、函数在区间)23,(ππ上递减。
6、给出下列命题:①“R x ∈∃,使x 2>3”的否定是“R x ∈∀,使人x2≤3”; ②函数)26sin()32sin(x x y -+=ππ的最小正周期是π;③命题“函数)(x f 在0x x =处有极值,则0)(0='x f ”的否命题是真命题;④已知函数)(x f '是函数)(x f 在R 上的导函数,若)(x f 是偶函数,则)(x f '是奇函数。
【恒心】【好卷速递】山东省泰安市2012届高三第一次模拟考试_数学(文)
泰安市高三第一轮复习质量检测数 学 试 题(文)2012.03一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若a 、b 为实数,则“a b <1”是“0<a <b1”的 A.充分而不必要条件B.必要而不充分条件C.充分条件D.既不充分也不必要条件2.已知i 是虚数单位,则ii+-221等于 A.i -B.i -54C.i 5354-D.i3.过点A (2,3)且垂直于直线052=-+y x 的直线方程为 A.042=+-y x B.072=-+y x ] C.032=+-y xD.052=+-y x4.设{}{}R x y y Q R x x y y P x∈==∈+-==,2,,12,则 A.Q P ⊆B.P Q ⊆C.Q P C R ⊆D.P C Q R ⊆5.已知向量()()k ,1,1,2-==,若()-⊥2,则k 等于 A.6B.—6C.12D.—126.函数x y 2log =的图象大致是7.设偶函数()x f 满足()()042≥-=x x x f ,则不等式()2-x f >0的解集为 A.{x x <2-或x >}4 B.{x x <0或x >}4 C.{x x <0或x >}6D.{x x <2-或x >}28.下列说法:①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;②设有一个回归方程x y53ˆ-=,变量x 增加一个单位时,y 平均增加5个单位; ③线性回归方程a x b yˆˆˆ+=必过()y x ,; ④在一个22⨯列联表中,由计算得K 2=13.079,则有99%的把握确认这两个变量间有关系;其中错误..的个数是 A.0 B.1 C.2 D.39已知βα,是两平面,n m ,是两直线,则下列命题中不正确...的是 A.若,m n m α⊥,//则α⊥mB.若,,βα⊥⊥m m 则βα//C.若,α⊥m 直线m 在面β内,则βα⊥D. 若n m =⋂βαα,//,则n m //10.执行如图所示的程序框图,输出的S 值为A.3B.—6C.10D.15-11.在面积为S 的矩形ABCD 内随机取一点P ,则PBC ∆的面积小于4S的概率是 A.61 B.41 C.31D.21 12.函数()(a x y a 13log -+=>0,且)1≠a 的图象恒过定点A ,若点A 在直线01=++ny mx 上(其中m ,n >0),则nm 21+的最小值等于 A.16 B.12 C.9 D. 8二、填空题:本大题共4个小题,每小题4分,共16分.请把答案填在答题纸的相应位置.13.等比数列{}n a 中,已知1,214321=+=+a a a a ,则87a a +的值为 ▲ .14.一个棱锥的三视图如图所示,则这个棱锥的体积为 ▲ .15.函数()()ϕω+=x A x f sin (ϕω,,A 为常数,A >0,ω>0)的部分图象如图所示,则⎪⎭⎫⎝⎛6πf 的值是 ▲ . 16.F 1、F 2为双曲线C :12222=-by a x (a >0,b >0)的焦点,A 、B 分别为双曲线的左、右顶点,以F 1F 2为直径的圆与双曲线的渐近线在第一象限的交点为M ,且满足∠MAB=30°,则该双曲线的离心率为 ▲ .找家教,可以找柯南东升,可以关注824135830空间,更多精彩请加821435830三、解答题:本大题共6个小题满分74分.解答应写出必要的文字说明、证明过程或演算步骤.请将解答过程写在答题纸的相应位置. 17.(本小题满分12分)已知数列{}n a 是等差数列,满足.13,542==a a 数列{}n b 的前n 项和是T n ,且.3=+n n b T (1)求数列{}n a 及数列{}n b 的通项公式; (II )若n n n b a c ⋅=,试比较n c 与1+n c 的大小.18.(本小题满分12分)在△ABC 中,角A 、B 、C 所对应的边分别为a 、b 、c ,且满足.cos cos cos 2B c C b B a += (I )求角B 的大小;(II )求函数()⎪⎭⎫ ⎝⎛+-⎪⎭⎫⎝⎛+=62cos 4sin 22ππA A A f 的最大值及取得最大值时的A 值.19.(本小题满分12分)在三棱锥P —ABC 中,PB ⊥平面ABC ,AB ⊥BC ,AB=PB=2,BC=23,E 、G 分别为PC 、PA 的中点.(I )求证:平面BCG ⊥平面PAC ;(II )在线段AC 上是否存在一点N ,使PN ⊥BE ?证明你的结论.20.(本小题满分12分)为了增强学生的环境意识,某中学随机抽取了50名学生举行了一次环保知识竞赛,本次竞赛的成绩(得分均为整数,满分100分)整理,制成下表:(II )若从成绩在[)50,40中选一名学生,从成绩在[)100,90中选出2名学生,共3名学生召开座谈会,求[)50,40组中学生A 1和[)100,90组中学生B 1同时被选中的概率?21.(本小题满分12分)已知函数()().ln 122x a x a x x f ++-=(I )当2=a 时,求曲线()x f y =在点()()1,1f 处的切线方程; (II )求函数()x f 的单调区间.22.(本小题满分14分)已知椭圆12222=+by a x (a >b >0)与抛物线x y 42=有共同的焦点F ,且两曲线在第一象限的交点为M ,满足.35=MF (I )求椭圆的方程;(II )过点P (0,1)的直线l 与椭圆交于A 、B 两点,满足25-=⋅,求直线l 的方程. 找家教,可以找柯南东升,可以关注824135830空间,更多精彩请加821435830。
山东省泰安市高三一模(数学理)(word版)
泰安市高三第一轮复习质量检测数 学 试 题(理科)一、选择题:本大题共12个小题。
每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若复数2()1aia i+∈-R 是纯虚数(i 是虚数单位),则a 的值为 A .2- B .1- C .1 D .22.已知a b c 、、均为实数,则""a b >是22""ac bc >成立的 A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分又不必要条件3.已知双曲线22221x y a b-=的一条渐近线方程为43y x =,则双曲线的离心率为A .53 BC .54D4.若右面的程序框图输出的S 是126,则①应为 A .5?n ≤ B .6?n ≤ C .7?n ≤ D .8?n ≤5.如图,设D 是图中边长为4的正方形区域,E 是D 内函数2y x = 图象下方的点构成的区域。
在D 中随机取一点,则该点在E 中的 概率为 A .15B .14C .13D .126.在ABC ∆中,a b c 、、分别是三内角A B C 、、的对边,且22sin sin (sin sin )sin A C A B B -=-,则角C 等于A .6π B .3π C .56π D .23π 7.定义在R 上的函数(1)y f x =+的图像如图所示,它在定义域上 是减函数,给出如下命题:①(0)1f =;②(1)1f -=;③若0x >,则()0f x <;④若0x <,则()1f x >。
其中正确的命题是A .②③B .①④C .②④D .①③8.如图,在棱长均为1的三棱锥S ABC -中,E 为棱SA 的中点,F 为ABC ∆的中心,则直线EF 与平面ABC 所成角的正切值是 A.B .1CD.29.定义在R 上的函数()f x 满足()()()2(,),(1)2,f x y f x f y xy x y f +=++∈=R 则(2)f -等于 A .2B .3C .6D .910.已知非零向量,a b 满足:2=||||a b ,若函数3211()32f x x x x =++⋅||a a b 在R 上有极值,设向量,a b 的夹角为θ,则cos θ的取值范围为 A .[1[,1]2B .1(,1]2C .1[1,]2- D .1[1,)2-11.如果直线1y kx =+与圆2240x y kx my +++-=交于M N 、两点,且M N 、关于直线0x y +=对称,则不等式组 10,0,0,kx y kx my y -+≥-≤≥表示的平面区域的面积是A .14B .12C .1D .212.某钢厂的年产量由1990年的40万吨增加到2000年的50万吨,如果按照这样的年增长率计算,则该钢厂2010年的年产量约为A .60万吨B .61万吨C .63万吨D .64万吨二、填空题:本大题共4个小题,每小题4分,共16分。
山东省泰安市高三数学第一次高考模拟 理(泰安一模)
山东省泰安市2012届高三第一次模拟考试数 学 试 题(理)2012.03一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若a 、b 为实数,则“a b <1”是“0<a <b1”的 A.充分而不必要条件 B.必要而不充分条件 C.充分条件D.既不充分也不必要条件2.已知i 是虚数单位,则i i+-221等于 A.i -B.iC.i 5354- D.i -54 3.过点A (2,3)且垂直于直线052=-+y x 的直线方程为 A.042=+-y x B.072=-+y x ] C.032=+-y xD.052=+-y x4.设{}{}R x y y Q R x x y y P x∈==∈+-==,2,,12,则 A.Q P ⊆B.P Q ⊆C.Q P C R ⊆D.P C Q R ⊆5.+=≠=,0,且⊥,则向量与的夹角为 A.30° B.60°C.120°D.150°6.函数x xy cos 1⋅=在坐标原点附近的图象可能是7.设偶函数()x f 满足()()042≥-=x x x f ,则不等式()2-x f >0的解集为 A.{x x <2-或x >}4B.{x x <0或x >}4C.{x x <0或x >}6D.{x x <2-或x >}28.下列说法:①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;②设有一个回归方程x y53ˆ-=,变量x 增加一个单位时,y 平均增加5个单位; ③线性回归方程a x b yˆˆˆ+=必过()y x ,; ④在一个22⨯列联表中,由计算得K 2=13.079,则有99%的把握确认这两个变量间有关系;其中错误..的个数是 A.0 B.1 C.2 D.39.正方体ABCD —A 1B 1C 1D 1中,CC 1与面BDA 1所成角的余弦值是A.32 B.33 C.32 D.36 10.执行如图所示的程序框图,输出的S 值为 A.3 B.—6 C.10 D.15-11.已知(){}1,1,≤≤=Ωy x y x ,A 是曲线2x y =与21x y =围成的区域,若向区域Ω上随机投一点P ,则点P 落入区域A 的概率为 A.31 B.41 C.81 D.121 12.函数()(a x y a 13l o g -+=>0,且)1≠a 的图象恒过定点A ,若点A 在直线01=++ny mx 上(其中m ,n >0),则nm 21+的最小值等于 A.16 B.12 C.9 D. 8二、填空题:本大题共4个小题,每小题4分,共16分.请把答案填在答题纸的相应位置.13.431⎪⎭⎫ ⎝⎛-x x 展开式中常数为 ▲ .14.一个棱锥的三视图如图所示,则这个棱锥的体积为▲ .15.函数()()ϕω+=x A x f sin (ϕω,,A 为常数,A >0,ω>0)的部分图象如图所示,则⎪⎭⎫⎝⎛6πf 的值是 ▲ . 16.F 1、F 2为双曲线C :12222=-by a x (a >0,b >0)的焦点,A 、B 分别为双曲线的左、右顶点,以F 1F 2为直径的圆与双曲线的渐近线在第一象限的交点为M ,且满足∠MAB=30°,则该双曲线的离心率为 ▲ .三、解答题:本大题共6个小题满分74分.解答应写出必要的文字说明、证明过程或演算步骤.请将解答过程写在答题纸的相应位置. 17.(本小题满分12分)已知数列{}n a 是等差数列,满足.13,542==a a 数列{}n b 的前n 项和是T n ,且.3=+n n b T (1)求数列{}n a 及数列{}n b 的通项公式; (II )若n n n b a c ⋅=,试比较n c 与1+n c 的大小.18.(本小题满分12分)在△ABC 中,角A 、B 、C 所对应的边分别为a 、b 、c ,且满足.cos cos cos 2B c C b B a += (I )求角B 的大小;(II )求函数()⎪⎭⎫ ⎝⎛+-⎪⎭⎫⎝⎛+=62cos 4sin 22ππA A A f 的最大值及取得最大值时的A 值.19.(本小题满分12分)在三棱锥P —ABC 中,PB ⊥平面ABC ,AB ⊥BC ,AB=PB=2,BC=23,E 、F 、G 分别为PC 、AC 、PA 的中点. (I )求证:平面BCG ⊥平面PAC ;(II )在线段AC 上是否存在一点N ,使PN ⊥BE ?证明你的结论. 20.(本小题满分12分)为缓解某路段交通压力,计划将该路段实施“交通银行”.在该路段随机抽查了50人,了解公众对“该路段限行”的态度,将调查情况进行整理,制成下表:(I )作出被调查人员年龄的频率分布直方图;(II )若从年龄在[)[)35,25,25,15的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“交通银行”的人数为ξ,求随机变量ξ的分布列和数学期望.21.(本小题满分12分)已知椭圆12222=+by a x (a >b >0)与抛物线x y 42=有共同的焦点F ,且两曲线在第一象限的交点为M ,满足.35=MF (I )求椭圆的方程;(II )过点P (0,1)的直线l 与椭圆交于A 、B 两点,满足25-=⋅PB PA ,求直线l 的方程.22.(本小题满分14分)已知函数()().ln 122x a x a x x f ++-=(I )当2=a 时,求曲线()x f y =在点()()1,1f 处的切线方程; (II )求函数()x f 的单调区间;(III )若对任意()2,3--∈a 及[]3,1∈x 时,恒有()x f ma -<1成立,求实数m 的取值范围.。
考点26 线线、线面、面面的位置关系(教师版) 新课标
2013年新课标数学40个考点总动员考点26 线线、线面、面面的位置关系(教师版)【高考再现】热点一平行关系1.(2012年高考四川卷理科6)下列命题正确的是()A、若两条直线和同一个平面所成的角相等,则这两条直线平行B、若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C、若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D、若两个平面都垂直于第三个平面,则这两个平面平行2. (2012年高考山东卷文科19) (本小题满分12分)如图,几何体E ABCD-是四棱锥,△ABD为正三角形,CB CD EC BD=⊥.,(Ⅰ)求证:BE DE=;(Ⅱ)若∠120BCD=︒,M为线段AE的中点,求证:DM∥平面BEC.【方法总结】1.证明线线平行的方法:(1)平行公理;(2)线面平行的性质定理;(3)面面平行的性质定理;(4)向量平行.要注意线面、面面平行的性质定理的成立条件.2.线面平行的证明方法:(1)线面平行的定义;(2)线面平行的判断定理;(3)面面平行的性质定理;(4)向量法:证明这条直线的方向向量和这个平面内的一个向量互相平行;证明这个直线的方向向量和这个平面的法向量相互垂直.线面平行的证明思考途径:线线平行⇔线面平行⇔面面平行.3.面面平行的证明方法:①反证法:假设两个平面不平行,则它们必相交,在导出矛盾;②面面平行的判断定理;③利用性质:垂直于同一直线的两个平面平行;平行于同一平面的两个平面平行;④向量法:证明两个平面的法向量平行. 热点二 垂直关系3.(2012年高考浙江卷理科10)已知矩形ABCD ,AB =1,BC 将∆ABD 沿矩形的对角线BD 所在的直线进行翻着,在翻着过程中,( )A .存在某个位置,使得直线AC 与直线BD 垂直B .存在某个位置,使得直线AB 与直线CD 垂直C .存在某个位置,使得直线AD 与直线BC 垂直D .对任意位置,三直线“AC 与BD ”,“AB 与CD ”,“AD 与BC ”均不垂直4.(2012年高考安徽卷理科6)设平面α与平面β相交于直线m ,直线a 在平面α内,直线b 在平面β内,且b m ⊥,则“αβ⊥”是“a b ⊥”的( )()A充分不必要条件()B必要不充分条件D即不充分不必要条件()C充要条件()5.(2012年高考北京卷文科16)(本小题共14分)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
泰安市高三第一轮复习质量检测
数 学 试 题(理)
2012.03
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若a 、b 为实数,则“a b <1”是“0<a <b
1”的
A.充分而不必要条件
B.必要而不充分条件
C.充分条件
D.既不充分也不必要条件
2.已知i 是虚数单位,则i i +-221等于
A.i -
B.i
C.i 5354-
D.
i -5
4
3.过点A (2,3)且垂直于直线052=-+y x 的直线方程为 A.042=+-y x B.072=-+y x ] C.032=+-y x
D.052=+-y x
4.设{}{}R x y y Q R x x y y P x
∈==∈+-==,2,,12
,则 A.Q P ⊆
B.P Q ⊆
C.Q P C R ⊆
D.P C Q R ⊆
5.若b a c +=≠=,0,且a c ⊥,则向量a 与b 的夹角为 A.30° B.60° C.120° D.150°
6.函数x x
y cos 1⋅=
在坐标原点附近的图象可能是
7.设偶函数()x f 满足()()042≥-=x x x f ,则不等式()2-x f >0的解集为 A.{x x <2-或x >}4 B.{x x <0或x >}4 C.{x x <0或x >}6
D.{x x <2-或x >}2
8.下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程x y 53ˆ-=,变量x 增加一个单位时,y 平均增加5个单位;
③线性回归方程a x b y
ˆˆˆ+=必过()y x ,; ④在一个22⨯列联表中,由计算得K 2=13.079,则有99%的把握确认这两个变量间有关系;其中错误..的个数是 A.0 B.1 C.2 D.3 本题可以参考独立性检验临界值表
9.正方体ABCD —A 1B 1C 1D 1中,CC 1与面BDA 1所成角的余弦值是
A.
3
2 B.
3
3 C.
3
2 D.
3
6
10.执行如图所示的程序框图,输出的S 值为 A.3
B.—6
C.10
D.15-
11.已知(){}1,1,≤≤=Ωy x y x ,A 是曲线2
x
y =与21
x y =围
成的区域,若向区域Ω上随机投一点P ,则点P 落入区域A 的
概率为 A.
3
1 B.
4
1 C.8
1 D.12
1
12.函数()(a x y a 13lo g -+=>0,且)1≠a 的图象恒过定点A ,若点A 在直线01=++ny mx 上(其中m ,n >0)
,则n
m 21+的最小值等于
A.16
B.12
C.9
D. 8
二、填空题:本大题共4个小题,每小题4分,共16分.请把答案填在答题纸的相应位置.
13.4
31⎪⎭⎫
⎝
⎛-x x 展开式中常数为 ▲ .
14.一个棱锥的三视图如图所示,则这个棱锥的体积为
▲ .
15.函数()()ϕω+=x A x f sin (ϕω,,A 为常数,A >0,ω
>0)的部分图象如图所示,则⎪⎭
⎫
⎝⎛6πf 的值是 ▲ . 16.F 1、F 2为双曲线C :
12
22
2=-
b
y a
x (a >0,b >0)的焦点,A 、B 分别为双曲线的左、右
顶点,以F 1F 2为直径的圆与双曲线的渐近线在第一象限的交点为M ,且满足∠MAB=30°,则该双曲线的离心率为 ▲ .
找家教,可以找柯南东升,可以关注824135830空间,更多精彩请加821435830
三、解答题:本大题共6个小题满分74分.解答应写出必要的文字说明、证明过程或演算步骤.请将解答过程写在答题纸的相应位置. 17.(本小题满分12分)
已知数列{}n a 是等差数列,满足.13,542==a a 数列{}n b 的前n 项和是T n ,且.3=+n n b T (1)求数列{}n a 及数列{}n b 的通项公式; (II )若n n n b a c ⋅=,试比较n c 与1+n c 的大小.
18.(本小题满分12分)
在△ABC 中,角A 、B 、C 所对应的边分别为a 、b 、c ,且满足.cos cos cos 2B c C b B a += (I )求角B 的大小;
(II )求函数()⎪⎭⎫ ⎝
⎛
+-⎪⎭⎫
⎝⎛
+
=62cos 4sin 22ππA A A f 的最大值及取得最大值时的A 值.
19.(本小题满分12分)
在三棱锥P —ABC 中,PB ⊥平面ABC ,AB ⊥BC ,AB=PB=2,BC=23,E 、F 、G 分别为PC 、AC 、PA 的中点. (I )求证:平面BCG ⊥平面PAC ;
(II )在线段AC 上是否存在一点N ,使PN ⊥BE ?证明你的结论. 20.(本小题满分12分)
为缓解某路段交通压力,计划将该路段实施“交通银行”.在该路段
随机抽查了50人,了解公众对“该路段限行”的态度,将调查情况进行整理,制成下表:
(I )作出被调查人员年龄的频率分布直方图;
(II )若从年龄在[)[)35,25,25,15的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“交通银行”的人数为ξ,求随机变量ξ的分布列和数学期望.
21.(本小题满分12分) 已知椭圆
12
22
2=+
b
y a
x (a >b >0)与抛物线x y 42
=有共同的焦点F ,且两曲线在第一象
限的交点为M ,满足.3
5=MF
(I )求椭圆的方程;
(II )过点P (0,1)的直线l 与椭圆交于A 、B 两点,满足2
5-=⋅PB PA ,求直线l 的方程.
22.(本小题满分14分)
已知函数()().ln 122
x a x a x x f ++-=
(I )当2=a 时,求曲线()x f y =在点()()1,1f 处的切线方程; (II )求函数()x f 的单调区间;
(III )若对任意()2,3--∈a 及[]3,1∈x 时,恒有()x f ma -<1成立,求实数m 的取值范围.
找家教,可以找柯南东升,可以关注824135830空间,更多精彩请加821435830。
