广义相对论之6v3_测地线方程与联络的计算
爱因斯坦的测地线方程

爱因斯坦的测地线方程全文共四篇示例,供读者参考第一篇示例:爱因斯坦的测地线方程是广义相对论的一个重要概念,它描述了时空中物质粒子运动的轨迹。
爱因斯坦在其相对论理论中提出了测地线方程,并通过这一方程推导出了引力场方程,从而揭示了引力的本质。
测地线,又称为测地曲线,是时空中物体或光线运动的轨迹。
在经典物理学中,测地线通常指的是在弱引力场下的运动轨迹。
在相对论物理学中,受到引力场影响的测地线通常指的是在强引力场下的运动轨迹,这个运动轨迹是由时空的几何性质决定的。
爱因斯坦在他的相对论中提出了一个重要的概念,即质量(或能量)引起了时空的弯曲。
这种弯曲导致了物体在重力场中运动时所遵循的轨迹,在数学上可以用测地线方程来描述。
爱因斯坦的测地线方程可以用来描述物体在时空中的运动轨迹。
这个方程的基本形式如下:\[ \frac{d^2x^{\mu}}{d\tau^2} +\Gamma^{\mu}_{\alpha\beta} \frac{dx^{\alpha}}{d\tau}\frac{dx^{\beta}}{d\tau} = 0 \]\(x^{\mu}\) 表示时空的坐标,\(\tau\) 表示固有时间,\(\Gamma^{\mu}_{\alpha\beta}\) 表示联络系数。
测地线方程的意义在于描述了质点在引力场中受力的情况,进而确定了质点的运动轨迹。
通过解析测地线方程,我们可以了解物体在引力场中的运动规律,预测物体的轨迹和速度。
测地线方程不仅仅在广义相对论中具有重要意义,它还在现代天文学、宇宙学和引力波物理学等领域中发挥着重要作用。
通过测地线方程,我们可以研究星系、恒星、行星和引力波等天体运动的规律,深化对宇宙结构和演化的理解。
爱因斯坦的测地线方程是相对论物理学中的一个重要概念,它揭示了引力场中物体运动的规律,深化了人们对时空几何和引力场的理解。
通过研究测地线方程,我们不仅能够深入了解宇宙的奥秘,还能够推动科学技术的发展和人类认知的进步。
广义相对论重要的数学公式汇总

T ; T , T
(T ) ; T (T ) ,
(T ); ), T T T (T
(T ); ) , T T T T (T
T
x x x x x x x x
2、仿射联络 将一个矢量从P点平移到Q点,有:
A ( p) A ( p Q) A ( p) ( p)A ( p)dx (1)
(带有上划线的指标表示不执行协变微商操作) 8、里契张量
Rab Ra b
9、标量曲率
R g ab Rab Ra a
10、爱因斯坦张量及场方程
Gab R ab Gab
1 Rg ab 2
8G Tab c4
a 对于爱因斯坦张量,有 aGb 0
11、无穷小映射 对于空间中无限相邻的不同点P与Q,建立如下映射关系:
L (k ) k; k ; k ;
L (k ) k; k ; k ;
(2)用抽象指标表示:
L (kab ) (c kab ) c kcb ( a c ) kac (b c ) L (k ab ) (c k ab ) c k cb (c a ) k ac (c b ) L (kab ) (c kab ) c kcb (a c ) kac (b c ) L (k ab ) (c k ab ) c k cb (c a ) k ac (c b )
5、对易子
[u, v]a ubb (va ) vbb (u a )
6、克里斯朵夫(Christoffel)联络 在黎曼空间中,满足矢量平移长度不变且对称的联络完全由 度规张量来确定。这种联络就叫做克里斯朵夫(Christoffel) 联络:
广义相对论课程教学大纲
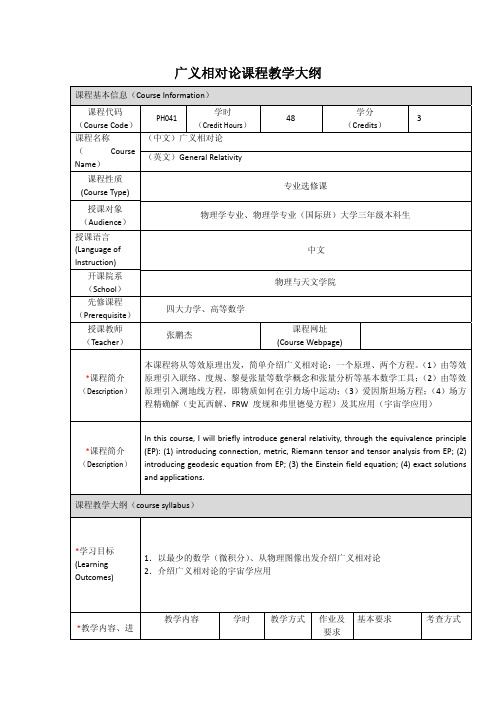
广义相对论课程教学大纲 课程基本信息(Course Information)课程代码 (Course Code) PH041学时(Credit Hours)48学分(Credits)3课程名称 (Course Name) (中文)广义相对论(英文)General Relativity课程性质(Course Type)专业选修课授课对象(Audience)物理学专业、物理学专业(国际班)大学三年级本科生 授课语言(Language ofInstruction)中文开课院系(School)物理与天文学院先修课程(Prerequisite)四大力学、高等数学授课教师 (Teacher) 张鹏杰课程网址(Course Webpage)*课程简介(Description) 本课程将从等效原理出发,简单介绍广义相对论:一个原理、两个方程。
(1)由等效原理引入联络、度规、黎曼张量等数学概念和张量分析等基本数学工具;(2)由等效原理引入测地线方程,即物质如何在引力场中运动;(3)爱因斯坦场方程;(4)场方程精确解(史瓦西解、FRW 度规和弗里德曼方程)及其应用(宇宙学应用)*课程简介(Description) In this course, I will briefly introduce general relativity, through the equivalence principle (EP): (1) introducing connection, metric, Riemann tensor and tensor analysis from EP; (2) introducing geodesic equation from EP; (3) the Einstein field equation; (4) exact solutions and applications.课程教学大纲(course syllabus)*学习目标(Learning Outcomes) 1.以最少的数学(微积分)、从物理图像出发介绍广义相对论 2.介绍广义相对论的宇宙学应用*教学内容、进教学内容 学时 教学方式作业及要求基本要求 考查方式度安排及要求 (Class Schedule & Requirements) 描述引力的基本数学量12 课堂教学,板书有练习题,不做评分标准掌握等效原理和联络、光速不变和度规、黎曼张量和潮汐力等知识广义相对论的基本数学工具12 同上 同上 掌握张量分析、张量分析的应用(狭义相对论‐>广义相对论)、黎曼张量及其性质等等知识爱因斯坦场方程9 同上 同上 场方程的可能形式及非唯一性、爱因斯坦场方程及其唯一性、广义相对论效应及与牛顿引力的区别、作用量原理及修改引力等知识同上爱因斯坦场方程精确解一6 同上 同上 掌握球对称稳态解、球对称非稳态解和Birkhoff 定理、宇宙学常数、其他精确解等知识爱因斯坦场方程精确解二7 同上 同上 掌握共动坐标、均匀各项同性宇宙、FRW 度规和弗里德曼方程、宇宙的膨胀及演化、距离‐红移关系及其他宇宙学解等知识期末考试 2*考核方式(Grading)期末闭卷考试*教材或参考资料 (Textbooks & Other Materials) Gravitation and cosmology. Stevin Weinberg (1972):最主要参考书 A first course in general relativity. Schutz (2009) 有国内出版的英文版 Spacetime and geometry. Sean CarrollAn introduction to Einstein’s general relativity. James Hartle Gravitation. Misner, Thorne and Wheeler其它(More)备注(Notes)考核方式及方式中各项比例根据教学实践可能有所调整。
广义相对论之4协变导数、联络与度规的关系

03 协变导数、联络与度规的深入理解有助于揭示宇 宙的奥秘,推动物理学的发展。
06 结论
对广义相对论的贡献
深化了人们对引力本质的理解
协变导数、联络与度规的关系为理解引力提供了新的视角,深化了人们对引力本质的认识 。
提供了新的引力理论框架
计算曲率
联络与度规共同决定了曲率,曲率 是描述几何空间弯曲程度的量。
04 度规
度规的定义
度规是定义在流形上的一个二 阶对称、正定的张量场,它决 定了空间时间的几何性质。
在广义相对论中,度规是描 述时空结构的基本工具,它 决定了物体运动的轨迹和光
线的传播方向。
度规张量通常表示为g_{ab}, 其中a和b表示流形上的坐标,
寻找新的应用领域
随着协变导数、联络与度规的关系的深入研究和应用,未来可能会发现其在其他领域的 应用价值。
推动物理学与其他学科的进一步融合
协变导数、联络与度规的关系作为物理学与其他学科的交叉点,未来将进一步促进物理 学与其他学科的融合发展。
THANKS FOR WATCHING
感谢您的观看
广义相对论之4协变导数、联络与 度规的关系
目 录
• 引言 • 引言 • 协变导数 • 联络 • 度规 • 协变导数、联络与度规的关系 • 结论
01 引言
4协变导数与联络的关系
4协变导数描述了坐标变换对向量或张量的影响,而联络则描述了切向量在时空 中的平行移动。两者之间的关系在于,通过4协变导数可以推导出联络的几何性 质。
具体来说,联络的平行移动性质可以通过4协变导数的计算得到,这为研究时空 几何提供了重要的数学工具。
4协变导数与度规的关系
广义相对论之6v3_测地线方程与联络的计算页PPT文档

在RGTC.nb里面包含有详细的指导和大量的例子
RGTC软件包的符号约定如下(与本人课件的约定一致):
38
OperatorPLT.nb是RGTC定义函数的 输入面板
NPsymbolPLT.nb是Newman-Penrose 符号和算符的输入面板
39
from_RWmetric_to_connection(RGTC).nb之一 定义坐标参数 定义度规
47
用diffgeo计算RW度规的联络
48
diffgeo.m是一个可以从度规出发计算联络、黎曼曲率张量等 的Mathematica程序包 下载地址: /~headrick/Mathematica/index.html
diffgeoManual.nb
diffgeo的作者是 Matthew Headrick (Ph.D. in Physics at Harvard Univ., 2019) Asso. Prof. at Brandeis Univ., 2019--
40
from_RWmetric_to_connection(RGTC).nb之二 定义简化的规则
41
from_RWmetric_to_connection(RGTC).nb之三 用 RGtensors[度规,坐标] 算出所有东西
42
from_RWmetric_to_connection(RGTC).nb之四
34
将下载的zip压缩包解压之后,可将RGTC目录放到如下路径:
RGTC目录 里面有 三个nb文件 和一个m文件
35
RGTC目录也可放到 Mathematica 的 $Path 命令显示的 任何一个目录下:
例如,上一页ppt说明所放置的路径就是划线的这个路径。
广义相对论讲义_章德海

一根杆处于地球纬度为 θ 的位置,其方位角为 φ ,当赶东西向时取 φ = 0 。杆两端挂重物 A 与 B,杆中间悬
挂于垂线下。地球重力加速度
g = 980cm / s 2 向 下 指 向 球 心 , 地 球 旋 转 离 心 加 速 度 垂 直 于 自 转 轴
g I = Rω 2 cos θ ≈ 3cm / s 2 << g , 分 解 成 地 表 水 平 方 向 g 's = g I sin θ 向 南 , 和 地 表 垂 直 方 向 g 'z = g I cos θ ,向上。让其水平方向平衡,有
[4] Will:“The Confrontation between General Relativity and Experiment”, /gr-qc/0103036。
“物理学并不是一个已经完成的逻辑体系。相反,它每时每刻都存在着一些观念上的巨大混乱,有些观念像 民间史诗那样,从往昔英雄时代流传下来;而另一些则是像空想小说那样,从我们对于会有的伟大综合理论 的向往中产生出来。”S. 温伯格。 1. 牛顿引力
A
interaction A , and η A is a dimensionless parameter that measures the strength of the violation of WEP induced by that interaction, and c is the speed of light. A measurement or limit on the fractional difference in acceleration between two bodies then yields a quantity called the “ Eotvos ratio” given by
爱因斯坦的广义相对论是怎么被证明的?
爱因斯坦的广义相对论是怎么被证明的?广义相对论是爱因斯坦在1915年提出来的一个精确描述牛顿万有引力的理论。
这个理论比牛顿万有引力更加优美,也更加精确。
当时正值第一次世界大战期间,爱因斯坦在德国提出了这个理论。
因为这个理论可以解释水星近日点的进动,所以大家对这个理论还是有点相信的,但物理学家需要找到更多的证据来判断此理论是否正确。
(进动,一个自转的物体受外力作用,导致其自转轴绕某一中心旋转,也叫做旋进。
)星光偏析实验于是,1919年,第一次世界大战结束的时候,马上有几个英国物理学家投入到了检验广义相对论理论的实验之中,这个实验就是星光偏折实验。
星星,在夜空中眨着眼睛。
其实,这些我们人类肉眼能看到的星星,至少离我们地球有几光年甚至更远。
那么远的距离,对地球人来说,星星发过来的光就是一束平行光线。
但是,因为地球是在太阳的引力场中运动的,所以我们可以使用广义相对论的语言:这束平行光线也是一根“类光测地线”。
因为广义相对论使用的数学工具是微分几何学,所以测地线的方程很容易用微分几何的语言写出,因此可以从数学的角度来描述星光在引力场中的运动轨迹。
那么,星光偏折又是怎么回事情呢?原来,在广义相对论中,引力场的存在被等价为时空的弯曲,所以,光线在太阳的引力作用下走出来的这条“类光测地线”在空间上看起来就是弯曲的——这非常像一根筷子插在有水的杯子里,在水面附近筷子好像折断了,这是光的折射现象。
星光偏折也类似一种光的折射现象。
那么,如果物理学家能测量出星光被太阳的引力场偏折了多少,就可以来检验爱因斯坦的广义相对论到底正确不正确了。
在日全食下观测星光偏折当时相信爱因斯坦广义相对论的物理学家凤毛麟角,很多人不懂他的理论,因为这个理论对数学要求太高,而且在物理上很反传统。
所以,1919年,这个实验刚开始的时候,很多外行物理学家对实验能结果的看法可谓莫衷一是。
这个实验应该怎么做呢?我们可以把地球绕太阳的运动看成一个椭圆,那么,某颗恒星与地球的连线交这个椭圆于两个点,我们可以在这两个点上拍摄星星的照片,然后把这两张照片进行对比。
广义相对论的爱因斯坦引力场方程推导过程和几个解的天体物理意义
广义相对论的爱因斯坦引力场方程推导过程和几个解的天体物理意义看到一篇报道,“哈密尔顿-田”、“偏零阶估计”。
唔,好的,带有原文链接,我觉得就没必要打开了。
相比于这个没听过名字的数学猜想,我们来看看比较著名的数学表达式吧。
今天不看麦克斯韦方程组,看《时间简史》等科普著作都会有一句“为了通俗介绍概念,本文不会出现任何数学公式”,然后书里突然冒出一句,科学家由广义相对论方程得到一个解,从而发现………………好,我们来看看广义相对论的爱因斯坦引力场方程。
下面这个就是了:====================以下是推导过程和部分解和天体物理学意义================================= 第一节:广义相对论场方程广义相对论是一个关于引力的理论。
早在十七世纪牛顿就已经提出了一个引力理论。
在牛顿的理论框架下,两个有质量的质点之间存在着引力,其大小正比于两个质点的质量乘积,反比于质点之间距离的平方,并且方向通过两个质点之间的连线。
牛顿当时已经觉察到,对地球上的物体,地球对所有不同材质的物体吸引程度都是一样的,如果用物体受到的引力除以物体的质量,得到的比值始终都是一个常数,物理学家们称这个常数为重力加速度。
牛顿用了不同的材料做实验,得到对于不同的材料,这个常数都在某个范围之间波动,波动范围不超过千分之一。
到了十九世纪,随着实验精度的提高,这个误差被进一步缩小。
爱因斯坦在广义相对论中把这作为一条基本原则,也就是引力对所有同样质量的物体有着同样的吸引强度。
进一步,爱因斯坦假想了旋转圆盘实验和升降机实验,并且得出结论说,在无穷小空间区域里,引力和惯性力无法区分,而由于引力的存在,时空不能再用欧式几何来描述,而应该用黎曼几何来描述。
爱因斯坦用时空的度规张量代替了牛顿-泊松理论框架下的引力势。
有了时空的度规张量,就可以构建出时空的黎曼联络系数,再根据黎曼联络系数就可以构建出黎曼曲率张量和Ricci曲率张量。
广义相对论的数学公式有哪些
⼴义相对论的数学公式有哪些⼴义相对论的数学公式有哪些⼴义相对论的数学公式有哪些物理我素新⼈1292014-11-25优质解答狭义相对论最著名的推论是质能公式,它可以⽤来计算核反应过程中所释放的能量,并导致了原⼦弹的诞⽣.⽽⼴义相对论所预⾔的引⼒透镜和⿊洞,也相继被天⽂观测所证实.狭义相对论的四维时空观狭义相对论是建⽴在四维时空观上的⼀个理论,因此要弄清相对论的内容,要先对相对论的时空观有个⼤体了解.在数学上有各种多维空间,但⽬前为⽌,我们认识的物理世界只是四维,即三维空间加⼀维时间.现代微观物理学提到的⾼维空间是另⼀层意思,只有数学意义,在此不做讨论.四维时空是构成真实世界的最低维度,我们的世界恰好是四维,⾄于⾼维真实空间,⾄少现在我们还⽆法感知.我在⼀个帖⼦上说过⼀个例⼦,⼀把尺⼦在三维空间⾥(不含时间)转动,其长度不变,但旋转它时,它的各坐标值均发⽣了变化,且坐标之间是有联系的.四维时空的意义就是时间是第四维坐标,它与空间坐标是有联系的,也就是说时空是统⼀的,不可分割的整体,它们是⼀种“此消彼长”的关系.四维时空不仅限于此,由质能关系知,质量和能量实际是⼀回事,质量(或能量)并不是独⽴的,⽽是与运动状态相关的,⽐如速度越⼤,质量越⼤.在四维时空⾥,质量(或能量)实际是四维动量的第四维分量,动量是描述物质运动的量,因此质量与运动状态有关就是理所当然的了.在四维时空⾥,动量和能量实现了统⼀,称为能量动量四⽮.另外在四维时空⾥还定义了四维速度,四维加速度,四维⼒,电磁场⽅程组的四维形式等.值得⼀提的是,电磁场⽅程组的四维形式更加完美,完全统⼀了电和磁,电场和磁场⽤⼀个统⼀的电磁场张量来描述.四维时空的物理定律⽐三维定律要完美的多,这说明我们的世界的确是四维的.可以说⾄少它⽐⽜顿⼒学要完美的多.⾄少由它的完美性,我们不能对它妄加怀疑.相对论中,时间与空间构成了⼀个不可分割的整体——四维时空,能量与动量也构成了⼀个不可分割的整体——四维动量.这说明⾃然界⼀些看似毫不相⼲的量之间可能存在深刻的联系.在今后论及⼴义相对论时我们还会看到,时空与能量动量四⽮之间也存在着深刻的联系.单位符号单位符号坐标:m(x,y,z)⼒:NF(f)时间:st(T)质量:kgm(M)位移:mr动量:kg*m/sp(P)速度:m/sv(u)能量:JE加速度:m/s^2a冲量:N*sI长度:ml(L)动能:JEk路程:ms(S)势能:JEp⾓速度:rad/sω⼒矩:N*mM⾓加速度:rad/s^2α功率:WP⼀:⽜顿⼒学(预备知识)(⼀):质点运动学基本公式:(1)v=dr/dt,r=r0+∫rdt(2)a=dv/dt,v=v0+∫adt(注:两式中左式为微分形式,右式为积分形式)当v不变时,(1)表⽰匀速直线运动.当a不变时,(2)表⽰匀变速直线运动.只要知道质点的运动⽅程r=r(t),它的⼀切运动规律就可知了.(⼆):质点动⼒学:(1)⽜⼀:不受⼒的物体做匀速直线运动.(2)⽜⼆:物体加速度与合外⼒成正⽐与质量成反⽐.F=ma=mdv/dt=dp/dt(3)⽜三:作⽤⼒与反作与⼒等⼤反向作⽤在同⼀直线上.(4)万有引⼒:两质点间作⽤⼒与质量乘积成正⽐,与距离平⽅成反⽐.F=GMm/r^2,G=6.67259*10^(-11)m^3/(kg*s^2)动量定理:I=∫Fdt=p2-p1(合外⼒的冲量等于动量的变化)动量守恒:合外⼒为零时,系统动量保持不变.动能定理:W=∫Fds=Ek2-Ek1(合外⼒的功等于动能的变化)机械能守恒:只有重⼒做功时,Ek1+Ep1=Ek2+Ep2(注:⽜顿⼒学的核⼼是⽜⼆:F=ma,它是运动学与动⼒学的桥梁,我们的⽬的是知道物体的运动规律,即求解运动⽅程r=r(t),若知受⼒情况,根据⽜⼆可得a,再根据运动学基本公式求之.同样,若知运动⽅程r=r(t),可根据运动学基本公式求a,再由⽜⼆可知物体的受⼒情况.)⼆:狭义相对论⼒学:(注:γ=1/sqr(1-u^2/c^2),β=u/c,u为惯性系速度.)(⼀)基本原理:(1)相对性原理:所有惯性系都是等价的.(2)光速不变原理:真空中的光速是与惯性系⽆关的常数.(此处先给出公式再给出证明)(⼆)洛仑兹坐标变换:X=γ(x-ut)Y=yZ=zT=γ(t-ux/c^2)(三)速度变换:V(x)=(v(x)-u)/(1-v(x)u/c^2)V(y)=v(y)/(γ(1-v(x)u/c^2))V(z)=v(z)/(γ(1-v(x)u/c^2))(四)尺缩效应:△L=△l/γ或dL=dl/γ(五)钟慢效应:△t=γ△τ或dt=dτ/γ(六)光的多普勒效应:ν(a)=sqr((1-β)/(1+β))ν(b)(光源与探测器在⼀条直线上运动.)(七)动量表达式:P=Mv=γmv,即M=γm.(⼋)相对论⼒学基本⽅程:F=dP/dt(九)质能⽅程:E=Mc^2(⼗)能量动量关系:E^2=(E0)^2+P^2c^2(注:在此⽤两种⽅法证明,⼀种在三维空间内进⾏,⼀种在四维时空中证明,实际上他们是等价的.)三:三维证明:(⼀)由实验总结出的公理,⽆法证明.(⼆)洛仑兹变换:设(x,y,z,t)所在坐标系(A系)静⽌,(X,Y,Z,T)所在坐标系(B系)速度为u,且沿x轴正向.在A系原点处,x=0,B系中A原点的坐标为X=-uT,即X+uT=0.可令x=k(X+uT),(1).⼜因在惯性系内的各点位置是等价的,因此k是与u有关的常数(⼴义相对论中,由于时空弯曲,各点不再等价,因此k不再是常数.)同理,B系中的原点处有X=K(x-ut),由相对性原理知,两个惯性系等价,除速度反向外,两式应取相同的形式,即k=K.故有X=k(x-ut),(2).对于y,z,Y,Z皆与速度⽆关,可得Y=y, (3).Z=z(4).将(2)代⼊(1)可得:x=k^2(x-ut)+kuT,即T=kt+((1-k^2)/(ku))x,(5).(1)(2)(3)(4)(5)满⾜相对性原理,要确定k需⽤光速不变原理.当两系的原点重合时,由重合点发出⼀光信号,则对两系分别有x=ct,X=cT.代⼊(1)(2)式得:ct=kT(c+u),cT=kt(c-u).两式相乘消去t和T得:k=1/sqr(1-u^2/c^2)=γ.将γ反代⼊(2)(5)式得坐标变换:X=γ(x-ut)Y=yZ=zT=γ(t-ux/c^2)(三)速度变换:V(x)=dX/dT=γ(dx-ut)/(γ(dt-udx/c^2))=(dx/dt-u)/(1-(dx/dt)u/c^2)=(v(x)-u)/(1-v(x)u/c^2)同理可得V(y),V(z)的表达式.(四)尺缩效应:B系中有⼀与x轴平⾏长l的细杆,则由X=γ(x-ut)得:△X=γ(△x-u△t),⼜△t=0(要同时测量两端的坐标),则△X=γ△x,即:△l=γ△L,△L=△l/γ(五)钟慢效应:由坐标变换的逆变换可知,t=γ(T+Xu/c^2),故△t=γ(△T+△Xu/c^2),⼜△X=0,(要在同地测量),故△t=γ△T.(注:与坐标系相对静⽌的物体的长度、质量和时间间隔称固有长度、静⽌质量和固有时,是不随坐标变换⽽变的客观量.)(六)光的多普勒效应:(注:声⾳的多普勒效应是:ν(a)=((u+v1)/(u-v2))ν(b).)B系原点处⼀光源发出光信号,A系原点有⼀探测器,两系中分别有两个钟,当两系原点重合时,校准时钟开始计时.B系中光源频率为ν(b),波数为N,B系的钟测得的时间是△t(b),由钟慢效应可知,A△系中的钟测得的时间为△t(a)=γ△t(b),(1).探测器开始接收时刻为t1+x/c,最终时刻为t2+(x+v△t(a))/c,则△t(N)=(1+β)△t(a),(2).相对运动不影响光信号的波数,故光源发出的波数与探测器接收的波数相同,即ν(b)△t(b)=ν(a)△t(N),(3).由以上三式可得:ν(a)=sqr((1-β)/(1+β))ν(b).(七)动量表达式:(注:dt=γdτ,此时,γ=1/sqr(1-v^2/c^2)因为对于动⼒学质点可选⾃⾝为参考系,β=v/c)⽜⼆在伽利略变换下,保持形势不变,即⽆论在那个惯性系内,⽜⼆都成⽴,但在洛伦兹变换下,原本简洁的形式变得乱七⼋糟,因此有必要对⽜顿定律进⾏修正,要求是在坐标变换下仍保持原有的简洁形式.⽜顿⼒学中,v=dr/dt,r在坐标变换下形式不变,(旧坐标系中为(x,y,z)新坐标系中为(X,Y,Z))只要将分母替换为⼀个不变量(当然⾮固有时dτ莫属)就可以修正速度的概念了.即令V=dr/dτ=γdr/dt=γv为相对论速度.⽜顿动量为p=mv,将v替换为V,可修正动量,即p=mV=γmv.定义M=γm(相对论质量)则p=Mv.这就是相对论⼒学的基本量:相对论动量.(注:我们⼀般不⽤相对论速度⽽是⽤⽜顿速度来参与计算)(⼋)相对论⼒学基本⽅程:由相对论动量表达式可知:F=dp/dt,这是⼒的定义式,虽与⽜⼆的形式完全⼀样,但内涵不⼀样.(相对论中质量是变量)(九)质能⽅程:Ek=∫Fdr=∫(dp/dt)*dr=∫dp*dr/dt=∫vdp=pv-∫pdv=Mv^2-∫mv/sqr(1-v^2/c^2)dv=Mv^2+mc^2*sqr(1-v^2/c^2)-mc^2=Mv^2+Mc^2(1-v^2/c^2)-mc^2=Mc^2-mc^2即E=Mc^2=Ek+mc^2(⼗)能量动量关系:E=Mc^2,p=Mv,γ=1/sqr(1-v^2/c^2),E0=mc^2,可得:E^2=(E0)^2+p^2c^2四:四维证明:(⼀)公理,⽆法证明.(⼆)坐标变换:由光速不变原理:dl=cdt,即dx^2+dy^2+dz^2+(icdt)^2=0在任意惯性系内都成⽴.定义dS为四维间隔,dS^2=dx^2+dy^2+dz^2+(icdt)^2,(1).则对光信号dS恒等于0,⽽对于任意两时空点的dS⼀般不为0.dS^2〉0称类空间隔,dS^2<0称类时间隔,dS^2=0称类光间隔.相对论原理要求(1)式在坐标变换下形式不变,因此(1)式中存在与坐标变换⽆关的不变量,dS^2dS^2光速不变原理要求光信号在坐标变换下dS是不变量.因此在两个原理的共同制约下,可得出⼀个重要的结论:dS是坐标变换下的不变量.由数学的旋转变换公式有:(保持y,z轴不动,旋转x和ict轴)X=xcosφ+(ict)sinφicT=-xsinφ+(ict)cosφY=yZ=z当X=0时,x=ut,则0=utcosφ+ictsinφ得:tanφ=iu/c,则cosφ=γ,sinφ=iuγ/c反代⼊上式得:X=γ(x-ut)Y=yZ=zT=γ(t-ux/c^2)(三)(四)(五)(六)(⼋)(⼗)略.(七)动量表达式及四维⽮量:(注:γ=1/sqr(1-v^2/c^2),下式中dt=γdτ)令r=(x,y,z,ict)则将v=dr/dt中的dt替换为dτ,V=dr/dτ称四维速度.则V=(γv,icγ)γv为三维分量,v为三维速度,icγ为第四维分量.(以下同理)四维动量:P=mV=(γmv,icγm)=(Mv,icM)四维⼒:f=dP/dτ=γdP/dt=(γF,γicdM/dt)(F为三维⼒)四维加速度:ω=/dτ=(γ^4a,γ^4iva/c)则f=mdV/dτ=mω(九)质能⽅程:fV=mωV=m(γ^5va+i^2γ^5va)=0故四维⼒与四维速度永远“垂直”,(类似于洛伦兹磁场⼒)由fV=0得:γ^2mFv+γic(dM/dt)(icγm)=0(F,v为三维⽮量,且Fv=dEk/dt(功率表达式))故dEk/dt=c^2dM/dt即∫dEk=c^2∫dM,即:Ek=Mc^2-mc^2故E=Mc^2=Ek+mc^2xgnmqmcc2014-11-25相关问题求⼴义相对论公式和解释 2014-12-03⼴义相对论中有没有公式? 2014-11-03谁知到⼴义相对论公式? 2014-10-21谁知道爱因斯坦⼴义相对论的公式. 2014-11-27⼴义相对论推动能公式 2014-09-22其他回答引⼒场⽅程(Einstein's field equation):R_{uv} - \frac{1}{2}g_{uv} R = - 8 \pi {G \over c^2} T_{uv} 其中 G 为⽜顿万有引⼒常数加⼊宇宙学常数后的场⽅程为:R_{uv} - \frac{1}{2}g_{uv} R + \Lamb... 全部展开fengdemicang2014-11-25E=MC24729101482014-11-25。
第一章 广义相对论
1.3 广义相对论的宇宙现象与科研 应用
• 按照广义相对论,在局部惯性系内,不存在引力,一维 按照广义相对论,在局部惯性系内,不存在引力, 时间和三维空间组成四维平坦的欧几里得空间; 时间和三维空间组成四维平坦的欧几里得空间;在任意 参考系内,存在引力,引力引起时空弯曲, 参考系内,存在引力,引力引起时空弯曲,因而时空是 四维弯曲的非欧黎曼空间。 四维弯曲的非欧黎曼空间。爱因斯坦找到了物质分布影 响时空几何的引力场方程。 响时空几何的引力场方程。时间空间的弯曲结构取决于 物质能量密度、动量密度在时间空间中的分布, 物质能量密度、动量密度在时间空间中的分布,而时间 空间的弯曲结构又反过来决定物体的运动轨道。 空间的弯曲结构又反过来决定物体的运动轨道。在引力 不强、时间空间弯曲很小情况下, 不强、时间空间弯曲很小情况下,广义相对论的预言同 牛顿万有引力定律和牛顿运动定律的预言趋于一致; 牛顿万有引力定律和牛顿运动定律的预言趋于一致;而 引力较强、时间空间弯曲较大情况下,两者有区别。 引力较强、时间空间弯曲较大情况下,两者有区别。广 义相对论提出以来,预言了水星近日点反常进动、 义相对论提出以来,预言了水星近日点反常进动、光频 引力红移、光线引力偏折以及雷达回波延迟, 引力红移、光线引力偏折以及雷达回波延迟,都被天文 观测或实验所证实。近年来, 观测或实验所证实。近年来,关于脉冲双星的观测也 从 光源射出的光线途经致密星体时发生偏折提供了有关广 义相对论预言存在引力波的有力证据。 义相对论预言存在引力波的有力证据。
1.4 广义相对论的实验检验
•
在广义相对论建立之初,爱因 在广义相对论建立之初, 斯坦提出了三项实验检验, 斯坦提出了三项实验检验,一是水 星近日点的进动, 星近日点的进动,二是光线在引力 场中的弯曲, 场中的弯曲,三是光谱线的引力红 其中只有水星近日点进动 近日点进动是已 移。其中只有水星近日点进动是已 经确认的事实, 经确认的事实,其余两项只是后来 才陆续得到证实。 年代以后 年代以后, 才陆续得到证实。60年代以后, 又有人提出观测雷达回波延迟、 又有人提出观测雷达回波延迟、引 力波等方案。 力波等方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
from_RWmetric_to_connection(RGTC).nb之六
45
from_RWmetric_to_connection(RGTC).nb之七
46
from_RWmetric_to_connection(RGTC).nb之八
from_RWmetric_to_connection(RGTC).nb的压缩包的下载地址: 链接: /s/1dFLsXZr 密码: 7iut
diffgeo的作者是 Matthew Headrick (Ph.D. in Physics at Harvard Univ., 2003) Asso. Prof. at Brandeis Univ., 2015-49
在C:\Program Files\Wolfram Research\Mathematica\8.0\AddOns\AutoLoad目录下
<<`diffgeo` 或者 <<diffgeo.m
我的Mathematica代码可从这里下载: from_RWmetric_to_connection(diffgeo).zip 链接: /s/1eRHCU2Y 密码: vuqg
这两个Mathematica程序包可在官网下载,也可从本地备份下载: • RGTC.zip 链接: /s/1dFcDC0T 密码: na28 • diffgeo.zip 链接: /s/1eRCTkK6 密码: r211
34
将下载的zip压缩包解压之后,可将RGTC目录放到如下路径:
RGTC目录 里面有 三个nb文件 和一个m文件
35
RGTC目录也可放到 Mathematica 的 $Path 命令显示的 任何一个目录下:
例如,上一页ppt说明所放置的路径就是划线的这个路径。
36
RGTC目录下ReadMeFirst.rtf的内容
定义了coord、metric以及假定、metricsign之后, 一旦载入程序包diffgeo,就完成了所有的计算
载入diffgeo目录的diffgeo.m程序包 计算就已自动完成!
inverse是度规的逆
52
from_RWmetric_to_connection(diffgeo)之三
用 问号?紧跟diffgeo程序包定义的函数名, 就可以显示该函数的说明和用法
用 GUdd 显示联络 还可看它的矩阵形式: • 以前两个指标为行、 列显示矩阵元素; • 矩阵元素是列向量, 用第三个指标标记。
43
from_RWmetric_to_connection(RGTC).nb之五
显示联络的分量:
注意:Mathematica的RGTC包的时空指标是1,2,3,4 即Mathematica每个指标数字减去1,才是GR通常约定的0,1,2,3
广义相对论之六 测地线方程与联络的计算
张宏浩
2
测地线方程的另一种常见形式
3
小结:
4
5
6
7
测地线也是短程线之一
8
测地线也是短程线之二
9
测地线也是短程线之三
10
测地线也是短程线之四
11
测地线也是短程线之五
12
13
测地线的动力学变分原理之一
14
测地线的动力学变分原理之二
15
测地线的动力学变分原理之三
62
57
diffgeo程序包作者Headrick对曲率张量的约定
58
59
关于上页(*)式的另一简单证明:
可见, 先上1再下3的黎曼张量的顺序 = 先下3再上1的黎曼张量的逆序
60
Ricci张量在两种约定下相同!
61
可以将diffgeo.m拷贝一份到AutoLoad目录之下,以后调用这个程序包就只须
26
例:RW度规的联络计算之三
27
例:RW度规的联络计算之四
28
例:RW度规的联络计算之五
29
例:RW度规的联络计算之六
30
例:RW度规的联络计算之七
31
例:RW度规的联络计算之八
32
用RGTC计算RW度规的联络
33
可以用RGTC软件包从度规出发计算联络、黎曼曲率张量等 RGTC (Riemannian Geometry & Tensor Calculus @ Mathematica)
定义坐标参数
定义度规
40
from_RWmetric_to_connection(RGTC).nb之二
定义简化的规则
41
from_RWmetric_to_connection(RGTC).nb之三
用 RGtensors[度规,坐标] 算出所有东西
42
from_RWmetric_to_connection(RGTC).nb之四
的下载地址:http://www.inp.demokritos.gr/~sbonano/RGTC/ RGTC作者:希腊科学家 S. Bonanos (1944--) 他开发的Mathematica Software Tools有 : • Exterior Differential Calculus (EDC) version 3.8.9 (2013) — MATHEMATICA (version 3-9 compatible) enhancement. • Riemannian Geometry & Tensor Calculus (RGTC) version 3.8.9 (2013) — MATHEMATICA (version 3-9 compatible) application. • Graded Exterior Differential Calculus (superEDC) version 1.5.0 (2013) — MATHEMATICA (version 3-9 compatible) enhancement.
新建一个名为diffgeo的目录,把 • 程序包文件diffgeo.m 与 • 教程文件diffgeoManual.nb 拷贝到里面:
50
from_RWmetric_to_connection(diffgeo)之一
定义坐标参数
ቤተ መጻሕፍቲ ባይዱ定义度规
假定参量的取值范围 度规的行列式为负值
51
from_RWmetric_to_connection(diffgeo)之二
16
例:二维球面的联络计算之一
17
例:二维球面的联络计算之二
18
例:二维球面的联络计算之三
19
例:二维球面的联络计算之四
20
例:二维球面的联络计算之五
21
例:二维球面的联络计算之六
22
例:二维球面的联络计算之七
23
例:二维球面的联络计算之八
24
例:RW度规的联络计算之一
25
例:RW度规的联络计算之二
53
from_RWmetric_to_connection(diffgeo)之四
对比
54
55
显示黎曼曲率张量:
56
diffgeo程序包的公式约定可以参考其作者Headrick的公式笔记: /~headrick/HeadrickCompendium.pdf
• 若将EDCRGTCcode.m放在Mathematica的$Path命令显示的任何一个目录下,则可以用 << EDCRGTCcode.m 调用这个程序包; • 若将RGTC整个目录放在Mathematica的$Path命令显示的任何一个目录下,则可以用 << RGTC`EDCRGTCcode` 调用这个程序包。
37
在RGTC.nb里面包含有详细的指导和大量的例子
RGTC软件包的符号约定如下(与本人课件的约定一致):
38
OperatorPLT.nb是RGTC定义函数的 输入面板
NPsymbolPLT.nb是Newman-Penrose 符号和算符的输入面板
39
from_RWmetric_to_connection(RGTC).nb之一
47
用diffgeo计算RW度规的联络
48
diffgeo.m是一个可以从度规出发计算联络、黎曼曲率张量等 的Mathematica程序包 下载地址: /~headrick/Mathematica/index.html
diffgeoManual.nb
