沉降_时间曲线呈_S_型的证明_从一维固结理论角度
《土力学与基础工程》复习资料和答案-选择题

1. 土力学与地基基础成为一门独立学科的奠基人是( )。
A .法国的库仑B .法国的布辛奈斯克C .英国的朗金D .美国的太沙基2. 评价粘性土软硬状态的物理指标是( )。
A .含水量B .孔隙比C .液性指数D .内聚力3.颗粒级配曲线较平缓的土,表示( )。
A .颗粒大小相差悬殊B .颗粒大小相差不多C .颗粒级配不好D .不均匀系数较小4. 在无限均布荷载作用下,地基中的附加应力分布特点是( )。
A .曲线分布B .正三角形分布C .倒三角形分布D .沿深度不变5. 高耸建(构)筑物应主要验算的地基变形特征是( )。
A .沉降量B .沉降差C .倾斜D .局部倾斜6. 对于软土,沉降计算深度即受压层厚度按( )标准确定。
A .σz ≤0.2σczB .σz <0.05σczC .σz <0.15σczD .σz ≤0.1σcz7.均质土体剪切破坏时,其破坏面一般为( )。
A .剪应力最大面B .抗剪强度最小面C .与大主应力作用面成2/45ϕ+ 角的面D .与大主应力作用面成2/45ϕ- 角的面8. 当地基塑性区的最大开展深度为基础宽度的四分之一时,相应的基底压力记为( )。
A .cr pB .4/1pC .4/1pD .u p9. 在直剪试验中,对试样施加竖向压力后让试样充分排水,待其固结稳定后,再快速施加水平剪应力使试样破坏,这种试验方法属于( )。
A .快剪B .固结慢剪C .慢剪D .固结快剪10. 某一重力式挡土墙,若墙后填土性质相同,则静止土压力E 0、主动土压力E a 和被动土压力E p 的大小关系是( )。
A. E 0>E a >E pB. E P >E a >E 0C. E p >E 0>E aD. E a >E 0>E p11. 对于中心受压的矩形基础,地基土中竖向附加应力最小是( )。
A .基础角点下深为一倍基础宽度处B .矩形基础角点基底处C .基础中心点下深为一倍基础宽度处D .矩形基础中心点基底处12. 对无粘性土土坡(坡角β,内摩擦角ϕ),满足土坡稳定的条件是( )。
2.5时间与沉降的关系详解

t2
t=∞
测 压 管
在水排出的同时,弹簧相应受压变形,承担部分 外荷,此时各点的。 u p 孔隙水压力:
u1 u2 u3 u4 p
p t1 σz 带孔活塞 水 H σ´ u 1 2 3 4 t=t1 弹簧 容器 测 压 管 h t2
求解思路: 有效应力原理 总应力已知 超静孔隙水压力的时空分布
多层渗透模型
1)加荷前,测压管中的水位与容器中的水位相同, 即土层中的孔隙水压力等于静水压力。 2)在施加荷载强度σ的瞬间,即t=0时刻,容器中 的水尚来不及排出,弹簧未受力和引起变形,外 荷全部由孔隙水承担。各测压管中水位都升高 了 h0 p w 。这表明土层不同深度处的超静水压力 都相同,即;
有效应力:
σz
t=∞
4)随着时间的延长,测压管中的水位又都恢复 到与静水位齐平。此时容器中的水不再向外排出, 弹簧也因之受力稳定,承担了全部外荷,相应于 各点的超静水压力已全部消散,荷载强度完全转 化为土中的有效应力,即
u1 u 2 u 3 u 4 0
2 3 4 p 1
1渗透固结模型
太沙基(Terzaghi,K.,1925)为研究土的固结问 1.试验装置—— 题提出了一维渗透模型。
带孔活塞 水 弹簧 容器 测压管 σ
△h
带有测压管并装满水的圆筒 带孔的活塞板 弹簧 2.模拟情况 弹簧模拟土骨架所承受的 压力,即有效应力σ´’ 筒中的水模拟孔隙水, u表 示外荷引起的超静水压力 ,即孔隙水压力。 小孔模拟土孔隙
2.5 沉降与时间的关系
Consolidation Theory of Saturated Soil
土力学-地基沉降与时间的关系

∞ o
H
σ′z
p
∞
排水面 不透水
初始条件
边界条件
σ′z σ′z=p u
u
u0=p
z
u :超静孔压 σ′z :有效应力 p :总附加应力 u0:初始超静孔压
t =0
u+ σ′z =p
0 ≤ z ≤ H: u=p
0<t <∞
z=0: u=0 z=H: ∂u⁄∂ =0 ⁄∂z=0 ⁄∂
t →∞
0 ≤ z ≤ H: u=0
饱和土体的渗流固结理论 - 一维渗流固结理论
土体的固结
p
物理模型
p 初始状态 边界条件 相间相互作用
侧限条件 土骨架 孔隙水 排水顶面 渗透性大小
钢筒 弹簧 水体 带孔活塞 活塞小孔大小
渗透固结过程
Terzaghi一维渗流固结模型 一维渗流固结模型
饱和土体的渗流固结理论 - 一维渗流固结理论
p
h=
o
M
H
σ′z u
uz,t σ′z σz − uz,t Uz,t = = = 1− σz σz σz
Uz,t=0~1:表征一点超静孔 ~ :表征一点超静孔 压的消散程度
z
H
σz
一层土的平 均固结度— 均固结度 地基平均固 结度
z 有效应力分布面积 ∫0 σ′ ,tdz ∫ uz,tdz Ut = = 1− = H 总应力分布面积 σ dz ∫ σzdz
均布荷载单向排水
∞
8 1 1 • 一般解: Ut= − 2 ∑ 2 e 一般解: π m=1 m
π2 −m2 Tv 4
Ut
∫ u dz = 1− ∫ σ dz
z,t 0 H 0 z
土的沉降与时间的关系

Tv 0.196
4cv t Tv 2 H
可得:
Tv H 2 t 181.6days 4cv
即 在181.6天内建筑物的固结沉降量为最终沉降量的一半。
试简述如何用固结理论求解下列两种课题的步骤:(1)已知历时求沉降量;(2) 估算达到某沉降量的历时。 答: (1) 已知历时求沉降量的步骤 a 估计该土层的最终沉降量S; b 计算该土层的竖向固结系数 c 计算竖向固结时间因数 Tv d 应用公式 U z 1
h k u z w z u
Soil mechanics
(d)
3、根据达西定律
q ki k
(超静孔隙水头 h
w
)
(e)
将式(d)、 (e)代入式(4-49),得
k (1 e1 ) 2u u 或者 a w z 2 t
Cv
2u u Cv 2 z t
u z ,t 4p 1 m z sin e m1 m 2H
2 m2 T 4 v1
4p
sin
z
2H
e
2 T 4 v1
P取附加应力平均值
一、习题评述
Soil mechanics
上层粘土
下层粘土
计算10天后沉降量时,应是三层土沉降之和,只是第二层(中 砂)不 考虑固结问题而已。
Soil mechanics
二、小测验 (30分钟)
Soil mechanics
三、方法讨论
沉降量、固结度计算法
三、方法讨论 课堂讨论题1:
沉降量、固结度计算法
Soil mechanics
在如图所示的厚10m的饱和粘土层表面瞬时大面积均匀堆载p0, 若干年后用测压管分别测得土层中的孔隙水压力uA=51.6kPa、 uB=94.2kPa、uC=133.8kPa、uD=170.4kPa,uE=198.0kPa
土力学-第四章地基的沉降计算3

z k p0
II. 荷载不是瞬时施加。 因此,不同的附加应力条件下,其固结度的公式也不同。
那么,怎么求解其他应力条件下的固结度呢?
叠加原理
U F U a Fa U b Fb
任意随深度而变的应力图形可以分解为若干个图形,则 总应力图形的固结度乘上其总应力面积,等于各分力应 力图形的固结度乘上各应力面积之和。
1 U (t ) 1 2 Hp
udz
0
并代入u的表达式
U (t ) 1 2
1 exp( M 2Tv ) U (Tv ) (U与Tv为一一对应关系) 2 m0 M
近似式
U (Tv ) 1
8
exp( 2
2
4
Tv ) (U (t ) 30%)
U(t)是Tv的单值 函数,Tv可反映 固结的程度
(2)有效应力逐渐增大,最终与总应力相等。 (3)变形随固结过程逐渐增大,最终达到稳定。
11
2、Terzaghi一维渗透固结数学模型
基本假定: 1. 土层是均质且完全饱和
2. 3. 4. 5. 6. 土颗粒与水不可压缩 水的渗出和土层压缩只沿竖向发生 渗流符合达西定律且渗透系数k保持不变 压缩系数av是常数 荷载均布,瞬时施加,总应力不随时间变化
de av du
dV
故孔隙体积变化与孔隙水压的关系为
1 ∂e dz 1 e ∂t
av u u dV dz mv dz 1 e t t
16
(3)由dQ=dV 建立固结方程
k 2u dQ dz 2 w z
由此得到固结方程
u dV mv dz t
∂ 2u ∂ u Cv 2 ∂z ∂t
地基沉降与时间关系 共24页文档
p
h 0
t 0
附加应力:σz=p 超静孔压: u = σz=p 有效应力:σ’z=0
渗流固结过程
0t
附加应力:σz=p 超静孔压: u <p 有效应力:σ’z>0
t
附加应力:σz=p 超静孔压: u =0 有效应力:σ’z=p
基本假定:
基本假设
①土层均匀、各向同性且完全饱和 ②土颗粒与水不可压缩 ③变形是单向压缩(水的渗出和土层压缩是单向的)
H
H
排水面
u0=p
z
双面排水时孔隙水压力分布
固结度
▪在某一固结应力作用下,经某一时间 t
后,土体发生固结或孔隙水应力消散的程
度。对于土层任一深度 z 处经时间 t 后 H z ,t u z ,t M
的固结度:
U z,t
z ,t z
Uz,t z zuz,t 1uz,t
z
z
z
z
Uz,t=0~1:表征总应力中有效应力所占比例
边界与初始条件
u C 4 cA o s C Z 5 sA in ) e z C v A 2 t
当t 0和0 z H 0<t 和z 0
u u0 z
u0
C5 z P
C4 0
0t 和z H u 0 z
A m
2H
t 和0 z H u 0
m=1,3,5,7……
uz,t
z
sinm z 2H
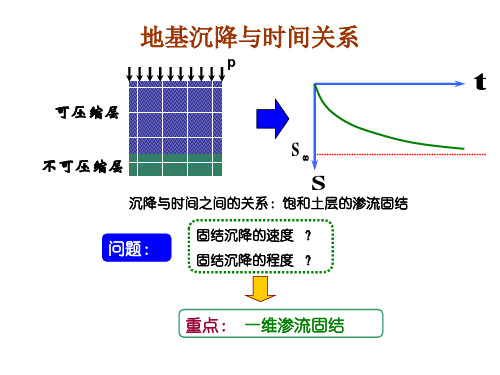
地基沉降与时间关系
p
t
可压缩层
不可压缩层
S
S
沉降与时间之间的关系:饱和土层的渗流固结
问题:
固结沉降的速度 ? 固结沉降的程度 ?
重点: 一维渗流固结
土力学_第5章(固结与压缩)

P0 P H
③计算地基中自重应力σsz分布
不排水
孔隙水压力
孔隙水压力
(五)三轴压缩试验成果—应力--应变关系
1 3
(1 3 ) y
1 3
f
E
1
b c
②-超固结土或密实砂 b ③-正常固结土或松砂
①-理想弹塑性
a O
b点为峰值强度
土 的 本 构 模 型
线弹性-理想塑性 1 3 1 2
1
应变硬化段
应变软化段
C
s
p
lg '
(五)三轴压缩试验
三轴试验测定: 轴向应变 轴向应力 体应变或孔隙水压力
轴向加压杆 顶帽
压力室
试 样
有机玻璃罩 橡皮膜 加压进水
类型 固结排水 施加σ3时 固结
透水石 排水管
量测体应变或 孔隙水压力
阀门
施加σ1-σ3时 排水
量 测 体应变
固结不排水
不固结不排水
固结
不固结
不排水
将地基分成若干层,认为整个地基 的最终沉降量为各层沉降量之和。
n n
o
s si i H i
i 1 i 1
ΔS1 ΔS2 ΔS3 ΔS4 Δ Si ΔSn
i第i层土的
压缩应变
z v
e e1 e2 1 e1 1 e1
z
取基底中心点下的附加应力进行计算,以基底中点的沉降代
400
e-p曲线
p(kPa)
(σ')
Δp
(σ')
p(kPa)
Δ p相等而 ΔeA> ΔeB,所以曲线A的压缩性 >曲线B的压缩性
土力学问答题_名词解释

一、名词解释1 . 塑限答:粘性土从可塑状态转变为半固体状态的界限含水率,也就是可塑状态的下限含水率。
2 . 不均匀系数答:定义为Cu= d60/ d10, d10 , d60分别为粒径分布曲线上小于某粒径土的土颗粒含量分别为10%和60%。
3 . 有效应力原理答:由外荷在研究平面上引起的法向总应力为σ,那么它必由该面上的孔隙力u和颗粒间的接触面共同分担,即该面上的总法向力等于孔隙力和颗粒间所承担的力之和,即σ=σ'+u。
4. 被动土压力答:当挡土墙向沿着填土方向转动或移动时,随着位移的增加墙后受到挤压而引起土压力增加,当墙后填土达到极限平衡状态时增加到最大值,作用在墙上的土压力称为被动土压力。
5 . 代替法答:代替法就是在土坡稳定分析重用浸润线以下,坡外水位以上所包围的同体积的水重对滑动圆心的力矩来代替渗流力对圆心的滑动力矩。
6 . 容许承载力答:地基所能承受的最大的基底压力称为极限承载力,记为fu.将f除以安全系数fs后得到的值称为地基容许承载力值fa,即fa=fu/fs7. 塑性指数液限和塑限之差的百分数值(去掉百分号)称为塑性指数,用表示,取整数,即:—液限,从流动状态转变为可塑状态的界限含水率。
—塑限,从可塑状态转变为半固体状态的界限含水率。
8. 临界水力坡降土体抵抗渗透破坏的能力,称为抗渗强度。
通常以濒临渗透破坏时的水力梯度表示,称为临界水力梯度。
9.不均匀系数不均匀系数的表达式:式中:和为粒径分布曲线上小于某粒径的土粒含量分别为60%和10%时所对应的粒径。
10.渗透系数当水力梯度i等于1时的渗透速度(cm/s或m/s)。
11.砂土液化液化被定义为任何物质转化为液体的行为或过程。
对于饱和疏松的粉细砂,当受到突发的动力荷载时,一方面由于动剪应力的作用有使体积缩小的趋势,另一方面由于时间短来不及向外排水,因此产生很大的孔隙水压力,当孔隙水压力等于总应力时,其有效应力为零。
根据太沙基有效应力原理,只有土体骨架才能承受剪应力,当土体的有效应力为零时,土的抗剪强度也为零,土体将丧失承载力,砂土就象液体一样发生流动,即砂土液化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∫
H
0
u dz H
(3)
≤ t 时: (1) 当 0 < t ≤ 0
32 p u= 4 0 ð TV 0
m =1, 3, 5
∑
∞
∞
ð 2 m 2 1 − 1 exp − 4 TV m4
(4)
d(u ) 32 p0 = 4 dt ð TV 0
m =1, 3, 5
∑
∞
1 m4
ð 2 m2 1 − exp − 4 TV 0 ⋅
(2) 当 t > t 0 时: u= 32 p0 ð 4 TV 0
ð 2 m2 ð 2 m 2 CV exp (TV − TV0 ) < 0 − − 2 4 H 4 (9) d 2 (u ) 32 p0 = 4 d t2 ð TV0
(17) 因− ð m ð m TV TV < 0 , 故 exp − 从而有: <1, 4 4
2 2 2 2
m =1, 3, 5
∑
∞
ð m 1 1 exp < − TV 2 2 4 m m =1,3,5 m
2 2
∑
∞
(18)
附 录:
可证明:
由: d(u ) 32 p0 = d t ð 4 TV 0 = 8 p0 ð 2 t0
p0 亦为一常数,故对时间 t 求导,可得: =− 1 ⋅du u0 d t
m =1, 3, 5
∑
∞
ð 2 m2 1 ð 2 m 2 CV exp − 4 TV m4 4 H 2
(1. 南京工业大学土木工程学院,江苏 南京 210009;2. 河海大学岩土工程研究所,江苏 南京 210098; 3. 南京水利科学研究院土工所,江苏 南京 210024;4. 香港理工大学土木结构工程系,香港)
摘 关
要:从一维固结理论出发,严格证明了在线性加载或近似线性加载情况下(这和工程实际加载相类似) ,沉降-时间曲线 键 词:固结理论;线性加载;沉降-时间曲线 文献标识码:A
∑
将 f ( x) = x 2 按余弦展开成傅立叶级数有: f ( x) = x 2 =
2
∑
∞
(-π≤x≤π)
(1) 将 f ( x) = x 在区间(0, 2π)内展开成傅立叶级数 有: f ( x) = x 2 = 4ð 2 cos( nx) +4 − 4ð 3 n2 n =1 (0≤x≤2π)
第 25 卷第 1 期 2004 年 1 月
文章编号: 1000-7598-(2004) 01―0020―03
岩 土 力 学 Rock and Soil Mechanics
Vol.25 No.1 Jan. 2004
沉降-时间曲线呈“S”型的证明
——从一维固结理论角度 梅国雄 1, 3, 4,宰金珉 1,殷宗泽 2,赵维炳 3,殷建华 4
1
引 言
目前, 大多数的沉降-时间关系的预测模型都是 基于瞬时加载的情形, 为了模拟实际的工程情况 (线 性加载或近似线性加载过程) ,通常需进行时间修 正。 笔者曾建立了一个考虑施工全过程的沉降-时间 预测新方法[1],但对曲线的性状,仅进行了机理上 的探讨,没有详细的数学力学证明。本文将从一维 固结理论出发,严格地证明在线性加载或近似线性 加载情况下,沉降-时间曲线呈“S”型。
(2) 当 t > t0 时: u= 16 p0 ð 3 TV0 ð 2 m2 1 mð z sin 1 − exp − TV0 3 ⋅ m 4 2H m =1, 3, 5
2
从一维固结角度证明线性加载下 沉降-时间曲线呈“S”型
p po
ð 2 m2 ð 2 m 2 CV exp (TV − TV0 ) > 0 − − 2 4 H 4 (10) 因−
S∞ < 0 为一负值,故: p0
d(S t ) d 2 (S t ) >0和 <0 dt d t2
(2) 当 0 < t ≤ ≤ t 0 时:
保持不变,如图 1 所示。按一维固结理论可以求得 任一时刻的孔隙水压力[2]: (1) 当 0 < t ≤ ≤ t0 时: u= 16 p0 ð 3 TV 0
∞
m =1, 3, 5
∑m
1
3
ð 2 m2 mð z sin TV ) 1 − exp( − 2 4 H (1)
≤ t0 范围内,
(0≤x≤2π) 从而有:
(2) (3)
()
(7)
m =1, 3, 5
∑
∞
ð 2 m2 1 exp − 4 TV m2 (15)
22
岩
土
力
学
2004 年
32 p d2 u =− 4 0 2 dt ð TV0
()
1 m4 m =1, 3, 5
∑
∞
ð 2 m 2 CV 4 H2 ⋅
m =1, 3, 5
∑
∞
1 ð2 = (见附录) ,故: m2 8
∑
n =1
∞
1 ð2 = 的数学证明 2 ( 2n − 1) 8 ð2 (−1) n cos n x +4 3 n2 n =1
∞ ð 2 m 2 p dS t 1 8 = mV h 0 1 − 2 exp − 4 TV t 0 ð m =1,3, 5 m 2 dt 2 p 8 ð > mV h 0 1− 2 ⋅ =0 t0 ð 8 (19) d(S t ) 即 >0 dt
呈“S”型。 中图分类号:TU433
Proof of s-t curve appearing “S” shape based on one-dimensinal consolidation theory
MEI Guo-xiong1, 3, 4, ZAI Jin-min1, YIN Zong-ze2, ZHAO Wei-bing3, YIN Jin-hua4
∑
∞
2.1 数学模型的建立 假定荷载在施工期荷载呈直线上升,完工后便
ð 2 m2 exp − (TV − TV 0 ) 4 (2)
收稿日期:2002-9-26. 基金项目:国家自然科学基金(50279021、50278042) 作者简介:梅国雄:男,1975 年出生,博士后,主要从事固结理论,土压力理论,土与结构物共同作用方面的研究和教学工作。
m =1, 3, 5
∑
∞
ð m 1 exp − T V m2 4
2 2
[1] [2] [3]
宰金珉, 梅国雄. 全过程的沉降量预测方法研究[J]. 岩 土力学, 2000, 20(4): 322-325. 殷宗泽. 土体沉降与固结[M]. 北京: 中国电力出版社, 1998. Das B M. Advanced Soil Mechanics[M]. New York: McGraw-Hill Book Company, 1983.
p u = (1 − ) S ∞ = mV h 0 t − umV h t0 u0 故: dS t p du = mV h 0 − mV h dt t0 dt d 2 St d2u = − m h V dt 2 dt 2
(12)
孔压定义的固结度 U u 相等,有: (6)
(13)
(14)
∫
H 0
σ dz = H
2
性加载或近似线性加载情况下,沉降- 时间曲线呈 (16) “S”型,为文献[1]建立新的沉降-时间预测模型奠 定了坚实的理论基础。
ð 2 m2 exp − 4 TV <0 有: dS t p 8 = mV h 0 1 − 2 dt t0 ð
参 考 文 献
Abstract: Based on one-dimensional consolidation theory, that the settlement-time curve appears “S” shape under linear loading or nearly linear loading is proved strictly. Key words: consolidation theory; linear loading; S-t curve
∑
∞
∑
n =1
∞
d 2 (S t ) 32 p d 2 (u ) = − m h = mV h 4 0 ⋅ V 2 2 dt dt ð TV0
sin( nx) n
m =1, 3, 5
∑
∞
1 m4
ð 2 m 2 CV ð 2 m2 ⋅ exp 4 − 4 TV >0 H2
2
(20)
在式(1)中令 x = ð ,有: ð2 = ð2 (−1) n ð2 1 n +4 ( − 1 ) = +4 2 3 n 3 n2 n =1 n =1
d(S t ) d 2 (S t ) 故 >0和 >0 dt d t2
∑
∞
∑
∞
d(S t ) >0和 dt d 2 (S t ) d(S t ) d 2 (S t ) > 0 ; 在 t > t 范围内, > 0 和 < 0。 0 d t2 dt d t2 沉降量 S t 在整个过程中,不断地增长,但在前期 综上所述: St 在 0 < t
(1.College of Civil Engineering, Nanjing University of Technolgy, Nanjing 210009, China; 2.Research Institute of Geotechnical Engineering, Hohai University, Nanjing 210098,China; 3. Geotechnical Engineering Department, Nanjing Hydraulic Research Institute, Nanjing 210024, China; 4. Department of Civil & Structural Engineering, The Hong Kong Polytechnic University, Hong Kong, China)
