第五章对流换热分析
传热学第5章讲解
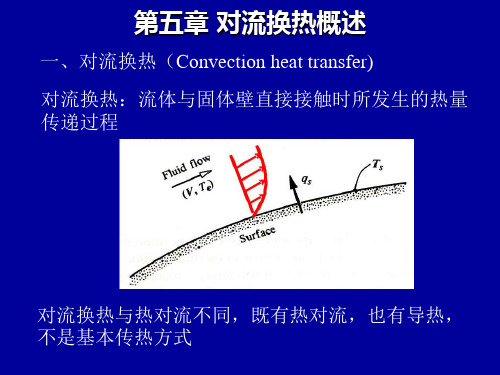
A qxdA
A
hx
tw
tf
x
dA
tw tf
A hxdA
等壁温,tw
tf
x
tw
tf
常数
对照式 = A h( tw-tf ) 可得
h 1 A
A hxdA
如何确定表面传热系数的大小是对流换热计算的
核心问题,也是本章讨论的主要内容。
5-1 对流换热概述
h t tw t y y0
上面两式建立了对流换热表面传热系数与温度场 之间的关系。而流体的温度场又和速度场密切相关, 所以对流换热的数学模型应该包括描写速度场和温度 场的微分方程。
5-2.对流换热过程的数学描述
一、连续性微分方程(质量守恒) y
u v 0
dy
x y
(2) 流动的状态 层流 :流速缓慢,流体分层地平行于壁面方 向流动,垂直于流动方向上的热量传递 主要靠分子扩散(即导热)。
6
紊流
:流体内存在强烈的脉动和旋涡,使各 部分流体之间迅速混合,因此紊流对流 换热要比层流对流换热强烈,表面传热 系数大。
7
(3) 流体有无相变 沸腾换热 凝结换热
(4) 流体的物理性质
q = h( tw-tf ) =h tm
h—整个固体表面的平均 表面传热系数;
tw—固体表面的平均温度 ; tf —流体温度,对于外部绕流,tf 取远离壁面的 主流温度;对于内部流动,tf 取流体的平均温度。
tm—平均换热温差。
对于局部对流换热,
qx
hx
tw
tf
x
4
ut 0
dx cp x dxdy
第5章-对流换热分析

二、连续性方程(质量守恒方程) A
流体的连续流动遵循质量守恒定律 从流场中 (x, y) 处取出边长为 dx、dy 、1的微元体,对进出 微元体的流量进行分析 (流入的质量=流出的质量)。
Mx M x dx x
M y vdx
二维、不可压缩ρ=C 、稳态流动时:
u v 0 x y
4个假设:(1)体积力(重力)作的功、表面力作的功, 流体不可压缩,流体不做功 W=0
(2)流体的热物性均为常量,热力学能变化由温度引起 (3)一般工程问题,流速低 ΔU动能=0
(4)无化学反应等qv
Φ内热源=0
能量微分方程式
y
Φ 导热 + Φ 对流 = U热力学能
2t 2t 1 ) 导热 2 dxdy+ 2 dxdy x y 2)单位时间,左侧面,进入的流体热量: x udycp t cp t udy
t hx ( ) t x y
w ,x
2 W m K
对流换热过程 微分方程式 D
对流换热过程微分方程
t hx ( ) t x y
梯度。
w,x
W m 2 K ( 5 2a )
hx 取决于流体λ、温度差Δt=( tw – tf )、贴壁流体的温度
( tu ) ( tv ) c p dxdy c p dxdy x y
由于对流进入 单元的净热量
t t u t v t u v c p u t v t dxdy c p u v t( ) dxdy y y y x y x x x t t u v c p u v dxdy ( 应用连续性方程: 0 ) y x y x
《传热学》第五章 对流换热分析PPT演示课件

24
求解结果 局部表面传热系数:
或可写成:
其中:
——准则方程
——无量纲流速 ——无量纲物性 ——无量纲换热强度
准则方程的意义——
把微分方程所反映的众多因素间的规律用少数几个准则来概括, 从而减少变量个数,以便于进行对流换热问题的分析、实验研究 和数据处理。
将上式在x,y两个方向代入牛顿第二定律,得到Navier-Stokes方程: 对于不可压缩流体:
11
将其代入Navier-Stokes方程,并采用连续方程化简,得到:
对稳态流动:
惯性力
体积力 压强梯度 黏滞力
当只有重力场作用时:
12
四、能量微分方程式
推导依据—— 内能增量=导热热量+对流热量 1.导热热量:
外掠平板全板长平均换热准则方程:
29
第六节 相似理论基础
相似原理的意义——通过实验寻找现象的规律以及指导推广应用实验。
一、物理相似的基本概念
1.几何相似
LA、LB——几何相似准则
30
2.物理现象相似
以管内流动为例,当两管各r之比满足下列 关系时:
若: 则速度场相似。 以外掠平板为例,当x,y坐标满足下列关系时:
《传热学》
1
第五章 对流换热分析
研究对象——流体与固体壁面之间的传热过程
研究目的——确定牛顿冷却定律
中的h
对流表面 传热系数
局部对流表面传热系数hx 平均对流表面传热系数
Isaac Newton(1642-1727)
确定对流表面传热系数的四种方法
分析法
类比法 数值法 实验法
第5章对流换热分析2讲

t Pr 1 3
( 层 流 、 0.6 Pr 50 )
第五章 对流换热 (李琼主讲) 20
δt<<L; 边界层内温度梯度变化显著,用能量微分方程描述; 边界层外温度梯度约为零,传热忽略不计。
因为膝盖处的热边界层很薄(相当 于外掠物体的前驻点),换热能力较 强,该处与空气的热交换量较大。 摩托车手的膝盖需要特别的保温, 你知道为什么吗?
u u u p 2u 2u ( u v ) X ( 2 2 ) x y x x y v v v p 2v 2v ( u v ) Y ( 2 2 ) x y y x y
2 2t t t t t c p u v 2 2 x y y x
这就是关于udydudy第五章对流换热李琼主讲39边界层积分方程组求解在常物性情况下动量积分方程可以独立求解即先求出然后求解能量积分方程获得dycy第五章对流换热李琼主讲40dydure64dydure323第五章对流换热李琼主讲41在工程中场使用局部切应力与流体动压头之比这个无量纲量并称之为范宁摩擦系数简称摩擦系数re646re292平均摩擦系数
第五章 对流换热 (李琼主讲) 21
三 数量级分析与边界层换热微分方程
1.数量级分析:比较方程中各量或各项的量级的相对大小;保 留量级较大的量或项;舍去那些量级小的项,方程大大简化 例:二维、稳态、强制对流、层流、忽略重力
u ~ 0(1); 5个基本量的数量级: 主流速度:
温度:t ~ 0(1); 边界层厚度: 壁面特征长度:l ~ 0(1);
边界层概念也可以用于分析其他情况下的流动和换热: 如:流体在管内受迫流动、流体外掠圆管流动、流体 在竖直壁面上的自然对流等
第五章对流换热分析

程,简称N-S方程,又称不可压缩粘性流体的运动微分方
程)
据牛顿第二定律:F=ma及相关流体力学知识推出。
第二节 对流换热的数学描写
一、运动微分方程
2.动量微分方程
u
u
u x
u y
X
p x
2u x2
2u 2 y
u
边界层的形成、发及区域划分
u∞
u∞
o
u∞=f(x,u,)
紊流核心层
o
缓冲层
u c
xc
层流底层
层流边界层 过渡段
紊流边界层
自O点开始边界层逐渐加厚,并随着粘滞力对外影响的减弱, 在某处开始层流开始不稳定起来。
临界距离xc:O点距层流向紊流过渡点的水平距离; 临界雷诺数Rec:层流向紊流过渡点的雷诺数值。Rec=u∞·xc/
b.粘滞力项:<3>式粘滞力可略去,且<2>中只须保留第二项;
c.压力梯度:<3>式中可略去,此时说明压力仅沿x方向发生变 化,故可将P/x改写成dP/dx,其值可由伯努利方程得出:
-dP/dx=u∞du∞/dx
N-S方程可写成:
u
u x
u y
1
dp dx
2u 2y
<2>.能量微分方程的简化:可忽略式右侧第一项,即沿x向
第三节 边界层换热微分方程组的解
一、流动边界层
6.流体受迫横掠圆管时的边界层
发生绕流脱体 形成卡门涡街
第三节 边界层换热微分方程组的解
第五章-传热学
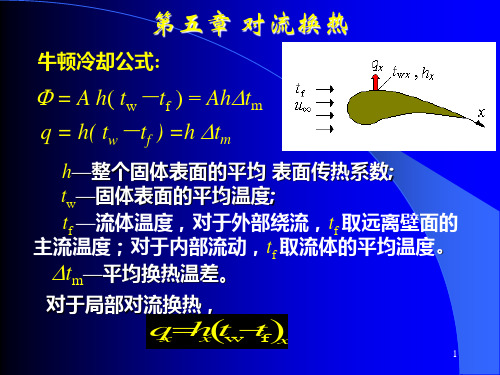
h
' h,x
' h,y
cpuxtvytdxdy
8
单位时间内微元体热力学能的增加为
dU
d
cp
t
dxdy
于是根据微元体的能量守恒
h
dU
d
可得
2t x2
2t y2
dxdy
cpuxtvytdxdy
cp
t
dxdy
cptux tvy ttu xv y
2t x2
2t y2
2
20
cp
uxt
v t y
=
2t x2
2t y2
1
11 1
1
2
1 1
1
2
对流换热微分方程组简化为
h t tw tf y w
u v 0 x y
简化方程组只有4个方
程,但仍含有h、u、v、 p、t 等5个未知量,方
程组不封闭。如何求解?
uuxvuy1ddpxy2u2
u t x
v t y
26
第六节 相似理论基础
相似原理指导下的实验研究仍然是解决复杂对流换 热问题的可靠方法。
相似原理回答三个问题: (1)如何安排实验? (2)如何整理实验数据? (3)如何推广应用实验研究结果?
一、 相似原理的主要内容
1.物理现象相似的定义 2.物理现象相似的性质 3.相似特征数之间的关系 4.物理现象相似的条件
三、解的函数形式——特征数关联式
特征数是由一些物理量组成的无量纲数,例如毕 渥数Bi和付里叶数Fo。对流换热的解也可以表示成 特征数函数的形式,称为特征数关联式。
通过对流换热微分方程的无量纲化可以导出与对 流换热有关的特征数。
第五章对流传热分析

第五章对流换热分析通过本章的学习,读者应熟练掌握对流换热的机理及其影响因素,边界层概念及其应用,以及在相似理论指导下的实验研究方法,进一步提出针对具体换热过程的强化传热措施。
5.1 内容提要及要求5.1.1 对流换热概述1.定义及特性对流换热指流体与固体壁直接接触时所发生的热量传递过程。
在对流换热过程中,流体内部的导热与对流同时起作用。
牛顿冷却公式q h(t w t f ) 是计算对流换热量的基本公式,但它仅仅是对流换热表面传热系数h 的定义式。
研究对流换热的目的是揭示表面传热系数与影响对流换热过程相关因素之间的内在关系,并能定量计算不同形式对流换热问题的表面传热系数及对流换热量。
2.影响对流换热的因素(1)流动的起因:流体因各部分温度不同而引起密度差异所产生的流动称为自然对流,而流体因外力作用所产生的流动称为受迫对流,通常其表面传热系数较高。
(2)流动的状态:流体在壁面上流动存在着层流和紊流两种流态。
(3)流体的热物理性质:流态的热物性主要指比热容、导热系数、密度、粘度等,它们因种类、温度、压力而变化。
(4)流体的相变:冷凝和沸腾是两种最常见的相变换热。
(5)换热表面几何因素:换热表面的形状、大小、相对位置及表面粗糙度直接影响着流体和壁面之间的对流换热。
综上所述,可知表面传热系数是如下参数的函数h f u, t w , t f , , c p , ,,, l这说明表征对流换热的表面传热系数是一个复杂的过程量,不同的换热过程可能千差万别。
3.分析求解对流换热问题分析求解对流换热问题的实质是获得流体内的温度分布和速度分布,尤其是近壁处流体内的温度分布和速度分布,因为在对流换热问题中“流动与换热是密不可分”的。
同时,分析求解的前提是给出正确地描述问题的数学模型。
在已知流体内的温度分布后,可按如下的对流换热微分方程获得壁面局部的表面传热系数由上式可有h xtt x yW/(m 2 K)w,x其中为过余温度,h xxyW/(m 2 K)w,x对流换热问题的边界条件有两类,第一类为壁温边界条件,即壁温分布为已知,待求的是流体的壁面法向温度梯度;第二类为热流边界条件,即已知壁面热流密度,待求的是壁温。
第五章 对流换热

Pr 1
t
边界层具有以下几个特征:
• 边界层的厚度与壁面特征长度l相比是很小的量; • 流场划分为边界层区和主流区; • 根据流动状态,边界层分为层流边界层和紊流 边界层。紊流边界层分为层流底层、缓冲层与紊流核
热边界层和流动边界层都从平板前沿开始同时形成 和发展,两种边界层厚度的相对大小取决于; 1. 流体运动粘度 。反映流体动量扩散的能力, 值 越大,流动边界层越厚。 •
2. 热扩散率 a 反映物体热量扩散的能力, 热边界层越厚。 具有相同的量纲m2/s
a 值越大,
普朗特数
a
Pr
无量纲数 ,流体的动量扩散能力与热量扩散能力之比. 对于层流边界层:
惯性力 体积力 压力梯度 粘性力
(3) 能量微分方程
• 根据微元体的能量守恒导出。不考虑位能和动能变化:
dU h d
导热 对流 热力学能的增加
2t 2t t t t c p u x v y x 2 y 2
• 对于局部对流换热
于是
q x hx t w t f x
q x dA hx t w t f x dA
A A
如果固体表面温度均匀(等壁温边界)
t w tf x t w tf
常数
t w t f hx dA
A
将该式与前式比较,可以得出固体表面温度均匀条件下平均表面传热系数与 局部表面传热系数之间的关系式:
x。 c
2 105 ~ 3 106
2) 热边界层(温度边界层 )
• 当温度均匀的流体与它所流过的固体壁面温度 不同时,在壁面附近将形成一层温度变化较大 的流体层。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
wton’s law of cooling:−=W/m 2dxdtq λ−=Contents第一节对流换热概述Analysis on Convection第二节对流换热微分方程组The Convection Heat Transfer Equations第三节边界层换热微分方程组Convection Differential Equations of Boundary Layer 第四节边界层换热积分方程(自学)第五节动量传递和热量传递的类比(自学)第六节相似理论基础Basis of similarity theoryConvection is the mode of energy transfer between a solid surface and the adjacent liquid or gas that is in motion, and it involves the combined effects of conduction and fluid motion.(流体与固体壁直接接触时所发生的热量传递过程,称为对流换热)The faster the fluid motion, the greater the convection heat transfer.We will study how to calculate the convection heat-transfer coefficient h in Chapter 5 and Chapter 6.5-1 Analysis on Convection(对流换热概述) Convection transfer problemHeat exchangers Tubes in steamboiler (蒸汽锅炉的管束)Tube-shell heat exchanger (管壳式换热器)Condenser ofrefrigerator Tubes withfins (翅片管束)图5-1几种常见的换热设备示意图Factors influencing convection heat transfer :Flow causes of fluid (流体流动的起因)、flow states ( 流动状态)、properties of fluid (流体物性)、change of phase of fluid (流体物相变化)、geometry parameters (壁面的几何参数),and so on 。
1.Causes and States of Flow (流动的起因和状态)(1) Causes of flow(流动起因)Forced convection(受迫对流):if the fluid is forced to flow over the surface by external means such as a fan ,pump,or the wind .naturalforced h h >Natural (or free) convection(自然对流):if the fluid motion is caused by buoyancy (浮力) forces that is induced(引起) by density difference due to the variation of the temperature in the fluid.Examples :air free convection :h=5~25W/(m 2.K )air forced convection :h=10~100W/(m 2.K )(2) flow states ( 流动状态)Whatever the causes of flow are ,the flow states are consist of laminar flow (层流)and turbulent flow (紊流)Laminar flow ——characterized by smooth streamlines (流线) and highly ordered motion due to the fluid flowing in laminae(层) or layers(整个流场呈一簇互相平行的流线)Turbulent flow ——characterized by velocity fluctuation (波动) and highly disordered motion (流体质点做复杂无规则的运动)lt h h >2.The thermal properties of fluid (流体热物性)Properties:density(密度) ρ[kg/m 3], specific heat(比热) c [J/(kg. ℃)]thermal conductivity(导热系数) λ[ W/(m. ℃)],dynamic viscosity(动力粘度) μ[kg/(s.m)]kinematic viscosity(运动粘度) ν(m 2/s ),volume expansion coefficient (体积膨胀系数) α(1/K),ρμ=v p p T T ⎟⎠⎞⎜⎝⎛∂∂−=⎟⎠⎞⎜⎝⎛∂∂=ρρυυα11自然对流换热增强↑⇒α)( 多能量单位体积流体能携带更、↑↑⇒h c ρ)( 热对流有碍流体流动、不利于↓↑⇒h μ↑↑⇒h λ)(间导热热阻小流体内部和流体与壁面where Ideal gasα=1/T***Characteristic temperature (定性温度)Average temperature of fluid (流体平均温度)t fthe surface temperature of wall (壁表面温度)t wthe arithmetic average temperature of the fluid and the wall surface (流体与壁的算术平均温度)(t f +t w )/2.3.Change of phase (流体的相变)Change of phase heat transfer(相变换热):Condensation (凝结)、Boiling(沸腾)、sublimation(升华)、freeze(凝固)、thaw(融化) and so onSingle phase heat transfer (单相换热)glechange h h sin >4. Geometry parameters of convection surface(换热表面几何因素)shape, sizes, position and roughnessExterior flow (外掠): flow across the flat plate,flow across cylinders and tubes (外掠平板、外掠圆管及管束)Interior Flow (内流): flow in a pipe ,flow in slot (管内、槽内流动)。
Forced convectionNatural convectionLower surface of a hot plateUpper surface of a hot plate Flow in a pipe Flow across a pipe***Characteristic Length (定型尺寸) l由于壁面几何形状的影响,在分析计算中可采用对换热有决定意义的特征尺寸作为依据,这个尺寸称定型尺寸。
Example :for a flat plate, l is the length of the plate in the flow direction .If the fluid flow in a pipe , l is the diameter d of the pipe, l=d),,,,,,,,(l c t t u f h p f w μαρλ=5. Sorts of ConvectionGenerally ,the convection heat transfer coefficient h can be expressed the function of those factors mentioned above5-2 The Convection Heat Transfer Equations对流换热微分方程组To simplify the analysis we assume:(1)The fluid is incompressible and Newton-style ;(2)The properties of fluid are constant and no heat resources. ;(3)The energy generated by viscosity is negligible (粘性耗散产生的耗散热可以忽略不计)。
**Newton-style fluid (牛顿型流体)服从y u∂∂=μτ定律的流体称牛顿型流体。
The viscous forces are described in terms of a shear stress between the fluid layers ,that this stress is assumed to be proportional to the normal (法线)velocity gradient .yu∂∂=μτ2-1 Differential Equation for the convection heat transfer process(对流换热过程微分方程式)xy q u Where y=0,u=0,no-slip conditionHeat transfer from the solid surface to the fluid layer adjacent to the surface is by pure conductionThe fluidlayer ismotionlessHeat transfer can be expressed as xw x y t q ,⎟⎟⎠⎞⎜⎜⎝⎛∂∂−=λ:0=y W/㎡λis thermal conductivityof fluidx w y t ,⎟⎟⎠⎞⎜⎜⎝⎛∂∂——is the temperature gradient at the surface x from leading edge of the flat plate(x 点帖壁处流体的温度梯度,K/m)According to Newton’s law of coolingxx x f w x x t h t t h q Δ⋅=−=)(h x ——the local convection heat transfer coefficient at surface x (壁面x 处的局部表面传热系数),W/(m 2.K )。
