植树问题(1)
2021人教版小学五年级上册数学第七单元第一课时《植树问题》课件

学习方法指导
同学们,天道酬勤,一个人学习成绩的优劣取决于 他的学习能力,学习能力包括三个要素:
规范的学习行为; 良好的学习习惯; 有效的学习方法。
只要做好以上三点,相信你一定会成为学习的强者。
加油!加油!加油!
下课了!
—— 小朋友们再见——
2000÷50=40(个) 40+1=41(盏) 41×2=82(盏) 答:一共要安装82盏路灯。
做一做
2.小明家门前有一条35m的小路,绿化队要在 路旁栽一排树。每隔5m栽一棵树(一端栽一端 不栽)。一共要栽多少棵?
做完后,可以画线 段图验证一下。
35÷5=7(棵) 答:一共要栽7棵树。
拓展训练
5 555
20÷5=4 要栽5棵
再看看25m可以栽几棵。
你发现了什么规律?不画图,你知道30m、35m 要栽几棵树吗?
新知探究
100m共有20个间隔,两端都要
栽,所以一共要栽 21 棵树。
因为两端都要栽,所以 栽树的棵数比间隔数多1。
规范解答 100 ÷ 5 +1 =21(棵) 答:一共要栽21棵树。
3.填空。
1.在一条长80米的小路上植树,每两端都植,每隔
10米植一棵,一共需要____9____棵;这条路被分 成了____8____段,棵数比段数____多____。
2.在相距50米的两楼之间栽一排树,每隔5米栽一
棵树,共可栽____9____棵树。
3.计划在长600米的一条堤上,从头到尾每隔6米
课堂小结
通过前面的学习,你有什么发现吗? 小结:1.不封闭路线两端都植树的解题方法:
总距离÷株数=间隔数 棵数=间隔数+1 2.不封闭路线两端都不植树的解题方法:
小学奥数6-1-13 植树问题(一).专项练习及答案解析

1.封闭与非封闭植树路线的讲解及生活运用。
2.掌握空心方阵和实心方阵的变化规律.3.几何图形的设计与构造一、植树问题分两种情况:(一)不封闭的植树路线.① 若题目中要求在植树的线路两端都植树,则棵数比段数多1.全长、棵数、株距之间的关系就为:棵数=段数1+=全长÷株距1+全长=株距⨯(棵数1-)株距=全长÷(棵数1-)② 如果题目中要求在路线的一端植树,则棵数就比在两端植树时的棵数少1,即棵数与段数相等.全长、棵数、株距之间的关系就为:全长=株距⨯棵数;棵数=段数=全长÷株距;株距=全长÷棵数.③ 如果植树路线的两端都不植树,则棵数就比②中还少1棵.全长、棵数、株距之间的关系就为:棵数=段数1-=全长÷株距1-.株距=全长÷(棵数1+).全长=株距⨯(棵数+1)(二)封闭的植树路线.在圆、正方形、长方形、闭合曲线等上面植树,因为头尾两端重合在一起,所以种树的棵数等于分成的段数.全长、棵数、株距之间的关系就为:棵数=段数=周长÷株距.知识点拨教学目标5-1-3.植树问题(一)二、解植树问题的三要素(1)总路线长(2)间距(棵距)长(3)棵数,只要知道这三个要素中任意两个要素,就可以求出第三个.三、方阵问题(1)明确空心方阵和实心方阵的概念及区别.(2)每边的个数=总数÷41+”;(3)每向里一层每边棋子数减少2;(4)掌握计算层数、每层个数、总个数的方法,及每层个数的变化规律。
例题精讲【例 1】大头儿子的学校旁边的一条路长400米,在路的一边从头到尾每隔4米种一棵树,一共能种几棵树?【考点】直线上的植树问题【难度】1星【题型】解答【解析】从图上可以看出,每隔4米种一棵树,如果20米长的路的一边共种了6棵树,这是因为我们首先要在这条路的一端种上一棵,就是说种树的棵树要比间距的个数多1,所以列式为:400÷4+1=101(棵).【答案】101棵【巩固】在一条长240米的水渠边上植树,每隔3米植1棵。
植树问题1(1)
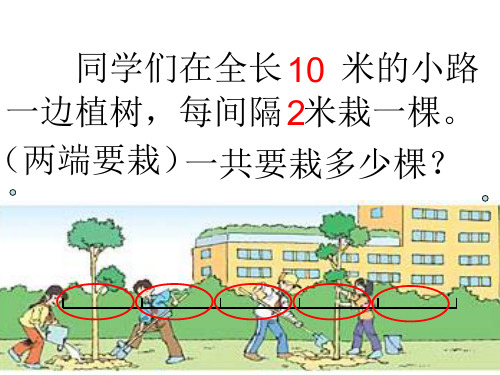
(两端要栽)一共要栽多少棵?
同学们在全长10 米的小路一边植 树,每间隔2米栽一棵。(两端要栽) 一共要栽多少棵?
同学们在全长10 米的小路一边植 树,每间隔5米栽一棵。(两端要栽) 一共要栽多少棵?
同学们在全长375米的小路 一边植树,每间隔 5 米栽一棵。
(两端要栽)一共要栽多少棵?
同学们在全长1307050米的小路 一边植栽花树,每间隔 150 米栽一棵。
(两端要栽)一共要栽多少棵?
(1)同学们做广播操,其中一列队伍
√ 长为60米,相邻的两个学生之间距离是2米,这一列一共有多少个学生?
√ (2)园林工人沿公路一侧植树,每隔2
米种一棵,一共种了6棵。从第1棵到最 后一棵的距离有多远?
× (3)一共有25个小组,每组种了5棵树苗,
购买花了1250元,每棵树苗多少元?
同学们在全长10米的小路一边植树,每间隔2米栽一棵。
回想一下我们今天学 过的内容
能不能用最简单的线 段图表示出棵数和间隔数 的关系?
2000÷50+1
植树问题1

植树问题以植树为内容,研究植树的棵树,棵与棵之间的距离(棵距)和需要植树的总长度(总长)等数量间关系的问题,称为植树问题。
其实,植树问题只是一个习惯上的称呼,并不一定每个问题都是谈植树,不过,植树问题的模型还是以植树最为形象。
植树问题在生活中应用很广泛,主要有两种情况:1、在直线上或不封闭的曲线上植树。
如果首尾两端都可以种1棵树,那么植树的棵树要比分的段数多1。
即:棵树=总长÷棵距+12、在封闭线路(如长方形、正方形、圆)上植树。
因为首尾两端重合在一起,所以植树的棵树就等于可分的段数。
即:棵树=总长÷棵距例1一条路长1000米,在路的一边从头到尾每隔5米种一棵树,一共可以种多少棵树?(1)将1000米的路每5米分成一段,一共分成了多少段?(2)一共可以种多少棵树?【课堂练习】1.有一条长1800米的公路,在公路的一侧从头到尾每隔25米栽一棵树,一共需要准备多少棵树苗?2.忆江南小区两座楼房之间相距36米,物业管理公司每隔2米栽1株花,一共要栽多少株花?例2一个湖泊周围长3200米,沿湖泊周围每隔4米栽一棵杨树,每两棵杨树中间栽一棵柳树,湖泊周围杨树和柳树各栽了多少棵?【课堂练习】一个圆形花圃周长36米,每隔3米放一盆花,一共放了多少盆花?例3某学校在道路的一侧栽树,每隔6米栽一棵,从起点到终点共栽了12棵。
求这条道路长多少米?【课堂练习】1.公园路边的一侧放了一些椅子,从起点到终点一共有68把,每两把椅子之间都相距10米,求这条路长多少米?2.沿一个花园四周每隔6米栽一棵树,一共栽了65棵,求这个花园的周长是多少米?例4为迎接国庆节,园林部门在一条长500米的道路两旁放置花盆,一共放置了102盆,问两个花盆间间隔多少米?(1)道路的一侧放了多少盆花?(2)道路的一侧一共有多少个间隔?(3)两个花盆间的间距是多少米?1.在600米长的公路两边从头到尾栽101棵树,每两棵树之间距离相等,每两棵之间相距多少米?2.两棵大树之间相距120米,园林部门计划在两棵大树中间补栽14棵小树,每两棵树的间隔距离相等,树的间隔是多少米?例5在一块正方形池塘的四周种树,每边都种18棵,并且四个顶点都种有一棵树。
植树问题一

植树问题(一)
2段,要锯几次?
锯成3段呢?锯成4段呢?锯成5段呢?
你发现什么了?
练习:
1. 把4条绳子连接成一条长绳子,要打几个结呢?
2. 一根6米长的竹竿,每隔1米做一个标记,一共需要做几个标记?
3.公园路边放了一些椅子,从起点到
终点共21把,每2把椅子之间有一头石狮子,这条路边一共有多少头石狮子?
一共挂了5个灯笼,每相邻2个灯
笼之间相距1米,学校大门款多
少米?
练习:
1. 一条街道的一侧有12盏路灯,再每两盏路灯之间有2课树,有多少棵树?
2.在一条街道的一旁植树,从一头到另一头一共植6课树,每相邻2课树之间相距5米,这条街道长多少米?
小林家住在6楼,从1楼到6楼一共要上多少层?从1楼到30楼一共要上多少层?
练习:
1、小芳家住在30楼,从1楼到30楼
一共要上多少层?
2、小亮从一楼到三楼用了2分钟,照
这样的速度,他从一楼到6楼需要
几分钟?
3、南校区的教学楼共有5层,每层有
16个台阶。
李红的教室在3楼。
算一算,李红从1楼到3楼要走多
少个台阶?冲关我最棒
1、植树节这天,同学们在一段马路的一边种树,从马路的一头到另一头一共种了6课树,每相邻2课树之间相距3米。
这段马路长有多少米?
2、小明家住在5楼,小明从1楼到2楼用了10秒,那么小明从1楼到5楼用了多少秒?
3、一张纸条想下图那样撕成1下成为2段,那么撕2下成为几段?撕5下呢?自己撕撕看。
1.植树问题(一)

学
过
程
一、揭示课题,导入新课
这节课我们来探索植树中的数学问题,揭示课题,板书:《植树问题》。
二、操作探究,感知规律
1.动手操作,发现规律。
出示例题:同学们在全长20米的小路一边种树,每隔4米种一棵。一共需要多少棵树苗?
想一想有几种情况,画一画图,再解答。(图上的20厘米表示20米)
(1)学生独立活动,动手“植树”,感知规律。
பைடு நூலகம்教学内容
植树问题(一)
教学
目标
1.通过探究发现一条线段上两端要种和两端不种两种情况植树问题的规律。
2.使学生经历和体验“复杂问题简单化”的解题策略和方法。
3.培养渗透数形结合的思想,培养学生借助图形解决问题的意识和能力。
教学重点
探究发现一条线段上两端要种和两端不种两种情况植树问题的规律
教学准备
课件,白纸和尺子
都符合“棵树=段数+1”的规律吗?板书:结论
三、应用规律,适当提升
1.同学们在全长100米的小路一边种树,每隔5米种一棵(两端要栽)。一共需要多少棵树苗?
2.有一条50米的小路,在小路的两旁每隔5米放一盆兰花(两头都放),一共要多少盆兰花?
3.想一想:
(1)园林工人沿公路一侧植树,每隔6米种一棵,一共种了36棵。从第1棵到最后一棵的距离有多远?
预计:两头都栽棵树=段数+1
两头不栽棵树=段数-1
只栽一头棵树=段数
(2)小组交流,说明“植树”规律
(3)汇报植树棵数,结合课件理解,教师将情境图转化为线段图。
(4)思考:为什么同样是20米的一段,有的种6棵,有的种5棵,有的种4棵?在生活中,什么情况下可能会一端种,一端不种?什么情况下可能两端都不种或两端都种?
典型应用题(一):植树问题

典型应用题(一):植树问题在不封闭路线上植树【例1】园林工人在长96米的公路两边每隔6米栽一棵树(首尾都栽)现在要改成每隔4米栽一棵树,那么不用移裁的树有多少棵?思路引导因为4和6的最小公倍数是12,故是12的整数倍的地方不需要移动,所以求出一侧栽树的棵数再乘2,即可得出不用移栽的树的总棵数。
正确解答:因为4和6的最小公倍数是12,所以96÷12=8(棵)(8+1)×2=9×2=18(棵)答:不用移栽的树有18棵。
解决这类问题的关键是要明白求4和6的最小公倍数是解决问题的关键,其次要掌握植树问题中两端都植树的数量关系式。
【变式1】园林工人在长60米的小路两边每隔5米栽一棵树(首尾都栽),现在要改成每隔4米栽一棵树,那么不用移栽的树有多少棵?【例2】为了美化乡村环境,王张村准备给一条长800m的村道两侧栽树,每隔20m栽一棵(只栽一端)。
一共需要多少棵树苗?思路引导只栽一端的植树问题,公式是:植树棵数=间隔数,两侧的棵数=一侧的棵数×2,据此计算即可。
正确解答:800÷20×2=40×2=80(棵)答:一共需要80棵树苗。
本题主要考查植树问题,关键分清植树棵数和间隔数的关系做题,并且看清楚是路的两侧还是一侧植树。
【变式2】聪聪家门前有一条长60米的小路,绿化队要在小路的两旁栽树(一端栽,一端不栽)。
相邻两棵树之间的距离是5米,一共要栽多少棵树?【例3】“一根木头要把它平均分成5段,每锯一段需要5分钟,锯完这根木头需要多少分钟?”这题属于植树问题中的()。
A.两端都不栽B.两端都栽C.一端栽一端不栽思路引导锯木头,锯1次,平均分成2段;锯2次,平均分成3段……锯的次数=段数-1;属于植树问题中的两端都不栽,棵数=间隔数-1,锯木头的次数=段数-1,相当于植树问题中的两端都不栽的情况,列式为:5-1=4(次),5×4=20(分钟)。
植树问题(一)

植树问题(一)姓名
1.同学们在32米条的小路旁栽树,每隔8米栽一棵。
如果两端都要栽,需要()棵树。
2.小丽给路边的小树浇水,这条路长20米,每两棵小树之间相隔4米,路的两端都有小树,小丽一共要浇()棵。
3.小强在学校一条长27米的路的一边插上彩旗,每隔3米插1面,如果只有一端插,另一端不插,需要()面彩旗。
4.在一条长18米的线上挂气球,每隔2米挂一个,如果只有一端挂,另一端不挂,需要()气球。
5.一条长45米的道路一侧,每间隔5米摆一盆鲜花,如果两端都不摆放,需要()鲜花。
6.一条公路长48米,在路的两边每隔8米安装一根电线杆,路的两端都不安装,需要()根电线杆。
7.小红用同样的速度在学校林荫道上散步,她从第1棵走到第6棵用了5分钟,当她走了9分钟时,应到达第()棵树。
8.小军用同样的速度走在插着彩旗的一条路上,他从第1面旗走到第4面旗用了6分钟,当他走了14分钟时,应到达第()面彩旗。
9.妈妈用同样的速度参观一条路上新建的多幢住房,她从第1幢楼房走到第4幢时用了9分钟。
当她走了24分钟时,看了()幢楼房。
10.在长45米的道路一侧栽了一排柳树,起点和终点都栽了,一共是10棵,相邻两棵的距离都相等,相邻两棵之间的距离是()米。
11.在学校一条长30米的道路一边挂小旗,起点和终点都挂了,一共是11面,相邻两面旗的距离都相等地,每两面旗之间的距离是()米。
12.体育馆门前的一条长40米路的一边在竖木桩,在起点和终点都竖了一根,一共是9根,相邻两根木桩的距离都相等,相邻两根木桩之间的距离是()米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
植树问题
教学内容:《义务教育课程标准实验教科书数学(五年级上册)》第106页
教学目标:
知识技能目标:
1、利用学生熟悉的生活情境,通过动手操作的实践活动,使他们发现间隔数与植树棵数之间的关系;
2、通过小组合作、交流,在理解间隔数与棵数之间规律的基础上解决简单的植树问题。
过程目标:
1、使学生经历感知、理解知识的过程,培养学生从实际问题中发现规律,并应用规律来解决问题的水平;
2、渗透数形结合的思想,培养学生借助图形解决问题的意识;
3、培养学生的合作意识,养成良好的交流习惯。
情感目标:
1、通过实践活动激发热爱数学的情感;
2、感受日常生活中处处有数学,体验学习成功的喜悦。
教学重点:理解“植树问题(两端要种)”的特征,应用规律解决问题
教学难点:理解“间隔数+1=棵数,棵数-1=间隔数”
教学准备:课件
教学过程:
一、课前导入
猜谜语:两棵小树十个杈,不长叶子不开花。
能写会算还会画,天天干活不说话。
二、创设原型
1、教学“间隔”的含义
师:是的,每位同学都有一双灵巧的手,在手里面还藏着有趣的数学知识,你想了解他吗?请举起你的右手。
(五指伸直、并拢、张开)
师:在张开的五指中你看到了什么?数学中我们把这个“空隙”叫“间隔”。
(板
书),数一数一只手中有几个这样的间隔?“4”在数学上称作“间隔数”,那么4根手指呢?3根呢?2根呢?
2、举例生活中的“间隔”
师:“间隔”在生活中处处可见,孩子们你们能说说生活中相关间隔的现象吗?老师也收集了一些,请同学们看。
那孩子们我们在站队的时候有间隔吗?(请生站起来示范),通过这个活动你们发现了什么?
3、引入课题
师:像这样跟间隔相关的问题在数学上统称为“植树问题”,这节课我们就一起来研究植树问题。
(板书课题)
三、构建模型
1、教学例1
课件出示:同学们要在全长20米的小路一边植树,每隔5米栽一棵(两端要栽)。
一共需要多少棵树?
师:春天,是植树的大好季节,为了美化校园,孩子们在干什么?同学们是怎样植树的?(生读)
(1)这道题告诉了我们什么信息呢?
分析题目:老师用尺子解释“一边”和“两端”的意思,让学生指一指。
并说明这节课主要研究两端种树的问题。
(2)先让学生们大胆猜想种多少棵?老师板书。
(3)学生以小组为单位讨论验证学生们猜想的方法,并请同学上台来演示。
(4)老师再用多媒体课件展示线段图。
并总结出两个关系式:
间隔数=全长÷间隔长度栽树的棵树=间隔数+1(板书)
2、试一试
师:如果老师把题目改一改,看看谁还会?
例2、同学们在全长100米的小路一边植树,每隔5米栽一棵(两端要栽)。
一共需要栽多少棵树?
(1)生轻轻读题,说说从这个题目中你了解了些什么信息?
(2)学生独立画线段图解决问题。
三、利用模型解决问题
师:恭喜大家,顺利通过挑战!接下来我们来到智慧大闯关?
课件出示:第一关:我会选
第二关:我会填
第三关:我会解决
第四关:问题角逐(这题设计有三种植树的方法,为下节课学习留下悬念)
四、全课小结
通过这节课的学习,你有什么收获?。
