线性网络的讲义几个定理
第2章 线性网络的基本分析方法和定理

2.1.1 电阻串联
图2.2 开关闭合后的实物图 如图2-2所示,当开关闭合时,两个灯泡都亮。把两只小灯泡顺次连接在电路 里,一只灯泡亮时,另一只灯泡也亮。像这样把元件逐个顺次连接起来的电路 称串联电路。
6
2.1.1 电阻串联
图2.3 调换开关位置后的实物图 如图2-3所示,当调换开关位置后,两个灯泡都亮。由以上现象可以得出,串 联电路的电流只有一条路径,通过一个元件的电流同时也通过另一个;串联电 路中只需要一个开关,且开关的位置对电路没有影响。
7
2.1.1 电阻串联
S
I U
U1
U2
I1
R1
I2 R2
图2-4 实例2-2电路图
在电路中,把几个电阻元件依次首尾连接起来,中间没有分支,在电源的作用 下流过各电阻的是同一电流,这种连接方式叫做电阻的串联,如图2-4所示为 两个电阻串联后由一个电源供电的串联电路,通过测量得知总电压U=U1+U2, 电流I=I1=I2,等效电阻R=R1+R2,因此串联电路的特点如下:
R = R1 + R2
(2-3)
由式(2-3)表明:串联电路中的等效电阻等于各个电阻之
和。
实例2-3 将3Ω,6Ω和9Ω三个电阻串联在电路中,其等效
电阻R为多少?
解:因为串联电路中的等效电阻等于各个电阻之和,所以
R=3+6+9=18Ω
12
2.1.1 电阻串联
4.串联电路的功率分配
如图2-4所示,设R1上的电压为U1,功率为P1;R2上的电压为U2,功率为P2 。 根据 U = U1+ U2 得 IR= IR1+IR2 等式两边同时乘以I,得 I2R = I2R1 + I2 R2
第四章 网络定理

a
-
1K 0.5 i1 u (b)
i b+
列方程:
2.5i1 i u 1Ki1
解得: Ro 0.4K 41
如果要用开短路法,求短路电流。
i1 1K
a
+
10V 1K 0.5 i1
iSC
(c)
-
列方程:1.5i1 iSC
i1
10 1K
解得: iSC 15mA 42
例:图(a)电路中,N为有源线性二端
25
端口电压电流关联
u Roi uoc
26
证明如下:。
端口支路用电流源i 替代,如图(a),根
据叠加定理,电流源单独作用产生
u’=Roi [图(b)],网络内部全部独立电
源共同作用产生u”=uoc [图(c)]。由此
得到
u u' u" Roi uoc
27
例6 求图(a)网络的戴维南等效电路。
isc
i2
i3
iS2
R1 R1 R2
iS1
uS R3
iS2
求Ro,图(b)求得
Ro
(R1 R2 )R3 R1 R2 R3
画出诺顿等效电路,如图(c)所示。
33
含源线性电阻单口网络的等效电路 只要确定uoc,isc或Ro 就能求得两种等 效电路。
34
戴维南定理和诺顿定理注意几点:
1. 被等效的有源二端网络是线性
2.求电阻Ro 图b网络的独立
电压源置零,
得图c,设端口 电压为u',端 上电流为 i '
1 2 - 6 i1’ +
i’ +
4
u’
i1’
3-4线性网络的叠加定理
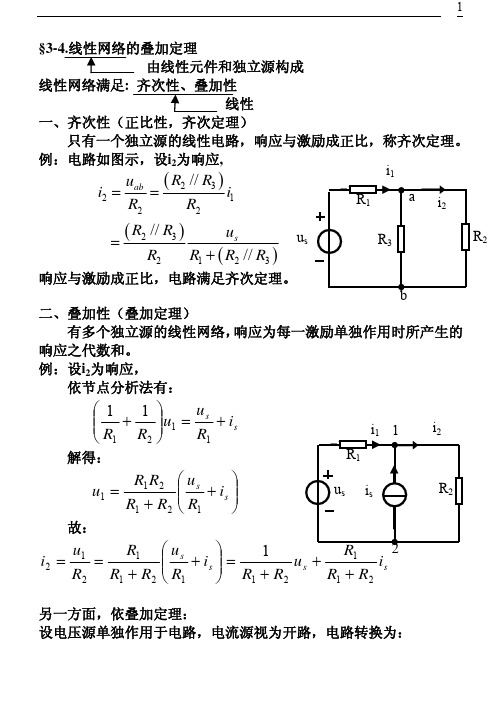
只有一个独立源的线性电路,响应与激励成正比,称齐次定理。
例:电路如图示,设i 2为响应,()()()232122232123//// //ab sR R u i i R R R R u R R R R ===+二、叠加性(叠加定理) 有多个独立源的线性网络,响应为每一激励单独作用时所产生的响应之代数和。
例:设i 2为响应,依节点分析法有:21211212⎠⎝i 2=另一方面,依叠加定理:设电压源单独作用于电路,电流源视为开路,电路转换为:2112R R u i s+=−s i R R R i 21122+=−依叠加定理,当两个独立源同时作用于电路时,有:12212212121s s R i i i u i R R R R −−=+=+++与节点电位分析法求得的结论一致。
注:在使用叠加定理时,应注意以下几点:1) 线性电容()视为端电压随时间变化的理想电压源;c q u ∝线性电感(L i ψ∝)视为端电流随时间变化的理想电流源。
2)当某一激励源单独作用时,其它激励源视为零值(电压源视为短路;电流源视为开路)。
3)受控源不能视为激励。
4)叠加定理不适合功率计算(非线性 22Ri RuP ==∵)。
5)多个激励时,只有当所有激励都扩大k 倍时,响应才扩大k 倍。
例3-17用叠加定理求图中电压U 1及电流源的功率解:设电压源单独作用,电流源视为开路,电路为右图所示:依分压公式有: V U 102510//201010//2011=×+=−设电流源单独作用,电压源视为短路,电路为下图所示:()V U 65.110//10//2021=×=−设电压源和电流源同时作用:V U U U 1661021111=+=+=−−电流源的端电压:V U U 91625251=−=−=电流源吸收的功率(注意:电流源为关联参考方向):9 1.513.5P U I W =×=×=例3-18用叠加定理求I x解:设电压源单独作用(受控源不能单独作用),电路如右图所示:()AI I I X X X 2010212 111=∴=−++−−−设电流源单独作用,电路为右图示:用节点分析法,有:⎪⎩⎪⎨⎧−=+=⎟⎠⎞⎜⎝⎛+−−补充212311212121X X I U I U解得:A I X 6.02−=−()A I I I X X X 4.16.0221=−+=+=−−例3-19设,利用响应与激励成比例的性质求:V U S 4−=?=IIA I 1=V U S 36=,由图可推得:解:设依齐次定理:S S S U I U I k kU I 361361=⇒==⇒=依题意: ()A I V U S 9143614−=−=⇒−=作业:3-14,3-17。
线性网络的一般分析方法和网络定理

② 对各独立节点按节点方程的一般形 式列写节点方程;
③ 解方程求出各节点电压;
④ 根据节点电压求出各支路电压和电 流。
3.节点方程的特殊处理方法
(1) 含理想电压源电路的节点方程
在应用节点分析法分析电路时,有时 遇到电路中含有理想电压源支路的情况, 如用上述常规方程来列写节点方程将产生 困难。因为节点方程是根据KCL导出的, 理想电压源支路的电流事先并未给出。
-
图 3
1
节 点 分 析 法 用 图
2.节点方程
以图3-1所示的直流电路为例,阐 明节点方程的导出步骤。
① 选定参考节点(本例以节点4为 参考节点),标明各支路电流的参考方 向,如图3-1所示。
② 根据欧姆定律,将各支路电流 用节点电压和支路电导表示。
③ 将式(3-2)代入式(3-1)。
现将节点分析法的解题步骤归纳如下:
第三章 线性网络的一般分析 方法和网络定理
3.1 节点分析法 3.2 回路分析法 *3.3 割集分析法 3.4 叠 加 定 理 3.5 替 代 定 理 3.6 戴维南定理与诺顿定理 3.7 互 易 定 理 3.8 电路的对偶性
3.1 节点分析法
1.节点电压
以图3-1所示的直流网络 为例。这个网络具有4个节点, 6条支路。标明各支路电流参 考方向,如图3-1所示。
图3-20网络的拓扑图
2.割集与基本割集
根据定义,树不能包含闭合回路, 因此,树支电压之间不能用KVL相联系。 就KVL来说,树支电压线性无关,即树 支电压是一组完备的独立电压变量。
一个具有n个节点的网络,其树支数 为(n-1),因此选出树后,就有(n-1)个树 支电压,如何写出求解这些电压变量所 需的(n-1)个独立方程呢?
线性网络电路的基本分析方法

法和定理 3.4叠加定理 3.4叠加定理
定理内容: 在线性电路中,当有两个或两个 以上的独立电源工作时,则任意支 路的电流或电压都可以认为是电路 中各个电源单独工作而其他电源不 作用时,在该支路中产生的各电流 或电压分量的代数和!!!
定理刨析:
1、条件: a、在线性电路中,非线性电路不能用叠加定理分析
•U (V)
•O
•I (A)
b、两个或两个以上电源工作
定理刨析:
2、各个电源单独工作而其他电源不作用, 对“不作用”的理解: a:电压源不作用相当于将电压源做短路处 理。 b:电流源不作用相当于将电流源做断路处 理。
定理刨析:
3、叠加代数和,如何确立正负号?
a 先看所给电路图是否给出参考方向,当给出时 我们可直接利用,若没给出我们必须先进行标注 (可任意给出)。 b 当各个电压源单独工作时,各负载上电流或电 压的实际方向与参考方向相同时取正,反之取 负!!! C 进行叠加后,若电流或电压取正表明此时电路 的实际流向与参考方向相同,反之取负,表明实 际流向与参考方向相反
注意了!!!!!!!
原电路的功率不等于各分电路计算所得的 功率的叠加
例. 求图中电压 u 。
6Ω
解:
6Ω
(1) 10V电压源单独作用, 电压源单独作用, 4A电流源开路 电流源开路
4Ω
u
10V
4A
4Ω
u(1)4 u源自= × 10 4+6(1)
10V
= 4V
u
4Ω
( 2)
(2) 4A电流源单独作用, 电流源单独作用, 电流源单独作用 10V电压源短路 电压源短路 共同作用: 共同作用:
6Ω
第四章 线性网络定理 电路理论 教学课件-精品文档

例3
求电压Us 。
+ 10V –
I1 6
4
10 I1 + –
Us
+ – 4A
解: (1) 10V电压源单独作用: (2) 4A电流源单独作用:
I1'
+ 10V –
6
4
10 I1' + –
I1'' 6
4
10 I1'' + –
Us '
–
+
+ Us' ' –
4A
Us'= -10 I1'+U1'
2.5A
10V
2
1A
不满足
2.5A
5 10V
2
?
5V
5V
1.5A
1A
满足
?
A +
5V
1A
A + 1V B
+ _1V
A + 1V B
1
1A
不满足
?
B
1A
2) 被替代的支路和电路其它部分应无耦合关系。
§4—2 叠加定理 (Superposition Theorem)
概念:在多个电源同时作用的线性电路(由线 性元件组成的电路)中,任何支路的电流或 任意两点间的电压,都是各个电源单独作用 时所得结果的代数和。
I1 R1
+ I2
I3
I1 R1
I2
I3
+
R2
R3
8V 4// 4 R2 // R3 = 4V × 8 = U= 8 4// 4) R1 +R2 // R3 ( 2+
第03章 线性网络的一般分析方法和网络定理

(2) 解方程,得: UA=21.8V, UB=-21.82V (3) 各支路电流: I2= (UA- UB)/10k= 4.36mA I1=(120-UA)/20k= 4.91mA I3=(UB +240)/40k= 5.45mA I4= UB /40=0.546mA I5= UB /20=-1.09mA
iS22=-iS3
—
… …节点2 … … … … … … … … 。
* 流入节点取正号,流出取负号。
由节点电压方程求得各节点电压后,各支路电流可用 节点电压表示: iS3
un1 i1 R1 un1 i2 R2 un1 un2 i3 R3 un1 un2 i4 R4 un2 i5 R5
5s 3s 3s
2s 4s
8s 6A
例1. 用节点法求各支路电流。 I1 20k UA 10k UB 40k I3 +120V I4 I2 40k I5 20k -240V + * 可先进行 电源变换。
解: (1) 列节点电压方程:
(
1 1 1 1 120 )U A UB 20 K 40 K 10 K 10 K 20 K 1 1 1 1 240 UA ( )U B 10 K 10 K 20 K 40 K 40 K
* 当电路含受控源时,系数矩阵一般不再为对称阵。
iS3 i1 un1 + uS1 R1 iS2 1 i3 i4 R4 0 变换 iS3 i1 G1uS1 un1 1 i3 R3 R3 un2 2 i5 R5
若电路中含电压源与 电阻串联的支路: 记Gk=1/Rk,得: 等效电流源
i2 R2
(G1+G2+G3+G4)un1-(G3+G4) un2 = G1 uS1 -iS2+iS3 -(G3+G4) un1 + (G3+ G4+ G5)un2= -iS3
第四章线性网络的基本定理

除去独立电源,有 u 6I 6(i I)
Ro
u i
=6
画出等效电路,有 R=Ro =6
⊥
Pm =3/8W
3/ 6 6I / 6
6
1/ 6 1/ 31/ 6s
I
0.5V
IsUc oc 3V
3
i 5 A PL 30%
12
Ps
24
Uoc Io Uo
Ro Isc
-
(1)等效变换法(除源) u
(2)外加电源法
Ro
(除源)
i
(3) 开路短路法( Uoc 、 Isc
)(注不意除:电源R压o )与 U电Isocc流方向关联
3、含受控源有源单口网络不一定同时存在两种等效电源
4、含源单口网络与外电路应无耦合; 线 性
5、含源单口网络应为线性网络;
20
练习: 图示电路分别求R=2、6 、18 时的电流I和R
所吸收的功率P。
解:U oc
144 6 36
144 2
24V
Ro
36 36
8 2
6
I 当R=2时: I=3A ,P=18W; 当R=6时: I=2A ,P=24W; 当R=18时:I=1A ,P=18W.
+ Uoc -
21
4-4 最大功率传输定理
Uoc=-1V Ro
Ro= 1
13
例2:已知图示网络的伏安关系为:
含
U=2000I+10
源
并且 Is=2mA.求网络N的戴维南等效电路。
Is
网 络
解: 设网络N 的戴维南等效电路参
N
数为Uoc和Ro,则有
U Uoc (I Is )Ro
