正交各向异性材料介绍
【国家自然科学基金】_正交各向异性材料_基金支持热词逐年推荐_【万方软件创新助手】_20140801
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
科研热词 正交各向异性 损伤 非线性黏弹性 蜂窝夹层结构 耳蜗主动机制 耳蜗 编织复合材料 织构系数 立方晶粒 界面脱粘 界面力学 渐进损伤 混凝土 正交板材 正交各向异性材料 柯蒂氏器 本构模型 本构方程 本构关系 数值模拟 数值分析 拉深 弯曲振动 应力强度因子 复合材料 基本特性 基底膜 土 固有频率 动态 制耳 三维正交机织玻璃纤维 三维五向 ansys
科研热词 正交各向异性 屈曲 各向异性 面内压缩荷载 轴对称 轴向压缩 解析计算 节理岩体 组构张量 精确解 等效连续应变理论 等效变形参数 稳态热传导 破坏准则 电磁场与微波技术 特征值 点应力破坏准则 正交各向异性板 正交各向异性材料 正交化方法 杂交应力元 机织物 时域有限差分 悬垂 强度准则 强度 应变速率 应变率 应力集中 应力场 应力分布 多尺度 复变应力函数 含孔正交各向异性板 含孔复合材料结构 含圆孔正交各向异性板 各向异性介质 各向同性材料 反演 压应力 功能梯度圆板 力学性能 分离变量法 假设应力场 修正偏应力 保角映射 仿真分析 仿真 不同杨氏模量 不变量 ptfe膜材
推荐指数 3 3 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
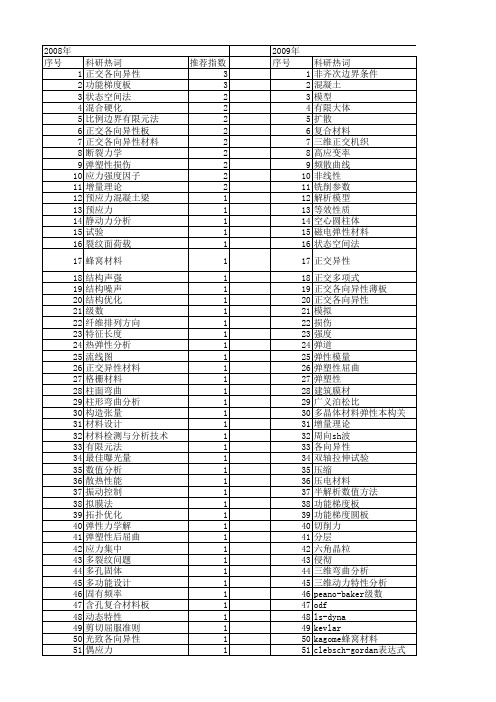
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51
正交各向异性材料粘塑性统一本构模型

正交各向异性材料粘塑性统一本构模型摘要:本文探讨了正交各向异性材料的粘塑性统一本构模型。
通过考虑粘弹性失效机制,实现全应力状态下本构参数的确定,并介绍基于拉伸和压缩试验数据的参数校正方法。
利用多类材料测试数据,探究模型表现在不同应变速率、应变比,以及偏移系数下的变化趋势。
结果表明,本构模型能够准确描述不同类型的材料受力时的本构响应,且对多类材料在不同应变速率、应变比等多种条件下的响应都有很好的模拟表现,可作为弹性失效后材料粘性本构行为模拟的基础理论。
关键词:正交各向异性材料;粘塑性;统一本构模型;应变速率;应变比正文:1. 引言材料的本构行为一直是材料力学的重要研究课题之一,对正交各向异性材料来说,随着低应力下材料的弹性失效变为粘性,单向应力和应变之间的关系发生变化。
因此,必须建立一种新的粘性本构模型,以准确预测材料在粘性本构加载情况下的变形特性。
2. 粘塑性统一本构模型本文探讨正交各向异性材料的粘塑性统一本构模型,考虑全应力状态下材料的粘弹性失效机制,实现全应力状态下本构参数的确定。
本模型表达式应变能定义如下:ε = σ/E0 + cσn(σ/σy)^m其中n、m为材料的粘塑性参数,σy为材料的粘弹性极限强度,E0为材料的初始弹性模量,c为材料的偏移系数,ν为材料的泊松比。
3. 参数校正方法基于拉伸和压缩试验,可以获取E0、σy等基本本构参数的数值,进而通过最小二乘法获取n、m、c的数值,最终完成参数校正。
4. 结果及结论本文利用多类材料测试数据,探究模型表现在不同应变速率、应变比,以及偏移系数下的变化趋势。
结果表明,本构模型能够准确描述不同类型的材料受力时的本构响应,且对多类材料在不同应变速率、应变比等多种条件下的响应都有很好的模拟表现,可作为弹性失效后材料粘性本构行为模拟的基础理论。
应用方面,正交各向异性材料的粘塑性统一本构模型可以在工程界得到广泛应用。
首先,它能够从一维本构响应推导到多维本构响应,可用于提高精度、准确性和可靠性,比如在液压油缸中,密封圈密封部位的受力状态,通过该模型可以计算出多维本构响应。
Ansys材料参数的定义问题

材料参数的定义问题我想用过ANSYS的人都知道:ANSYS计算结果的精度,不仅与模型,网格,算法紧密相关,而且材料参数的定义正确与否对结果的可靠性也有决定性的作用,为方便大家的学习,本人就用过的一些材料模型,作出一些总结,并给出相关的命令操作,希望对从事ANSYS应用的兄弟姐妹们有所帮助,水平有限,不对之处还望及时纠正.先给出线性材料的定义问题,线性材料分为三类:1.isotropic:各向同性材料2.orthotropic:正交各向异性材料3.anisotropic:各向异性材料1. isotropic各向同性材料的定义:这种材料比较普遍,而且定义也非常简单,只需定义两个常数:EX, NUXYNUXY默认为0.3,剪切模量GXY默认为EX/(2(1+NUXY)),如果你定义的是各向同性的弹性材料的话,这个参数一般不用定义.如果要定义,一定要和公式: EX/(2(1+NUXY))的值匹配,否则出错,另泊松比的定义一般推荐不要超过0.5.相关命令,例如:mp,ex,1,300e9mp,nuxy,1,0.252.orthotropic:正交各向异性材料:这种材料也是比较常见的,不过定义起来稍微麻烦一点,需定义的常数有: EX, EY, EZ, NUXY, NUYZ, NUXZ, GXY, GYZ, GXZ注意:在这里没有默认值,就是说,如果你某些参数不定义的话,程序会提示出错,比如:XY平面的平面应力问题,如果你只定义了EX, EY,程序将提示你,这是正交各向异性材料, GXY, NUXY是必须的.相关命令,例如:mp,ex,1,300e9mp,ey,1,200e9mp,nuxy,1,0.25mp,gxy,1,170e9…3.anisotropic:各向异性材料:各向异性材料定义起来较为复杂,这里我只作些简单的说明,更详细的资料,大家可以去看帮助.对于各向异性弹性材料的定义,需要定义弹性系数矩阵,这个矩阵是一个对称正定阵,因而输入的值一定要为正值.弹性常数矩阵如下图所示,各向异性体只有21个独立的弹性常数,因而我们也就只需输入21个参数即可,而且对于二维问题,弹性常数缩减为10个.弹性系数矩阵可以用刚度或柔度两种形式来定义,自己根据情况选用,输入的时候,可以通过菜单或者TB命令的TBOPT选项来控制.相关的命令流,例如:tb,anel,1tbdata,1, 110e6, 120e6, 130e6, 140e6, 150e6, 160e6tbdata,7, 220e6, 230e6, 240e6, 250e6, 260e6tbdata,12, 330e6, 340e6, 350e6, 360e6tbdata,16, 440e6, 450e6, 460e6tbdata,19, 550e6, 560e6tbdata,21, 660e6另:需注意一下各个参数的编号顺序和起始位置,不要搞错了,输入的时候,是按照上三角阵来录入的,即:D11,D12,D13,D14,D15,D16,D22,D23…。
ANSYS命令流学习笔记14-shell单元的铺层复合材料分析

!ANSYS命令流学习笔记 14-shell 单元的铺层复合材料分析!学习重点:!1、熟悉复合材料的材料特点工程应用中典型的复合材料为纤维增强复合材料。
玻璃纤维增强塑料(玻璃钢)、碳纤维、石墨纤维、硼纤维等高强度和高模量纤维。
复合材料各层为正交各向异性材料(O rthotropic )或者横向各向异性材料( Transversal Isotropic),材料的性能与材料主轴的取向有关。
各向异性 Anisotropic,一般的各项同性材料需要两个材料参数弹性模量而各向异性在 XYZ有着不同的材料属性,而且拉伸行为和剪切行为互相关联。
程需要 21 个参数。
E 和泊松比v。
定义其几何方正交各向异性 orthotropic,在XYZ有着不同的材料属性,而且拉伸行为和剪切行为无关,定义材料需要 9 个参数: Ex, Ey, Ez, Vxy, Vyz,Vxz, Gxy, Gyz, Gxz。
横向各向异性 Transversal Isotropic,属于各向异性材料,但是在某个平面上表现出二维上的各向同性。
!2、熟悉复合材料分析所用的ANSYS单元复合材料单元关键在于能够实现铺层。
不同截面属性的梁单元(beam188, beam189, elbow290 ),2D 对称壳单元( shell208, shell209 ),3D 铺层壳单元( shell181, shell281, shell131, shell132),3D 铺层实体单元( solid185, solid186, solsh190, solid278, solid279 ),均能实现复合材料的搭建。
其中Beam 单元和2D 对称壳单元很少使用。
SHELL91、 SHELL99、 SOLID46、SOLID191 用于一些以前的分析教程中,但是现在这些单元已经被淘汰,最好选择下列单元区替代他们。
用越来越少的单元做越来越多的事情也是趋势。
Shell208 和 shell209, 2D 对称壳单元前者为 2 节点 3 自由度单元,后者为 3 节点 3 自由度单元,均能用于薄板和中厚板结构(L/h > 5-8 )。
各向同性

各向同性、各向异性理解1、orthotropic和anisotropic的区别isotropic各向同性orthotropic正交各向异性的anisotropic各向异性的uniaxial单轴的我只说一下orthotropic和anisotropic的区别:orthotropic主要是材料在不同垂直方向上有着不同的物理性质和参数,意思就是如果处在同一个角度的平面上,那么同平面的材料是具有着相同的物理性质的.anisotropic则是完全有方向角度决定的物理参数,只要方向有不同,物理性质则完全不同.2、各向同性和各向异性物理性质可以在不同的方向进行测量。
如果各个方向的测量结果是相同的,说明其物理性质与取向无关,就称为各向同性。
如果物理性质和取向密切相关,不同取向的测量结果迥异,就称为各向异性。
造成这种差别的内在因素是材料结构的对称性。
在气体、液体或非晶态固体中,原子排列是混乱的,因而就各个方向而言,统计结果是等同的,所以其物理性质必然是各向同性的。
而晶体中原子具有规则排列,结构上等同的方向只限于晶体对称性所决定的某些特定方向。
所以一般而言,物理性质是各向异性的。
例如,α-铁的磁化难易方向如图所示。
铁的弹性模量沿[111]最大(7700kgf/mm),沿[100]最小(6400kgf/mm)。
对称性较低的晶体(如水晶、方解石)沿空间不同方向有不同的折射率。
而非晶体(过冷液体),其折射率和弹性模量则是各向同性的。
晶体的对称性很高时,某些物理性质(例如电导率等)会转变成各向同性。
当物体是由许多位向紊乱无章的小单晶组成时,其表观物理性质是各向同性的。
一般合金的强度就利用了这一点。
倘若由于特殊加工使多晶体中的小单晶沿特定位向排列(例如金属的形变“织构”、定向生长的两相晶体混合物等),则虽然是多晶体其性能也会呈现各向异性。
硅钢片就是这种性质的具体应用。
介于液体和固体之间的液晶,有的虽然分子的位置是无序的,但分子取向却是有序的。
正交各向异性C

2023年第47卷第4期Journal of Mechanical Transmission正交各向异性C/SiC汽车通风式制动器仿真分析朱玉玲1,2王优强1,2赵涛1,2李梦杰1,2何彦1,2(1 青岛理工大学机械与汽车工程学院,山东青岛266520)(2 工业流体节能与污染控制教育部重点实验室,山东青岛266520)摘要运用热力耦合及传热学相关理论,利用有限元软件Abaqus建立正交各向异性C/SiC材料的汽车通风式制动器模型;以此为基础,对该模型在紧急制动过程中不同制动初速度、不同制动压力以及制动盘的不同纵向膨胀系数进行了模拟和分析。
结果显示,在热力耦合作用下,制动盘节点单元温度曲线呈现出“锯齿状”波动,热应力主要出现在摩擦副接触的中间区域;在紧急制动过程中,制动压力和初速度越大,制动盘面温度上升越明显,而不同制动盘膨胀系数对制动盘最高温度的影响不显著。
关键词C/SiC 制动盘热力耦合Abaqus 温度场Simulation Analysis of Orthotropic Anisotropic C/SiC for Automotive Ventilated Brakes Zhu Yuling1,2Wang Youqiang1,2Zhao Tao1,2Li Mengjie1,2He Yan1,2(1 School of Mechanical and Automotive Engineering, Qingdao University of Technology, Qingdao 266520, China)(2 Key Lab of Industrial Fluid Energy Conservation and Pollution Control Ministry of Education, Qingdao 266520, China)Abstract Using the theory related to thermal coupling and heat transfer, the finite element software Abaqus is used to establish an orthogonal anisotropic C/SiC model of an automotive ventilated brake disc. Based on this model, different braking initial velocities, different braking pressures and different longitudinal expan⁃sion coefficients of the brake disc during emergency braking are simulated and analyzed. The results show that the temperature profile of the nodal unit of the brake disc exhibited "sawtooth" fluctuations under the effect of thermal coupling, and the thermal stresses mainly appeared in the middle region of the friction contact. The high⁃er the braking pressure and initial speed during emergency braking are, the higher the temperature rise of the disc surface will be. However, the effect of different disc expansion coefficients on the maximum disc tempera⁃ture is not significant.Key words C/SiC Brake disc Thermodynamic coupling Abaqus Temperature field0 引言拥有一个安全高效的制动系统是汽车稳定行驶的重要前提。
正交各向异性孔板的材料参数识别

二维正交各向异性材料及其结构 材料参数识别的算法
如果正交各向异性材料平面结构的材料主轴
能从中切出一个试件,进行参数测定。随着计算机 技术的飞速发展,采用数值—实验反分析方法进行 正交各向异性材料性能参数的识别引起人们的广 泛关注。由于参数识别问题是非线性的,在迭代求 解时,导致计算工作量很大。边界元法有其独到的 长处: (1) 整个问题降维,网格划分仅在边界上。 象孔板这样几何形状发生突变的结构,会出现应力 集中现象,用边界元法计算分析,计算工作量小的 优势比较明显; (2) 精度高; (3) 域内点的位移和应 力可按需计算。因此,对于仅需布置若干个测点和 需要迭代计算的参数识别问题,边界元法是很有利 的。 本文以优化技术和边界元分析为基础,识别正 交各向异性孔板的材料参数。选择孔板结构的位移 为目标变量,以测量位移与边界元计算相应的位移 之 差 的 平 方 和 作 为 目 标 函 数 。 采 用 Levenberg-Marquardt 方法极小化目标函数,迭代计 算得出材料参数。优化计算中,基于离散的边界元 代数矩阵方程对识别的材料参数求导,计算得出灵 敏度。算例表明本文提出的方法是有效的。
∂hij ∂s m = ˆ ∂h = ij kl ∂x m
∗ ∂t kl
b
i, j = 1,2, L , n
(11)
用 Levenberg-Marquardt 方法可以得到一系列 的迭代步。当给定的某种收敛准则满足时,迭代即 终止。第 k 次迭代的材料参数值可以由下列方程计 算 [ J ( s ( k ) ) T J ( s ( k ) ) + µ ( k ) I ]ä ( k ) = − J ( s ( k ) ) T f ( s ( k ) ) (17)
复合材料力学2-5章

第二章单向层合板的正轴刚度本章的一些讲法与讲义次序不同,请同学们注意,另外一些在材料力已阐明的概念,如应力、应变等在这里不再强调,希望大家能自学与复习。
§2—1 正交各向异性材料的特点●各向同性材料●各向异性材料我们这里所指的各向异性材料的特点仅仅是指在不同方向上材料的力学性质不同(机械性能)。
●正交各向异性材料正交各向异性材料是一种特殊的各向异性材料。
其特点为: 这类材料有三个互相垂直的弹性对称面(与弹性对称面对称的点性质相同),在平行方向上的弹性质(力学特性)均相同。
如多层单向板,当不考虑纤维与基体性质的不均匀性,粘结层又很薄可以忽略,即把它写作“连续匀质”材料看,则三个弹性对称面分别为:与单层平行的面及与它垂直的纵向、横向的两个切面。
板上任何两点,在平行方向上的力学性质是一样的。
把这三个弹性平面相交的三个轴称为弹性主轴,也称为正轴。
下图是一种典型的正交个向异性材料,当厚度很小时可处理为正交个向异性板。
用宏观力学处理连续纤维增强复合材料层压板结构时,总是把单向层板作为基本单元来分析层合板。
层合板的组成增强纤维排列方向一致所粘合的薄层称单向(单层)板(层),有时把很多单层粘合在一起,各层的纤维排列方向均一致,也称单向板。
正轴的弹性常数正交各向异性弹性体,1、2、3轴为它的弹性主轴,则沿这三个轴共有9各独立弹性常数。
1E 、2E 、3E ——杨氏模量; 12G 、13G 、23G ——剪切模量; 21v 、31v 、32v ——泊松系数。
21v 表示在1方向拉伸时在2方向产生的收缩效应系数;同样,12v 表示在2方向拉伸时在1方产生的收缩效应系数。
1221v v ≠ 这点与各向同性材料不同。
并有关系式212121E v E v = 313131E v E v = 323232E v E v = ∴ 12v、13v 、23v 是不独立的系数。
顺便指出,有的文献定义12v 为1方向拉伸时在2方向的收缩系数。
