第10章 Panel Data 模型
面板数据模型理论

5.2 面板数据模型理论5.2.1 面板数据模型及类型。
面板数据(panel data )也称时间序列截面数据(time series and cross section data )或混合数据(pool data )。
面板数据是同时在时间和截面空间上取得的二维数据。
面板数据从横截面(cross section )上看,是由若干个体(entity, unit, individual )在某一时刻构成的截面观测值,从纵剖面(longitudinal section )上看是一个时间序列。
面板数据用双下标变量表示。
例如:it y , N i ,,2,1 =;T t ,,2,1 =其中,N 表示面板数据中含有的个体数。
T 表示时间序列的时期数。
若固定t 不变,•i y ),,2,1(N i =是横截面上的N 个随机变量;若固定i 不变,t y •,),,2,1(T t =是纵剖面上的一个时间序列。
对于面板数据来说,如果从横截面上看,每个变量都有观测值,从纵剖面上看,每一期都有观测值,则称此面板数据为平衡面板数据(balanced panel data )。
若在面板数据中丢失若干个观测值,则称此面板数据为非平衡面板数据(unbalanced panel data )。
面板数据模型是建立在面板数据之上、用于分析变量之间相互关系的计量经济模型。
面板数据模型的解析表达式为:it it it it it x y μβα++= T j N i ,2,1;,2,1==其中,it y 为被解释变量;it α表示截距项,),,,(21k it it itit x x x x =为k ⨯1维解释变量向量;'21),,,(k it it it it ββββ =为1⨯k 维参数向量;i 表示不同的个体;t 表示不同的时间;it μ为随机扰动项,满足经典计量经济模型的基本假设),0(~2μσμIIDN it 。
面板数据模型通常分为三类。
panel data

平行数据(Panel Data)模型厦门大学财政系王艺明平行数据(Panel Data)§平行数据是指对不同时刻的横截面个体作连续观测所得到的多维数据。
由于这类数据有着独特的优点,使平行数据模型目前已在计量经济学、社会学等领域有着较为广泛的应用。
§平行数据在EViews中被称为时序与横截面混合数据(pooled time series and cross-section data)。
平行数据模型是一类利用平行数量分析变量间相互关系并预测其变化趋势的计量经济模型。
模型能够同时反映研究对象在时间和横截面单元两个方向上的变化规律及不同时间、不同单元的特性。
Panel Data模型的基本设定§平行数据模型的基本假设:参数齐性假设,即被解释变量y由某一参数的概率分布函数P(y|θ)。
§假定时间序列参数齐性,及参数值不随时间的不同而变化,则平行数据模型可表示为:§yit =αi+βi’xit+εiti=1,…,N; t=1,…,T§xit ’=(x1it,x2it,…,xKit),为外生变量向量,βi’=(β1i ,β2i,…,βKi),为参数向量,K是外生变量个数,T是时期总数§其中参数αi 和βi都是个体时期恒量(individual time-invariant variable),其取值只受到截面单元不同的影响§E(εit )=0; E(εit2)=σi2; E(εitεjt)=σij; E(εitεjt-s)=0Panel Data 模型的基本设定I §根据模型的不同设定通常有三类估计方法§T 较大,N 较小。
通常采用时间序列模型的假设,即T 趋于无穷大,而N 固定、有限。
§该假设下,标准的方法是Zellner 的似无相关回归方法(Zellner Seemingly Unrelated Regression, SUR ),该方法考虑到回归方程间残差的相关性,即E(εit εjt )=σij ,采用GLS 方法估计似无相关回归(SUR)§假设要估计以下方程组§y1t=α1+β1’x1t+u1t§y2t=α2+β2’x2t+u2t§y3t=α3+β3’x3t+u3t§由于各种经济形态中存在的共同事件对不同横截面误差的影响方式类似,所以它们是同期相关的§Cov(u1t ,u2t)=σ12, Cov(u2t,u3t)=σ23,Cov(u1t,u3t)=σ13§这种情况下可采用Zellner(1962)的似无相关回归(SUR)方法进行参数估计似无相关回归(SUR)§其步骤为§1、使用OLS方法分别估计每个方程并求残)差(uit§2、使用残差估计方差和协方差(σ)ij§3、使用第2步中求得的估计值求所有参数的广义最小二乘估计值(FGLS)§在EViews中可以直接进行SUR估计Panel Data 模型的基本设定II §N 较大而T 较小。
面板数据模型.讲课文档

其中,
称为复合误差(composite error)。
这一结果与1987年数据的横截面OLS回归结果不一 样。注意,使用混合OLS并不解决遗漏变量问题。
两时期面板数据分析(续4)
另一种方法,考虑了非观测效应与解释变量相关性。
(面板数据模型主要就是为了考虑非观测效应与解 释变量相关性的情形)例如在犯罪方程中,让ai中
为两类:一类是恒常不变的;另一类则随时间而变。
d2t表示当t=1时等于0而当t=2时等于1的一个虚拟变 量,它不随i而变。ai概括了影响yit的全部观测不到 的、在时间上恒定的因素,通常称作非观测效应, 也称为固定效应,即ai在时间上是固定的。特质误 差uit表示随时间变化的那些非观测因素。
两时期面板数据分析(续2)
第三,Panel Data Model可以通过设置虚拟变量对 个别差异(非观测效应)进行控制;即面板数据模 型可以用来有效处理遗漏变量(omitted varaiable) 的模型错误设定问题。
遗漏变量
使用面板数据的一个主要原因是,面板数据可以用 来处理某些遗漏变量问题。
例如,遗漏变量是不随时间而变化的表示个体异质 性的一些变量,如国家的初始技术效率、城市的历 史或个人的一些特征等。这些不可观测的不随时间 变化的变量往往和模型的解释变量相关,从而产生 内生性,导致OLS估计量有偏且不一致。
2000 4203.555 8206.271 5522.762 4361.555 3890.580 4077.961 5317.862 3612.722 4360.420 3877.345 5011.976 8651.893 3793.908 6145.622 6950.713
2001 4495.174 8654.433 6094.336 4457.463 4159.087 4281.560 5488.829 3914.080 4654.420 4170.596 5159.538 9336.100 4131.273 6904.368 7968.327
Panel Data模型EViews操作过程(2013)

Data模型的EViews操作过程两种模式:Ⅰ. 关于Panel工作文件;Ⅱ. 关于Pool对象。
数据的预处理1.在EXCEL文件中,将每个变量各年的原始数据按照年份顺序排成一列,称之为堆积数据(见表“汇总0”)。
2.输入截面单元的标识(表示地区的符号,前面加_;如:_HB、_NMG等)。
3.将数据表按照时间分类(即排序,见表“汇总”)。
Ⅰ. 关于Panel工作文件的操作过程案例1:我国农村居民消费函数(2000-2010年,27个省市数据,工作文件:NXF)一、输入数据1、创建Panel工作文件选择File / New / Workfile,在出现的创建工作文件对话框中:(1)在文件结构类型中,选择“平衡面板(Balanced Panel)”;(2)输入起始、终止期,截面单元个数。
2.更改截面标识(可以省略)序列crossid 中是以数字1、2、…标记截面标识,为了便于区分,可以重新定义一个字符串序列。
(1)点击object / New object ,选择series Alpha 并输入序列名(设为dq ); (2)双击dq 序列,在打开的序列窗口中粘贴截面标识的字符串序列;(3)双击工作文件窗口中的Range ,在弹出的对话框中,将截面标识的的ID 序列改成新的标识序列:dq3.输入数据键入命令:DATA Y X ,然后用复制+粘贴方式从Excel 文件中将各个变量的堆积数据(注意:数据事先要按照截面单元堆积,本例中是按照“地区”)复制到工作文件之中;此时工作文件中各个变量都是堆积数据。
工作文件中将生成分别表示截面标识和时期标识的两个序列:Crossid — 截面标识 dateid — 时期标识二、模型估计过程1.估计混合模型直接在命令窗口键入命令:LS Y C X2.估计变截距模型在方程窗口中点击Estimate按钮,在弹出的方程描述框中选择Panel Options选项卡,此时可以在截面和时期列表中选择None、Fixed、Random,用来选择单因素(或双因素)固定效应、随机效应变截距模型;同时可以选择GMM、GLS、SUR等估计方法。
(整理)PanelData模型的估计过程.
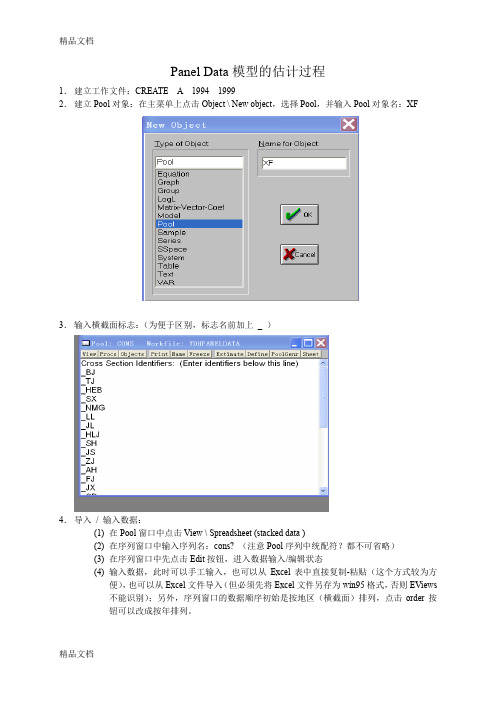
Panel Data模型的估计过程1.建立工作文件:CREATE A 1994 19992.建立Pool对象:在主菜单上点击Object \ New object,选择Pool,并输入Pool对象名:XF3.输入横截面标志:(为便于区别,标志名前加上_ )4.导入/ 输入数据:(1)在Pool窗口中点击View \ Spreadsheet (stacked data )(2)在序列窗口中输入序列名:cons? (注意Pool序列中统配符?都不可省略)(3)在序列窗口中先点击Edit按钮,进入数据输入/编辑状态(4)输入数据,此时可以手工输入,也可以从Excel表中直接复制-粘贴(这个方式较为方便),也可以从Excel文件导入(但必须先将Excel文件另存为win95格式,否则EViews不能识别);另外,序列窗口的数据顺序初始是按地区(横截面)排列,点击order按钮可以改成按年排列。
5.输入/ 生成其他变量数据:(1)再次点击View \ Spreadsheet (stacked data )(2)在序列窗口中输入新序列名:INC?(3)点击Procs \ Generate Pool Serise,生成新的Pool序列——上期消费CONS1:6.估计Panel Data模型:(1)打开Pool对象XF(2)点击Estimate按钮(3)在Estimation窗口中依次估计不同形式的模型:混合模型:在常系数栏(common coefficients)输入解释变量名cons1? inc?,在截据项栏(intercept)选择常数(common)变截据模型:在常系数栏(common coefficients )输入解释变量名cons1? inc?,在截据项栏(intercept )选择固定效应(fixed effects )变系数模型:在截面单元系数栏(cross section specific coefficients )输入解释变量名cons1? inc?, 在截据项栏(intercept )选择固定效应(fixed effects )7.8. Panel Data 模型的识别:∵ F 2={(1148951-299023) /[(28-1)(2+1)]}/[299023/28*5-28*3]=1.965 而 F 2 = 1.965 > F 0.05(81,56)=1.52 (利用Excel 的FINV 函数计算)∴ 拒绝H 20,模型不是混合回归模型又 ∵ F 1={(643899-299023) /[(28-1)*2]}/[299023/28*5-28*3]=1.196而 F 1 =1.196 < F 0.05(54,56)=1.56∴ 接受H 10,模型是变截据模型,而不是变系数模型,即各地区的边际消费倾向相同,差异只表现在平均水平上。
PanelData模型课件

– 面板数据模型 – 综列数据模型 – 平行数据模型 – 时空数据模型
• 常用Panel Data 模型
– 变截矩模型(Variable-Intercept Models)
固定影响(Fixed-Effects) 随机影响(Random-Effects)
– 变系数模型(Variable-Coefficient Models)
. 条件:
. 如果随机项在不同横截面个体之间的协方差不为 零, GLS估计比每个横截面个体上的经典单方程 估计更有效。
. 为什么?
问题的关键是然后求得V矩阵。 各种文献中提出各种V矩阵的方
法,形成了各种FGLS估计
. 当n很大,甚至成千上万, OLS计算可能超过任何 计算机的存储容量。此时,可用分块回归的方法 进行计算。
. 分块回归的思路是:设法消去数量很多的αi ,估计 β,然后利用每个个体的时间序列数据计算αi 。
e’e=T
这是一个不含高阶的 Qi ,只含β的模型,
可以估计β
• 分块估计的思路:
– 首先构造1个不含αi ,只包含β的模型,对其进行OLS。 – 然后分别在每个个体上计算αi ,分块的含义体现于此。
§7.3 Panel Data 模型
一、概述 二、模型的设定——F检验 三、固定影响变截距模型 四、固定影响变系数模型
一、 Panel Data 模型概述
1、关于Panel Data Model
• 独立的计量经济学分支
– 比较多地用于宏观经济分析——统计数据 – 也可以用于微观经济分析——调查数据
• 情 形 4 : 不 讨 论 。 Because it is seldom
meaningful to ask if the intercepts are the same when the slopes are unequal, we shall ignore the
面板数据模型panel data model
自由度K为模型中解释变量(不包括截距项)的个数。
计量经济学,面板数据模型,王少平
24
六、动态面板数据模型
动态面板模型:解释变量中包含被解释变量的滞后 项。 一般形式:
Yit 1 2 X 2it k X kit Yit 1 it
it i t uit
Iit 1 2 Fit 3Cit Iit 1 i t uit i 1, 2,, N t 1, 2,, T
(5)
计量经济学,面板数据模型,王少平
11
四、静态面板数据模型估计
面板数据一般模型:
Yit 1 2 X 2it k X kit it
计量经济学,面板数据模型,王少平
26
2. LSDV估计的有偏和非一致性
模型(17)可以表示为: Yit 1 D1 N DN Yi,t 1 uit 等价于模型:
Y Y
* i ,t
* i ,t 1
* it
* it
其中:
1 T * Yi ,t 1 Yi ,t 1 Yi ,t T t 1
(18)
其中:uit 为经典误差项, E(i ) 0 E(iuit ) 0
要得到 的一致估计量:需为 Yi,t 1 寻找适当的工具变 量。 GMM以工具变量为基础,核心思想在于利用正交条件 估计未知参数。
计量经济学,面板数据模型,王少平
28
六、动态面板-IV估计
固定效应:如果个体效应或时间效应与模型中的解释变量相关 随机效应:如果个体效应或时间效应与模型中的解释变量不相 关
面板数据的模型(panel data model)
面板数据的模型(panel data model)王志刚 2004年11月11日一. 混合数据模型和面板数据模型如果扰动项it ε服从独立同分布假定,而且和解释变量不相关,那么就可以采用混合最小二乘法估计(Pooled OLS ),但是这里要注意POLS 暗含着一个假定就是,截距项和解释变量的系数是相同的,不随着个体和时间而变化。
我们一般采用单因子(one-way effects )模型,假定截距项具有个体异质性,也就是:这种模型是最常见的面板模型(又称为纵列数据longitudinal data ),因为面板数据往往要求个体纬度 N>>T(时间纬度),下面我们基本上以这种模型为例。
it u 是独立同分布,而且均值为0,方差为2u σ。
如对截距项和解释变量系数均有个体的异质性,那么要采用随机系数模型(Random coefficient model ),stata 的xtrchh 过程提供了相应的估计。
双因子模型(two-way ):it t i it u ++=γαε二. 固定效应(Fixed effects ) vs 随机效应(Random effects)如果个体效应i α是一个均值为0,方差为2ασ的独立同分布的随机变量,也就是()0,cov =it i x α,该模型就称为随机效应模型(又称为error component model );如果相关,则称为固定效应模型。
1.在随机效应模型中,it ε在每个个体内部存在着一阶自相关,因为他们都包含着相同的个体效应;此时OLS 无效,而且标准差也失真,应该采用广义最小二乘估计(GLS)其中:是个体按时间的均值;有待估计;我们可以通过对组内和组间估计得到相应的残差,从而可以计算出方差;T k n e e e e nnk nT ubetween between between between within within u 22222,,ˆˆ1σσσσσα-=-'='--=;组间估计:εβ+=..i i x y ;组内估计如下;2.如果个体效应和解释变量相关,OLS 和GLS 都将失效,此时要采用固定效应模型。
EVIEWS面板数据分析操作教程及实例
除此项 外均支 持协整
16
表10.8 Johansen面板协整检验结果
(选择序列有确定性趋势而协整方程只有截距的情况)
支
原假设
Fisher联合迹统计 Fisher联合-max统计
量(p值)
量(p值)
持 协
整
0个协整向量
133.4 (0.0000)*
128.7 (0.0000)*
至少1个协整向量 65.74 (0.2266)
yi m xi β i* ui
由于自变量前 系数不变,所 以自变量填写
在此处
◎POOL/ESTIMATE如右 窗口 点确定结果请点 结果
说明 软件给出的固定影响分为: 一 总体均值 二 个体对总体的偏离
31
记下:自 由度为N (T-1)-K
记下 S2
32
附注:包含时期个体恒量的固定影响变截距模型
F1=((S2-S1)/8)/(S1 /85) = 3.29 F2=((S3-S1)/12)/(S1 /85) = 25.73 界到相点利应,用的k1函和临数k界2是值@自为qf由:di度st(。d,k在1,k给2)定得5%到的F分显布著的性临水界平值下,(d其=0中.9d5),是临得 F2(12, 85) = 1.87 F1(8, 85) =2.049 H1。由因于此,F2例>11.807.5,的所模以型拒应绝采H用2;变又系由数于的形F1式>2。.049,所以也拒绝28
10
思路一:变量之间是非同阶单整 :序列变换
◎变量之间是非同阶单整的指即面板数据中有些序列平稳而有些序列不平稳,
此时不能进行协整检验与直接对原序列进行回归。
◎对序列进行差分或取对数使之变成同阶序列
若变换序列后均为平稳序列可用变换后的序列直接进行回归
《计量经济分析方法与建模》课件第二版第10章 Panel Data 模型
面板数据含有横截面、时间和指标三维信息,利用
面板数据模型可以构造和检验比以往单独使用横截面数
据或时间序列数据更为真实的行为方程,可以进行更加 深入的分析。正是基于实际经济分析的需要,作为非经 典计量经济学问题,同时利用横截面和时间序列数据的 模型已经成为近年来计量经济学理论方法的重要发展之
一。
3
时间)信息的数据结构称为面板数据( panel data )。 有的书中也称为平行数据。本章将利用面板数据的计量
模型简称为Panel Data 模型。
1
经典线性计量经济学模型在分析时只利用了面板数据
中的某些二维数据信息,例如使用若干经济指标的时间序 列建模或利用横截面数据建模。然而,在实际经济分析中,
例10.4 研究企业投资需求模型
5家企业:
GM:通用汽车公司 CH:克莱斯勒公司 GE:通用电器公司 WE:西屋公司 US:美国钢铁公司 I :总投资 M :前一年企业的市场价值 (反映企业的预期利润) K :前一年末工厂存货和设备的价值 (反映企业必要重置投资期望值)
3个变量:
创建Pool对象,选择Objects/New Object/Pool…并在编辑
17
(3) 打开Pool序列的堆积式数据表。需要的话还可以单
击Order+/-按钮进行按截面成员堆积和按日期堆积之间的转 换。 (4) 单击Edit+/-按钮打开数据编辑模式输入数据。 如果有一个Pool包含识别名_CM,_CH,_GE,_WE,
_US,通过输入:I? M? K?,指示EViews来创建如下序列:
选择View/Spreadsheet(stacked data),EViews会要求输
入序列名列表
确认后EViews会打开新建序列的堆积式数据表。我们看 到的是按截面成员堆积的序列,Pool序列名在每列表头,截面
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4. 观察或编辑Pool定义
要显示Pool中的截面成员识别名称,单击工具条的
Define按钮,或选择View/Cross-Section Identifiers。如果需 要,也可以对识别名称列进行编辑。
5. Pool序列数据
Pool中使用的数据都存在普通 EViews序列中。这些序列
可以按通常方式使用:可以列表显示,图形显示,产生新序
变量)信息的数据结构称为面板数据( panel data )。 有的书中也称为平行数据。本章将利用面板数据的计量
模型简称为Panel Data 模型。
1
经典线性计量经济学模型在分析时只利用了面板数据
中的某些二维数据信息,例如使用若干经济指标的时间序 列建模或利用横截面数据建模。然而,在实际经济分析中,
第十章
Panel Data模型
在进行经济分析时经常会遇到时间序列和横截面两 者相结合的数据。例如,在企业投资需求分析中,我们 会遇到多个企业的若干指标的月度或季度时间序列;在 城镇居民消费分析中,我们会遇到不同省市地区的反映 居民消费和居民收入的年度时间序列。本章将前述的企
业或地区等统称为截面,这种具有三维(截面、时期、
必须注意,Pool对象本身不包含序列或数据。一个 Pool对象只是对基本数据结构的一种描述。因此,删除一 个Pool并不会同时删除它所使用的序列,但修改Pool使用的 原序列会同时改变Pool中的数据。
6
1. 创建Pool对象 在本章中,使用的是一个研究投资需求的例子,包括了五 家企业和三个变量的20个年度观测值的时间序列:
2
面板数据含有横截面、时期和变量三维信息,利用
面板数据模型可以构造和检验比以往单独使用横截面数
据或时间序列数据更为真实的行为方程,可以进行更加 深入的分析。正是基于实际经济分析的需要,作为非经 典计量经济学问题,同时利用横截面和时间序列数据的 模型已经成为近年来计量经济学理论方法的重要发展之
一。
3
4
10.1.1 含有Pool对象的工作文件
Pool对象在EViews中扮演着两种角色。首先,Pool对
象中包含了一系列的标识名。这些标识名描述了工作文件
中的面板数据的数据结构。在这个角色中,Pool对象在管 理和处理面板数据上的功能与组对象有些相似。其次,利 用Pool对象中的过程可以实现对各种Panel Data模型的估 计及对估计结果的检验和处理。在这个角色中,Pool对象 与方程对象有些相似
21
10.1.3 输出Pool数据
按照和上面数据输入相反的程序可进行数据输出。由于
EViews可以输入输出非堆积数据,按截面成员堆积和按日期
堆积数据,因此可以利用EViews按照需要调整数据结构。
22
10.1.4 使用Pool数据
每个截面成员的基础序列都是普通序列,因此EViews中对 各单个截面成员序列适用的工具都可使用。另外,EViews还有 专门适用于Pool数据的专用工具。可以使用EViews对与一特定 变量对应的所有序列进行类似操作。 1. 检查数据 用 数 据 表 形 式 查 看 堆 积 数 据 。 选 择 View/Spreadsheet (stacked data),然后列出要显示的序列。序列名包括普通序列 名和Pool序列名。 2. 描述数据 可以使用 Pool对象计算序列的描述统计量。在 Pool 工具栏 选择View/Descriptive Statistics…,EViews会打开如下对话框: 23
10.1 Pool对象
EViews对Panel Data模型的估计是通过含有Pool对象 的工作文件和具有面板结构的工作文件来实现的。 处理面板数据的EViews对象称为Pool。通过Pool对象 可以实现对各种变截距、变系数时间序列模型的估计,但 Pool对象侧重分析“窄而长”的数据,即截面成员较少, 而时期较长的侧重时间序列分析的数据。 对于截面成员较多,时期较少的“宽而短”的侧重截 面分析的数据,一般通过具有面板结构的工作文件 (Panel workfile)进行分析。利用面板结构的工作文件 可以实现变截距Panel Data模型以及动态Panel Data模型 的估计。
的数据从上到下依次堆积,每一列代表一个,单击Order+/-实现堆 积方式转换,也可以按日期堆积数据:
每一列代表一个变量,每一列内数据都是按年排列的。如果 数据按年排列,要确保各年内截面成员的排列顺序要一致。
16
3. 手工输入/剪切和粘贴 可以通过手工输入数据,也可以使用剪切和粘贴工具输
I_CM,I_CH,I_GE,I_WE,I_US;M_CM,M_CH, M_GE,M_WE,M_US;K_CM,K_CH,K_GE,K_WE, K_US:
18
4. 文件输入
可以使用Pool对象从文件输入堆积数据到各单独序列。当 文件数据按截面成员或时期堆积成时,EViews要求: (1) 堆积数据是平衡的 (2) 截面成员在文件中和在Pool中的排列顺序相同。 平衡的意思是,如果按截面成员堆积数据,每个截面成员 应包括正好相同的时期;如果按日期堆积数据,每个日期应包 含相同数量的截面成员观测值,并按相同顺序排列。 特别要指出的是,基础数据并不一定是平衡的,只要在输 入文件中有表示即可。如果观测值中有缺失数据,一定要保证 文件中给这些缺失值留有位置。 要使用 Pool 对象从文件读取数据,先打开 Pool ,然后选择 Procs/Import Pool Data(ASCII,.XLS,.WK?)… ,要使用与 Pool 19 对象对应的输入程序。
3. Pool序列概念 一旦选定的序列名和 Pool中的截面成员识别名称相对应, 就可以利用这些序列使用 Pool了。其中关键是要理解 Pool 序 列的概念。 一个 Pool序列实际就是一组序列 , 序列名是由基本名和 所有截面识别名构成的。 Pool序列名使用基本名和“?”占位 符,其中“ ?” 代表截面识别名。如果序列名为 GDPJPN , GDPUSA,GDPUK,相应的Pool序列为GDP?。如果序列名 为JPNGDP,USAGDP,UKGDP,相应的Pool序列为 ?GDP。 当使用一个Pool序列名时,EViews认为将准备使用Pool 序列中的所有序列。EViews会自动循环查找所有截面识别名 称并用识别名称替代“?”。然后会按指令使用这些替代后的 名称了。Pool序列必须通过Pool对象来定义,因为如果没有 截面识别名称,占位符“?”就没有意义。 10
17
(3) 打开Pool序列的堆积式数据表。需要的话还可以单
击Order+/-按钮进行按截面成员堆积和按日期堆积之间的转 换。 (4) 单击Edit+/-按钮打开数据编辑模式输入数据。 如果有一个Pool包含识别名_CM,_CH,_GE,_WE,
_US,通过输入:I? M? K?,指示EViews来创建如下序列:
5
Pool对象的核心是建立表示截面成员的名称表。为明 显起见,名称要相对较短。例如,国家作为截面成员时,
可以使用USA代表美国,CAN代表加拿大,UK代表英国。
定义了 Pool的截面成员名称就等于告诉了 EViews ,模 型的数据结构。在上面的例子中, EViews 会自动把这个
Pool理解成对每个国家使用单独的时间序列。
在编辑框内输入计算描述统计量的序列。 EViews 可以
入:
(1) 通过确定工作文件样本来指定堆积数据表中要包含哪 些时间序列观测值。
(2) 打开Pool,选择View/Spreadsheet(stacked data),
EViews会要求输入序列名列表,可以输入普通序列名或 Pool 序列名。如果是已有序列,EViews会显示序列数据;如果这 个序列不存在,EViews会使用已说明的 Pool序列的截面成员 识别名称建立新序列或序列组。
列,或用于估计。也可以使用Pool对象来处理各单独序列。
11
10.1.2 输入Pool数据
有很多种输入数据的方法,在介绍各种方法之前,首 先要理解面板数据的结构,区别堆积数据和非堆积数据形 式。 面板数据的数据信息用三维表示:时期,截面成员, 变量。例如:1950年,通用汽车公司,投资数据。 使用三维数据比较困难,一般要转化成二维数据。有 几种常用的方法。 1. 非堆积数据 存在工作文件的数据都是这种非堆积数据,在这种形 式中,给定截面成员、给定变量的观测值放在一起,但和 其他变量、其他截面成员的数据分开。例如,假定我们的 数据文件为下面的形式:
20
通过附录 A的学习,大家对这个对话框应该比较熟悉, 填写说明如下: 注明Pool序列是按行还是按列排列,数据是按截面成 员堆积还是按日期堆积。 在编辑框输入序列的名称。这些序列名应该是普通序 列名或者是Pool名。 填入样本信息,起始格位置和表单名(可选项)。 如果输入序列用Pool序列名,EViews会用截面成员识 别名创建和命名序列。如果用普通序列名,EViews会创建 单个序列。 EViews会使用样本信息读入文件到说明变量中。如果 输入的是普通序列名,EViews会把多个数据值输入到序列 中,直到从文件中读入的最后一组数据。
这种仅利用二维信息的模型在很多时候往往不能满足人们
分析问题的需要。例如,在生产函数分析中,仅利用横截 面数据只能对规模经济进行分析,仅利用混有规模经济和 技术革新信息的时间序列数据只有在假设规模收益不变的 条件下才能实现技术革新的分析,而利用面板数据可以同 时分析企业的规模经济(选择同一时期的不同规模的企业 数据作为样本观测值)和技术革新(选择同一企业的不同 时期的数据作为样本观测值),可以实现规模经济和技术 革新的综合分析。
窗口中输入截面成员的识别名称:
7
对截面成员的识别名称没有特别要求,但必须能使用这 些识别名称建立合法的EViews序列名称。此处推荐在每个识 别名中使用“_”字符,它不是必须的,但把它作为序列名的 一部分,可以很容易找到识别名称。
