第二讲 基本几何体
基本几何体

基本几何体几何学是一门讨论物体形状以及相互作用的学科,在其中,基本几何体起到至关重要的作用。
基本几何体指的是多维平面几何图形的构成,如平面、空间三角形、空间四边形、正方体、棱柱体、圆锥体、椎体等。
它们是多维平面几何图形的基础,研究它们可以帮助我们更好地理解物体的形状。
平面是基本几何体的一种,它由点、线、线段和弧线构成,是最基本的物体形状,平面可以在二维空间内表示,它的宽度和长度可以通过座标系来表示。
它的高度、半径、斜率等等有用的信息也可以从座标系中获得。
空间三角形是基本几何体中的另一种,它是由三条边和三个顶点构成的,这三条边一般称作顶边,起始点和结束点称为顶点。
三角形可以在三维空间内表示,它可以描述物体的表面形状,可以帮助我们更好地理解物体的形状。
空间四边形是基本几何体的另一种,它由四条边和四个顶点构成,称为多边形。
它可以在三维空间中描述物体的表面形状,可以用来描述物体的结构与外形,四边形的面积可以通过其各条边的长度和夹角来计算。
正方体是基本几何体中的另一种,它由六个面和八个角构成,一般把八个角和六个面分别称为端点和面。
正方体可以在三维空间内展示,它可以用来描述物体的整体形状,可以知道物体的长、宽、高,可以通过体积的计算来计算物体的重量。
棱柱体是基本几何体的另一种,它由两个圆面加上一条棱组成,其中圆面可以是圆、椭圆、圆环等,棱柱体可以在三维空间中描述,它可以帮助我们更好地理解物体的整体形状。
另外,还可以通过它的体积来计算物体的重量。
圆锥体是基本几何体中的另一种,它是由一个圆面和一个椭圆面组成的,圆锥体也可以在三维空间中描述,它可以帮助我们更好地理解物体的外形,也可以通过它的体积来计算物体的重量。
椎体是基本几何体中的另一种,它由三个圆面和一个椭圆面组成,椎体也可以在三维空间中描述,它可以帮助我们更好地理解物体的外形,还可以通过它的体积和表面积计算物体的重量。
以上就是基本几何体的基本特征,它们是多维平面几何图形的基础,可以用来描述物体的形状,并且可以结合物理学中的相关定理,用来计算物体的面积、体积、重量等。
基本立体图形+第2课时++圆柱、圆锥、圆台、球、简单组合体(2019)必修第二册

②是由一个长方体截去一个三棱锥后得到的几何体;
③是由一个圆柱挖去一个三棱锥后得到的几何体.
典例精析
题型三:旋转体的有关计算
例3
一个圆台的母线长为12 cm,两底面面积分别为4π cm2和25π cm2,求:
(1)圆台的高;(2)将圆台还原为圆锥后,圆锥的母线长.
解
圆台的轴截面是等腰梯形ABCD.
由已知可得O1A=2 cm,OB=5 cm.
挖去
一部分而成.
典例精析
题型一:旋转体的结构特征
例1 (1)下列说法正确的是________.(填序号)
①以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台;
②圆柱、圆锥、圆台的底面都是圆;
③以等腰三角形的底边上的高线所在的直线为旋转轴,其余各边旋转一周形成的
曲面所围成的几何体是圆锥;
④半圆面绕其直径所在直线旋转一周形成球;
例4 有一根高为3π cm,底面半径为1 cm的圆柱形铁管,用一段铁丝在铁管上缠绕2圈,
并使铁丝的两个端点落在圆柱的同一母线的两端,求铁丝的最短长度.
解 把圆柱侧面及缠绕其上的铁丝展开,在平面上得到矩形ABCD(如图所示),
由题意知BC=3π cm,AB=4π cm,点A与点C分别是铁丝的起、止位置,
8.1 基本立体图形
第2课时 圆柱、圆锥、圆台、球、
简单组合体
新知探索
圆柱的结构特征
圆柱
图形及表示
定义:以 矩形的一边 所在直线为旋转轴,其余三边旋转形
成的面所围成的旋转体叫做圆柱
相关概念:
圆柱的轴:________
旋转轴
圆柱的底面:_________的边旋转而成的圆面
垂直于轴
圆柱的侧面:_________的边旋转而成的曲面
高中数学必修2《空间几何体》知识点
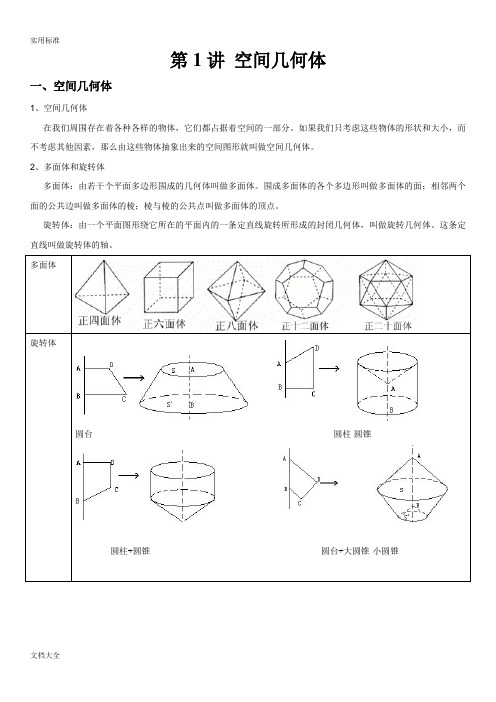
第1讲空间几何体一、空间几何体1、空间几何体在我们周围存在着各种各样的物体,它们都占据着空间的一部分。
如果我们只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体。
2、多面体和旋转体多面体:由若干个平面多边形围成的几何体叫做多面体。
围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点。
旋转体:由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体,叫做旋转几何体。
这条定直线叫做旋转体的轴。
多面体旋转体圆台圆柱-圆锥圆柱+圆锥圆台+大圆锥-小圆锥二、柱、锥、台、球的结构特征1.棱柱定义图形表示分类性质有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
两个互相平行的平面叫做棱柱的底面,其余各面叫做棱柱的侧面。
用平行的两底面多边形的字母表示棱柱,如:棱柱ABCDEF-A1B1C1D1E1F1。
棱柱的分类一(底面):棱柱的底面可以是三角形、四边形、五边形、……我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、……棱柱的分类二(根据侧棱与底面的关系):斜棱柱: 侧棱不垂直于底面的棱柱.直棱柱: 侧棱垂直于底面的棱柱叫做直棱柱正棱柱: 底面是正多边形的直棱柱叫做正棱柱(1)上下底面平行,且是全等的多边形。
(2)侧棱相等且相互平行。
(3) 侧面是平行四边形。
三棱柱四棱柱五棱柱斜棱柱直棱柱正棱柱2.棱锥定义图形表示性质分类有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
用顶点及底面各顶点字母表示棱锥,如:棱锥S-ABC侧面是三角形,底面是多边形。
按底面多边形的边数分类可分为三棱锥、四棱锥、五棱锥等等,其中三棱锥又叫四面体。
特殊的棱锥-正棱锥定义:如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面中心三棱锥四棱锥五棱锥直棱锥2.棱台定义图形表示分类性质用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫做棱台。
第2讲 空间几何体运动轨迹与长度问题(原卷版)

第2讲 空间几何体运动轨迹与长度问题一、单选题1.(2022·全国·高三专题练习(理))已知正方体ABCD A B C D ''''-的棱长为4,E ,F 分别为BB ',C D ''的中点,点P 在平面ABB A ''中,=PF N 在线段AE 上,则下列结论正确的个数是( )①点P 的轨迹长度为2π;①线段FP 的轨迹与平面A B CD ''的交线为圆弧;①NP ;①过A 、E 、F 作正方体的截面,则该截面的周长为103A .4 B .3 C .2 D .12.(2022·江西·模拟预测(理))已知正方体1111ABCD A B C D -的棱长为3,点P 在11A C B △的内部及其边界上运动,且DP =P 的轨迹长度为( )AB .2πC .D .3π 3.(2022·河南河南·三模(理))已知正四棱柱1111ABCD A B C D -,2AB =,1AA a =,点M 为1CC 点的中点,点P 为上底面1111D C B A 上的动点,下列四个结论中正确的个数为( )①当a =P 位于上底面的中心时,四棱柱P ABCD -外接球的表面积为25π3; ①当2a =时,存在点P 满足4PA PM +=;①当2a =时,存在唯一的点P 满足90APM ∠=︒;①当2a =时,满足BP AM ⊥的点P .A .1B .2C .3D .4 4.(2022·四川泸州·三模(理))已知三棱锥P ABC -的底面ABC 为等腰直角三角形,其顶点P 到底面ABC 的距离为3,体积为24,若该三棱锥的外接球O 的半径为5,则满足上述条件的顶点P 的轨迹长度为( )A .6πB .30πC .(9π+D .(6π+5.(2022·重庆·模拟预测)已知棱长为3的正四面体A BCD -,P 是空间内的任一动点,且满足2PA PD ≥,E 为AD 中点,过点D 的平面α∥平面BCE ,则平面α截动点P 的轨迹所形成的图形的面积为( )A .πB .2πC .3πD .4π6.(2022·浙江温州·高三开学考试)如图,正方体1AC ,P 为平面11B BD 内一动点,设二面角11A BD P --的大小为α,直线1A P 与平面11BD A 所成角的大小为β.若cos sin βα=,则点P 的轨迹是( )A .圆B .抛物线C .椭圆D .双曲线二、多选题 7.(2022·湖北·高一阶段练习)已知正方体1111ABCD A B C D -的棱长为2,E 为线段1AA 的中点,AP AB AD λμ=+,其中,[0,1]λμ∈,则下列选项正确的是( )A .12μ=时,11A P ED ⊥B .14λ=时,1B P PD +C .1λμ+=时,直线1A P 与面11BDE D .1λμ+=时,正方体被平面1PAD 截的图形最大面积是8.(2022·湖南岳阳·三模)如图,在直棱柱1111ABCD A B C D -中,各棱长均为2,π3ABC ∠=,则下列说法正确的是( )A .三棱锥1A ABC -B .异面直线1AB 与1BCC .当点M 在棱1BB 上运动时,1MD MA +最小值为D .N 是ABCD 所在平面上一动点,若N 到直线1AA 与BC 的距离相等,则N 的轨迹为抛物线9.(2022·广东·高二阶段练习)已知正方体1111ABCD A B C D -的棱长为2,点P 为正方形ABCD 所在平面内一动点,则下列命题正确的有( )A .若点P 总满足11PD DC ⊥,则动点P 的轨迹是一条直线B .若点P 到直线1BB 与到直线DC 的距离相等,则点P 的轨迹为抛物线C .若点P 到直线1DD 的距离与到点C 的距离之和为2,则动点P 的轨迹是椭圆D .若1D P 与AB 所成的角为π3,则点P 的轨迹为双曲线 10.(2022·江苏南通·模拟预测)设正方体ABCD —1111D C B A 的棱长为2,P 为底面正方形ABCD 内(含边界)的一动点,则( )A .存在点P ,使得A 1P ∥平面11B CDB .当PC PD ⊥时,|A 1P |2的最小值是10-C .若1APC 的面积为1,则动点P 的轨迹是抛物线的一部分D .若三棱锥P —111A B C 的外接球表面积为41π4,则动点P 的轨迹围成图形的面积为π11.(2022·山东·高一阶段练习)如图,在棱长为1111ABCD A B C D -中,点P 是平面11A BC 内一个动点,且满足15DP PB +=+ ) (参考数据:4sin 535︒=,3sin 375︒=)A .1PB B D ⊥B .点P 的轨迹是一个圆C .直线1B P 与平面11A BC 所成角为53°D .设直线1B P 与直线1AD 所成角为θ,则3790θ︒≤≤︒12.(2022·广东·佛山市南海区艺术高级中学模拟预测)如图,若正方体的棱长为1,点M 是正方体1111ABCD A B C D -的侧面11ADD A 上的一个动点(含边界),P 是棱1CC 的中点,则下列结论正确的是( )A .沿正方体的表面从点A 到点PB .若保持||PM =M 在侧面内运动路径的长度为3π C .三棱锥1B C MD -的体积最大值为16 D .若M 在平面11ADD A 内运动,且111MD B B D B ∠=∠,点M 的轨迹为抛物线13.(2022·广东佛山·高二期末)如图,在棱长为2的正方体1111ABCD A B C D -中,M 为1D D 的中点,连接BM ,设BM 的中点为E ,动点N 在底面正方形ABCD 内(含边界)运动,则下列结论中正确的是( )A .存在无数个点N 满足0AN BM ⋅=B .若2AN NC =,则1A ,E ,N 三点共线C .若NB ND +=,则1A ND .若MN 与平面ABCD 所成的角为3π,则点N 的轨迹为抛物线的一部分 14.(2022·全国·模拟预测)如图,点M 是棱长为1的正方体1111ABCD A B C D -中的侧面11ADD A 上的一个动点(包含边界),则下列结论正确的是( )A .存在无数个点M 满足1CM AD ⊥B .当点M 在棱1DD 上运动时,1||MA MB +1C .在线段1AD 上存在点M ,使异面直线1B M 与CD 所成的角是30D .满足1||2MD MD =的点M 的轨迹是一段圆弧15.(2022·福建·厦门一中高一阶段练习)如图,在棱长为2的正方体1111ABCD A B C D -中,O 为正方形ABCD 的中心,P 为棱1AA 上的动点.则下列说法正确的是( )A .点P 为1AA 中点时,1PO DC ⊥B .当P 点运动时,折线段1D P PC +长度的最小值是3C .当P 点运动时,三棱锥1P BDC -外接球的球心总在直线1A C 上D .当P 为1AA 的中点时,正方体表面到P 点距离为2的轨迹的总长度为43π⎛ ⎝16.(2022·山东聊城·三模)在直四棱柱1111ABCD A B C D -中,所有棱长均2,60BAD ∠=︒,P 为1CC 的中点,点Q 在四边形11DCC D 内(包括边界)运动,下列结论中正确的是( )A .当点Q 在线段1CD 上运动时,四面体1A BPQ 的体积为定值B .若AQ//平面1A BP ,则AQ 的最小值为5C .若1A BQ △的外心为M ,则11A B AM ⋅为定值2D .若1AQ =,则点Q 的轨迹长度为23π 17.(2022·全国·华中师大一附中模拟预测)如图,在四棱锥P -ABCD 中,底面ABCD 是边长为2的正方形,PA ⊥平面ABCD ,且2PA =.点E ,F ,G 分别为棱AB ,AD ,PC 的中点,下列说法正确的是( )A .AG ⊥平面PBDB .直线FG 和直线AC 所成的角为3π C .过点E ,F ,G 的平面截四棱锥P -ABCD 所得的截面为五边形D .当点T 在平面ABCD 内运动,且满足AGT △的面积为12时,动点T 的轨迹是圆 18.(2022·福建三明·模拟预测)已知棱长为4的正方体1111ABCD A B C D -中,14AM AB =,点P 在正方体的表面上运动,且总满足0MP MC ⋅=,则下列结论正确的是( ) A .点P 的轨迹所围成图形的面积为5 B .点P 的轨迹过棱11A D 上靠近1A 的四等分点C .点P 的轨迹上有且仅有两个点到点C 的距离为6D .直线11B C 与直线MP 所成角的余弦值的最大值为3519.(2022·重庆巴蜀中学高一期中)在正方体1111ABCD A B C D -中,M ,N ,P 分别为棱111,,AB CC C D 的中点,动点Q ∈平面MNP ,2DQ AB ==,则( )A .1AC MNB .直线∥PQ 平面11A BCC .正方体被平面MNP 截得的截面为正六边形D .点Q 的轨迹长度为2π 20.(2022·云南·昭通市第一中学高一阶段练习)(多选)如图,若正方体的棱长为1,点M 是正方体1111ABCD A B C D -的侧面11ADD A 上的一个动点(含边界),P 是棱1CC 的中点,则下列结论正确的是( )A .沿正方体的表面从点A 到点PB .若保持PM M 在侧面内运动路径的长度为3π C .三棱锥1B C MD -的体积最大值为16 D .若点M 满足111MD B B D B ∠=∠,则点M 的轨迹为线段21.(2022·山东·模拟预测)如图,正方体1111ABCD A B C D -的棱长为2,点M 是其侧面11ADD A 上的一个动点(含边界),点P 是线段1CC 上的动点,则下列结论正确的是( )A .存在点P ,M ,使得平面11B D M 与平面PBD 平行B .存在点P ,M ,使得二面角--M DC P 大小为23π C.当P 为棱1CC 的中点且PM =M 的轨迹长度为23πD .当M 为1A D 中点时,四棱锥M ABCD - 22.(2022·广东·三模)在正方体1111ABCD A B C D -中,1AB =,点P 满足1CP CD CC λμ=+,其中[][]0,1,0,1λμ∈∈,则下列结论正确的是( )A .当1//B P 平面1A BD 时,1B P 可能垂直1CDB .若1B P 与平面11CCD D 所成角为4π,则点P 的轨迹长度为2πC .当λμ=时,1||DP A P +D.当1λ=时,正方体经过点1A 、P 、C 的截面面积的取值范围为 23.(2022·重庆巴蜀中学高三阶段练习)已知正四面体A BCD -的棱长为2,底面BCD 所在平面上一动点P 满足AP = )A .点PB .直线AP 与底面BCD 所成角的正弦值为13C .DPD .直线AP 与直线CD 所成角的取值范围为ππ,32⎡⎤⎢⎥⎣⎦ 24.(2022·福建·莆田二中模拟预测)在棱长为1的正方体1111ABCD A B C D -中,点M 是11A D的中点,点P ,Q ,R 在底面四边形ABCD 内(包括边界),1PB ∥平面1MC D ,1D Q =,点R 到平面11ABB A 的距离等于它到点D 的距离,则( )A.点P B .点Q 的轨迹的长度为4πC .PQ 12D .PR 25.(2022·全国·高三专题练习)如图,若正方体的棱长为1,点M 是正方体1111ABCD A B C D -的侧面11ADD A 上的一个动点(含边界),P 是棱1CC 的中点,则下列结论正确的是( )A .沿正方体的表面从点A 到点PB .若保持PM M 在侧面内运动路径的长度为π3C .三棱锥1B C MD -的体积最大值为16D .若M 在平面11ADD A 内运动,且111MD B B D B ∠=∠,点M 的轨迹为线段26.(2022·福建·厦门一中高二期中)在四棱锥P ABCD -中,底面ABCD 是边长为2的正方形,PA ⊥平面ABCD ,且2PA =.若点E ,F ,G 分别为棱AB ,AD ,PC 的中点,则( ) A .AG ⊥平面PBDB .直线FG 和直线AB 所成的角为4π C .当点T 在平面PBD 内,且2TA TG +=时,点T 的轨迹为一个椭圆D .过点E ,F ,G 的平面与四棱锥P ABCD -表面交线的周长为27.(2022·全国·模拟预测)如图,在棱长为1的正方体1111ABCD A B C D -中,P 为棱1BB 的中点,Q 为正方形11BB C C 内一动点(含边界),则下列说法中正确的是( )A .若1D Q ∥平面1A PD ,则动点Q 的轨迹是一条线段B .存在Q 点,使得1D Q ⊥平面1A PDC .当且仅当Q 点落在棱1CC 上某点处时,三棱锥1Q A PD -的体积最大D .若1D Q =Q 点的轨迹长度为428.(2022·湖南益阳·一模)已知正方体1111ABCD A B C D -的棱长为2,点E 、F 分别是棱AB 、11A B 的中点,点P 在四边形ABCD 内(包含边界)运动,则下列说法正确的是( ) A .若P 是线段BC 的中点,则平面1AB P ⊥平面DEFB .若P 在线段AC 上,则异面直线1D P 与11A C 所成角的范围是ππ,42⎡⎤⎢⎥⎣⎦C.若1PD 平面11A C E ,则点PD .若PF 平面11B CD ,则PF 长度的取值范围是 29.(2022·湖南·长沙市南雅中学高三阶段练习)已知正方体1111ABCD A B C D -的棱长为1,E 为线段1AA 的中点,AP AB AD λμ=+,其中,[0,1]λμ∈,则下列选项正确的是( ) A .12μ=时,11A P ED ⊥B .14λ=时,1B P PD +C .λμ=时,三棱锥1D EBP -的体积为定值D .1λμ+=时,直线1A P 与面11B DE 30.(2022·湖北·襄阳五中模拟预测)如图,在棱长为1的正方体ABCD —111A B C D 中,E 为侧面11BCC B 的中心,F 是棱11C D 的中点,若点P 为线段1BD 上的动点,N 为ABCD 所在平面内的动点,则下列说法正确的是( )A .PE ·PF 的最小值为148B .若12BP PD =,则平面P AC 截正方体所得截面的面积为98C .若1D N 与AB 所成的角为4π,则N 点的轨迹为双曲线的一部分 D .若正方体绕1BD 旋转θ角度后与其自身重合,则θ的最小值是23π31.(2022·广东珠海·高三期末)如图,在直棱柱1111ABCD A B C D -中,各棱长均为2,3ABC π∠=,则下列说法正确的是( )A .三棱锥1A ABC -外接球的表面积为283π B .异面直线1AB 与1BC 所成角的余弦值为12C .当点M 在棱1BB 上运动时,1MD MA +最小值为D .N 是平面ABCD 上一动点,若N 到直线1AA 与BC 的距离相等,则N 的轨迹为抛物线 32.(2022·浙江杭州·高二阶段练习)如图,在正四棱柱ABCD -A 1B 1C 1D 1中,AB =3,1AA =P 是该正四棱柱表面或内部一点,直线PB ,PC 与底面ABCD 所成的角分别记为α,β,且sin β=2sin α,记动点P 的轨迹与棱BC 的交点为Q ,则下列说法正确的是( )A .Q 为BC 中点B .线段P A 1长度的最小值为5C .存在一点P ,使得PQ ①平面AB 1D 1D .若P 在正四棱柱ABCD -A 1B 1C 1D 1表面,则点P 33.(2022·全国·高三专题练习)如图,若正方体的棱长为1,点M 是正方体1111ABCD A B C D -的侧面11ADD A 上的一个动点(含边界),P 是棱1CC 的中点,则下列结论正确的是( )A .当M 为AD 中点时,三棱锥M -BDP 的体积为124B .沿正方体的表面从点A 到点PC .若保持PM =M 在侧面内运动路径的长度为3π D .若M 在平面11ADD A 内运动,且111MD B B D B ∠=∠,点M 的轨迹为抛物线34.(2022·全国·高三专题练习)如图,已知直四棱柱ABCD -EFGH 的底面是边长为4的正方形,CG m =,点M 为CG 的中点,点P 为底面EFGH 上的动点,则( )A .当4m =时,存在点P 满足8PA PM +=B .当4m =时,存在唯一的点P 满足2APM π∠=C .当4m =时,满足BP ①AM 的点P 的轨迹长度为D .当m 时,满足2APM π∠=的点P35.(2022·浙江丽水·高二期末)如图,在正四棱柱1111ABCD A B C D -中,=3AB ,1AA =P 是该正四棱柱表面或内部一点,直线PB ,PC 与底面ABCD 所成的角分别记为,αβ,且sin 2sin βα=,记动点P 的轨迹与棱BC 的交点为Q ,则下列说法正确的是( )A .Q 为BC 中点B .线段1PA 长度的最小值为5C .存在一点P ,使得//PQ 平面11AB DD .若P 在正四棱柱1111ABCD A B C D -表面,则点P 36.(2022·江苏·扬州中学高三开学考试)如图,点P 是棱长为2的正方体1111ABCD A B C D -的表面上一个动点,则( )A .当P 在平面11BCCB 上运动时,四棱锥11P AA D D -的体积不变B .当P 在线段AC 上运动时,1D P 与11A C 所成角的取值范围是,62ππ⎡⎤⎢⎥⎣⎦C.当直线AP 与平面ABCD 所成的角为45°时,点P 的轨迹长度为π+D .若F 是11A B 的中点,当P 在底面ABCD 上运动,且满足PF ∥平面11B CD 时,PF 长度的三、双空题37.(2022·山东潍坊·模拟预测)如图,将正四面体每条棱三等分,截去顶角所在的小正四面体,余下的多面体就成为一个半正多面体,亦称“阿基米德体”.点A ,B ,M 是该多面体的三个顶点,点N 是该多面体外接球表面上的动点,且总满足MN AB ⊥,若4AB =,则该多面体的表面积为______;点N 轨迹的长度为______.38.(2022·湖南·雅礼中学二模)已知菱形ABCD 的各边长为2,60D ∠=.如图所示,将ACB △沿AC 折起,使得点D 到达点S 的位置,连接SB ,得到三棱锥S ABC -,此时3SB =.则三棱锥S ABC -的体积为__________,E 是线段SA 的中点,点F 在三棱锥S ABC -的外接球上运动,且始终保持EF AC ⊥,则点F 的轨迹的周长为__________.39.(2022·浙江·1111ABCD A B C D -中,P 为侧面11BCC B 内的动点,且直线1A P 与AB 的夹角为30°,则点P 的轨迹长为___________;若点1A 与动点P 均在球O 表面上,球O 的表面积为___________.40.(2022·江苏无锡·高三期末)正四面体ABCD 的棱长为12,在平面BCD 内有一动点P ,且满足AP =则P 点的轨迹是__________;设直线AP 与直线BC 所成的角为θ,则cos θ的取值范围为__________.四、填空题41.(2022·广东·广州六中高二期中)在矩形ABCD 中,E 是AB 的中点,1,2AD AB ==,将ADE 沿DE 折起得到A DE ',设A C '的中点为M ,若将A DE '绕DE 旋转90,则在此过程中动点M 形成的轨迹长度为___________.42.(2022·全国·高三专题练习)在棱长为a 的正方体1111ABCD A B C D -中,M ,N 分别为1BD ,11B C 的中点,点P 在正方体表面上运动,且满足MP CN ⊥,点P 轨迹的长度是___________.43.(2022·湖北·黄冈中学二模)如图,棱长为1的正方体1111ABCD A B C D -,点P 沿正方形ABCD 按ABCDA 的方向作匀速运动,点Q 沿正方形11B C CB 按111B C CBB 的方向以同样的速度作匀速运动,且点,P Q 分别从点A 与点1B 同时出发,则PQ 的中点的轨迹所围成图形的面积大小是________.44.(2022·湖南师大附中三模)已知棱长为3的正四面体ABCD ,E 为AD 的中点,动点P 满足2PA PD =,平面α经过点D ,且平面//α平面BCE ,则平面α截点P 的轨迹所形成的图形的周长为_________.45.(2022·江西萍乡·三模(理))如图,在正方形ABCD 中,点M 是边CD 的中点,将ADM △沿AM 翻折到PAM △,连接,PB PC ,在ADM △翻折到PAM △的过程中,下列说法正确的是_________.(将正确说法的序号都写上)①点P 的轨迹为圆弧;①存在某一翻折位置,使得AM PB ⊥;①棱PB 的中点为E ,则CE 的长为定值;46.(2022·安徽·合肥一中模拟预测(文))如图,点M 是正方体1111ABCD A B C D -中的侧面11ADD A 内(包括边界)的一个动点,则下列命题正确的是___________(请填上所有正确命题的序号).①满足1BM A D ⊥的点M 的轨迹是一条线段;①在线段1AD 上存在点M ,使异面直线1B M 与CD 所成的角是6π;①若正方体的棱长为1,三棱锥1B C MD -的体积最大值为13; ①存在无数个点M ,使得点M 到直线AD 和直线11C D 的距离相等. 47.(2022·河南·鹤壁高中模拟预测(文))如图,在棱长为1的正方体1111ABCD A B C D -中,P 为棱1BB 的中点,Q 为正方形11BB C C 内一动点(含边界),则下列说法中正确的是______.①若1//D Q 平面1A PD ,则动点Q 的轨迹是一条线段①存在Q 点,使得1D Q ⊥平面1A PD①当且仅当Q 点落在棱1CC 上某点处时,三棱锥1Q A PD -的体积最大①若1D Q =Q 48.(2022·北京·高三专题练习)如图,正方体ABCD -A 1B 1C 1D 1的棱长为2,点O 为底面ABCD 的中心,点P 在侧面BB 1C 1C 的边界及其内部运动.给出下列四个结论:①D 1O ①AC ;①存在一点P ,D 1O ①B 1P ;①若D 1O ①OP ,则①D 1C 1P①若P 到直线D 1C 1的距离与到点B 的距离相等,则P 的轨迹为抛物线的一部分. 其中所有正确结论的序号是_________________.49.(2022·四川南充·二模(理))已知正方体1111ABCD A B C D -的棱长为,M N 为体对角线1BD 的三等分点,动点P 在三角形1ACB 内,且三角形PMN 的面积PMN S =△P 的轨迹长度为___________. 50.(2022·宁夏·石嘴山市第三中学高三期末(理))如图正方体1111ABCD A B C D -的棱长为4,点M 是棱11A D 的中点,点P 在面ABCD 内(包含边界),且MP =则下列四个命题中:①点P 的轨迹的长度为2π①存在P ,使得1MP AC ⊥①直线MP 与平面11BDD B ①沿线段MP 的轨迹将正方体1111ABCD A B C D -切割成两部分,挖去体积较小部分,剩余部分几何体的表面积为881)+π其中正确命题的序号是___________.51.(2022·四川省叙永第一中学校模拟预测(文))正方体1111ABCD A B C D -棱长为3,点E 在边BC 上,且满足BE =2EC ,动点M 在正方体表面上运动,并且总保持1ME BD ⊥,则动点M 的轨迹的周长为__.52.(2022·青海·海东市教育研究室一模(理))已知P 为正方体1111ABCD A B C D -表面上的一动点,且满足,2PA AB =,则动点P 运动轨迹的周长为__________.。
人教A版高中数学必修二 《基本立体图形》立体几何初步(第二课时旋转体及简单组合体的结构特征)

[解析] ①以直角三角形的一条直角边为轴旋转一周才可以得到圆锥,故错误;②以 直角梯形垂直于底边的一腰为轴旋转一周可得到圆台,故错误;③它们的底面为圆 面,故正确;④正确;作球的一个截面,在截面的圆周上任意取四点,则这四点就 在球面上,故⑤错误;球面上任意三点一定不共线,故⑥错误.
[答案] ③④
课前 • 自主探究 课堂 • 互动探究 课后 • 素养培优 课时 • 跟踪训练
[教材提炼] 知识点一 圆柱的结构特征 预习教材,思考问题 圆柱是由几个平面围成的吗?若不是,它又是怎么构成的呢?
[提示] 圆柱的面不都是平的,如侧面就是曲的.它是以矩形的一条边为旋转轴, 其余三条边旋转一周形成的面围成的旋转体.
2.已知 AB 是直角梯形 ABCD 中与底边垂直的一腰,如图.分别 以 AB、BC、CD、DA 为轴旋转,试说明所得几何体的结构特征.
解析:(1)以 AB 为轴旋转所得旋转体是圆台.如图①所示. (2)以 BC 边为轴旋转所得的旋转体是一组合体:下部为圆柱,上部为圆锥.如图② 所示. (3)以 CD 边为轴旋转所得的旋转体为一组合体:上部为圆锥,下部为圆台,再挖去 一个小圆锥.如图③所示.
若本例中蚂蚁围绕圆柱转两圈,如图,则它爬行的最短距离是多少?
解析:可把圆柱展开两次,如图,则 AB′即为所求. ∵AB=2,BB′=2×2π×1=4π, ∴AB′= AB2+BB′2= 4+16π2=2 1+4π2. 故蚂蚁爬行的最短距离为 2 1+4π2.
一般地,沿多面体或旋转体的表面最短距离(路程)问题,用侧面展开解决.
答案:C
3.如图所示的组合体,其结构特征是 ( ) A.两个圆锥 B.两个圆柱 C.一个棱锥和一个棱柱 D.一个圆锥和一个圆柱
解析:题图所示的几何体是由一个圆锥和一个圆柱构成的组合体.
人教版高中数学必修2《基本立体图形—多面体》PPT课件

(4)棱台 定义及分类
定义:用一个平行于棱锥底面的平面去截
棱锥,底面与截面之间那部分多面体叫做
棱台.
分类:由三棱锥、四棱锥、五棱锥……截
得的棱台分别为三棱台、四棱台、五棱
台……
记作棱台
正棱台
ABCD-A′B′C′D′
例题
将下列各类几何体之间的关系用Venn图表示出来:
多面体、长方体、棱柱、棱锥、棱台、直棱柱、四面体、 平行六面体.
基本立体图形(多面体)
高一年级 数学
立体几何是研究现实世界中物体的形状、大小与 位置关系的数学分支,在解决实际问题中有着广泛的 应用,在小学和初中我们已经认识了一些从现实物体 中抽象出来的立体图形,立体图形各式各样、千姿百 态,本节课我们将从空间几何体的整体观察入手,研 究它们的结构特征,学习它们的表示方法.
我们把棱柱中两个互相平行的面叫做棱柱的底面,它 们是全等的多边形;其余各面叫做棱柱的侧面,它们 都是平行四边形;相邻侧面的公共边叫做棱柱的侧棱, 侧面与底面的公共顶点叫做棱柱的顶点.
记作棱柱 ABCDEFA′B′C′D′E′F′
分类:直棱柱,斜棱柱,正棱柱,平行六面体.
像金字塔这样的多面体,均由平面图形围成,其中一个面 是多边形,其余各面都是有一个公共顶点的三角形,这样 的多面体就是棱锥.
剩余部分是一个侧棱长为2的三棱柱,并指出截去的几何 体的特征.
立体几何中常用割补法解题,将一个不规则的几何体 用一个平面分割成规则的几何体,这种方法蕴含了一 种构造思想,有利于提高同学们的创新思维品质.
如果我们用一个平行于棱锥底面的平面去截棱锥,其 中一部分还是棱锥,那么另一部分又是什么几何体呢? 我们把底面和截面之间的部分多面体就叫做棱台.
几何体知识点总结
几何体知识点总结几何体是三维空间中的物体,有长、宽、高三个方向的尺寸。
在数学中,研究几何体的性质和关系是几何学的基本内容之一。
几何体包括了诸如球体、立方体、长方体、圆柱体、圆锥体等多种形态,它们在我们日常生活中随处可见,比如水杯、球、汽车等。
在学习几何体的知识时,需要了解和掌握一些基本概念和性质,这样才能更好地理解和应用几何体的相关知识。
本文将按照几何体的性质、表面积和体积来进行概括总结。
一、几何体的性质1. 点、线、面和体的概念在几何学中,点是没有长、宽、高的,只有位置没有大小。
线是由一系列点按照一定的顺序排列而成,线没有宽度,有长没有高。
面是由无数个线相交而成,面没有高。
几何体是由无数个面所围成,几何体有三个维度,即长、宽和高。
2. 顶点、边和面几何体的顶点是几何体的交点,可以用来表示几何体的各个部分。
边是连接几何体不同部分的线段,用来表示几何体的边界。
面是由边相交而成,表明几何体的表面。
3. 直线、平面与空间的关系几何体的性质和关系中有一些概念是离不开直线、平面以及空间的。
直线是由点连成的,平面是由直线连成的,空间是由无数个平面相互连接而成的。
几何体存在于三维空间中,有着三个维度。
4. 对称性几何体的对称性是指在某种变化下,几何体仍能保持不变的性质。
对称性包括了轴对称和中心对称,这在研究几何体的构造、性质和应用中都有着重要意义。
5. 体积的概念几何体的体积是指几何体所占据的空间大小,它是几何体重要的属性之一。
体积的计算需要根据不同的几何体结构和性质进行不同的推算和计算。
二、几何体的表面积1. 表面积的概念几何体的表面积是指几何体所有表面的总面积,它是一个重要的指标,可以用来描述几何体的大小和形状。
表面积的计算需要根据几何体的不同结构和性质进行不同的推算和计算。
2. 三棱柱、四棱柱、六面体等的表面积计算方法不同的几何体表面积的计算方法是不同的,比如三棱柱、四棱柱、六面体等。
这些几何体的表面积计算方法需要根据每个几何体的特点和性质进行具体的计算。
第2讲 空间几何体轨迹问题(解析版)
第2讲 空间几何体轨迹问题一.选择题(共7小题)1.(2020秋•西城区期末)在棱长为1的正方体1111ABCD A B C D -中,M ,N 分别为1BD ,11B C 的中点,点P 在正方体的表面上运动,且满足MP CN ⊥,则下列说法正确的是( )A .点P 可以是棱1BB 的中点 B .线段MPC .点P 的轨迹是正方形D .点P 轨迹的长度为2【解析】解:在正方体1111ABCD A B C D -中,以D 为坐标原点,分别以DA ,DC ,1DD 为x 轴,y 轴,z 轴建立空间直角坐标系,因为该正方体的棱长为1,M ,N 分别为1BD ,11B C 的中点, 则(0D ,0,0),1111(,,),(,1,1),(0,1,0)2222M N C ,所以1(,0,1)2CN =,设(P x ,y ,)z ,则111(,,)222MP x y z =---,因为MP CN ⊥,所以111()0,2430222x z x z -+-=+-=,当1x =时,14z =, 当0x =时,34z =, 取1133(1,0,),(1,1,),(0,1,),(0,0,)4444E F G H ,连结EF ,FG ,GH ,HE ,则(0,1,0)EF GH ==,1(1,0,)2EH FG ==-,所以四边形EFGH 为矩形,则0,0EF CN EH CN ⋅=⋅=,即EF CN ⊥,EH CN ⊥,又EF 和EH 为平面EFGH 中的两条相交直线, 所以CN ⊥平面EFGH ,又111111(,,),(,,)224224EM MG =-=-,所以M 为EG 的中点,则M ∈平面EFGH , 所以为使MP CN ⊥,必有点P ∈平面EFGH , 又点P 在正方体表面上运动, 所以点P 的轨迹为四边形EFGH , 因此点P 不可能是棱1BB 的中点, 故选项A 错误;又1EF GH ==,EH FG ==,所以EF EH ≠,则点P 的轨迹不是正方形,且矩形EFGH 的周长为222+= 故选项C 错误,选项D 正确;因为1(,0,1)2CN =,111(,,)222MP x y z =---,又MP CN ⊥,则111()0,2430222x z x z -+-=+-=,所以322x z =-,点P 在正方体表面运动,则30212z -,解得1344z,且01y ,所以MP =故当14z =或34z =,0y =或1时,MP 取得最大值为34, 故选项B 错误; 故选:D .2.(2020•5月份模拟)棱长为1的正方体1111ABCD A B C D -中,P 为正方体表面上的一个动点,且总有1PC BD ⊥,则动点P 的轨迹所围成图形的面积为( )A B .C D .1【解析】解:连接1AB ,AC ,1B C ,则可证1BD ⊥平面1ACB , 故P 点轨迹围成图形为△1AB C ,又11AC AB B C ===12AB CS∴. 故选:C .3.(2020•山西模拟)已知长方体1111ABCD A B C D -,2AB AD ==,14AA =,M 是1BB 的中点,点P 在长方体内部或表面上,且//MP 平面11AB D ,则动点P 的轨迹所形成的区域面积是( )A .6B .C .D .9【解析】解:如图所示,E ,F ,G ,H ,N 分别为11B C ,11C D ,1DD ,DA ,AB 的中点, 则11////EF B D NH ,1////MN B A FG , 所以平面//MEFGHN 平面11AB D ,所以动点P 的轨迹是六边形MEFGHN 及其内部. 因为2AB AD ==,14AA =,所以EF HN ==EM MN FG GH ===GM =E 到GM =所以229EFGH S S ===梯形. 故选:D .4.(2020•5月份模拟)棱长为1的正方体1111ABCD A B C D -中P 为正方体表面上的一个动点,且总有1PC BD ⊥,则动点P 的轨迹的长度为( )A .34πB .4πC .D .【解析】解:P 点的轨迹为过点C 与直线1BD 垂直的截面与正方体的交线,就是图形中点三角形1ACB ,它的周长为:. 故选:C .5.(2020•天河区一模)如图所示,在棱长为a 的正方体1111ABCD A B C D -中,E 是棱1DD 的中点,F 是侧面11CDD C 上的动点,且1//B F 面1A BE ,则F 在侧面11CDD C 上的轨迹的长度是( )A .aB .2aC D 【解析】解:设G ,H ,I 分别为CD 、1CC 、11C D 边上的中点则1A BEG 四点共面, 且平面1//A BGE 平面1B HI 又1//B F 面1A BE ,F ∴落在线段HI 上,正方体1111ABCD A B C D -中的棱长为a ,1122HI CD ∴==.即F 在侧面11CDD C . 故选:D .6.(2020•大观区校级模拟)已知在三棱锥P ABC -中,O 为AB 中点,PO ⊥平面ABC ,90APB ∠=︒,2PA PB ==,下列说法中错误的是( )A .若O 为ABC ∆的外心,则2PC =B .若ABC ∆为等边三角形,则AP BC ⊥C .当90ACB ∠=︒时,PC 与平面PAB 所成角的范围为(0,]4πD .当4PC =时,M 为平面PBC 内动点,若//OM 平面PAC ,则M 在三角形PBC 内的轨迹长度为2【解析】解:O 为ABC ∆的外心,可得OA OB OC ===PO ⊥平面ABC ,可得PO OC ⊥,即有2PC =,A 正确;若ABC ∆为等边三角形,若AP BC ⊥,又AP PB ⊥,可得AP ⊥平面PBC ,即AP PC ⊥,由PO OC ⊥可得PC AC ===,矛盾, 故B 错误;若90ACB ∠=︒时,设PC 与平面PAB 所成角为θ,可得OC OA OB ===2PC =,设C 到平面PAB 的距离为d , 由C PAB P ABC V V --=,可得11112223232d AC BC =, 即有222242AC BC AC BC +==,当且仅当2AC BC ==取得等号,可得d 2sin 22d θ=,即有θ的范围为(0,]4π,C 正确; 取BC 的中点N ,PB 的中点K ,连接OK ,ON ,KN ,由中位线定理可得//ON AC ,//OK PA ,可得平面//OKN 平面PAC , 可得M 在线段KN 上,而122KN PC ==,可得D 正确. 故选:B .7.(2020•昌平区模拟)如图,正方体1111ABCD A B C D -的棱长为3,点E 在棱BC 上,且满足2BE EC =,动点M 在正方体表面上运动,且1ME BD ⊥,则动点M 的轨迹的周长为( )A .B .C .D .【解析】解:由正方体的特点可知1BD ⊥平面1ACB ,在AB ,1BB 上分别取点P ,Q ,使得2BP PA =,12BQ QB =, 连接PE ,PQ ,EQ ,则//PE AC ,1//EQ B C , ∴平面1//AB C 平面PEQ ,1BD ∴⊥平面PEQ ,M ∴的轨迹为PEQ ∆.正方体棱长为3,AC ∴=, 23PE AC ∴==,PEQ ∴∆的周长为3PE =故选:A .二.多选题(共4小题)8.(2020秋•济南期末)已知正方体1111ABCD A B C D -的棱长为2,点E ,F 在平面1111A B C D 内,若||AE =AC DF ⊥,则( )A .点E 的轨迹是一个圆B .点F 的轨迹是一个圆C .||EF 1D .AE 与平面1A BD【解析】解:对于选项A ,在正方体1111ABCD A B C D -中,1AA ⊥平面1111A B C D ,1A E ⊂平面1111A B C D , 所以11AA A E ⊥, 故22211AE AA A E =+, 则有11A E =,所以点E 的轨迹是以1A 为圆心,1为半径的圆, 故选项A 正确;对于选项B ,在正方体中,AC ⊥平面11B BDD , 因为AC DF ⊥, 则DF ⊂平面11B BDD , 故F 在11B D 上,所以F 的轨迹是线段11B D , 故选项B 错误;对于选项C ,||EF 的最小值即为求线段11B D 上的点到以1A 为圆心,1为半径的圆的最小距离,又圆心1A 到线段11B D 的距离为d ,所以||EF 1, 故选项C 正确;建立如图所示的空间直角坐标系,因为点E 的轨迹是以1A 为圆心,1为半径的圆, 故设(cos E θ,sin θ,2),[0,]2πθ∈,则(0A ,0,0),1(0A ,0,2),(2B ,0,0),(0D ,2,0),所以(cos ,sin ,2)AE θθ=,1(2,0,2),(2,2,0)A B BD =-=-, 设平面1A BD 的法向量为(,,)n x y z =, 则有1220220A B n x z BD n x y ⎧⋅=-=⎪⎨⋅=-+=⎪⎩,令1x =,则1y =,1z =, 故(1,1,1)n =,设AE 与平面1A BD 所成的角为α,则)2|||cos sin |cos ,|||||AE n AE n AE nπθθα++⋅=<===, 当4πθ=时,sin α=,故AE 与平面1A BD ,故选项D 正确. 故选:ACD .9.(2020秋•开福区校级月考)已知正方体1111ABCD A B C D -的棱长为1,动点P 在其表面上运动,且||PAx =,其中点P 的轨迹长度为()f x ,给出下列结论正确的有( ) A .13()216fπ=B .f (1)32π=C .f = D.f =【解析】解:动点P 在其表面上运动,且||PA x =,∴点的轨迹是以A 为球心,PA 为半径的球的球面与正方体的面的交线,当01x <时,点的轨迹如图,则13()3242f x x x ππ=⨯⨯=,所以13()24f π=,故选项A 不符合题意; f (1)32π=,故选项B 符合题意;x <时,点P 的轨迹是三段相等圆弧,在与点A 不相邻的三个面上,圆弧半径R ==,圆弧的圆心角为6π,124f π∴=⨯=,故选项D 符合题意;当x =时,点P 的轨迹是三段相等圆弧,圆弧的长是四分之一个圆,半径是1,如图,∴这条轨迹的长度是:1332142ππ⨯⨯⨯=,故选项C 不符合题意.故选:BD .10.(2020秋•胶州市期中)已知四面体ABCD 的所有棱长均为2,则下列结论正确的是( ) A .异面直线AC 与BD 所成角为60︒B .点A 到平面BCDC .四面体ABCDD .动点P 在平面BCD 上,且AP 与AC 所成角为60︒,则点P 的轨迹是椭圆 【解析】解:如图,由题意,四面体ABCD 为正四面体,取底面BCD 的中心为G ,连接CG 并延长,角BD 于E , 则E 为BD 的中点,且CE BD ⊥,连接AG ,则AG ⊥底面BCD ,得AG BD ⊥, 又AGCE G =,BD ∴⊥平面ACG ,则AC BD ⊥,故A 错误;由四面体的所有棱长为2,可得23CG CE =,又2AC =,AG ∴=,即点A 到平面BCD ,故B 正确;设四面体ABCD 的外接球的球心为O ,半径为R ,连接OC ,则222)R R =-+,解得R =ABCD 的外接球体积为343π⨯=,故C 正确; AP 与AC 所成角为60︒,AP 可看作以AC 为轴的圆锥的母线所在直线,P 的轨迹为平面BCD 截圆锥所得曲线,由AP 与AC 所成角为60︒,且1cos 2ACG ∠=>,可知平面BCD 仅与圆锥一侧面有交点,P 的轨迹为双曲线, 故D 错误. 故选:BC .11.(2020秋•靖江市校级月考)如图1AC 是棱长为2的正方体,M 为11B C 的中点,下列命题中正确的命题有( )A .1AB 与1BC 成60︒角B .若113CN NC =,面1A MN 交CD 于E ,则13CE =C .P 点在正方形11ABB A 边界及内部运动,且1MP DB ⊥,则PD .E ,F 分别在1DB 和11A C 上,且1112A F DE EB FC ==,直线EF 与1AD ,1A D 所成角分别是α,β,则2παβ+= 【解析】证明:连接1AD ,11B D ,则11//AD BC , 则△11AB D 是正三角形,则1AD 与1AB 所成的角即为1AB 与1BC 成的角, 即1AB 与1BC 成60︒角;故A 正确,若113CN NC =,面1A MN 交CD 于E ,则13CE =;建立以1D 为坐标原点,11D A ,11D C ,1D D 分别为x ,y ,z 轴的空间直角坐标系如图: 则1(2A ,0,0),(1M ,2,0),(0N ,2,3)2,设DE t =,则(0E ,t ,2),1A ,M ,N ,E 四点共面,∴存在实数x ,y 使111A E xA M y A N =+,即(2-,t ,2)(1x =-,2,0)(2y +-,2,3)2,则2222322x y x y t y ⎧⎪--=-⎪+=⎨⎪⎪=⎩,得234343x y t ⎧=-⎪⎪⎪=⎨⎪⎪=⎪⎩,则43DE =,42233CE =-=,故B 错误,取11A B 的中点H ,1BB 的中点K , 连接HM ,HM ,HK , 则1DB HM ⊥,1DB KM ⊥, 则1DB ⊥平面HKM ,若1MP DB ⊥,则M 在平面HKM 中,则M HK ∈,则1HK ==即P 点在正方形11ABB A 边界及内部运动,且1MP DB ⊥,则P正确,故C 正确;建立如图的空间坐标系如图,则1(2A ,0,0),(0D ,0,2),(2A ,0,2),1(2B ,2,0), 则1(2D A =,0,2),1(2DA =,0,2)-,E ,F 分别在1DB 和11A C 上,且1112A FDE EB FC ==,∴122(233DE DB ==,2,42)(3-=,43,4)3-,则4(3E ,43,2)3,11122(233A F AC ==-,2,40)(3=-,43,0), 则2(3F ,43,0),则2(3EF =-,0,2)3-,则cos |cos EF α=<,122448||122224()()22333D A -->===-+-, 则0α=cos |cos EF β=<,1244||024()3DA -+>==-+, 则2πβ=,即2παβ+=,故D 正确,故选:ACD .三.填空题(共9小题)12.(2020秋•鼓楼区校级期末)如图,在棱长为1的正方体1111ABCD A BC D -中,点E ,F 分别是棱BC 、1CC 的中点,P 是侧面11BCC B 内一点(含边界),若1//A P 平面AEF ,点P 的轨迹长度为 .直线1A P 与平面11BCC B 所成角的正切值的取值范围是 .【解析】解:如图,分别取棱1BB ,11B C 的中点M ,N ,连接1A M ,1A N ,MN ,1BC ,NE ,M ,N ,E ,F 分别是其所在棱的中点,1//MN BC ∴,1//EF BC ,//MN EF ∴,MN ⊂/平面AEF ,EF ⊂平面AEF ,//MN ∴平面AEF ,1//AA NE ,1AA NE =,∴四边形1AENA 为平行四边形,1//A N AE ∴, 1A N ⊂/平面AEF ,AE ⊂平面AEF ,1//A N ∴平面AEF , 1A NM N N =,∴平面1//A MN 平面AEF ,P 是侧面11BCC B 内一点,且1//A P 平面AEF ,∴点P 必在线段MN 上,∴点P的轨迹长度为1122MN BC ==. 点P 的轨迹是线段MN ,11A B ⊥平面11BCC B ,∴直线1A P 与平面11BCC B 所成角的正切值为11A B 与P 到1B 的距离之比,设O 是MN的中点,则2MO NO ==, 111A B =,P 到1B 的距离的最大值为1112MB NB ==, ∴直线1A P 与平面11BCC B 所成角的正切值的最小值为1212=, P 到1B的距离的最小值为1B O == ∴直线1A P 与平面11BCC B=∴直线1A P 与平面11BCC B 所成角的正切值的取值范围是[2,.;[2,.13.(2020秋•桃城区校级月考)在三棱锥P ABC -中,PA AB ⊥,4PA =,3AB =,二面角P AB C --的大小为30︒,在侧面PAB ∆内(含边界)有一动点M ,满足M 到PA 的距离与M 到平面ABC 的距离相等,则M 的轨迹的长度为. 【解析】解:如图,过M 作MN PA ⊥ 于N ,MO ⊥平面ABC 于O , 过O 作OQ AB ⊥ 于Q ,连接MQ , 则MQO ∠ 为二面角P AB C -- 的平面角, 由30MQO ∠=︒, 得2MQ MO =.又MO MN =,所以2MQ MN =,在PAB ∆ 中,以AB 所在直线为x 轴,AP 所在直线为y 轴建立平面直角坐标系, 则直线AM 的方程为2y x =, 直线PB 的方程为43120x y +-=,所以直线AM 与PB 的交点坐标为612(,)55R ,所以M 的轨迹为线段AR ,14.(2020•浙江二模)在棱长为6的正三棱锥P ABC-中,D为棱PA上一动点,E为BC上一动点,且满足32AD BE=,则线段DE的中点Q的运动轨迹的测度||L L为曲线、平面图形、几何体时,||L 分别对应长度、面积、体积).【解析】解:取AB,AC,PB,PC的中点,H,I,G,F,由题意可知,Q在平面FGHI内运动,设2AD x=,3BE x=,在平面FGHI内,32HM x=,MQ x=,所以线段DE的中点Q的轨迹为线段.当E运动到C点时,132HM HI BC===,4AD=,则2MQ=,由正三棱锥的性质,可知PA BC⊥,所以HI MQ⊥,所以||L==15.(2020•河南模拟)在直四棱柱1111ABCD A B C D -中,侧棱长为6,底面是边长为8的菱形,且120ABC ∠=︒,点E 在边BC 上,且满足3BE EC =,动点M 在该四棱柱的表面上运动,并且总保持1ME BD ⊥,则动点M的轨迹围成的图形的面积为 MC 与平面ABCD 所成角最大时,异面直线1MC 与AC 所成角的余弦值为 .【解析】解:如图,在直四棱柱1111ABCD A B C D -中,底面是菱形,侧棱垂直底面, AC ∴⊥平面11BDD B ,1BD AC ∴⊥,在AB 上取F ,使得3BF FA =,连接EF ,则//EF AC ,1BD EF ⊥, 记AC 与BD 的交点为O ,以O 为坐标原点,建立如图所示的空间直角坐标系,则(4B ,0,0),1(4D -,0,6),(1E ,0), 在1BB 上取一点G ,记为(4G ,0,)t ,∴1(8BD =-,0,6),(3EG =,-,)t ,由12460BD EG t =-+=,解得4t =,即12BG GB =, EFG ∴∆的边为点M 的运动轨迹,由题意得FG =3344EF AC ==⨯=动点M 的轨迹围成的面积为12S =⨯∴当M 与G 重合时,MC 与平面ABCD 所成角最大,(4M,0,4),1(0C,6),∴1(4MC=-,,2),AC的一个方向向量为(0n =,1,0),11143cos,||||68MC nMC nMC n∴<>===,∴异面直线1MC与AC故答案为:16.(2020•高密市模拟)在四棱锥P ABCD-中,PA⊥平面ABCD,2AP=,点M是矩形ABCD内(含边界)的动点,且1AB=,3AD=,直线PM与平面ABCD所成的角为4π.记点M的轨迹长度为α,则tanα= P ABM-的体积最小时,三棱锥P ABM-的外接球的表面积为.【解析】解:如图所示,因为PA⊥平面ABCD,垂足为A,则PMA∠为直线PM与平面ABCD所成的角,所以4PMAπ∠=;因为2AP=,所以2AM=,所以点M位于底面矩形ABCD内的以点A为圆心,2为半径的圆上,记点M的轨迹为圆弧EF,连接AF,则2AF=;因为1AB=,3AD=,所以6AFB FAEπ∠=∠=;则弧EF的长度为263ππα=⨯=,所以tanα.当点M位于F时,三棱锥P ABM-的体积最小,又2PAF PBFπ∠=∠=,所以三棱锥P ABM-的外接球球心为PF的中点;因为PF =所以三棱锥P ABM -的外接球的表面积为248S ππ==.8π.17.(2020•南昌三模)已知长方体1111ABCD A B C D -中,32AB =,2AD =,1AA =已知P 是矩形ABCD内一动点,14PA =,设P 点形成的轨迹长度为α,则tan α= -1C P 的长度最短时,三棱锥1D DPC -的体积为 .【解析】解:在长方体的底面矩形ABCD 内一动点P ,连接AP ,14PA =,1AA =2AP ∴,P ∴点的轨迹为以A 为圆心,以2为半径的圆,与底面矩形BC 的交点为E ,D ,即P 的轨迹为圆弧DE ,连接AE , 在ABE ∆中,332cos 24AB EAB AE ∠===,3sin cos 4DAE EAB ∴∠=∠=,得3arcsin 4DAE ∠=, 2DE DAE α∴==∠,α为钝角, 373sin sin(2arcsin )2448DAE α∴=∠==1cos 8α==-,得tan α=-当1C P 的长度最短时,P 在AC 上,此时52AC ==,则51222PC =-=,:1:5PC AC =.又11132322D DAC V -=⨯⨯⨯⨯∴1115D DPC D DAC V V --==故答案为:-.18.(2020•中卫二模)古希腊数学家阿波罗尼奥斯发现:平面上到两定点A ,B 距离之比为常数(0λλ>且1)λ≠的点的轨迹是一个圆心在直线AB 上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体1111ABCD A B C D -中,1226AB AD AA ===,点E 在棱AB 上,2BE AE =,动点P 满足BP =.若点P 在平面ABCD 内运动,则点P 所形成的阿氏圆的半径为 P 在长方体1111ABCD A B C D -内部运动,F 为棱11C D 的中点,M 为CP 的中点,则三棱锥1M B CF -的体积的最小值为 .【解析】解:①若点P 在平面ABCD 内运动时,如图以A 为原点距离平面直角坐标系,可得(2,0)E ,(6,0)B .设(,)P x y ,由BP =可得223BP PE =.即22223(2)3(6)x y x y -+=-+,2212x y ⇒+=.则点P 所形成的阿氏圆的半径为A ,②若点P 在长方体1111ABCD A B C D -内部运动,由①可得点P在半径为A 球上. 如图建立空间直角坐标系,可得(3A ,0,0),(0F ,3,3),(0C ,6,0),1(3B ,6,3) 则1(0,3,3),(3,3,0)FC FB =-=,(3,6,0)AC =-设面1FB C 的法向量为(,,)m x y z =,1330330m FC y z m FB x y ⎧=-=⎪⎨=+=⎪⎩,可得(1,1,1)m =--. A 到面1FCB的距离为||9||3m AC d m ===则P 到面1FCB 的距离的最小值为=, M 为CP 的中点,M ∴到面1FCB . 则三棱锥1M B CF -的体积的最小值为1213193234FCB S =⨯=. 故答案为:,94.19.(2020•柯城区校级一模)若四棱锥P ABCD-的侧面PAB内有一动点Q,已知Q到底面ABCD的距离与Q到点P的距离之比为正常数k,且动点Q的轨迹是抛物线,则当二面角P AB C--平面角的大小为30︒时,k的值为12.【解析】解:如图,设二面角P AB C--平面角为θ,点Q到底面ABCD的距离为||QH,点Q到定直线AB得距离为d,则||sinQH dθ=,即||sinQHdθ=.点Q到底面ABCD的距离与到点P的距离之比为正常数k,∴||||QHkPQ=,则||||QHPQk=,动点Q的轨迹是抛物线,||PQ d∴=,即||||sinQH QHkθ=.则sin kθ=.∴二面角P AB C--的平面角的余弦值为cos cos30θ===︒解得:1(0)2k k =>.故答案为:12.20.(2019秋•舟山期末)若四棱锥P ABCD-的侧面PAB内有一动点Q,已知Q到底面ABCD的距离与Q到点P的距离之比为正常数k,且动点Q的轨迹是抛物线,则当二面角P AB C--平面角的大小为60︒时,k的值为.【解析】解:如图,设二面角P AB C--平面角为θ,点Q到底面ABCD的距离为||QH,点Q到定直线AB得距离为d,则||sinQH dθ=,即||sinQHdθ=.点Q到底面ABCD的距离与到点P的距离之比为正常数k,∴||||QHkPQ=,则||||QHPQk=,动点Q的轨迹是抛物线,||PQ d∴=,即||||sinQH QHkθ=,则sin kθ=.∴二面角P AB C--的平面角的余弦值为1 cos cos602θ=︒=.解得:0)k k>..。
基本几何体优秀课件
基本几何体优秀课件xx年xx月xx日•引言•基本几何体概述•平面几何基础知识•立体几何基础知识•基本几何体的教学应用•基本几何体的扩展知识•教学反思与总结目录01引言几何学是数学的重要分支,研究空间形状、大小、性质等基本元素几何学在科学、工程、艺术、医学等领域有广泛应用课程背景掌握基本几何学概念、定理和证明方法理解几何学在各个领域中的应用课程目的教学内容与目标让学生掌握几何学的基本思想和方法教授平面几何、立体几何和球面几何等基本内容提高学生空间想象能力和逻辑推理能力培养学生具备解决几何问题的能力02基本几何体概述定义几何体亦称立体,是几何学中研究具有某种性质的空间形态的构成要素及其组合规律的基本概念分类分为平面几何体和空间几何体定义与分类常见基本几何体•长方体•由六个矩形围成的封闭图形,面和棱的数目均为六•体积 = 长 × 宽 × 高•球体•由一个半圆绕直径旋转而成,球体的直径是球体的最大直径•体积 = (4/3)πr^3•表面积 = 4πr^2在受力后不易变形基本几何体的性质稳定性各部分密度均匀,即质量均匀分布均匀性形状规则,内部结构有序规则性03平面几何基础知识1定义与基本概念23在平面几何中,点是一个基本元素,表示位置和概念。
点线是平面几何中的基本元素之一,表示方向和连接。
线平面是平面几何中的基本元素之一,表示一个广阔的区域。
平面在任意两个点之间,只有一条直线。
欧几里得定理平行公设三角形内角和定理经过一条直线外的一点,只有一条直线与原直线平行。
三角形内角和等于180度。
03平面几何的基本定理0201利用平面几何知识,可以测量距离、角度、面积等。
测量利用平面几何知识,可以画出各种图形,如直线、圆、三角形等。
画图利用平面几何知识,可以证明各种命题,如勾股定理、三角形相似等。
证明平面几何的应用04立体几何基础知识定义立体几何是几何学的一门分支,研究三维空间中物体的形状、大小和位置关系。
必修二几何体初步知识点整理
必修二几何体初步知识点整理本文档旨在整理必修二几何体的初步知识点,以帮助学生快速回顾和理解相关概念。
一、基本概念1. 几何体:几何体是由面、棱和顶点组成的三维图形。
2. 面:几何体的平面表面,可以是平面、弯曲面或曲面。
3. 棱:连接两个相邻顶点的线段。
4. 顶点:几何体的尖端或拐角点。
二、常见的几何体1. 立方体:所有的边长相等,所有的面都是正方形。
2. 正方体:所有的边长相等,所有的面都是正方形。
3. 圆柱体:两个平行的圆底,连接底部的是直圆柱,连接侧面的是斜圆柱。
4. 圆锥体:由一个圆锥面和一个顶点组成。
5. 球体:所有点到球心的距离相等。
三、特性和公式1. 表面积:- 立方体:$6a^2$,其中 $a$ 是边长。
- 正方体:$6a^2$。
- 圆柱体:$2\pi rh+2\pi r^2$,其中 $r$ 是底圆半径,$h$ 是高度。
- 圆锥体:$\pi r^2 + \pi rl$,其中 $r$ 是底圆半径,$l$ 是斜高度。
- 球体:$4\pi r^2$,其中 $r$ 是球半径。
2. 体积:- 立方体:$a^3$。
- 正方体:$a^3$。
- 圆柱体:$\pi r^2h$。
- 圆锥体:$\frac{1}{3}\pi r^2h$。
- 球体:$\frac{4}{3}\pi r^3$。
3. 对面积和体积的关系:相似几何体的面积和体积之比等于相应边长的比的立方。
四、示例问题1. 如何计算一个正方体的表面积?答:正方体的表面积等于 $6$ 乘以一个面的面积,即 $6a^2$。
2. 如何计算一个圆柱体的体积?答:圆柱体的体积等于底圆的面积乘以高度,即 $\pi r^2h$。
3. 如果两个立方体边长的比为$2:3$,它们的体积之比是多少?答:由于边长比为 $2:3$,则体积之比等于 $(\frac{2}{3})^3 =\frac{8}{27}$。
五、总结本文档对必修二几何体的初步知识点进行了整理和概述,包括基本概念、常见的几何体、特性和公式,以及示例问题的解答。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
扩展体
了解扩展体
• 圆角
案例1:四色球
• 案例2:办公桌
案例3:算盘
床
小结:
• 本章主要掌握最基本的建模方法及概念
作业:
• 标准几何体的分类 • 标准工具的使用及技巧
• 创建方法
– 立方体 – 长方体
• 键盘输入 • 参数
– 长、宽、高 – 长度分段、宽度分段、高度分 段
3.1.2 创建其他标准几何体
• • • • • • • • • 球体 几何球体 圆柱体 管状体 圆环 圆锥 四棱锥 茶壶 平面
• 球体
– 半径 – 分段 – 半球 – 切片 – 平滑 – 轴心在底部
– 半径 – 高度 – 高度分段 – 端面分段 – 边数 – 切片
• 四棱锥的创建
– 宽度 – 深度 – 高度 – 宽度分段 – 深度分段 – 高度分段
• 茶壶的创建
– 半径 – 分段 – 平滑 – 茶壶部件
• 平面的创建
– 长度 – 宽度 – 分段 – 渲染倍增
小结: 小结:
• 3ds的面有正面和反面之分,正面可见,反面 不可见 方法*:在文字上点右键----配置—选
择强制双面即可
基本工具
快捷键: Q————选择 W————移动 E————旋转 R————缩放
•
1. 2. 3. 4. 5. 6. 7. 8.
选取
选取工具 名称选取 选择方式 窗口/交叉选择切换 选择过滤器 锁定 加选、减选(ctrl、alt) 菜单选择
缩放
XYZ 等比例 非等比例 XY/XZ/YZ X/Y/Z 压缩
基本几何体
3.1.1 长方体的创建
长方体生成最简单的基本体。 长方体生成最简单的基本体。立方体是长方体的唯一变 但是,可以改变缩放和比例以制作不同种类的矩形对象, 量。但是,可以改变缩放和比例以制作不同种类的矩形对象, 类型从大而平的面板和板材到高立柱和小块。 类型从大而平的面板和板材到高立柱和小块。
• 1. “修改”面板 • 2. “创建”面板 • 3. 对象类别
视图控制区 基本几何体的使用 基本工具的使用 了解扩展体
视图控制区
• • • • • • • •
缩放视口 缩放所有视图 最大化显示 所有视口最大化显示 区域缩放 平移视图 弧形旋转视图 最大化视口切换
<[ 放大; ] 缩小>
<Shift+Ctrl+Z> <Ctrl+W> <Ctrl+P> <Alt+鼠标中键> <Alt+W>
• 几何球体
– 半径 – 分段 – 基点面类型 – 平滑 – 半球 – 轴心在底部
• 圆柱体
– 半径 – 高度 – 分段 – 边数 – 平滑 – 切片
• 管状体
– 半径 – 高度 – 分段 – 边数 – 平滑 – 切片
• 圆环的创建
– 半径 – 旋转 – 扭曲 – 分段 – 边数 – 切片
• 圆锥体的创建
