2010年全国初中数学联赛江西省初赛试题及详细解答
2010年全国初中数学竞赛试题参答案
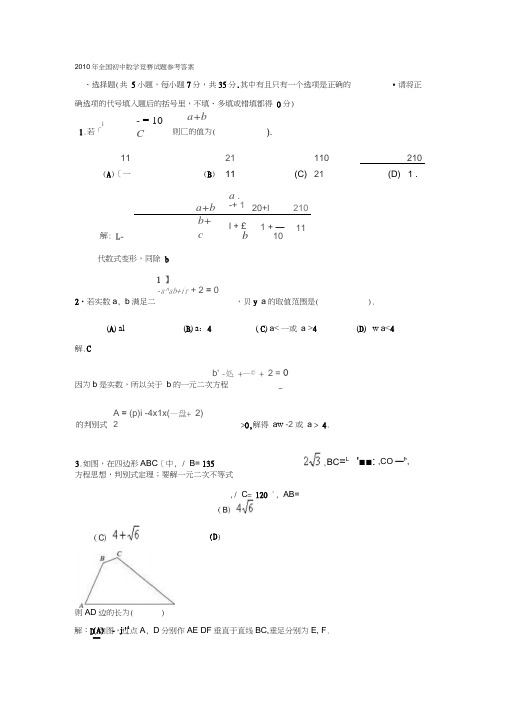
2010年全国初中数学竞赛试题参考答案、选择题(共 5小题,每小题7分,共35分.其中有且只有一个选项是正确的 •请将正确选项的代号填入题后的括号里,不填、多填或错填都得 0分)j- = 10 a+b1.若「C则匚的值为().1121110 210 (A )[一(B ) 11(C) 21(D) 1 .a+b a .-+ 1 20+l 210解: L-b+cl + £b1 + — 1011代数式变形,同除 b1 】-a^ab+ir + 2 = 02•若实数a , b 满足二,贝y a 的取值范围是().(A ) al _(B ) a :4 ( C ) a < 一或 a >4 (D ) _w a <4解.Cb' -处 +—© + 2 = 0因为b 是实数,所以关于 b 的一元二次方程_A = (p)i -4x1x(—盘+ 2)2>0,解得 a w -2 或 a > 4.方程思想,判别式定理;要解一元二次不等式则AD 边的长为()解:D 如图,过点A , D 分别作AE DF 垂直于直线BC,垂足分别为E, F .的判别式 3.如图,在四边形ABC [中, / B= 135,BC =L'■■: ,CO —f ',(D ),/ C = 120 °, AB=(A) - j'1■由已知可得BE=AE= J . , C =?述,DI 2J .,于是 EF = 4+ JI .过点A 作AGL DF 垂足为G 在Rt △ AD (中,根据勾股定理得AD 」一"「"】:A —匸:=_丨一,;勾股定理、涉及双重二次根式的化简,补全图形法4.在一列数 ……中,已知冷二,且当k >2时,疋-1~4~因为 2010=4X 502+2,所以 尬(I =2. 高斯函数;找规律。
5•如图,在平面直角坐标系 xOy 中,等腰梯形 ABC 啲顶点坐标分别为 A (1, 1), B( 2, —1), C (-2, - 1), D (- 1, 1). y 轴上一点 P ( 0, 2)绕点 A 旋转 180。
2010年全国初中数学联赛试题

②
②-①,得 ,所以 ,
代入①中,得 ,解得 , .
当 时, ,在Rt△PAE中,由勾股定理可得 .
当 时, ,此时 ,所以点P在△ABC的外面,不符合题意,舍去.
因此 .
4.将若干个红、黑两种颜色的球摆成一行,要求两种颜色的球都要出现,且任意中间夹有5个或10个球的两个球必为同一种颜色的球.按这种要求摆放,最多可以摆放_______个球.
(2)当 时, , .又 为三角形的三边长,所以 ,即 ,解得 .又因为三角形的周长不超过30,即 ,解得 .因此 ,所以 可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形.
综合可知:符合条件且周长不超过30的三角形的个数为5+6=11.……………………20分
二.(本题满分25分)题目和解答与(A)卷第二题相同.
解由已知等式可得
①
令 ,则 ,其中 均为自然数.
于是,等式①变为 ,即
②
由于 均为自然数,判断易知,使得等式②成立的 只有两组: 和 …………10分
(1)当 时, , .又 为三角形的三边长,所以 ,即 ,解得 .又因为三角形的周长不超过30,即 ,解得 .因此 ,所以 可以取值4,5,6,7,8,对应可得到5个符合条件的三角形.…………15分
故 ,即 .
又 ,所以 ,即
②………………………20分
如果m为正整数,则 , ,从而 ,与②式矛盾.
如果m为负整数,则 , ,从而 ,与②式矛盾.
因此, 时,方程 不可能有整数根.
综上所述, .………………………………25分
如果球的个数多于15个,则一方面,16号球与10号球应同色,另一方面,5号球与16号球中间夹有10个球,所以5号球与16号球同色,从而1到16号球的颜色都相同,进一步可以知道:所有的球的颜色都相同,与要求不符.
2010全国初中数学竞赛题及答案

三、解答题(共4题,每题20分,共80分)11.如图,△ABC 为等腰三角形,AP 是底边BC 上的高,点D 是线段PC 上的一点,BE 和CF 分别是△ABD 和△ACD 的外接圆直径,连接EF . 求证: tan EF PAD BC∠=.证明:如图,连接ED ,FD . 因为BE 和CF 都是直径,所以ED ⊥BC , FD ⊥BC ,可得…………(20分)12.如图,抛物线2y ax bx =+(a >0)与双曲线y x=相交于点A ,B . 已知点A 的坐标为(1,4),点B 在第三象限内,且△AOB 的面积为3(O 为坐标原点).(1)求实数a ,b ,k 的值;(2)过抛物线上点A 作直线AC ∥x 轴,交抛物线于另一点C ,求所有满足△EOC ∽△AOB 的点E 的坐标.(第11题)解:(1)因为点A (1,4)在双曲线k y x=上, 所以k=4. 故双曲线的函数表达式为xy 4=. 设点B (t ,4t ),0t <,AB 所在直线的函数表达式为y mx n =+,则有 44m n mt n t =+⎧⎪⎨=+⎪⎩,, 解得4m t =-,4(1)t n t +=. 于是,直线AB 与y 轴的交点坐标为4(1)0,t t +⎛⎫ ⎪⎝⎭,故 ()141132AOB t S t t∆+=⨯-=(),整理得22320t t +-=, 解得2t =-,或t =1(舍去).所以点B 的坐标为(2-,2-). ⎧⎨⎩=B '(2-,2)是CO 的延长1OA 到点1E ,使得1OE =12OA ,这时点1E (8,2-)是符合条件的点.(ii )作△BOA 关于x 轴的对称图形△2B OA ',得到点2A (1,4-);延长2OA 到点2E ,使得2OE =22OA ,这时点E 2(2,8-)是符合条件的点.所以,点E 的坐标是(8,2-),或(2,8-). …………(20分)13.求满足22282p p m m ++=-的所有素数p 和正整数m ..解:由题设得(21)(4)(2)p p m m +=-+, 所以(4)(2)p m m -+,由于p 是素数,故(4)p m -,或(2)p m +. ……(5分)(1)若(4)p m -,令4m kp -=,k 是正整数,于是2m kp +>,2223(21)(4)(2)p p p m m k p >+=-+>,故23k <,从而1k =. 所以4221m p m p -=⎧⎨+=+⎩,,解得59.p m =⎧⎨=⎩, …………(10分) (2)若(2)p m +,令2m kp +=,k 是正整数.当5p >时,有46(1)m kp kp p p k -=->-=-,223(21)(4)(2)(1)p p p m m k k p >+=-+>-,故(1)3k k -<,从而1k =,或2.由于(21)(4)(2)p p m m +=-+是奇数,所以2k ≠,从而1k =.于是4212m p m p -=+⎧⎨+=⎩,, 这不可能.当5p =时,2263m m -=,9m =;当3p =,2229m m -=,无正整数解;当2p =时,2218m m -=,无正整数解.综上所述,所求素数p =5,正整数m =9. …………(20分)14.从1,2,…,2010这2010个正整数中,最多可以取出多少个数,使得所取出的数中任意三个数之和都能被33整除?解:首先,如下61个数:11,1133+,11233+⨯,…,116033+⨯(即1991)满足题设条件. …………(5分)另一方面,设12n a a a <<< 是从1,2,…,2010中取出的满足题设条件的数,对于这n 个数中的任意4个数i j k m a a a a ,,,,因为33()i k m a a a ++, 33()j k m a a a ++,所以 33()j i a a -.因此,所取的数中任意两数之差都是33的倍数. …………(10分)设133i i a a d =+,i =1,2,3,…,n . 由12333()a a a ++,得12333(33333)a d d ++, …………(15分)故20分)。
2010年全国初中数学联赛试题

2010年全国初中数学联赛试题说明:评阅试卷时,请依据本评分标准.第一试,选择题和填空题只设7分和0分两档;第二试各题,请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数.第一试一、选择题:(本题满分42分,每小题7分)1. 若,,a b c 均为整数且满足1010()()1a b a c -+-=,则||||||a b b c c a -+-+-= ( )A .1.B .2.C .3.D .4.【答】B.因为,,a b c 均为整数,所以a b -和a c -均为整数,从而由1010()()1a b a c -+-=可得 ||1,||0a b a c -=⎧⎨-=⎩或||0,|| 1.a b a c -=⎧⎨-=⎩ 若||1,||0,a b a c -=⎧⎨-=⎩则a c =,从而|||a b b c c -+-=|||a b b a a a -+-+-=. 若||0,||1,a b a c -=⎧⎨-=⎩则a b =,从而||||||a b b c c a -+-+-=||||||2||2a a a c c a a c -+-+-=-=.因此,||||||a b b c c a -+-+-=2.2.若实数,,a b c 满足等式3||6b =,9||6b c =,则c 可能取的最大值为 ( )A .0.B .1.C .2.D .3.【答】C.32(3),||(2)55c b c =+=-,而||0b ≥,所以2c ≤. 当2c =时,可得9,0a b ==,满足已知等式.所以c 可能取的最大值为2.3.若b a ,是两个正数,且 ,0111=+-+-a b b a 则 ( )A .103a b <+≤. B .113a b <+≤. C .413a b <+≤. D .423a b <+≤. 【答】C. 由1110a b b a--++=可得b a b ab a +=++22,则 2()()()(1)ab a b a b a b a b =+-+=++-①由于b a ,是两个正数,所以,0>ab 0a b +>,所以10a b +->,从而.1>+b a 另一方面,由22()()44a b a b ab ab +=-+≥可得4)(2b a ab +≤,结合①式可得14a b a b +≥+-,所以.34≤+b a 因此,413a b <+≤.4.若方程2310x x --=的两根也是方程420x ax bx c +++=的根,则2a b c +-的值为 ( )A .-13.B .-9.C .6.D . 0.【答】A.设m 是方程2310x x --=的一个根,则2310m m --=,所以231m m =+.由题意,m 也是方程420x ax bx c +++=的根,所以420m am bm c +++=,把231m m =+代入此式,得22(31)0m am bm c ++++=,整理得2(9)(6)10a m b m c +++++=. 从而可知:方程2310x x --=的两根也是方程2(9)(6)10a x b x c +++++=的根,这两个方程实质上应该是同一个一元二次方程,从而有22(9)(6)1(31)a x b x c k x x +++++=--(其中k 为常数),故961131a b c +++==--,所以333,10b a c a =--=--.因此,2(333)2(10)13a b c a a a +-=+-----=-.5.在△ABC 中,已知︒=∠60CAB ,D ,E 分别是边AB ,AC 上的点,且︒=∠60AED ,CE DB ED =+,CDE CDB ∠=∠2,则=∠DCB( )A .15°.B .20°.C .25°.D .30°.【答】 B.如图,延长AB 到F ,使BF =ED ,连CF ,EF .∵ ︒=∠=∠60AED EAB ,∴︒=∠60EDA ,︒=∠=∠120CED EDB ,BF ED AE AD ===,DF BF DB DB ED CE =+=+=,于是,AF AC =,︒=∠=∠60AFC ACF .又∵︒=∠120EDB ,CDE CDB ∠=∠2,∴ ︒=∠︒=∠80,40CDB CDE ,︒=∠-∠-︒=∠20180EDC CED ECD .在△CDA 和△CBF 中,CA=CF ,︒=∠=∠60CFB CAD ,AD=BF ,∴ △CDA ≌△CBF , ∴ ︒=∠=∠20ACD FCB .于是,︒=∠-∠-︒=∠2060FCB CDE DCB .6.对于自然数n ,将其各位数字之和记为n a ,如2009200911a =+++=,201020103a =+++=,则123a a a a ++++( ) A .28062. B .28065. C .28067. D .28068.【答】D.把1到2010之间的所有自然数均看作四位数(如果不足四位,则在前面加0,补足四位,这样做不会改变n a 的值).1在千位上出现的次数为310,1在百位上出现的次数为2210⨯,1在十位和个位上出现的次数均为22101⨯+,因此,1出现的总次数为3210210321602+⨯⨯+=.2在千位上出现的次数为11,2在百位和十位上出现的次数均为2210⨯,2在个位上出现的次数为22101⨯+,因此,2出现的总次数为21121031612+⨯⨯+=.类似的,可求得(3,4,5,6,7,8,9)k k =出现的总次数均为221031601⨯⨯+=.因此11a a ++=28068.二、填空题:(本题满分28分,每小题7分)1.已知实数,x y 满足方程组3319,1,x y x y ⎧+=⎨+=⎩则22x y += .【答】 13.由3319x y +=得2()[()3]19x y x y xy ++-=,把1x y +=代入,可得6xy =-. 因此,,x y 是一元二次方程260t t --=的两个实数根,易求得这两个实数根分别为3和2-,所以22223(2)13x y +=+-=.2.二次函数c bx x y ++=2的图象与x 轴正方向交于A ,B 两点,与y 轴正方向交于点C .已知AC AB 3=,︒=∠30CAO ,则c = . 【答】 19. 由题意知,点C 的坐标为),0(c ,c OC =.设B A ,两点的坐标分别为)0,(1x ,)0,(2x ,则21,x x 是方程02=++c bx x 的两根. 由根与系数的关系得c x x b x x =-=+2121,.又︒=∠30CAO ,则c AC AB c AC 323,2===. 于是,c AC OA x 330cos 1=︒==,c AB OA OB x 332=+==. 由c c x x ==2219,得91=c . 3.在等腰直角△ABC 中,AB =BC =5,P 是△ABC 内一点,且PAPC =5,则PB =______.【答】作P E ⊥AB ,交AB 于点E ,作P F ⊥BC ,交BC 于点F ,设,PE mPF n ==,分别在△PAE 、△PCF 中利用勾股定理,得22(5)5m n +-= ①22(5)25m n -+= ②②-①,得10()20n m -=,所以2m n =-,代入①中,得27120n n +-=,解得13n =,24n =. 当3n =时,21m n =-=,在Rt △PAE中,由勾股定理可得PB ==当4n =时,22m n =-=,此时PE AE >,所以点P 在△ABC 的外面,不符合题意,舍去.因此PB =4.将若干个红、黑两种颜色的球摆成一行,要求两种颜色的球都要出现,且任意中间夹有5个或10个球的两个球必为同一种颜色的球.按这种要求摆放,最多可以摆放_______个球.【答】 15.将这些球的位置按顺序标号为1,2,3,4,…….由于1号球与7号球中间夹有5个球,1号球与12号球中间夹有10个球,12号球与6号球中间夹有5个球,7号球与13号球中间夹有5个球,13号球与2号球中间夹有10个球,2号球与8号球中间夹有5个球,8号球与14号球中间夹有5个球,14号球与3号球中间夹有10个球,3号球与9号球中间夹有5个球,9号球与15号球中间夹有5个球,15号球与4号球中间夹有10个球,4号球与10号球中间夹有5个球,因此,编号为1,7,12,6, 13,2,8,14,3,9,15,4,10的球颜色相同,编号为5,11的球可以为另外的一种颜色.因此,可以按照要求摆放15个球.如果球的个数多于15个,则一方面,16号球与10号球应同色,另一方面,5号球与16号球中间夹有10个球,所以5号球与16号球同色,从而1到16号球的颜色都相同,进一步可以知道:所有的球的颜色都相同,与要求不符.因此,按这种要求摆放,最多可以摆放15个球.第二试 (A )一.(本题满分20分)设整数,,a b c (a b c ≥≥)为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长不超过30的三角形的个数.解 由已知等式可得222()()()26a b b c a c -+-+-=①令,a b m b c n -=-=,则a c m n -=+,其中,m n 均为自然数.C于是,等式①变为222()26m n m n +++=,即 2213m n mn ++=②由于,m n 均为自然数,判断易知,使得等式②成立的,m n 只有两组:3,1m n =⎧⎨=⎩和1,3.m n =⎧⎨=⎩ …………10分 (1)当3,1m n ==时,1b c =+,34a b c =+=+.又,,a b c 为三角形的三边长,所以b c a +>,即(1)4c c c ++>+,解得3c >.又因为三角形的周长不超过30,即(4)(1)30a b c c c c ++=++++≤,解得253c ≤.因此2533c <≤,所以c 可以取值4,5,6,7,8,对应可得到5个符合条件的三角形. …………15分(2)当1,3m n ==时,3b c =+,14a b c =+=+.又,,a b c 为三角形的三边长,所以b c a +>,即(3)4c c c ++>+,解得1c >.又因为三角形的周长不超过30,即(4)(3)30a b c c c c ++=++++≤,解得233c ≤.因此2313c <≤,所以c 可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形.综合可知:符合条件且周长不超过30的三角形的个数为5+6=11. ……………………20分二.(本题满分25分)已知等腰三角形△ABC 中,AB =AC ,∠C 的平分线与AB 边交于点P ,M 为△ABC 的内切圆⊙I 与BC 边的切点,作MD//AC ,交⊙I 于点D.证明:PD 是⊙I 的切线.证明 过点P 作⊙I 的切线PQ (切点为Q )并延长,交BC 于点N.因为CP 为∠ACB 的平分线,所以∠ACP =∠BCP.又因为PA 、PQ 均为⊙I 的切线,所以∠APC =∠NPC.又CP 公共,所以△ACP ≌△NCP , …………10分所以∠PAC =∠PNC.由NM =QN ,BA =BC ,所以△QNM ∽△BAC ,故∠NMQ =∠ACB ,所以MQ//AC.………………………………20分又因为MD//AC ,所以MD 和MQ 为同一条直线. NCA又点Q 、D 均在⊙I 上,所以点Q 和点D 重合,故PD 是⊙I 的切线. ……………………………25分三.(本题满分25分)已知二次函数2y x bx c =+-错误!未找到引用源。
2010年江西省中考数学试卷详解版

2010年江西省中考数学试卷参考答案与试题解析一、选择题(共8小题,每小题3分,满分24分)1.(3分)(2010•江西)计算﹣2﹣6的结果是()A.﹣8 B.8 C.﹣4 D.4【考点】:有理数M115【难易度】:容易题【分析】:根据有理数的减法法则得:﹣2﹣6=(﹣2)+(﹣6)=﹣(2+6)=﹣8.【解答】:答案A.【点评】:本题考查了有理数的减法运算法则,属于送分题,难度不大,熟知其运算法则:减去一个数等于加上这个数的相反数,可直接得出答案。
2.(3分)(2010•江西)计算﹣(﹣3a)2的结果是()A.﹣6a2B.﹣9a2C.6a2D.9a2【考点】:整式运算M11N【难易度】:容易题【分析】:由积的乘方运算,把每一个因式分别乘方,再把所得的幂相乘,则﹣(﹣3a)2=﹣(﹣3)2×a2=﹣9a2.【解答】:答案B.【点评】:此题考查了积的乘方的运算,难度不大,整式的运算是中考常见的考点,只要熟练掌握运算法则,运用公式即可直接解题.3.(3分)(2010•江西)沿圆柱体上底面直径截去一部分后的物体如图所示,它的俯视图是()A.B.C.D.【考点】:视图与投影M414【难易度】:容易题【分析】:由题意,找到从上面看所得到的图形即是答案,因为是从圆柱体上底面直径截去一部分,则显然视图与圆有关,从直径处分为两个半圆.【解答】:答案D.【点评】:本题考查了几何体的三视图的识别,属于基础题,难度不大,需要熟记:几何体正视图、左视图、俯视图是从物体的正、左侧、上面看得到的视图,注意看得到的棱画实线.4.(3分)(2010•江西)已知等腰三角形的两条边长分别是7和3,则下列四个数中,第三条边的长是()A.8 B.7 C.4 D.3【考点】:等腰三角形性质与判定M327;三角形三边的关系M322【难易度】:容易题【分析】:因为腰长与底边不确定,所以分①7为腰长,3为底边,②7为底边,3为腰长两种情况,则①当7为腰长,3为底边时,三边为7、7、3,能组成三角形,故第三边的长为7,②当3为腰长,7为底边时,三边为7、3、3,3+3=6<7,根据三角形任意两边之和大于第三边,两边之差小于第三边,所以不能组成三角形.【解答】:答案B.【点评】:本题了三角形满足的条件以及等腰三角形的性质,难度不大,基本图形的性质是中考必考知识点,注意在没有边角关系,需要进行分类讨论.5.(3分)(2010•江西)不等式组的解集是()A.x>﹣3 B.x>3 C.﹣3<x<3 D.无解【考点】:一元一次不等式(组)的解及解集M12K【难易度】:容易题.【分析】:先求出各不等式的解集,再求其公共部分即为不等式组的解集.则由﹣2x<6,化系数为1解得,x>﹣3,由﹣2+x>1,移项、合并同类项得,x>3,故原不等式组的解集为:x>3.【解答】:答案B.【点评】:此题考查了一元一次不等式组的解集,属于基础题,难度不大,是中考的常规题目,正确解出不等式的解集是解决本题的关键.求不等式组的解集时,先求出各不等式的解集。
2010年全国 初中数学联赛(含答案)

12010年全国初中数学联合竞赛试题参考答案第一试一、选择题:(本题满分42分,每小题7分)1.若a ,b ,c 均为整数且满足1010()()1a b a c -+-=,则||||||a b b c c a -+-+-=( )A .1B .2C .3D .4【答案】 B【解析】 因为()()10101a b a c ---=,而左边的两个加数都是非负整数,所以一个等于0,另一个等于1,也就是说,a ,b ,c 三个数中有两个相等,另一个和它们相差1.因此,所求的和式中,两项等于1,另一项等于2,结果为2.2.若实数a ,b ,c 满足等式3||6a b =,49||6a b c =,则c 可能取的最大值为( )A .0B .1C .2D .3【答案】 C【解析】 为了使c 尽量大,a 应该尽量大,b 应该尽量小.因为它们都是非负数,3a ,0b =,不难观察到所求答案为2.3.若a ,b 是两个正数,且1110,a b b a--++= 则( )2A .103a b <+≤B .113a b <+≤C .413a b <+≤D .423a b <+≤. 【答案】 C【解析】 去分母之后得到()()110a a b b ab -+-+=,即220a ab b a b ++--=.给定a 和b 是两个正数,那么如果让它们中的一个等于0,则另一个等于0或14.若方程2310x x --=的两根也是方程420x ax bx c +++=的根,则2a b c +-的值为 ( )A .13-B .9-C .6D .0【答案】 A【解析】 这需要使得前者是后者的因式,用综合除法可得,余式为()()33310a b x a c +++++,它应该等于0.所以两个系数都为0,特别地,()()333210a b a c ++-++,所以所求答案为13-.5.在ABC △中,已知60CAB ∠=︒,D ,E 分别是边AB ,AC 上的点,且60AED ∠=︒,ED DB CE +=,2CDB CDE ∠=∠,则DCB ∠= ( )A .15oB .20oC .25oD .30o【答案】 B【解析】 观察可得ADE △为正三角形,6.对于自然数n ,将其各位数字之和记为n a ,如2009200911a =+++=,201020103a =+++=,则312320092010a a a a a +++++=L ( )A .28062B .28065C .28067D .28068.【答案】 D【解析】 根据弃九法,它和1到2010的和被9除的余数相等.每连续9个自然数之和被9整除,2010被9除余3,1236++=,所以只有D 符合.二、填空题:(本题满分28分,每小题7分)1.已知实数x ,y 满足方程组33191x y x y ⎧+=⎨+=⎩,,则22x y += .【答案】 13【解析】 第一式除以第二式可得2219x xy y -+=,第二式平方可得2221x xy y ++=,那么所求答案就是()1921313⨯+÷=.2.二次函数2y x bx c =++的图象与x 轴正方向交于A ,B 两点,与y 轴正方向交于点C .已知3AB ,30CAO ∠=︒,则c = .【答案】 19【解析】 观察可知A 必须在B 左边,否则B 会跑到x 轴负半轴上.设A 的横坐标为a ,则C 的纵坐标3,23AC =,2AB a =.因此,考虑两根之积,33a a ⨯,3a =319=. 3.在等腰直角ABC △中,5AB BC ==,P 是ABC △内一点,且5PA ,5PC =,则PB = .4【答案】 10【解析】 设()00B ,,()50A ,,()05C ,,根据熟知的勾三股四弦五,可观察到()31P ,,(另一个点在三角形外,不符合),所以10PB =.4.将若干个红、黑两种颜色的球摆成一行,要求两种颜色的球都要出现,且任意中间夹有5个或10个球的两个球必为同一种颜色的球.按这种要求摆放,最多可以摆放 个球.【答案】 15【解析】 也就是说,编号之差为6或11的两个球颜色相同.下面从1号球开始,依次写出颜色相同的球的编号:11261711516104159314821371→→→→→→→→→→→→→→→→→也就是说,如果有17个球,则全部同色;如果超过17个,则任何连续17个同色,也不行.如果有16个,则上面的圈去掉17号球仍然是一条链,仍然不行;如果有15个,则上面的圈去掉17号球和16号球后断成两部分,所以可以.第二试 (A )一.(本题满分20分)设整数()a b c a b c ≥≥,,为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长5不超过30的三角形的个数.【解析】 由已知等式可得222()()()26a b b c a c -+-+-= ①令a b m -=,b c n -=,则a c m n -=+,其中m ,n 均为自然数.于是,等式①变为222()26m n m n +++=,即2213m n mn ++= ②由于m ,n 均为自然数,判断易知,使得等式②成立的m ,n 只有两组:31m n =⎧⎨=⎩,,和13.m n =⎧⎨=⎩,⑴ 当3m =,1n =时,1b c =+,34a b c =+=+.又a ,b ,c 为三角形的三边长,所以b c a +>,即(1)4c c c ++>+,解得3c >.又因为三角形的周长不超过30,即(4)(1)30a b c c c c ++=++++≤,解得253c ≤. 因此2533c <≤, 所以c 可以取值4,5,6,7,8,对应可得到5个符合条件的三角形.6⑵ 当1m =,3n =时,3b c =+,14a b c =+=+.又a ,b ,c 为三角形的三边长,所以b c a +>,即(3)4c c c ++>+,解得1c >.又因为三角形的周长不超过30,即(4)(3)30a b c c c c ++=++++≤,解得233c ≤. 因此2313c <≤, 所以c 可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形.综合可知:符合条件且周长不超过30的三角形的个数为5611+=.二.(本题满分25分)已知等腰三角形ABC △中,AB AC =,C ∠的平分线与AB 边交于点P ,M 为ABC △的内切圆I e 与BC 边的切点,作MD AC ∥,交I e 于点D .证明:PD 是I e 的切线.【解析】 过点P 作I e 的切线PQ (切点为Q )并延长,交BC 于点N .因为CP 为ACB ∠的平分线,所以ACP BCP ∠=∠.又因为PA 、PQ 均为I e 的切线,所以APC NPC ∠=∠.IP QNB7又CP 公共,所以ACP NCP △≌△,所以PAC PNC ∠=∠.由NM QN =,BA BC =,所以QNM BAC △≌△,故NMQ ACB ∠=∠,所以MQ AC ∥.又因为MD AC ∥,所以MD 和MQ 为同一条直线.又点Q 、D 均在I e 上,所以点Q 和点D 重合,故PD 是I e 的切线.三.(本题满分25分)已知二次函数2y x bx c =+-的图象经过两点()1P a ,,()210Q a ,. ⑴ 如果a ,b ,c 都是整数,且8c b a <<,求a ,b ,c 的值.⑵ 设二次函数2y x bx c =+-的图象与x 轴的交点为A 、B ,与y 轴的交点为C .如果关于x 的方程20x bx c +-=的两个根都是整数,求ABC △的面积.【解析】 点()1P a ,、()210Q a ,在二次函数2y x bx c =+-的图象上,故1b c a +-=,4210a c a +-=,解得93b a =-,82c a =-.⑴ 由8c b a <<知8293938a a a a -<-⎧⎨-<⎩,,解得13a <<.又a 为整数,所以2a =,9315b a =-=,8214c a =-=.⑵ 设m ,n 是方程的两个整数根,且m n ≤,旗开得胜8由根与系数的关系可得39m n b a +=-=-,28mn c a =-=-,消去a ,得98()6mn m n -+=-,两边同时乘以9,得8172()54mn m n -+=-,分解因式,得(98)(98)10m n --=.所以9819810m n -=⎧⎨-=⎩,,或982985m n -=⎧⎨-=⎩,,或9810981m n -=-⎧⎨-=-⎩,,或985982m n -=-⎧⎨-=-⎩,,解得12m n =⎧⎨=⎩,,或109139m n ⎧=⎪⎪⎨⎪=⎪⎩,,或2979m n ⎧=-⎪⎪⎨⎪=⎪⎩,,或19323m n ⎧=⎪⎪⎨⎪=⎪⎩,,又m ,n 是整数,所以后面三组解舍去,故1m =,2n =.因此,()3b m n =-+=-,2c mn =-=-,二次函数的解析式为232y x x =-+.易求得点A 、B 的坐标为()10,和()20,,点C 的坐标为()02,, 所以ABC △的面积为1(21)212⨯-⨯=.第二试 (B )旗开得胜9一.(本题满分20分)设整数a ,b ,c 为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长不超过30的三角形的个数(全等的三角形只计算1次).【解析】 不妨设a b c ≥≥,由已知等式可得222()()()26a b b c a c -+-+-= ①令a b m -=,b c n -=,则a c m n -=+,其中m ,n 均为自然数.于是,等式①变为222()26m n m n +++=,即2213m n mn ++= ②由于m ,n 均为自然数,判断易知,使得等式②成立的m ,n 只有两组:31m n =⎧⎨=⎩,,和13.m n =⎧⎨=⎩,⑴ 当3m =,1n =时,1b c =+,34a b c =+=+.又a ,b ,c 为三角形的三边长,所以b c a +>,即(1)4c c c ++>+,解得3c >.又因为三角形的周长不超过30,即(4)(1)30a b c c c c ++=++++≤,解得253c ≤. 因此2533c <≤,旗开得胜10所以c 可以取值4,5,6,7,8,对应可得到5个符合条件的三角形.⑵ 当1m =,3n =时,3b c =+,14a b c =+=+.又a ,b ,c 为三角形的三边长,所以b c a +>,即(3)4c c c ++>+,解得1c >.又因为三角形的周长不超过30,即(4)(3)30a b c c c c ++=++++≤,解得233c ≤. 因此2313c <≤, 所以c 可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形.综合可知:符合条件且周长不超过30的三角形的个数为5611+=.二.(本题满分25分)题目和解答与(A )卷第二题相同.三.(本题满分25分)题目和解答与(A )卷第三题相同.第二试 (C )11一.(本题满分20分)题目和解答与(B )卷第一题相同.二.(本题满分25分)题目和解答与(A )卷第二题相同.三.(本题满分25分)设p 是大于2的质数,k 为正整数.若函数2(1)4y x px k p =+++-的图象与x 轴的两个交点的横坐标至少有一个为整数,求k 的值.【解析】 由题意知,方程2(1)40x px k p +++-=的两根1x ,2x 中至少有一个为整数.由根与系数的关系可得12x x p +=-,12(1)4x x k p =+-,从而有()()()()12121222241x x x x x x k p ++=+++=- ①⑴ 若1k =,则方程为22(2)0x px p ++-=,它有两个整数根2-和2p -.⑵ 若1k >,则10k ->.因为12x x p +=-为整数,如果1x ,2x 中至少有一个为整数,则1x ,2x 都是整数.又因为p 为质数,由①式知1|2p x +或2|2p x +.不妨设1|2p x +,则可设12x mp +=(其中m 为非零整数),则由①式可得212k x m-+=,12故()()12122k x x mp m -+++=+,即1214k x x mp m-++=+. 又12x x p +=-,所以14k p mp m--+=+, 即1(1)4k m p m-++= ② 如果m 为正整数,则(1)(11)36m p ++⨯=≥,10k m->, 从而1(1)6k m p m-++>,与②式矛盾. 如果m 为负整数,则(1)0m p +<,10k m-<, 从而1(1)0k m p m-++<,与②式矛盾. 因此,1k >时,方程2(1)40x px k p +++-=不可能有整数根.综上所述,1k =.旗开得胜13。
2010 年全国初中数学竞赛预赛试题.

2010 年全国初中数学竞赛预赛试题参考答案及评分标准一、选择题(共5小题,每小题6分,共30分) 1.B 2.A 3.C 4.C 5.D二、填空题(共5小题,每小题6分,共30分)6. 7.8% 7. +, 1 8. 51 9. 100 10. 48t << 三、 解答题(共4小题,每小题15分,共60分)11.解:(1)设y kx b =+,∵x =4时,y =400;x =5时,y =320. ∴4004,3205.k b k b =+⎧⎨=+⎩解之,得80,720.k b =-⎧⎨=⎩ ∴y 与x 的函数关系式为80720y x =-+ ………………… 5分 (2)该班学生买饮料每年总费用为50×120=6000(元),当y =380时,38080720x =-+,得 x =4.25,该班学生集体饮用桶装纯净水的每年总费用为380×4.25+780=2395(元), 显然,从经济上看饮用桶装纯净水花钱少. .……………………………… 10分(3)设该班每年购买纯净水的费用为W 元,则W =xy =x (-80x +720) =2980()16202x --+,∴当 x =92时,W 最大值=1620,要使饮用桶装纯净水对学生一定合算,则 50a ≥W 最大值+780,即 50a ≥1620+780, 解之,得 a ≥48.所以a 至少为48元时班级饮用桶装纯净水对学生一定合算,由此看出,饮用桶装纯净水不仅能省钱,而且能养成勤俭节约的好习惯……………1 5分12.证明:连结CG. ∵BD ⊥AC ,EF 垂直平分BC ,∴BG=CG ,BE=EC=21BC ∵DF=21BC ,∴DF=BE .……………………………… 5分在△BEG 和△FDG 中⎪⎩⎪⎨⎧=∠=∠∠=∠FD BE FDG BEG FGD BGE∴△BEG ≌△FDG (AAS )∴∠F=∠GBE=∠GCB , GE=GD .………………… 10分 而GE ⊥BC ,GD ⊥AC ,∴CG 平分∠ACB ,∴∠ACB=2∠F. ………………… 15分13.解:(1) 当x =-1和x =3时, y 值相同 , 即y =a -b +c =9a +3b +c . ∴b=-2a , 则 x M = -1222=--=aa ab .∵ 点M 在y=3x -7上 , ∴ y M = 3-7=-4 , ∴M(1,-4) . 设y = a (x -1)2-4 ,∵当x = 4时, y =3×4-7= 5 .把当x = 4 , y = 5 代入上式 , 5 = a (4-1)2-4 , a=1.∴ y = (x -1)2-4 或y =x 2-2x -3 . .……………………………… 4分(2) 当x = 0时 y =-3 , ∴ C(0,-3).当y = 0时 x 1=-1, x 2=3 . ∴ A(-1,0) , B (3,0).∴ 直线BM 为 y=2x -6 . ∵ x P = OQ = t , ∴ y P = 2t -6.∴ S = S △AOC +S 梯OCPQ =12 ×1×3+12×(3+│2t -6│)×t = 32 +9-2t 2 ·t = -t 2+92 t +32. .……………………………… 8分 (3)P 1(2,-2), P 2(75 ,-165 ), P 3(520102,5105-+)……………………… 12分 (4)(-1,-3)或 (910 ,-2710 ) 、(-110 ,310) …………………………… 15分 14.解:(1) ∵AE ⊥B D ,∴BE⌒ =DE ⌒ ,∴∠E B D=∠EC B . ∵∠A B H=∠D B H ,∠B HE=∠EC B +∠C B H ,∠H B E=∠D B H+∠E B D ,∴∠B HE=∠H B E. ∴B E=HE. ……………………………5分(2) 连结QC 、T B ,则∠B CQ+∠C B Q=90°,又∠B DQ+∠ATD=90°,而∠B CQ=∠B DQ ,∴∠C B Q=∠ATD=∠AT B ,∴ΔA B G ∽ΔAT B ,∴A B 2=A G•AT , ∵AH ⊥CE ,∴H 为CE 的中点,∴B E=12 EC ,∴ΔB EO ∽ΔC B E ,∴OE BO =BE EC =12设⊙A 的半径为R ,由A B 2-OA 2=B O 2,OE=R -3,得R 2-32=4(R -3)2,解得,R=5,或R=3(不合题意,舍去).∴A T•AG=A B 2=25. ……………………………… 10(方法二提示:可连结AD,CD 证ΔB AG ∽ΔTAD)(3)答:②MN R的值不变. 证明:作O 1K ⊥MN 于K ,连结O 1N 、PN 、B M ,则MN=2NK , 且∠N O 1K=∠NPM ,∴MN R =2NK O 1N=2sin ∠NO 1由直线y=34x +3 得 O B =OD=4,OM ⊥B D ,∴∠B MO=∠DMO ,又∠B MO=∠A B M+∠B AM ,∠DMO=∠MPN+∠PNM ,∵∠A B M=∠PNM ,∴∠MPN=∠B AM=∠NO 1K ,MN R=2sin ∠B AM=2×BO AB = 85 , 所以 MN R 的值不变,其值为 85. ……………15分 Q O H G F E D C B A x y T。
江西省2010年中考数学真题及答案解析

机密2010年6月19日江西省2010年中等学校招生考试数学试题卷说明:1.本卷共有六个大题,25个小题,全卷满分120分,考试时间120分钟.2.本卷分为试题卷和答题卷,答案要求写在答题卷上,不得在试题卷上作答,否则不给分.一、选择题(本大题共8个小题,每小题3分,共24分)每小题只有一个正确选项. 1.(2010江西,1,3分) 计算 -2- 6的结果是( )A .-8B . 8C . -4D . 4【分析】把有理数的减法运算转化为加法运算,即8)6(262-=-+-=--【答案】A【涉及知识点】有理数的减法运算【点评】本题属于基础题,主要考查学生对有理数的加减运算是否掌握,考查知识点单一 【推荐指数】★2. (2010江西,2,3分) 计算 -(-3a)2的结果是( )A .-6a 2B . -9a 2C . 6a 2D . 9a 2【分析】根据“积的乘方等于积中各因式的乘方的积”可知22229)3()3(a a a -=--=-- 【答案】B【涉及知识点】积的乘方运算【点评】本题属于基础题,主要考查幂的运算,考查知识点单一,但对负数的幂运算容易出错。
【推荐指数】★3.(2010江西,3,3分) 沿圆柱体上面直径截去一部分的物体如图所示,它的俯视图是( ) 3. 沿圆柱体上底面直径截去一部分的物体如图所示,它的俯视图是( )A B C D(第3题)【分析】根据俯视图的定义,沿圆柱体上面直径截去一部分的物体后,它的俯视图仍然是一个圆,且增加了直径这条边。
【答案】D【涉及知识点】三视图【点评】本题考查了三视图的概念,题小但新颖且有一定思考,学生很容易错选A 或B 。
【推荐指数】★★★★4. (2010江西,4,3分) 已知等腰三角形的两条边长分别是7和3,则下列四个数中,第三条边的长是( )A .8B .7C . 4D .3【分析】等腰三角形的两条边长分别是7和3,第三边要么是7,要么是3,但当第三边为3时构不成三角形,所以第三边只能是7. 【答案】B【涉及知识点】等腰三角形,三角形三边关系【点评】本题把等腰三角形知识与三角形三边关系有机地结合在一起,简单地综合,同时考查了数学分类思想。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年全国初中数学联赛江西省初赛试题解答第 一 试一. 选择题(每小题7分,共42分)1、化简35134862+-++的结果是( ).()A 、2; ()B 、22; ()C 、2; ()D 、12.答案:D解:221348(23)143(123)+=++=+,25(123)423(31)-+=-=-,22423(31)623(31)23222⎛⎫++++-=+=== ⎪ ⎪⎝⎭,因此原式12=. 2、ABC ∆是一个等腰直角三角形,DEFG 是其内接正方形,H 是正方形的对角线交点;那么,由图中的线段所构成的三角形中相互全等的三角形的对数为( ).()A 、12; ()B 、13; ()C 、26; ()D 、30.答案:C .解:设3AB =,图中所有三角形均为等腰直角三角形,其中,斜边长为1的有5个,它们组成10对全等三角形;斜边长为2的有6个,它们组成15对全等三角形;斜边长为2的有2个,它们组成1对全等三角形;共计26对.3、设0ab ≠,且函数21()24f x x ax b =++与22()42f x x ax b =++有相同的最小值u ;函数23()24f x x bx a =-++与24()42f x x bx a =-++有相同的最大值v ;则u v +的值( ).()A 、必为正数; ()B 、必为负数; ()C 、必为0; ()D 、符号不能确定.答案:C .解:2221()()44f x x a b a b a =++-≥-,2222()(2)2424f x x a b a b a =++-≥-, 由22424b a u b a -==-,得223b a -= ……①2223()()44f x x b a b a b =--++≤+,2224()(2)2424f x x b a b a b =--++≤+;由22424a b v a b +==+,得223a b = ……②HD GFA C E B②-①得,222()3()a b b a +=-,所以0a b += ……③,或23b a -=……④ 若0a b +=,则222()(65)(65)()[65()]0u v b a a b a b b a +=-++=++-=; 若23b a -=,据②④,222()33b b -=,即2(31)30b -+=,矛盾! 4、若关于x 的方程227100x ax a ++-=没有实根,那么,必有实根的方程是( ).()A 、22320x ax a ++-=; ()B 、22560x ax a ++-=; ()C 、2210210x ax a ++-=; ()D 、22230x ax a +++=.答案:A .解:由方程227100x ax a ++-=无实根,得其判别式0<,于是25a <<, 方程,,,A B C D 的判别式分别是:4(1)(2)A a a ∆=--,4(2)(3)B a a ∆=--,4(3)(7)C a a ∆=--,4(1)(3)D a a ∆=+-,显然,对于满足25a <<的每个a 值,可以确保0A ∆>,但不能保证,,B C D ∆∆∆非负,(即使得方程,,B C D 无实根的a 的区间与区间(2,7)都有重叠部分,而使方程A 无实根的a 的区间(1,2)与区间(2,7)无重叠部分),所以A 必有实根,其余方程不一定有实根.5、正方形ABCD 中,,E F 分别是,AB BC 上的点,DE 交AC 于M ,AF 交BD 于N ;若AF 平分BAC ∠,DE AF ⊥;记BE x OM =,BN y ON =,CF z BF=,则有( ).()A 、x y z >>; ()B 、x y z ==;()C 、x y z =>; ()D 、x y z >=. 答案:D解:由角平分线,2BN AB AC CFON AO AB BF====,即2y z ==,又AME ∆的角分线与高重合,则AME ∆为等腰三角形,AM AE =,作OP ∥AB ,交OE 于P ,则OP 为DBE ∆的中位线,OMP ∆∽AME ∆,2BE BEx OM OP===,所以x y z >=. 6、将1,2,3,4,5,6,7,8这八个数分别填写于一个圆周八等分点上,使得圆周上任两个相邻P NM EFODA B CNMEFODABC位置的数之和为质数, 如果圆周旋转后能重合的算作相同填法,那么不同的填法有( ). ()A 、4种; ()B 、 8种; ()C 12种、; ()D 、16种. 答案:B解:相邻两数和为奇质数,则圆周上的数奇偶相间,于是8的两侧为3,5,而7的两侧为4,6;剩下两数1,2必相邻,且1与4,6之一邻接;考虑三个模块[4,7,6],[5,8,3],[1,2]的邻接情况,得到8种填法.二、 填空题(每小题7分,共28分)1、若k 个连续正整数之和为2010,则k 的最大值是 . 答案:60.解:设(1)2010(1)(2)()2k k n n n k kn +=++++++=+,则(21)4020k n k ++=, 注意21k n k <++,而2402023567=⨯⨯⨯,为使k 值最大,当把4020表成最接近的一对因数之积,为40206067=⨯,所以60k =.2、单位正三角形中,将其内切圆及三个角切圆(与角两边及三角形内切圆都相切的圆)的内部挖去,则三角形剩下部分的面积为 . 答案:349S π=-解:单位正三角形内切圆半径为36r =,其面积为212s r ππ==,而O 为其中心,故OD OH AH r ===,因此,AEF ∆与ABC ∆的相似比为1:3,于是每个小圆面积等于O面积的19,故四个圆面积之和为439s π=,因此,所求三角形剩下部分的面积为349S π=-.3、圆内接四边形ABCD 的四条边长顺次为:2,7,6,9AB BC CD DA ====,则四边形的面积为 .答案:30.解:由于2222768592+==+,即2222BC CD DA AB +=+,所以BCD ∆与DAB ∆都是直角三角形,因此,四边形面积1(7692)302BCD DAB S S =+=⋅⨯+⨯=. 4、在123520±±±±±中,适当选择+、-号,可以得到不同代数和的个数是 . 答案:24个.解:1,2,3,5,20中,有奇数三个,故其代数和必为奇数;由1,2,3,5可以得到绝对值11≤OH BA D CFE的所有奇数:这是由于11235=--+,31235=-+-+,51235=+-+,71235=-++,91235=-+++,111235=+++;以上各式通乘1-,可得1,3,5,7,9,------的表达式;而据题意,表达式中,1,2,3,5及20都必须参与,那么,能得到的整数应是±20加或减135,7,9,11,,,即得到十二个正奇数9,11,13,,31 和十二个负奇数9,11,,31--- ;因此可表出的数共计24个.第 二 试一、(20分)边长为整数的直角三角形,若其两直角边长是方程2(2)40x k x k -++=的两根,求k 的值并确定直角三角形三边之长.解:设直角边为,a b ,(a b <)则2,4a b k ab k +=+=,因方程的根为整数,故其判别式为平方数,设()()22(2)166613221648k k n k n k n +-=⇒-+--=⨯=⨯=⨯,66,k n k n -+>--63261k n k n -+=⎧∴⎨--=⎩或61662k n k n -+=⎧⎨--=⎩或63261k n k n -+=⎧⎨--=⎩解得1452k =(不是整数,舍去),2315,12k k == 215k =时,17,605,12,13a b ab a b c +==⇒=== 312k =时,14,486,8,10a b ab a b c +==⇒===二、(25分)如图,自ABC ∆内的任一点P ,作三角形三条边的垂线:,,PD BC PE CA PF AB ⊥⊥⊥,若,BD BF CD CE ==;证明:AE AF =.证:注意如下事实:若四边形的两条对角线互相垂直,则其两组对边的平方和相等. 连,,PA PB PC ,则有2222PA BF PB AF +=+;2222PB CD PC BD +=+,2222PC AE PA CE +=+;三式相加得222222AE CD BF AF CE BD ++=++, 利用条件,BD BF CD CE ==,代入上式,得AE AF =.三、(25分)已知,,a b c 为正整数,且33a bb c++为有理数,证明222a b c a b c ++++为整数.证:因3是无理数,则 30b c -≠,而223(3)(3)33a b a b b c b c b c++-=-+ 22233()3ab bc b ac b c-+-=-为有理数,所以20b ac -=,于是 222222()2()()2()a b c a b c ab bc ac a b c ab bc b ++=++-++=++-++FEPBCADFEPBCAD2()2()()()a b c b a c b a b c a b c=++-++=++-+,因此,222a b ca b ca b c++=-+++为整数.。
