ARCH模型
ARCH学习总结

ARCH 学习1. ARCH 模型 定义:均值方程t t ε= ~..t i i d ν 2()0()1t t E E νν== 01at j t jj h ααε-==+∑ 特性:A.无条件均值 B.条件均值 C.无条件方差 D.条件方差高铁梅版本总结自回归条件异方差(Autoregressive Conditional Heteroscedasticity Model , ARCH)模型是特别用来建立条件方差模型并对其进行预测的。
自相关的问题是时间序列数据所特有,而异方差性是横截面数据的特点,但时间序列同样也存在异方差特征,在金融数据上这一特征很明显。
为了刻画这种相关性,恩格尔提出自回归条件异方差(ARCH)模型。
ARCH 的主要思想是时刻 t 的ut 的方差(= σ2 t )依赖于时刻(t -1)的扰动项平方的大小,即依赖于 û2t - 1 。
ARCH 模型如果 ut 的均值为零,对 y t 取基于(t -1)时刻的信息的期望,即Et -1(yt ),有如下的关系: 即第一个方程式为均值方程。
假设在时刻 ( t -1 ) 所有信息已知的条件下,扰动项 ut 的条件分布是:~ 也就是,ut 遵循以0为均值,(α0+α1u 2t-1 )为方差的正态分布。
由于(6.1.7)中 ut 的方差依赖于前期的平方扰动项,我们称它为ARCH(1)过程: 通常用极大似然估计得到参数γ0, γ1, γ2, ⋯⋯, γk , α0, α1的有效估计。
容易加以推广,ARCH (p )过程可以写为: (6.1.8) 这时方差方程中的(p +1)个参数α0, α1, α2, ⋯⋯, αp 也要和回归模型中的参数γ0, γ1, γ2, ⋯⋯, γk 一样,利用极大似然估计法进行估计。
如果(6.1.8)中方差不存在异方差,则02)var(ασ==t t u即: 相应的检验,对(6.1.8)建立方程,如果显著为0,即不存在异方差,否则存在异方差,等价于存在ARCH 效应。
数学建模EViews中估计ARCH模型

(EViews4.0)的对话框
第15页/共75页
(EViews5)的对话框
第16页/共75页
与选择估计方法和样本一样,需要指定均值方程和方差
方程。
(一)均值方程 在因变量编辑栏中输入均值方程形式,均值方程的形式可 以用回归列表形式列出因变量及解释变量。如果方程包含常 数,可在列表中加入C。如果需要一个更复杂的均值方程,可 以用公式的形式输入均值方程。 如果解释变量的表达式中含有ARCH—M项,就需要点 击对话框右上方对应的按钮。EViews4.0中,只有3个选项: 1.选项None表示方程中不含有ARCH−M项;
恩格尔和克拉格(Kraft, D., 1983)在分析宏观数据时,发现这样一些 现象:时间序列模型中的扰动方差稳定性比通常假设的要差。恩格尔的结 论说明在分析通货膨胀模型时,大的及小的预测误差会大量出现,表明存 在一种异方差,其中预测误差的方差取决于后续扰动项的大小。
从事于股票价格、通货膨胀率、外汇汇率等金融时间序列预测的研究 工作者,曾发现他们对这些变量的预测能力随时期的不同而有相当大的变 化。预测的误差在某一时期里相对地小,而在某一时期里则相对地大,然 后,在另一时期又是较小的。这种变异很可能由于金融市场的波动性易受 谣言、政局变动、政府货币与财政政策变化等等的影响。从而说明预测误 差的方差中有某种相关性。
SAS实验指导-Arch建模要点

ARCH建模及SAS实现一.Arch模型Arch模型即自回归条件异方差模型,是金融市场中广泛应用的一种特殊非线性模型。
1982年,R.Engle在研究英国通货膨胀率序列规律时提出ARCH模型,其核心思想是残差项的条件方差依赖于它的前期值的大小。
1986年,Bollerslev在ARCH模型基础上对方差的表现形式进行了线性扩展,并形成了更为广泛的GARCH模型。
1. 金融时间序列的异方差性特征金融时间序列,无恒定均值(非平稳性),呈现出阶段性的相对平稳的同时,往往伴随着出现剧烈的波动性;具有明显的异方差(方差随时间变化而变化)特征:尖峰厚尾:金融资产收益呈现厚尾和在均值处呈现过度波峰;波动丛聚性:金融市场波动往往呈现簇状倾向,即波动的当期水平往往与它最近的前些时期水平存在正相关关系。
杠杆效应:指价格大幅度下降后往往会出现同样幅度价格上升的倾向。
因此,传统线性结构模型(以及时间序列模型)并不能很好地解释金融时间序列数据。
2. ARCH(p)模型考虑k 变量的回归模型011t t k kt t y x x γγγε=++++若残差项t ε的均值为0,对y t 取基于t-1时刻信息的期望:1011()t t t k kt E y x x γγγ-=+++该模型中,y t 的无条件方差是固定的。
但考虑y t 的条件方差:22110111var(|)()t t t t t k kt t t y Y E y x x E γγγε---=----=其中,1var(|)t t y Y -表示基于t-1时刻信息集合Y t-1的y t 的条件方差,若残差项t ε存在自回归结构,则y t 的条件方差不固定。
假设在前p 期所有信息的条件下,残差项平方2t ε服从AR(p )模型:22211t t p t p t εωαεαεν--=++++ (*)其中t ν为0均值、2νσ方差的白噪声序列。
则残差项t ε服从条件正态分布:()2211~0,t t p t p N εωαεαε--+++ 残差项t ε的条件方差:22211var()t t t p t p εσωαεαε--==+++由两部分组成:(1)常数项ω;(2)ARCH 项——变动信息,前p 期的残差平方和21pi t i i αε-=∑注:未知参数01,,,p ααα和01,,,k γγγ利用极大似然估计法估计。
ARCH和GARCH模型

2.2 ARCH模型的导出
yt b0 b1x1,t b2 x2,t ,... ut
E(ut ) 0
2,t
意是:ut的ut条是件一方个差白随噪时声间,而其变无化条,件假方设差是ut一2 服个从常数。
AR(1)过程(模型的名称来源)
ut2 0 1ut21 wt
0
0 1 1, 0 0
18
ARCH的参数的约束
▪ 残差序列ut的无条件峰度K
k m4
3
2 0
(1
1
)
( 0 )2
[ 2 ]2 (11)(1 312 ) 11
3 1 12 1 312
3, (Q
0 12
1) 3
该ARCH模型估计的残差序列的无条件分布具有尖 峰厚尾特性,进一步
19
ARCH与厚尾性
自回归:残差平方服从AR(p)过程: ut=ρ0+ρ1ut-1+ρ2ut-2+……+εt
▪ 若线性回归模型的误差实际上是异方差,却被假定为同 方差,这就意味着标准误差的估计值是错误的。
▪ 此时,参数的估计量的方差是有偏估计(或者不收敛, 是时变的),统计检验和置性区间就不正确!
8
yt b0 b1xt ut , ut : iidN (0, 2 ),b0 0
)
2
xt2
9
▪ 普通最小二乘估计(OSL):回归直线要使得残差 平方和最小。
▪ 异方差存在时,普通最小二乘估计法给误差方差大 的观测值以较大的权重,给误差方差小的观测值以 较小的权重。
▪ 回归结果:使得残差平方和最小,故产生一个后果, 只要方差大的那部分数据得到很好的拟合,这样普 通最小二乘不再是有效的——参数估计量的方差不 再是最小的方差。
ARCH模型 计量经济学 EVIEWS建模课件

例如Engle-Ito-Lin(1990)在对日元兑美元汇率
的研究中得到如下结果,
st2= 0.0006 + 0.1169et-12- 0.0627 et-22 - 0.0047 et-32 0.0181 et-42 + 0.9581st-12
虽然参数的和是0.9895,小于1。但δi, i = 2, 3, 4 是负的。Nelson-Cao(1992)认为参数非负的约束
可以放宽要求。对于GARCH(1, q) 模型,
t2
=
δ0
+
δ1
εt
–1
2
+
…
+
δq
εt
–q
2
+
1
t
2 -1
t2非负的充分与必要条件是:δ0 0;1 0;
k
ki i1 1
0, k
0,1,q
1
i0
二、ARCH模型的建立
㈠检验均值模型的残差ARCH效果
⒈ 残差的分布及其假设 选择Y=XB或A(L)Y=W(L)ε对均值模型的估计会 得到残差的估计值,如果模型的残差具有异方差 性,那么使用非线性的估计才是有效的。 在模型的误差项服从ARCH过程的情况下,如 果模型仍然服从其他的基本假设,则OLS估计仍然 有效,即使误差项非正态也会渐近有效。
1
2ht
exp
(Yt
Yt )2
2ht
⑵对于误差服从t分布的GARCH(1,1)过程,在 k→∞时,接近正态分布,其对数似然函数为:
容量为T。
εt ARCH (q)可以表示为:εt=σtvt。要注意:
E(εt) = 0;vt iidN(0, 1);2t = E(ε2t) = ht;
arch模型
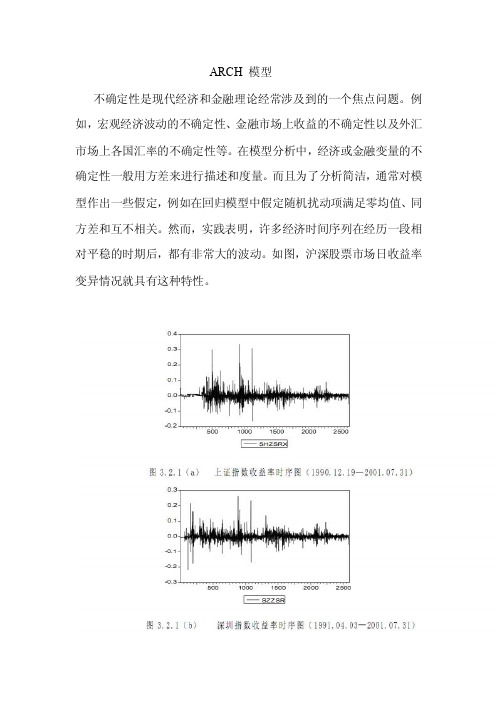
ARCH 模型不确定性是现代经济和金融理论经常涉及到的一个焦点问题。
例如,宏观经济波动的不确定性、金融市场上收益的不确定性以及外汇市场上各国汇率的不确定性等。
在模型分析中,经济或金融变量的不确定性一般用方差来进行描述和度量。
而且为了分析简洁,通常对模型作出一些假定,例如在回归模型中假定随机扰动项满足零均值、同方差和互不相关。
然而,实践表明,许多经济时间序列在经历一段相对平稳的时期后,都有非常大的波动。
如图,沪深股票市场日收益率变异情况就具有这种特性。
在这种情况下,同方差假定是不恰当的。
在这种情况下,人们关心的是如何预测序列的条件方差。
例如,作为资产持有者,他既关心收益率的预测值,同时也关心持有期内方差的大小。
如果一位投资者计划在第 t 时期买入某项资产,在第 t+1 时期售出,则无条件方差(即方差的长期预测值)对他来讲就不重要了。
对于这一类问题,可以使用自回归条件异方差模型 (autoregressive conditiona heteroskedastic model ,简称 ARCH 模型)来进行分析。
最早的 ARCH 模型是由 Robert Engle 于 1982 年建立的,因此它的发展历史不长。
但是,这种模型及其各种推广形式已被广泛应用于经济和金融数据序列的分析,ARCH 模型族已成为研究经济变量变异聚类特性的有效工具。
第一节 ARCH 模型的概念与性质 1、ARCH 过程ARCH 模型的一般性定义如下。
假设时间序列{}t y 服从如下回归模型:'t t ty x u ξ=+(8.1.1)其中 t x 是外生变量向量,它可以包含被解释变量的滞后项,ξ是回归参数向量。
如果扰动项序列{}t u 满足:11|~(0,)(,,)t t t t t t q u N h h h u u ---Ω= (8.1.2)其中:11122{,',,'}t t t t t y x y x -----Ω= 为t 时期以前的信息集。
ARCH模型综述改进版PPT课件

E-GARCH模型文档仅供参考,如有不当之处,请联系本人改正。
EGARCH或指数(Exponential)GARCH模型由纳尔什(Nelson,1991) 提出。条件方差被指定为:
log
2 t
0log
2
t 1
ARCH(m)模型
模型假定
a , a L a 2
2
t tt t 0 1 t 1
m t 2 m 0> 0 ,对 i> (0 ,有 3. 1i.> 30 )
t 独立同分布随机变量序列,均值为0,方差为1,0> 0 ,对 i> 0 ,有 i> 0
2)ARCH模型对参数的限制是相当严格的。例如不同阶距 对a1的限制。
3)对于弄清一个金融时间序列的变化的来源, ARCH模型 不能提供任何新见解。它只是提供一个机械的方式来描 述条件方差的状态,而对由什么引起这种变化没有给出 任何启示。
4)ARCH模型会过高估计波动率,因为它对收益率序列大 的孤立的抖动反应缓慢。
第二次则是长记忆在经济学上的研究取得突破,与ARCH 模型相结合所产生的一系列长记忆ARCH的研究从1996年 至今方兴未艾ARCH类模型因其良好的统计特性和对波动 现象的准确描述,被广泛地应用于对经济类时间序列数据, 如利率、外汇汇率、通货膨胀率等的回归分析及预测中。
我们将把介绍的重点放在ARCH模型早期阶段及第一次突 破进展阶段。
GARCH模型认为,在一定时期内,误 差项的方差不仅取决于误差项过去的 方差,而且还取决于过去的误差项本 身。
GARCH(1,1)模型 文档仅供参考,如有不当之处,请联系本人改正。
【时间序列】波动率建模之ARCH模型

【时间序列】波动率建模之ARCH模型1. ARCH1.1 异方差在传统计量经济学模型中,都假设干扰项的方差为常数(同方差)。
但是在现实世界中,许多经济时间序列的波动具有丛聚性等特征。
例如:股市中可能存在的涨跌,当遇到结构性风险,股票价格可能存在大涨或者大跌的情况,这种类时间序列被称为条件异方差,即使无条件异方差是恒定的,但是也会存在方差相对较高的时候,而这个波动率是通常会呈现出持续性,这被称为波动丛聚性。
1.2 ARCH过程ARCH (atuoregressive conditional heteroskedastic,自回归条件异方差)模型可以描述一个序列阶段性的稳定和波动:表示白噪音过程,满足 ;相互独立,和都为常数,且把代入到中可得:这便是序列的一阶自回归异方模型ARCH(1),推广到高阶则可得我们为什么要用条件异方差呢,首先来考虑估计一个平稳的ARMA模型,则的条件均值为,用条件均值去预测下一期,则预测误差的方差为如果使用无条件预测,结果一般是时间序列的长期均值。
则无条件预测误差方差为其中白噪音过程,,,可得由此可得无条件预测方差大于条件预测方差,所以使用条件预测结果更好。
所以针对一些时间序列的异方差性,可以使用一些模型去拟合条件方差。
1.3 ARCH性质1.ARCH模型,误差项的条件均值和无条件均值都等于0.对于所有,因此,序列具有序列不相关性,但是误差并不相互独立(误差),换个角度看, ARCH(1) 的方差是等于AR(1)的:2.为条件异方差将导致也为异方差,所以ARCH模型可以表示出序列中阶段性的稳定和波动3.ARCH误差和序列的自相关参数相互作用。
的变化和序列的持续较大的方差有关,越大,持续时间越长,的变化越持久。
ARCH是使用AR(P)来对条件方差建模,如果加上MA(q) 过程又会如何呢?由此衍生出了GARCH2. GARCH假设误差过程为:表示白噪音过程,均值为0,方差为1,因此的条件与无条件均值都为0.此模型将自回归以及异方差的移动平均项结合了起来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ARCH 模型
对于一般的回归模型
t t y x u ='β+ 其中t 1t 2t kt x x x x '=⋯⋯(,,,) (18.1.1) 如果随即扰动项的2t ε平方服从AR (q )过程,即:
222t 01t-1q t-q t u u u t=1,2=α+α+⋯⋯+α+η⋯⋯ (18.l.2) 其中t η独立同分布,并且满足E (t η)=0,V (t η)=2λ,则称模型为自回归条件异方差模型,简称为ARCH 模型。
称序列t u 服从q 阶的ARCH 过程,记作t u ~ARCH (q )。
(18.1.1)和(18.l.2)构成的模型称为回归一ARCH 模型。
ARCH 模型通常用于对主体模型的随机扰动项进行建模,以便提取残差中的有用信息,最终使模型的残差t η项成为白噪声。
这样,对于AR (p )模型:
t 1t-1p t-p t y y y u =φ+⋯⋯+φ+ (18.l.3) 如果t u ~ARCH (q ),则序列t y 可用AR (p )-ARCH (q )模型描述。
ARCH (q )模型又可建华表示为
t t t u h v = (18.l.4)
q
2
2
2t 01t-1
q t-q 0t-i i 1
h u
u u ==α+α+⋯⋯+α=α+∑
(18.1.5) 其中t v 独立同分布,且E (t v )=0,V (t v )=1;0a 0>,i 0α≥(i=1,2,3,⋯⋯,q ),并且q
i i 11=α<∑以保证ARCH 的平稳性。
对于任意时刻t ,t u 的条件期望:
t t-1t t E u u h E v ∣⋯⋯=∙(,)()=0 (18.1.6) 条件方差:
222t t-1t t t E u u h E v h ∣⋯⋯=∙(,)()= (18.1.7) (18.1.7)反映了序列条件方差随时间变化的性质。
