字典排序法 (1)
字典序排序规则

字典序排序规则字典序,也称为英文字母顺序,是一种使用字母表进行顺序排列的方式。
它也被称为字母表排序法,其有效性已经被大量应用于信息管理、文件组织和文本处理等领域。
字典序是一种以字母表为基础的排序方式,它可以比较任何一个特定的字符串,并以正确的顺序进行排序。
字典序排序,从简单的角度来说,就是把所有出现的字符按照字母表的顺序排列,并以此排序来确定字母表中字符出现的次序。
字典序排序将字母表按照字母顺序依次排列,由a开始,最后以z结束,顺序如下:a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z。
字典序排序按照字母顺序来排列,字母表中可有大写字母、小写字母、数字以及其他特殊符号。
由于大写字母的键位在小写字母的键位之前,因此大写字母会被首先显示出来,比如“A-Za-z”,这样先被显示出来的字母就是A,而且,比如“0-9A-Za-z”,这样先被显示出来的字母就是0。
字典序排序可以对英文字母及多种字符进行排列,但是只有当所有字符都处于统一的字符集中才能有效地实施这种排序。
比如,如果所有字符都是中文的话,就不能使用字典序排序法。
字典序排序比较的的是字符的拼写顺序,而不是字符的语义意义。
这种排序方式一般使用于一些信息类或文件文本的参考目录,因为这样可以使用字典序比较查找的效率更高,它广泛地应用在数据库和文件管理领域。
字典序排序与其他排序方式所不同的是,它不会重复叠加排序,即便是在一些特定场景下,字典序在短时间内也能达到排序的效果,它也不消耗多余的时间。
字典序排序是利用字母表对字符进行排序的一种方式,它可以有效的节省时间和空间,提高查找效率,被广泛应用于信息管理、文件组织和文本处理等领域。
字典序排序比较简便,相比其他排序方式,它具有较高的效率,应用范围广泛,因此得到了广大用户的认可。
字典序排序规则

字典序排序规则字典序排序规则,也称为字母表排序规则,是指将语文中所有书写单节字(包括汉字和英文字母)按照一定的规则进行排序的一种排序方式。
其中,英文字母按照其所代表的音节从A到Z的顺序进行排列,而汉字按照其在《现代汉语常用字表》中的编号从1到11,035的顺序来排序。
字典序排序规则的由来字典序排序规则也有一定的历史背景:第一个汉字字典,即《说文解字》是由著名汉学家、篆书研究家白求恩在古代经典里发现的,它是中国最早的汉字字典,最早的汉字字典排序规则的基础就是在《说文解字》的基础上进行构建的,当时,按照《说文解字》的排序规则,汉字按照构音节→部首→字形来排列,在实践的过程中受到了很多限制,所以,在20世纪初,英文字典序排序规则出现了。
字典序排序规则的应用字典序排序规则也有广泛应用:例如,在新闻报刊和文学类书籍出版中,经常会用字典序排列文章,不同文章之间的先后顺序便可以很快速、简单地按照字典序列出来;又如,词典、书目及文献的索引等,都会采用字典序排序规则来进行索引查询,以便用户容易、快速地查找某个词条;此外,在编程语言的程序开发中,字典序排序规则也有着广泛的应用,例如,通过字典序排序规则,可以实现文件的快速查找。
字典序排序规则的优点字典序排序规则具有一定的优势:首先,可以满足大多数索引查询的需求;其次,字母表中英文字母的排列是有规律的,而汉字在《现代汉语常用字表》中的编号也是有序的,能够有效地避免汉字书写时的混乱;再次,排序的过程简单易行,可以大大节省排序的时间;最后,字典序排序规则也具有良好的可读性,它能在有限的空间里产生多种排序效果,节约人力和财力。
总结总而言之,字典序排序规则是一种非常有用的排序方式,它受到英文字典序排序规则的启发,通过字母表中英文字母和《现代汉语常用字表》中汉字排列的有序序号,能够有效地缩小排序的范围,满足不同排序需求,具有很强的可读性和可操作性,能够大大节省人力和时间。
字典排序法

字典排序法
《字典排序法》是一种经常用在计算机编程中的排序算法,它是指给定一个列表或者数组,按照字典顺序,由最低到最高的方式对所有元素进行排序。
这种方法可以比较容易地实现,并且排序效率也比较高,有许多应用场景。
字典排序法是根据元素的值来进行排序,通常情况下,排序会按照字母表顺序,由最低到最高,从而获得排序结果。
它可以被用在多种编程语言中,比如 c++ 、 c# 、 java 、 python 中的列表/数组排序等。
字典排序法的实现很简单,看下面的实现,这是一个python实现的示例:
def sort_dict(x):
x.sort(key=lambda x:x[0])
return x
上面提供的示例函数接受一个由多个元组组成的列表,用key参数传递lambda函数,以输入列表中的每个元组中的第一个元素作为排序标准,这是一个非常常见的字典排序的实现。
字典排序法的应用非常广泛,常见的应用场景如下:
1)字典排序法可以用于对元素的排序,比如对字符串的排序,或者对计算机系统中的文件名称的排序;
2)字典排序法也可以用于多个字典的排序,比如对数据库中的表格字段值的排序,或者对JSON对象中字段值的排序;
3)字典排序法还可以用于对有序列表进行排序,比如进行排序后可以借助有序列表快速搜索对应的值;
4)字典排序法也可以用于对树结构中的节点进行排序,使得后续进行搜索操作更加轻松高效;
5)字典排序法还可以用于实现元素的组合排序,因为字典排序法可以在元素的排序上实现可控的灵活性。
以上就是《字典排序法》的具体介绍,它的实现非常简单,并且具有广泛的应用,因此可以用于解决各种问题,是一种非常有用的算法之一。
字典序排列
9
7
3. 将a[i]与a[k]互换位置
void exchange(int a[],int i,int k) { int temp; temp=a[i]; a[i]=a[k]; a[k]=temp; a); len = sizeof(a)/sizeof(int); for(m=i+1,n=len-1;m<n;m++,n--) { temp=a[m]; a[m]=a[n]; a[n]=temp; }
1
图1.11是一棵高度为4的树,按从根节点到叶子节点依次向下搜索并 读出边的标号顺序,自左向右,依次为1234,1243,1324,134…,即 1,2,3,4的全排列。
问题:已知一个排列,如何得出下一个排列
2
字典序法算法
求(p)= p1…pj-1 pjpj+1pk-1 pkpk+1…pn的下一个排列:
5
字典序算法实现
1. 找出从右到左第一个小于它右边数的数,返回其数组下标 i1 int search1(int a[]) { int i; for(i=len-1;i>=1;i--) { if(a[i-1]<a[i]) //数组下标从0开始 return i-1; } return -1; }
6
2. 找到 a[i]右边比a[i]大的下标最大的数,返回其数组下标k int search2(int a[],int n) { int k; for(k=len-1;k>n;k--){ if(a[k]>a[n]) return k; } return -1; }
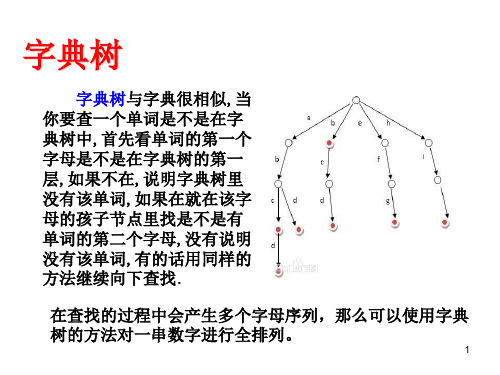
字典树
字典树与字典很相似,当 你要查一个单词是不是在字 典树中,首先看单词的第一个 字母是不是在字典树的第一 层,如果不在,说明字典树里 没有该单词,如果在就在该字 母的孩子节点里找是不是有 单词的第二个字母,没有说明 没有该单词,有的话用同样的 方法继续向下查找. 在查找的过程中会产生多个字母序列,那么可以使用字典 树的方法对一串数字进行全排列。
字典顺序0比1小

字典顺序0比1小
字典排序是一种对于随机变量形成序列的排序方法。
即按照字母顺序,或者数字小大顺序,由小到大的形成序列。
以问题中提到的序列为例,“ilove”的第一个字母是“i”,“baray”的第一个字母是“b",在字母表中,”i“是排到”b“前面的,所以”ilove“就应该排到”baray“前面。
字母表序列:
A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z。
字典序:在数学中,字典或词典顺序(也称为词汇顺序,字典顺序,字母顺序或词典顺序)是基于字母顺序排列的单词按字母顺序排列的方法。
这种泛化主要在于定义有序完全有序集合(通常称为字母表)的元素的序列(通常称为计算机科学中的单词)的总顺序。
字典序的形式定义:
给定两个偏序集A和B,(a,b)和(a′,b′)属于笛卡尔积A×B,则字典序定义为:(a,b) ≤ (a′,b′) 当且仅当a<a′ 或(a=a′ 且b≤b′)。
结果是偏序。
如果A和B是全序, 那么结果也是全序。
第二讲 字典排列法与树形图

第二讲字典排列法与树形图知识点总结1、枚举法:字典排列法、分类枚举、树形图都是枚举法中的一种,使用各种枚举法需要注意有条理、不重复、不遗漏,使人一目了然。
2、字典排列法:从首位开始,按一定的顺序(比如从小到大)枚举第一位,对于每种情况再按从小到大的顺序枚举第二位,依次类推。
3、分类枚举:先有序分类,再有序枚举。
4、树形图:确定起点,按照一定的顺序一一罗列,最后数终点个数。
例题精讲【例1】汤姆、杰瑞和得鲁比都有蛀牙,他们一起去牙医诊所看病,医生发现他们一共有8颗蛀牙,他们三人可能分别有几颗蛀牙?【分析】三人情况:都有蛀牙说明每个人的蛀牙数目不能为0,每人至少有1颗,一共有8颗蛀牙,所以最多的蛀牙数是6。
题中有三个人的名字,所以三个人是有次序的,我们将汤姆看成是首位,杰瑞看成第二位,德鲁比看成第三位,则可以运用字典排列法枚举。
汤姆: 1 1 1 1 1 1 汤姆: 2 2 2 2 2杰瑞: 1 2 3 4 5 6 杰瑞: 1 2 3 4 5得鲁比:6 5 4 3 2 1 得鲁比: 5 4 3 2 1汤姆: 3 3 3 3 汤姆: 4 4 4杰瑞: 1 2 3 4 杰瑞: 1 2 3得鲁比:4 3 2 1 得鲁比:3 2 1汤姆: 5 5 汤姆: 6杰瑞: 1 2 杰瑞: 1 得鲁比:2 1 得鲁比:1总共有6+5+4+3+2+1=21种情况。
【例2】下午茶的时候,老师给同学们准备了苹果,香蕉和橘子三种水果,每种都有足够多个,昊昊想挑3个水果吃,请问:他一共有多少中选择?【分析】分类枚举:先有序分类,再有序枚举。
一种水果:苹苹苹,香香香,橘橘橘两种水果:苹香香,苹苹香,苹橘橘,苹苹橘,香橘橘,香香橘三种水果:苹香橘一共:3+6+1=10(种)【例3】一个人在三个城市A、B、C中游览。
他今天在这个城市,明天就必须到另一个城市。
这个人从A城出发,4天后还回到A城,那么这个人有几种旅游路线?【分析】列出树形图如下,共有6种路线。
【思维拓展】小学数学三年级思维拓展之字典排序法(附答案)

三年级思维拓展之字典排序法
1.用数字1,2,3可以组成多少个不同的三位数?(数字可以重复使用)
2.在某地有1分,2分,4分,8分四种面值的硬币,假如你恰有这四种硬币各1枚。
问共能组成都少种不同的钱数?请你用加法算式一个一个列举出来
3.小悦、东东、阿奇三个人共有7本课外书,每个人至少有一本。
问小悦、东东、阿奇分别有几本课外书?
4.汤姆、杰瑞和得鲁比都有蛀牙,他们一起去牙医诊所看病,医生发现他们一共有8颗蛀牙,他们三人可能分别有几颗蛀牙?
5.设S=1,2,3,4,用字典序法求出S的全部排列。
6.解答下列各题.
(1)用1、2、3三张数字卡片可以组成多少个不同的三位数?
(2)用1、2、3三种数字卡,每种都有足够数量,可以组成多少个不同的三位数?
7.解答下列各题
(1)用数字1、2、3可以组成多少个不同的三位数?
(2)用数字1、3、6可以组成多少个不同的三位数?
(3)数字用1、3、6可以组成多少个不同的无重复数字的三位数?
8.用数字1、2、3可以组成多少个不同的无重复数字的自然数?。
字典序排序规则

字典序排序规则字典序是一种常用的文本排序方法,也叫作字母排序、字符排序或词典顺序,它是指按照字符串中第一个字母的字母表顺序来排序。
它是一种通用的方法,可以用于排序不同语言中的字符串。
字典序排序规则可以分为三个基本概念:字母表顺序,比较原则和大小写规则。
字母表顺序是指排序时按照英文字母的出现次序来排列,如A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z,以及分隔符。
比较原则是按照字符串中每个字符的字母表顺序来比较,比较的结果可以是相等、小于或者大于,这取决于字符串中比较字符的出现次序。
如果比较字符之间出现相等,就比较下一个字符。
这样就能确定字典序排序的位置。
大小写规则是指对于有些排序系统,小写字母比大写字母优先,反之大写字母比小写字母优先。
字典序排序规则可以用于排序各种字符串,包括单词表、英文文章、文件名、文件路径、网址和编程语言中的符号标识符。
它也可以用于查找文本中的某个字符串,例如使用搜索引擎搜索某个关键字时。
字典序排序规则也可以用于排序多种数据类型,如整数、日期和浮点数。
由于字符串和数字可以转换为一个字符串,因此可以将这些数据类型排序成字母序。
这样就可以利用字典序排序规则来比较多种数据类型。
字典序排序规则对于数据库、文件系统和其他应用有很多用处,它可以极大地提高检索准确性,也可以减少搜索所需的时间。
另外,字典序排序规则可以用于排序不可见的数据,这也有助于检索文本中的信息。
字典序排序是一种有用的排序算法,它可以应用于多种情境中,并帮助解决检索的效率问题。
它的好处是简单,易于理解,易于实现,可以应用于排序不同语言的字符串,以及各种数据类型,这些都使它成为一种非常流行的文本排序算法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对于使用递归解决排列和组合的问题,俺看了很多篇参考资料,可惜的是有点难以理解别人的写法,跟MSDN一样,字都是中文,可是合起来就不知道是啥意思了,同样都是代码,每一句都能看明白,可就是不知道,他在这里为啥要写这一句,这一句在整个程序中的地位,还是脑子不好使,中学的时候数学没学好,这么些年又没好好的锻炼脑子,生锈了。
对于全排列来说,咱们还是从最简单的开始吧。
序列中只有一个元素:那么全排列就只有一种,{1}就是这个序列本身。
序列中有两个元素:那么全排列有两种方式,{1,2},{2,1}。
序列中有三个元素:那么全排列有六种方式,{1,2,3},{1,3,2},{2,1,3},{2,3,1},{3,1,2},{3,2,1}。
如果将排列的结果做成一个整数的话,那么对于三个元素的全排列结果应该是:{123},{132},{213},{231},{312},{321},这六个数有没有什么特点?当然有。
1.它们都是由1,2,3这几个字符组成的。
2.3>2>1。
3.123<132<213<231<312<321。
这个垃圾结论能替我们解决问题吗?当然能。
还记得我们怎么理解二进制的吗?还记得我们怎么理解八进制的吗?还记得我们怎么理解十六进制的吗?二进制中包含两个字符:0,1。
八进制中包含八个字符:0,1,2,3,4,5,6,7。
十六进制中包含十六个字符:0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F。
俺的乖乖,数字么呢?字母都来咧,那些个A呀,B呀,C呀,只是一些符号而已,它们在十六进制中代表的是10,11,12,13,14,15而已。
为嘛非得用ABCDEF呢?能不能用其他的字符呢?当然可以。
甚至于我们把ABCDEF可以改成“啊吧才的饿飞”,只有它依然代表的是10,11,12,13,14,15就行了。
为嘛会用的上ABCDEF呢?呵呵,简单了,因为咱们平常用的数字中没有一个单独的符号用来表达10,11,12,13,14,15而已,咱们为这些值找了个代表而已。
好了,扯的够远了,往回扯。
回到八进制中,为嘛八进制中没有ABCDEF呢?简单的回答是:咱们平常用的数字可以完全拿来表达八进制中的每个单独的数字,就是说,够用了,用不着折腾了复杂的回答是:可以有ABCDEF这些字母,反正这些字母仅仅是个代表而已。
改成{1,2,3,4,5,6,7,8}行不?当然行。
不就是个符号么。
二进制的改成{1,2}行不,也行;改成{2,3}行不,也行。
无论是{1,2}还是{2,3}仅仅是个符号,咱们要做的工作是保证符号中的大小关系,比如1<2,2<3就行了。
那么再次变态一点:{1,4}行不?当然行,对于二进制来说,只要1<4就行了。
那么{3,8}也行喽?当然。
好了,我们已经够变态的了,不妨再变态一点。
既然都已经有了二进制,八进制,十六进制,为嘛不能整个三进制呢?三进制中有几个符号呢?根据二进制,八进制,十六进制推理而来,三进制当中肯定有三个符号。
那是那三个呢?呵呵,你喜欢哪三个呢?俺喜欢{0,1,2}行不?行,呵呵,这娃还比较传统。
那俺要是喜欢{1,2,3}行不?行,呵呵,娃可教也。
二进制中的两位数有哪些啊(使用的符号为{0,1})?不就是:10,11,01,00么。
那么数字不重复的两位数的二进制数有哪些?不就是:10,01么,00和11都有重复。
对于三进制中的不重复的三位数有哪些呢?不就是:{123},{132},{213},{231},{312},{321}。
可是还有很多三位数没写出来呢?知道。
按照完全的三进制来说,123的下一个数字应该是131。
可是如果我们手头的可以使用的字符有限,不是每个字符都可以使用很多次的话,那我们的三位数的序列就应该是{123},{132},{213},{231},{312},{321}。
如果我们将{123},{132},{213},{231},{312},{321}看做连续的三位数,那么{123}<{132}<{213}<{231}<{312}<{321},那么比123大的下一个数就是132,比132大的下一个数就是213......到了这里,我们的结论是什么?结论是:如果要做n个元素的全排列,那么排列的结果一定是一组用n个元素表达的数字的数组,而且每个数字中用上了这n个元素,没有遗漏,没有重复,而且这个数组应该是升序的(或降序),第一个数字小于第二个数字,第二个数字小于第三个数字......第n-1个数字小于第n个数字。
目标有了,现在必须得想办法拼出咱们的目标。
抽象一下问题:如果我们已经有了一个数字了,通过什么手段得到一个比这个数字大一点点的新数字。
如果我们能解决这个问题,再次将新数字作为基础,找一个比新数字大一点点的新新数字。
剩下的工作就是使劲循环,这样我们就可以找到从某个数字开始的所有的比它大的数字了。
那啥时候可以停止了呢?直到找不到一个比现有数字还大的数字,就结束,换种说法,直到找到的数字是最大的。
使用给定的那么几个元素怎么能排出来一个最大的数字呢?呵呵,这不就很简单么。
把最大的元素放在最高位,把次大的放在第二位,把次次大的放在第三位......把最小的放在最低位。
呵呵,看懂了没?不就是一个将所有的元素以降序方式排列么。
如果我们要全排列,那就应该从最小值跑到最大值就可以了,最大值就是降序排列,那最小值很显然的应该是升序排列。
还是从实例开始吧。
二进制:最小值是01,最大值10;分析出从小数得到大数的过程中一定有交换。
三进制:{1,2,3,}{1,3,2,}:有交换,交换2,3。
{2,1,3,}:有交换,交换的比较复杂。
{2,3,1,}:有交换,交换1,3。
{3,1,2,}:有交换,交换的比较复杂。
{3,2,1,}:有交换,交换1,2。
中间有两步“交换的比较复杂”,比较难于总结,先放下。
四进制:{1,2,3,4,}{1,2,4,3,}:有交换,交换3,4。
{1,3,2,4,}:有交换,交换的比较复杂。
{1,3,4,2,}:有交换,交换2,4。
{1,4,2,3,}:有交换,交换的比较复杂。
{1,4,3,2,}:有交换,交换2,3。
{2,1,3,4,}:有交换,交换的比较复杂。
{2,1,4,3,}:有交换,交换3,4。
{2,3,1,4,}:有交换,交换的比较复杂。
{2,3,4,1,}:有交换,交换1,4。
{2,4,1,3,}:有交换,交换的比较复杂。
{2,4,3,1,}:有交换,交换1,3。
{3,1,2,4,}:有交换,交换的比较复杂。
{3,1,4,2,}:有交换,交换2,4。
{3,2,1,4,}:有交换,交换的比较复杂。
{3,2,4,1,}:有交换,交换1,4。
{3,4,1,2,}:有交换,交换的比较复杂。
{3,4,2,1,}:有交换,交换1,2。
{4,1,2,3,}:有交换,交换的比较复杂。
{4,1,3,2,}:有交换,交换2,3。
{4,2,1,3,}:有交换,交换的比较复杂。
{4,2,3,1,}:有交换,交换1,3。
{4,3,1,2,}:有交换,交换的比较复杂。
{4,3,2,1,}:有交换,交换1,2。
从简单的交换看,每次交换都是把大的数交换到前面了,小的数交换到后面了,如果规律相同的话,那么“有交换,交换的比较复杂。
”也应该遵循将大的数交换到前面,小的数交换到后面。
那我们随便找一个“有交换,交换的比较复杂。
”过程来详细分析。
比如从{3,1,4,2,}怎么到的{3,2,1,4,},先找到不动的元素3,反正它没有参与交换,所以,干掉它;问题简化为:{1,4,2}怎么到的{2,1,4},根据交换的规律,一定是大的向前,小的向后。
咱们从后向前看,前面的元素有没有比后面小的?有,谁?1么,那1应该和谁换,应该和比1大的最小的那个进行交换,那这个数是谁?是2,那就换吧,换完的结果是{2,4,1},这个结果和咱们的目标有一点点差别,就是1和4的位置有差别,咱们的目标是{2,1,4},可是中间结果是{2,4,1},那很容易啊,不就是把刚才中间结果中的1和4换一下就OK了。
问题在于:为嘛要换呢?回到咱们的目标上,咱们想找一个数,比142稍微大一点点的数,不是找一个比142大很多的数,在得到全排列的过程,其实是一个将数组的元素从升序更改到降序的过程,如果没有完全排好的话,那么一定有左侧元素小于右侧元素的现象,在找到的左侧元素的右边一定是已经降序排列的,要找一个比当前数大的数,那可以将找到的左侧元素和右侧序列中的一个元素进行交换,以达到比原数大的效果,可是选哪个元素呢?只能选一个比左侧元素还大的元素交换过去才能比原来的数大,那么这样交换完成的数的确比原来的数大;但是不是仅仅大于原来的数吗?呵呵,难说,因为左侧元素的右侧已经以降序的方式排列,那么它们组成的数字肯定不是较小的数字,而是较大的数字,怎么能让这个数字是个比原数稍微大一点点的数呢?交换完成以后,将左侧元素右边的所有数字直接从降序改成升序,不就是一个较小的数了么。
总结总结。
1.从右向左找,找到第一个比下一个元素还小的地方,记下位置,标注为左元素。
2.从右向左找,找到第一个比左元素大的元素,记下位置,标注为右元素。
3.交换左元素和右元素。
4.不管现在左元素位置上放的是谁,将左元素右边的序列逆序。
5.这样就得到了一个新数了。
6.可以继续重复1-5,来继续得到下一个排列。
7.如果再也找不到一个比下一个元素还小的地方,那么意味着这个序列已经降序了,排列完成了,那就结束吧。
可算到代码实现了。
static void Main(string[] args){int[] ary ={ 1, 2, 3,4 };while (true){Print(ary);if (!Next(ary)){break;}}}static void Print(int[] ary){Console.Write("{");for (int i = 0; i <ary.Length; i++){Console.Write("{0},",ary[i]);}Console.Write("}");Console.WriteLine();}staticbool Next(int[] ary){//因为序列一开始是升序的,等排序完成以后就应该是降序的//所以排完的标志是序列中从后向前找,找不到后面比前面大//的元素,如果真的找不到了,那就结束了。
intleftIndex = -1;for (int i = ary.Length - 1; i > 0; i--){if (ary[i - 1] <ary[i]){leftIndex = i - 1;break;}}//找不到了,那就结束了if (leftIndex< 0){return false;}//如果能运行到这里,说明序列还没有被完全排完//还有后面比前面大的情况//下面的工作是从序列的后面向前面找,找到刚才//leftIndex的位置就结束了;找什么呢?找一个比//leftIndex还大的元素,也就是在已经降序排列的//那一部分中找一个比leftIndex 还大的元素,这个//一定能找到。
