小学五年级平面图形面积
五年级下册数学-平面图形的面积练习

平行图形的面积
一、练习题
1、如图所示,已知四边形ABCD 是平行四边形,BC 的长度为10,高AE 的长度为6,求平行四边形ABCD 的面积。
2、如图所示,四边形ABCD 是梯形,AD 的长度是4,BC 的长度是8,高AE 的长度是6,求梯形ABCD 的面积。
A B D C E A B D E C
3、如图所示,已知平行四边形ABCD 的面积是24,CD 边上的高AE 的长度是3,求AB 的长度。
4、如图所示,已知长方形的周长是18,宽是4,求长方形的面积。
A B C D E
5、如下图,已知AC=10,BD=6,BE=6,求AD 的长度。
B A D
C E
二、答案
1、答案解析:因为平行四边形面积=底×高,所以平行四边形ABCD的面积=10×6=60。
2、答案解析:因为梯形面积=(上底+下底)×高÷2,所以梯形ABCD的面积=(4+8)×6÷2=36。
3、答案解析:平行四边形面积=底×高,即3×CD=24,则CD=24÷3=8,AB=CD=8。
4、答案解析:因为长方形周长=(长+宽)×2,所以长+宽=18÷2=9,宽=4,长=9-4=5,长方形面积=长×宽=5×4=20。
5、答案解析:三角形ABD面积=BD×AC÷2=6×10÷2=30,三角形ABD面积=AD×BE÷2=30,所以AD=30×2÷6=10。
五年级数学平面图形的面积计算(PPT)5-2
应用题:
1. 一块梯形木板面 积为9.2平方米,中 位线长2.3米,求梯 形木板的高是多少?
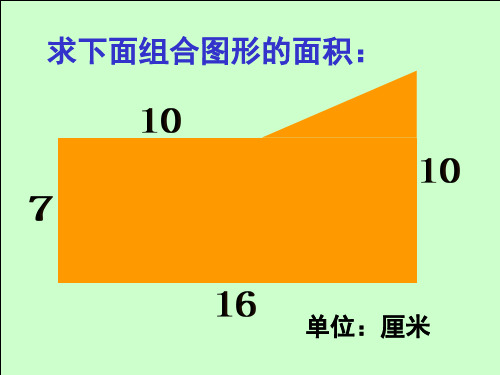
求下面组合图形的面积:
单位:厘米
年国际上以国际协议原点()作为地极原点,经度起点实际上不变。 【本岛】名几个岛屿中的主要岛屿,其名称和这几个岛屿总体的名称相同。例如我国的 湾湾包括湾湾本岛和澎湖列岛、绿岛、兰屿等许多岛屿。 【本地】名人、物所在的地区;叙事时特指的某个地区:~人|~口音|~特产。 【本分】①名本 身应尽的责任和义务:守~|~的工作。②形安; 大语文加盟品牌有哪些 大语文加盟品牌有哪些 ;于所处的地位和环境:~人|这个人 很~。 【本固枝荣】ī树木主干强固,枝叶才能茂盛,比喻事物的基础巩固了,其他部分才能发展。 【本行】名①个人一贯从事的或长期已经熟习的行业: 他原来是医生,还是让他干老~吧。②现在从事的工作:三句话不离~|熟悉~业务。 【本纪】名纪传体史书中帝王的传记,一般按年月编排重要史实,列 在全书的前面,对全书起总纲的作用。 【本家】名同宗族的人:~兄弟|他们俩住在一个村,是~。 【本家儿】〈方〉名指当事人:~不来,别人不好替他 做主。 【本金】ī名①存款者或放款者拿出的钱(区别于“利息”)。②经营工商业的本钱;营业的资本。 【本科】名大学或学院的基本组成部分(区别于 “预科、专科”等)。 【本来】①形属性词。原有的:~面貌|~的颜色。②副原先;先前:他~身体很瘦弱,现在很结实了|我~不知道,到了这里才听 说有这么回事。③副表示理所当然:~就该这样办。 【本利】名本金和利息。 【本领】名技能;能力:有~|~高强。 【本名】名①本来的名字;原来的 名字(区别于“别号、官衔”等)。②给本人起的名儿:有些外国人的全名分三部分,第一部分是~,第二部分是父名,第三部分是姓。 【本命年】名我国 习惯用十二生肖记人的出生年,每十二年轮转一次。如子年出生的人属鼠,再遇子年,就是这个人的本命年。参看页〖生肖〗。 【本末】名①树的下部和上 部,东西的底部和顶部,比喻事情从头到尾的经过:详述~|纪事~。②比喻主要的与次要的:不辨~|~颠倒。 【本末倒置】比喻把主要事物和次要事物 或事物的主要方面和次要方面弄颠倒了。 【本能】①名人类和动物不学就会的本领,如初生的婴儿会哭会吃奶,蜂酿蜜等都是本能的表现。②副机体对外界刺激不知不觉地、无意识地(做出反应):他看见红光一闪,~地闭上了眼睛。 【本票】名出票人签发的,并承诺在见票时向收款人或持票人无条件支付确 定金额的票据。 【本钱】名①用来营利、生息、等的钱财:做买卖得有~。②比喻可以凭借的资历、能力、条件等:强壮的身体是做好工作的~。 【本人】 代人称代词。①说话人指自己:这
五年级数学 平面几何图形的面积 基础+拔高例题 带作业(带详细答案)

平面几何图形的面积板块一:基础巩固1、一个三角形的面积比与他等底等高的平行四边形的面积少12平方分米,则平行四边形的面积是(24 )平方分米,三角形的面积是(12 )平方分米。
2、李叔叔在院子里靠着墙边围城了一个鸡笼,围鸡笼的网子长20.5米,求这个鸡笼的占地面积是多少平方米?上底+下底=20.5-8.5=12(米)梯形面积=12×8.5÷2=51(平方米)3、有一个长方形,如果宽减少2米,或长减少3米,则面积均减少24平方米,求这个长方形的是是多少平方米?32原长方形的长:24÷2=12(米)原长方形的宽:24÷3=8(米)原来长方形的面积:12×8=96(平方米)4、如图是由边长分别为4厘米、8厘米的两个正方形组成的图形,求阴影部分面积。
方法一:可以分割成两个钝角三角形第一个钝角三角形的底是4,高是4,第二个钝角三角形的高是8,底是8-4=4,所以总共的面积是:4×4÷2+8×(8-4)÷2=24(平方厘米)方法二:两个正方形的面积-2处空白的面积=4×4+8×8-8×8÷2-4×(4+8)÷2=24(平方厘米)5、如图是由边长分别为4、8、6厘米的三个正方形组成的图形,求阴影部分面积。
方法一:可以分割成三个钝角三角形第一个钝角三角形的底是4,高是4,面积是:4×4÷2=8(平方厘米)第二个钝角三角形的高是8,底是(8-4),面积:8×(8-4)÷2=16(平方厘米)第三个钝角三角形的高是8,底是6,面积是:6×8÷2=24(平方厘米)一共的面积:8+16+24=48(平方厘米)方法二:把右上角补起来阴影面积=三个正方形的面积+小长方形面积-两处空白的面积=4×4+8×8+6×6+6×(8-6)-(8+4)×4÷2-8×(6+8)÷2=48(平方厘米)板块二:拓展提高【例题1】下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.208 5阴影部分+中间空白=中间空白+下面空白所以阴影部分=下面空白20-5=15(厘米)(15+20)×8÷2=140(平方厘米)【例题2】右图中甲的面积比乙的面积大__________平方厘米.乙甲6厘米8厘米4厘米利用同增同减差不变甲-乙=(甲+空白)-(乙+空白)=大三角形面积-小三角形面积=6×8÷2-4×8÷2=24-16=8(平方厘米)【例3】右图中,矩形ABCD 的边AB 为4厘米,BC 为6厘米,三角形ABF 比三角形EDF 的面积大9平方厘米,求ED 的长.A B CDEF利用同增同减差不变三角形ABF-三角形EDF 的面积=9平方厘米同时增加梯形BCDF 的面积,则:长方形ABCD-三角形BCE=9长方形ABCD 的面积=4×6=24(平方厘米)则三角形BCE 的面积=24-9=15(平方厘米)EC=15×2÷6=5(厘米)ED=5-4=1(厘米)【巩固】如图所示,CA=AB=4厘米,△ABE 比△CDE 的面积小2平方厘米,求CD 的长为多少厘米?A BECD利用同增同减差不变三角形CDE-三角形ABE 的面积=2平方厘米同时增加三角形BCE 的面积,则:三角形BCD-三角形ABC=2三角形ABC 的面积=4×4÷2=8(平方厘米)则三角形BCD 的面积=8+2=10(平方厘米)CD=10×2÷4=5(厘米)【例4】一块长方形铁板,长15分米,宽12分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?1215222原来的面积=15×12=180(平方分米)现在的的面积=(15-2)×(12-2)=130(平方厘米)减少的面积:180-130=50(平方厘米)【巩固】一个长方形,如果长减少5厘米,宽减少2厘米,那么面积就减少66平方厘米,这时剩下的部分恰好成为一个正方形,求原来长方形的面积?5×22566-2×5=56(平方厘米)设剩下的部分正方形的边长为x厘米5x+2x=56X=8原来长方形的长:8+5=13(厘米)原来长方形的宽:8+2=10(厘米)原来长方形的面积:13×10=130(平方厘米)【例5】下面图形中,长方形ABCD的面积是32平方厘米,EF都是所在边的中点,求三角形AEF的面积。
五年级数学平面图形的面积

8.在下图中,阴影部分的面积是 21平方厘米,直角梯形的面积是 多少平方厘米?
单位:厘米
谢谢观赏
应用题:
5. 一座拦河大坝横截面
是梯形,面积是30平方米, 它的高是8米,下底比上底 多1.5米,梯形的下底是多 少?
6.在下图中,梯形的面积是60平 方厘米,周长是36厘米,两腰长 度之和是16厘米。求梯形的高。
7.如下图,梯形ABCD的面积等于72平 方厘米,AB=4厘米,DC=8厘米。求三 角形ABD平方米,中 位线长2.3米,求梯 形木板的高是多少?
应用题:
2. 一个梯形的上底为6 厘米,下底为9厘米,面 积为45平方厘米,它的 高是多少厘米?
应用题:
3. 已知梯形的面积是 21平方米,高6米,下底 长4米,求上底长多少?
应用题:
4. 某梯形上底与下 底的和为100米,面积 为1500平方米,它的 高是多少米?
五年级第二学期
求下面组合图形的面积:
单位:厘米
求下图中阴影部分的面积:
单位:厘米
求下图中阴影部分的面积:
单位:厘米
; 苹果售后维修点 / 苹果售后维修点 ;
顿写一封内容尖刻的信回敬那家伙。 “可以狠狠地骂他一顿。”林肯说。 斯坦顿立刻写了一封措辞强烈的信,然后拿给总统看。 “对了,对了。”林肯高声叫好,“要的就是这个!好好训他一顿,真写绝了,斯坦顿。” 但是当斯坦顿把信叠好装进信封里时,林肯却 叫住他,问道:“你要干什么?” “寄出去呀。”斯坦顿有些摸不着头脑了。 “不要胡闹。”林肯大声说,“这封信不能发,快把它扔到炉子里去。凡是生气时写的信,我都是这么处理的。这封信写得好,写的时候你己经解了气,现在感觉好多了吧,那么就请你把它烧掉,再 写第二封信吧。” 6、果断 有一个6岁的小男孩,一天在外面玩耍时,发
小学五年级数学 平面图形的面积计算

算法(2):12×5÷2=30(平方厘米)
× 算法(3):10×5÷2=25(平方厘米)
练习:选取有效的条件进行计算它们的面积。(单位:厘米)
5 4 8
5
8
12
6 5 10
8 4
1、平行四边形面积:8×4=32(平方厘米) 2、梯形面积:(8+12)×4÷2=40(平方厘米) 3、三角形面积:10×5÷2=25(平方厘米)
Байду номын сангаас
练习: 12
6分米
(?)
10
5米
S=10平方米
(1): 6×10÷12=5(分米) 或:12x=6×10
(2): 5x÷2=10 或:10×2÷5=4(米)
1.5米
2米
3米
(1)求梯形面积: (1.5+2)×3÷2=5.25(平方米)=525(平方分米) (地板面积)
(2)求地砖面积: 20×20=400(平方厘米) =4(平方分米) (3)单位转换:(想一想) (4)求砖的块数: 525÷4=131.25≈132(块)
长方形、正方形 平行四边形 三角形 梯形
长方形
长方形面积=长×宽
S=ab
平行四边形
平行四边形面积=底×高
S=ah
正方形
正方形面积=边长×边长 S=a 2(a的平方)
三角形
三角形面积=底×高÷2
S=ah÷2
梯形
梯形面积=(上底+下底)×高÷2
S=(a+b)h÷2
练习:求下面图形的面积
单位:厘米
12 65
五年级数学教案——《图形的面积》

五年级数学教案——《图形的面积》【教学内容】北师大版小学数学五年级上册P16-17 “比较图形的面积”。
【教学目标】1、借助方格纸,能直接判断图形面积的大小。
2、通过交流,知道比较图形面积大小的基本方法。
3、体验图形形状的变化与面积大小变化的关系。
【教学重点】掌握比较图形面积大小的方法。
会用不同的方法去比较图形的面积大小【教具准备】课件、方格纸、直尺、各种平面图形的硬纸板、七巧板等【教学设计】教学过程教学过程说明一、复习旧知,揭示新课。
1、课件播放已经学过的各种平面图形(长方形、正方形、三角形、梯形等),让学生说出图形的名称以及特征。
2、让学生拿出准备的长方形的硬纸板。
跟同桌说说哪儿是它的周长,哪儿是它的面积。
并且用手比划一下这个长方形的周长有多长?用手摸一摸它的面积有多大?(注:明确图形的周长是指绕图形一周的长度;图形的面积是指所占平面的大小。
)3、师:任意拿出两个图形纸板,说说哪个面积大?哪个面积小?让学生进行直观判断。
如果两个形状不同,大小很难区分时,你有什么办法?--揭示课题:我们今天来探讨图形面积的比较。
二、自主探究:比较图形面积的大小。
1、出示课本16页网格中的13个图形。
2、自主探究活动:这些图形的面积之间有什么关系呢?请同学们先仔细观观察、比较,看谁的发现最多多!3、小组交流:在小组里交流你的发现。
①全班交流,归纳比较图形面积的方法:各组派代表说说你们组找到了哪些图形之间的面积大小关系?是怎么知道的?依据同学的回答,归纳学生所使用的比较方法如下:②板书:A、数方格的方法;(重点说明这个方法,为今后学习面积公式的推导作好铺垫。
)B、重叠法;(通过旋转、平移、翻转等操作方法,使两个图形重叠,再观察比较出图形面积的大小)C、转化法;(通过割补、拼合转化为规则的图形后,再做比较)三、实践活动:比较图形面积的大小。
1、活动一:课件出示课本17页1题:师:同学们观察得很仔细,总结了这么多的比较图形面积大小的方法,那我要考考大家的眼力,下列图形中哪些与图1的面积一样?为什么?你用的是什么方法得到的?(注:重点要引导学生怎样对图形进行平移和分割,让学生体会形状变化而面积不变的事实,培养学生图形的转化思想,为后续运用转化思想学习面积公式的推导打下基础。
五年级数学上册平面图形的面积归纳与练习

姓名:1、求下面图形的面积。
3、量出所需要的数据,再求图形的面积。
面积公式在生活中的运用。
1、有一块平行四边形菜地,底是240m,宽是125m,在这块地里共收油菜7.38吨。
这块菜地有多少公顷?平均每公顷收油菜多少吨?2、有一块麦田的形状是平行四边形。
它的底是250m,高是84m,共收小麦14.7吨。
这块菜地平均每公顷收小麦多少吨?3、一块玻璃的形状是一个三角形,它的底是12.5dm,高是7.8dm。
每平方米玻璃的价格是68元,买这块玻璃要用多少钱?4、小雨的书房需要用一些同样大小的平行四边形地砖铺地,每块砖的第是7dm,高是4dm,每平方米地砖的价格是0.25元,小雨带了200元钱去建材城买地砖,他最多能买多少块这样的地砖?5、一架滑翔机模型的尾翼是由两个完全相同的梯形组成的。
它的面积是多少?6、一个果园的形状是梯形。
它的上底是160米,下底是180米,高是50米。
如果每棵果树占地10平方米,这个果园共有多少棵果树?7、如图,靠墙围成一个花坛,围成花坛的篱笆长46米,求这个花坛的面积?8、有一块梯形地,上底长64米,比下底短16米,高50米。
平均每15平方米种一棵果树,这块地共种多少棵果树?基础题型三、已知周长,求平面图形的面积。
注:“已知周长,求图形的面积这一类题型”,我们先要根据“周长”,求出计算“面积”所需要的条件,再代入面积公式计算。
另外,在求计算面积所需要的条件时,列方程来求解可以降低出错率。
【例题】已知一个等边三角形的周长是15cm,高约是4.3cm。
求三角形的面积。
分析与解:等边三角形的周长是其边长的3倍,所以等边三角形的边长是:15÷3=5(cm),所以三角形的面积是:S=ah÷2=5×÷2=10.75(2cm)1、一个等腰直角三角形的两条直角边的和是8.4dm,求三角形的面积?2、一个等腰梯形的周长是34cm,一腰长度是5cm,等腰梯形的高是3cm。
五年级数学面积求解技巧

五年级数学面积求解技巧五年级数学面积求解技巧在五年级的数学学习中,面积是一个重要的概念。
从求解简单的平面图形面积到复杂的立体图形面积,都需要掌握一些基本的技巧。
本文将介绍五年级数学面积求解的一些技巧。
一、平面图形面积的求解1. 长方形和正方形面积的求解长方形的面积等于长度乘以宽度,即面积=长×宽。
正方形的面积等于边长的平方,即面积=边长×边长。
2. 三角形面积的求解三角形的面积等于底边长度乘以高的一半,即面积=底边×高÷2。
当底边和高的长度已知时,直接代入公式即可求得面积。
当底边和顶点的坐标已知时,可以通过计算底边和高的长度来求得面积。
可以利用勾股定理或者直角三角形的特性来计算。
当三角形的三个顶点的坐标已知时,可以利用向量运算来求解。
可以通过顶点坐标的向量表示来计算面积。
3. 梯形面积的求解梯形的面积等于上底加下底的平均值乘以高,即面积=(上底+下底)×高÷2。
当上底和下底的长度已知时,直接代入公式即可求得面积。
当上底、下底和高的长度已知时,可以直接代入公式求得面积。
4. 长度单位的转换在求解面积时,有时需要将图形的尺寸从一种单位转换为另一种单位。
例如,将图形的尺寸从厘米转换为米,或者从毫米转换为厘米。
转换单位时,需要根据单位之间的比例关系来计算。
例如,1米=100厘米,1厘米=10毫米,根据这些比例可以进行单位的转换。
二、立体图形面积的求解1. 立方体面积的求解立方体的表面积等于6个面的面积之和。
每个面的面积可以根据上述的平面图形面积求解方法来计算。
2. 矩形长方体面积的求解矩形长方体的表面积等于底面的面积加上四个侧面的面积。
可以通过计算底面的面积和四个侧面的面积来求解总面积。
3. 圆柱体面积的求解圆柱体的表面积等于底面圆的周长乘以高,再加上两个底面的面积。
可以通过计算底面圆的周长和两个底面的面积来求解总面积。
4. 球体面积的求解球体的表面积等于4πr²,其中π是圆周率,r是球的半径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面图形面积
练习1:
例二:
图中正方形的边长为10cm,ED=8cm,△EFC 的面积是45平方厘米,求梯形BCDF的面积。
练习2:
练习3:
例四:
长方形ABCD的长为5厘米、宽为3厘米,设其对角线BD对折后得到的图形如下所示:则图中阴影部分的周长是_______厘米。
练习4:
如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点F处,且点F在△ABC外部,则阴影部分图形的周长为()cm。
图中,E、F分别为AD、BC边上一点,连接AF和BE,相交于P;连接CE和DF,相交于Q。
已知三角形ABP的面积是20平方厘米,三角形CDQ的面积是35平方厘米。
求阴影部分EPFQ 的面积。
练习5:
如图: ABCD是平行四边形,三角形EBC是直角三角形,EC长8厘米,BC长10厘米,阴影部分的面积比三角形EFG的面积大10平方厘米。
平行四边形的面积是多少平方厘米
例六:
已知长方形的长是15厘米,宽是8厘米,四边形EFGH的面积是12平方厘米,求空白部分的面积
如图,ABCD为平行四边形,三角形DCE的面积是97平方厘米,阴影部分的面积是多少平方厘米
当堂检测
一.如图,在四边形ABCD中,DCFG为正方形,ADEB为梯形,DE=30厘米,DG=24厘米,AB=39厘米,求梯形ABED的面积
二.在四边形ABCD中,AB=BC=10厘米,BE=8厘米,AD的长是______厘米。
三.一个长方形被两条直线分成四个长方形,其中三个的面积分别是20亩,25亩,30亩,另一个长方形的面积是多少亩。
四.如图所示,梯形中的两个小三角形的面积为3、9平方厘米,梯形ABCD的面积是 ___.
面积计算:
如图7—;11,正方形abcd的边长是4厘米,cg=3厘米求长方形defg的面积。
