实验1 卷积积分运算
实验报告信号卷积实验

一、实验目的1. 理解卷积的概念及其物理意义。
2. 掌握卷积运算的原理和方法。
3. 通过实验加深对卷积运算在实际应用中的理解。
二、实验原理1. 卷积的定义:卷积是一种线性运算,它描述了两个信号在时域上的相互作用。
对于两个连续时间信号f(t)和g(t),它们的卷积定义为:F(t) = ∫f(τ)g(t-τ)dτ其中,F(t)是卷积结果,f(τ)是信号f(t)的任意时刻的值,g(t-τ)是信号g(t)在时刻t-τ的值。
2. 卷积的性质:卷积具有交换律、结合律和分配律等性质。
其中,交换律是指f(t)和g(t)的卷积与g(t)和f(t)的卷积相等;结合律是指三个信号f(t)、g(t)和h(t)的卷积可以分别进行两两卷积后再进行一次卷积;分配律是指一个信号与两个信号的卷积等于该信号分别与两个信号卷积后的和。
三、实验内容1. 实验一:连续时间信号卷积实验(1)选用信号:选取两个连续时间信号f(t)和g(t),其中f(t)为矩形脉冲信号,g(t)为指数衰减信号。
(2)卷积计算:根据卷积的定义,计算f(t)和g(t)的卷积F(t)。
(3)结果分析:观察F(t)的波形,分析卷积结果的物理意义。
2. 实验二:离散时间信号卷积实验(1)选用信号:选取两个离散时间信号f[n]和g[n],其中f[n]为单位阶跃信号,g[n]为矩形脉冲信号。
(2)卷积计算:根据离散时间信号卷积的定义,计算f[n]和g[n]的卷积F[n]。
(3)结果分析:观察F[n]的波形,分析卷积结果的物理意义。
3. 实验三:MATLAB仿真实验(1)选用信号:选取两个连续时间信号f(t)和g(t),其中f(t)为正弦信号,g(t)为余弦信号。
(2)MATLAB编程:利用MATLAB的信号处理工具箱,编写程序实现f(t)和g(t)的卷积运算。
(3)结果分析:观察MATLAB仿真得到的卷积结果,分析其物理意义。
四、实验结果与分析1. 实验一:连续时间信号卷积实验(1)实验结果:通过计算得到f(t)和g(t)的卷积F(t)的波形。
卷积信号实验报告

信号与系统上机实验报告一连续时间系统卷积的数值计算140224 班张鑫学号 14071002 一、实验原理计算两个函数的卷积卷积积分的数值运算实际上可以用信号的分段求和来实现,即:如果我们只求当 t = n∆ t1 是r ( t )的值,则由上式可以得到:∆t足够小时,r(t2)就是e(t)和f(t)卷积积分的数值近似值由上面的公式可当1以得到卷积数值计算的方法如下:(1)将信号取值离散化,即以为周期,对信号取值,得到一系列宽度间隔为的矩形脉冲原信号的离散取值点,用所得离散取值点矩形脉冲来表示原来的连续时间信号;(2)将进行卷积的两个信号序列之一反转,与另一信号相乘,并求积分,所得为t=0时的卷积积分的值。
以为单位左右移动反转的信号,与另一信号相乘求积分,求的t<0和t>0时卷积积分的值;(3)将所得卷积积分值与对应的t标在图上,连成一条光滑的曲线,即为所求卷积积分的曲线。
1信号与系统上机实验报告一二、处理流程图三、C程序代码#include"stdafx.h"#include"stdio.h"//#include "stdilb.h"float u(float t){while (t>= 0) return(1);while (t<0) return(0);}float f1(float t){return(u(t+2)-u(t-2));}float f2(float t){return(t*(u(t)-u(t-2))+(4-t)*(u(t-2)-u(t-4)));}int_tmain(int argc, _TCHAR* argv[]){FILE *fp;fp=fopen("juanji.xls","w+");float t,i,j,result=0;for(i=-2;i<=6;i=i+0.1){result=0;for(j=0;j<=4;j=j+0.1)result+=f2(j)*f1(i-j)*0.1;printf("%.1f\t%.2f\t",i,result);fprintf(fp,"%.1f\t%.2f\n",i,result);}printf ("\n");return 0;}四、运行结果五、卷积曲线六、感想与总结卷积是信号与系统时域分析的基本手段,主要用于求解系统的零状态响应。
电路原理课件-卷积积分

7) t≥7时,
y(t ) 0
注意:积分上下限应由被 积函数存在的时域范围的 上下限确定。
卷积积分在电路分析中的应用
例1、电路如图所示,uS=15e-0.25t(t)V。采用卷积计算uC。
解:以uC为响应,求单位阶跃响应
uC (0 ) uC (0 ) 0
uCf 40 1 0.5V 40 40
t t
t t
t 0
d dt t t
卷积积分上下限分析
t
0
r t h t f t f t h t
卷积符合交换律
δ t f t δ f t dτ τ τ
k 0
f (t ) f a (t )
f ( k ) ( t k ) ( t ( k 1) )
k 0 n 1
k 0 n 1
k 0
n 1
(t k ) (t (k 1) ) f (k )
例2、电路如图,R=10,L=1H,激励uS的波形如图 所示,求零状态响应i(t)。
解:以电流i 为响应,求单位阶跃响应为:
R t 1 g( t ) (1 e L ) ( t ) R 0.1(1 e 10 t ) ( t )
则单位冲激响应为:
dg( t ) h (t ) e 10 t ( t ) dt
40 40 RC 0.05 1s 40 40
uC ( t ) uCf (1 e ) ( t ) 0.5(1 e t ) ( t )V
t
单位阶跃响应为:
g(t ) 0.5(1 e t ) (t )
信号与系统实验

信号与系统实验实验一 信号的时域基本运算一、 实验目的1.掌握时域内信号的四则运算基本方法;2.掌握时域内信号的平移、反转、倒相、尺度变换等基本变换;3.注意连续信号与离散信号在尺度变换运算上区别。
二、 实验原理信号的时域基本运算包括信号的相加(减)和相乘(除)。
信号的时域基本变换包括信号的平移(移位)、反转、倒相以及尺度变换。
(1) 相加(减): ()()()t x t x t x 21±= [][][]n x n x n x 21±= (2) 相乘: ()()()t x t x t x 21∙= [][][]n x n x n x 21∙=(3) 平移(移位): ()()0t t x t x -→ 00>t 时右移,00<t 时左移[][]N n x n x -→ 0>N 时右移,0<N 时左移(4) 反转:()()t x t x -→ [][]n x n x -→ (5) 倒相:()()t x t x -→ [][]n x n x -→ (6) 尺度变换: ()()at x t x →1>a 时尺度压缩,1<a 时尺度拉伸,0<a 时还包含反转[][]mn x n x → m 取整数1>m 时只保留m 整数倍位置处的样值,1<m 时相邻两个样值间插入1-m 个0,0<m 时还包含反转三、实验结果1、连续时间信号时域的基本运算 (1) 相加减X1(t)=t+2 , x2(t)=cos(2*pi*t) , x(t)=x1(t)+x2(t).验证:由理论得x(t)=t+2+cos(2*pi*t),而上图x(t)满足该表达式,故得证。
(2)相乘X1(t)=t+2 , x2(t)=cos(2*pi*t) , x(t)=x1(t)*x2(t).验证:由理论得x(t)=(t+2)*cos(2*pi*t),而上图x(t)满足该表达式,故得证。
卷积积分及零状态响应的卷积计算法.
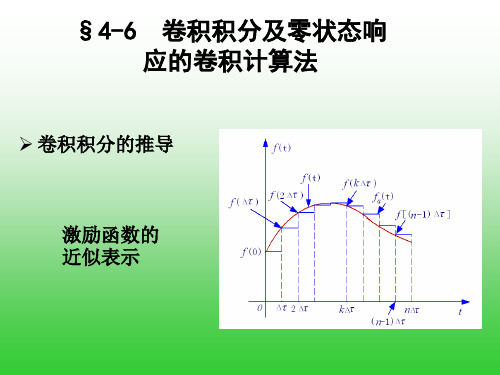
e
t T
t
e RC
ε(t)
➢卷积积分的图解
求f(t)与h(t)的卷积,实质上是求一个新函数
f()h(t)在 由0到t的区间内的定积分。根据定积分的 几何意义,函数在0到t区间内的定积分值,决定于被积 函数f()h(t)的曲线在该区间内与 轴之间所限定的面
积。
设 f (t) ε(t)
h(t ) etε(t )
计算。
解: 当 0<t <1 时
r(t ) te(t )ε(t )d 0 t e(t )d 1 et 0
当 t >1 时
r(t ) e1 (t )ε(t )d 0 1 e(t )d e(t1) et 0
注意:积分上下限应由被 积函数存在的时域范围的 上下限确定,用作图的方 法可方便地确定出积分上 下限。
δt
f
t
t
0
δ
f
t
d
0δ f 0
t d
f
t
δt f t f t
f tδt f t
δt
t0
f
t
t
0
δ
t 0
f
t
d
δ t0
t0
t0
f
t
d
f t t0
例1 求卷积 [e tε(t)] ε(t)
解: [e tε(t)] ε(t) t e ε( )ε(t )d 0
t ed 0
h(t)
1
t
e RC ε(t )
RC
零状态响应电压为
t
uC (t)
u( )h(t ) d
0
t 0
u0e T
ε(
)
1 RC
实验1卷积算法实验
实验1卷积算法实验一.实验目的1、掌握用窗函数法设计卷积算法的原理和方法;2、熟悉卷积算法特性;3、了解各种窗函数对卷积算法的影响。
二.实验设备计算机,Code Composer Studio 系统。
三.实验原理1、卷积的基本原理和公式卷集和:对离散系统“卷积和”也是求线性时不变系统输出响应(零状态响应)的主要方法。
()()()()*()Y n x m h n m x n h n +∞-∞=-=∑卷积和的运算在图形表示上可分为四步:1)翻褶 先在自变量坐标M 上作出x(m)和h(m),将m=0的垂直轴为轴翻褶成h(-m)。
2)移位 将h(-m)移位n ,即得h(n-m)。
当n 为正整数时,右移n 位。
当n 为负整数时,左移n 位。
3)相乘 再将h(n-m)和x(m)的相同m 值的对应点值相乘。
4)相加 上所有对应点的乘积叠加起来,即得y (n)值。
依上法,取n=…,-2,-1,0,1,2,3,…各值,即可得全部y(n)值。
2、程序流程图实验1流程图3、程序的自编函数及其功能1)processing1(int *input2,int *output2)调用形式:processing1(int *input2,int *output2)参数解释:intput2、output2为两个整型指针数组。
返回值解释:返回了一个“TRUN”,让主函数的while循环保持连续。
功能说明:对输入的input2buffer波形进行截取m点,再以零点的Y轴为对称轴进行翻褶,把生成的波形上的各点的值存入以OUTPUT2指针开始的一段地址空间中。
2)processing2(int *output2,int *output3)调用形式:processing2(int *output2,int *output3)参数解释:output2、output3为两个整型指针数组。
返回值解释:返回了一个“TREN”,让主函数的while循环保持连续。
连续时间系统卷积的数值计算实验报告.docx

实验报告实验名称:连续时间系统卷积的数值计算一、实验目的:1、加深对卷积概念及原理的理解;2、掌握借助计算机计算任意信号卷积的方法。
二、实验原理:卷积积分不仅可以通过直接积分或查表的方法来求解,还可以用积分的数值计算方法来求解。
在线性系统的分析过程中,有时会遇到复杂的激励信号,或者有时只是一组测试数据或曲线,冲激响应也可能出现同样的情况。
显然,此时直接计算积分或查表都有困难,而采用近似的数值计算方法可以解决这个问题,求得卷积积分。
1、卷积的定义卷积积分可以表示为2卷积计算的几何算法卷积积分的计算从几何上可以分为四个步骤:翻转→平移→相乘→叠加。
3卷积积分的应用卷积积分是信号与系统时域分析的基本手段,主要用于求系统零状态响应,它避开了经典分析方法中求解微分方程时需要求系统初始值的问题。
设一个线性零状态系统,已知系统的单位冲激响应为h(t),当系统的激励信号为e(t)时,系统的零状态响应为由于计算机技术的发展,通过编程的方法来计算卷积积分已经不再是冗繁的工作,并可以获得足够的精度。
因此,信号的时域卷积分析法在系统分析中得到了广泛的应用。
卷积积分的数值运算实际上可以用信号的分段求和来实现,即:如果我们只求当t = nΔt (n为正整数,nΔt 记为t )时r(t)的值,则由上式可以得到:当Δt 足够小时,r(t )就是e(t)和h(t)卷积积分的数值近似,由上面的公式可以得到卷积数值计算的方法如下:1 将信号取值离散化,即以 Ts 为周期,对信号取值,得到一系列宽度间隔为 Ts 的矩形脉冲原信号的离散取值点,用所得离散取值点矩形脉冲来表示原来的连续时间信号;2 将进行卷积的两个信号序列之一反转,与另一信号相乘,并求积分,所得为 t=0 时的卷积积分的值。
以 Ts 为单位左右移动反转的信号,与另一信号相乘求积分,求的t<0和t>0时卷积积分的值;3 将所得卷积积分值与对应的t 标在图上,连成一条光滑的曲线,即为所求卷积积分的曲线。
卷积实验报告

1.理解卷积的概念及物理意义;
2.通过实验的方法加深对卷积运算的图解方法及结果的理解。
二、实验内容:(请将实验的题目内容、实验及过程代码、实验结果(必要时可以进行拷屏)、实验体会等填写到此处。页面空间不够,可另附页或另附文件。
卷积积分的物理意义是将信号分解为冲激信号之和,借助系统的冲激响应,求解系统对任意激励信号的零状态响应。设系统的激励信号为 ,冲激响应为 ,则系统的零状态响应为 。
实验步骤:
(1)连接P04和P101;
(2)调节信号源,使P04输出f=1KHz,占空比为50%的脉冲信号,调节W701使信号幅度为4V;
(3)按下SW101按钮,使程序指示灯D3D2D1D0=0100,指示灯对应系统卷积;
(4)将示波器的CH1接于TP801,CH2接于TP802,分别观察系统冲击响应 波形与卷积后的输出信号 * 的波形;
信号 为矩形脉冲信号, 为锯齿波信号,如图9-2所示。根据卷积积分的运算方法得到 和 的卷积积分结果 ,如图9-2(c)所示。
图10-2矩形脉冲信号与锯齿脉冲信号的卷积积分的结果
3.本实验进行的卷积运算的实现方法
在本实验装置中采用了DSP数字信号处理芯片,因此在处理模拟信号的卷积积分运算时,是先通过A/D转换器把模拟信号转换为数字信号,利用所编写的相应程序控制DSP芯片实现数字信号的卷积运算,再把运算结果通过D/A转换为模拟信号输出。结果与模拟信号的直接运算结果是一致的。数字信号处理系统逐步和完全取代模拟信号处理系统是科学技术发展的必然趋势。图9-3为信号卷积的流程图。
(5)按下SS702,使频率表右侧t/T指示灯亮,之后旋转SS702,调节P04输出信号的占空比,改变激励信号的脉宽,观测卷积后波形,记录到表10-2中;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、实验目的
(1)理解掌握卷积的概念及物理意义。
(2)理解单位冲激响应的概念及物理意义。
二、实验原理
根据前述知识,连续信号卷积运算定义为
τττd t f
f t f t f t f ⎰∞
∞
--=
=)()()(*)()(2
1
21
卷积计算可以通过信号分段求和来实现,即
∆
•∆-•∆=-=
=∑⎰∞
-∞
=→∆∞
∞
-)()(lim
)()()(*)()(2
1
2
1
21k t f
k f d t f
f t f t f t f k τττ 如果只求当∆=n t (n 为整数)时)(t f 的值)(∆n f ,则由上式可得
∑∑∞
-∞
=∞
-∞
=∆-•∆•
∆=∆-∆•∆=
∆k k k n f k f k n f
k f n f ])[()()()()(2
1
2
1
式(9-3)中的
∑∞
-∞
=∆-•∆k k n f k f ])[()(2
1
实际上就是连续信号)(1t f 和
)(2t f 经等时间间隔∆均匀抽样的离散序列)(1∆k f 和)(2∆k f 的卷积和。
当∆足够小时,)(∆n f 就是卷积积分的结果——连续时间信号)(t f 的较好的数值近似。
三、实验程序
四、实验例题
已知函数t t f 2)(1=,t t f 2)(2=,求)(*)()(21t f t f t f =,并求)(t f 的时域波形图。
(1)解:分别画出)(1τf 和)(2τ-t f 的时域波形
①当0<t 时,)(1τf 和)(2τ-t f 的时域波形为
此时
0)(*)()(21==t f t f t f
②当10<<t 时,)(1τf 和)(2τ-t f 的时域波形为
此时,
30
2132
)(22)(*)()(t d t t f t f t f t
=-•==⎰τττ
③当21<<t 时,)(1τf 和)(2τ-t f 的时域波形为
此时,
38
432)(22)(*)()(31
1
21-
+-=-•==⎰-t t d t t f t f t f t τττ
④ 当2>t 时,)(1τf 和)(2τ-t f 的时域波形为
此时,
0)(*)()(21==t f t f t f
所以,时域波形图如下
(2)通过MATLAB求解
输入公式:
得到:
综上,通过MATLAB仿真与计算结果一致。
五、实验小结
实验结果表明,用Mathlab计算出的结果与理论结果一致。
通过实验,我更深刻地理解了卷积的概念及其物理意义。
并且学习了Matlab在卷积运算中的用法,熟悉了Matlab的有关知识,、受益匪浅。
