第二章-卷积与与卷积积分
信号与系统课后题解第二章

⑺
对⑺式求一阶导,有:
de(t ) d 2 i 2 (t ) di (t ) du (t ) =2 +2 2 + c 2 dt dt dt dt de(t ) d 2 i2 (t ) di (t ) =2 + 2 2 + 2i1 (t ) + 2i 2 (t ) 2 dt dt dt
⑻
将⑸式代入⑻式中,有:
λ 2 + 2λ + 1 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1
y h (t ) = C1e −t + C2 te− t
由初始状态为 y (0 ) = 1, y ' (0 ) = 0 ,则有:
C1 = 1 − C 1 + C 2 = 0
由联立方程可得 故系统的零输入响应为:
由联立方程可得 故系统的零输入响应为:
A1 = 2, A2 = −1
y zi (t ) = 2e − t − e −2 t
(2)由原微分方程可得其特征方程为
λ 2 + 2λ + 2 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1 ± i
y h (t ) = e −t (C1 cos t + C2 sin t )
(− 3C1 + 3C2 )δ (t ) + (C1 + C2 )δ ' (t ) − (− 2C1 + C 2 )δ (t ) = δ (t )
(
(
( + C e )δ (t ) + (C e
2 1
)
−2 t
+ C2 e t δ ' (t )
卷 积 积 分

1.1 卷积积分的推导
函数分解为窄脉冲
解:将 反折,得
,如图(c)所示。由
图可见, 保持不动,将 平移 ,得
,如图(d)所示。
其计算结果如下:
1.2 卷积积分的性质 (1)卷积的代数运算 ①交换律
即:
例:
,求
。
解法一:将 反褶
由于
所以 同理可得 于是
②分配律 ③结合律 (2)卷积的微分与积分 ①卷积的微分
信号与系统
卷积积分
根据LTI系统的性质,如果将作用于LTI系 统的输入信号分解,而且每个分量作用于系统 的响应容易求得。那么,根据叠加原理,将各 个分量产生的响应求和即可得原输入信号引起 的响应。
卷积法的原理就是将信号分解成许多冲激 信号之和,借助系统的冲激响应,求解线性时 不变系统对任意激励信号的零状态响应。它也 是时域与变换域方法之间相联系的重要手段。
② 卷积的积分例:设有源自个函数分别为求这两个函数的卷积
。
利用卷积的微分得
信号与系统
卷积及其性质

f1()
f2(t
)d
iii) 若t 0, f1(t)0, f2(t)0,则
S(t) 0,
t
0
t
S(t) 0
f1() f2(t )d,
t
0
精选PPT
2
§2.7 卷积及其性质
2, 卷 积 及 分 的 求 取 方 法
(1) 函 数 计 算 法
例,已知
f1 (t )
1 [u (t 2
2 ) u (t 5)]
二,离散卷积和
1,定义
两个序列x1(n),x2(n) 得卷积和定义为
x1(n)*x2(n) x1(m)x2(nm) m
如果两个序列都是因果的,即 x1(n) x1(n)u(n),x2(n) x2(n)u(n) 则有
n
x1(n)*x2(n) x1(m)x2(nm) m0
精选PPT
13
§2.7 卷积及其性质
解 : s(t) f1 (t)* f1 (t) d fd 1 ( tt)* t f2 ()d
f1(t)
f2(t)
2
1
0 123
t
1
2
01
t
精选PPT
11
§2.7 卷积及其性质
f1'(t) 2
1
0 12 3
t
f2'(t)
1
2
01
t
s(t) 2
45
1 23
t
-2
精选PPT
12
§2.7 卷积及其性质
f1( ) f2 (t )d
举例说明。
精选PPT
6
§2.7 卷积及其性质
(1)分配律:f1(t)[ f2(t) f3(t)] f1(t) f2(t) f1(t) f3(t) 物理意义:几个系统并联,可等效为一个冲激响应
信号与系统王明泉版本~第二章习题解答
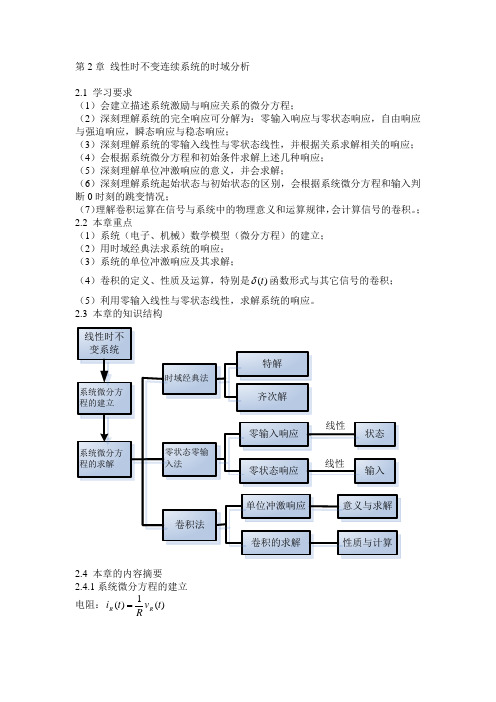
第2章 线性时不变连续系统的时域分析2.1 学习要求(1)会建立描述系统激励与响应关系的微分方程;(2)深刻理解系统的完全响应可分解为:零输入响应与零状态响应,自由响应与强迫响应,瞬态响应与稳态响应;(3)深刻理解系统的零输入线性与零状态线性,并根据关系求解相关的响应; (4)会根据系统微分方程和初始条件求解上述几种响应; (5)深刻理解单位冲激响应的意义,并会求解;(6)深刻理解系统起始状态与初始状态的区别,会根据系统微分方程和输入判断0时刻的跳变情况; (7)理解卷积运算在信号与系统中的物理意义和运算规律,会计算信号的卷积。
; 2.2 本章重点(1)系统(电子、机械)数学模型(微分方程)的建立; (2)用时域经典法求系统的响应; (3)系统的单位冲激响应及其求解;(4)卷积的定义、性质及运算,特别是()t δ函数形式与其它信号的卷积; (5)利用零输入线性与零状态线性,求解系统的响应。
2.3 本章的知识结构2.4 本章的内容摘要2.4.1系统微分方程的建立电阻:)(1)(t v Rt i R R =电感:dtt di L t v L L )()(= )(d )(1)(0t i v Lt i L tL L +=⎰∞-ττ 电容:dtt dv C t i C C )()(= ⎰+=tt L C C t i i Ct v 0)(d )(1)(0ττ 2.4.2 系统微分方程的求解 齐次解和特解。
齐次解为满足齐次方程t n t t h e c e c e c t y 32121)(λλλ+⋅⋅⋅++=当特征根有重根时,如1λ有k 重根,则响应于1λ的重根部分将有k 项,形如t k t k t k t k h e c te c e t c e t c t y 111112211)(λλλλ++⋅⋅⋅++=--- 当特征根有一对单复根,即bi a +=2,1λ,则微分方程的齐次解bt e c bt e c t y at at h sin cos )(21+= 当特征根有一对m 重复根,即共有m 重ib a ±=2,1λ的复根,则微分方程的齐次解bt e t c bt te c bt c t y at m m at h cos cos cos )(121-+⋅⋅⋅++= bt e t d bt te d bt e d at m m at at sin sin sin 121-+⋅⋅⋅+++ 特解的函数形式与激励函数的形式有关。
第二章 (4)卷积积分的性质

f 1 (t )
f 2 (t )
2
1
0
2
0 1
1
2 3
t
1
3
t
解法一: 解法一:图示法
f 1 (τ
t <1 ,
)
f (t ) = 0
2
0
1
2 3
τ
f 2 (t τ
t2
)
1
t 0
1
τ
解法一: 解法一:图示法
f 1 (τ
t <1 ,
)
t
f (t ) = 0
1< t < 2 ,
f (t ) = ∫ 2dτ = 2(t 1)
(2) e ε(t + 3) ε(t 5) 2t e ε (t + 3) ε (t 5) ∞ 2τ = ∫ e ε (τ + 3) ε (t τ 5)dτ ∞
2t
=∫t 53e2τ1 2(t 5) 6 e = e 2 6 1 2( t 2) = e 1 e 2
[
1 2τ dτ = e 2
' ∞ ∞
上式称为杜阿密尔积分. 上式称为杜阿密尔积分. 杜阿密尔积分 其物理含义为: 其物理含义为:LTI系统的零状态响应等于激励的 系统的零状态响应等于激励的
f ' (t )与系统的阶跃响应 g(t )的卷积积分. 的卷积积分. 导数
例2.4-4 求图示函数 f1(t ) 与 f2 (t ) 的卷积 f (t ) .
若f (t ) = f1(t ) f2(t ),则 f1(t t1 ) f2(t t2 ) = f1(t t2 ) f2 (t t1 ) = f (t t1 t2 )
推广4 推广
卷积积分的定义

卷积积分的定义卷积积分是数字信号处理中最常见的数学运算之一,其定义可以简单地描述为:将一个信号与另一个信号“褶积”在一起,以求出它们之间的关系或者产生的效果。
在实际应用中,卷积积分广泛用于信号处理、图像处理和通信工程等领域,是数字信号处理基础重要的处理运算。
首先,我们来看一下离散信号的卷积积分,以了解其定义和运算步骤。
假设有两个离散信号f[n]和g[n],它们的长度依次为M和N。
那么它们的卷积积分定义为:s[n] = ∑(f[k]g[n-k]),k从0到M-1上式表示的是,将g[n]相对于f[n]做移位运算,按其对应的系数f[k]进行加权之后,再将所有元素相加,就可以得到卷积积分结果s[n]。
这个过程实际上是一种加权和计算,位于g[n]的每一个系数都和f[n]的相应系数进行乘积,然后将它们相加以得到最终的卷积积分结果。
卷积积分运算可以理解为一个滑动窗口,它在f[n]中移动,并将窗口大小限定为g[n]的长度。
随着滑动窗口移动,计算得到的结果被放置到s[n]中,这个过程一直持续到窗口完全移出f[n]。
在计算过程中,g[n]每移动一次,窗口中的每个元素将会和f[n]的相应元素进行乘积,然后将它们相加来得到s[n]中的一个元素。
需要注意的是,在卷积积分的定义中,n的取值是从0到M+N-2,这是因为卷积积分的长度为(M+N-1)。
如果n的取值超过了这个范围,那么最终的结果将会是无效和不必要的。
除了离散信号卷积积分之外,连续信号卷积积分也是数字信号处理中常见的一种运算。
其计算过程与离散信号相似,只是在信号中,连续时间变量t所涉及的积分替换掉离散时间变量n:s(t) = ∫ f(τ)g(t-τ)dτ,τ从负无穷到正无穷上式表示的是,将g(t)相对于f(t)做移位运算,按其对应的函数f(τ)进行加权之后,再将所有元素相加,就可以得到连续信号卷积积分结果s(t)。
这个过程和离散信号的卷积积分类似,只是积分替换了离散信号中的累加。
第二章第3讲 卷积

[ f () * f ()]d f (t) * f ()d f (t) * f ()d
1 2 1 2 2 1
t
t
t
证明:
[ f ( ) * f
1 t 1
t
2
( )]d [ f1 ( ) f 2 ( )d ]d
[ f1 (t )u(t t1 )] [ f 2 (t )u(t t2 )]
信号与系统 同济大学汽车学院 魏学哲 weixzh@
g (t ) f1 ( )u( t1 ) f 2 (t )u(t t2 )d
结合律应用于系统分析,相当于串联系统的冲激响 应,等于串联的各子系统冲激响应的卷积
信号与系统 同济大学汽车学院 魏学哲 weixzh@
卷积的微分与积分
df2 (t ) df1 (t ) d [ f1 (t ) * f 2 (t )] f1 (t ) * f 2 (t ) * dt dt dt
t t2
t1
f1 ( ) f 2 (t )d
t1 t t2
t
积分限是: 例:
f1(t ) 2e u(t )
g (t )
f 2 (t ) u(t ) u(t 2)
求
f1 ( ) f 2 (t )d
信号与系统 同济大学汽车学院 魏学哲 weixzh@
f1( ) 1 f2(1-) 2
f1( ) 1 f2(2-) 2
f1( )
f2(3-)
2
c
c
c
c
-1
0
f1() f2(-)
信号第二章3卷积

若将此信号作用到冲激信号为h(t)的线性时不 变系统,则系统的响应为
r (t ) H [e(t )] H [ e( ) (t )d ]
e( ) H [ (t )]d
e( )h(t )d
零状态响应:rzs (t ) e( )h(t )d h(t ) e(t )
def
2.算子符号基本规则
(1)算子多项式可以进行因式分解 ( p 2)( p 3) p 2 5 p 6 例如: (2)等式两端的算子符合因式不能相消 ( p 2) r (t ) ( p 1) e(t ) ( p 2)( p 3) r (t ) ( p 2 4 p 3) e(t ) 不能简化为: (3)算子的乘除顺序不能随意颠倒
(3)结合律: f1(t) f2 (t) f3 (t) f1(t) f2 (t) f3 (t)
e(t)
h1(t)
h2(t)
r(t)
串联系统 r (t ) e(t ) h1 (t ) h2 (t )
2.卷积的微分与积分
d f1 (t ) f 2 (t ) df 2 (t ) (4)微分性: f1 (t ) dt dt df1 (t ) (适于高阶微分) f 2 (t ) dt
r (t ) e( )h(t )d
1 (a) t 2
e(t ) * h(t ) 0
h(t )
e( )
1
1 2
t 2
(b)
0
1 t 1 2
相乘
t
1
1 t 1 2 t 1 e(t ) * h(t ) 1 1 (t )d 2 2 t2 t 1 4 4 16 (b)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明:
x(tt1)(tt2)
x(t1)(tt2)d
x(tt1t2
')(')d'
x(tt1t2)
(令tt2 ')
(4)
若x(t: )x1(t)*x2(t) 则 :x1(tt1)x2(tt2)x(tt1t2)
1. 图解法: 2. 以一个例子说明这个方法。已知:
2
x[n]
1
1
h[n] 11
012 n
012 n
求y: f[n]x[n]h[n]
( 1)反h折 [k] : h[k]
h[-k] 11
-2 -1 0 n
( 2)时 h[- 移 k] : h[nk]
例:设x(t)与h(t)如图所示,求y(t)=x(t)*h(t)
x (t)
h(t)
1
1
1 2
反折:
01t h( ) 1
-2
0
0
时移
2t
h(t )
1
-2+t
t 0
(1)
h(t )
x( )
1
(2)
-2+t
t
1 2
0
1
h(t )
1
x( )
-2+t1 20 Nhomakorabeat
1
(3)
h (t ) x ( )
2、将h(-τ)沿τ轴时延t秒,得得h(t-τ)
3、将x(τ)与 h(t-τ)相乘 ,得x(τ) h(t-τ) 4、沿τ轴对x (τ) h(t-τ)积分
h(t)
1 1
x(t) t
2 1
2 4t
h(t-) t= 0
x()
t-1 t
t< 1
1< t< 2
2< t< 3
3< t< 4
4< t< 5
yf(t) x()h(t)d
上述积分是x(t)与h(t)之间的一种二元运算,用 y(t)=x(t)*h(t)表示。即
y(t)x(t)*h(t) x()h(t)d
❖卷积积分的图解法 卷积的图解法有助于我们理解卷积的物理意义以及求
解步骤,以x(t)*h(t)为例:
1、将h(τ)反折,得h(-τ)
(5 ) x(t) '(t)x'(t)
例
h(t)
已知:h(t)1 t 2
0 t 2
-2
2
t
x(t)3 (t)(t3 )
解:将h(t)写成与阶跃函数乘积的形式:
h (t) u (t 2 ) u (t 2 )
y(t) x(t)h(t)
(3(t)(t 3))[u(t 2)u(t 2)] 3(t)u(t 2)3(t)u(t 2) (t 3)u(t 2)(t 3)u(t 2)
h(t) L[{0},(t)] cetu(t)的形式。 这里,=-2。即h(t) ce-2tu(t)代入方程中: -2ce-2tu(t)+c (t) 2ce-2tu(t) 3 (t)
c 3 h(t) 3e-2tu(t)
注意:单位冲击响应为系统的零状态响应。
2.3 卷积积分
对于线性系统,可以将输入信号分解为许多简单 信号之和。如果求得简单信号作用于系统的响应, 那么,所有这些响应叠加起来就是该输入作用于系 统的响应。
以及满足:
x[n][n]x[n] x[n][nn1]x[nn1] x[nn1][nn2]x[nn1 n2]
x1[nn1]x2[nn2]x[nn1 n2]
下面分析卷积和的几种运算方法:
从卷积和的表达式:
yf [n] x[n]h[n] x[k]h[n k] k
可知,卷积和也要经过以下四个步骤:
反 折 移 位 相 乘 求 和
第二章 线性时不变系统 (LTI:Linear Time Invarient)
重点: ❖理解并掌握卷积积分与卷积和的概念与相关性质; ❖掌握LTI系统的性质; 难点: ❖深刻理解卷积积分与卷积和的概念;
2.1 线性时不变连续系统的时域解法
连续时间系统处理连续时间信号,通常用微分 方程来描述系统。
❖微分方程的经典解。
若: 0
0 t1
tn t
tn t
n 1
x ( t) ( t t1 ) ( t t2 ) ( t tn 1 ) ( t ti)
i 1
n 1
y ( t) h ( t t1 ) h ( t t2 ) h ( t tn 1 ) h ( t ti) i 1
设x(t)为无时限的信号,将它分解为一系列宽度为 的
4.与冲激函数或阶跃函数的卷积
(1)函数x(t)与单位冲激函数δ(t)卷积的结 果仍然是x(t)本身。即:
x(t)(t)x(t)
证明:
x(t)(t)
x()(t
)d
x()(
t)d
x(t) ( t)d
x(t)
((t) (t))
(2 ) x ( t)( t t0 ) x ( t t0 )
x(t) h1(t)
h2(t) y(t)
(4)卷积的微分:
两个函数卷积后的导数等于其中一函数导数 与另一函数之卷积。即:
( x ( t ) h ( t ) ) x '( t ) ' h ( t ) x ( t ) h '( t )
(5)卷积的积分:
t
t
t
( x () h ()d )x () d h ( t) x ( t) h () d
在离散系统中,由于离散信号本身就是不连续 的序列,对应每个样值序列,每一响应也是一个 离散时间序列,把这些序列叠加即得离散系统的 零状态响应。
离散单位冲激函[数 n]
[n]
1 0
n0 n0
1 [n]
-1 0 1
n
移位的单位冲激[函 n数k]
[n-k]
1 0
nk nk
1 [nk]
…-1 0 1… k
1
y(t)
1(t)dt2t3
t22
4 24
t3时y, (t)0
1 2
0
1 -2+t
t
y(t)
5
16
y(t)的时域波形如图所示:
9
16
1 2
0 13 2
2
3t
例:
x1(t) 1
x2(t) 1
-1
01t
-2
0 2t
求
y1(t)x1(t)*x1(t) y2(t)x1(t)*x2(t)
y1(t)
y2(t)
窄脉冲之和。
x (t )
x(k )
0
k
t
当 0 则: x(t)x(k)..(tk) k
设系统的单位冲激响应为h(t),则系统对应于tk 的
冲激响应为
x(k) ..h(tk)
则系统对输入x(t)的总响应为所有冲激响应之和:
yf(t)x(k)..h(tk) k
当: d,k 求和符号改为积分符号
x(t)x()(t)d
应用类似的推演可以到处卷积的高阶导数或 多重积分之运算规律:
设 y(t)x1(t)x2(t) ,则有: y(i)(t)x1 (j)(t)x2(ij)(t)
此处,当i 、j取正整数时为导数的阶次,取负 整数时为重积分的次数。 一个简单的例子为:
y ( t) x 1 '( t) x 2 ( 1 )( t) x 1 ( 1 )( t) x 2 '( t)
eat ai
Ae at
eat ai i为 i重根
i
A jt je at
j0
L
L
Cktk
A jt j
k0
j0
t
tp cost()
A0+A1t A0+A1t+A2t2+……APtp
B 1 co t s) (B 2 sitn )(
❖系统的零输入响应与零状态响应
一个线性系统可以将系统的响应分解为零输入响应和零 状态响应。即:
k
的响应为 x [ k ]h [ n k ]
k
即:
y f [n ] x[k ]h[n k ]
k
定义将 : yf[n]x[n]h[n]x[k]h[nk] k 称为卷积和。
2 卷积和的性质:
与连续函数的卷积积分的性质类似,离散函数 的卷积和也满足交换律,结合律以及分配律。
( 1 ) 交换 x [n ] 律 h [n ] h [ : n ]x [n ]
( 2 ) 结 ( : x [ n ] h 合 1 [ n ] ) h 2 [ n ] = x [ n ] 律 ( h 1 [ n ] h 2 [ n ] ( 3 ) 分 : x [ n ] ( h 1 配 [ n ] + h 2 [ n ] ) x [ n ] 律 h 1 [ n ] + x [ = n ] h 2 [ n ]
解:
2
2
-2 0
2t
-3
-1 1
3t
例:已知 x(t)eau t(t)
h(t)u(t)
a0
求: y(t)x(t)*h(t)
x( τ )
1
h( τ )
1
t
t
例:已知
x(t) e2tu(t) h(t) u(t 3)
求: y(t)x(t)*h(t)
x()e2u() h()u(3)
1 1
t
3
t
2.卷积积分运算的性质
3u(t 2)3u(t 2)u(t 1)u(t 5)
例:已知 x1(t)e3tu(t) x2(t)u(t 3)u(t 5)
