STL文件上有限元网格的生成
HYPERMESH的一些常见问题的解答

1、如何将.igs文件或.stl文件导入hypermesh进行分网?files\import\切换选项至iges格式,然后点击import...按钮去寻找你的iges文件吧。
划分网格前别忘了清理几何2、导入的为一整体,如何分成不同的comps?两物体相交,交线如何做?怎样从面的轮廓产生线(line)?都用surface editSurface edit的详细用法见HELP,点索引,输入surface edit3、老大,有没有划分3D实体的详细例子?打开hm,屏幕右下角help,帮助目录下hyperworks/tutorials/hyermesh tutorials/3D element,有4个例子。
4、如何在hypermesh里建实体?hm的几何建模能力不太强,而且其中没有体的概念,但它的曲面功能很强的.在2d面板中可以通过许多方式构建面或者曲面,在3D面板中也可以建造标准的3D曲面,但是对于曲面间的操作,由于没有"体"的概念,布尔运算就少了,分割面作就可以了5、请问怎么在hypermesh中将两个相交平面到圆角啊?defeature/surf fillets6、使用reflect命令的话,得到了映射的另一半,原先的却不见了,怎么办呢?法1、在选择reflect后选择duplicate复制一个就可以法2、先把已建单元organize〉copy到一个辅助collector中,再对它进行reflect,将得到的新单元organize〉move到原collector中,最后将两部分equivalence,就ok拉。
7、请问在hypermesh中如何划分装配体?比如铸造中的沙型和铸件以及冷铁,他们为不同材质,要求界面单元共用,但必须能分别开?你可以先划分其中一个部件,在装配面上的单元进行投影拷贝到被装配面上8、我现在有这样一个问题,曲线是一条线,我想把它分成四段,这样可以对每一段指定density,网格质量会比直接用一条封闭的线好。
marc有限元软件-网格生成

3 3 网格生成网格生成(MESH GENERATION)菜单用于建立和/或修改模型的几何形状或有限元模型。
网格生成菜单由以下子菜单和命令构成。
命令说明Mentat 3.1Main Menu ArrayMesh Generation图3.1 网格生成菜单命令说明Mentat 3.1Main MenuMesh Generation 节点(Nodes)在某一特定位置加一个节点。
注意:节点的坐标为当前所定义的坐标系。
缺省设置为总体直角坐标系。
如果GRID按钮被激活,则可以用鼠标在屏幕上直接点节点的位置。
从模型中删除节点。
必须指定一系列要删除的节点。
只有那些与单元没有联系的节点才可以被删除掉。
在删除节点之前一定要先将与其有关联的单元删掉。
对已存在的节点重新定位。
必须选择节点并输入新的坐标值。
显示被选择节点在总体坐标系和用户坐标系下的x、y、z坐标值。
单元(Elements)将单元加到当前的模型中去。
所加单元的类型取决于当前所定义的单元阶次。
选择相应的节点以定义单元的拓扑关系。
定义单元所需的节点数目取决于单元的阶次。
如果GRID按钮被激活,则可以用鼠标来添加单元。
如果选择的几何点上没有定义节点,则节点将会被自动建立。
注意:定义二维单元时必须注意要按逆时针方向在x-y或z-r 平面内选节点。
命令说明Mentat 3.1Main Menu ArrayMesh Generation从模型中删除单元。
必须选择要删除的单元。
重新定义单元中的节点连接情况。
旧节点将从单元中被去除,但仍然保留在模型中。
使用清除节点(SWEEP NODES)命令可以将多余的节点从模型中删除。
使用编辑(EDIT)命令时必须选择要修改的单元以及新的节点号。
显示所选单元的信息。
可以显示单元号、单元阶次、单元类型。
另外单元的节点连接情况也会被显示出来。
几何点(Points)在网格的某一特定位置加一个几何点。
注意:点的坐标为当前所定义的坐标系。
缺省设置为总体直角坐标系。
有限元网格自动生成的典型方法与研究前瞻_张玉峰

第38卷第2期2005年4月武汉大学学报(工学版)Enginee ring Jour nal of W uhan U niver sity Vo l .38N o .2A pr .2005收稿日期:2004-05-11作者简介:张玉峰(1966-),男,甘肃礼县人,博士,副教授,主要从事CAD /CA E 、造型技术研究.文章编号:1671-8844(2005)02-054-06有限元网格自动生成的典型方法与研究前瞻张玉峰,朱以文(武汉大学土木建筑工程学院,湖北武汉 430072)摘要:回顾了有限元网格自动生成的典型方法,分析了这些方法的优缺点,结合当前的研究现状,指出了今后一段时期内,有限元网格自动生成研究的重点和方向.关键词:有限元;网格;自动生成;特征造型;非流形几何造型中图分类号:T B 115 文献标识码:AReview for typical methods of finite element mesh automaticgeneration and research topics in futureZH ANG Yu -feng ,ZH U Yi -wen(Scho ol o f Civil and A r chitec tur al Eng ineering ,W uhan U niver sity ,Wuhan 430072,China )A bstract :This paper first review s the ty pical methods of finite element mesh autom atic generation ,and discusses the advantages and the disadvantages of them .Finally ,acco rding to the current status o f the investig ation ,some research topics are presented .Key words :finite element ;mesh ;auto matic generation ;feature based modeling ;non -m anifold geometricmodeling 有限元法作为一种高效的工程计算与分析方法,已广泛地应用于机械、电子、水利、土木建筑、热传导及电磁学等工程领域.用有限元法进行工程问题分析时,其基本过程大体分为三个阶段:有限元模型的建立和数据输入(即生成有限元模型),用分析软件进行工程计算,分析结果的后处理及评判.有限元分析的主要困难是分析模型的建立,传统的有限元分析模型的建立需要花费大量的时间和精力.根据经验,有限元分析各阶段所用的时间为[1]:40%~45%用于模型的建立和数据输入(即前处理),50%~55%用于分析结果判读和评定(即后处理),而分析计算只占5%左右;而文献[2]指出有限元建模工作量占FEA 工作量的一半以上,甚至达到80%.因此,有限元分析的前后处理长期以来一直成为FEA 的一大瓶颈,严重地阻碍着FEA 技术的应用和发展.有限元网格的自动生成是有限元建模的关键,因此,有限元网格自动生成技术一直是有限元法研究的热门课题之一.目前二维分析域的网格生成算法已经比较成熟,有不少方法已被许多FEA 系统所采用,但三维网格的全自动生成算法还远未成熟,是人们近年来普遍关注的重点研究方向[3-5].本文仅对众多网格生成方法中典型方法的算法思想进行回顾和总结,并结合当前的研究现状提出未来的研究主题.1 有限元网格的要求有限元网格生成是有限元分析的关键环节,生成的网格应满足以下要求[1]:(1)单元之间不能相互重叠;(2)单元要与原物体的占有空间相容,即单元既不能落在原区域之外,也不能在原区域边界内出现空洞; 第2期张玉峰等:有限元网格自动生成的典型方法与研究前瞻(3)单元应尽可能精确逼近原物体;(4)单元的形状合理.每个单元尽量趋近于正多边形或正多面体,不能出现面积很小的二维尖角元或体积很小的三维薄元;(5)网格的密度分布合理,分析值变化梯度大的区域需要细化网格;(6)相临单元的边界相容,即不能从一个单元的边或面的内部产生另一单元的顶点.2 网格生成典型方法回顾网格生成算法的研究已有30多年的历史,国内外研究者先后提出了许许多多网格生成算法.总体来说,若按网格生成方法所产生的单元类型可以分为生成结构化(Construction)网格的方法和生成非结构化(Non-Co nstructio n)网格的方法.若按生成单元的维数不同分为二维平面网格生成法、三维曲面网格生成法和三维实体网格生成法,其中,二维平面网格生成法又可以分为三角形网格生成法和四边形网格生成法,三维实体网格生成法又可以分为四面体网格生成法、五面体网格生成法和六面体网格生成法.若按网格生成的自动化程度可分为手工网格生成法、半自动化网格生成法及全自动化网格生成法.有限元网格生成法难以准确分类,而且目前的网格生成法分类中,对某一具体的网格生成法叫法不一致,如有人将结点连元法叫做填充法,将拓扑分解法叫做结构分解法.本节只对普遍公认的几种典型的有限元网格生成方法作一简要综述和分类.典型的有限元网格生成方法有:结点连元法、Delaunay三角划分法、网格模板法、映射法、拓扑分解法、几何分解法、基于栅格法、前沿位移法、旋转平移法、混合方法等等.2.1 结点连元法结点连元法总的过程是先生成结点,再将结点连接成单元.即在二维、三维形体的边界上和有效区域内按照需要的网格密度变化规律尽量均匀地布点,然后,根据一定的准则将这些点连接成三角形网格(三维中是四面体网格),在二维网格的划分中,最早提出的结点生成法是随机布点法[6].随机布点法先将分析域根据问题的特点划分为若干个子域,每个子域具有一个网格密度控制参数,在各子域以网格密度控制参数为步长分割区域的内外边界先得到边界结点,再对各子域的最小外接长方形以该子域的网格密度参数为步长划分正方形网格,每个正方形方格内随机产生一个内部结点.随机布点法不能保证布点均匀,同时为了确定可用结点,要进行点距检查和多次试探,算法效率低.为此,S haw R D和Pitchen R G提出了更为简单的长方形网格直接布点法[7].用这种方法布点能在子域内生成等边三角形单元.除了这种长方形网格直接布点法外,Lo S H提出了另外一种更简单和直接的等距水平扫描线直接布点法[8].然而,不管是长方形网格直接布点还是等距水平扫描线法直接布点,总会留下一部分不能用固定模式填充的空白地带,为弥补这一缺点,直接布点常用的另一种方法是硬币填充法[9].二维分析域的结点生成后,按一定规则和方法将结点连接成三角形单元,相临三角形单元合并后可以形成四边形单元.形成三角形单元时,Caven-dish J C提出了由外到里,逐层推进的内部结点优选法,该方法先在边界正方向上任选两个相临结点为顶点形成三角形一边,然后在区域边界内的内部结点中采用优选法选择最优的结点作为三角形的另一顶点,从而保证网格的总体形状最优.结点优选法计算量很大,效率不高.Lo S H在利用等距水平扫描线法生成内部结点的基础上采用了一种比较简单的算法生成三角形单元,即网格生成前沿法,与顶点优选法相比它的优点是不再需要检查新生成的三角形是否与已生成的单元相交,而且使生成过程更加稳定.总之,结点连元法形成网格的过程是先布点,后将结点连线生成单元.随机布点法不能保证布点均匀,且点距检查计算耗时效率低,直接布点法中,长方形网格直接布点法和等距水平线扫描法虽然方法简单、算法快速、布点比较均匀,但单一死板,不能避免产生最后剩余的空白地带,硬币填充法布点均匀,能较好地避免产生最后剩余的空白地带.总的来讲,结点连元法的优点是:对于复杂形体适应能力强,与其他方法相比能容易实现网格生成的自动化,所以也有人将该方法直接叫做自动化网格划分方法,此外该方法生成的单元形状良好;缺点是计算量大,效率低.2.2 Delaunay三角划分法这种方法实质上也是结点连元法.Delaunay 三角划分在散乱数据场的可视化、逆向工程、地理信息系统(如地貌的不规则网格建模)、VRM L产55武汉大学学报(工学版)2005品建模等领域都有十分广泛的应用,尤其在有限元网格自动生成方面广为流行.在平面域的Delau-nay三角划分中,理论上已经严格证明,只要给定的结点分布中不存在四点及四点以上共圆时,有最优解,即所有三角形单元中最小内角之和可达到最大值.在Delaunay三角划分后,形成许许多多彼此相连的Voro noi多边形,每个只有一个结点,每一个Voro noi多边形的边实际上就是其内结点与相临Vo ronoi多边形内结点连线的中垂线,所有Voronoi多边形的集合叫做Dirichlet图,连接相临Voronoi多边形内的结点便形成三角形网格.实现Delaunay三角剖分的方法很多,常用的一种算法是逐个插入结点的递归算法.该算法要求生成的Delaunay三角形的外接圆内不允许存在其他结点,若有其他结点,则应局部修改原来的剖分.基本过程为:先构造一个大外接圆,将所有结点都包含进去,然后找出已有三角形中哪些三角形的外接圆内包含新加入的结点,删除这些三角形内离新结点距离最近的一条边,将新结点与周围的老结点连线形成新的三角剖分.除了逐个插入结点的递归算法,在二维Delaunay三角形划分中,Joe采用的方法是先将复杂域分解为凸多边形域[10],再对每个凸域用缩小多边形生成内部结点并形成凸域的Delaunay划分.Sapidis等人用增加边界点的方法来保证边界一定包含在Delaunay三角划分中[11].在三维划分中,若用逐点插入递归算法,将二维情况推广到三维,则采用四面体的外接球内不包含其他点的准则来生成四面体网格.不过应注意一些特殊情况的处理,第一种特殊情况是,新加入的结点恰好落在外接球表面,处理办法是少量摄动新结点位置,再让程序继续运算;第二种特殊情况是四面体的四个顶点接近共面,尽管四个表面的三角形形状良好,但四面体的体积近于0,称其为薄元,必须要消除薄元,方法为:若与薄元四面体相临的两个四面体有公共顶点,则删除该薄元,在薄元所接近的平面内,置换对角线,形成两个新的相临四面体单元;若与薄元相临的四面体的任何两个无公共顶点,采用增加薄元厚度的方法处理[1].若将二维的硬币填充算法扩展到三维形体的情况,就是球填充法[9],同样从边界开始逐层向里铺点,该算法具有灵活的填充能力,可以有效防止薄元的产生,计算效率高.2.3 网格模板法这是目前商品化网格生成器都提供的一种基本功能.该方法要求,首先用交互方式将待分区域划分为若干个形状简单的子区域.每个子域分别用定型的网格模板作出规整的网格剖分,再用补充措施使得相邻子域在结合面上共享公共结点,并且保证网格相容.2.4 映射法映射法出现于20世纪70年代,是最早采用的网格生成方法.从70年代开始应用于商品化系统中,比如FEMG EN.目前映射法在现有的商品化系统中仍占统治地位,它是根据形体边界的参数方程,利用适当的映射函数,将待分区域映射到参数空间中形成规则参数域,对规则参数域进行网格剖分,将参数域的网格(二维是正方形,三维是立方体)反向映射回欧氏空间,从而生成实际的网格.映射法可分为三大类:保角映射法、基于偏微分方程法、代数插值法.三维网格划分的许多方法都是先将形体的表面离散化,所以曲面映射是三维映射的基础.在空间参数曲面网格的生成中,根据曲面边界的性质有单线性映射、双线性映射、三线性映射.映射法的优点是:计算效率高,网格分布均匀,排列整齐,便于直接生成四边形、六面体等高精度单元.但是映射法对于形状较为复杂的形体适应性差,需要将复杂形体事先分解成若干形状简单的子域.子域分解繁琐费时,人工交互多,难以实现全自动化.2.5 拓扑分解法也有人称其为结构分解法,最早由英国剑桥大学的Wordenweber[12]提出,用于二维平面问题,现已推广至三维空间.拓扑分解法,顾名思义就是从形体的拓扑因素着手进行分割,而不过问元素的具体形状.这种方法在保证拓扑结构连续性的基础上每次切下一个三角形单元.当整个形体已被粗分解后,再用对半分割、中心分割、对角线置换等手段进一步作细化分解.拓扑分解法的原理简单,易于处理.但它只从拓扑关系入手,不考虑几何因素,因此难以获得良好形状的单元剖分,也难以应用于含有曲面的三维形体.2.6 几何分解法几何分解法是同时产生结点和元素的方法.该56 第2期张玉峰等:有限元网格自动生成的典型方法与研究前瞻方法较多地考虑了待分域的几何特征.Bykat A最早提出了一种递归对半分割法[13,14],他将每个凸多边形域递归分割成两个子域,并在分割线上按网格密度要求插入一组新的结点,分割的最终结果为三角形网格.为保证递归分割算法的正确性和三角剖分网格的质量,要采取以下措施:第一是先根据网格密度要求生成边界结点,并将边界结点按一定方向顺序连接形成多边形域;第二是若区域非凸,则由程序将其分割成凸多边形;第三是对凸多边形正确选择对半分割边的首末端点.使得凸多边形区域每次都能分割成大致相等的两个子域.文献[15]提供了另一种对半分割算法,据此开发的商用软件T riquamesh被纳入I-DEAS的S upe rtab系统,它可以剖分三维形体.几何分解法由于从几何因素着手划分单元,每次都能得到良好形状的局部结果.因此,该方法单元形状好,但是对复杂区域和不规则形体要分割成简单的子域,人工干预多,效率低.此外,逐层循环分割法只能做到每次取出的单元有优良形状,但不能保证最终剩余的部分是合理的,即空白地带难以解决好.2.7 基于栅格法该算法也叫空间分解法,最早由Thacker, Go nzalez和Putland[16]提出,它是将放置于物体之上,即可在栅格的规则点处布置结点,也可在栅格单元中随机布置结点,容易得到均匀网格,不过在边界处需要对结点位置作适当调整,以满足边界的几何定义.基于栅格的各种算法虽然区别很大,但所产生的网格却是基本类似的,因为内部单元完全一样,只是边界单元有所不同.Ki Kucki N[17]利用矩形栅格产生了以四边形为主体单元,同时含有一些三角形单元的混合型网格.Baehmann等人及Shpitalni[18]分别在提高算法对复杂形体处理的可靠性和减少单元数目方面进行了改进,同时又用八叉树编码法将其推广到三维的情形.特别值得一提的是,他们提出的“修正的八叉树”法容易生成高质量的单元,虽然它的边界单元需要进一步处理以免质量太差,但该法产生的网格具有阶梯结构和空间可访问性,可以实现与实体造形系统的集成,而且易于精整网格质量.缺点是复杂形体的边界单元的质量不易控制.2.8 前沿位移法这种方法的基本思想是将形体的边界向域内移动一段距离,在两个边界之间形成网格单元.在二维划分中Saeed[19]等人讨论了造型中的凸域的位移及其应用于网格的划分,但网格质量较差. Jo hnsto n[20]等人用位移法实现了复杂域的三角划分,其方法是将所有的边界都向域内移动,但该法包含性检查和消除畸形单元比较费时.Taiber t[21]等人用基于环位移法生成四边形网格,该法的基本思想是将一个连续环分解为小环,直到形成四边形.在实现时先对边界位移,再用切分线将内部切分,使得两部分尽可能为矩形,该法的边界离散采用等差数列法.它的不足是不适合狭长形体,多连通域变为单连通域需要加入切割线,形成连续环也要用户指定,难以实现全自动化.在三维网格划分中,Peraire[22]等人的算法是层次性的,先生成边界上的结点,再用二维前沿法生成曲面单元,然后用前沿法生成三维网格,网格密度得到一定的传播.前沿法对非凸域有时会有出现凹陷单元的问题.2.9 扫描法扫描法是将离散化的二维形体进行旋转、扫描、拉伸等操作得到三维网格的一种方法,扫描过程中,扫面断面还可以进行扭曲与变形,形成特殊形状的实体网格.这种方法难度较低,容易实现,在当今大多数商用CAD软件和有限元前置处理软件中均有这种功能.但是这种方法只适于形状简单的三维物体,且主要靠人机交互来实现,自动化程度低.2.10 混合方法上述方法大多对特定形状的分析域有其各自的优势.现实的分析域形状一般都很复杂.具体剖分网格时,可针对具体分析域各部分的几何特性,利用几何变换和拓扑变换,根据情况对各部分分别运用上述算法进行网格生成,再将各个子网格缝合起来而得到最终的网格.这样可以充分利用各算法的优点,得到质量优良的网格,也是今后发展的趋势.现有的全自动网格生成方法在效率、稳定性、通用性等方面与实用要求都有较大差距,在三维情况下尤为突出.二维全自动网格划分已日益成熟,在商品化软件中正逐步取代作为半自动化的映射法的主导地位.但四边形单元的全自动生成比三角57武汉大学学报(工学版)2005单元的全自动生成更加困难.目前的算法中仅有少数可生成四边形单元.三维全自动网格划分要在商用软件中占主导地位,还要待以时日.关键在于开发可靠、高效的划分方法,这有待进一步的研究和发展.3 有限元网格自动生成的研究前沿理想化的有限元网格生成方法应具有以下功能特点:(1)自动化程度高.最好实现全自动化,无需任何人工干预.(2)单元形状和整体网格形状最优.如单元最好是等边三角形、正方形、正四面体、立方体等等,三角形网格中所有单元最小内角之和达到最大值.不存在细长尖角、薄体元等畸变单元.(3)网格密度易于控制,网格疏密过渡均匀.(4)算法效率高,速度快.(5)通用性强,可以划分任意形状的单元网格,对任何形状分析域都有很强的适应性.(6)程序可靠、稳定.(7)能实现自适应网格剖分.(8)有利于和CAD造型软件、优化分析软件等的集成.但要达到上述功能很困难,所以,有限元建模技术将是一个漫长的发展过程.其中,有限元网格生成的全自动化、提高计算精度是有限元分析研究的两大主题.目前,有限元模型自动生成的前沿及发展趋势如下:(1)能够直接将CAD造型系统提供的具有完备几何信息和非几何信息的特征模型自动转换成有限元模型.目前的有限元建模技术不能满足这一要求.由于CAD设计模型和有限元分析模型在表达模型的侧重点上有很大的不同,二者之间存在联系的沟壑.从设计模型进行有限元模型的抽象,需要模型的细节编辑和减维操作.细节编辑即将形体中对特定分析问题来说无需关注、不太重要的细节(如小孔、圆角等)简化或去除,这将大大提高网格生成的速率和质量;减维操作就是对设计模型中的部分或全部区域降低维数,从而减小有限元分析的复杂度及规模.目前的造型系统尚不具备这种功能.特征造型技术的发展为二者的无缝集成提供了实现的基础.(2)非流形几何造型技术在有限元自动建模中的应用研究.在基于特征的有限元自动建模中,属性定义和减维操作后自然会产生具有悬边、悬面、孤点的混合维模型.因而,基于特征的非流形几何造型技术的研究对实现有限元模型的自动生成具有十分重要的意义.目前的研究尚不深入.(3)网格生成的全自动化.现有的全自动网格生成方法在效率、稳定性、通用性等方面离要求都有不少差距,特别是三维网格的生成更是如此.二维网格的全自动生成已日趋成熟,三维网格的全自动生成是未来研究的重点.此外,基于特征的非流形混合维网格的全自动生成将是长期研究的重大课题.(4)网格精整优化技术.要提高有限元的计算精度,在现有技术基础上需要进一步进行网格精整措施的研究.目前,各种方法自动生成的网格单元受其边界条件的制约较大,尽管可以通过单元光滑法和单元修正技术进行调整,但在复杂区域和复杂边界时这是有限的,因此,如何进一步提高生成单元的精度仍是有限元前处理中的重要课题之一.(5)网格密度控制技术.网格密度控制是网格自动生成的一个难点,要解决如下问题:如何合理定义网格密度;如何自适应地控制网格;如何控制生成的网格接近正则单元,并且使其平滑过渡.(6)网格剖分自适应技术.在对工程结构进行力学分析时,人们事先并不知道应力集中程度及其位置,只能凭借以往的经验,在自己认为应力梯度大的地方将网格划分得密一些.而有限元网格自适应技术通过有限元计算结果的后误差分析,重新划分有限元网格,使得在控制误差允许范围内,以最少的自由度获得最优的计算结果,避免应力梯度大的地方网格密度过小,或应力梯度小的地方网格过密.有限元网格自动调整技术依然是未来研究的重要方向.但计算结果的误差估算是实现自适应技术的一个难点,各个领域中分析的问题不同,误差估算也不一样.(7)有限元自动建模中的人工智能和专家系统.合理而高效地建立有限元模型需要依靠计算力学专家和工程技术人员长期积累的知识和经验,若引入专家的经验,建立知识库,采用专家系统实58 第2期张玉峰等:有限元网格自动生成的典型方法与研究前瞻行知识推理机制和人工智能将大大提高有限元自动建模的效率和提高模型的正确性.(8)三维网格的可视化及正确性的检测.目前,三维网格缺乏有效的可视化技术.现有的可视化手段都不能较好地显示三维网格的正确性,因而三维网格正确性检测显得十分重要,但目前尚无有效方法.(9)造型系统、有限元网格自动生成、自适应分析技术的集成.4 结束语有限元网格的全自动生成是有限元建模中的关键,也将是长期研究的热点课题.相信随着FEA技术的发展,采用特征造型技术、人工智能和专家系统等多种技术的交叉综合应用,必将取得较大的发展.参考文献:[1] 唐荣锡.CA D/CA M技术[M].北京:北京航空航天大学出版社,1994.[2] Benny Raphael,K rishanmoo rthy C S.A uto mating fi-nite element development using object oriented tech-niques[J]puta tion,1993,10:267-278. [3] 李笑牛,赵 伟.六面体有限元网格生成方法综述[J].大连民族学院学报,2003,5(3):1-2.[4] 雷永刚,卫原平,阮雪榆.三维有限元网格自动生成典型方法与发展方向[J].机械科学与技术,1999,18(2):311-313.[5] 汤劲松,油新华.空间有限元网格自动生成算法的初步研究[J].石家庄铁道学院学报,2000,13(4):71-74.[6] Cavendish J C.A utoma tic triangulation of arbitraryplanar domains fo r the finite element method[J].In-ternatio nal Jo urna l fo r Numerica l M e tho ds in Eng i-neering,1974(8):679-696.[7] Shaw R D,P itchen R G.M o dificatio ns to the Suha-ra-F ukuda me thod of netwo rk ge nera tion[J].Inter-na tional Jour nal fo r Numerical M e tho ds in Engineer-ing,1978(12):93-99.[8] Lo S H.A new mesh genera tion scheme fo r arbitraryplanar domains[J].Inte rnational Jour nal f or N umeri-cal M ethods in Enginee ring,1985(21):1403-1426. [9] 刘剑飞.有限元前置处理的研究与实现[D].北京:北京航空航天大学,1991.[10]Ba rry Jo e.Te trahedr al mesh g ener atio n in po ly hedralreg io ns based o n co nv ex po ly hedro n deco mpo sitio ns[J].I nter na tional Journal fo r Numerica l M ethods inEng ineering,1994,37(4):693-713.[11]Sapidis,Renato Pe bining recur sive spa-tia l decom po sition's and do main delaunay te trahedr iza-tio ns fo r meshing arbitrarily shaped curv ed so lid mod-els[J].Comp.M e th.in applied mech.and Eng.,1993,108:281-302.[12]W ordenw eber B.Finite element me sh ge nera tion[J].CA D,1984,16(5):285-291.[13]By ka t A.A uto matic g ene ratio n of tria ng ular g rid:Ⅰ—subdiv isio n o f a general polyg on into co nve x sub-reg io ns.Ⅱ—t riangula tion o f convex poly g ons[J].Int.J.N umer.M eth.Eng.,1976,10:1329-1342.[14]By kat A.Desig n of a recur siv e shape contro llingmesh g ener ator[J].Int.J.Numer.M e th.Eng.,1983,19:1375-1390.[15]Sluiter M L C,Hansen D L.A general purpose auto-matic mesh genera to r fo r shell and solid finite ele-ments[J].Co mputer s in Enginee ring ASM E,1982,3:29-34.[16]T hacke r W C,et al.A method for auto mating theco nstructio n o f ir regular computatio nal grids fo rsto rm surge fo reca st models[J].Journal of Computa-tio na l Phy sics,1980,37:371-387.[17]Jose M iranda g uides,N obo ru ki kuchi.P reprocessingand po stpr ocessing fo r materials ba sed o n the ho mog-eniza tion me tho d with adaptive finite eleme nt metho ds[J].N um.M e th.in A pplid M echanics and Eng.,1990,83:143-198.[18]Shpitalni M.Finite element mesh ge nera tion viaswitching function representatio n[J].Finite Eleme ntin A naly sis and Desig n,1989,5(2):119-130. [19]Jeffrey T alber t,Alan R P arkinson.Develo pment ofan automa tic two-dimensio nal finite element meshg ene rator using quadrilater al e lements and Beziercurve bounda ry definitio n[J].Int.J.N um.M eth.Eng.,1990,29(7):1551-1567.[20]Johnston B P,Sullivan J M.Fully automatic two dimen-sional mesh generation using no rmal offsetting[J].Int.Journal Num.M eth.Eng.,1992,33(2):425-442. [21]Ta lbert J A,P arkinson A R.Develo pment o f an au-toma tic two dimensio nal finite element mesh g ener a-to r using quadrilater al elements and Bezie r curveboundar y definitio n[J].I nt.J.N um.M eth.Eng.,1990,29(7):1551-1567.[22]P eraire R,e t al.Finite element Eule r co mputations inthr ee dimensions[J].I nt.Jour nal.Num.M eth.Eng.,1998,26(10):2135-2159.59。
有限元设计软件生成网格的PAVING算法
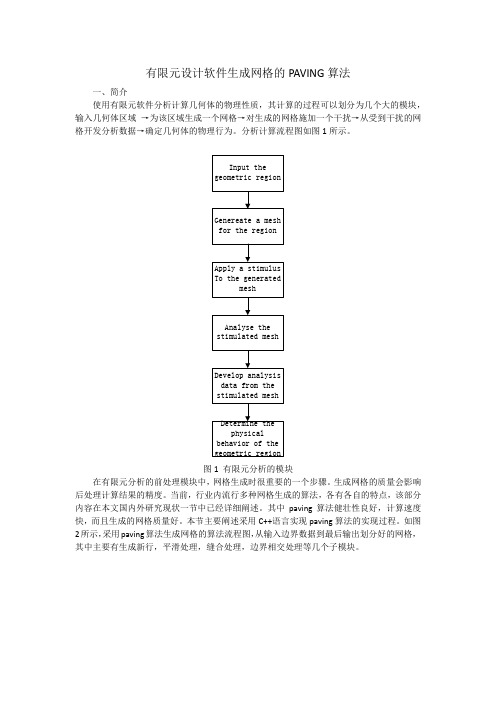
有限元设计软件生成网格的PAVING算法一、简介使用有限元软件分析计算几何体的物理性质,其计算的过程可以划分为几个大的模块,输入几何体区域→为该区域生成一个网格→对生成的网格施加一个干扰→从受到干扰的网格开发分析数据→确定几何体的物理行为。
分析计算流程图如图1所示。
图1 有限元分析的模块在有限元分析的前处理模块中,网格生成时很重要的一个步骤。
生成网格的质量会影响后处理计算结果的精度。
当前,行业内流行多种网格生成的算法,各有各自的特点,该部分内容在本文国内外研究现状一节中已经详细阐述。
其中paving算法健壮性良好,计算速度快,而且生成的网格质量好。
本节主要阐述采用C++语言实现paving算法的实现过程。
如图2所示,采用paving算法生成网格的算法流程图,从输入边界数据到最后输出划分好的网格,其中主要有生成新行,平滑处理,缝合处理,边界相交处理等几个子模块。
图2 Flow chart of paving algorithm为了清晰理解上述paving算法的流程,以图3所示为例,图a当中为输入的原始外边界数据,围成待划分网格的区域。
选择边界上的一行节点为基础,添加生成一行新的浮动节点,生成顺序为沿着外边界按逆时针方向进行。
对新生成的浮动节点进行平滑处理,使节点围成的单元的internal angle以及aspect ratio变得更为合理,单元更趋近于规则四边形。
对剩余的待划分网格区域进行缝合,检查单元是否相交,对相交的单元进行处理,对单元进行调整,直到整个区域生成高质量的网格为止。
图3 paving算法铺筑单元示意图依据图2所示流程图,生成相应的伪代码:DoRow choiseWhile add row is not completeAdd row portionSmooth row portionSeam boundaryIf intersection occurs thenConnect overlapsSeam boundaryEnd ifRow adjustmentIf intersection occursConnect overlapsSeam boundaryEnd ifWhile (closure check is negative)Clean-up mesh二、分部详细说明1.输入边界数据根据算法的流程图中,首先要输入待划分网格的边界数据,确定区域的内边界和外边界。
有限元的网格划分技术

有限元的网格划分技术对于有限元分析来说,网格划分是其中最关键的一个步骤,网格划分的好坏直接影响到解算的精度和速度。
网格化有三个步骤:定义单元属性(包括实常数)、在几何模型上定义网格属性、划分网格。
定义网格的属性主要是定义单元的外形、大小。
单元大小基本上在线段上定义,可以用线段数目或长度大小来划分,可以在线段建立后立即声明,或整个实体模型完成后逐一声明。
采纳BottOm-UP方式建立模型时,采纳线段建立后立即声明比较便利且不易出错。
例如声明线段数目和大小后,叁制对象时其属性将会一•起夏制,完成上述操作后便可进行网格化命令。
网格化过程也可以逐步进行,即实体模型对象完成到某个阶段就进行网格话,如所得结果满足,则连续建立其他对象并网格化。
网格的划分可以分为自由网格(free meshing)、映射网格(mapped meshing)和扫略网格(SWeeP meshing)等。
一、自由网格划分自由网格划分是自动化程度最高的网格划分技术之一,它在面上可以自动生成三角形或四边形网格,在体上自动生成四周体网格。
通常状况下,可采用ANSYS的智能尺寸掌握技术(SMARTSIZE命令)来自动掌握网格的大小和疏密分布,也可进行人工设置网格的大小(AESIZE、LESIZE、KESIZE、ESIZE等系列命令)并掌握疏密分布以及选择分网算法等( MOPT 命令)。
对于简单几何模型而言,这种分网方法省时省力,但缺点是单元数量通常会很大,计算效率降低。
同时,由于这种方法对于三维简单模型只能生成四周体单元,为了获得较好的计算精度,建议采纳二次四周体单元(92号单元)。
假如选用的是六面体单元,则此方法自动将六面体单元退化为阶次全都的四周体单元,因此,最好不要选用线性(•阶次)的六面体单元(没有中间节点,比如45号单元),由于该单元退化后为线性的四周体单元,具有过大的刚度,计算精度较差;假如选用二次的六面体单元(比如95 号单元),由于其是退化形式,节点数与其六面体原型单元全都,只是有多个节点在同一位置而己,因此,可以采用TCHG命令将模型中的退化形式的四周体单元变化为非退化的四周体单元(如92号单元),削减每个单元的节点数量,提高求解效率。
STL文件上有限元网格的生成

STL文件上有限元网格的生成摘要:这些被提议的方法的是为了展示一个适合有限元方法的且关于物体近似边界表示的直接由CAD软件生成的曲面网格产生的可能性。
首先,我们将描述由一个简单的物体表面三角剖分组成的边界表示法。
接着我们将展示如何获得一个相容的形状适应网格。
形状适应是考虑到几何逼近和由一个误差估计量的各向同性的尺寸映射做出的。
网格可以被用来用于有限元计算(通过壳体元素),或者可以用来作为一个启动体积网格算法(Delaunay 或advancing front)曲面的网格。
这个用来产生网格的原则是基于与求精算法相关的Delaunay 方法和光滑化原则。
最后,我们将展示不用用于克服常规的基于一个几何特定表示法的网格化软件的限制的几何模型的参数表示法。
关键字:网格产生;STL文件格式Bisection算法;Delaunay 三角剖分。
1.CAD接口1.1基于CAD的数据集市面上的大多数CAD软件可以产生STL文件,且这些大体上用作实现样机研究和绘制图形的目的。
这些文件表现了立体的三角剖分的边界。
STL三角剖分的生产算法都是高效的,而且如果可以接受大规模数据集的话平面可以被精确地逼近。
但是,这不是一个真正几何模型是因为STL文件格式仅由一个扩展的三角平面列组成。
这些小平面除了一般立体外部定向的座标外,还由三个三角顶点座标组成。
这种三角剖分法是建立用来最小化一个关于立体(图1)真实边界的几何逼近准则的。
(见图1)1.2 STL三角剖分的特性STL三角剖分不能直接用在有限元方法(FEM)中,主要是因为它要求在计算域的几何描述上的特殊性。
在FEM中,几何和函数支持由元(三角形或其他)提供,且它们必须有一特殊形状,也就是就计算误差估算量的固有大小和固有品质因子应该越低越好。
在这项工作中,我们利用如下三角形的品质因子,在此di,i=0…2代表三角形每边的长度。
我们假定:品质因子就是:这个品质因子在0(对于所有退化三角形而言)和1(对等边三角形而言)之间。
marc有限元软件-网格生成

3 3 网格生成网格生成(MESH GENERATION)菜单用于建立和/或修改模型的几何形状或有限元模型。
网格生成菜单由以下子菜单和命令构成。
命令说明Mentat 3.1Main Menu ArrayMesh Generation图3.1 网格生成菜单命令说明Mentat 3.1Main MenuMesh Generation 节点(Nodes)在某一特定位置加一个节点。
注意:节点的坐标为当前所定义的坐标系。
缺省设置为总体直角坐标系。
如果GRID按钮被激活,则可以用鼠标在屏幕上直接点节点的位置。
从模型中删除节点。
必须指定一系列要删除的节点。
只有那些与单元没有联系的节点才可以被删除掉。
在删除节点之前一定要先将与其有关联的单元删掉。
对已存在的节点重新定位。
必须选择节点并输入新的坐标值。
显示被选择节点在总体坐标系和用户坐标系下的x、y、z坐标值。
单元(Elements)将单元加到当前的模型中去。
所加单元的类型取决于当前所定义的单元阶次。
选择相应的节点以定义单元的拓扑关系。
定义单元所需的节点数目取决于单元的阶次。
如果GRID按钮被激活,则可以用鼠标来添加单元。
如果选择的几何点上没有定义节点,则节点将会被自动建立。
注意:定义二维单元时必须注意要按逆时针方向在x-y或z-r 平面内选节点。
命令说明Mentat 3.1Main Menu ArrayMesh Generation从模型中删除单元。
必须选择要删除的单元。
重新定义单元中的节点连接情况。
旧节点将从单元中被去除,但仍然保留在模型中。
使用清除节点(SWEEP NODES)命令可以将多余的节点从模型中删除。
使用编辑(EDIT)命令时必须选择要修改的单元以及新的节点号。
显示所选单元的信息。
可以显示单元号、单元阶次、单元类型。
另外单元的节点连接情况也会被显示出来。
几何点(Points)在网格的某一特定位置加一个几何点。
注意:点的坐标为当前所定义的坐标系。
缺省设置为总体直角坐标系。
第3章:几何实体模型生成网格模型

中南大学
第3章
生成有限元网格模型
中南大学
弹性模量
泊松比
在材料属性对话框窗口的左边,同样用树型结构文件夹方式显 示已经定义的参数的材料,默认的时候会有材料1,要添加、删除 或者拷贝相近的材料,使用材料特性窗口的菜单命令。需要修改材 料特性的时候,可以双击要修改的材料文件夹,选择其中所定义的 特性,双击进行修改。
第3章
生成有限元网格模型
中南大学
二次单元假定位移是二阶变化的,因此单元上的应变、应 力是线性变化的。 P-单元的位移可以在2~8阶间选择,而且具有求解收敛精 度自动控制功能。在许多情况下,同线性单元相比,采用高阶 类型的单元可以得到更好的计算结果。细的说明。 进入帮助文档有2种方法: (1)单击工具栏中的 (2)通过应用菜单Help进入 按钮
定义了单元类型后,ANSYS会自动生成一个与此单元类型 对应的单元类型参考号,如果模型中定义了多种单元类型,则 与这些单元类型相对应的类型参考号组成的表称为单元类型表。 在创建实际单元时(直接创建单元或者划分网格),需要从单 元类型表中为其分配一个类型参考号以选择对应的单元类型生 成有限元模型。
第3章
第3章 3.2 划分网格
生成有限元网格模型
中南大学
网格划分是建模中非常重要的一个环节,它将几何模型转化 为由节点和单元构成的有限元模型。网格划分的好坏将直接影 响到计算结果的准确性和计算速度,甚至会因为网格划分不合 理而导致计算不收敛。 网格划分主要包含以下3个步骤: (1)分配单元属性 包括单元类型、分配实常数或者截面属性(对有些单 (1)分配单元属性 分配单元属性(
元类型)、分配材料属性等); ;
(2)设定网格尺寸控制和网格形状(可选择的,由ANSYS确定单元尺 (2)设定网格尺寸控制和网格形状
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
STL文件上有限元网格的生成摘要:这些被提议的方法的是为了展示一个适合有限元方法的且关于物体近似边界表示的直接由CAD软件生成的曲面网格产生的可能性。
首先,我们将描述由一个简单的物体表面三角剖分组成的边界表示法。
接着我们将展示如何获得一个相容的形状适应网格。
形状适应是考虑到几何逼近和由一个误差估计量的各向同性的尺寸映射做出的。
网格可以被用来用于有限元计算(通过壳体元素),或者可以用来作为一个启动体积网格算法(Delaunay 或advancing front)曲面的网格。
这个用来产生网格的原则是基于与求精算法相关的Delaunay 方法和光滑化原则。
最后,我们将展示不用用于克服常规的基于一个几何特定表示法的网格化软件的限制的几何模型的参数表示法。
关键字:网格产生;STL文件格式Bisection算法;Delaunay 三角剖分。
1.CAD接口1.1基于CAD的数据集市面上的大多数CAD软件可以产生STL文件,且这些大体上用作实现样机研究和绘制图形的目的。
这些文件表现了立体的三角剖分的边界。
STL三角剖分的生产算法都是高效的,而且如果可以接受大规模数据集的话平面可以被精确地逼近。
但是,这不是一个真正几何模型是因为STL文件格式仅由一个扩展的三角平面列组成。
这些小平面除了一般立体外部定向的座标外,还由三个三角顶点座标组成。
这种三角剖分法是建立用来最小化一个关于立体(图1)真实边界的几何逼近准则的。
(见图1)1.2 STL三角剖分的特性STL三角剖分不能直接用在有限元方法(FEM)中,主要是因为它要求在计算域的几何描述上的特殊性。
在FEM中,几何和函数支持由元(三角形或其他)提供,且它们必须有一特殊形状,也就是就计算误差估算量的固有大小和固有品质因子应该越低越好。
在这项工作中,我们利用如下三角形的品质因子,在此di,i=0…2代表三角形每边的长度。
我们假定:品质因子就是:这个品质因子在0(对于所有退化三角形而言)和1(对等边三角形而言)之间。
当然,这些要求是和应用相关的。
比如,在流体力学中很普遍地应用在边界层的各向异性元和冲激波当中。
很显然一个由最小化几何准则得到的网格不能适合FEM的要求,因为它依赖于表面的的曲率和拓扑,且生成的三角形在某方向上会大大伸长(见图2-4)。
但是,得到的网格一般都是一致的。
1.3 STL网格中的几何恢复STL文件内容包含每个三角形顶角座标和相应法线。
为了达到曲面的完全网格化,我们需要获得关于被网格化曲面的拓扑和曲率的有关数据。
三角形间的拓扑和连通度可以通过避免在STL文件间的顶角冗余得到。
这可以通过利用一个利用字典法排序和储存了的顶角的二叉树做出的。
在这个过程结束时,我们得到了一物体表面的网格及所有类型的可被重新网格化所需的连通度,特别是用来作邻接查找的连通度(见小节三)。
由于许多工业制品有棱与边,我们需要决定它们定位的位置。
这可以通过一个边测定程序考查在三角剖分中的实体间的连通度得到。
在保持它们原貌以用于重新网格化的过程中模型边的查找显得十分重要。
也就是说它们不能被Delaunauy重新网格化法切割。
这种查找是基于邻接三角形的角的计算。
两三角形的公共部分被认为是一个边,如果在此两个三角形的法向量间的角比一个特定的值(一般为20。
)大的话。
另外还应该注意的是我们可以处理诸如在一个集合(比如为了应用边界条件)中的两个不同部分间的接触部分的面积。
这些部分将被认为是边,且将被保留在最后的网格中(图5)。
接着曲率通过寻找其它与之连接的三角剖分的每个元素来求值且检查它们的法向量(图6)。
接下来的程序是用来:对于每个三角形Ti,我们在它的三个顶点(Vj(j=0…2)进行迭代。
在每个顶点,有两个边Sjk(k=0…1),与之相关的三角与Ti,Tjk邻接。
如果Sjk是个陡沿,我们定义一个变量r jk为0;不然就是1。
曲率C Tt通过下式计算出来:θj是在Sj0和Sj1间的角,θ’ j是法向量Tj0和Tj1间的角。
在这之后,曲率在每个项点V i外推(Cvi),应用连接Vi的n个三角形的最大曲率:我们应该注意到在这里考虑的曲率是关于曲面的曲率张量范数(也就是说我们不用在意曲率产生的效应方向),要注意到得到的曲率不是十分准确的。
这是因为几何曲面表示(平面集)是离散。
实际上,这些曲率不仅驱动一任选网格的细化。
在较少弯曲平面上的结果是粗糙的,在其它地方可得到改善。
图六描绘了利用上面提到的公式得到的一个穿过每个三角形的线性插值的结果。
在这方面,我们需要的用于网格生成的程序的信息是关于目标网格的各向同性尺寸映射的信息。
既然这不是当前研究工作的目的,我们假定或者常尺寸映射是由用户提供的,或者一个尺寸映射是基于一个已被提供的误差估计量(从先前的FEM算得)。
我们也考虑当密度映射是基于一个几何准则(控制在STL网格和三角剖分间的最大距离)的情形,描述在2.5节。
2. 细化方法网格三角形是通过缩减尺寸比率(在真实大小和目标大小之间的比率)来分类的。
最差三角形(最大的)是第一个用Bisection算法在2.1部分处理的。
在每个阶段,排序一直在更新(因为总有新三角产生且一些已经毁坏了)且处理可以一直持续直到所有三角形都无法符合准则。
当所有的三角形符合准则时,我们应用一个光滑程序。
最终网格将准备用来处理FEM(见小节三)。
2.1Bisection算法新垂直线是在平分已经在网格上存在的一个线段上生成的。
垂直线在线段中部生成,线段也不必成为曲面的一部分。
垂直线然后必须插入网格且投影到一个初始STL网格上(图7,8)。
我们将用来生成顶点的线段可以应用以下从参照9中的算法中找到。
首先,我们寻找上面已定义的用于细化的与目标大小最无关系的三角形T,接着我们寻找包含有一边长于T的路径。
这些定义了一个序列(Ti)。
让Sn为三角形Tn最长的线段。
三角形Tn+1与Tn沿着它最长的线段Sn相邻。
当Sn 和Sn+1是相同的线段时序列停止。
序列当然在T0=T时开始。
首先用来二等分的线段是在序列(Si)中的最后的线段。
算法一直重复到我们考虑的第一条线段,即二等分了的S0。
这导致了一准确的面积的加细(图9,10)。
2.2 关于Delaunay准则在每次二分之后,曲面将被局部地处理以达到更好的正则性。
这可以通过遵循著名的关于2D网格的Delaunay准则完成。
但是,我们正在处理曲面因而常规的Delaunay准则要改变。
为了处理曲面的曲率和它的离散表示实际上是必要的。
让我们回到在两维情况下关于Delaunay三角剖分的原始定义[4,5,6]。
定义一:空圆特性:让T为一个顶点集S的凸面的任意三角剖分。
如果空圆的特性已经对每个三角形T的两相邻三角形的每个布局作了检验,这意味着这已经对整个三角剖分作了检验。
三角剖分T被认为是一个Delaunay相容三角剖分。
考虑到它们的曲率话,定义可以被用来匹配曲面。
如果我们改变了度量的定义,Delaunay 准则仍然是有效的[2,6],这点十分重要。
我们应该考虑外接圆的一个新的定义。
在这个情况下,外接圆是曲面所有点的存储单元,这些点它们到中心的曲线距离也就是半径是一样的。
曲线距离是通过积分计算出来的。
在参数空间(如果它能局部被地被认为是常量)上,半接圆的映射如上被定义为一个椭圆。
不幸的是,仅通过STL三角剖分知道曲面,这样的参量化不能很好定义。
我们打算应用另一个准则,当然不能够比前一个准则精确,但是对于在三角形旁的拓扑测试来说已经足够好了。
这组成了由参照八定义二和三的基础。
定义二:空圆的特性:让Ts成为位于曲面上的顶点集S凸面的一个任意三角剖分。
如果空接球的特性可由三角剖分Ts的两个邻接三角来检验。
那么Ts被认为是一个弱Delaunay相容三角剖分。
定义三:另外,如果空球特性可通过全三角剖分来检验,那么Ts被认为是在曲面上的一个强Delaunay相容三角剖分。
定义四:一个三角形的外接球是和外接圆有一样相同中心和相同直径的球体。
我们注意到三角剖分是弱Delaunay相容且在定义二中一般不遵循在全曲面上的空球准则。
它们在定义三上并不是强Delaunay相容的。
在只处理曲面网格时这并不困难,但是如果后来我们要用一个3Ddelaunay方法产生一个体积网格,一些三角形将最后被切割成如[8]的样子。
如果我们处理平面几何,定义2成了无条件限制的定义一,我们可以断定在这种情况下,三角剖分是Delaunay相容的,在定义2中是弱Delaunay相容的。
在定义2中,距离是在3维欧几空间中测量的。
因此,除了用一个准确的Delaunay准则来测定一个交点,我们只有当它不在位于交点附近的三角形的外接球内的情况下可以检验它。
这种相邻性是与网格的拓扑有关的。
事实上,在三角形之间的连通关系定义了其相邻性(壳概念,[6])(图11,12)。
局部重啮合法是基于对角线交换[1]的。
用于交换的对角线是通过查找与变址Delaunay 准则有关而与新顶点无关的三角形决定的。
我们完成了由前先找到的三角形组成的顶点域上的一种“星式”重网格化算法法。
这就是“Watson”算法[11]。
为了防止弱几何逼近的产生,查找与变址Delunay准则无关的三角形是只在方向没有极大不同于在新顶点即时邻接的三角形的方向的三角形上完成的,一般地15。
到60。
之间的差异是正常的(图13,14)。
为了防止物体边缘的破坏,在如上1.3节定义的在算法中交换属于边缘的线段序列是不允许的。
图十三到十六展示了在们于初始网格化步骤间的曲面逼近临界角的效果。
如预计的,那些边缘没有破坏。
事实上三角形并不都与变址Delaunay准则相关,这并不是问题,是因为初始STL网格将被优化。
确切地说,从优化了算法的一些点上,三角形并不与变址Delaunay准则有关将不被考虑,这是因为在那点上三角形间方向之间的不同将小于临界角。
在优化步骤的后期,三角剖分将是弱Delaunay相容的。
这是配合在[9]中描述的曲面算法的关键。
2.3投影算法我们在图十五可以看Delaunay重网格化导致了弱几何逼近。
经常地,当我们在并不是一个初始STL网格的线段上产生一个交点,这并不是位于原始STL模型上的。
因而,当我们需要一个投影算法用于在由初始STL三角剖分描述的曲面上重定位交点。
这种操作是需要消耗时间的,这是因为在顶点将被投影的初始STL网格上的目标三角形不能预先知道。
一邻接查找算法可用来防止检验所有的在初始STL网格上的三角形。
这个算法在当用于网格化的以非常小体积为特点的立体上是非常有用的(见样例3.4:交叉存取四面体)。
我们应当避免属于内表面到到外表面的交点投影。
投影算法是基于每个新交点是在一线段上产生的事实(归因于Bisection算法)。
事实上,当一个新的交点产生的地方我们已知道STL三角形。
