用直角三角形构造勾股定理的证明
三角形勾股定理证明方法

勾股定理是一个基本的几何定理,它指出直角三角形的两条直角边的平方和等于斜边的平方。
以下是几种常见的勾股定理证明方法:
1. 拼接证明:将两个直角三角形拼接成一个矩形,然后利用矩形的性质来证明勾股定理。
2. 边长比例证明:利用相似三角形的性质,通过边长比例来证明勾股定理。
3. 辅助圆证明:以直角三角形的直角顶点为圆心,直角边为半径作圆,然后利用圆的性质来证明勾股定理。
4. 面积合成证明:将直角三角形与两个小三角形组合成一个大三角形,然后利用大三角形的面积公式来证明勾股定理。
5. 鞋带公式证明:利用高斯面积公式(即鞋带公式)来证明勾股定理。
6. 行列式证明:利用二阶行列式的性质来证明勾股定理。
7. 切割定理证明:通过将直角三角形切割成两个小三角形,然后利用切割定理来证明勾股定理。
8. 无穷级数证明:利用极限定理和无穷级数的性质来证明勾股定理。
以上是几种常见的勾股定理证明方法,每种方法都有其独特的思路和证明步骤。
在实际应用中,可以根据具体情况选择适合的方法来进行证明。
勾股定理证明方法大全

勾股定理证明方法大全
勾股定理是数学中比较基础的内容,下面介绍几种证明方法: 1. 几何证明法
构造直角三角形ABC,其中∠ABC=90度,AB=c,AC=a,BC=b,则根据勾股定理,有:
c = AB + AC
即:
c = a + b
这个方法是最常见的证明方法,也是最直观的。
2. 代数证明法
将勾股定理转化为代数式,如下所示:
设直角三角形的两条直角边分别为a和b,斜边为c,则根据勾股定理,有:
c = a + b
将c用另一种方式表示,如下所示:
c = sqrt(a + b)
将c代入原式,并进行平方操作可以得到:
c = a + b
因此,勾股定理成立。
3. 数学归纳法
首先,在直角三角形中,当一条直角边为0时,另外两条直角边的长度必然相等,而且都为0,勾股定理显然成立。
接下来,假设当直角边长为n时,勾股定理成立,即:
c = a + b
考虑当直角边长为n+1时,如何证明勾股定理仍然成立。
此时,可以将直角边长为n+1的直角三角形划分成以一条边长为n的直角三角形和一个长度为1的小直角三角形。
根据勾股定理,前者的斜边平方和等于两直角边平方和,后者的斜边平方就是1。
组合起来就得到:
(c + 1) = a + b + 1
即:
c + 2c + 1 = a + b + 1
移项可得:
c = a + b
因此,当直角边长为n+1时,勾股定理仍然成立。
根据数学归纳法,勾股定理对所有正整数均成立。
几种简单证明勾股定理的方法

几种简单证明勾股定理的方法勾股定理是一个著名的数学定理,它描述了直角三角形三条边的长度之间的关系。
下面是几种简单证明勾股定理的方法:方法一:特例验证法对于任意一个直角三角形,我们可以列出它的两条直角边的长度的平方和,以及斜边的长度的平方,验证它们是否相等。
例如,对于一个直角边分别为3和4的直角三角形,我们可以计算出它的斜边的长度为5,然后验证3²+4²=5²。
这种方法虽然简单,但是只适用于特例,不能推广到一般情况。
方法二:几何构造法将两个大小相同的直角三角形放在同一直线上,使得它们的斜边成为一条直线。
这时,我们可以证明两个三角形的面积之和等于底边长度之和的两倍。
由于两个三角形面积相等,因此可以得出底边长度之和等于斜边长度。
例如,对于两个直角边分别为a和b的直角三角形,它们的斜边长度分别为c,将它们放在同一直线上,使得它们的斜边成为一条直线。
可以证明两个三角形的面积之和等于底边长度之和的两倍,即ab/2+ab/2=c²/2。
因此,可以得出a²+b²=c²。
方法三:代数推导法通过代入特殊值的方式,可以得到勾股定理的公式。
例如,当直角三角形的两条直角边分别为3和4时,可以得出斜边的长度为5,然后代入公式3²+4²=5²得到验证。
这种方法虽然简单,但是只适用于已知直角三角形两条直角边长度的特殊情况。
方法四:平方法通过平方法证明勾股定理的思路是:将直角三角形的一条直角边平移到斜边所在的直线上方,与斜边重合。
这时,可以将直角三角形的一条直角边看作是斜边减去一条直角边的长度所得的差,因此可以得出斜边的平方等于两条直角边的平方和。
例如,对于一个直角边分别为a和b的直角三角形,可以将其一条直角边平移到斜边所在的直线上方,与斜边重合。
这时,可以将直角三角形的一条直角边看作是斜边减去一条直角边的长度所得的差,即a²+b²=c²。
勾股定理几种证明方法

勾股定理几种证明方法勾股定理的证明【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c,再做三个边长分别为a、b、c的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a+b,所以面积相等.即11a2+b2+4×ab=c2+4×ab22,整理得a2+b2=c2.【证法2】(邹元治证明)以a、b为直角边,以c为斜边做四个全等的直角三角形,则每个直角三角形的面积1ab2等于.把这四个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上,B、F、C三点在一条直线上,C、G、D三点在一条直线上.∵RtΔHAE≌RtΔEBF,∴∠AHE=∠BEF.∵∠AEH+∠AHE=90º,∴∠AEH+∠BEF=90º.∴∠HEF=180º―90º=90º.∴四边形EFGH是一个边长为c的正方形.它的面积等于c2.∵RtΔGDH≌RtΔHAE,∴∠HGD=∠EHA.∵∠HGD+∠GHD=90º,∴∠EHA+∠GHD=90º.又∵∠GHE=90º,∴∠DHA=90º+90º=180º.2∴.∴a+b=c.【证法3】(赵爽证明)以a、b为直角边(b>a),以c为斜边作四个全等的直角三角形,则每个直角(a+∴ABCD是一个边长为a+b的正方形,它的面积等于(a+b)2=4×1ab+c22221ab2三角形的面积等于.把这四个直角三角形拼成如图所示形状.∵RtΔDAH≌RtΔABE,∴∠HDA=∠EAB.∵∠HAD+∠HAD=90º,∴∠EAB+∠HAD=90º,2∴ABCD是一个边长为c的正方形,它的面积等于c.∵EF=FG=GH=HE=b―a,∠HEF=90º. 2(b−a)∴EFGH是一个边长为b―a的正方形,它的面积等于.14×ab+(b−a)2=c22∴.222∴a+b=c.【证法4】(1876年美国总统Garfield证明)以a、b为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面1ab2积等于.把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上.∵∴∵∴∴∴RtΔEAD≌RtΔCBE,∠ADE=∠BEC.∠AED+∠ADE=90º,∠AED+∠BEC=90º.∠DEC=180º―90º=90º.ΔDEC是一个等腰直角三角形,12c2它的面积等于.又∵∠DAE=90º,∠EBC=90º,∴AD∥BC.1(a+b)2∴ABCD是一个直角梯形,它的面积等于2.1(a+b)2=2×1ab+1c222.∴2∴a+b=c.【证法5】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c.把它们拼成如图那样的一个多边形,使D、E、F在一条直线上.过C作AC的延长线交DF于点P.∵D、E、F在一条直线上,且RtΔGEF≌RtΔEBD,∴∠EGF=∠BED,∵∠EGF+∠GEF=90°,222∴∴又∵∴∴∵∴∴即又∵∠BED+∠GEF=90°,∠BEG=180º―90º=90º.AB=BE=EG=GA=c,ABEG是一个边长为c的正方形.∠ABC+∠CBE=90º.RtΔABC≌RtΔEBD,∠ABC=∠EBD.∠EBD+∠CBE=90º.∠CBD=90º.∠BDE=90º,∠BCP=90º,BC=BD=a.∴BDPC是一个边长为a的正方形.同理,HPFG是一个边长为b的正方形.设多边形GHCBE的面积为S,则1a2+b2=S+2×ab,21c2=S+2×ab2,∴a2+b2=c2.【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a、b(b>a),斜边长为c.再做一个边长为c的正方形.把它们拼成如图所示的多边形,使E、A、C三点在一条直线上.过点Q作QP∥BC,交AC于点P.过点B作BM⊥PQ,垂足为M;再过点F作FN⊥PQ,垂足为N.∵∠BCA=90º,QP∥BC,∴∠MPC=90º,∵BM⊥PQ,∴∠BMP=90º,∴BCPM是一个矩形,即∠MBC=∵∠QBM+∠MBA=∠QBA=90º,∠ABC+∠MBA=∠MBC=90º,∴∠QBM=∠ABC,又∵∠BMP=90º,∠BCA=90º,BQ=BA=c,∴RtΔBMQ≌RtΔBCA.同理可证RtΔQNF≌RtΔAEF.从而将问题转化为【证法4】(梅文鼎证明).【证法7】(欧几里得证明)做三个边长分别为a、b、c的正方形,把它们拼成如图所示形状,使H、C、B三点在一条直线上,连结BF、CD.过C作CL⊥DE,交AB于点M,交DE于点L.∵AF=AC,AB=AD,∠FAB=∠GAD,∴ΔFAB≌ΔGAD,12a∵ΔFAB的面积等于2ΔGAD的面积等于矩形ADLM的面积的一半,2∴矩形ADLM的面积=a.2b同理可证,矩形MLEB的面积=.∵正方形ADEB的面积=矩形ADLM的面积+矩形MLEB的面积222222∴c=a+b,即a+b=c.【证法8】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a、b(b>a),斜边长为c.再做一个边长为c的正方形.把它们拼成如图所示的多边形.过A作AF⊥AC,AF交GT于F,AF交DT于R.过B作BP⊥AF,垂足为P.过D作DE与CB的延长线垂直,垂足为E,DE交AF于H.∵∠BAD=90º,∠PAC=90º,∴∠DAH=∠BAC.又∵∠DHA=90º,∠BCA=90º,AD=AB=c,∴RtΔDHA≌RtΔBCA.∴DH=BC=a,AH=AC=b.由作法可知,PBCA是一个矩形,所以RtΔAPB≌RtΔBCA.即PB=CA=b,AP=a,从而PH=b―a.∵RtΔDGT≌RtΔBCA,RtΔDHA≌RtΔBCA.∴RtΔDGT≌RtΔDHA.∴DH=DG=a,∠GDT=∠HDA.又∵∠DGT=90º,∠DHF=90º,∠GDH=∠GDT+∠TDH=∠HDA+∠TDH=90º,∴DGFH是一个边长为a的正方形.∴GF=FH=a.TF⊥AF,TF=GT―GF=b―a.∴TFPB是一个直角梯形,上底TF=b―a,下底BP=b,高FP=a+(b―a).用数字表示面积的编号(如图),则以c为边长的正方形的面积为c2=S1+S2+S3+S4+S5①∵S8+S3+S4=1[b+(b−a)]•[a+(b−a)]b2−1ab22,=S5=S8+S9,1S3+S4=b2−ab−S8b2−S−S18.2∴=②把②代入①,得c2=S1+S2+b2−S1−S8+S8+S92b+S2+S9=b2+a2.=222∴a+b=c.【证法9】(李锐证明)设直角三角形两直角边的长分别为a、b(b>a),斜边的长为c.做三个边长分别为a、b、c的正方形,把它们拼成如图所示形状,使A、E、G三点在一条直线上.用数字表示面积的编号(如图).∵∠TBE=∠ABH=90º,∴∠TBH=∠ABE.又∵∠BTH=∠BEA=90º,BT=BE=b,∴RtΔHBT≌RtΔABE.∴HT=AE=a.∴GH=GT―HT=b―a.又∵∠GHF+∠BHT=90º,∠DBC+∠BHT=∠TBH+∴∠GHF=∠DBC.∵DB=EB―ED=b―a,∠HGF=∠BDC=90º,∴RtΔHGF≌RtΔBDC.即S7=S2.过Q作QM⊥AG,垂足是M.由∠BAQ=∠BEA=90º,可知∠ABE=∠QAM,而AB=AQ=c,所以RtΔABE≌RtΔQAM.又RtΔHBT≌RtΔABE.所以RtΔHBT≌RtΔQAM.即S8=S5.由RtΔABE≌RtΔQAM,又得QM=AE=a,∠AQM=∠BAE.∵∠AQM+∠FQM=90º,∠BAE+∠CAR=90º,∠AQM=∠BAE,∴∠FQM=∠CAR.又∵∠QMF=∠ARC=90º,QM=AR=a,∴RtΔQMF≌RtΔARC.即S4=S6.222c=S+S+S+S+Sa=S+Sb1234516∵,,=S3+S7+S8,又∵S7=S2,S8=S5,S4=S6,22a+b=S1+S6+S3+S7+S8∴=S1+S4+S3+S2+S5=c,222即a+b=c.【证法10】(利用反证法证明)如图,在RtΔABC中,设直角边AC、BC的长度分别为a、b,斜边AB的长为c,过点C作CD⊥AB,垂足是D.222222假设a+b≠c,即假设AC+BC≠AB,则由AB2=AB•AB=AB(AD+BD)=AB•AD+AB•BD22可知AC≠AB•AD,或者BC≠AB•BD.即AD:AC≠AC:AB,或者BD:BC≠BC:AB.在ΔADC和ΔACB中,∵∠A=∠A,∴若AD:AC≠A C:AB,则∠ADC≠∠ACB.在ΔCDB和ΔACB中,∵∠B=∠B,∴若BD:BC≠BC:AB,则∠CDB≠∠ACB.又∵∠ACB=90º,∴∠ADC≠90º,∠CDB≠90º.222AC+BC≠AB这与作法CD⊥AB矛盾.所以,的假设不能成立.222∴a+b=c.【证法15】(辛卜松证明)DD2设直角三角形两直角边的长分别为a、b,斜边的长为c.作边长是a+b的正方形ABCD.把正方形ABCD划分成上方左图所示的几个部分,则正方形ABCD的面积为(a+b)2=a2+b2+2ab;把正方形ABCD划分成上方右图所示的几个部分,则正方形ABCD 的面积为∴∴(a+b)21=4×ab+c222=2ab+c.a2+b2+2ab=2ab+c2,【证法11】(陈杰证明)设直角三角形两直角边的长分别为a、b(b>a),斜边的长为c.做两个边长分别为a、b的正方形(b>a),把它们拼成如图所示形状,使E、H、M三点在一条直线上.用数字表示面积的编号(如图).在EH=b上截取ED=a,连结则AD=c.∵EM=EH+HM=b+a,ED=∴DM=EM―ED=(b+a)―a=b.又∵∠CMD=90º,CM=a,∠AED=90º,AE=b,∴RtΔAED≌RtΔDMC.∴∠EAD=∠MDC,DC=AD=c.∵∠ADE+∠ADC+∠MDC=180º,∠ADE+∠MDC=∠ADE+∠EAD=90º,∴∠ADC=90º.∴作AB∥DC,CB∥DA,则ABCD是一个边长为c的正方形.∵∠BAF+∠FAD=∠DAE+∠FAD=90º,∴∠BAF=∠DAE.连结FB,在ΔABF和ΔADE中,∵AB=AD=c,AE=AF=b,∠BAF=∠DAE,∴ΔABF≌ΔADE.∴∠AFB=∠AED=90º,BF=DE=a.∴点B、F、G、H在一条直线上.在RtΔABF和RtΔBCG 中,∵AB=BC=c,BF=CG=a,∴RtΔABF≌RtΔBCG.2c=S2+S3+S4+S5,∵S1=S5=S4=S6+S7,b2=S1+S2+S6,a2=S3+S7,22a+b=S3+S7+S1+S2+S6∴=S2+S3+S1+(S6+S7)∴=S2+S3+S4+S52=c。
勾股定理9种证明(有图)
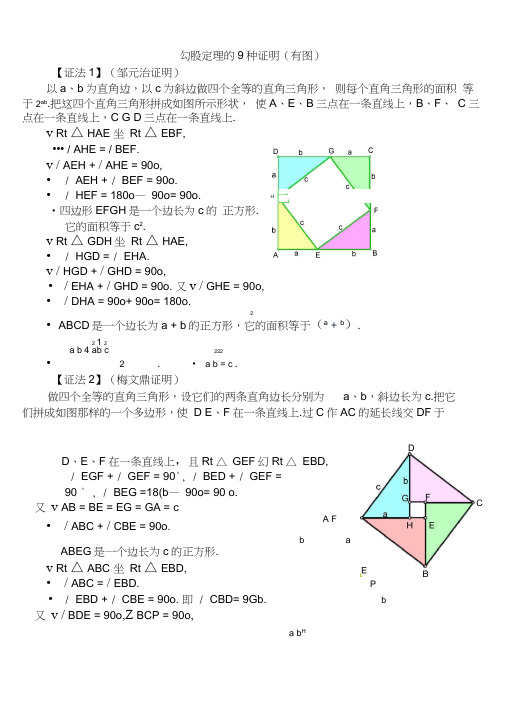
勾股定理的9种证明(有图)【证法1】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形, 则每个直角三角形的面积 等于2ab .把这四个直角三角形拼成如图所示形状, 使A 、E 、B 三点在一条直线上,B 、F 、 C 三点在一条直线上,C G D 三点在一条直线上.v Rt △ HAE 坐 Rt △ EBF, ••• / AHE = / BEF.v / AEH + / AHE = 90o, • / AEH + / BEF = 90o.• / HEF = 180o — 90o= 90o.•四边形EFGH 是一个边长为c 的 正方形.它的面积等于c 2.v Rt △ GDH 坐 Rt △ HAE, • / HGD = / EHA. v / HGD + / GHD = 90o,• / EHA + / GHD = 90o. 又v / GHE = 90o, • / DHA = 90o+ 90o= 180o.2• ABCD 是一个边长为a + b 的正方形,它的面积等于(a + b ).21 2a b 4 ab c222•2. • a b = c .【证法2】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为 a 、b ,斜边长为c.把它 们拼成如图那样的一个多边形,使 D E 、F 在一条直线上.过C 作AC 的延长线交DF 于/ EGF + / GEF = 90°, / BED + / GEF = 90 ° , / BEG =18(b — 90o= 90 o. 又 v AB = BE = EG = GA = c• / ABC + / CBE = 90o.v Rt △ ABC 坐 Rt △ EBD, • / ABC = / EBD.• / EBD + / CBE = 90o. 即 / CBD= 9Gb. 又 v / BDE = 90o ,Z BCP = 90o ,D 、E 、F 在一条直线上,且Rt △ GEF 幻Rt △ EBD, ABEG 是一个边长为c 的正方形.a b HH匕DA FbaP bCBC = BD = a.••• BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCB 的面积为S,则21 b S2 ab, 2 1=S 2 ab2 ,a 2 +b 2 =c 2【证法3】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为 a 、b (b>a )c.再做一个边长为c 的正方形.把它们拼成如图所示的多边形,使 直线上. 过点Q 作QP// BC 交AC 于点P. 过点B 作BML PQ 垂足为M ;再过点 F 作FNL PQ 垂足为N.v / BCA = 90o , QP// BC • / MPC = 90o , v BM 丄 PQ• / BMP = 90o ,• BCPM 是一个矩形,即/ MBC = 90o.v / QBM + / MBA = / QBA = 90o , / ABC + / MBA = / MBC = 90o , • / QBM = / ABC又 v / BMP = 90o ,/ BCA = 90o , BQ = BA = c , • Rt △ BMQ 坐 Rt △ BCA.同理可证Rt △ QNF 幻Rt △ AEF.从而将问题转化为【证法4】(梅文鼎证明). 【证法4】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使 在一条直线上,连结BF CD.过 C 作 CL L DE 交AB 于点M 交DE 于点L.v AF = AC , AB = AD,/ FAB = / GAD• △ FAB 坐△ GADE 、A ,斜边长为C 三点在一条 H 、C B 三点 v △ FAB 的面积等于K△ GAD 的面积等于矩形ADLM 的面积的一半,二矩形ADLM 的面积二 同理可证,矩形 MLEE 的面积 v 正方形ADEB 勺面积 =矩形ADLM!勺面积+ /. c 2 a 2 b 2,即 a 2 -【证法5】(杨作玫证明) 做两个全等的直角三角形,设它们的两条直角边长分别为 a 、b (b>a ),斜边长为c. 再做一个边长为c 的正方形.把它们拼成如图所示的多边形.过A 作AF 丄AC AF 交GT 于F , AF 交DT 于 R.过B 作BP 丄AF,垂足为 E , DE 交 AF 于 H. v / BAD = 90o ,Z PAC = 90o , ••• / DAH = / BAC. 又 v / DHA = 90o ,Z BCA = 90o , AD = AB = c ,• Rt △ DHA 坐 Rt △ BCA. • DH = BC = a , AH = AC = b. 由作法可知,PBCA 是一个矩形, 所以 Rt △ APB 坐 Rt △ BCA.即 PB = CA = b , AP= a ,从v Rt △ DGT 坐 RtRt △ DHA 坐 Rt• Rt △ DGT 坐 Rt • DH = DG = a , 又 v / DGT = 90o ,2 a . =b 2 矩形MLEB 勺面积 b 2 =c 2. PH = b — a. △ BCA , △ BCA. △ DHA . / GDT = / HDA . / DHF = 90o ,P.过D 作DE 与CB 的延长线垂直,垂足为 / GDH = / GDT + / TDH = / HDA+Z TDH = 90o ,• DGFH 是一个边长为a 的正方形.• GF = FH = a . TF 丄AF , TF = GT — GF = b — a .• TFPB 是一个直角梯形,上底 TF=b-a ,下底BP= b ,高FP=a + (b —a ).用数字表示面积的编号(如图),则以c 为边长的正方形的面积为 c 2 = Si S 2 S 3 S 4 S 51S 8 +S 3 +S 4 =- b + (b - a )】• a + (b -a /v2S5 - S 8' S 9丄21 .S 3S 4-b 2 ab・・ 2把②代入①,得c^S iS 2b 2 -S^S 8S 8S 9①b 2 -1 ab2 ,2=bS2S 9 = b 2 川 a 2【证法6】(李锐证明)设直角三角形两直角边的长分别为 a 、b (b>a ),斜边的长为c.做三个边长分别为a 、 b 、c 的正方形,把它们拼成如图所示形状,使 A 、E 、G 三点在一条直线上.用数字表示 面积的编号(如图).v / TBE = / ABH = 900, ••• / TBH = / ABE. 又 v / BTH = / BEA = 900,BT = BE = b , • Rt △ HBT 坐 Rt △ ABE. • HT = AE = a. • GH = GT — HT = b — a. 又 v / GHF + / BHT = 900,/ DBC + / BHT = / TBH + • / GHF = / DBC.v DB = EB — ED = b — a , / HGF = / BDC = 90o , • Rt △ HGF 坐 Rt △ BDC.即 S ^ S 2.过 Q 作 QM L AG 垂足是 M.由/ BAQ = / BEA = 90o ,可知 / ABE =/ QAM 而 AB = AQ = c ,所以 Rt △ ABE 幻 Rt △ QAM .又 Rt △ HBT 幻Rt △ ABE.所以 Rt △ HBT 幻 Rt △ QAM .即 S 8 二 S 5.由 Rt △ ABE 坐 Rt △ QAM 又得 QM = AE = a ,/ AQM = / BAE.v / AQM + / FQM = 90o ,Z BAE + / CAR = 90o ,Z AQM = / BAE • / FQM = / CAR.【证法7】(利用多列米定理证明)• Rt △ QMF 坐 Rt △ ARC.即 S 4 =S6.• • c 2 =S 1 S 2 S 3 S 4 S 5 a 2 S 6又v S 7 二 S 2 S g 二 S 5 S 4 二 S 6> > >• a 2 b 2 = S ! S 6 S 3 S 7 S 8=S iS 4 S 3 S 2 S 52=c ,即a 2 + b 2 =c 2.又 v / QMF = / ARC = 90o , QM = AR = a , b^ S 3 S 7 S 8R a A在Rt △ ABC 中,设直角边 BC= a , AC= b ,斜边AB = c (如图).过点A 作AD// CB, 过点B 作BD//CA 则ACBD 为矩形,矩形ACBD 内接于一个圆.根据多列米定理,圆内接 四边形对角线的乘积等于两对边乘积之和,有AB ・DC 二 AD ・BC AC *BD ,AB = DC = c , AD = BC = a , AC = BD = b ,AB 2 =BC 2 +AC 2,即 c 2 =a 2 +b 2 a 2 +b 2 =c 2【证法8】(利用反证法证明) 如图,在Rt △ ABC 中,设直角边 AG点C 作CDL AB 垂足是D.假设a 2 b 2=c 2,即假设AC 2 BC —AB 2,则由AB^AB *AB =AB AD BD =AB ・AD AB * BD可知 AC 2 式 AB ・AD ,或者 BC 2 式 AB ・BD .即 AD : AO AG AB 或者 BD : BO BC AB. 在厶ADC 和△ ACB 中, v / A = / A,.若 AD : AW AC AB 」 / AD 字/ ACB.在厶CDB 和△ ACB 中, v / B = / B ,.若 BD BW BC AB,贝S / CDB^Z ACB. 又v / ACB = 90o ,. / AD& 90o ,Z CD 字 90o. 这与作法CDLAB 矛盾.所以,/. a 2 b 2 = c 2.【证法9](辛卜松证明)设直角三角形两直角边的长分别为 a 、b,斜边的长为c.作边长是a+b 的正方形ABCD. 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为 (a +bf =a +b +2ab ;把正方形ABCD 划分成上方右图所示的几个部分,则正方形 ABCD 勺21 2,.十.(a +b 『=4 乂一ab+c 2面积为 2= 2ab c .2 2 2.. a b 2ab 二 2ab c ,BC 的长度分别为a 、b ,斜边AB 的长为c ,过 AC 2 • BC 2 = AB 2的假设不能成立..a2+b2=c2.。
证明勾股定理的多种方法

证明勾股定理的多种方法勾股定理是数学中一条重要的几何定理,它是数学中的基础知识之一。
勾股定理的形式可以简洁地表达为:直角三角形的斜边的平方等于两直角边的平方和。
本文将探索并介绍证明勾股定理的多种方法。
方法一:几何证明最常见的证明勾股定理的方法之一是几何证明。
该方法利用了直角三角形的特性,根据三角形的几何关系和平行线的性质,从而得出勾股定理的结论。
以直角三角形ABC为例,其中∠C为直角,假设∠A=α,∠B=β,边长分别为a, b, c。
根据正弦定理和余弦定理,可以推导出以下关系式:sinα = a / c,sinβ = b / c,cosα = b / c,cosβ = a / c由此可得:sin²α + cos²α = a² / c² + b² / c² = (a² + b²) / c²根据三角恒等式sin²α + cos²α = 1,可得:(a² + b²) / c² = 1即 a² + b² = c²,从而证明了勾股定理。
方法二:代数证明除了几何证明外,勾股定理还可以通过代数方法进行证明。
假设直角三角形的边长分别为a, b, c,且∠C为直角。
根据勾股定理,我们有:a² + b² = c²我们可以将其转化为代数方程组,从而进行证明。
构造方程组如下:x² + y² = 1²(x+c)² + y² = a²x² + (y+c)² = b²解方程组可得:x = (a² - b² + c²) / (2c)y = ±√(a² - x²)因此,可得到:a² + b² = (a² - b² + c²)² / (4c²) + (a² - (a² - b² + c²)² / (4c²) = c² · [(a² + b²) / (4c²) + (a² + b² - 2ab)/(4c²)]将a² + b² = c²带入上式,得到:c² = (c² · [(c² + 2ab) / (4c²)])化简后可得:c² = (c² + 2ab) / 4即 a² + b² = c²,从而证明了勾股定理。
勾股定理的证明方法带图

勾股定理的证明方法带图勾股定理是数学中一个非常重要的定理,它在几何学、物理学和工程学等领域都有广泛的应用。
勾股定理主要用于解决直角三角形的边长关系问题,它的常见表述是:直角三角形斜边的平方等于直角边的平方和。
在这篇文档中,我们将通过多个证明方法来证明勾股定理,并且将每个步骤都用图示来说明。
1. 证明方法一:几何学证明首先,我们来介绍一种几何学证明勾股定理的方法。
我们假设有一个直角三角形ABC,其中∠C为直角。
通过在边AC上作高CD,我们可以将三角形ABC分成两个矩形ACDE和BCFD。
接下来,我们将使用几何学的原理来证明∆ABC的边长关系。
我们知道,由于三角形ACD和BFC是矩形ACDE和BCFD的对角线,所以ACD和BFC是相似三角形。
因此,我们可以建立以下比例方程:AC/AD = BC/BF由于AD和BF都是三角形ABC的直角边,我们将其记为a和b,因此可以得到以下等式:AC/a = BC/b将上述等式两边都乘以a和b,得到:AC^2 = BC^2 + a^2 - - - (1)所以,通过几何学证明,我们可以得到勾股定理的一个解释:直角三角形的斜边的平方等于直角边的平方和。
为了更加清晰地理解这个几何学证明过程,让我们来看一个图示。
图示如下:```C|\\| \\a | \\ b| \\|____\\A c B```在上面的图示中,我们可以看到三角形ABC以及直角边a和b以及斜边c之间的关系。
通过几何学证明的过程,我们可以看到三角形ACD和BFC的构造,以及通过相似三角形的比例关系建立的方程式。
最终,我们得到了勾股定理的证明:直角三角形斜边的平方等于直角边的平方和。
2. 证明方法二:代数学证明除了几何学证明之外,我们还可以通过代数学方法来证明勾股定理。
在这种方法中,我们将使用代数方程和平方的运算来证明。
我们假设一个直角三角形ABC,其中∠C为直角。
假设直角边a的长度为x,直角边b的长度为y,斜边c的长度为z。
勾股定理的三种证明方法过程

勾股定理的三种证明方法过程勾股定理是初中数学中一个重要的定理,它描述了一个直角三角形中的边长关系。
勾股定理的三种证明方法为:几何证明、代数证明和物理证明。
下面将分别介绍这三种证明方法。
几何证明是最早被使用的一种方法,我们可以通过几何图形来证明勾股定理。
首先,我们画一个直角三角形ABC,其中∠ABC为直角。
然后,我们可以通过重复使用等腰直角三角形的特性来得到边长关系。
具体来说,我们可以将三角形ABC分成两个等腰直角三角形,分别记作三角形ABD和三角形CBD。
根据等腰直角三角形的性质,我们可以得出以下等式:BD=AD、BD=CD。
再根据两个等式,我们可以得到AD=CD,即a²=b²+c²,这就是勾股定理的一种几何证明方法。
代数证明是一种通过代数运算来证明勾股定理的方法。
我们可以用代数变量表示直角三角形的边长,假设直角边为a、b,斜边为c。
根据勾股定理,我们有a²+b²=c²。
接下来,我们可以使用代数运算来推导这个等式。
首先,我们可以将直角边的平方展开,得到a²=b²+c²-2bc。
然后,我们可以将等式两边同时加上2bc,得到a²+2bc=b²+c²。
再将两边同时除以2,得到(a²+2bc)/2=(b²+c²)/2。
由于等式两边相等,我们可以得到a²+bc=b²+c²/2。
最后,我们将等式两边同时减去c²/2,得到a²-bc=b²-c²/2,再整理一下得到a²-bc=b²-c²,即a²=b²+c²,这就得到了勾股定理。
物理证明是一种较为特殊的证明方法,它通过实验来验证勾股定理。
首先,我们需要准备一个光滑的斜面,并且在斜面上放置一个小球。
