多元函数极值的充分条件
多元函数取得极值的条件

序列可行方向的性质 性 质 1 处可微, 设ci(x)在x处可微,则 ∀d ∈SFD(x, X )有 在 处可微
∇cj (x)T d ≥ 0, (∀j ∈I (x)) T ∇cj (x) d = 0, (∀j ∈E)
证明
∀d ∈SFD(x, X ), dk (k =1,2,L 和δk X, 且有dk →d和δk →0,则
由于该方程组的系数矩阵的行向量组线性无关, 由于该方程组的系数矩阵的行向量组线性无关,所以该方程组有解
∀d ∈S*,则d ≠ 0,且d与∇ci (x*)(i ∈E)正交。
{∇c1(x*),L, ∇cme (x*), d} 成 e +1 空 , 法 间 n − me −1 空 , 生 m 维 间 其 空 是 为 间 在 空 中 取 组 准 交 di (i =1,2,L, n − me −1), 考 函 方 组 法 间 任 一 标 正 基 虑 数 程
∇f (x*) = 0
设 元 数 (x)存 二 连 偏 数 x*是 小 n 函 f 在 阶 续 导 , 极
值点,则
∇f (x*) = 0,且∇2 f (x*)半正定
证明: f (x*) = 0显然。 ∇ ∀d ∈Rn , 令x = x *+αd,由Taylor公式有 1 2 T 2 0 ≤ f (x) − f (x*) = α d ∇ f (x *+θαd)d 2
若函数z= 在点P(x 若函数 f(x,y) 在点 0,y0)的某邻域内连续且存在一 的某邻域内连续且存在一
f x′(x0 , y0 ) = 0
′′ ′′ ′′ A = f xx (x0 , y0 ), B = f xy (x0 , y0 ), C = f yy (x0 , y0 )
多元函数取到条件极值的充分条件

多元函数取到条件极值的充分条件
在数学及经济学中,多元函数取到条件极值的充分条件是一直在学术界引发热
议的话题。
由于大多数多元函数的性质是复杂的,因此解决条件极值问题时,往往需要结合统计学研究多元函数的性质来获得解决方案。
多元函数取到条件极值的充分条件,通常就是要求函数符合一定的条件函数,
并且函数必须满足一定的变量不等式要求,才能取得最优解。
具体来说,要求偏导函数满足Kaplans-Kronrod方程,以及函数的条件必须在第四范式函数中满足等式,才能保证能使函数取得条件极值。
此外,通过多元math解析法求解多元函数取到条件极值的充分条件,可以从
解析、符号、数值几方面来考虑极值问题。
首先,通过解析法,我们可以确定函数的步调和步长,以及函数形式最合理时的极值情况;其次,通过符号学计算,可以推算出条件函数面上极值的取值空间大小与选择;最后,通过数值计算,可以进一步改善求解准确性和精度,从而有效精确求解出条件极值的充分条件。
通过恰当的多元函数处理可以使得机器学习的算法具有有效的收敛性,从而有
效抑制模型可能出现的偏差。
此外,取得条件极值的充分条件还可以使机器学习更加准确,提高系统性能,完善互联网体验。
因此,多元函数取到条件极值的充分条件对当今互联网来说,十分重要。
多元函数极值的充分条件

多元函数极值的充分条件马丽君(集宁师范学院 数学系)我们知道,一元函数()y f x =在点0x x =取得极值的充分条件是:函数()f x 在点0x 处具有一阶二阶连续导数,0x 是()f x 驻点,即0()0f x '=。
若0()0(0)f x ''><,则0x 为()f x 的极小值点(或极大值点)对于多元函数()Y f X =,其中12(,,,)n X x x x =,有与上面一元函数取得极值的充分条件相对应的结论。
定义 1.设n 元函数()Y f X =,其中12(,,,)n X x x x =,对各自变量具有一阶连续偏导数,则称12,,,Tn f ff x x x ⎛⎫∂∂∂⎪∂∂∂⎝⎭为()f X 的梯度,记作gradf 。
引理 设n 元函数()f X ,其中12(,,,)n X x x x =,对各自变量具有一阶连续偏导数,则()f X 在点000012(,,,)n X x x x =取得极值的必要条件是:0112(),,,0Tn n X X f ff gradf X x x x ⨯=⎛⎫∂∂∂== ⎪∂∂∂⎝⎭证明:引理成立是显然的,即极值点函数可导,则该点的偏导数等于零。
定义 2.设n 元函数()f X ,对各自变量具有二阶连续偏导数,000012(,,,)n X x x x =是()f X 的驻点,现定义()f X 在点0X 处的矩阵为:222000211212222000202122222000212()()()()()()()()()()f N n n n f X f X f X X X X X X f X f X f X H X X X X X X f X f X f X X X X X X ⎧⎫∂∂∂⎪⎪∂∂∂∂∂⎪⎪⎪⎪∂∂∂⎪⎪=∂∂∂∂∂⎨⎬⎪⎪⎪⎪⎪⎪∂∂∂⎪⎪∂∂∂∂∂⎩⎭由于各二阶偏导数连续,即22(,1,2,,)i j j if fi j n x x x x ∂∂==∂∂∂∂,所以0()f H X 为实对称矩阵。
等约束条件下多元函数条件极值的充分条件

0
0
0
0
f +λφ 烎
0 2 2
0 0 2 2
2 三元函数的条件极值
2. 1 单等式约束条件下极值 三元函数 u=f( x, z)在 φ( x, z) =0 下取到极值的充分条件 。 y, y,
2 2 2 定理 2 设函数 u=f( x, z), x, z)存在二阶连续偏导数 , a r a n e 函数 y, y, g g x +φ z ≠0且L y +φ φ( φ 是空间区域 Ω 的内点且是 L( L( x, z, x, z) x, z), M0( x z x, z, =f( +λ λ) λ λ)的稳 y, y, y, y y, 0, 0, 0, 0) φ(
在大学数学许多教材中 , 关于等约束条件极值几乎只是给出了其必要条件 , 而要求出极值通常是采 至于是极大值还是极小值往往是结合实际问题来讨论 , 而要 用L a r a n e 乘数法求出其可能的极值点 , g g
1] 2] 2 。 通常的方法是采用二阶微分法 [ 从理论上准确判断出其是极大 、 极小值往往比较困难 [ 求出d L并
u z, ) 将 z=ψ( x x, x, z)得 : u=f( x, x, =f y y)代入 u=f( y, y, y) 0, 0 ), x +f z ψ( ψ( x x
2 2 u z u z ( z) z z ; =f + f +f 2 =f z x x +f x z z x +f z z z y +f 2 x x x x x y y 2 2 z ( z) z u z ; =f + f +f x x z z z z z y +f y +f x x x y y y y 2 2 z ( z) z u z ; + f +f f z z z z z y +f y y +f y 2 = 2 y y y y y 2 z z x y x x z -2 x z z z z φ φx φz +φ φx ; 又将以下几式 =-φ , =-φ 2 =-φ φ 3 x x y φz φz φz 2 2 x y z-( x z y z z +φ z z y y y z z z z z φ φy +φ φx ) φ φx φy ; φ φz -2 φ φy φz +φ φx 代入 ( ) 、 ( ) 、 ( ) 式 4 5 6 =-φ φ 3 2 =- 3 x y y z z φ φ 2 2 2 2 2 2 f 1 u 1 u 2 2 2 2 (x 且令λ=- z u L L L = z x z -2 x z x z +L z z x) 2 ; 2 = ( z -2 z +L z z y y y y y) 2 ; 2= L φ φ φ φ φ φ φ φ x x y y z z φz φ φ 2 2 2 u u 1 u 2 ( 其中μ= L A, B, 2 C, = = = x x z z z z y y 2 φz -L φx φz -L φy φz +L φx φy ) 2 μ μ μ , ) x , ) , ) x( y( x y( x x z 0y 0 φ 0y 0 0y 0 2 2
多元函数极值条件的充分及必要条件

多元函数极值条件的充分及必要条件一、引言在数学中,多元函数的极值问题是一个重要的研究方向。
求解多元函数的极值可以帮助我们了解函数的性质和优化问题。
本文将介绍多元函数极值的充分条件和必要条件,并通过数学推导和具体案例进行说明。
二、充分条件对于一个多元函数,如果它在某一点处取得极值,那么该点的梯度向量为零。
这是多元函数极值的充分条件之一,也称为驻点条件。
假设函数为$f(x_1,x_2,...,x_n)$,我们定义其梯度向量为:$$\n ab la f=\l ef t(\f ra c{{\pa rt ia lf}}{{\p ar ti al x_1}},\f ra c {{\p ar ti al f}}{{\p a rt ia lx_2}},...,\fr ac{{\p ar ti alf}}{{\pa r t i al x_n}}\ri gh t)$$如果存在一个点$(x_1^*,x_2^*,...,x_n^*)$,使得$\na bl af(x_1^*,x_2^*,...,x_n^*)=\m at hb f{0}$,那么该点为函数$f$的驻点。
然而,驻点并不一定是极值点。
还需要进一步考察该点的二阶偏导数信息。
三、必要条件1.H e s s i a n矩阵H e ss ia n矩阵是多元函数在某个点处的二阶偏导数构成的矩阵。
对于函数$f(x_1,x_2,...,x_n)$,其He ssi a n矩阵定义为:$$H(f)=\be gi n{bma t ri x}\f ra c{{\pa rt ia l^2f}}{{\p ar ti al x_1^2}}&\f ra c{{\par t ia l^2 f}}{{\pa rt ia lx_1\p ar ti al x_2}}&\cd o ts&\fr ac{{\p art i al^2f}} {{\p ar ti al x_1\par t ia lx_n}}\\\f ra c{{\pa rt ia l^2f}}{{\p ar ti al x_2\pa rt ia lx_1}}&\f r ac{{\p a rt ia l^2f}}{{\pa r ti al x_2^2}}&\cd o ts&\fr ac{{\p art i al^2f}} {{\p ar ti al x_2\par t ia lx_n}}\\\v do ts&\vd ot s&\dd o ts&\vd ot s\\\f ra c{{\pa rt ia l^2f}}{{\p ar ti al x_n\pa rt ia lx_1}}&\f r ac{{\p a rt ia l^2f}}{{\pa r ti al x_n\p a rt ial x_2}}&\cd ot s&\fr a c{{\pa rt i al^2f}}{{\pa rti a lx_n^2}}\e nd{b ma tr ix}$$2.S y l v e s t e r定理S y lv es te r定理给出了判别He ss ia n矩阵正定、负定和不定的条件。
88多元函数极值
在点(1, 2)处, AC–B2=12(–6)<0, 在点(–3, 0)处,
AC–B2=(–12)6<0, 所以f(–3, 0)和f(1, 2)不是极值;
在点(–3, 2)处, AC–B2= –12(–6)>0, 且A= –12<0,
所以函数在点(–3, 2)处有极大值f(–3, 2)=31.
推广: 如果三元函数 u=f(x, y, z) 在点P(x0, y0, z0)处 具有偏导数, 则它在点P(x0, y0, z0)处有极值的必要条件 为: fx(x0, y0, z0)=0, fy(x0, y0, z0)=0, fz(x0, y0, z0)=0.
仿照一元函数, 凡能使一阶偏导数同时为零的点, 称为此函数的驻点.
的存在性可知: 这时长方体在第一卦限顶点的坐标为:
(a , b , c )
333
最大长方体的长宽高分别为: 2a , 2b , 2c .
最大体积为:
8abc . 3
3
3
解二:
作变量替换:
33 X
x,
Y y,
Z z.
a
b
c
问题变成在单位球面X2+Y2+Z2=1内求内接长方体
的最大体积问题.
例2: 求由方程 x2+y2+z2–2x+2y–4z–10=0 确定的隐
函数z=f(x, y)的极值.
解: 在方程两边分别对x, y求偏导, 得
2 x 2 y
2z 2z
zx zy
2 2
4zx 4zy
0 0
由函数取极值的必要条件知, 求驻点. 令
zx 0, zy 0, 得驻点P(1, –1). 在上述方程组两边再分别对x, y求偏导数, 得
第八节极值与最值

• 使函数的各偏导数同时为0的点,称为驻点.
• 具有偏导数的函数的极值点必定是驻点,但驻点不
一定是极值点。例如,
有驻点( 0, 0 )
• 极值点也可能是偏导数不存在的点。
• 极值点只可能在驻点或使偏导数不存在的点中产生.
例: f ( x, y ) y 2 x 2 1 解: f x 2 x 0 , f y 2 y 0 ,
例3 求由方程 x2 y2 z2 2 x 2 y 4z 10 0
确定的函数z f ( x, y)的极值
解 将方程两边分别对 x, y 求偏导
2x 2z zx 2 4zx 0 2 y 2z zy 2 4zy 0
zx' 0, z'y 0, 代入上式,解得驻点为 P(1,1),
的极值.
解方程组
得驻点: (1, 0) , (1, 2) , (–3, 0) , (–3, 2) .
第二步 求二阶偏导数及判别.
B
C
f xx (x, y) 6x 6, f xy (x, y) 0, f yy (x, y) 6 y 6
A
在点(1,0) 处
AC B2 12 6 0, A 0,
zx
(x2 y2 1)2
0,
zy
(x2
y2 1) 2y(x (x2 y2 1)2
y)
0,
得驻点 (
1, 2
1 2
)
和
(
1 , 2
1 2
)
,
x y
因为
lim
x
x2
y2
1
0
y
即边界上的值为零. z( 1 , 1 ) 1 , z( 1 , 1 ) 1 ,
22 2
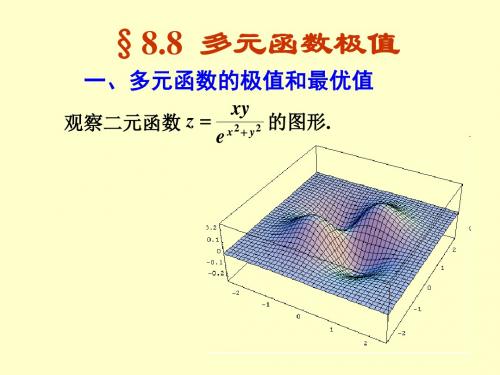
06 第六节 多元函数的极值及其求法

第六节 多元函数的极值及其求法在实际问题中,我们会大量遇到求多元函数的最大值、最小值的问题. 与一元函数的情形类似,多元函数的最大值、最小值与极大值、极小值密切的联系. 下面我们以二元函数为例来讨论多元函数的极值问题.分布图示★ 引例 ★ 二元函数极值的概念 例1-3★ 极值的必要条件 ★ 极值的充分条件★ 求二元函数极值的一般步骤 ★ 例4 ★ 例5★ 求最值的一般步骤 ★ 例6 ★ 例7★ 例8 ★ 例9 ★ 例10 ★ 例11 ★ 条件极值的概念 ★ 拉格郎日乘数法 ★ 例12★ 例 13 ★ 例 14 ★ 例 15 ★ 例 16*数学建模举例★ 线性回归问题 ★ 线性规划问题★ 内容小结 ★ 课堂练习★ 习题6-6内容要点一、二元函数极值的概念定义1 设函数),(y x f z =在点),(00y x 的某一邻域内有定义, 对于该邻域内异于),(00y x 的任意一点),(y x , 如果),,(),(00y x f y x f <则称函数在),(00y x 有极大值;如果),,(),(00y x f y x f >则称函数在),(00y x 有极小值; 极大值、极小值统称为极值. 使函数取得极值的点称为极值点.定理1 (必要条件) 设函数),(y x f z =在点),(00y x 具有偏导数, 且在点),(00y x 处有极值, 则它在该点的偏导数必然为零,即.0),(,0),(0000==y x f y x f y x (6.1)与一元函数的情形类似,对于多元函数,凡是能使一阶偏导数同时为零的点称为函数的驻点.定理2 (充分条件) 设函数),(y x f z =在点),(00y x 的某邻域内有直到二阶的连续偏导数,又,0),(00=y x f x .0),(00=y x f y 令.),(,),(,),(000000C y x f B y x f A y x f yy xy xx === (1) 当02>-B AC 时,函数),(y x f 在),(00y x 处有极值,且当0>A 时有极小值),(00y x f ;0<A 时有极大值),(00y x f ;(2) 当02<-B AC 时,函数),(y x f 在),(00y x 处没有极值;(3) 当02=-B AC 时,函数),(y x f 在),(00y x 处可能有极值,也可能没有极值.根据定理1与定理2,如果函数),(y x f 具有二阶连续偏导数,则求),(y x f z =的极值的一般步骤为:第一步 解方程组,0),(,0),(==y x f y x f y x 求出),(y x f 的所有驻点;第二步 求出函数),(y x f 的二阶偏导数,依次确定各驻点处A 、 B 、 C 的值,并根据2B AC -的符号判定驻点是否为极值点. 最后求出函数),(y x f 在极值点处的极值.二、二元函数的最大值与最小值求函数),(y x f 的最大值和最小值的一般步骤为:(1)求函数),(y x f 在D 内所有驻点处的函数值;(2)求),(y x f 在D 的边界上的最大值和最小值;(3)将前两步得到的所有函数值进行比较,其中最大者即为最大值, 最小者即为最小值. 在通常遇到的实际问题中,如果根据问题的性质,可以判断出函数),(y x f 的最大值(最小值)一定在D 的内部取得,而函数),(y x f 在D 内只有一个驻点,则可以肯定该驻点处的函数值就是函数),(y x f 在D 上的最大值(最小值).三、条件极值 拉格朗日乘数法前面所讨论的极值问题,对于函数的自变量一般只要求落在定义域内,并无其它限制条件,这类极值我们称为无条件极值. 但在实际问题中,常会遇到对函数的自变量还有附加条件的的极值问题. 对自变量有附加条件的极值称为条件极值.拉格朗日乘数法设二元函数),(y x f 和),(y x ϕ在区域D 内有一阶连续偏导数,则求),(y x f z =在D 内满足条件0),(=y x ϕ的极值问题,可以转化为求拉格朗日函数),(),(),,(y x y x f y x L λϕλ+=(其中λ为某一常数)的无条件极值问题.于是,求函数),(y x f z =在条件0),(=y x ϕ的极值的拉格朗日乘数法的基本步骤为:(1) 构造拉格朗日函数),(),(),,(y x y x f y x L λϕλ+=其中λ为某一常数;(2) 由方程组⎪⎩⎪⎨⎧===+==+=0),(,0),(),(,0),(),(y x L y x y x f L y x y x f L y y y x x x ϕλϕλϕλ解出λ,,y x , 其中x , y 就是所求条件极值的可能的极值点.注:拉格朗日乘数法只给出函数取极值的必要条件, 因此按照这种方法求出来的点是否为极值点, 还需要加以讨论. 不过在实际问题中, 往往可以根据问题本身的性质来判定所求的点是不是极值点.拉格朗日乘数法可推广到自变量多于两个而条件多于一个的情形:四、数学建模举例例题选讲二元函数极值的概念例1 (E01) 函数2232y x z +=在点(0, 0)处有极小值. 从几何上看,2232y x z +=表示一开口向上的椭圆抛物面,点)0,0,0(是它的顶点.(图7-6-1).例2 (E02) 函数22y x z +-=在点(0,0)处有极大值. 从几何上看,22y x z +-= 表示一开口向下的半圆锥面,点)0,0,0(是它的顶点.(图7-6-2).例3 (E03) 函数22x y z -= 在点(0,0)处无极值. 从几何上看,它表示双曲抛物面(马 鞍面)(图7-6-3)例4 (E04) 求函数x y x y x y x f 933),(2233-++-=的极值.解 先解方程组解得驻点为),0,1(),2,1(),0,3(-).2,3(-再求出二阶偏导数),(y x f xx ,66+=x ),(y x f xy ,0=),(y x f yy .66+-=y在点 (1, 0) 处, ,06122>⋅=-B AC 又,063),(0963),(22⎪⎩⎪⎨⎧=+-==-+=y y y x f x x y x f y x ,0>A 故函数在该点处有极小值;5)0,1(-=f在点 (1, 2) 处, )0,3(-处,,06122<⋅-=-B AC 故函数在这两点处没有极值;在点)2,3(-处,,0)6(122>-⋅-=-B AC 又,0<A 故函数在该点处有极大值.31)2,3(=-f例5 证明函数 y y ye x e z -+=cos )1(有无穷多个极大值而无一极小值.二元函数的最大值与最小值.证 由⎪⎩⎪⎨⎧=--='=+-='0)1(cos 0sin )1(y x e z x e z y y y x).(1)1(Z k y k x k ∈⎩⎨⎧--==π 又,cos )1(x e z A y xx +-=''=,sin x e z B y xy -=''=).2(cos y x e z C y yy--=''= 在点))(0,2(z n n ∈π处,,2-=A ,0=B ,1-=C ,022>=-B AC又,0<A 所以函数z 取得极大值;在点))(2,)12((z n n ∈-+π处,,12-+=e A ,0=B ,2--=e C ,0422<--=---e e B AC 此时函数无极值.证毕.二元函数的最大值与最小值例6 求函数y xy x y x f 22),(2+-=在矩形域 |),{(y x D =}20,30≤≤≤≤y x上的最大值和最小值.解 先求函数),(y x f 在D 内驻点.由,022=-=y x f x 022=+-=x f y 求得f 在D 内部的唯一驻点 (1, 1),且.1)1,1(=f 其次求函数),(y x f 在D 的边界上的最大值和最小值.如图所示.区域D 的边界包含四条直线段.,,,4321L L L L在1L 上,0=y ,)0,(2x x f =.30≤≤x 这是x 的单调增加函数,故在1L 上f 的最大值为,9)0,3(=f 最小值为.0)0,0(=f同样在2L 和4L 上f 也是单调的一元函数,易得最大值、最小值分别为,9)0,3(=f 1)2,3(=f (在2L 上),,4)2,0(=f 0)0,0(=f (在4L 上),而在3L 上,2=y ,44)2,(2+-=x x x f ,30≤≤x 易求出f 在3L 上的最大值,4)2,0(=f 最小值.0)2,2(=f将f 在驻点上的值)1,1(f 与4321,,,L L L L 上的最大值和最小值比较,最后得到f 在D 上的最大值,9)0,3(=f 最小值.0)2,2()0,0(==f f例7 求二元函数)4(),(2y x y x y x f z --==在直线6=+y x , x 轴和y 轴所围成的闭区域D 上的最大值与最小值.解 先求函数在D 内的驻点,解方程组 ,0)4(),(0)4(2),(222⎩⎨⎧=---='=---='y x y x x y x f y x y x xy y x f xx 得唯一驻点),1,2(且,4)1,2(=f 再求),(y x f 在D 边界上得最值,在边界6=+y x 上,即,6x y -=于是),2)(6(),(2--=x x y x f由,02)6(42=+-='x x x fx 得4,021==x x ,264=-==x x y 而,64)2,4(-=f 所以4)1,2(=f 为最大值,64)2,4(-=f 为最小值.例8 求函数 32233),(x y x y x f -+=在区域16:22≤+y x D 上的最小值.解 先求),(y x f 在D 内的极值.由,36),(2x x y x f x -=',6),(y y x f y =' 解方程组⎩⎨⎧==-060362y x x 得驻点(0, 0), (2, 0). 由于,6)0,0(=''xxf ,0)0,0(=''xy f ,6)0,0(=''yy f ,6)0,2(-=''xxf ,0)0,2(=''xy f .6)0,2(=''yy f 所以, 在点 (0, 0) 处,0362<-=-AC B ,06>=A 故在 (0, 0) 处有极小值.0)0,0(=f 在点 (2, 0) 处,0362>=-AC B 故函数在点 (2, 0)处无极值.再求),(y x f 在边界1622=+y x 上的最小值.由于点),(y x 在圆周1622=+y x 上变化,故可解出),44(1622≤≤--=x x y 代入),(y x f 中,有z ),(y x f =32233x y x -+=348x -=),44(≤≤-x这时z 是x 的一元函数,求得在]4,4[-上的最小值.164-==x z 最后比较可得,函数32233),(x y x y x f -+=在闭区间D 上的最小值.16)0,4(-=f例9 求 122+++=y x yx z 的最大值和最小值.解 x z 22222)1()(2)1(+++-++=y x y x x y x ,0=y z 22222)1()(2)1(+++-++=y x y x y y x ,0=解得驻点 ⎪⎪⎭⎫ ⎝⎛21,21和,21,21⎪⎪⎭⎫ ⎝⎛-- 因为,01lim 22=+++∞→∞→y x y x y x 即边界上的值为零.又 ,2121,21=⎪⎪⎭⎫ ⎝⎛z ,2121,21-=⎪⎪⎭⎫ ⎝⎛--z 所以最大值为,21最小值为.21-例10 (E05) 某厂要用铁板做成一个体积为32m 的有盖长方体水箱. 问当长、宽、高各 取怎样的尺寸时, 才能使用料最省.解 设水箱的长为,xm 宽为,ym 则其高应为./2xym 此水箱所用材料的面积 A ⎪⎪⎭⎫ ⎝⎛⋅+⋅+=xy x xy y xy 222⎪⎪⎭⎫ ⎝⎛++=y x xy 222).0,0(>>y x 此为目标函数.下面求使这函数取得最小值的点).,(y x 令,0222=⎪⎭⎫ ⎝⎛-=x y A x .0222=⎪⎪⎭⎫ ⎝⎛-=y x A y 解这方程组,得唯一的驻点,23=x .23=y根据题意可断定,该驻点即为所求最小值点. 因此当水箱的长为m 32、宽为m 32、高为=⋅33222m 32时,水箱所用的材料最省.注: 体积一定的长方体中,以立方体的表面积为最小.例11 (E06) 设1q 为商品A 的需求量, 2q 为商品B 的需求量, 其需求函数分别为,10420,4216212211p p q p p q -+=+-=总成本函数为2123q q C +=,其中21,p p 为商品A 和B 的价格, 试问价格21,p p 取何值时可使利润最大?解 按题意,总收益函数为),10420()42216(2122112211p p p p p p q p q p R -+++--=+=于是总利润函数为)2()3(2211-+-=-=p q p q C R L).10420)(2()4216)(3(212211p p p p p p -+-++--=为使总利润最大,求一阶偏导数,并令其为零:,08414211=+-=∂∂p p p L )2(10)10420()3(422111---++-=∂∂p p p p p L ,02082821=-+=p p由此解得 ,14,26321==p p 又因 .0)20)(4(8)(22<---=''⋅''-''yy xx xy L L L 故取价格14,26321==p p 时利润可达最大,而此时得产量为.6,921==q q例12 求函数xyz u =在附加条件a z y x /1/1/1/1=++ ()0,0,0,0>>>>a z y x (1)下的极值.解 作拉格朗日函数),,,(λz y x L )./1/1/1/1(a z y x xyz -+++=λ由.3.3/.0)/1/1/1(30/0/0/222a x y x a xyz z y x xyz z xy L y xz L x yz L zy x ===⇒=⇒=++-⇒⎪⎩⎪⎨⎧=-==-==-=λλλλλ故)3,3,3(a a a 是函数xyz u =在条件(1)下唯一驻点.把条件(1)确定的隐函数记作),,(y x z z =将目标函数看作),,(),(y x F y x z xy u =⋅=再应用二元函数极值的充分条件判断,知点,3,3(a a )3a 是函数xyz u =在条件(1)下的极小值点.而所求极值为.273a条件极值 拉格朗日乘数法例13 (E07) 求表面积为2a 而体积为最大的长方体的体积.解 设长方体的三棱长为,,,z y x 则问题就是在条件 ),,(z y x ϕ2222a xz yz xy -++=0=(1) 下, 求函数)0,0,0(>>>=z y x xyz V 的最大值.作拉格朗日函数),,,(λz y x L ),222(2a xz yz xy xyz -+++=λ 由..,0)(20)(20)(2z y x z x y x z y z y z x y x x y xy L z x xz L z y yz L zy x ==⇒++=++=⇒⎪⎩⎪⎨⎧=++==++==++=λλλ代入 (1) 式,得唯一可能的极值点:,6/6a z y x ===由问题本身意义知,此点就是所求最大值点.即,表面积为2a 的长方体中,以棱长为6/6a 的正方体的体积为最大,最大体积.3663a V =例14 在经济学中有个Cobb-Douglas 生产函数模型,),(1a a y cx y x f -=式中x 代 表劳动力的数量, y 为资本数量(确切地说是y 个单位资本), c 与)10(<<a a 是常数, 由各工厂的具体情形而定. 函数值表示生产量.现在已知某制造商的Cobb-Douglas 生产函数是=),(y x f ,1004143y x 每个劳动力与每单位资本的成本分别是150元及250元. 该制造商的总预算是50000元. 问他该如何分配这笔钱用于雇用劳动力与资本,以使生产量最高.解 这是个条件极值问题,求函数4143100),(y xy x f =在条件50000250150=+y x 下的最大值. 令)25015050000(100),,(413y x y x y x L --+=λλ,由方程组⎪⎩⎪⎨⎧=--==-==-=--0250150500000250250150754343141y x L yx L y x L xx x λλ 中的第一个方程解得,21411y x -=λ将其代入第二个方程中,得 ,0125254141343=---y x y x 在该式两边同乘,4341y x 有,012525=-y x 即.5y x =将此结果代入方程组的第三个方程得,50,250==y x 即该制造商应该雇用250个劳动力而把其余得部分作为资本投入,这时可获得最大产量.16719)50,250(=f例15 (E08) 设销售收入R (单位:万元)与花费在两种广告宣传的费用y x ,(单位:万元) 之间的关系为yy x x R +++=101005200 利润额相当五分之一的销售收入, 并要扣除广告费用. 已知广告费用总预算金是25万元, 试问如何分配两种广告费用使利润最大?解 设利润为,z 有 z y x R --=51.1020540y x y y x x --+++=,限制条件为.25=+y x 这是条件极值问题.令),,(λy x L )25(1020540-++--+++=y x y x yy x x λ 从,01)5(2002=+-+=λx L x 01)10(2002=+-+=λy L y22)10()5(y x +=+又,25x y -=解得,15=x .10=y 根据问题本身的意义及驻点的唯一性即知,当投入两种广告的费用分别为15万元和10万元时,可使利润最大.例16 设某电视机厂生产一台电视机的成本为c , 每台电视机的销售价格为p , 销售量为x .假设该厂的生产处于平衡状态, 即电视机的生产量等于销售量. 根据市场预测, 销售量x 与销售价格为p 之间有下面的关系:ap Me x -= )0,0(>>a M (1) 其中M 为市场最大需求量, a 是价格系数. 同时, 生产部门根据对生产环节的分析, 对每台电视机的生产成本c 有如下测算: x k c c ln 0-= (1,0>>x k ), (2) 其中0c 是只生产一台电视机时的成本, k 是规模系数. 根据上述条件, 应如何确定电视机的售价p , 才能使该厂获得最大利润?解 设厂家获得的利润为,u 每台电视机售价为,p 每台生产成本为,c 销售量为,x 则.)(x c p u -=于是问题化为利润函数x c p u )(-=在附加条件(1)、(2) 下的极值问题.利用拉格朗日乘数法,作拉格朗日函数:),,,,(μλc p x L ).ln ()()(0x k c c Me x x c p ap +-+-+-=-μλ令x L x k c p /)(μλ++-=,0=p L ap aMe x -+=λ,0=c L μ+-=x .0=将 (1) 代入 (2),得 ).(ln 0ap M k c c --= (3)由 (1) 及0=p L 知 ,1-=a λ即./1a -=λ (4)由0=c L 知,μ=x 即 .1/=μx将 (3)、(4)、(5) 代入,0=x L 得,0/1)(ln 0=+--+-k a ap M k c p由此得 *p .1/1ln 0akk a M k c --+-=由问题本身可知最优价格必定存在,故这个*p 就是电视机的最优价格.数学建模举例1.最小二乘法数理统计中常用到回归分析,也就是根据实际测量得到的一组数据来找出变量间的函数关系的近似表达式. 通常把这样得到的函数的近似表达式叫做经验公式. 这是一种广泛采用的数据处理方法. 经验公式建立后,就可以把生产或实践中所积累的某些经验提高到理论上加以分析,并由此作出某些预测. 下面我们通过实例来介绍一种常用的建立经验公式的方法.例17 (E09) 测定刀具的磨损速度,按每隔一小时测量一次刀具厚度的方式,得到如下 实测数据:8.243.257.251.263.265.268.260.27)(76543210)(76543210毫米刀具厚度小时时间顺序编号i i y t i试根据这组实测数据建立变量y 和t 之间的经验公式).(t f y =解 观察散点图,易发现所求函数)(t f y =可近似看作线性函数,因此可设,)(b at t f +=其中a 和b 是待定常数,但因为图中各点并不在同一条直线上,因此希望要使偏差)7,,2,1,0()(Λ=-i t f y i i 都很小.为了保证每个这个的偏差都很小,可考虑选取常数,,b a 使∑=+-=702)]([i i i b at yM 最小.这种根据偏差的平方和为最小的条件来选择常数b a ,的方法叫做最小二乘法.求解本例:可考虑选取常数,,b a 使∑=+-=702)]([i i i b at yM 最小.把M 看成自变量a和b 的一个二元函数,那么问题就可归结为求函数),(b a M M =在那些点处取得最小值.令,0)]([20)]([2707⎪⎪⎩⎪⎪⎨⎧=+--=∂∂=+--=∂∂∑∑==i i i i i i i b at y b M t b at y a M即 .0)]([0)]([77⎪⎪⎩⎪⎪⎨⎧=+-=+-∑∑==i i i i i i i b at y t b at y 整理得.871717171712⎪⎪⎩⎪⎪⎨⎧=+=+∑∑∑∑∑=====i i i i i i i i i i i y b t a t y t b t a (1) 计算,得.0.717,5.208,140,28717171271====∑∑∑∑====i ii i i iii ity ytt代入(1),得 ⎩⎨⎧=+=+5.20882871728140b a b a.125.27,3036.0=-=b a于是,所求经验公式为 .125.273036.0)(+-==t t f y (2) 根据上式算出的)(i t f 与实测的i y 有一定的偏差,见下表:注:偏差的平方和,108165.0=M 其平方根.392.0=M 我们把M 称为均方误差,它的大小在一定程度上反映了用经验公式近似表达原来函数关系的近似程度的好坏.注:本例中实测数据的图形近似为一条直线,因而认为所求函数关系可近似看作线性函数关系,这类问题的求解比较简便.有些实际问题中,经验公式的类型虽然不是线性函数,但我们可以设法把它转化成线性函数的类型来讨论.2.线性规划问题求多个自变量的线性函数在一组线性不等式约束条件下的最大值最小值问题,是一类完全不同的问题,这类问题叫做线性规划问题. 下面我们通过实例来说明.例18 (E10) 一份简化的食物由粮和肉两种食品做成, 每份粮价值30分, 其中含有4单位醣, 5单位维生素和2单位蛋白质; 每一份肉价值50分, 其中含有1单位醣, 4单位维生素和4单位蛋白质. 对一份食物的最低要求是它至少要由8单位醣, 20单位维生素和10单位蛋白质组成, 问应当选择什么样的食物, 才能使价钱最便宜.解 设食物由x 份粮和y 份肉组成,其价钱为.5030y x C +=由食物的最低要求得到三个不等式约束条件,即:为了有足够的醣,应有;84≥+y x 为了有足够的维生素,应有;2045≥+y x为了有足够的蛋白质,应有;1042≥+y x 并且还有.0,0≥≥y x 上述五个不等式把问题的解限制在平面上如图的阴影区域中,现在考虑直线族.5030y x C +=当C 逐渐增加时,与阴影区域相交的第一条直线是通过顶点S 的直线,S 是两条直线 2045=+y x 和1042=+y x 的交点,所以点S 对应于C 的最小值的坐标是),65,310(即这种食物是由313份粮和65份肉组成. 代入y x C 5030+=即得到所要求的食物的最低价格32141655031030min =⨯+⨯=C 分.下面的例子是用几何方法来解决的.例19 (E11) 一个糖果制造商有500g 巧克力, 100g 核桃和50g 果料. 他用这些原料生产三种类型的糖果. A 类每盒用3g 巧克力, 1g 核桃和1g 果料, 售价10元. B 类每盒用4g 巧克力和1g 核桃, 售价6元. C 类每盒是5g 巧克力, 售价4元. 问每类糖果各应做多少盒, 才能使总收入最大?解 设制造商出售C B A ,,三类糖果各为z y x ,,盒,总收入是z y x R 4610++=(元). 不等式约束条件由巧克力、核桃和果料的存货限额给出,依次为 .50,100,500543≤≤+≤++x y x z y x当然,由问题的性质知,y x ,和z 也是非负的,所以 .0,0,0≥≥≥z y x 于是,问题化为:求R 的满足这些不等式的最大值.上述不等式把允许的解限制在Oxy 空间中的一个多面体区域之内(如图).在平行平面R z y x =++4610中只有一部分平面和这个区域相交,随着R 增大,平面离原点越来越远.显然,R 的最大值一定出现在这样的平面上,这种平面正好经过允许值所在多面体区域的由图可见,R 的最大值是920元,相应的点是,)30,50,50(所以A 类50盒,B 类30盒,C 类30盒时收入最多.课堂练习1.求函数)(2)(),(22222y x y x y x f --+=的极值.2.求函数)sin(sin sin ),(y x y x y x f z +-+==在由x 轴, y 轴及直线π2=+y x 所围成三角形中的最大值.3.某工厂生产两种产品A 与B, 出售单价分别为10元与9元, 生产x 单位的产品A 与生产y 单位的产品B 的总费用是:)()33(01.03240022元y xy x y x +++++求取得最大利润时, 两种产品的产量各多少?。
