理论力学 第13章
理论力学习题册答案

理论力学习题册答案班级姓名学号第一章静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体,还适用于变形体。
()2、作用于刚体上三个力的作用线汇交于一点,该刚体必处于平衡状态。
()3、刚体是真实物体的一种抽象化的力学模型,在自然界中并不存在。
()4、凡是受两个力作用的刚体都是二力构件。
()5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。
()二.选择题1、在下述公理、法则、原理中,只适于刚体的有()①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
(a)球A(b)杆AB- 1 -(c)杆AB、CD、整体(d)杆AB、CD、整体(e)杆AC、CB、整体(f)杆AC、CD、整体四.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
(a)球A、球B、整体(b)杆BC、杆AC、整体- 2 -班级姓名学号第一章静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
(a)杆AB、BC、整体(c)杆AB、CD、整体CAFAxDBFAyFBWEW(b)杆ABOriginal Figure、BC、轮E、整体FBD of the entire frame(d)杆BC带铰、杆AC、整体- 3 -(e)杆CE、AH、整体(g)杆AB带轮及较A、整体(f)杆AD、杆DB、整体(h)杆AB、AC、AD、整体- 4 -班级姓名学号第二章平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F= - F’,所以力偶的合力等于零。
()2、用解析法求平面汇交力系的合力时,若选用不同的直角坐标系,则所求得的合力不同。
()3、力偶矩就是力偶。
第十三章动量矩定理_理论力学

式中
分别为作用于质点上的内力和外力。求 n 个方程的矢量和有
式中
,
于 点的主矩。交换左端求和及求导的次序,有
为作用于系统上的外力系对
令 (13-3)
为质系中各质点的动量对 点之矩的矢量和,或质系动量对于 点的主矩,称为质系对 点的动量矩。由此得
(13-4) 式(13-4)为质系动量矩定理,即:质系对固定点 的动量矩对于时间的一阶导数等于外力 系对同一点的主矩。
设 Q 为体积流量, 为密度, 和 分别为水流进口处和出口处的绝对速度, 和 分别为涡轮外圆和内圆的半径, 为 与涡轮外圆切线的夹角, 为 与涡轮内圆切线的
夹角,则
由动量矩定理 得
为叶片作用于水流上的力矩。若水涡轮共有 个叶片,则水流作用于涡轮的转动力矩为
方向与图示方向相反。 §13-2 刚体绕定轴转动微分方程
解:取两叶片间的水流为研究对象(图 13-4 中的兰色部分)。作用于质系上的的外力有 重力和叶片的约束力,重力平行于 z 轴,对转动轴之矩为零。所以外力主矩为叶片对水流
的约束力对 z 轴之矩 。
计算 时间间隔内动量矩的增量 。设 t 瞬时占据 ABCD 的水流,经过 时间间隔
后,运动至占据
,设流动是稳定的,则
有
式中
得
(13-8)
或
(13-9)
此式称为刚体绕定轴转动的微分方程。
为刚体绕定轴转动的角加速度,所以上式
可写为
(13-10)
1.由于约束力对 z 轴的力矩为零,所以方程中只需考虑主动力的矩。 2.比较刚体绕定轴转动微分方程与刚体平动微分方程,即
与
形式相似,求解问题的方法和步骤也相似。 转动惯量与质量都是刚体惯性的度量,转动惯量在刚体转动时起作用,质量在刚体平动
《理论力学》第十三章--虚位移试题及答案
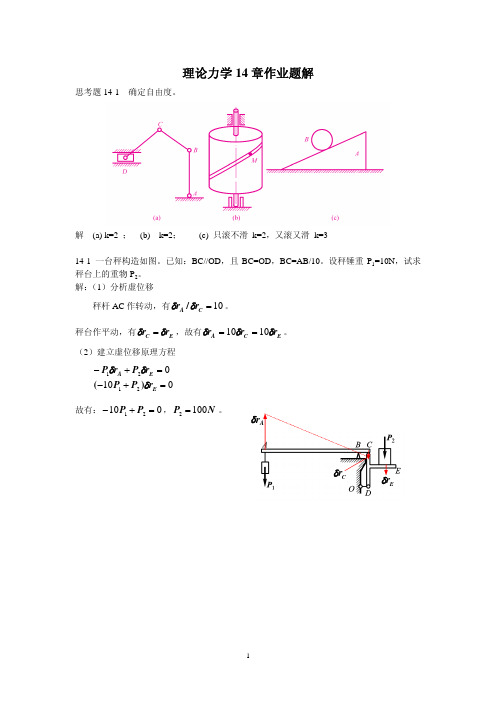
理论力学14章作业题解思考题14-1 确定自由度。
解 (a) k=2 ; (b) k=2; (c) 只滚不滑 k=2,又滚又滑 k=314-1 一台秤构造如图。
已知:BC//OD ,且BC=OD ,BC=AB/10。
设秤锤重P 1=10N ,试求秤台上的重物P 2。
解:(1)分析虚位移 秤杆AC 作转动,有10=C A r r d d /。
秤台作平动,有E C r r d d =,故有E C A r r r d d d 1010==。
(2)建立虚位移原理方程1002121=+-=+-E E A r P P r P r P d d d )(故有:01021=+-P P ,N P 1002=。
Cr d Er14-5 OA=l ,OC=R满足的条件。
解: (用虚位移原理求解)(1) 运动分析(虚位移关系分析)A 处虚位移关系用合成运动的理论分析。
A 为动点,OC 为动系。
r e A r r r r r r d d d +=f d d cos A e r r =另外:R r l r C e /d d = (2) 虚功方程fd f f d d d d cos /)cos /(cos /R l F F r R l F F R r l F r F r F r F C C C A C 21212121000==-=-=-14-9 已知:AC=BC=EC=GC=DE=DG=l ,荷载F 2。
求平衡时的F 1。
解 用解析法,1个自由度,选q 为广义坐标。
建立坐标,如图。
(1) 计算虚位移qdqd q qdq d q sin ,cos cos ,sin l y l y l x l x A A D D 2233-====(2) 计算力的投影 2211F F F F x y -=-= , (3) 建立虚位移原理方程qqdq q q d d sin cos )cos sin (230320212121F F l F l F x F y F D x A y ==×-×=+Oxy14-12 F=4kN, AO=OE=5m. 求D 解:(1) 接触D 处水平约束,代之约束力。
13.2转动惯量(重庆大学土木理论力学课件)解析

3、性质
转动惯量的性质与刚体的质量以及质量相对于转动
轴的分布状况有关。
4、单位:kg·m2;kg·cm2
若单位制不同,则Jz的单位不同, 为了避免不同的单位制引起错误, 也为了便于记忆,将 Jz /m,就变 成只与长度有关的量(而各单位制
z
zi
xi x
mi
yi y
中长度都是基本量)因此就可统一 表示。
J z' mi[xi2 ( yi d )2 ]
mi (xi2 yi2) ( mi )d 2 2d mi yi
mi m , mi yi myC 0
J z' J zC md 2
刚体对通过质心轴的转动惯量具有最小值。
推论: J z J zC md 2
m
对于均质物体,其密度r为常量,如以V表示物体 的体积,则有,
Jz
r 2dV
V
m V
r 2dV
V
7、常见情形
①均质等截面细直杆对于通过中点且与杆垂直的y轴的转动惯 量。
Jz
m V
r2dV m
V
Al
r2 Adr
V
m 0.5l r2dr 1 ml2
l 0.5l
由式(13-5)可知,在所有相互平行的轴中,物 体对于通过其质心的轴的转动惯量为最小。
例如,均质等截面细 直杆对于通过杆端且 与杆垂直的z′轴的 转动惯量为:
J z
J zC
md 2
1 12
ml 2
m( l )2 2
1 3
ml 2
z 0.577l
3、其他方法
理论力学-第13章 动力学普遍方程和第二类拉格朗日方程

*第13章 动力学普遍方程和第二类拉格朗日方程
第二类拉格朗日方程
返回
第二类拉格朗日方程
在动力学普遍方程中,由于系统存在约束,一般情形下,各 质点的虚位移并不完全独立,应用时须建立各虚位移与广义坐标 之间的关系。
第二类拉格朗日方程
N
(Qk Qk*) δ qk 0
k 1
其中Qk为对应于广义所标qk的广义力(generalized forces); Qk*为广义惯性力(generalized inertia forces)
Qk
n i 1
Fi
ri qk
Qk*
n i 1
miai
ri qk
由于在完整约束下,δq1, δq2,…, δqN 相互独立,
Qk*
n i 1
miri
ri qk
d dt
n
(
i 1
miri
ri qk
)
n i 1
miri
d dt
( ri qk
)
d dt
n i1
mi
ri
ri qk
n i1
mi
ri
ri qk
d dt
qk
n
(
i 1
1 2
miri2 )
qk
n
(
i 1
1 2
miri2 )
d dt
(
T qk
理论力学
第3篇 工程动力学基础
第3篇 工程动力学基础
*第13章 动力学普遍方程 和第二类拉格朗日方程
*第13章 动力学普遍方程和第二类拉格朗日方程
理论力学第13章动能定理

在理论力学中,动能被定义为物体运动时的能量,其大小与物体的质量和速度有关。根据牛顿第二定律,物体的动量改变量等于作用在物体上的外力的冲量。因此,如果一个力在一段时间内作用在一个物体上,那么这个力就会使物体的动量发生改变,从而产生动能的变化。
动能的定义
外力的功
外力的功等于力的大小与物体在力的方向上发生的位移的乘积。
总结词
外力的功是指力对物体运动所产生的效应,其大小等于力的大小与物体在力的方向上发生的位移的乘积。这是物理学中功的定义,也是计算外力对物体所做功的基本方法。
详细描述
VS
系统动能的增量等于合外力对系统所做的功。
详细描述
系统动能的增量是指在一个过程中,系统动能的增加量。这个增量可以通过计算合外力对系统所做的功来得到。如果合外力对系统做正功,则系统动能增加;如果合外力对系统做负功,则系统动能减少。因此,系统动能的增量与合外力对系统所做的功有直接的关系。
总结词
系统动能的增量
03
CHAPTER
动能定理的应用
适用于单个质点在力的作用下运动的情况,计算质点的动能变化。
单个质点的动能定理指出,质点在力的作用下运动时,外力对质点所做的功等于质点动能的增量。这个定理是理论力学中研究质点运动的基本定理之一,可以用来解决各种实际问题。
总结词
详细描述
单个质点的动能定理
动能定理是能量守恒定律在动力学中的具体表现,是解决动力学问题的有力工具。
动能定理适用于一切宏观低速的物体,对于微观、高速适用于狭义相对论。
动能定理适用于直线运动,对于曲线运动需要积分形式进行处理。
动能定理的适用范围
02
CHAPTER
动能定理的基本内容
总结词
理论力学练习册及答案
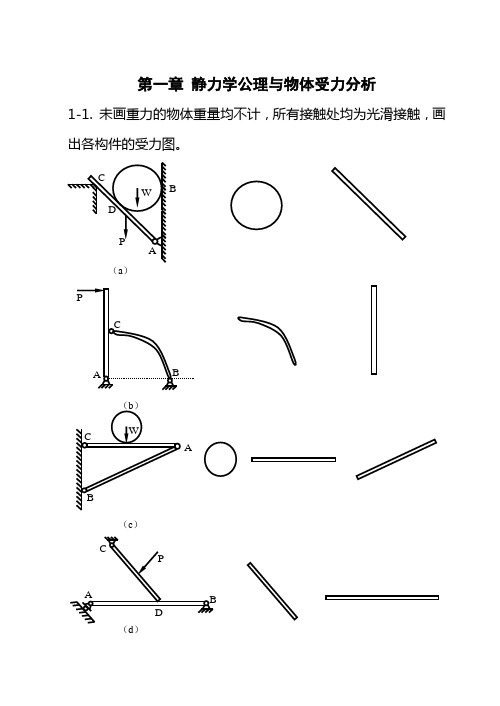
8-8.图示机构中,设当OA与水平线成450角的瞬时,曲柄OA有反时针方向的匀角速度ω=25 rad/s,连杆AB水平,扇形板BD铅垂。求扇形板绕定轴D转动的角加速度ε。
解:将力系向A点简化,并过A点建立如图所示坐标系。
由矢量式可得力系简化的最终结果为力螺旋,
作用点为:
3-2.已知A(1,0,1),B(0,1,2)(长度单位为米),F= kN。求力F对x、y、z轴的矩?
解:
3-3.如图所示,长方体边长为a、b、c,力F沿BD,试计算力F对AC轴之矩MAC(F)
解:力F对C点的矩为:
4-3.置于铅垂面内的均质正方形簿板重P= 100kN,与地面间的摩擦系数f= 0.5,欲使簿板静止不动,求作用在点A的力F的最大值?
4-4.折梯放在水平地面上,其两脚与地面的摩擦系数分别为fA= 0.2,fB= 0.6,折梯一边AC的中点D上有一重为P= 500N的重物,折梯重量不计,问折梯能否平衡?如果折梯平衡。试求出两脚与地面间的摩擦力。
第六章 刚体基本运动
6-1.在如图所示中,已知ω、。在图上标示出A、B两的速度、加速度。
6-2.在如图所示的平面机构中,半径为r的半圆盘在A和B处与杆铰接,已知 , ,曲柄O1A以匀角速度ω转动。求图示瞬时圆盘上M点的速度和加速度。
6-3.在如图所示的平面机构中,齿轮1紧固在杆AC上, ,齿轮1与半径为r2的齿轮2啮合,齿轮2可绕O2轴转动,。设 , ,试确定 时,轮2的角速度和角加速度。
解:动点取曲柄OA上A点,
理论力学(机械工业出版社)第十三章达朗伯原理习题解答

习 题13-1 如图13-16所示,一飞机以匀加速度a 沿与水平线成仰角b 的方向作直线运动。
已知装在飞机上的单摆的悬线与铅垂线所成的偏角为f ,摆锤的质量为m 。
试求此时飞机的加速度a 和悬线中的张力F T 。
图13-16ma F =I 0cos sin 0I T =-=∑βϕF F F xϕβsin cos IT F F =0sin cos 0I T =--=∑mg F F F y βϕ0sin cos sin cos I I =--mg F F βϕϕβ0sin )cos(I=-+mg F ϕβϕ mgma=+ϕβϕsin )cos()cos(sin βϕϕ+=g amg maF F )cos(cos sin cos sin cos I T βϕβϕβϕβ+===13-2 球磨机的简图如图13-17所示,滚筒作匀速转动,内装钢球及被粉碎的原料,当钢球随滚筒转到某一角度f 时,将脱离筒壁作抛射运动,由于钢球的撞击,从而破碎与研磨原料。
已知钢球脱离筒壁的最佳位置'4054︒=ϕ,滚筒半径R =0.6m 。
试求使钢球在'4054︒=ϕ处脱离滚筒的滚筒转速。
图13-172n I ωmR ma F == 0cos 0I N n =-+=∑F mg F F ϕ)cos (cos cos 22I N ϕωϕωϕg R m mg mR mg F F -=-=-=令0N =F0cos 2=-ϕωg RR g ϕωcos =min r/35.296.00454cos 8.9π30cos π30π30='︒⨯===R g n ϕω13-3 一质量为m 的物块A 放在匀速转动的水平转台上,如图13-18所示。
已知物块的重心距转轴的距离为r ,物块与台面之间的静摩擦因数为s μ。
试求物块不致因转台旋转而滑出时水平转台的最大转速。
图13-182n I ωmr ma F == 00N =-=∑mg F F ymg F =N00I =-=∑F F F x0N s 2=-F mr μω 0s 2=-mg mr μωrgs μω=rgn s max π30π30μω==13-4 离心调速器的主轴以匀角速度w 转动,如图13-19所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
rr
mrC aC
r
惯性力系向质心简化:M IC 0
只简化为一个力:FIR maC
平移刚体的惯性力系可以简化为通过质心的 合力,其大小等于刚体的质量与加速度的乘积, 合力的方向与加速度方向相反。
2.刚体定轴转动
z
切向惯性力:FIit miait miri
法向惯性力:FIin
mi
an i
1.96N
应用静力学写平衡 方程的方法求解动力
v
FTl sin 2 2.1m/s
m
学问题,这种方法称 为动静法。
§ 13-2 质点系的达朗贝尔原理
Fi FNi FIi 0
i 1,2, ,n
—— 质点系的达朗贝尔原理
质点系中每个质点上作用的主动力,约束力和 惯性力在形式上组成平衡力系.
例13-1
已知: m 0.1kg ,l 0.3m, 60 求: v, FT.
解: 法向惯性力的大小:
FI
man
v2 m
l sin
根据质点的达朗贝尔原理:
mg
FT
FI
0
在自然轴上投影:
F b 0, FT cos mg 0
F n 0, FT sin FI 0
FT
mg
cosቤተ መጻሕፍቲ ባይዱ
第十三章 达朗贝尔原理
§ 13-1 惯性力·质点的达朗贝尔原理
由牛顿第二定律,有
令:FFImaFmN aFmaF惯N 0性力
FI m
有:F
FN
FI
0
FN
—— 质点的达朗贝尔原理
F
ma
作用在质点的主动力、约束力和虚加的惯性 力在形式上组成平衡力系.
注意:质点并非处于平衡状态,达朗贝尔原理只 是将动力学问题转化为静力学问题求解
这个力偶的矩等于刚体对转轴的转动惯量与 角加速度的乘积,转向与角加速度相反。
思考: 对于具有质量对称平面的刚体:
1.刚体匀速转动,转轴不通过质心。
FIR maC
作用点在转轴上。
2.转轴通过质心,但 。0
M IO JO
3.刚体作匀速转动,且转轴通过质心。
FIR 0 , MIO 0
3.刚体作平面运动(平行于质量对称面)
D
解: 刚好离开地面时,地面约束力为零.
研究 AB 杆,杆为平移,加惯性力:
FIC m2a
按达朗贝尔原理列平衡方程:
M A 0 m2aR sin 30 m2gR cos30 0
解得:a 3g
研究整体,加惯性力和惯性力矩:
FIA
m1a,
MIA
1 2
m1R2
a R
D
按达朗贝尔原理列平衡方程:
记 Fi(e) 为作用于第i个质点上质点系外部物体的作用力.
Fi
(i)为作用于第i个质点上质点系内部的力.
F (e) i
F (i) i
FIi
0
i 1,2, , n
对于质点系,由静力学可知,空间任意力系 平衡的充分必要条件为:
F (e) i
0Fi(i)
FIi 0
MO
F (e) i
求:支座A,B受到的附加约束力.
解: 重物平移,加惯性力:FI ma
转子定轴转动,加惯性力矩:M IO J
由质点系的达朗贝尔原理,列平衡方程:
J
a R
MB 0 mgl2 FIl2 Pl3 MIO FA l1 l2 0
Fy 0 FA FB mg P FI 0
静约束力 附加动约束力
向质心简化 随同质心平移运动
FIR
maC
绕质心转动
M IC JC
有质量对称平面的刚体,平行于此平面运动 时,刚体的惯性力系简化为在此平面内的一个力 和一个力偶。
这个力通过质心,其大小等于刚体质量与质 心加速度的乘积,方向与质心加速度方向相反;
这个力偶的矩等于刚体对过质心且垂直于质 量对称面的轴的转动惯量与角加速度的乘积,转 向与角加速度相反。
M0O
F (i) i
M O FIi 0
F (e) i
FIi 0
M O
F (e) i
M O FIi 0
作用在质点系上的所有外力与虚加在每个 质点上的惯性力在形式上组成平衡力系
例13-2 已知:如图所示,定滑轮的半径为r ,质量为m 均匀分布
在轮缘上,绕水平轴O转动.垮过滑轮的无重绳的两端
挂有质量为m1 和m2 的重物(m1>m2),绳与轮间不打 滑,轴承摩擦忽略不计。 求:重物的加速度.
解: 对两重物加惯性力,大小分别为:
FI1 m1a, FI2 m2a
记滑轮边缘上任一点的质量为 mi ,加速度
有切向、法向之分,惯性力大小分别为:
FIit mir mia
列平衡方程:
,
FIin
r
FIR
r Fi
e
mi ar i
marC
M IO
MO
F (e)
i
d LO dt
主矢 主矢的大小和方向与简化中心的位置无关
FIR
maC
主矩 主矩的大小和方向与简化中心的位置一 般有关
1.刚体平移
惯性力系向点O 简化:
r
M IO
rri
r FIi
rri (miarC ) ( mirri ) arC
FA
mgl2 Pl3 l1 l2
l1
a l2
ml2
J R
FB
mgl1
Pl1 l2
l1 l2
l3
l1
a l2
ml1
J R
附加动约束力决定于惯性力系
§ 13-4 绕定轴转动刚体的轴承动约束力
如果绕定轴转动的机械在转动起来后轴承受 力与不转时轴承受力一样,则一般来说这些机械 不会产生破坏,也不会产生振动与噪声。
MD 0 FR FIA R MIA FIC R sin 30o m2gR cos30o 0
aCn
aCt
注意
在画虚加的惯性力系的主矢和主矩时,必须按照 和质心加速度的方向相反以及与角加速度转向相反 (考虑负号)的原则画出。在方程中只需按其数值 的大小带入,不能再带负号!
解题步骤及要点
1.选取研究对象:原则与静力学相同。 2.受力分析:画出全部主动力和外约束力。 3.运动分析:主要是刚体质心加速度,刚体角加速度, 标出方向或转向。 4.虚加惯性力:在受力图上画上惯性力和惯性力偶。 5.列动静法方程:选取适当的矩心和投影轴。 6.建立补充方程:运动学补充方程(运动量之间的关 系)。 7.求解未知量。
因 t, 得: Fx m2e2 sint
Fy m1 m2 g m2e 2 cost
M m2gesin t m2e 2h sin t
例13已知5:如图所示,电动绞车安装在梁上,梁的两端搁在 支座上, 绞车与梁共重为P.绞盘半径为R,与电机转子 固结在一起,转动惯量为J ,质心位于O 处.绞车以加速 度a提升质量为m的重物,其它尺寸如图.
解: 对转子,匀速转动,角加
速度为零,无需加惯性力 矩,只需加惯性力:
FI me2
根据质点系的达朗贝尔原理,此 电动机上的外力与惯性力形成一个平 衡力系,列平衡方程:
Fx 0, Fx FI sin 0
Fy 0, Fy (m1 m2)g FI cos 0
M A 0, M m2gesin FI hsin 0
则惯性力系简化的主矩为:
M IO M Iz J z
工程中绕定轴转动的刚体常常有质量对称平面。
结论
当刚体有质量对称平面且绕垂直于此对称面 的轴作定轴转动时,惯性力系向转轴与对称平面 交点简化时,得位于此平面内的一个力和一个力 偶。
这个力等于刚体质量与质心加速度的乘积, 方向与质心加速度方向相反,作用线通过转轴;
由静约束力与动约束力的概念,对绕定轴转 动的刚体,如果能消除轴承附加动约束力,使轴 承只收到静约束力作用,就可以做到这一点。
为此,先把任意一个绕定轴转动刚体的轴承 全约束力求出来,然后再推出消除附加动约束力 的条件。
O点为简化中心 根据动静法,平衡方程如下:
Fx 0 FAx FBx FRx FIx 0 Fy 0 FAy FB y FR y FI y 0
FBx
1 AB
M y FRxOA
M Iy FIxOA
FBy
1 AB
M x FRyOA M Ix FIyOA
FBz FRz
由
FIR
,
M
引起的轴承约束力称为附加动约束力
IO
附加动约束力为零的条件为: FIx FIy 0, M Ix M Iy 0
即: FIx maCx 0 FIy maCy 0
2
s1
158
m s2
惯性力大小为:
FI man 3160N
由质点系的动静法,列平
衡方程可得:
FNA
FNB
1 2
mg FI
1 20 9.8 3160N 1680N
2
• 作业 • 13-11 13-18
例13已6知:均质圆盘 m1, 纯R,滚动.均质杆 l 2R, m2. 求:F 多大,能使杆B 端刚好离开地面? 纯滚动的 条件?
Fz 0 FBz FRz 0 M x 0 FB yOB FAyOA M x MIx 0 M y 0 FAxOA FBxOB M y MI y 0 Mz 0
解得轴承全约束力为:
FAx
1 AB
M y FRxOB
M Iy FIxOB
FAy
1 AB
M x FRyOB M Ix FIyOB
miri 2
FItiO
ri
zi
惯性力系对x轴的矩为:
x
yi xi
