全微分和热力学
热力学一般关系

热力学一般关系本章提要及安排本章提要:1.工质的平衡热力性质是指工质状态参数间的函数关系,特别以可测参数为独立变量的热力学能、焓、熵函数在工程应用中尤为重要。
2.对热力学状态函数的研究通常从它们的偏微商着手。
在常用状态函数的偏微商中,有的是可以通过实验测定的,常将它们定义为各种热系数;有的则不能用实验的方法得出。
3.工质在准平衡变化中的热力学基本定律表达式同时也表达了热力学状态函数之间的基本关系,又称基本热力学关系式。
通过勒让德变换,基本热力学关系可以用不同的组合参数表达。
基本热力学关系的一阶偏微商和二阶混合偏微商给出状态函数偏微商之间的一般关系。
当然,与热力学基本定律一样这些一般关系对任何工质都是适用的。
4.按照基本热力学关系,可以用可测的状态参数和热系数来表达不能通过实验直接得出的偏微商,从而将各常用状态函数的全微分式用可测的参数及免系数表达出来。
这样,就为在实验测定数据的基础上得出工质的状态函数开辟了道路。
5.在工质热力性质研究中,并非所有热系数都是必需沤过实验测定的,应用热系数间的一般关系可以由少虽测得的热系数得到所需的其它热系数。
这样,可以大大减少研究中的实验工作量.同时减小由于有限的实验精确度带来的误差。
6.依据本章所导出的一般关系式,应用所讲述的推导方法,还可导得工程中需用的各种函数关系。
7.本章所导出的一般关系式只适用于简单可压缩系统。
本章要求:1.了解热力学一般关系的内容及其在工质热力性质研究中的地位和作用;2.掌握导出热力学一般关系的思路和推导方法;3.熟悉简单可压缩工质基本的和常用的热力学一般关系。
学习建议:本章学习时间建议共2学时:1.常用状态函数的偏微商;基本热力学关系; 1学时2.热力学能、焓和熵的微分式;热系数之间的一般关系; 1学时4.1 常用状态函数的偏微商本节知识点:状态方程的偏微商热力学能函数的偏微商焓函数的偏微商熵函数的偏微商本节参考图片:麦克斯韦汤姆逊汤姆逊实验本节疑问解答:思考题4.1.1 思考题4.1.2 思考题4.1.3本节基本概念:定温压缩系数压力的温度系数绝热压缩系数比定容热容比定压热容绝热节流系数工程中常用的状态函数有状态方程 F(p ,v ,T )=0,和以可测参数为独立变量的热力学能、焓、熵函数,通常热力学能函数u(T ,v ),焓函数h(T ,p),和熵函数s(T ,v),s(T ,p)的导得较为方便。
热力学基本概念

(vi) 对抗恒定外压过程 始终态压力不相等。
psu=常数。
状态2
(vii)自由膨胀过程(向真空膨胀过程)。
如图1-1所示,
状态1 循环过程 图1-1气体向真空膨胀
以后我们会讲到,此过程没有体积功。
(自由膨胀)
气体 真空
(3)相变化过程与饱和蒸气压 相变化过程:一定条件下聚集态的变化过程。如
气体
(T,p)
(i) 对于一定量组成不变的均相流体系统,系统的任意宏观
性质是另外两个独立的宏观性质的函数: Z=f(x,y),如
理想气体
V nRT p
就是说,这些状态函数之间是有一定的内在联系和制约关系的, 所以一个体系的状态不需要把所有的量都确定,可以通过他们 之间的关系来确定其它的量。联系它们之间关系的方程式称为 状态方程。除PV=nRT外,热力学中还要讲到许多状态方程。
压力—临界压力(pc), pc(CO2)=7.38MPa 体积—临界摩尔体积(Vm,c),Vm,c(CO2)=94×10-6m3·mol-1
Tc , pc , Vm,c 统称临界参量。一些物质的临界参量见表1.2。
表1.2 一些物质的临界参量
物质
He H2 N2 O2 H2O CH4 C2H 4 C6H6 C2H5 OH
b 图1-3
a g
{Vm,c} CO2 定温p-Vm,c 图
温度升高,如T2 ,p-V 线上定压水平段缩短,到温度T2缩
为一点c,此几即为临界状态。临界状态是气液不可分的状态。
T1 T2 Tc T3 {p}
c l
b 图1-3
a g {Vm,c}
CO2 定温p-Vm,c 图
临界状态:
温度—临界温度(Tc),Tc(CO2)=304.2K
6.热力学基本关系式
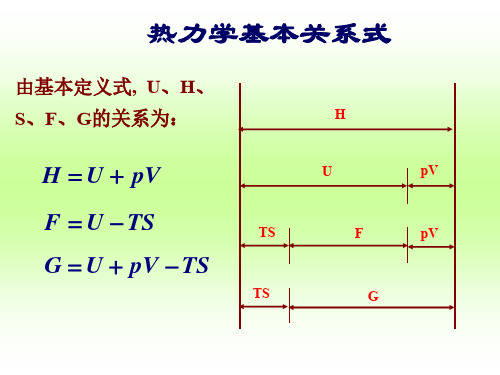
G U pV TS
dG S dT V d p
U、H、F、G这些热力学函数之间的关系实质是勒让德变换 勒让德变换实际上是在我们得到了一个不变量后,要得到它的对偶自变量下的 不变量的一个重要的变换。
热力学四个基本关系式(Gibbs关系式)如下:
d U T d S p dV
S p V T T V
(1)
U p V T T p T V
得证
几个重要的偏导关系式
1.与S有关的
S p V T T V
S V T p p T
d H T d S V d p
(1)
(2) (3)
d F S d T p dV dG S dT V d p
(4)
条件: 简单封闭系统,只作体积功。
• 基本关系式实质上是 U 、 H 、 F 和 G 的数学全 微分展开式。 • 简单的封闭系统, 状态只需两个独立变量即可 决定, 这两个变量可以任意选取. • 从四个关系式的微分变量可知, 对不同的状态 函数, 在作全微分展开时, 选取的独立变量是 不一样的:
例: 试证明:
U p V T T p T V
解:有基本热力学关系式
d U T d S p dV
在等温条件下,求内能对体积的偏微商:
U S V T V p T T
由麦克斯韦关系式: 代入(1)式得:
Wf 0
Qr T d S
将上式代入内能的全微分:
W p dV
d U T d S p dV
(1)
热力学函数间的普遍关系式

不可逆过程 可逆过程 不可能过程
此式热力学第二定律的数学表达式之一,其中δQ为微循环中系 统从外界吸收的热量,T为吸热时热源的温度。
孤立系统的熵增原理:
孤立系统所进行的一切实际过程都朝着系统熵增 加的方向进行,在有限的情况下,系统的熵维持 不变,任何使系统熵减小的过程都是不可逆的。
S iso
0 0 0
U P V S H V p S A P V T G V p T
下变量N常常省略
A S T V G S T
因为U、H、A和G为热力学函数,因此他们的微分式是全 微分,因全微分的二阶偏导数与求导次序无关,从而得 到下列麦克斯韦关系式:
U U (S ,V ) H H ( S , p) A A(T ,V ) G G(T , p)
上述热力学基本关系式仅适用于摩尔数不变的均匀 系,如果考虑单组元系统摩尔数的变化,系统的广 延参数将取决于其摩尔数,这样上式就可扩展为:
U U ( S ,V , N ) H H ( S , p, N ) A A(T ,V , N ) G G (T , p, N )
V , S p, T V , T V , T p, S p, T
S T T V S V pT
p
由于热熔:
CV T S
并有:
T
V
C p T S
dH d (U pV ) TdS Vdp
dG SdT Vdp
dA SdT pdV
这四个式子,是组成固定物质的热力学基本微分关系式。
高等工程热力学-第二章 热力学微分方程及工质的通用热力性质

(2) 在充进入C2H4的过程中所交换的热量;
(3) 在充进入C2H4的过程中总的熵产和火用损。
分析:
(1)本题的不可逆性体现在 哪里? (2)充气过程中所交换的热量、总的熵产和 火用损与焓基准、熵基准是否有关?
(3)理想气体方程是否适用?
当 当 当 >0,dT<0,节流冷效应; <0,dT>0,节流热效应; <0,dT = 0,节流零效应;
§2-6 克拉贝龙方程
克拉贝龙方程建立了相变过程中不可测参数的变化量ds 及dh,与可测参数的变化量dp、dT及dv之间的一般关系式, 它是确定相变过程中不可测参数s与h的数值及制定相应的热力 性质表所不可缺少的工具。
第二章 热力学微分方程 及工质的通用热力性质
热力学微分方程
建立了状态参数之间的一般关系式, 与过程的性质及途径无关; 适用于任何工质,任何过程。
§2-1 §2-2 §2-3 §2-4 §2-5 §2-6
特性函数 热物性参数 热力学能、焓及熵的一般关系式 有关比热的热力学关系式 焦尔—汤姆孙系数 克拉贝龙方程
(11-32)
§2-4 有关比热的热力学关系式
( 4-42)
( 4-44) ( 4-45)
结论: (1)对于气体,
恒为负值,所以cp>cv; ≈0,
(2)对于液体及固体,压缩性很小, 因此有cp≈cv; (3)当T→0时,cp≈cv。
§2-5 焦尔—汤姆孙系数
一、绝热节流过程的基本性质
二、绝热节流的温度效应
则
方程
吉布斯方程组 方程
纯质,可逆与不可逆均可
①吉布斯方程组具有高度的正确性和普遍性。 ②吉布斯方程组建立了热力学中最常用的8个状 态参数之间的基本关系式,在此基础上,可以 导出许多其它的普遍适用的热力学函数关系。
热力学与统计物理学-第二章
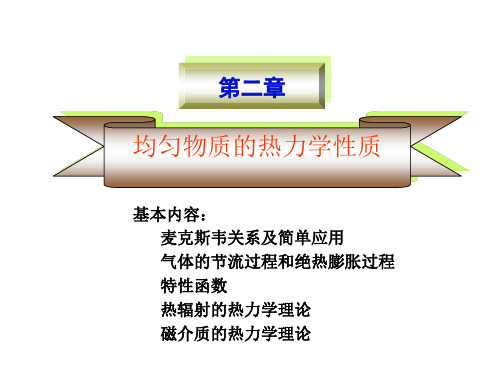
dG=-SdT+VdP
S V
P T
T P
Good Physicists Have Studied Under Very Fine Teachers
太阳照在小树上
(
S V
)T
(
p T
)V
(河流)由山峰流向山谷
照向和流向方向一致取正号,否则取负号。看对 方的分母,取自己的脚标。
T
p
T
V
( V
)S
( S
)V
;
( p )S ( S ) p
( S V
)T
(
p T
)V
;
( V T
)p
(
S p
)T
——麦克斯韦关系
Sun
太阳 peak
山峰
Tree
小树 Valley
山谷
§2-2 麦克斯韦关系的简单应用
麦克斯韦关系的应用有:
⑴用实验可测量的量(如状态方程,热容量
Summary
dU=TdS-PdV dH=TdS+VdP
P T S V V S
T V
P S
S P
G
T
P
F
H
V
S
U
dF=-SdT -PdV
S P
V T
T V
一.能态方程和定容热容量
U T p p V T T V
CV
T S T
V
第一式给出了温度不变时, 系统内能随体积的变化率与物态方程的关系,称 为能态方程;第二式是定容热容量。
热力学基础

王 华
《工程热力学》
The Zeroth Law of Thermodynamics 如果两个系统分别与第三个系统处于热平 衡,则两个系统彼此必然处于热平衡。
If two bodies are in thermal equilibrium with a third body, they are also in thermal equilibrium with each other.
2014-5 Henan Polytechnic University
王 华
《工程热力学》
为什么引入平衡概念? Why introduce equilibrium? 如果系统平衡,可用一组确切的参数 (压力、温度)描述 但平衡状态是死态,没有能量交换 能量交换 状态变化
《工程热力学》
§1-2 状态和状态参数 State and state properties
状态:某一瞬间热力系所呈现的宏观状况
状态参数:描述热力系状态的物理量
状态参数的特征:
1、状态确定,则状态参数也确定,反之亦然 2、状态参数的积分特征:状态参数的变化量 与路径无关,只与初终态有关 3、状态参数的微分特征:全微分
《工程热力学》
平衡Equilibrium与均匀Even
平衡:时间上 均匀:空间上
平衡不一定均匀,单相平衡态则一定是均匀的
2014-5 Henan Polytechnic University 王 华
《工程热力学》
平衡状态
内部存在热平衡 内部存在力平衡 系统内一定具有均匀一致的温度 系统内一定具有均匀一致的压力 工程上,常是气体组成的系统
V v= m
比容
/kmol
U u= m
比内能
热力学与统计物理第二章均匀物质的热力学性质

(1)(3)两式比较,即有
H V ( )T T ( ) p V p T
H S CP T T P T P
定压膨胀系数: 1 ( V ) P
V T
焓态方程:
H ( )T TV V p
dH CP dT [T 1]Vdp (可测)
dG SdT VdP
dF SdT pdV
(1)由热力学的基本微分方程: dU=TdS-pdV 内能:U=U(S,V),全微分为
U U dU dS dV S V V S
U U 对比可得: S T , V P V S
五、求证:
CP CV T
P T V
2
P V T
证明:
( S , P) S CP T T T (T , P) P
( S , P) T (T , V )
(T , P) (T , V )
(3)麦氏关系记忆 • 规律:相邻3个变量为一组,按顺序(顺、逆时针都可 以)开始第一变量放在分子,中间变量作分母,末尾 量放在括号外作下标,构成一偏导数.则此偏导数等 于第4个变量按相反方向与相邻的另两个量构成的 偏导数(符号:广延量对广延量正号,否则负号).
§2.2 麦氏关系的简单应用
上节导出了麦氏关系:
u (u , y ) 性质: ( 1 ) ( ) y= x ( x, y ) (u, y ) u y u y u 证明: ( ) y ( )x ( )x ( ) y ( ) y ( x, y ) x y y x x (u, v) (v, u ) (u , v) (u , v) ( x, s ) (2) (3) ( x, y ) ( x, y ) ( x, y ) ( x, s ) ( x, y ) (u, v) 1 (4) ( x, y ) ( x, y ) (u , v)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014届本科毕业论文全微分与热力学姓名:高盼系别:物理与电气信息学院专业:物理学学号:100314015指导教师:王保玉2014年2月9日目录摘要与关键字 (II)0 引言....................................................... 错误!未定义书签。
1 全微分函数的基本性质....................................... 错误!未定义书签。
2 热力学基本方程及辅助热力学方程 (3)2.1 物态方程 (3)2.2 态函数内能U和熵S (4)2.3 热力学基本微分方程 (5)3 内能、焓、自由能及吉布斯函数的全微分和麦克斯韦关系 (5)4 麦克斯韦关系的简单应用 (7)4.1 熵的一般关系式 (7)4.2 内能的一般关系式 (9)4.3 焓的一般关系式 (10)4.4 定压比热与定容比热的关系 (13)摘要 (II)关键词 (II)参考文献 (14)致谢 (15)全微分与热力学摘要基本热力学状态函数及其辅助函数许多都是不可测量,必须将它们与可测量联系起来才便于确定,但数学推导过于复杂。
本文从四个热力学基本方程出发, 利用函数全微分性质,对比研究可得出八个对应系数关系式,再对其二次微分得出四个麦克斯韦关系式,方便对热力学系统进行研究。
关键词热力学基本方程;全微分;麦克斯韦关系;不可测量;可测量;热力学系统Total differential and thermodynamicsAbstractMany basic thermodynamic state function and the auxiliary function are measured, they must be linked with measurable just easy to determine, but the mathematical deduction is too complex.In this paper, in four fundamental equations of thermodynamics, the total differential properties, functions comparative study can be concluded that eight corresponding coefficient relation, again the second time differential draw four maxwell's equation, is convenient to study thermodynamics system.Key wordsThe thermodynamic basic equations; Total differential; Maxwell relations; Immeasurability; Measurability; Thermodynamic system0 引言热力学是研究热能与其他形式能量的转换规律的科学,着重阐述工质的热力学性质、基本热力过程以及热工转换规律,最终找出提高能量利用效率的方法,从而促进为人类文明的进步。
[1]热力学函数全微分关系式的推证,是要把热力学体系不易测量的热力学函数的全微分用实验易于测量的物理量如P 、V 、T 、S 、等温膨胀系数、等温压缩系数、等体热容、等压热容等表示出来,这样就可以研究热力学系统求解实际问题了,如工质的性质、最大功的计算等。
[2]在这方面已有许多教材和报告给出证明,但是其中的数学推导步骤过于复杂,对于初学者来说很难接受。
我作为一个学生,站在学生的角度,在在不失科学性的前提下,用尽量简单的数理知识总结出“四-八-四”关系式,通过此式,同学们不仅轻松接受,而且对热力学基本方程及其完整的微分性质有更加清晰的理解。
此外熵、内能和焓的一般关系式中均含有定压比热或者定容比热,定压比热的测定较易,因此我们要设法找到两个比热的关系,从而由定压比热计算出定容比热,以避开实验测定定容比热的困难,最后根据利用“四-八-四”关系式导出基本热力学函数,就可以对热力学系统进行研究了。
1全微分函数的基本性质设函数(,)z f x y =在点(,)x y 的某邻域内有定义,如果函数在点(,)x y 的全增量z (,)(,)f x x y y f x y ∆=+∆+∆- 可以表示为 z ()A x B y O ρ∆=∆+∆+其中A 、B 不依赖于y x ∆∆、而仅与y x 、有关,则称函数(,)z f x y =在点(,)x y 可微分,而x A B y ∆+∆称为函数(,)z f x y =在点(,)x y 的全微分,记作dz 即z y x z z d dx dy x y ⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭[3]状态函数的全微分性质状态参数,当我们强调它们与独立变量的函数关系时,常称它们为状态函数。
从数学上说,状态函数必定具有全微分性质。
这一数学特性十分重要,利用它可导出一系列很有实用价值的热力学关系式。
下面我们扼要介绍全微分的一些基本定理。
[4]设函数),(y x f z=具有全微分性质z y xz z d dx dy x y ⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭ (1) 则必然有(1) 互易关系令式(1)中()1,y z f x y x ∂⎛⎫=⎪∂⎝⎭, ()2,xz f x y y ⎛⎫∂= ⎪∂⎝⎭则 12y x f f y x ⎛⎫∂∂⎛⎫=⎪ ⎪∂∂⎝⎭⎝⎭ (2)互易关系与⎰=0dz 等价。
它不仅是全微分的必要条件,而且是充分条件。
因此,可反过来检验某一物理量是否具有全微分。
(2) 循环关系当保持z 不变,即0=dz 时,由式(1),得0=⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫⎝⎛∂∂z xz y dy y z dx x z 则 xy zy z x z x y ⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂1z yx z y x y x z ⎛⎫∂∂∂⎛⎫⎛⎫=-⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭(3) 此式的功能是:若能直接求得两个偏导数,便可确定第三个偏导数。
结果也很容易记忆,只需将三个变量依上、下、外次序,即))()((xzy yxz zyx 循环就行了。
(3) 变换关系将式(1)用于某第四个变量ω不变的情况,可有ωωωdy y z dx x z dz xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫⎝⎛∂∂= 两边同除以ωdx ,得y x z z z y x x y x ωω⎛⎫∂∂∂∂⎛⎫⎛⎫⎛⎫=+ ⎪⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭ (4)式中:y x z ⎪⎭⎫ ⎝⎛∂∂是函数),(y x z 对x 的偏导数;ω⎪⎭⎫ ⎝⎛∂∂x z 是以),(ωx 为独立变量时,函数),(ωx z 对x 的偏导数。
上面的关系可用于它们之间的变换。
(4) 链式关系按照函数求导法则,可有下述关系:1=⎪⎭⎫⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂yy z x x z (5)1y y yz x x z ωω∂∂∂⎛⎫⎛⎫⎛⎫=⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭(6) 这是在同一参数(如y )保持不变时,一些参数),,,( ωx z 循环求导所得偏导数间的关系。
若将关系式中每个偏导数视为链的一环,则链式关系的环数可随所涉及参数的个数而增减。
2 热力学基本方程及辅助热力学方程2.1物态方程在介绍具体物质的物态方程前,先介绍几个与物态方程有关的物理量体胀系数(压强保持不变的情况下,温度升高1K 所引起的物体体积的相对变化)1P V V T α∂⎛⎫=⎪∂⎝⎭压强系数(体积保持不变的情况下,温度升高1K 所引起的物体压强的相对变化)1V p p T β∂⎛⎫=⎪∂⎝⎭等温压缩系数(温度保持不变情况下增加单位压强所引起的物体体积的相对变化)1T T V V P κ∂⎛⎫=- ⎪∂⎝⎭[3]由微分性质循环关系式(3)得1T V PV P T P T V ∂∂∂⎛⎫⎛⎫⎛⎫=- ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭ (7)因此 T Pακβ= 三者之间可以转换(1)理想气体的物态方程PV nRT = (8) (2)简单固体和液体由于固体和液体的膨胀系数是温度的函数,与压强近似无关,等温压缩系数可以近似看作常量,因为 (,,)0f p V T = (,)V V p T = p TV V dV dp dT p T ⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭11T pT dV V V dp dT dp dT V V p V T κα⎛⎫∂∂⎛⎫=+=-+ ⎪ ⎪∂∂⎝⎭⎝⎭两端积分得000Vp T T V p T dV dp dT V κα=-+⎰⎰⎰ 00(p p )(0T T T V V e κα--+-=) 00(p p )()000,)(T ,)T T T V T p V p e κα--+-=( 令00p =00(p p )()00,)(T ,0)T T T V T p V e κα--+-=( 利用泰勒公式展开得000(,)(,0)[1()]T V T P V T TT p ακ=+-- (9)(3)顺磁性固体(,,)0f M H T = H 表示磁场强度 M 表示磁化强度 T 表示温度实验测得一些物质的磁物态方程为 CM HT =(10)(C 为常数,其值因物质的不同而异)此式又称为居里定律。
[5]2.2态函数内能U 和熵S(1)内能:焦耳所做实验表明,系统经绝热过程从初态到末态,在此过程中外界对系统所作的功仅取决于系统的初、末态,而与过程无关,这个事实表明,可以用绝热过程中外接对系统所作的功S W 定义一个态函数U 在末态B 与初态A 之差B A SU U W -=如果系统经历的过程不是绝热过程,初、末态的内能变化等于外接对气体做的功与从外界吸收的热量之和,即:B A U U W Q-=+ (11)其微分形式是:dU dQ dW =+ (12)(2)熵函数:对于可逆过程有0dQT =⎰,dQ 为系统从温度为T 的热源所吸收的热量。
设想系统从初始状态A 经过可逆过程1到达终态B 后,又经过另一可逆过程2回到初始状态A ,这两个过程构成一个循环过程,根据上式 有 120BAA B dQ dQ T T +=⎰⎰由于1、2是由A 态到B 态的两个任意过程,上式表明,在初始状态A 和终态B 给定后积分BA dQ T ⎰与可逆过程的路径无关。
克劳修斯根据此性质引入一个态函数:BA B AdQS S T -=⎰ 对上式取微分得dQdS T =(13)此式表明在无穷小的可逆过程中,系统的熵变ds 与其温度T 及其在过程中吸取的热量dQ 的关系。
