第06章 热力学微分关系式
热力学一般关系(热学高等数学偏微分)word版本

第二部分工质的热力性质六热力学函数的一般关系式由热力学基本定律引出的一些基本热力学状态函数(如内能U、熵S)及其为某一研究方便而设的组合函数(如焓H、自由能F、自由焓G等)许多都是不可测量,必须将它们与可测量(如压力p、体积V、温度T等)联系起来,否则我们将得不到实际的结果,解决不了诸如上一章讲的最大功计算等一些具体的问题。
这就需要发展热力学的数学理论以将热力学基本定律应用到各种具体问题中去。
热力学函数一般关系式 全微分性质+基本热力学关系式6.1 状态函数的数学特性对于状态参数,当我们强调它们与独立变量的函数关系时,常称它们为状态函数。
从数学上说,状态函数必定具有全微分性质。
这一数学特性十分重要,利用它可导出一系列很有实用价值的热力学关系式。
下面我们扼要介绍全微分的一些基本定理。
设函数),(y x f z =具有全微分性质dy y z dx x z dz xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂= (6-1) 则必然有(1) 互易关系令式(6-1)中),(y x M x z y=⎪⎪⎭⎫ ⎝⎛∂∂, ),(y x N y z x =⎪⎪⎭⎫ ⎝⎛∂∂ 则 y x x N y M ⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂ (6-2)互易关系与⎰=0dz 等价。
它不仅是全微分的必要条件,而且是充分条件。
因此,可反过来检验某一物理量是否具有全微分。
(2) 循环关系当保持z 不变,即0=dz 时,由式(6-1),得0=⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂z xz y dy y z dx x z则 xy z y z x z x y ⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂ 故有 1-=⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂y z x z x x y y z (6-3)此式的功能是:若能直接求得两个偏导数,便可确定第三个偏导数。
结果也很容易记忆,只需将三个变量依上、下、外次序,即))()((xzy yxz zyx 循环就行了。
工程热力学第六章 热力学微分关系式及实际气体性质

第一节 主要数学关系式
简单可压缩系统,所有状态是二个独立参数 的函数。状态参数都是点函数,微分是全微 分,设;z=f(x,y),则:
dz
z x
y
dx
z y
x
dy
dz
Mdx
Ndy; M
z x
y
,N
z y
x
M
y
x
y2zx;N xy
x2zyM y x
M y x
完成一个循环则: dzxzy
V
G p
T
三、麦克斯韦关系式
T V
s
p S
v
T
p
s
V S
p
S V
T
p T
v
S p
T
V T
p
四、热系数
系统的三个基本状态参数p、v、T之间应用
函数关系式:
v p
T
p T
v
T v
p
1
v p
或
v
dv
p 常 数 时 q p cpdTp
c pdT p
cvdT p
T
p T
v
d
v
p
得
:
cp
cv
T
p T
v v T
p
理想气体:
cp
cv
T
R v
R=R p
第五节 克拉贝龙方程
纯物质在定压相变过程中温度保持不变,说 明相变时压力和温度存在函数关系:
简化:
dp dT
h(β) h(α) T(v(β) v(α)
的比值,即z=v/vid=pv/RT或pv=zRT
对理想气体z=1,对实际气体z是状态函数, 可能大于1或小于1。z的大小表示实际气体性 质对理想气体的偏离程度
《工程热力学》第六章 实际气体性质及热力学普遍关系式

n
f b
气
C 界 1 A
2 B
汽液共存区
m
4
v
一、概念; 二线、三区、六参数 饱和状态 饱和蒸汽;饱和液体 饱和压力、饱和温度 临界点参数 二、几个区域 饱和蒸汽线、饱和液体线 饱和状态区(汽液共存区)、液相状态区、汽相 状态区
5
概念
归纳有:
P (水) 实际气体P-T图 固 相 一般物质
全微分条件(判据)
M N ( )x ( )y y x
17
2、链式关系---性质之二 x x 对函数x=x(y,z)展开 dx y dy z dz y z z z
dz dy dx x y y x z x y x y z x dy z dz y z y z x y x y dy x dy x
20
热系数
21
6-6 热力学的一般关系式
一、热力学能的普遍关系式 二、焓的普遍关系式 三、熵的普遍关系式 四、比热的普遍关系式
22
一、热力学能的普遍关系式
u u du ( ) v dT ( )T dv T v du Tds pdv s s s f (T , v ) ds dT dv T v v T s s du T dT T P dv T v v T s p u ; Cv v T T v T v u s p T P T P v T v T T v p du Cv dT T P dv T v
热力学函数基本关系式

V S ( ) p d p T
S V d p
p
从状态方程求得 ,V 与 p 的关系,就可求 ( S )T 或 S 。
上一内容
下一内容 回主目录 返回
2018/11/23
Maxwell 关系式的应用
物化课件
例如,对理想气体
pV nRT,
( S p )T
常用的特征变量为:
G(T , p)
U (S,V )
上一内容
下一内容
A(T ,V ) H (S, p)
回主目录
S(H, p)
返回
2018/11/23
特性函数
物化课件
例如,从特性函数G及其特征变量T,p,求H,U, A,S等函数的表达式。 G(T , p) dG SdT Vdp G 导出: V ( G ) T S ( ) p p T
V =C p dT [V T ( ) p ]dp T
V H C p dT [V T ( ) p ]dp T
知道气体状态方程,求出( V ) p 值,就可计算 H值。
T
上一内容
下一内容 回主目录 返回
2018/11/23
Maxwell 关系式的应用
等温对p求偏微分 ( H )T T ( S )T V
( S )T 不易测定,据Maxwell关系式 p
(
所以
H V ( )T V T ( ) p p T
只要知道气体的状态方程,就可求得 ( H )T p 值,即等温时焓随压力的变化值。
上一内容
下一内容 回主目录 返回
dA SdT pdV
(
(4) dG SdT Vdp
利用该关系式可将实验可测偏微商来代替那些不易直 接测定的偏微商。
6.热力学基本关系式
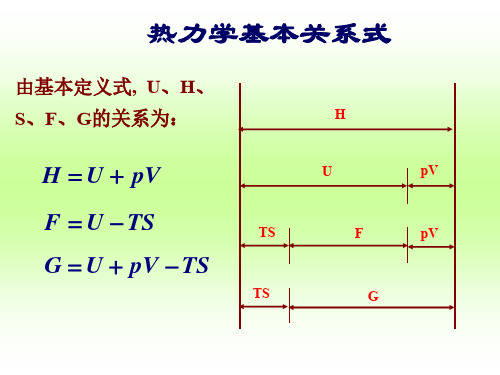
G U pV TS
dG S dT V d p
U、H、F、G这些热力学函数之间的关系实质是勒让德变换 勒让德变换实际上是在我们得到了一个不变量后,要得到它的对偶自变量下的 不变量的一个重要的变换。
热力学四个基本关系式(Gibbs关系式)如下:
d U T d S p dV
S p V T T V
(1)
U p V T T p T V
得证
几个重要的偏导关系式
1.与S有关的
S p V T T V
S V T p p T
d H T d S V d p
(1)
(2) (3)
d F S d T p dV dG S dT V d p
(4)
条件: 简单封闭系统,只作体积功。
• 基本关系式实质上是 U 、 H 、 F 和 G 的数学全 微分展开式。 • 简单的封闭系统, 状态只需两个独立变量即可 决定, 这两个变量可以任意选取. • 从四个关系式的微分变量可知, 对不同的状态 函数, 在作全微分展开时, 选取的独立变量是 不一样的:
例: 试证明:
U p V T T p T V
解:有基本热力学关系式
d U T d S p dV
在等温条件下,求内能对体积的偏微商:
U S V T V p T T
由麦克斯韦关系式: 代入(1)式得:
Wf 0
Qr T d S
将上式代入内能的全微分:
W p dV
d U T d S p dV
(1)
热力学一般关系(热学 高等数学 偏微分)(完整资料).doc

【最新整理,下载后即可编辑】第二部分 工质的热力性质六 热力学函数的一般关系式由热力学基本定律引出的一些基本热力学状态函数(如内能U 、熵S )及其为某一研究方便而设的组合函数(如焓H 、自由能F 、自由焓G 等)许多都是不可测量,必须将它们与可测量(如压力p 、体积V 、温度T 等)联系起来,否则我们将得不到实际的结果,解决不了诸如上一章讲的最大功计算等一些具体的问题。
这就需要发展热力学的数学理论以将热力学基本定律应用到各种具体问题中去。
热力学函数一般关系式←全微分性质+基本热力学关系式6.1 状态函数的数学特性对于状态参数,当我们强调它们与独立变量的函数关系时,常称它们为状态函数。
从数学上说,状态函数必定具有全微分性质。
这一数学特性十分重要,利用它可导出一系列很有实用价值的热力学关系式。
下面我们扼要介绍全微分的一些基本定理。
设函数),(y x f z =具有全微分性质dy y z dx x z dz xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂= (6-1)则必然有(1) 互易关系令式(6-1)中),(y x M x z y=⎪⎪⎭⎫ ⎝⎛∂∂, ),(y x N y z x =⎪⎪⎭⎫ ⎝⎛∂∂ 则 y x x N y M ⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂ (6-2)互易关系与⎰=0dz 等价。
它不仅是全微分的必要条件,而且是充分条件。
因此,可反过来检验某一物理量是否具有全微分。
(2) 循环关系当保持z 不变,即0=dz 时,由式(6-1),得0=⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂z xz y dy y z dx x z 则 xy z y z x z x y ⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂ 故有 1-=⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂y z xz x x y y z (6-3) 此式的功能是:若能直接求得两个偏导数,便可确定第三个偏导数。
热力学函数的基本关系式

⑵等温等压相变△G 对于等温等压的可逆相变,直接可得(△G)T,P=0.对于非等温 等压的非可逆相变或同温同压下两个相态的△G,可以通过设计可 逆过程进行计算,也可根据G---P关系公式求算。
1.8 热力学函数的基本关系式
H
U、H、S、A、G 、 p、V、T H =U+pV,A =U-TS,G =H-TS 1. 热力学基本方程
U
pV
TS A pV
TS
G
δWr ′=0时,则δWr=-pdV,于是
一微小可逆过程
dU=δQr+δWr,
dS δ Qr T
δWr ′ =0时,则δWr=-pdV,于是
=8586Jmol-1 故△G= △G1+ △G2 + △G3=8584Jmol-1 依Gibbs自由能减少原理,298K,1atm水不能经等温等压过程转变 为同温 同压的水蒸气,但其逆过程则是可以的。因此在298K, 1atm下液态水是稳定态。
⒊应用Gibbs--helmholtz方程求△G 将 G--H方程:{э(△G/T)/эT}P=- △H/T2
△S=0,△T=0,△H=0,
△G=0
⑵理气在等温等压的Gibbs自由能改变 △G = △H-T △S (△H=0) △S=-R∑nilnXi △G= RT∑nilnXi 其中ni为组分i的量,Xi为理想混合气中
为组分I的摩尔数。
⒌非等温等压两态的△G 若体系的两态温度,压力都不相等,根据G的定义:
工程热力学第六章(实际气体的性质及热力学一般关系式)09(理工)(沈维道第四版)

当氧气、氮气等超过10MPa时亦应按实际气体
●◆二、压缩因子
1、压缩因子
为反映实际气体与理想气体的偏离程度引入
压缩因子Z
2、压缩因子的 物理意义
理想气 Z pv pv v
体的pv0
RgT pv0 v0
Z 1 v v0 实际气体比理想气体难压缩
Z 1 v v0 实际气体比理想气体易压缩
H1
LA :液态(过冷液体)
共存
T2 G1 T1
v
(3)水平线HL的长度变化
临界压力pc
温度提高,水平线HL的长度缩短。临界温度Tc
(4)临界点
临界比体积vc
随着温度提高,水平线HL缩为一个点,此时温度Tc 超过此温度,无论怎样加压,◆物质确定,临界点确定
都不能使气体变为液体,故p
称此点为临界点。
压缩因子的大小与物质的种类和所处的状态有关
实际气体种类繁多,通过实验画出各气体的Z-p图, 不方便,下面介绍1个通用方法:对比态参数法
●◆1、临界状态
p
1896年安德鲁斯对二氧化 碳作等温压缩实验得到不 同温度下的p-v图。
液 A1
C L2
p pc
H2
T Tc
Tc 气
里方程的形式
理想气体
一切气体 p 0 Z 1
第三维里系数
Z pv 1 B' p C ' p2 D' p3 RgT
或 Z pv 1 B C 2 D 3
RgT
第二维里系数
1
B v
C v2
D v3
B,B',C,C',D,D'……与温度有关的量
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 热力学微分关系式
1.基本概念
自由能:F =U -TS ,F 称为自由能,或称亥姆霍兹(Helmholtz )函数。
自由焓:令G = H -TS ,G 称为自由焓,或称吉布斯(Gibbs )函数。
2.重要公式
热力学能的基本关系式:
V p U W U Q d d d +=+=δδ
V p S T U d d d -=
焓的基本关系式:
p V V p U H d d d d ++= p V S T H d d d +=
自由能基本关系式:
V p T S F d d d --=
自由焓的基本关系式:
P V T S G d d d +-=
麦克斯韦关系式:
v s )()(
S p V T ∂∂-=∂∂ p s )()(S V p T ∂∂=∂∂ v T )()(T p
V S ∂∂=∂∂ p T )()(T
V p S ∂∂=∂∂-
热系数:
⎪
⎪
⎪⎭
⎪⎪
⎪⎬⎫∂∂-=∂∂=∂∂=
T p v )(1)(1)(1p v v T v v T
p p μβα
式中
α——压力温度系数;
v )(
T
p
∂∂——物质在定容下压力随温度的变化率; β——容积膨胀系数,或称热膨胀系数;
p )(
T
v
∂∂——物质在定压下比体积随温度的变化率;
μ——定温压缩系数,或简称压缩系数;
T )(
p
v
∂∂——物质在定温下比体积随压力的变化率,表示物质在定温条件下受压后的压缩性。
这个偏导数为负值,加负号后,μ仍为正值。
熵方程:
v T
p
T T c s d )(d d v v ∂∂+=
p T
v
T T
c s
d )(
d d p p ∂∂-=
v v
T T c p p T
T c s d )(d )(d p p v v ∂∂+∂∂=
焓方程:
p T
v
T v T c h d ])(
[d d p p ∂∂-+= 热力学能的微分方程式:
⎰⎰-∂∂+=-2
1
21
d ])(
[d v v 12v v T T v p T
p
T T c u u 热量的微分方程式:
v v p p d d (
)d d d ()d p q T s c T T v T
v
q T s c T T p
T
δδ∂==+∂∂==-∂
上述两式适用于任意物质的任何可逆过程。
比热容与状态方程式的关系:
2T v 21()()v c p T v T ∂∂=∂∂ 2p T p 21()()c v T p T
∂∂=-∂∂ 2211
2p p T p 2()()d p p v
c c T p T
∂-=-∂⎰
比定压热容与比定容热容的关系:
T 2p v p )()(
v
p T v T c c ∂∂∂∂-=- μ
β2
v p Tv c c =
-
克拉贝龙方程:
)
(d d )
()()
()(s s αβαβv v T h h T p --= 克劳修斯-克拉贝龙方程:
s
s s s s s d )(ln d d d 1RT r
T p T p p ==。
