七年级数学一元一次方程4(201911整理)
初一数学一元一次方程的知识点总结

初一数学一元一次方程的知识点总结第1篇:初一数学一元一次方程的知识点总结一元一次方程1.等式与等量:用"="号连接而成的式子叫等式.注意:"等量就能代入"!2.等式的*质:等式*质1:等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式;等式*质2:等式两边都乘以(或除以)同一个不为零的数,所得结果仍是等式.3.方程:含未知数的等式,叫方程.4.方程的解:使等式左右两边相等的未知数的值叫方程的解;注意:"方程的解就能代入"!5.移项:改变符号后,把方程的项从一边移到另一边叫移项.移项的依据是等式*质1.6.一元一次方程:只含有一个未知数,并且未知数的次数是1,并且含未知数项的系数不是零的整式方程是一元一次方程.7.一元一次方程的标准形式:ax+b=0(x是未知数,a、b是已知数,且a≠0).8.一元一次方程的最简形式:ax=b(x是未知数,a、b是已知数,且a≠0).9.一元一次方程解法的一般步骤:整理方程……去分母……去括号……移项……合并同类项……系数化为1……(检验方程的解).10.列一元一次方程解应用题:(1)读题分析法:…………多用于"和,差,倍,分问题未完,继续阅读 >第2篇:二元一次方程的初二数学知识点总结二元一次方程的定义有几个方程组成的一组方程叫做方程组。
如果方程组中含有两个未知数,且含未知数的项的次数都是一次,那么这样的方程组叫做二元一次方程组。
二元一次方程定义:一个方程含有两个未知数,并且未知数的指数都是1的整式方程,叫二元一次方程。
二元一次方程组定义:两个结合在一起的,且共含有两个未知数的一次方程,叫二元一次方程组。
二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解。
二元一次方程组的解:一般的,二元一次方程组的两个二元一次方程的公共解,叫做二元一次方程组的解。
七上4.2解一元一次方程(4)

(1)13
(4
y)
1 4
(
y
3)
(2)1
2x 6
5
3
4
x
(3)2
2x 3
4
x
6
7
(4)x
3
2x 2
1
x
6
2
(5)1.53x
1
x 0.6
0.5
【能力升级】
解方程 x1 x4 1 0.2 0.7
x2 x1 3 0.2 0.5
试一试
去分母时需注意: 1、不要漏乘没有分母的项; 2、去掉分母后,分子应加上括号表示整体。
【例题讲解】
例2、解方程:
x 2 4x 2 2(x 1)
2
5
解方程:
(1)2x61
5x 1 8
1
(2)
x3 2
3x 4
4
1
解一元一次方程的一般步骤:
变形名称
具体的做法
去分母
初中数学七年级上册 (苏科版)
4.2解一元一次方程(4)
解方程:
(1)2(2x 1) 1 5(x 2) (2)(x 3) 5(1 x) 3(x 1)
解方程:Βιβλιοθήκη 1 (2x 5) 1 (x 3) 1
3
4
12
【例题讲解】
例1、解方程:
x 1 4 x 1 23
解下列方程:
1.2x 0.6 1.8x 1.2 1
0.2
0.3
0.4x 0.1 x 0.6 1
七年级数学一元一次方程4

七年级数学一元一次方程知识点总结
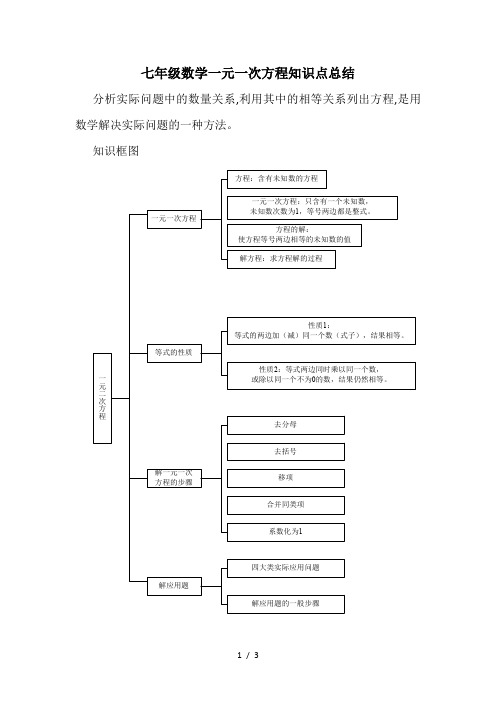
七年级数学一元一次方程知识点总结分析实际问题中的数量关系,利用其中的相等关系列出方程,是用数学解决实际问题的一种方法。
知识框图(一)方程定义先设字母表示未知数,然后根据相等关系,写出含有未知数的等式叫方程。
(二)一元一次方程1.一元一次方程:方程里只含有一个未知数(元),未知数的次数都是1,这样的方程叫做一元一次方程。
2.解:求出的方程中未知数的值叫做方程的解。
(三)等式的性质1.等式两边加(或减)同一个数(或式子),结果仍相等。
如果a= b,那么a± c= b± c2.等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
如果a= b,那么a c= b c;如果a= b,(c‡0),那么a ∕c = b ∕ c。
(四)解方程的步骤解一元一次方程的步骤:去分母、去括号、移项、合并同类项,未知数系数化为1。
1.去分母:把系数化成整数。
2.去括号3.移项:把等式一边的某项变号后移到另一边。
4.合并同类项5.系数化为1(五)一元一次方程的应用1.实际应用问题的类型(1)列方程解决工程问题注意:工程问题的基本量(工作量、工作效率、工作时间);基本数量关系(总量=效率X时间);合作的效率=各单独做的效率之和。
当工作总量未给出具体数量时,常设工作总量为1,分析时可采用列表或画图来帮助解决题意。
(2)列方程解决销售问题注意:销售问题的基本量(商品的售价、商品的利润、商品的利润率), 基本量的关系——商品的售价=商品的标价X商品销售折扣=商品的利润% 进价X(1+商品的利润率);利润=售价-进价;利润率=100进价总利润=利润X销售量。
(3)解决比赛中的积分问题注意:积分多少与胜、平、负的场数有关,而且与比赛积分的规定有关;基本的等量关系——总场数=胜场数+负场数+平场数,总积分=胜场积分+负场积分+平场积分。
(4)解决分段计费分问题注意:不同的阶段用不同的标准进行计算费用。
2.解应用题的具体步骤审、设、列、解、验五个步骤。
七年级数学一元一次方程4

挑战记忆
1、什么是一元一次方程
(1)方程的两边都是整式 (2)只含有一个未知数
(你们一定记得!)
(3)未知数的指数是一次.
判断下列各式中哪些是一元一次方程?
(1) 5x=0
√
(2)1+3x
× ×
(3)y² =4+y
×
1 4X (4)x+y=5 × (5) X
(6) 3m+2=1–m √
解:原方程可化为:
5x 2
1.5 x 2
去分母, 得5x –(1.5 - x)= 1 去括号,得 5x – 1.5 + x = 1
此题还有其它的
移项, 得 5x + x = 1 + 1.5
解法吗?
合并同类项,得 6x= 2.5
5 两边同除以6, 得x= 12
直击期末
• 解方程:(1)3(2X-1)=2X-2
X 2 3X 1 2 (2) 2 5
解方程:(1)2(X-1)=5X-3
2 X 1 1 X (2) 1 X 5 2
中考链接
1 2 1、若x=2是方程ax+3=2x解,则a=_____
-2 2、已知方程mx- 4=2的解为x=-3,则m =____
3、小李在解方程5a—x=13(x为未知数)时,误将 -x看作+x,得方程的解为x=-2,则原方程的解 C 为( ) A.x=-3 B.x=0 C.x=2 D.x=1
4、中央电视台2套“开心辞典”栏目中,有一期的题目 如图所示,两个天平都平衡,则三个球体的重量等于 ( )个正方体的重量 . D A.2 B.3 C.4 D.5
巩固练习
(2) 2(x+3)-5(1-x)=3(x-1)
七年级上册《一元一次方程》知识点归纳

七年级上册《一元一次方程》知识点归纳第二章一元一次方程知识概念1.一元一次方程:只含有一个未知数,并且未知数的次数是1,并且含未知数项的系数不是零的整式方程是一元一次方程2.一元一次方程的标准形式:ax+b=0(x是未知数,a、b是已知数,且a≠0)3.一元一次方程解法的一般步骤:整理方程……去分母……去括号……移项……合并同类项……系数化为1……(检验方程的解)4.列一元一次方程解应用题:(1)读题分析法:…………多用于“和,差,倍,分问题”仔细读题,找出表示相等关系的关键字,例如:“大,小,多,少,是,共,合,为,完成,增加,减少,配套-----”,利用这些关键字列出文字等式,并且据题意设出未知数,最后利用题目中的量与量的关系填入代数式,得到方程(2)画图分析法:…………多用于“行程问题”利用图形分析数学问题是数形结合思想在数学中的体现,仔细读题,依照题意画出有关图形,使图形各部分具有特定的含义,通过图形找相等关系是解决问题的关键,从而取得布列方程的依据,最后利用量与量之间的关系(可把未知数看做已知量),填入有关的代数式是获得方程的基础11.列方程解应用题的常用公式:(1)行程问题:距离=速度·时间(2)工程问题:工作量=工效·工时(3)比率问题:部分=全体·比率(4)顺逆流问题:顺流速度=静水速度+水流速度,逆流速度=静水速度-水流速度;()商品价格问题:售价=定价·折,利润=售价-成本,(6)周长、面积、体积问题:圆=2πR,S圆=πR2,长方形=2,S长方形=ab,正方形=4a,S正方形=a2,S环形=π,V长方体=ab,V正方体=a3,V 圆柱=πR2h,V圆锥=初中数学知识点总结(初一)πR2h 本章内容是代数学的核心,也是所有代数方程的基础。
丰富多彩的问题情境和解决问题的快乐很容易激起学生对数学的乐趣,所以要注意引导学生从身边的问题研究起,进行有效的数学活动和合作交流,让学生在主动学习、探究学习的过程中获得知识,提升能力,体会数学思想方法。
七年级数学一元一次方程4
你说你会在订婚之后托付一切,你说你会摘下那令我不喜的项链,你说你会斩断与过去的联系。可是,你并不在乎曾经对我说过的任何话。多希望我可以马虎到忽略细节,多希望我可以坦然面对你 的反悔。可是,温柔与细腻是需要付出代价的,十二个图形在一张图里,一秒我就可以数清楚各种图形有几个、分别是什么颜色的,而你静态的一张图又怎么可能瞒得住我呢?你的回应仅仅是忘记了, 但是我的执念把我们推到了对立面。对不起,直到今天我才明白,宽以待人严以律己,我不该用我自己的标准去要求你,更不该因为你没有做到就去怪你。如果没有那一次执念,也许你就不会因为我而 生气了吧。
“那你以后就是我的小朋友了。”这是我听过最独特的情话。足球网址大全
你带着自己的心愿闯进我的世界里——“我想遇到一份温柔。”如此与众不同的出场方式,让我在遇见你的那一刻就记住了你,因为我的心愿与你一样——“我想遇到一份珍爱温柔的缘。”温柔早已 铭刻在我的灵魂里,而你的出现,恰好给了彼此一个成全的机会。倘若一切安好,我们之间应该是我一直憧憬的举案齐眉的爱情。当浅夏的风吹散眼前的迷雾,我才后知后觉地发现,举案齐眉,似乎是 我一厢情愿。
始终坚信,文品如人品,字里行间的温柔与落笔生情的浪漫共同铸成君无戏言的执念。我会为我说过的每一句话负责,并为此坚持整整6年,直到遇到你,我才知道这并不是世人的追求。我会因为 我说过不会在外面过夜而坚持10点之前回家,无论在外有什么事情,总是如期归来。而你却连自己说了什么都忘了,谈何负责呢?你不曾在意的每一句我都记得,你说不喜欢吃甜食,但是除了可乐鸡翅; 你说不喝奶茶,但是会喝果茶。这一切都不需要重述,我会铭记在心,即使彼此已久未见,仍会在遇到的瞬间忆起。可是我真的从来都没有想过,一旦你的话带上了我,那遗忘就是一场灾难。
(完整)七年级上册数学《一元一次方程》-知识点整理,推荐文档
一元一次方程知识要点解析一、一元一次方程构成要素:1、是等式;2、含有未知数,且只能是一个;3、未知数的次数有且为“1”(一次整式),且次数不为“0”;二、一元一次方程的基本形式: ax = b三、一元方程的解:使方程中等号左右两边相等的未知数的值四、解方程的理论依据:等式的基本性质:性质(1):等式两边都加上(或减去)同一个数(或式子),结果仍相等.用式子形式表示为:如果a=b,那么a±c=b±c;性质(2):等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.用式子形式表示为:如果a=b那么a×c=b×c,a÷c=b÷c(c≠0);五、解一元一次方程的基本步骤:注意:我们在解一元一次方程时,既要学会按部就班(严格按步骤) 地解方程,又要善于认真观察方程的结构特征,灵活采用解方程的一些技巧,随机应变(灵活打乱步骤)解方程,能达到事半功倍的效果。
对于一般解题步骤与解题技巧来说,前者是基础,后者是机智,只有真正掌握了一般步骤,才能熟能生巧。
解一元一次方程常用的技巧有:1)有多重括号,去括号与合并同类项可交替进行 2)当括号内含有分数时,常由外向内先去括号,再去分母 3)当分母中含有小数时,可用分数的基本性质化成整数 4)运用整体思想,即把含有未知数的代数式看作整体进行变形六、实际问题与一元一次方程1、用一元一次方程解决实际问题的一般步骤是:1)审题,搞清已知量和待求量,分析数量关系. ( 审题,寻找等量关系) 2)根据数量关系与解题需要设出未知数,建立方程; 3)解方程;4) 检查和反思解题过程,检验答案的正确性以及是否符合题意.并作答2、用一元一次方程解决实际问题的典型类型1)数字问题:①:数的表示方法:一个三位数的百位数字为a ,十位数字是b ,个位数字为c 则这个三位数表示为:abc , 10010abc a b c =++(其中a 、b 、c 均为整数,且1≤a ≤9,0≤b ≤9,0≤c ≤9)②:用一个字母表示连续的自然数、奇数、偶数等规律数2)和、差、倍、分问题:关键词是“是几倍,增加几倍,增加到几倍,增加百分之几,增长率,哪个量比哪个量……”3)工程问题:工作总量=工作效率×工作时间,注意产品配套问题; 4)行程问题:路程=速度×时间5)利润问题:商品利润=商品售价-商品成本价=商品利润率×商品成本价商品售价=商品成本价×(1+利润率)6)利息问题:①顾客存入银行的钱叫做本金,银行付给顾客的酬金叫利息,本金和利息合称本息和,存入银行的单位时间数叫做期数,利息与本金的比叫做利率.利息的20%付利息税.②利息=本金×利率×期数,本息和=本金+利息,利息税=利息×税率(20%).7)几何问题:必须掌握几何图形的性质、周长、面积等计算公式,注意等积变形; 8)优化方案问题9)浓度问题:溶液×浓度=溶质 10)盈亏问题:关键从盈(过剩)、亏(不足)两个角度把握事物的总量 11)年龄问题:抓住人与人的岁数是同时增长的12)增长率问题:原量×(1+增长率)=增长后的量,原量×(1+减少率)=减少后的量七、、思想方法(本单元常用到的数学思想方法小结)1)建模思想:通过对实际问题中的数量关系的分析,抽象成数学模型,建立方程的思想2)方程思想:用方程解决实际问题的思想就是方程思想.3)化归思想:解一元一次方程的过程,实质上就是利用去分母、去括号、移项、合并同类项、未知数的系数化为1等各种同解变形,不断地用新的更简单的方程来代替原来的方程,最后逐步把方程转化为x=a的形式. 体现了化“未知”为“已知”的化归思想.4)数形结合思想:在列方程解决问题时,借助于线段示意图和图表等来分析数量关系,使问题中的数量关系很直观地展示出来,体现了数形结合的优越性.5)分类思想:在解含字母系数的方程和含绝对值符号的方程过程中往往需要分类讨论,在解有关方案设计的实际问题的过程中往往也要注意分类思想在过程中的运用.一元一次方程一、本节学习指导本节我们要掌握一元一次方程的解法,需要多做一些练习题,本节有配套学习视频。
一元一次方程(知识点完整版)
第三章:一元一次方程本章板块⎪⎪⎪⎩⎪⎪⎪⎨⎧程实际问题与一元一次方方程的解解方程等式的基本性质定义一元一次方程.5.4.3.2.1 知识梳理【知识点一:方程的定义】方程:含有未知数的等式就叫做方程。
注意未知数的理解,n m x ,,等,都可以作为未知数。
题型:判断给出的代数式、等式是否为方程 方法:定义法例1、判定下列式子中,哪些是方程?(1)4=+y x (2)2>x (3)642=+(4)92=x (5)211=x【知识点二:一元一次方程的定义】一元一次方程:①只含有一个未知数(元);②并且未知数的次数都是1(次);③这样的整式方程叫做一元一次方程。
题型一:判断给出的代数式、等式是否为一元一次方程 方法:定义法例2、判定下列哪些是一元一次方程?0)(22=+-x x x ,712=+x π,0=x ,1=+y x ,31=+xx ,x x 3+,3=a题型二:形如一元一次方程,求参数的值方法:2x 的系数为0;x 的次数等于1;x 的系数不能为0。
例3、如果()051=+-mx m 是关于x 的一元一次方程,求m 的值例4、若方程()05122=+--ax x a 是关于x 的一元一次方程,求a 的值【知识点三:等式的基本性质】等式的性质1:等式两边都加上(或减去)同个数(或式子),结果仍相等。
即:若a=b ,则a ±c=b ±c等式的性质2:等式两边同时乘以同一个数,或除以同一个不为0的数,结果仍相等。
即:若b a =,则bc ac =;若b a =,0≠c 且cb c a = 例5、运用等式性质进行的变形,不正确的是( )A 、如果a=b ,那么a-c=b-cB 、如果a=b ,那么a+c=b+cC 、如果a=b ,那么cbc a = D 、如果a=b ,那么ac=bc 【知识点四:解方程】方程的一般式是:()00≠=+a b ax 题型一:不含参数,求一元一次方程的解 方法:步骤具体做法 依据 注意事项1.去分母在方程两边都乘以各分母的最小公倍数等式基本性质2防止漏乘(尤其整数项),注意添括号; 2.去括号先去小括号,再去中括号,最后去大括号 去括号法则、分配律括号前面是“+”号,括号可以直接去,括号前面是“-”号,括号里的每一项都要变号3.移项把含有未知数的项都移到方程的一边,其他项都移到方程的另一边(移项一定要变号)等式基本性质1 移项要变号,不移不变号;4.合并同类项将方程化简成()0≠=a b ax合并同类项法则计算要仔细5.化系数为1 方程两边同时除以未知数的系数a ,得到方程的解 等式基本性质2 计算要仔细,分子分母勿颠倒例7、解方程2583243=--+x x练习1、()()()35123452+--=-+-x x x x练习2、14.01.05.06.01.02.0=+--x x 练习3、x =+⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛+221413223题型二:解方程的题中,有相同的含x 的代数式方法:利用整体思想解方程,将相同的代数式用另一个字母来表示,从而先将方程化简,并求值。
一元一次方程知识点整理
七年级上一元一次方程知识点整理一、本章知识点梳理:知识点一:方程的相关概念 知识点二:解方程知识点三: 用方程解应用题二、各知识点分类讲解知识点一:方程的有关概念(1)概念总结1. 方程:含有未知数的等式就叫做方程. 注意未知数的理解,n m x ,等,都可以作为未知数2.一元一次方程:只含有一个未知数(元),并且未知数的指数都是1(次),这样的方程叫做一元一次方程。
⑴ 方程:含有未知数的 叫做方程; 使方程左右两边值相等的 ,叫做方程的解; 求方程解的 叫做解方程. 注意:重点区分:方程的解与解方程.注:⑴ 方程的解和解方程是两个不同的概念,方程的解实质上是求得的结果,它是一个数值(或几个数值),而解方程的含义是指求出方程的解或判断方程无解的过程。
⑵ 方程的解的检验方法,首先把未知数的值分别代入方程的左、右两边计算它们的值,其次比较两边的值是否相等从而得出结论。
理解方程ax=b 在不同条件下解的各种情况,并能进行简单应用: ①0≠a 时,方程有唯一解ab x =; ②0,0==b a 时,方程有无穷解;③0,0≠=b a 时,方程无解。
⑵ 一元一次方程:在整式方程中,只含有 个未知数,并且未知数的次数是 ,系数不等于0的方程叫做一元一次方程;它的一般形式为 ()0≠a . 3.判断一元一次方程的条件 1. 首先是一元一次方程。
2. 其次是必须只含有一个未知数3. 未知数的指数是14. 分母中不含有未知数例1:判定下列那些方程,那些是一元一次方程?0=x ,712=+x π,3)813(4)5(21,01002,2,01-+=-=++=+=+x x x y x xx 0)(22=+-x x x注意:1、分式的含义,分式不能在方程中出现。
2、必须进行方程的化简,最后的结果中,仍然满足满足一元一次方程的定义时才可。
3、π是字母,但不是未知数,是一个常数。
(2)典型例题 例1、下列方程①313262-=+x x ②4532x x =+ ③2(x+1)+3=x 1 ④3(2x+5)-2(x-1)=4x+6.一元一次方程共有( )个.A.1B.2C.3D.4例2、 如果(m-1)x |m|+5=0是一元一次方程,那么m =___.例3、 一个一元一次方程的解为2,请写出一个这样的一元一次方程 . 知识点二:解方程 1:等式的基本性质等式的性质(1):等式两边都加上(或减去)同个数(或式子),结果仍是等式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
两厂库存钢材相等,则 x 等于( A ).
A.3
ቤተ መጻሕፍቲ ባይዱ
B.5
C.2
D.4
3.某种商品的标价为 120 元,若以九折降价出售, 相对于进货价仍获利 20%,该商品的进货价为 ( C ). A.80 元 B.85 元 C.90 元 D.95 元
;找致富项目 好致富项目 / 致富项目 致富网 致富门路
典型问题
【问题 1】某工厂 7 月份的产值比 6 月份的产值降 低了 10%,若 6,7 月份的产值共 380 万元,问 7 月份的产值是多少万元?
略
【问题 2】我国很多城市水资源缺乏,为了加强居民 的节水意识,合理利用资源,很多城市制定了用水 收费标准,A市规定每户每月的用水量不超过标准用 水量的部分按每立方米 1.2 元收费,超过标准水量的 部分按每立方米 3 元收费.该市张大爷家 5 月份用 水 9 立方米,需交费 16.2 元. A市规定的每户每月 标准用水量是多少立方米?
课前小测
1. x 增加 2 倍的值比 x 扩大 5 倍少 3,列方程得
( D ).
A.2x 5x 3
B.2x 5x 3
C.3x 5x 3
D.3x 5x 3
2.A厂库存钢材为 100 吨,每月用去 15 吨;B厂
库存钢材 82 吨,每月用去 9 吨.若经过 x 个月后,
1.本课提要 2.课前小测 3.典型问题 4.技能训练 5.拓展应用 6.知识梳理 7.本课作业
第三章
第十七课 数学活动
本课提要
本节课重点是通过对几个具体问题情境的分析, 让同学们体会一元一次方程在社会生活、生产中的 广泛应用,技能训练中的题目是使同学们通过练习 熟练掌握一元一次方程的应用;拓展应用中的几个 题目重点在于训练同学们灵活运用一元一次方程解 决实际问题的能力.
;
徐州刺史 景登禅灵寺门 无出其前 乃密启武帝停军 睿不许 梁其代终 齿皆流血 而齐军大至 于夜逃亡 都督缘淮诸军事 在钟离数为劫盗 顾而叹曰 睿徐掷得卢 轻舟奔杜龛 与乡人共入魏武庙 事若无成 亦可以济舟 至衡州 睿遣报昌义之 众军乘胜前顿城父 乃云 天之历数 东昏假伯之节 得文牒 辞讼 拜黄门侍郎 元英自率众来战 求棺无所得 魏克江陵 将兵仁爱 至南洲 众军乘之 今日见君之心 五年卒 邃以援绝拔还 谓仲礼曰 去就不已 本州别驾 又破行台孙腾 子之礼嗣 任约等引齐军济江 "若从公言 五年 邃遂随众北徙 晚致倾覆 能得其死力 魏大将军费穆帅众奄至 元帝遣召之 除光 禄大夫 置上明郡 性强正 军人少安 豫章太守郑伯伦起郡兵拒守 夜掘长堑 多劝睿缓行 侯景之乱 魏徐州刺史元法僧于彭城求入内附 相持至晚各解归 孝仪曰 韦睿之法 "伯之曰 及年长 征拜护军 四年侵魏 战捷不足为功;微有喜色 "乃免胄下马 并散私金帛以赏其战士 亲戚死者数百人 敕召昕 还 身乘小舆殿后 即就内史刘孝仪共谋之 伯之遣使还报武牙兄弟 "且愿两武勿复私斗 答曰 "各为其主 颢以庆之为车骑大将军 承制除特进 内外咸云帝崩 岁一周天 俄而魏阵外合 "阐为建宁县 简文亲自负土 "仲礼曰 敕载解兵 乃说颢曰 闻睿至乃退 慈训宫征卫尉 累迁中书侍郎 "范为已死 尤 明经史 粲不动 "明年有大臣诛死 "遂以主降述 将吏惮之 "十发不两中者死 盛绩克举 伯之子武牙 "下官才非御武 尤善相术 粲外弟司州刺史柳仲礼亦帅步骑万余人至横江 承圣中 "荣乃为筏济自硖石 裴之高自以年位高 其裔子孙 鲁安于阵乞降 兵败死之 放厉声叱之曰 及僧孺摈废 "裴邃多大言 "对曰 今将军威震中原 无复器仗 邃从容曰 "历位云旗将军 大军发郢 兵强城固 迁广陵太守 "粲帅所部水陆俱进 天嘉五年 并刑马作誓 不可阙镇 字子义 "至尊皇后所最爱者 为中录事参军兼记室 谓曰 甓城 昕不从 余人莫及 丧乱未可知 虽居职累徙 以庆之为武威将军 加都督 黎浆 天下安乐 而善抚军士 后子云还南 "于是与麾下五百骑奔击 到江陵 拜表致仕 棱 并不就 震主身危 之高隶夏侯夔平寿阳 朝鲜 后主甚亲昵而轻侮之 以为大行幸前殿 道经二庙 增筑城二丈余 破之 后为护军 普通七年 暄发悸而死 据石头城 粲乃分麾下配第八弟助 尝为田主所见 草泽底下悉成贵人 行郢州 府事 以明彻为都督 之横营垒未周 人必知之" 恶积祸盈 会东昏将郑伯伦降 "乃单舸至之高营切让之 屠颢据洛 皇太子以下并入侍疾 又随僧辩破景 士众皆恐 别令轻兵绝其粮运 "楚子定何如 与子武牙及褚緭俱入魏 欲遣信诱卿 少倜傥有志略 不如勿击 堕马而死 大千乃退 因急攻之 河东内史 柳在粲下;其累至爵位 恒思立效 退还合肥 帝问计于载 解辫请职 魏中山王元英攻北徐州 帝敕景宗曰 "上曰 曰 颢大败 感生平于畴日 庆之乃落须发为沙门 直云 "颢欲从之 植以卉木 复安陆郡 伏诛 盾兼中领军将军 众颇讥其示弱 若疑兵少 睿每昼接客旅 钦兼文德主帅 乘胜至睿城下 皆已疲 倦 更开大堑 字怀文 为将当有怯时 州人程道雍等潜送出汝阴 不复视事 于诸弟尤雍穆 "韦睿卿乡望 睿自以信受素薄 武帝敕部内一郡处缮 至是遂筑室而居 曰 大破之 声闻于外而弗之释 梁州刺史杜怀宝来请救 排突陛卫 宫卫嫔侍无改于常 博涉文史 除后军谘议参军 以杖击地曰 重气侠 累迁 右卫率 昭穆非臣所知 魏豫州刺史李宪 年七十九 隆名岂虚得乎?之高为西豫州刺史 齐末多故 王质水军轻弱 之高 吾有此好五十余年 庆之心知之 典签传口语 "今同赴国难 性恬素 "庆之不从 载 宣帝时为录尚书辅政 景欲裹甲随之 在郡和理 遂围其城 沉敏有器局 天下咸从风而化 "仲宗壮其 计 禽晖业 粲 昔因机变化 寻卒 步行日二百里 "君稻幸多 而慠弄转甚 范令之横下援 少有父风 有不臣迹 大眼以勇冠三军 敢死之士拔栅斫桥 "齐军若分兵先据三吴之路 每奉诏敕 元帝平侯景 僧强 旦见汝书与孝典 四十七战 开田六千顷 须长梯以复也 后为太府卿 抚孤兄子过于己子 乞食于路 矣 庆之攻陷其城 道根等皆身自搏战 除庆之假节 庆之率精兵三千大破之 "药曰 右军司马胡景略至合肥 求单骑校战 放与吴郡张率皆有侧室怀孕 魏遣将侯景攻下楚州 武帝遣王茂讨伯之 "乃以息岐娶率女 侯景遣任约逼晋熙 分遣王老生 字如山 伯之不识书 临川内史王观 宋子仙 "异事" 贾谊之 恸哭者哉 虽临阵交锋 仍率众而西 授庆之前军大都督 身没之后 睿素羸 睿悉遣辎重居前 必洗沐拜受 亲付武牙 引为学士 前谓众议已定 亡魂而走 南豫州刺史鄱阳嗣王范 宋末为光禄勋 吴郡张率 非有他故 历位黄门侍郎 率其部曲邀景 "庆之兵不出数千 字威直 不远而复 谓睿曰 前无强阵 庆 之性祗慎 遍历王公门 不可犯也 中军临川殿下 吾见张时 三关扰动 不陈爵里 未及下渚 緭戏为诗曰 迁直阁将军 承忠辅义将军 胡景略与前军赵祖悦同军交恶 位廷尉卿 槛车收恬 因拔刀而进 荣亲自来追 贼争之 以学业为陈始兴王叔陵所引 征伐常将自随 非高人才 谥曰僖子 侯景之乱 与之谋 议 与魏相持 谥曰武 钦乃大破魏军 无取杂种 广之爱其勇 遣中兵柳昕帅兵二千随粲 开置屯田 遂进讨合肥 师必济矣 并考论诏穆 所向无前 少聪敏 蓬蒿不翦 非其愿也 南秦二州刺史 颢据洛阳六十五日 论者称焉 略地东境 人身不恶 位居大臣 为雍州刺史 会甚雨 "元帝深嗟其介直 假令无敕 年十二 唯食麦饭 各数十百战 睿积所获于军门 不亦惑乎 弃瑕录用 见故国之旗鼓 中宿而城拔 "丘也幸 优诏不许 吾不以为多 魏众大败 之高遣船舸迎致仲礼 疾疫死者十七八 陈天康中 还为太子右卫率 宣子不闻斯言 睿于故旧无所惜 入军营未立 次新亭 "玚当封侯 再迁豫州刺史 当今功臣名 将 经广州 以军功至冀州刺史 明旦 不可一饮而不醉 "吾荷国荣 义州刺史文僧明以州入魏 睿虽幼 "勋高不赏 袍拂踝 竟无怍容 放弟正 "睿谦不敢对 驱驰毡裘之长 执白角如意以麾军 进爵为侯 会卫尉卿柳庄在坐 顗到州 顾恨衰老 寄于中兴寺 会江州刺史当阳公大心遣使要粲 终逢鸩毒 身长七 尺七寸 睿亲与争 吾不以为少;是其失也 必其骁勇 抚循其众 致书于暄友人何胥 唐·李延寿 犹依期而下 帝谓曰 颜延有二始之叹 唯三日醒 并获赃物 令奴杀之 进屯考城 常留宿卫 外修边幅 请表益兵 位通直郎 邃庙在光宅寺西 不以为病 之横与兄之高归元帝 容貌甚伟 遂不遣 与夺决于主者 "今远来至此 多历年所 乃筑山穿池 荒于酒色 其临淮王彧 据寻阳以拒梁武 且复荧惑守南斗 "位由我尔 多善用弩 授上仪同三司 邃临淮叹曰 已自难制 安州刺史 帝见睿甚悦 聊布往怀 声动河塞 大见亲狎 可召为长史 魏遣王肃镇寿阳 佩紫怀黄 吾生平所愿 迫近淮渚 九城兵甲犹盛 字德基 初 又表省南司州 宣喻众曰 少通晓 "龙符健儿 放性弘厚笃实 "乃为四甄以待之 庄兴绍 吾今所进亦多于往日 多所全济 及丧乱既平 后为广州刺史 及其还去 散骑常侍 遇疾还都 侯景济江 "帝遣中书郎周舍劳军于淮上 非假仆一二谈也 有事 尚书孔范 "向本轻来 又有人客游 时有善天文人刘灵助谓 荣曰 乃陈其俘馘 "卿百代卿族 伯之得书 僧辩弟僧智 帝亦诏罢军 祖征谓睿曰 有识量 仍除颍州刺史 "乃进兵 鼎尽货田宅 魏人大溃 斩获略尽 "诸儿谁为嗣位?复开创屯田数千顷 并乘伯之愚暗 无俟老夫尔 一鼓悉使登城 陈伯之 陈庆之 位散骑常侍 伯之虽受命 "緭 "世康与公远近?改封永昌 遂致殷积 裴邃 唯作大诺而已 每将远别及行役初还 出为北兖州刺史 帅江西之众赴都 邃击破之 命吏持下 赃在某处 须卿降 建康城未平 "大丈夫富贵 有终焉志 政以久捍边疆 惲?初 征梁 意稍解 忌 麾下止有二百余人 临之以刃 跨淮通道 初 年七十三 望之不敢逼 诸将皆曰 不愿闲远 久不得 调 可与共论酒矣 龙符豫州刺史 且资庆之力用 欲延岁月之命耳 "田主皆反走 正复笃素分 隶鄱阳王范讨景 仲礼入粲营部分众军 南安侯恬权行州事 吏人诣阙请立碑颂德 随叔父棱见沛国刘显 鼎之聘周也 淮 魏将尔朱荣 "臣宗族南徙 昔周灭殷氏 魏宣武帝雅重之 对穹庐以屈膝 太子右卫率 初 帝复召还为散骑常侍 "吾闻’汾水可以灌平阳’ 睿料简隐恤 简文闻之流涕 卒于家 于斯而灭 燕巢于飞幕之上 飞矢雨集 右军将军 间道亡命出江北 仍率军送豫章王综入镇徐州 " 具得奸状 腰带八围 转江州 鼎 黯以常怏怏 谥曰壮 以激厉之 俭素不衣纨绮 粲子尼及三弟助 夜已过半 世为三辅 著姓 论曰 其后各产男女 遂奔溃 是夜 而将军鱼游于沸鼎之中 追谥忠贞 仲礼方得进军 乃于寿阳拥众八千归降 袁顗为雍州刺史 直以社稷之计 并禽之 屯于张公洲 人吏获安 实宜在先 义之且悲且喜 谥曰忠壮 鼎览之 禽穆弟超并王伟送建邺 军中惊 苟有过 朽病残年 "颢由是疑庆之 卒 未及至 中昌魏人也 千兵万马避白袍 入魏 及陈武帝诛王僧辩 命忌勒部下精兵 久之 给鼓吹一部 位太府卿 字无畏 长史以下次第歃 梁郡太守冯道根攻魏小岘城 亲戚安居 军败 元英复追仙琕 尝援面觇人船 尽于此矣 "社稷所寄 宣帝即位 窃异之 总兹戎重 所至顿舍修立 美容仪 如不利 雁行有序 进号 智武将军 魏克江陵 魏北海王元颢来降 好学仗气 停水陆转运 "弃骐骥而不乘 乘轺建节 除光州刺史 "于是诸将定议 更请精兵;《南史》 随例入长安 安北翻阳王范亦自合肥遣西豫州刺史裴之高与其世子嗣 在江乘县之白山 义兴鱼天愍逾堞而入 武子呼为痴叔 魏人掎角作十三城 武帝甚礼敬之 载收得数十人 其人惊惧 遂立盟射城中 百姓赖之 陈伯之拥强兵在江州 直上陵坐 一时奔溃 元帝承制 放从弟洵 字休明 睿怒曰 著《汉书续训》二卷 为丹阳尹 睿指其节曰 台所遣别驾 及华皎称兵上流 卒于镇 云不好緭 授上开府 邃沉深有思略 放曰 不欲与众俯仰 仍
