利用轴对称求最小值
轴对称相关最值问题

与轴对称有关的最值问题【典型题型一】:如图,直线 l 和 l 的异侧两点 A、B,在直线 l 上求作一点 P,使 PA+PB最小。
APD BEC图(5)【典型题型二】如图,直线 l 和 l 的同侧两点 A、B,在直线 l 上求作一点 P,使 PA+PB最小。
【练习】 1、( 温州中考题 ) 如图( 5),在菱形 ABCD中,AB=4a,E 在 BC上,EC=2a,∠ BAD=1200, 点 P 在 BD上,则 PE+PC 的最小值是()解:如图( 6),由于菱形是轴对称图形,因此 BC中点 E 对于对角线 BD的对称点 E 必定落在 AB的中点 E1,只需连结 CE1,CE1 即为 PC+PE的最小值。
这时三角形 CBE1 是含有 30 角的直角三角形, PC+PE=C1E=23 a 。
因此选( D)。
2、如图( 13),一个牧童在小河南 4 英里处牧马,河水向正东方流去,而他正位于他的小屋 B 西 8 英里北 7 英里处,他想把他的马牵到小河畔去饮水,而后回家,他可以达成这件事所走的最短距离是()(A) 4+ 185 英里(B) 16 英里(C) 17 英里(D) 18 英里3.如图, C为线段 BD上一动点,分别过点 B、D作 AB⊥BD,ED⊥BD,连结 AC、EC。
已知 AB=5,DE=1,BD=8,设 CD=x.请问点 C知足什么条件时, AC+CE的值最小 ?AC' 4.如图,在△ ABC中,AC=BC=2,∠ACB=90°, D是 BC边的中点, E是 AB边上一动点,则 EC+ED的最小值为 _______。
E即是在直线 AB上作一点 E,使 EC+ED最小作点 C对于直线 AB的对称点 C' ,连结 DC'交AB E DC' EC+ED DBC' DB=1 BC=2 于点,则线段的长就是的最小值。
在直角△中,,依据勾股定理可得, DC'= 55.如图,等腰 Rt△ABC的直角边长为 2,E是斜边 AB的中点, P 是 AC边CBD A上的一动点,则 PB+PE的最小值为E 即在 AC上作一点 P,使 PB+PE最小P作点 B对于 AC的对称点 B' ,连结 B'E,交 AC于点 P,则 B'E = PB'+PE = PB+PEB'E 的长就是 PB+PE的最小值B' CBF在直角△ B'EF 中,EF = 1 ,B'F = 3 依据勾股定理, B'E = 10A D6.如下图,正方形 ABCD的面积为 12,△ ABE是等边三角形,点 E 在正方形 ABCD内,E 在对角线 AC上有一点 P,使 PD+PE的和最小,则这个最小值为()P A.2 3 B.2 6 C.3 D. 6B C即在 AC上求一点 P,使 PE+PD的值最小点 D对于直线 AC的对称点是点 B,连结 BE交 AC于点 P,则 BE = PB+PE= PD+PE,BE的长就是 PD+PE的最小值 BE = AB = 2 37.如图,若四边形 ABCD是矩形, AB = 10cm ,BC = 20cm,E 为边 BC上的一个动点, P 为C'BD上的一个动点,求 PC+PD的最小值;A D作点 C对于 BD的对称点 C' ,过点 C',作 C'B⊥BC,交 BD于点 P,则 C'E 就是 PE+PC的最小20值直角△ BCD中,CH= 错误!不决义书签。
利用轴对称破解最短路径问题

第一章平移、对称与旋转第4 讲利用轴对称破解最短路径问题一、学习目标1.理解“直线上同一侧两点与此直线上一动点距离和最小”问题通过轴对称的性质与作图转化为“两点之间,线段最短”问题求解。
2.能将实际问题或几何问题(对称背景图)中有关最短路径(线段之差最大值)问题借助轴对称转化为两点之间,线段最短问题分析与求解。
二、基础知识•轻松学与轴对称有关的最短路径问题关于最短距离,我们有下面几个相应的结论:(1)在连接两点的所有线中,线段最短(两点之间,线段最短);(2)三角形的两边之和大于第三边,两边之差小于第三边;(3)在三角形中,大角对大边,小角对小边。
(4)垂直平分线上的点到线段两端点的距离相等;【精讲】一般说来,线段和最短的问题,往往把几条线段连接成一条线段,利用“两点之间线段最短” 或者“三角形两边之和大于第三边”加以证明,关键是找相关点关于直线的对称点实现“折”转“直” 。
另外,在平移线段的时候,一般要用到平行四边形的判定和性质。
(判定:如果一个四边形的一组对边平行且相等,那么这个四边形是平行四边形;性质:平行四边形的对边相等。
)三、重难疑点•轻松破最短路径问题在平面图形中要解决最短路径问题,自然离不开构建与转化“两点之间,线段最短”的数学公理,通常将涉及到的两点中的任一点作出关于直线的对称点,从而运用两点之间,线段最短解决实际问题.在日常生活、工作中,经常会遇到有关行程路线的问题。
“最短路径问题”的原型来自于“饮马问题” 、“造桥选址问题” ,出题通常以直线、角、等腰(边)三角形、长方形、正方形、坐标轴等对称图形为背景。
(1)“一线同侧两点”问题例1如图,点A B在直线m的同侧,点B'是点B关于m的对称点,AB'交m于点P.(1)AB与AP+PB相等吗为什么(2)在m上再取一点N,并连接AN与NB比较AN+N有AP+PB的大小,并说明理由.解析:(1)T 点B'是点B 关于m 的对称点,••• PB=PB ,••• AB =AP+PB , ••• AB =AP+PB(2)如图:连接 AN, BN B ' N,TAB' =AP+PB• AN+NB=AN+NB> AB', • AN+N > AP+PB点评:两条线段之和最短,往往利用对称的思想,利用两点之间的线段最短得出结果。
13.4轴对称之最短路径问题人教版2024—2025学年八年级上册

13.4轴对称之最短路径问题人教版2024—2025学年八年级上册二、例题讲解例1.如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC,已知线段AB=4,DE=2,BD=8,设CD=x.(1)用含x的代数式表示AC+CE的长;(2)请问点C满足什么条件时,AC+CE最小?最小为多少?(3)根据(2)中的规律和结论,请构图求代数式的最小值.变式1.如图,C为线段BD上一动点,分别过点B,D作AB⊥BD,ED⊥BD,连结AC,EC,已知AB=5,DE=1,BD=8.(1)请问点C什么位置时AC+CE的值最小?最小值为多少?(2)设BC=x,则AC+CE可表示为,请直接写出的最小值为.例2.如图,直线l是一条河,P,Q是两个村庄,欲在l上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是()A.B.C.D.变式1.如图,在⊥ABC中,BA=BC,BD平分⊥ABC,交AC于点D,点M、N 分别为BD、BC上的动点,若BC=10,⊥ABC的面积为40,则CM+MN的最小值为.变式2.如图,等腰三角形ABC的底边BC长为8,面积是24,腰AC的垂直平分线EF分别交AC,AB于E,F点,若点D为BC边的中点,点M为线段EF 上一动点,则⊥CDM的周长的最小值为()A.7B.8C.9D.10变式3.如图,在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.(1)点D的坐标为;(2)若E为边OA上的一个动点,当⊥CDE的周长最小时,求点E的坐标.例3.如图,⊥AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若⊥PMN的周长是6cm,则P1P2的长为()A.6cm B.5cm C.4cm D.3cm变式1.已知点P在⊥MON内.如图1,点P关于射线OM的对称点是G,点P 关于射线ON的对称点是H,连接OG、OH、OP.(1)若⊥MON=50°,求⊥GOH的度数;(2)如图2,若OP=6,当⊥P AB的周长最小值为6时,求⊥MON的度数.变式2.如图,⊥MON=45°,P为⊥MON内一点,A为OM上一点,B为ON上一点,当⊥P AB的周长取最小值时,⊥APB的度数为()A.45°B.90°C.100°D.135°变式3.如图,⊥AOB=30°,P是⊥AOB内的一个定点,OP=12cm,C,D分别是OA,OB上的动点,连接CP,DP,CD,则⊥CPD周长的最小值为.变式4.如图,在五边形中,⊥BAE=140°,⊥B=⊥E=90°,在边BC,DE上分别找一点M,N,连接AM,AN,MN,则当⊥AMN的周长最小时,求⊥AMN+⊥ANM 的值是()A.100°B.140°C.120°D.80°例4.如图,在⊥ABC中,AB=AC,⊥A=90°,点D,E是边AB上的两个定点,点M,N分别是边AC,BC上的两个动点.当四边形DEMN的周长最小时,⊥DNM+⊥EMN的大小是()A.45°B.90°C.75°D.135°变式1.如图,在平面直角坐标系中,已知点A(0,1),B(4,0),C(m+2,2),D(m,2),当四边形ABCD的周长最小时,m的值是()A.B.C.1D.变式2.如图,在四边形ABCD中,⊥B=90°,AB⊥CD,BC=3,DC=4,点E 在BC上,且BE=1,F,G为边AB上的两个动点,且FG=1,则四边形DGFE 的周长的最小值为.例5.如图,⊥AOB=20°,点M、N分别是边OA、OB上的定点,点P、Q分别是边OB、OA上的动点,记⊥MPQ=α,⊥PQN=β,当MP+PQ+QN最小时,则β﹣α的值为()A.10°B.20°C.40°D.60°变式1.如图,∠AOB=20°,M,N分别为OA,OB上的点,OM=ON=3,P,Q分别为OA,OB上的动点,求MQ+PQ+PN的最小值。
中考数学经典几何模型之轴对称最值模型(解析版)

中考数学几何模型:轴对称最值模型名师点睛拨开云雾开门见山B'QDA'AP B C典题探究启迪思维探究重点例题1. 如图,在矩形ABCD中,AB=10,AD=6,动点P满足S△P AB=S矩形ABCD,则点P到A,B两点距离之和P A+PB的最小值为2.【解答】解:设△ABP中AB边上的高是h.∵S△P AB=S矩形ABCD,∴AB•h=AB•AD,∴h=AD=4,∴动点P在与AB平行且与AB的距离是2的直线l上,如图,作A关于直线l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.在Rt△ABE中,∵AB=10,AE=4+4=8,∴BE===2,即P A+PB的最小值为2.故答案为:2.变式练习>>>1.如图Rt△ABC和等腰△ACD以AC为公共边,其中∠ACB=90°,AD=CD,且满足AD⊥AB,过点D 作DE⊥AC于点F,DE交AB于点E,已知AB=5,BC=3,P是射线DE上的动点,当△PBC的周长取得最小值时,DP的值为()A.B.C.D.【解答】解:连接PB、PC、P A,要使得△PBC的周长最小,只要PB+PC最小即可,∵PB+PC=P A+PB≥AB,∴当P与E重合时,P A+PB最小,∵AD=CD,DE⊥AC,∴AF=CF,∵∠ACB=90°,∴EF∥BC,∴AE=BE=AB=2.5,∴EF=BC=1.5,∵AD⊥AB,∴△AEF∽△DEA,∴=,∴DE==,故选:B.例题2. 如图所示,凸四边形ABCD中,∠A=90°,∠C=90°,∠D=60°,AD=3,AB=,若点M、N分别为边CD,AD上的动点,求△BMN的周长的最小值.【解答】解:作点B关于CD、AD的对称点分别为点B'和点B'',连接B'B''交DC和AD于点M和点N,DB,连接MB、NB;再DC和AD上分别取一动点M'和N'(不同于点M和N),连接M'B,M'B',N'B和N'B'',如图1所示:∵B'B''<M'B'+M'N'+N'B'',B'M'=BM',B''N'=BN',∴BM'+M'N'+BN'>B'B'',又∵B'B''=B'M+MN+NB'',MB=MB',NB=NB'',∴NB+NM+BM<BM'+M'N'+BN',∴C△BMN=NB+NM+BM时周长最小;连接DB,过点B'作B'H⊥DB''于B''D的延长线于点H,如图示2所示:∵在Rt△ABD中,AD=3,AB=,∴==2,∴∠2=30°,∴∠5=30°,DB=DB'',又∵∠ADC=∠1+∠2=60°,∴∠1=30°,∴∠7=30°,DB'=DB,∴∠B'DB''=∠1+∠2+∠5+∠7=120°,DB'=DB''=DB=2,又∵∠B'DB''+∠6=180°,∴∠6=60°,∴HD=,HB'=3,在Rt△B'HB''中,由勾股定理得:===6.∴C△BMN=NB+NM+BM=6,变式练习>>>2.如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为()A.140°B.100°C.50°D.40°【解答】解:分别作点P关于OA、OB的对称点P1、P2,连接P1P2,交OA于M,交OB于N,则OP1=OP=OP2,∠OP1M=∠MPO,∠NPO=∠NP2O,根据轴对称的性质,可得MP=P1M,PN=P2N,则△PMN的周长的最小值=P1P2,∴∠P1OP2=2∠AOB=80°,∴等腰△OP1P2中,∠OP1P2+∠OP2P1=100°,∴∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N=100°,故选:B.例题3. 如图,在△ABC中,∠C=90°,CB=CA=4,∠A的平分线交BC于点D,若点P、Q分别是AC 和AD上的动点,则CQ+PQ的最小值是2.【解答】解:如图,作点P关于直线AD的对称点P′,连接CP′交AD于点Q,则CQ+PQ=CQ+P′Q=CP′.∵根据对称的性质知△APQ≌△AP′Q,∴∠P AQ=∠P′AQ.又∵AD是∠A的平分线,点P在AC边上,点Q在直线AD上,∴∠P AQ=∠BAQ,∴∠P′AQ=∠BAQ,∴点P′在边AB上.∵当CP′⊥AB时,线段CP′最短.∵在△ABC中,∠C=90°,CB=CA=4,∴AB=4,且当点P′是斜边AB的中点时,CP′⊥AB,此时CP′=AB=2,即CQ+PQ的最小值是2.故填:2.变式练习>>>3.如图,已知等边△ABC的面积为4,P、Q、R分别为边AB、BC、AC上的动点,则PR+QR的最小值是()A.3B.2C.D.4【解答】解:如图,作△ABC关于AC对称的△ACD,点E与点Q关于AC对称,连接ER,则QR=ER,当点E,R,P在同一直线上,且PE⊥AB时,PR+QR的最小值是PE的长,设等边△ABC的边长为x,则高为x,∵等边△ABC的面积为4,∴x×x=4,解得x=4,∴等边△ABC的高为x=2,即PE=2,故选:B.例题4. 如图,∠MON=30°,A在OM上,OA=2,D在ON上,OD=4,C是OM上任意一点,B是ON上任意一点,则折线ABCD的最短长度为2.【解答】解:作D关于OM的对称点D′,作A作关于ON的对称点A′,连接A′D′与OM,ON的交点就是C,B二点.此时AB+BC+CD=A′B+BC+CD′=A′D′为最短距离.连接DD′,AA′,OA′,OD′.∵OA=OA′,∠AOA′=60°,∴∠OAA′=∠OA′A=60°,∴△ODD′是等边三角形.同理△OAA′也是等边三角形.∴OD'=OD=4,OA′=OA=2,∠D′OA′=90°.∴A′D′==2.变式练习>>>4. 如图,在长方形ABCD中,O为对角线AC的中点,P是AB上任意一点,Q是OC上任意一点,已知:AC=2,BC=1.(1)求折线OPQB的长的最小值;(2)当折线OPQB的长最小时,试确定Q的位置.【解答】解:(1)作点B关于AC的对称点B′,作点O关于AB的对称点O′,连接AB′,QB′,AO′,PO′,B′O′,则QB=QB′,OP=O′P,折线OPQB的长=OP+PQ+QB=O′P+PQ+QB′,∴折线OPQB的长的最小值=B′O′.∵在长方形ABCD中,∠ABC=90°,在△ABC中,AC=2,BC=1,∠ABC=90°,∴∠BAC=30°,∵点B、B′关于AC对称,点O、O′关于AB对称,∴∠B′AC=30°,AB′=AB=,∠O′AB=30°,AO′=AO=1,∴∠B′AO′=90°,∴B′O′=,∴折线OPQB的长的最小值=2;(2)设B′O′交AC于点Q′,∵在Rt△AO′B′中,AO′=1,B′O′=2,∴∠AB′O′=30°,则∠AO′B′=60°,∵在△AO′Q′中,∠Q′AO′=∠Q′AB+∠BAO′=60°,∴△AO′Q′是等边三角形,∴AQ′=AO′=1=AO,∴点Q′就是AC的中点O.∴当折线OPQB的长最小时,点Q在AC的中点.例题5. 如图,矩形ABCD中,AB=4,BC=8,E为CD的中点,点P、Q为BC上两个动点,且PQ=3,当CQ=时,四边形APQE的周长最小.【解答】解:点A向右平移3个单位到M,点E关于BC的对称点F,连接MF,交BC于Q,此时MQ+EQ最小,∵PQ=3,DE=CE=2,AE==2,∴要使四边形APQE的周长最小,只要AP+EQ最小就行,即AP+EQ=MQ+EQ,过M作MN⊥BC于N,设CQ=x,则NQ=8﹣3﹣x=5﹣x,∵△MNQ∽△FCQ,∴=,∵MN=AB=4,CF=CE=2,CQ=x,QN=5﹣x,解得:x=,则CQ=故答案为:.变式练习>>>5.如图,已知A(3,1)与B(1,0),PQ是直线y=x上的一条动线段且PQ=(Q在P的下方),当AP+PQ+QB最小时,Q点坐标为()A.(,)B.(,)C.(0,0)D.(1,1)【解答】解:作点B关于直线y=x的对称点B'(0,1),过点A作直线MN,使得MN平行于直线y=x,并沿MN向下平移单位后得A'(2,0)连接A'B'交直线y=x于点Q,如图理由如下:∵AA'=PQ=,AA'∥PQ∴四边形APQA'是平行四边形∴AP=A'Q∵AP+PQ+QB=B'Q+A'Q+PQ且PQ=∴当A'Q+B'Q值最小时,AP+PQ+QB值最小根据两点之间线段最短,即A',Q,B'三点共线时A'Q+B'Q值最小∵B'(0,1),A'(2,0)∴直线A'B'的解析式y=﹣x+1∴x=﹣x+1,即x=∴Q点坐标(,)故选:A.例题6. 如图,点E、F是正方形ABCD的边BC上的两点(不与B、C两点重合),过点B作BG⊥AE于点G,连接FG、DF,若AB=2,求DF+GF的最小值为.【解答】解:取AB的中点O,点O、G关于BC的对称点分别为O'、G',∵G与G'关于BC对称,∴FG=FG',∴FG+DF=FG'+DF,∴当G(也就是G')固定时,取DG'与BC的交点F,此时能够使得FG+FD最小,且此时FG+DF的最小值是DG',现在再移动点E(也就是移动G),∵BG⊥AE,∴∠AGB=90°,∴当点E在BC上运动时,点G随着运动的轨迹是以O为圆心,OA为半径的90°的圆弧,点G'随着运动的轨迹是以O'为圆心,O'B为半径的90°的圆弧,∴当取DO'与交点为G'时,能够使得DG'达到最小值,且DG'的最小值=DO'﹣O'G'=﹣1=﹣1,即DF+GF的最小值为﹣1.故选:A.变式练习>>>6.如图,平面直角坐标系中,分别以点A(2,3)、点B(3,4)为圆心,1、3为半径作⊙A、⊙B,M,N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为()A.5﹣4B.﹣1C.6﹣2D.【解答】解:作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图,则此时PM+PN最小,∵点A坐标(2,3),∴点A′坐标(2,﹣3),∵点B(3,4),∴A′B==5,∴MN=A′B﹣BN﹣A′M=5﹣3﹣1=5﹣4,∴PM+PN的最小值为5﹣4.故选:A.例题7. 如图,AD为等边△ABC的高,E、F分别为线段AD、AC上的动点,且AE=CF,当BF+CE取得最小值时,∠AFB=()A.112.5°B.105°C.90°D.82.5°【解答】解:如图,作CH⊥BC,且CH=BC,连接BH交AD于M,连接FH,∵△ABC是等边三角形,AD⊥BC,∴AC=BC,∠DAC=30°,∴AC=CH,∵∠BCH=90°,∠ACB=60°,∴∠ACH=90°﹣60°=30°,∴∠DAC=∠ACH=30°,∵AE=CF,∴△AEC≌△CFH,∴CE=FH,BF+CE=BF+FH,∴当F为AC与BH的交点时,如图2,BF+CE的值最小,此时∠FBC=45°,∠FCB=60°,∴∠AFB=105°,故选:B.变式练习>>>7.如图,等边△ABC中,AD为BC边上的高,点M、N分别在AD、AC上,且AM=CN,连BM、BN,当BM+BN最小时,∠MBN=30度.【解答】解:如图1中,作CH⊥BC,使得CH=BC,连接NH,BH.∵△ABC是等边三角形,AD⊥BC,CH⊥BC,∴∠DAC=∠DAB=30°,AD∥CH,∴∠HCN=∠CAD=∠BAM=30°,∵AM=CN,AB=BC=CH,∴△ABM≌△CHN(SAS),∴BM=HN,∵BN+HN≥BH,∴B,N,H共线时,BM+BN=NH+BN的值最小,如图2中,当B,N,H共线时,∵△ABM≌△CHN,∴∠ABM=∠CHB=∠CBH=45°,∵∠ABD=60°,∴∠DBM=15°,∴∠MBN=45°﹣15°=30°,∴当BM+BN的值最小时,∠MBN=30°,故答案为30.例题8. (1)如图①,Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AB边上任意一点,则CD的最小值为.(2)如图②,矩形ABCD中,AB=3,BC=4,点M、点N分别在BD、BC上,求CM+MN的最小值.(3)如图③,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是BC边上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG、CG,四边形AGCD的面积是否存在最小值,若存在,求这个最小值及此时BF的长度.若不存在,请说明理由.【解答】解:(1)如图①,过点C作CD⊥AB于D,根据点到直线的距离垂线段最小,此时CD最小,在Rt△ABC中,AC=3,BC=4,根据勾股定理得,AB=5,∵AC×BC=AB×CD,∴CD==,故答案为;(2)如图②,作出点C关于BD的对称点E,过点E作EN⊥BC于N,交BD于M,连接CM,此时CM+MN=EN最小;∵四边形ABCD是矩形,∴∠BCD=90°,CD=AB=3,根据勾股定理得,BD=5,∵CE⊥BC,∴BD×CF=BC×CD,∴CF==,由对称得,CE=2CF=,在Rt△BCF中,cos∠BCF==,∴sin∠BCF=,在Rt△CEN中,EN=CE sin∠BCE==;即:CM+MN的最小值为;(3)如图3,∵四边形ABCD是矩形,∴CD=AB=3,AD=BC=4,∠ABC=∠D=90°,根据勾股定理得,AC=5,∵AB=3,AE=2,∴点F在BC上的任何位置时,点G始终在AC的下方,设点G到AC的距离为h,∵S四边形AGCD=S△ACD+S△ACG=AD×CD+AC×h=×4×3+×5×h=h+6,∴要四边形AGCD的面积最小,即:h最小,∵点G是以点E为圆心,BE=1为半径的圆上在矩形ABCD内部的一部分点,∴EG⊥AC时,h最小,由折叠知∠EGF=∠ABC=90°,延长EG交AC于H,则EH⊥AC,在Rt△ABC中,sin∠BAC==,在Rt△AEH中,AE=2,sin∠BAC==,∴EH=AE=,∴h=EH﹣EG=﹣1=,∴S四边形AGCD最小=h+6=×+6=,过点F作FM⊥AC于M,∵EH⊥FG,EH⊥AC,∴四边形FGHM是矩形,∴FM=GH=∵∠FCM=∠ACB,∠CMF=CBA=90°,∴△CMF∽△CBA,∴,∴,∴CF=1∴BF=BC﹣CF=4﹣1=3.达标检测领悟提升强化落实1. 如图,矩形ABCD中,AB=5,AD=10,点E,F,G,H分别在矩形各边上,点F,H为不动点,点E,G为动点,若要使得AF=CH,BE=DG,则四边形EFGH周长的最小值为()A.5B.10C.15D.10【解答】解:作点F关于CD的对称点F′,连接F′H交CD于点G,此时四边形EFGH周长取最小值,过点H作HH′⊥AD于点H′,如图所示.∵AF=CH,DF=DF′,∴H′F′=AD=10,∵HH′=AB=5,∴F′H==5,∴C四边形EFGH=2F′H=10.故选:D.2. 如图,平面直角坐标系中,分别以点A(﹣2,3),B(3,4)为圆心,以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于﹣3.【解答】解:作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图,则此时PM+PN最小,∵点A坐标(﹣2,3),∴点A′坐标(﹣2,﹣3),∵点B(3,4),∴A′B==,∴MN=A′B﹣BN﹣A′M=﹣2﹣1=﹣3,∴PM+PN的最小值为﹣3.故答案为﹣3.3. 如图,已知直线y=x+4与两坐标轴分别交于A、B两点,⊙C的圆心坐标为(2,0),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是8﹣2和8+2.【解答】解:y=x+4,∵当x=0时,y=4,当y=0时,x=﹣4,∴OA=4,OB=4,∵△ABE的边BE上的高是OA,∴△ABE的边BE上的高是4,∴要使△ABE的面积最大或最小,只要BE取最大值或最小值即可,过A作⊙C的两条切线,如图,当在D点时,BE最小,即△ABE面积最小;当在D′点时,BE最大,即△ABE面积最大;∵x轴⊥y轴,OC为半径,∴EE′是⊙C切线,∵AD′是⊙C切线,∴OE′=E′D′,设E′O=E′D′=x,∵AC=4+2=6,CD′=2,AD′是切线,∴∠AD′C=90°,由勾股定理得:AD′=4,∴sin∠CAD′==,∴=,解得:x=,∴BE′=4+,BE=4﹣,∴△ABE的最小值是×(4﹣)×4=8﹣2,最大值是:×(4+)×4=8+2,故答案为:8﹣2和8+2.4. 正方形ABCD,AB=4,E是CD中点,BF=3CF,点M,N为线段BD上的动点,MN=,求四边形EMNF周长的最小值++.【解答】解:作点E关于BD的对称点G,则点G在AD上,连接GM,过G作BD的平行线,截取GH=MN=,连接HN,则四边形GHNM是平行四边形,∴HN=GM=EM,过H作PQ⊥BC,交AD于P,交BC于Q,则∠HPG=∠HQF=90°,PQ=AB=4,∵∠PGH=∠ADB=45°,∴HP=PG==1,HQ=4﹣1=3,由轴对称的性质,可得DG=ED=2,∴AP=4﹣2﹣1=1,∴BQ=1,又∵BF=3CF,BC=4,∴CF=1,∴QF=4﹣1﹣1=2,∵当点H、N、F在同一直线上时,HN+NF=HF(最短),此时ME+NF最短,∴Rt△HQF中,FH===,即ME+NF最短为,又∵Rt△CEF中,EF===,∴ME+NF+MN+EF=++,∴四边形EMNF周长的最小值为++.故答案为:++.5. 如图,已知点D,E分别是等边三角形ABC中BC,AB边的中点,BC=6,点F是AD边上的动点,则BF+EF的最小值为3.【解答】解:过C作CE⊥AB于E,交AD于F,连接BF,则BF+EF最小(根据两点之间线段最短;点到直线垂直距离最短),由于C和B关于AD对称,则BF+EF=CF,∵等边△ABC中,BD=CD,∴AD⊥BC,∴AD是BC的垂直平分线(三线合一),∴C和B关于直线AD对称,∴CF=BF,即BF+EF=CF+EF=CE,∵AD⊥BC,CE⊥AB,∴∠ADB=∠CEB=90°,在△ADB和△CEB中,,∴△ADB≌△CEB(AAS),∴CE=AD,∵BC=6,∴BD=3,∴AD=3,即BF+EF=3.故答案为:3.6. 如图,在边长为1正方形ABCD中,E、F、G、H分别是AB、BC、CD、DA上的点,3AE=EB,有一只蚂蚁从E点出发,经过F、G、H,最后回到E点,则蚂蚁所走的最小路程是.【解答】解:延长DC到D',使CD=CD',G对应位置为G',则FG=FG',同样作D'A'⊥CD',D'A'=DA,H对应的位置为H',则G'H'=GH,再作A'B'⊥D'A',E的对应位置为E',则H'E'=HE.容易看出,当E、F、G'、H'、E'在一条直线上时路程最小,最小路程为EE'===27. 如图,在△ABC中,AC⊥BC,∠B=30°,点E,F是线段AC的三等分点,点P是线段BC上的动点,点Q是线段AC上的动点,若AC=3,则四边形EPQF周长的最小值是8.【解答】解:过E点作E点关于BC的对称点E′,过F点作F点关于AC的对称点F′,∵在△ABC中,AC⊥BC,∠B=30°,AC=3,∴AB=6,∵点E,F是线段AC的三等分点,∴EF=2,∵E′F′=AB=6,∴四边形EPQF周长的最小值是6+2=8.故答案为:8.8. 如图,长为1的线段AB在x轴上移动C(0,1)、D(0,2),则AC+BD的最小值是.【解答】解:如图所示,以AB,BD为边构造平行四边形ABDE,作点C关于x轴的对称点F,连接AF,则DE⊥y轴,OF=OC=1,∵四边形ABDE是平行四边形,∴BD=AE,DE=AB=1,∵AB垂直平分线CF,∴AC=AF,∴AC+BD=AE+AF,如图,当点E,A,F在同一直线上时,AE+AF=EF(最短),此时,∵Rt△DEF中,DE=1,DF=2+1=3,∴EF===,∴AC+BD的最小值是.故答案为:.9. 在矩形ABCD中,AB=8,BC=10,G为AD边的中点.如图,若E、F为边AB上的两个动点,且EF=4,当四边形CGEF的周长最小时,则求AF的长为.【解答】解:∵E为AB上的一个动点,∴如图,作G关于AB的对称点M,在CD上截取CH=4,然后连接HM交AB于E,接着在EB上截取EF=4,那么E、F两点即可满足使四边形CGEF的周长最小.∵在矩形ABCD中,AB=8,BC=10,G为边AD的中点,∴AG=AM=5,MD=15,而CH=4,∴DH=4,而AE∥CD,∴△AEM∽△DHM,∴AE:HD=MA:MD,∴AE===,∴AF=4+=.故答案为:.10. 如图,矩形ABCO的边OC在x轴上,边OA在y轴上,且点C的坐标为(8,0),点A的坐标为(0,6),点E、F分别足OC、BC的中点,点M,N分别是线段OA、AB上的动点(不与端点重合),则当四边形EFNM的周长最小时,点N的坐标为(4,6).【解答】解:如图所示:作点F关于AB的对称点F′,作点E关于y轴的对称点E′,连接E′F′交AB与点N.∵C的坐标为(8,0),点A的坐标为(0,6),点E、F分别足OC、BC的中点,∴OE=OE′=4,FB=CF=3,∴E′C=12,CF′=9.∵AB∥CE′,∴△F′NB∽△F′E′C.∴==,即=,解得BN=4,∴AN=4.∴N(4,6).故答案为:(4,6).11. 如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6.P为对角线BD上一点,则PM﹣PN的最大值为2.【解答】解:如图所示,作以BD为对称轴作N的对称点N',连接PN',MN',根据轴对称性质可知,PN=PN',∴PM﹣PN=PM﹣PN'≤MN',当P,M,N'三点共线时,取“=”,∵正方形边长为8,∴AC=AB=,∵O为AC中点,∴AO=OC=,∵N为OA中点,∴ON=,∴ON'=CN'=,∴AN'=,∵BM=6,∴CM=AB﹣BM=8﹣6=2,∴==∴PM∥AB∥CD,∠CMN'=90°,∵∠N'CM=45°,∴△N'CM为等腰直角三角形,∴CM=MN'=2,即PM﹣PN的最大值为2,故答案为:2.12. 如图,两点A、B在直线MN外的同侧,A到MN的距离AC=16,B到MN的距离BD=10,CD=8,点P在直线MN上运动,则|P A﹣PB|的最大值等于10.【解答】解:延长AB交MN于点P′,∵P′A﹣P′B=AB,AB>|P A﹣PB|,∴当点P运动到P′点时,|P A﹣PB|最大,∵BD=10,CD=8,AC=16,过点B作BE⊥AC,则BE=CD=8,AE=AC﹣BD=16﹣10=6,∴AB===10,∴|P A﹣PB|的最大值等于10,故答案为:10.11. 如图△ABC是边长为2的等边三角形,D是AB边的中点,P是BC边上的动点,Q是AC边上的动点,当P、Q的位置在何处时,才能使△DPQ的周长最小?并求出这个最值.【解答】解:作D关于BC、AC的对称点D′、D″,连接D′D″,DQ,DP.∵DQ=D″Q,DP=D′P,∴△DPQ的周长为PQ+DQ+DP=PQ+D″Q+D′P=D′D″,根据两点之间线段最短,D′D″的长即为三角形周长的最小值.∵∠A=∠B=60°,∠BED=∠AFD=90°,∴∠α=∠β=90°﹣60°=30°,∠D′DD″=180°﹣30°﹣30°=120°,∵D为AB的中点,∴DF=AD•cos30°=1×=,AF=,易得△ADF≌△QD''F,∴QF=AF=,∴AQ=1,BP=1,Q、P为AC、BC的中点.∴DD″=×2=,同理,DD′=×2=,∴△DD′D″为等腰三角形,∴∠D′=∠D″==30°,∴D″D′=2DD′•cos30°=2××=3.12. 如图,C 为线段BD 上一动点,分别过点B 、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=5,DE=1,BD=8,设CD=x.(1)用含x的代数式表示AC+CE的长;(2)请问AC+CE的值是否存在最小值?若存在,请求出这个最小值;若不存在请说明理由.(3)根据(2)中的规律和结论,请直接写出出代数式+的最小值为25.【解答】解:(1)由线段的和差,得BC=(8﹣x).由勾股定理,得AC+CE =+=+=+;(2)当A、C、E在同一直线上,AC+CE最小;当A、C、E在同一直线上时,延长AB,作EF⊥AB于点F,∵AB=5,DE=1,∴AF=6,∵∠ABD=90°,∴∠FBD=90°,∵∠BDE=∠BFE=90°,∴四边形BFED是矩形,∴BD=EF=8,∴AE===10;(3)如下图所示:作BD=24,过点B作AB⊥BD,过点D作ED ⊥BD,使AB=3,ED=4,连接AE交BD于点C,当BC=x,∵x+y=24,∴y=24﹣x,AE的长即为代数式的最小值,过点A作AF∥BD交ED的延长线于点F,得矩形ABDF,则AB=DF=3,AF=BD=24,所以AE===25,即代数式+的最小值为25,故答案为:25.- 21 -。
利用轴对称的性质求最小值

利用轴对称的性质求最小值。
生活中的轴对称》评课稿新课标指出:“数学课程不仅要考虑数学自身的特点,更应遵循学生学习数学的心理规律,强调从学生已有的生活经验出发……..”本节课的设计体现了新课程标准的精神,从学生的兴趣出发,通过“观察——操作——体会”来获取知识,遵循数学来源于生活,又应用于生活的理念,注重在培养学生实践能力和审美能力上作文章,现简单点评如下:一、在情境导入上,密切联系生活实际,让学生学有价值的数学。
对于本节课的起点张老师把握的相当好,充分考虑到了初中数学课改的目标要求贴近于生活、来源于生活。
教师用学生所熟识的天坛、剪纸,及京剧脸谱3个标志作为课题的引入是尊重学生原有认知基础的一个有力表现。
教师用课件把图形对折后能重合的是轴对称图形很好的演绎了出来。
在此基础上通过观察,操作,练习等一系列活动体验轴对称图形的基本特征。
这一知识的形成层层深入,逐步从生活走向数学;后面的巩固练习,让学生用学到的知识判断各种图形是否是轴对称图形,又把数学融入了生活。
真正实现了数学与生活的密切联系,让学生学有价值的数学。
二、在重点难点突破上,学生通过课下动手实验,剪出圆这样一个轴对称图形,然后折叠、分析,得出轴对称的概念,结合实例欣赏,仔细分析出轴对称概念中须注意的几点。
并总结出轴对称图形和轴对称的区别,轴对称图形是一个图形自身的对称,轴对称是两个图形关于某条直线对称。
教师在这个环节上充分利用了媒体教学和传统教学的结合,从实践过程中得出结论,符合学生认识事物的客观规律。
三、在学以致用上,张老师所设计的题目,与实际联系密切,联系到英语字母、数学中的数字、语文中的汉字,综合性强,增强了学生的趣味性。
在此,如果能对本题稍微进行一下扩展,给学生3分钟讨论时间,让他们联想一些生活中其他对称的字和英语中的字母,比比谁想的又快又多,会使学生在不知不觉中感受到轴对称图形不单单局限在图形上,身边很多事物也是可以看做是轴对称图形的,这样就更能加深学生对轴对称的认识。
专题复习1:利用轴对称求最值_

专题复习1:利用轴对称求最值Ⅱ. 请你设计一个用时最少的方案.二、关于两(多)条线段和最小问题思路指导:此类问题一般通过适当的几何变换实现“折”转“直”。
即将连接两点的折线转化为线段最短问题1.直接运用两点间线段最短解决问题.例:如图8,已知A(1,1)B(3,-3),C为x轴上一个动点,当AC+BC最小时,C点坐标为,此时AC+BC的最小值为.练习:如图9,四边形ABCD为边长为5的正方形,以B为圆心4为半径画弧交BA与M,交BC于N,P在MN上运动,则PA+PB+PC的最小值为.2.平移后应用两点间线段最短例:已知:如图10,A(1,2),B(4,-2),C(m,0),D(m+2,0)(1)在图中作出当AC+CD+DB最小时C点的位置,并求出此时m的值(2)求AC+CD+DB的最小值.练习:如图11,NP,MQ为一段河的两岸(河的两侧为平坦的地面,可以任意穿行),NP∥MQ,河宽PQ 为60米,在NP一侧距离河岸110米处有一处藏宝处A,某人从MQ一侧距离河岸40米的B处出发,随身携带恰好横穿(与河岸垂直)河面的绳索(将绳索利用器械投掷至河对岸并固定,人扶绳索涉水过河),请计算此人从出发到目的地最少的行进路程,并确定固定绳索处(MQ一侧)到B处的最近距离.3.旋转后应用两点间线段最短例:如图12,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.⑴求证:△AMB≌△ENB;⑵①当M点在何处时,AM+CM的值最小;②当M点在何处时,AM+BM+CM的值最小,并说明理由;⑶当AM+BM+CM的最小值为31+时,求正方形的边长.练习:点O 为正方形ABCD内一点,(1)正方形边长为4,求OB+OD的最小值(2)若OB+OC+OD的最小值为26+,求正方形的边长4.对称后应用两点间线段最短数学模型已知:如图14,直线l 及直线同侧两点P、Q,在直线l 上求作点M,使线段PM+QM最小,并说明理由关系探究上图中:相等的角:线段关系:类型一:单动点单对称轴(直线同侧两线段和转化为异侧,进而应用两点间线段最短)练习:1.如图15,已知菱形ABCD的边长为6,M、N 分别为AB、BC边的中点,P为对角线AC上的一动点,则PM+PN的最小值.2. 如图16,已知菱形ABCD的边长为6,点E为AB边的中点,∠BAD=60°,点P为对角线AC上的一动点,则PE+PB的最小值..3. 如图17,已知正方形ABCD的边长为2,点M为BC 边的中点,P为对角线BD上的一动点,则PM+PC的最小值4. 如图18,正方形ABCD的面积为a,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一动点P,PD+PE的和最小值为4,则a= .5.如图19,已知⊙O的半径为1,AB、CD为⊙O的两互相垂直的直径,点M在弧AD上,且∠MOD=30°,点P为半径OD上的一动点,则PM+PA的最小值.6. 如图20,已知⊙O的半径为1,AB为⊙O的直径,C是⊙O上的一点,且∠CAB=30°点M是弧CB的中点,,点P为直径AB上的一动点,则PM+PC的最小值.7.如图21,⊙O的直径为10,A,B在圆周上,AC⊥MN,BD⊥MN,AC=6,BD=8.P为MN上一个动点,则PA+PB的最小值为.8.如图22,已知∠AOB=60°,OA=6,C为OA的中点,OD平分∠AOB,M为OD上一动点,则AM+CM的最小值为9.如图23,从点A(0,2)发出的一束光,经x轴反射,过点B(4,3),则这束光从点A到点B所经过路径的长为.10.如图24,已知抛物线y=x2-2x-3,与x轴相交于点A、B两点(点A在点B的左边),与y轴相较于点C,P 为抛物线对称轴上的一点,则PO+PC的最小值是.11.如图25,以正方形ABCD中AB为边向外作等边三角形AMB,N为对角线BD上一点,若AN+MN的最小值为2226,则正方形边长为.12.一次函数y=kx+b的图象与x、y轴分别交于点A(2,0),B(0,4).(1)求该函数的解析式;(2)O为坐标原点,设C为AB的中点,P为OB上一动点,求PC+PA取最小值时P点的坐标.13.如图27,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.(1)求点B的坐标;(2)求经过A、O、B三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由14.如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.实验与探究:(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:B′、C′;归纳与发现:(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为(不必证明);运用与拓广:(3)已知两点D(1,-3)、E(-1,-4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.类型二:双动点单对称轴(在类型一基础上应用垂线段最短)例:如图,已知∠CAB=30°,BA=6,AF平分∠BAC,P,Q分别为AB,AF上的动点,则BQ+PQ的最小值为练习:1.如图29,正方形ABCD中,AE为∠BAC的平分线,M,N分别为AE,AB上的动点,若MN+BM最小值为3,则正方形边长为.2.如图30,在锐角△ABC中,AB=42,∠BAC=45°,∠BAC 的平分线交BC于点D, M、N分别是AD和AB上的动点,则BM+MN的最小值是___________ .3.如图31,矩形ABCD中,AB=6,BC=8,M,N分别为BD,BC上的动点,则CM+MN的最小值为. 类型三:单动点双对称轴例:如图32,已知:∠AOB=30°,P为∠AOB内一点,OP=6,M,N分别为OA,OB上的动点,则△PMN的周长最小值为.练习:1.如图33,已知:∠AOB=60°,P为∠AOB内一点,OP=10,M,N分别为OA,OB上的动点,则△PMN的周长最小值为.2.如图34,两个镜子成45°角,P为夹角内一个光源,P距离交点2米,光线从P发出后经过OB,OA反射后经过点P,则光线经过的路线长为.3.如图35,已知A(3,2)为坐标平面上一点,在x,y 轴上确定点M,N,使△AMN周长最小,并求出此时M,N坐标.类型四. 双动点双对称轴例:已知P,Q为∠AOB内两个定点,M,N分别为OA,OB上的动点。
(完整版)利用轴对称求最短距离问题

利用轴对称求最短距离问题基本题引入:如图(1),要在公路道a上修建一个加油站,有A,B两人要去加油站加油。
加油站修在公路道的什么地方,可使两人到加油站的总路程最短?你可以在a上找几个点试一试,能发现什么规律?·B ·A·B·Aa·B·Aa·A′图1M·A′MNa 图2图3思路分析:如图2,我们可以把公路a近似看成一条直线,问题就是要在a上找一点M,使AM与BM的和最小。
设A′是A的对称点,本问题也就是要使A′M与BM的和最小。
在连接A′B的线中,线段A′B最短。
因此,线段A′B与直线a的交点C的位置即为所求。
如图3,为了证明点C的位置即为所求,我们不妨在直线a上另外任取一点N,连接AN、BN、A′N。
因为直线a是A,A′的对称轴,点M,N在a上,所以AM= A′M,AN= A′N。
∴AM+BM= A′M+BM= A′B在△A′BN中,∵A′B<A′N+BN∴AM+BM<AN+BN即AM+BM最小。
点评:经过复习学生恍然大悟、面露微笑,不一会不少学生就利用轴对称知识将上一道中考题解决了。
思路如下:②∵BC=9(定值),∴△PBC的周长最小,就是PB+PC最小.由题意可知,点C关于直线DE的对称点是点A,显然当P、A、B三点共线时PB+PA最小.此时DP=DE,PB+PA=AB.由∠ADF=∠FAE,∠DFA=∠ACB=90°,得△DAF∽△ABC.EF∥BC,1159AB=,EF=.∴AF∶BC=AD∶AB,即6∶9=AD∶15.∴AD=10.Rt△ADF22292525中,AD=10,AF=6,∴DF=8.∴DE=DF+FE=8+=.∴当x=时,△PBC的周长222得AE=BE=最小, y值略。
数学新课程标准告诉我们:教师要充分关注学生的学习过程,遵循学生认知规律,合理组织教学内容,建立科学的训练系统。
使学生不仅获得数学基础知识、基本技能,更要获得数学思想和观念,形成良好的数学思维品质。
轴对称最值
作法
图形
原理
在直线 上求点A,在 上求B,使PA+AB的值最小.
作P点关于 的对称点 ,作 B⊥ 于B,交 于A.
点到直线的距离,垂线段最短.
【问题8】
作法
图形
原理
A为 上一定点,B为 上一定点,在 上求点M,在 上求点N,使AM+MN+NB的值最小.
作点A关于 的对称点 ,作点B关于 的对称点 ,连接 交 于M,交 于N.
轴对称的应用——最值问题
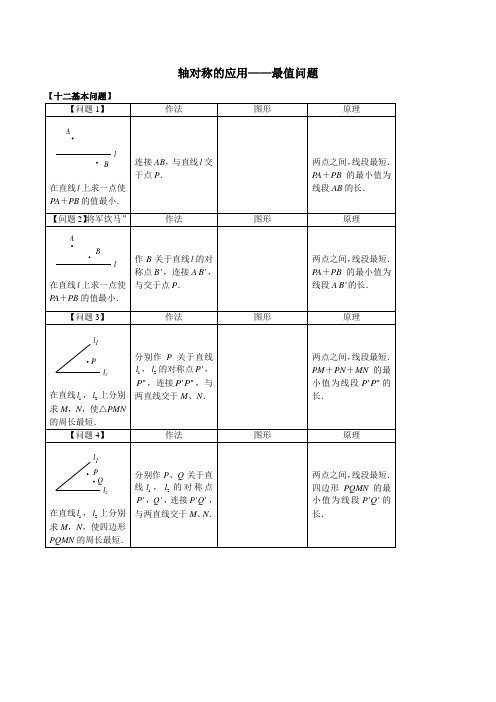
【十二基本问题】
【问题1】
作法
图形
原理
在直线 上求一点使PA+PB的值最小.
连接AB,与直线 交于点P.
两点之间,线段最短.
PA+PB的最小值为线段AB的长.
【问题2】将军饮马”
作法
图形
原理
在直线 上求一点使PA+PB的值最小.
作B关于直线 的对称点 ,连接A ,与交于点P.
17.(17-18-江汉-期中T24)如图,等腰△ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AC于点F,垂足为E,若M为BC边上一动点,D为EF上一动点,则BD+MD的最小值为cm.
18.(17-18-东西湖-期中T16)如图,∠AOB=30°,M、N分别是边OA、OB上的定点,P、Q分别是边OB、OA上的动点,记∠OPM=α,∠PON=β,当MP+PQ+QN最小时,则α,β之间的相等数量关系是
9.(17-18-华一寄-12月T16)如图,直线AB与x轴交于点A(2,0),与y轴交于点B(0,2),D为OC的中点,P是线段BC上一动点,则当OP+PD值最小时点P的坐标为__________
10.(17-18-粮道街-12月T16)(2017-2018粮道街中学八上月考)如图,在锐角三角形ABC中,AB=4,△ABC的面积为10,BD平分∠ABC.若M、N分别是BD、BC上的动点,则CM+MN的最小值为___________
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图(6)
C
B
图(5
)
C
B
一、课本原型:
如图(1)所示,要在街道旁修建一个奶站,向居民区A 、B 提供牛奶,奶站应建在什么地方,才能使从A ,B 到它的距离之和最短?
解:如图(2)①,只要画出A 点关于直线L 的对称点C ,连结BC 交直线L 于P ,则P 点就是所求。
这时PA+PB=PC+PB 为最小,(因为两点之间线段最短)。
证明:如图(2)②,在L 上任取一点P 1,连结P 1A ,P 1B ,P 1C ,
因为P 1A+P 1B=P 1C+P 1B >BC=PA+PB 。
这是根据三角形两边之和大于第三边,所以结论
成立。
二、应用和延伸: 例1、(七年级作业本题)如图(3),
∠AOB 内有一点P ,在OA 和OB 边上分别找出M 、N ,使ΔPMN 的周长最小。
解:如图(4),只要画出P 点关于OB 、OA 的对称点P 1,P 2 ,
连结P 1、P 2交OB 、OA 于M 、N ,
此时ΔPMN 的周长PM+PN+MN =P 1P 2为最小。
(证明略)
例2、如图,A 到直线L 的距离AC =3千米,B 到直线L 的距离BD =1千米,并且CD =4千米,在直线L 上找一点P ,使PA+PB 的值最小。
求这个最小值。
解:如图所示,只要过A 1点画直线L 的平行线与BD 的延长线交于H ,
在Rt △A 1BH 中,A 1H=4千米,BH=4千米,用勾股定理求得A 1B 的长度为42千米。
三、迁移和拓展:
例3、(温州2003年中考题)如图(5),在菱形ABCD 中,AB=4a,E 在BC 上,EC=2a ,∠
BAD=1200
,点P 在BD 上,则PE+PC (A ) 6a , (B) 5a , (C)4a (D)23a 。
解:如图(6),因为菱形是轴对称图形,所以BC 中点E 关于对角线BD 的对称点E 一定
落在AB 的中点E 1,只要连结CE 1,CE 1即为PC+PE 的最小值。
这时三角形CBE 1是含有300
角
的直角三角形,PC+PE=CE 1
=23a 。
所以选(D )。
②
l
街道
图(1)
B
A
街道
图(3
)
例4、如图(7), 在直角坐标系XOY 中,X 轴上的动点M (X ,0)到定点P (5,5)和到Q (2,1)的距离分别为MP 和MQ ,那么当MP+MQ 取最小值时,点M 的横坐标X=_ ___.(你能求出当MP-MQ 最大时点M 的横坐标X= ?)
Q 关于X 轴的对称点Q 1(2,-1),连结PQ 1 交X 于点M ,则M 点即为所求。
点M 的横坐标只要先求出经过PQ 1两点的直线的解析式,(y=2x-5),令y=0,求得x=5/2。
(也可以用勾股定理和相似三角形求出答案。
