材料力学-第七章弯曲变形 上课例题
秦飞编著《材料力学》第7章 弯曲应力

秦飞 编著《材料力学》 第7章 弯曲应力
14
7.1 弯曲正应力
弯曲正应力公式
各种型钢的Iz、Wz值均可以从附录的型钢规格表中查到。
常用截面:矩形截面
bh 3 Iz 12
y max
h 2
bh 2 Wz 6
h
b
对于直径为D的实心圆形截面
πD Iz 64
4
ymax
C
拉
z
M
z
C
压
拉 y y
秦飞 编著《材料力学》 第7章 弯曲应力 8
7.1 弯曲正应力
纯弯曲时梁横截面上的正应力
(2)静力平衡关系 由平面假设,横截面上只有正应力σ。纯弯曲情况下,梁横 截面上的内力只有Mz=M,轴力和 My等其他内力均为零,则
dA 0
A
中性轴
z dA 0
A
由这3个静力平衡方
y
与y成正比,沿截面高
度线性变化。
秦飞 编著《材料力学》 第7章 弯曲应力
ρ为中性层曲率半径
10
7.1 弯曲正应力
纯弯曲时梁横截面上的正应力
(4)物性关系
y 将 代入物性关系,得: y E E
可见,梁横截面上的弯曲正应力 (normal stress in bending) 与y成正比, 即 (1)沿截面高度线性分布; (2)在中性层处为零,在上、下表面 处最大。
My Iz
—弯曲正应力公式
此公式适用于所有横截面具有纵向对称轴的梁,如圆形截 面、工字形截面和T形截面。 由公式: 正比于y。 沿高度线性分布。 中性轴处=0。
秦飞 编著《材料力学》 第7章 弯曲应力 13
工程力学---材料力学(第七章- 梁弯曲时位移计算与刚度设计)经典例题及详解

得: D 0
Pl 2 得: C 16
AC段梁的转角方程和挠曲线方程分别为:
P 2 2 (4 x l ) 16 EI Px y (4 x 2 3 l 2 ) 48 EI
y
P
B
A
x
l 2
C
l 2
x
最大转角和最大挠度分别为:
max A B
ymax y
q 7qa 8k 384 EI
3
q/2
B C
q/2
A B C
顺时针
q/2
例16:图示梁B处为弹性支座,弹簧刚 度
EI k 求C端挠度fC。 2a 3
q
A
EI k
B
C
2a
a
解:(1)梁不变形,仅弹簧变形引起的C点挠度为 4 3 qa 3qa B处反力=qa fC 1 2 k EI
q
B
x
l
由边界条件: x 0时,y 0
x l时,y 0
得:
ql 3 C , D0 24
梁的转角方程和挠曲线方程分别为:
y
q 2 3 3 (6lx 4 x l ) 24 EI
q
x
A qx y (2lx 2 x 3 l 3 ) 24 EI
ql 3 24 EI
A a a
q
B C
a
qa 12 EI
顺时针
3 3
P=qa
A B
P=qa
m=qɑ²/2
qa qa C B 6 EI 4 EI
4
顺时针
B
q
C
qa 5qa fC B a 8EI 24 EI
材料力学第7章 弯曲变形[精]
![材料力学第7章 弯曲变形[精]](https://img.taocdn.com/s3/m/e8c1aae8d4d8d15abf234e2e.png)
dx
小变形梁可近似为
wfx 转角方程 2
材料力学
7.2 梁的挠曲线近似微分方程
由纯弯曲梁的曲率与弯矩的关系:
1M
EI
1
x
M x
EI
曲线曲率 计算公式
1
w
x
3
1w2 2
由曲率-弯矩 的符号关系:
小变形梁的近 似微分方程:
C、D积分常数,由梁上已知的挠度或转角确定,这些
已知的挠度或转角称为边界条件。
4
材料力学
以图示简支梁为例
x0, wA w00 xl, wB wl0
以图示悬臂梁为例
x0, wA w00 A w00
出版社 科技分社 5
材料力学
出版社 科技分社
材料力学
出版社 科技分社
22
8
材料力学
两次积 分得:
EIw1qx31qlx2C 64
EIw 1 qx41qlx3CxD 24 12
由简支梁的边界条件:
出版社 科技分社
(3) (4)
w 0, w 0
x0
xl
得积分常数
C 1 ql3,D0 24
9
材料力学
梁的转角方程
w q(4 x 3 6 lx 2 l3 ) 2 4 E I
当 a>b 时,B支座处截面的转角绝对值为最大
maxB=Fab 6lE lIa
简支梁的最大挠度应在dw/dx=0处,由 w1 0 得
x1
l2b2 3
aa2b
3
当 a>b 时,则有x1< a,由此可知最大挠度位于AC之间1。5
材料力学
出版社 科技分社
材料力学-第7章 弯曲变形

梁弯曲问题的近似和简化
q( x)
M0
ML
Q0
QL
弯曲问题中,不考虑轴向拉伸。因此,梁内力只有弯矩和剪力 下面,我们分别考虑弯矩和剪力引起的弯曲变形效果
材料力学-第7章 弯曲变形
挠度曲线 垂直于轴线的横截面弯曲后仍为平面,仍 垂直于轴线,只是相互间转动一个角度
M
弯矩引起的弯曲变形
M
剪力引起的弯曲变形
例题
2
已知:简支梁受力如 图所示。FP、EI、l均为已 知。 求:加力点B的挠度和 支承A、C处的转角。
材料力学-第7章 弯曲变形
§7- 3 计算梁位移的积分法
解:1. 确定梁约束力 首先,应用静力学方法求得 梁在支承A、C二处的约束力分别 如图中所示。 解:2. 分段建立梁的弯矩方程 因为B处作用有集中力FP,所以需要分为AB和BC两段 建立弯矩方程。 在图示坐标系中,为确定梁在0~l/4范围内各截面上的 弯矩,只需要考虑左端A处的约束力3FP/4;而确定梁在l/4~ l范围内各截面上的弯矩,则需要考虑左端A处的约束力 3FP/4和荷载FP。
Q
垂直于轴线的横截面弯曲后不垂直于轴线
Q
材料力学中一般考虑细长梁,顾而可以忽略剪力引起的变形,只 考虑弯矩引起的变形。因为所有横截面始终与轴线垂直,所以,梁的 弯曲变形可以仅用轴线来表征。空间的梁简化成一轴线。
材料力学-第7章 弯曲变形
挠度曲线
问题1: 如何表征梁的弯曲变形
-用什么物理量来描述梁的变形
( x)
w
x
x
( x)
w( x)
材料力学-第7章 弯曲变形
挠度曲线
* 弯曲变形的表征
梁在弯曲变形后,横截面的位置将发生改变,这种位置 的改变称为位移 (displacement) 。梁的位移包括三部分:
北京航空航天大学-材料力学课件ppt-14+第七章+弯曲变形
3. 求 wC
17 Fa 3
A
Fa
C
B
wC 2
wC1
wB
wC
wC1 wC 2
48EI
4EA
D
a
H
4. 比较弯曲与拉压位移 A bh, I bh3 12
设b×h矩形截面
17 Fa 3 48EI
Fa 4EA
17
a h
2
结论: (如果题意没有要求),拉压与弯曲共同
作用时,拉压引起的位移可以忽略。
18
第七章 弯曲变形
§7-6 简单静不定梁
• 静不定度与多余约束
q(x)
M
5-3=2 度静不定
q(x)
F
6-3 = 3 度静不定
静不定度 =支反力(力偶)数-有效平衡方程数 多余约束 多于维持平衡所必须的约束
静不定度=多余约束数 多余反力 与多余约束相应的支反力或支力偶矩
19
第七章 弯曲变形
静定基与相当系统
例: 求图示外伸梁C点 的挠度和转角
q
C B
l
a
q
仅考虑BC段变形(刚化AB,可
A
视BC为悬臂梁)
qa4 wC1 8EI ()
C1
qa 3 6EI
()
B
l
qa
仅考虑AB段变形(刚化BC)
A
B
C2
B2
qa2l 6EI
()
总挠度和转角
wC 2
B2a
qa3l 6EI
()
l
qa 3 wC wC1 wC 2 24EI (3a 4l ) ()
0
0
wB 0, B 0
A
B
25
材料力学经典习题册 弯曲变形
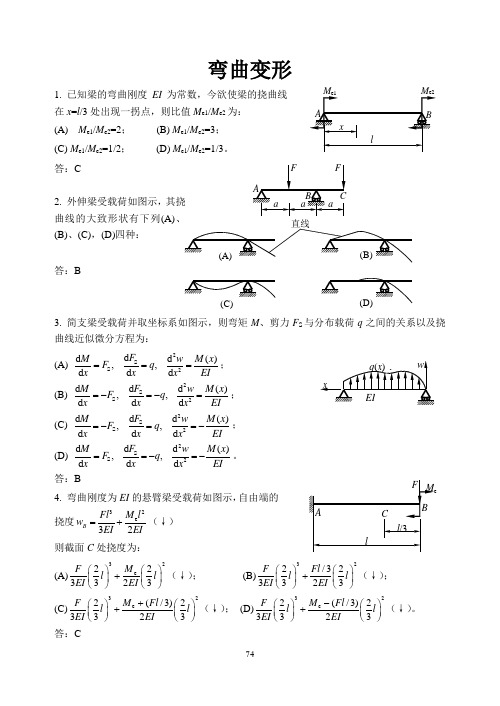
弯曲变形1. 已知梁的弯曲刚度EI为常数,今欲使梁的挠曲线在x=l/3处出现一拐点,则比值M e1/M e2为:(A) M e1/M e2=2;(B) M e1/M e2=3;(C) M e1/M e2=1/2;(D) M e1/M e2=1/3。
答:C2. 外伸梁受载荷如图示,其挠曲线的大致形状有下列(A)、(B)、(C),(D)四种:答:B3. 简支梁受载荷并取坐标系如图示,则弯矩M、剪力F S与分布载荷q之间的关系以及挠曲线近似微分方程为:(A)2SS2dd d(),,d d dFM w M xF qx x x EI===;(B)2SS2dd d(),,d d dFM w M xF qx x x EI=-=-=;(C)2SS2dd d(),,d d dFM w M xF qx x x EI=-==-;(D)2SS2dd d(),,d d dFM w M xF qx x x EI==-=-。
答:B4. 弯曲刚度为EI的悬臂梁受载荷如图示,自由端的挠度23e32BM lFlwEI EI=+(↓)则截面C处挠度为:(A)32e223323MFl lEI EI⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭(↓);(B)322/323323F Fll lEI EI⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭(↓);(C)32e(/3)223323M FlFl lEI EI+⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭(↓);(D)32e(/3)223323M FlFl lEI EI-⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭(↓)。
答:C5. 画出(a)、(b)、(c)三种梁的挠曲线大致形状。
答:6. 试画出图示梁的挠曲线大致形状。
答:7. 正方形截面梁分别按(a)、(b)两种形式放置,则两者间的弯曲刚度关系为下列中的哪一种: (A) (a)>(b); (B) (a)<(b); (C) (a)=(b); (D) 不一定。
答:C8. 试写出图示等截面梁的位移边界条件,并定性地画出梁的挠曲线大致形状。
材料力学习题弯曲变形

弯曲变形基本概念题一、选择题1.梁的受力情况如图所示,该梁变形后的挠曲线如图()所示(图中挠曲线的虚线部分表示直线,实线部分表示曲线)。
2. 如图所示悬臂梁,若分别采用两种坐标系,则由积分法求得的挠度和转角的正负号为()。
题2图题1图A.两组结果的正负号完全一致B.两组结果的正负号完全相反C.挠度的正负号相反,转角正负号一致D.挠度正负号一致,转角的正负号相反3.已知挠曲线方程y = q0x(l3 - 3lx2 +2 x3)∕(48EI),如图所示,则两端点的约束可能为下列约束中的()。
题3图4. 等截面梁如图所示,若用积分法求解梁的转角、挠度,则以下结论中()是错误的。
A.该梁应分为AB、BC两段进行积分B.挠度积分表达式中,会出现4个积分常数-26-题4图 题5图C .积分常数由边界条件和连续条件来确定D .边界条件和连续条件表达式为x = 0,y = 0;x = l ,0==右左y y ,0='y5. 用积分法计算图所示梁的位移,边界条件和连续条件为( ) A .x = 0,y = 0;x = a + l ,y = 0;x = a ,右左y y =,右左y y '=' B .x = 0,y = 0;x = a + l ,0='y ;x = a ,右左y y =,右左y y '=' C .x = 0,y = 0;x = a + l ,y = 0,0='y ;x = a ,右左y y =D .x = 0,y = 0;x = a + l ,y = 0,0='y ;x = a ,右左y y '=' 6. 材料相同的悬臂梁I 、Ⅱ,所受荷载及截面尺寸如图所示。
关于它们的最大挠度有如下结论,正确的是( )。
A . I 梁最大挠度是Ⅱ梁的41倍B .I 梁最大挠度是Ⅱ梁的21倍 C . I 梁最大挠度与Ⅱ梁的相等 D .I 梁最大挠度是Ⅱ梁的2倍题6图 题7图7. 如图所示等截面梁,用叠加法求得外伸端C 截面的挠度为( )。
弯曲内力—弯曲变形概述(材料力学)

平面弯曲及梁的分类 剪力和弯矩的定义及正负号规定 截面法和代数和法求剪力和弯矩 单一荷载下静定梁的内力图 分布荷载集度、剪力与弯矩之间的微分关系 利用内力图规律绘制剪力图和弯矩图 叠加原ห้องสมุดไป่ตู้绘制梁的弯矩图
弯曲变形实例 1 桥式吊车梁
弯曲变形概述
弯曲变形概述
弯曲变形实例 2 火车轮轴
弯曲变形概述
梁上所有横截面的竖向对称 轴形成了梁的纵向对称面
3. 梁的计算简图及梁的分类
弯曲变形概述
(1)简支梁:梁的一端是固定铰支座,另一端是可动铰支座。
(2)外伸梁:一端或两端伸出支座外的梁。
(3)悬臂梁:一端固定,另一端自由的梁。
Fq
FAx
A
FAy
Me B
FB
FAx A
FAy
q B FB
支座
固定铰支座 可动铰支座 固定端支座
1. 弯曲变形
受力特征
当杆件受到垂直于杆件轴线的横向力或位于杆轴平面内的外力偶时,杆件的轴线
将由直线变成曲线,这种变形称为弯曲,以弯曲为主要变形的构件,通常称为梁。
变形特征
弯曲变形概述
2.平面弯曲
若梁上所有外力都作用在纵向对称面内,则梁的轴线将在纵向对称面内由直线变 成曲线,这种弯曲称为平面弯曲。
FAx
A
MA
FAy
F
B
Me
弯曲变形概述
3.弯曲构件---梁
(1)可简化为简支梁的吊车大梁
(2)可简化为外伸梁的火车轮轴 (3)可简化为悬臂梁的化工反应塔
qF
A
B
F
A
F
B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
1
|x0
Fab(l 6lEI
b)
B
2
|xl
Fab(l 6lEI
a)
当 a > b 时, 右支座处截面的转角绝对值为最大
max
B
Fab(l 6lEI
a)
14
简支梁的最大挠度应在 w' 0处
先研究第一段梁,令 w1 0 得
1
w1'
Fb 6lEI
(3l 2
4b2 )
0.0625 Fbl 2 EI
wmax
y |xx1 9
Fb 3lEI
(l 2
b2 )3
Fbl 2 0.0642
EI
结论:在简支梁中, 不论它受什么荷载作用, 只要挠曲线上无 拐点, 其最大挠度值都可用梁跨中点处的挠度值来代替, 其精确度 是能满足工程要求的.
2
(4)
边界条件 x 0, w 0
x 0, w 0
将边界条件代入(3)(4)两式中,可得 C1 0 C2 0
梁的转角方程和挠曲线方程分别为
EIw Flx Fx2 EIw Flx2 Fx3
2
26
3
y
F
A
l
Bx
wmax
max
max 和 wmax都发生在自由端截面处
max
Fl 2 |xl EI
Fl 2 2EI
Fl 2 ( 2EI
)
Pl 3
wmax w |xl 3EI ( )
4
例题2 图示一抗弯刚度为 EI 的简支梁,在全梁上受集度为q 的
均布荷载作用.试求此梁的挠曲线方程和转角方程,并确定其 max
和 wmax
q
Aቤተ መጻሕፍቲ ባይዱ
B
l
5
q
解:由对称性可知,梁的两
个支反力为
A
B
FRA
FRB
ql 2
x
l
FRA
FRB
此梁的弯矩方程及挠曲线微分方程分别为
M ( x) ql x q x2 22
EIw ql x q x2 22
EIw ql x2 q x3 C 46
EIw ql x3 q x4 Cx D 12 24
F
b l
FRA
A
FRB
F
a l
两段梁的弯矩方程分别为
x
1 a
x
F
D
2
FRB
B
b l
M1
FRA x
F
b l
x
(0 x a)
M2
F
b l
x
F(x
a)
(a x l )
9
两段梁的挠曲线方程分别为 (a)(0 x a)
挠曲线方程 转角方程 挠度方程
EIw1
M1
F
b l
18
例题5 试利用叠加法,求图
C 2x
D2
11
D点的连续条件
在 x = a 处 w1 w2
FRA
1
w1 w2
A
边界条件
a
F
D
2 FRB
B
b
在 x = 0 处, w1 0
l
在 x = l 处, w2 0
代入方程可解得:
D1 D2 0
C
1
C
2
Fb 6l
(
l
2
b
2)
12
(a)(0 x a)
第七章 弯曲变形 上课例题
例题1 图示一抗弯刚度为 EI 的悬臂梁, 在自由端受一集中力 F
作用.试求梁的挠曲线方程和转角方程, 并确定其最大挠度 wmax
和最大转角 max
F w
A
Bx
l
1
解: (1) 弯矩方程为
w A
M( x) F (l x) (1)
(2) 挠曲线的近似微分方程为
16
例题4 一抗弯刚度为EI的简支梁受荷载如图所示.试按叠加原理
求梁跨中点的挠度 wC和支座处横截面的转角A , B 。
Me
q
A
B
C
l
17
解:将梁上荷载分为两
Me
项简单的荷载,如图所示
A
wC (wC)q (wC)Me
(a)
5ql 4 Mel 2 384EI 16EI
(
)
θ A (θ A)q (θ A)Me
(l 2
b2
3x2)
0
x1
l2 b2 3
a(a 2b) 3
当 a > b时, x1 < a 最大挠度确实在第一段梁中
wmax w |xx1 9
Fb 3lEI
(l 2 b2 )3 0.0642 Pbl 2 EI
15
梁中点 C 处的挠度为
wC
Fb 48EI
x
EIw1
F
b l
x2 2
C1
EIw1
F
b l
x3 6
C1x
D1
10
(b)( a x l )
挠曲线方程
EIw 2
M
2
F
b l
x
F
(
x
a)
转角方程 挠度方程
EIw 2
F
b l
x2 2
F
(
x 2
a)2
C
2
EIw 2
F
b l
x3 6
F
(
x 6
a)3
1
w1
Fb 6lEI
(l 2
b2
3x2)
w1
Fbx 6lEI
[l 2
b2
x2]
(b)( a x l )
2
w 2'
Fb 2lEI
[l b
(
x
a)2
x2
1 3
(l 2
b2)]
w
2
Fb 6lEI
[
l b
(
x
a
)3
x
3
(l
2
b
2
)
x]
13
将 x = 0 和 x = l 分别代入转角方程左右两支座处截面的转角
(b) A
( ql 3 Mel ) ( )
24EI 3EI
Me
θ B (θ B)q (θ B)Me
(c) A
ql 3 Mel ( )
24EI 6EI
q C l q
( A)q C (wC )q
l
( A ) C Me (wC )Me
l
B B ( B)q
B (B )Me
6
边界条件x=0 和 x=l时, w 0
q
wmax
梁的转角方程和挠曲线方程 A 分别为
q (6lx2 4x3 l 3 )
24EI w qx (2lx2 x3 l 3 )
24EI
A
x
FRA
B
B
l
FRB
最大转角和最大挠度分别为
在 x=0 和 x=l 处转角的绝对值相等且都是最大值,
x
l
EIw M( x) Fl Fx (2)
对挠曲线近似微分方程进行积分
EIw
Flx
Fx 2 2
C1
(3)
EIw
Flx 2 2
Fx 3 6
C 1x
C2
(4)
F
Bx
2
EIw
Flx
Fx 2 2
C1
(3)
EIw
Flx 2 2
Fx 3 6
C 1x
C
max
A
B
ql 3 24EI
在梁跨中点处有最大挠度值
wmax
w
x l 2
5ql4 384EI
7
例题3 图示一抗弯刚度为EI的简支梁, 在D点处受一集中力F的作 用.试求此梁的挠曲线方程和转角方程,并求其最大挠度和最大转 角.
F
A a
D
B
b
l
8
解: 梁的两个支反力为
FRA
