九年级中考数学考点提升训练——专题:《找规律:数字变化类》(三)(Word版,带答案)
2021年九年级数学中考二轮复习探索规律专题突破训练:数字的变化规律(附答案)

2021年九年级数学中考二轮复习探索规律专题突破训练:数字的变化规律(附答案)1.计算1+2﹣3﹣4+5+6﹣7﹣8+…+2017+2018﹣2019﹣2020的值为()A.0B.﹣1C.2020D.﹣20202.按一定规律排列的单项式:a,﹣a2,a3,﹣a4,a5,﹣a6,……第2020个单项式是()A.2020a B.﹣2020a C.a2020D.﹣a20203.已知函数f(x)=,若M=f(1)+f(2)+f(3)+…+f(2013)+f(2014),N=f ()+f()+f()+…+f()+f(),则M+N=()A.2014B.C.2013D.4.一列数1,5,11,19…按此规律排列,第7个数是()A.37B.41C.55D.715.在数列,,,,,,,,,,…中,请你观察数列的排列规律,推算该数列中的第5055个数为()A.B.C.D.6.将一列有理数﹣1,2,﹣3,4,﹣5,6,…,按如图所示进行排列,则﹣2021应排在()A.A位置B.B位置C.D位置D.E位置7.已知f(1)=2(取1×2的末位数字),f(2)=6(取2×3的末位数字),f(3)=2(取3×4的末位数字),…,则f(1)+f(2)+f(3)+…+f(2021)的值为()A.6B.4028C.4042D.40488.已知整数a1,a2,a3,a4,…,满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,…,依此类推,则a2035的值为()A.﹣2035B.2035C.﹣1018D.﹣10179.一个盒子里装有不多于200颗糖,如果每次2颗,3颗,4颗或6颗的取出,最终盒内都只剩下一颗糖,如果每次以11颗的取出,那么正好取完,则盒子里共有颗糖.10.按一定规律排列的一列数依次为,﹣,,﹣,,﹣,…,按此规律排列下去,这列数中第8个数是,第n个数是(n为正整数).11.一组按规律排列的式子:,,,,,其中第8个式子是,第n个式子是(用含的n式子表示,n为正整数).12.已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此类推,则a2019的值为.13.设第n行第m个数为a n,m.满足a n,n=a n,1=,a n,m=a n+1,m+a n+1,m+1,求a12,11=.14.正整数按如图所示的规律排列,则第29行第30列的数字为.15.已知a1=0,a n+1=﹣|a n+n|(n≥1,且n为整数),则a2020的值是.16.正整数按如图的规律排列.请写出第20行,第21列的数字.17.观察下列一组数:﹣,,﹣,,﹣,…,它们是按一定规律排列的,那么这一组数的第n个数是.18.如果a是不为1的有理数,我们把称为a的差倒数.如:2的差倒数是=﹣1,﹣1的差倒数是=.已知a1=4,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2022=.19.观察下列两个数的积(这两个数的十位上的数相同,个位上的数的和等于10);71×79=5609;24×26=624;35×35=1225;53×57=3021;…(1)计算83×87=,552=.(2)根据观察与计算能得出什么结论,请将它用文字或字母表示出来;(3)证明得出的结论.20.阅读材料:求1+2+22+23+…+22019+22020的值.解:设S=1+2+22+23+…+22019+22020①,将等式①的两边同乘以2,得2S=2+22+23+24+…+22020+22021②,用②﹣①得,2S﹣S=22021﹣1,即S=22021﹣1.即1+2+22+23+…+22019+22020=22021﹣1.请仿照此法计算:(1)请直接填写1+2+22+23的值为;(2)求1+5+52+53+…+510的值;(3)请直接写出1﹣10+102﹣103+104﹣105+…﹣102019+102020﹣的值.21.我们把按一定规律排列的一列数称为数列.若对于一个数列中任意相邻有序的三个数a,b,c总满足c=ab+2a﹣b,则称这个数列为“梦数列”.(1)若0,1,﹣1,2,y是“梦数列”,则y=;(2)如果数列…,x,3,6x﹣1,…是“梦数列”,求x的值;(3)如果数列…,2m,n,5…是“梦数列”,求代数式8m﹣2n+4mn﹣9的值.22.有一系列等式:第1个:52﹣12=8×3;第2个:92﹣52=8×7;第3个:132﹣92=8×11;第4个:172﹣132=8×15;……(1)请写出第5个等式:.(2)请写出第n个等式,并加以验证.(3)依据上述规律,计算:8×3+8×7+8×11+……+8×399.23.观察下列等式:=1,=,=.将以上三个等式的两边分别相加,得:+=1=1=.(1)直接写出计算结果:=.(2)计算:.(3)猜想并直接写出:=.(n 为正整数)24.阅读下列材料,然后回答问题:观察下列等式:=1,=,将以上三个等式相加得:=1=1=.(1)猜想并写出:=;(2)直接写出下列各式的结果:①=;②=;(3)探究并计算:.25.观察下列各式:12+32+42=2×(12+32+3);22+42+62=2×(22+42+8);32+52+82=2×(32+52+15);…(1)用a,b,c表示等式左边的由小到大的三个底数,发现c与a,b的数量关系是;(2)等式右边括号内的三个数可用a,b表示为:;(3)用a,b表示你发现的等式,并加以证明.26.定义一种新运算“⊙”,观察下列等式:①1⊙3=1×3﹣(﹣1)﹣(﹣3)=7,②(﹣1)⊙(﹣2)=(﹣1)×(﹣2)﹣1﹣2=﹣1,③0⊙(﹣2)=0×(﹣2)﹣0﹣2=﹣2,④4⊙(﹣3)=4×(﹣3)﹣(﹣4)﹣3=﹣11,…(1)计算(﹣5)⊙3的值;(2)有理数的加法和乘法运算满足交换律,“⊙”运算是否满足交换律?请说明理由.27.有一列数,按一定规律排成1,,,,,,….(1)这列数中的第7个数是,第n个数是.(2)若其中某三个相邻数的和是,则这三个数中最大的数是多少?28.观察下列等式:①1﹣1﹣=﹣;②﹣﹣=﹣;③﹣﹣=﹣;④﹣﹣=﹣;…根据上述规律解决下列问题:(1)完成第⑤个等式;(2)写出你猜想的第n个等式(用含n的式子表示)并证明其正确性.29.我们将不大于2020的正整数随机分为两组,第一组按照升序排列得到a1<a2<…<a1010,第二组按照降序排列得到b1>b2>…>b1010.求|a1﹣b1|+|a2﹣b2|+…+|a1010﹣b1010|的所有可能值.30.观察下列等式:12=;12+22=;12+22+32=;12+22+32+42=;…(1)根据上述规律,求12+22+32+42+52的值;(2)你能用一个含有n(n为正整数)的算式表示这个规律吗?请直接写出这个算式(不计算).(3)根据你发现的规律,计算下面算式的值:62+72+82+92+…+592+602.参考答案1.解:∵1+2﹣3﹣4=﹣4,5+6﹣7﹣8=﹣4,即每四项结果为﹣4,∵2020÷4=505,∴1+2﹣3﹣4+5+6﹣7﹣8+…+2013+2014﹣2015﹣2016=﹣4×505=﹣2020.故选:D.2.解:∵一列单项式为:a,﹣a2,a3,﹣a4,a5,﹣a6,…,∴第n个单项式为(﹣1)n+1•a n,当n=2020时,这个单项式是(﹣1)2020+1•a2020=﹣a2020,故选:D.3.解:根据题意可知:f(2)==,f()=÷(1+)=,∴f(2)+f()=+=1,…可得:f(2014)+f()=1,又∵f(1)=,∴M+N=2013+=.故选:D.4.解:1=1×2﹣1,5=2×3﹣1,11=3×4﹣1,19=4×5﹣1,…第n个数为n(n+1)﹣1,则第7个数是:55.故选:C.5.解:观察数列发现规律:第n组的分数有n个,它们的分子是从1开始的连续自然数,分母是从n开始的连续降序自然数,因为前100组有:1+2+3+…+100=5050个分数,所以5055个数在第101组的第5个,分母为101﹣4=97,分子是5,所以第5055个数为:.故选:B.6.解:由图可知,每个凸起对应5个数字,这些数字的奇数都是负数,偶数都是正数,∵(2021﹣1)÷5=2020÷5=404,∴﹣2021应排在E位置,故选:D.7.解:∵f(1)=2(取1×2的末位数字),f(2)=6(取2×3的末位数字),f(3)=2(取3×4的末位数字),f(4)=0(取4×5的末位数字),f(5)=0(取5×6的末位数字),f(6)=2(取6×7的末位数字),f(7)=6(取7×8的末位数字),f(8)=2(取8×9的末位数字),f(9)=0(取9×10的末位数字),f(10)=0(取10×11的末位数字),f(11)=2(取11×12的末位数字),…,可知末位数字以2,6,2,0,0依次出现,∵2021÷5=404…1,∴f(1)+f(2)+f(3)+…+f(2021)=(2+6+2+0+0)×404+2=10×404+2=4040+2=4042,故选:C.8.解:由题意可得,a1=0,a2=﹣|a1+1|=﹣1,a3=﹣|a2+2|=﹣1,a4=﹣|a3+3|=﹣2,a5=﹣|a4+4|=﹣2,…,∵(2035﹣1)÷2=2034÷2=1017,∴a2035=﹣1017,故选:D.9.解:已知如果每次11颗地取出正好取完,则盒子内糖数必为11的倍数.又知盒子里装有不多于200颗糖,则盒子内糖数可能为11、22、33、44、55、66、77、88、99、110、121、132、143、154、165、176、187、198.又已知如果每次2颗,3颗,4颗或6颗地取出,最终盒内都只剩一颗糖,则盒子内糖数为12的倍数+1.又知盒子里装有不多于200颗糖则盒子内糖数可能为13,25,37,49,61,73,85,97,109,121,133,145,157,169,181,193.取上面两组数的交集可得121,故盒子里共有121颗糖.故答案为:121.10.解:根据分析可知:一列数依次为:,﹣,,﹣,,﹣,…,按此规律排列下去,则这列数中的第8个数是﹣,所以第n个数是:(﹣1)n+1(n是正整数).故答案为:﹣;(﹣1)n+1.11.解:∵=(﹣1)2•,﹣=(﹣1)3•,=(﹣1)4•,…∴第8个式子是,第n个式子为:(﹣1)n+1•.故答案是:;(﹣1)n+1•.12.解:a1=0,a2=﹣|a1+1|=﹣|0+1|=﹣1,a3=﹣|a2+2|=﹣|﹣1+2|=﹣1,a4=﹣|a3+3|=﹣|﹣1+3|=﹣2,a5=﹣|a4+4|=﹣|﹣2+4|=﹣2,a6=﹣|a5+5|=﹣|﹣2+5|=﹣3,a7=﹣|a6+6|=﹣|﹣3+6|=﹣3,…,所以,n是奇数时,a n=﹣(n﹣1),n是偶数时,a n=﹣,∴a2019=﹣(2019﹣1)=﹣1009.故答案为:﹣1009.13.解:因为a n,n=a n,1=,所以a11,11=a11,1=,a12,12=a12,1=,因为a n,m=a n+1,m+a n+1,m+1,所以a12,11=a11,11﹣a12,12=﹣=.故答案为:.14.解:根据图表分析如下:第一行:首个数字1,横向箭头共有1个数字,第二行:首个数字4,横向箭头共有2个数字,第三行:首个数字9,横向箭头共有3个数字,第四行:首个数字16,横向箭头共有4个数字,可以发现每行首个数字是行数的平方,每行横向箭头数字个数等于行数,因此,第29行第30列的数字应该为第30行第1列上面的数字的平方减去30,302﹣30=870.故答案为:870.15.解:∵a1=0,a n+1=﹣|a n+n|(n≥1,且n为整数),∴a2=﹣|0+1|=﹣1,a3=﹣|﹣1+2|=﹣1,a4=﹣|﹣1+3|=﹣2,a5=﹣|﹣2+4|=﹣2,a6=﹣|﹣2+5|=﹣3,a7=﹣|﹣3+6|=﹣3,…,∴a2020=﹣=﹣1010,故答案为:﹣1010.16.解:第一行第二列对应的数字为:2=1×2,第二行第三列对应的数字为:6=2×3,第三行第四列对应的数字为:12=3×4,第四行第五列对应的数字为:20=4×5,…第20行,第21列对应的数字为:20×21=420;故答案为:420;17.解:观察下列一组数:﹣=﹣,=,﹣=﹣,=,﹣=﹣,…,它们是按一定规律排列的,那么这一组数的第n个数是:(﹣1)n.故答案为:(﹣1)n.18.解:∵a1=4a2===﹣,a3===,a4===4,…数列以4,﹣,三个数依次不断循环,∵2022÷3=674,∴a2022=a3=,故答案为:.19.解:(1)∵83×87=7221,552=3025,(2)可得规律为:十位上数字乘以十位上数字加一作为结果的千和百位数字,两个个位相乘作为结果的个位和十位.(3)设十位数字为x,个位数字为y,一个数为10x+y,则另一个数为10x+10﹣y=10(x+1)﹣y,(10x+y)[10(x+1)﹣y]=100x(x+1)+y(10﹣y),前一项就是十位上数字乘以十位上数字加一,后一项就是两个个位数字相乘.故答案为:(1)7221;3025.20.解:(1)1+2+22+23=1+2+4+8=15,故答案为:15;(2)设S=1+5+52+53+ (510)则5S=5+52+53+ (511)∴5S﹣S=511﹣1,∴4S=511﹣1,∴S=,即1+5+52+53+…+510=;(3)设S=1﹣10+102﹣103+104﹣105+…﹣102019+102020,则10S=10﹣102+103﹣104+105﹣…﹣102020+102021,∴S+10S=1+102021,∴11S=1+102021,∴S=,∴1﹣10+102﹣103+104﹣105+…﹣102019+102020﹣=﹣=.21.解:(1)∵0,1,﹣1,2,y是“梦数列”,∴y=﹣1×2+2×(﹣1)﹣2=﹣2+(﹣2)+(﹣2)=﹣6,故答案为:﹣6;(2)∵数列…,x,3,6x﹣1,…是“梦数列”,∴6x﹣1=3x+2x﹣3,解得x=﹣2,即x的值为﹣2;(3)∵数列…,2m,n,5…是“梦数列”,∴5=2mn+4m﹣n,∴8m﹣2n+4mn﹣9=2(2mn+4m﹣n)﹣9=2×5﹣9=1.22.解:(1)由题意可知:相间两个奇数的乘方差,等于这个两数的平均数的8倍,∴第5个等式为:212﹣172=8×19,故答案为:212﹣172=8×19;(2)第n个等式为:(4n+1)2﹣(4n﹣3)2=8(4n﹣1).验证:(4n+1)2﹣(4n﹣3)2=16n2+8n+1﹣(16n2﹣24n+9)=32n﹣8=8(4n﹣1),∴(4n+1)2﹣(4n﹣3)2=8(4n﹣1);(3)8×3+8×7+8×11+……+8×399=52﹣12+92﹣52+132﹣92+……+4012﹣3972=4012﹣12=402×400=160800.23.解:(1)=1﹣+…+=1﹣=,故答案为:;(2)=1﹣+…+=1﹣==;(3)=×(1﹣+…+)=×(1﹣)=×=×=,故答案为:.24.解:(1)由题意可得,=,故答案为:;(2)①=1﹣+…+=1﹣=,故答案为:;②==1﹣+…+=1﹣==,故答案为:;(3)=×(+…+)=×()=×=.25.解:(1)∵12+32+42=2×(12+32+3);22+42+62=2×(22+42+8);32+52+82=2×(32+52+15);…,∴用a,b,c表示等式左边的由小到大的三个底数,则c=a+b,故答案为:c=a+b;(2)∵12+32+42=2×(12+32+3);22+42+62=2×(22+42+8);32+52+82=2×(32+52+15);…,∴用a,b,c表示等式左边的由小到大的三个底数,则等式右边括号内的三个数可表示为a2+b2+ab,故答案为:a2+b2+ab;(3)a2+b2+(a+b)2=2(a2+b2+ab),证明:∵a2+b2+(a+b)2=a2+b2+a2+2ab+b2=2(a2+b2+ab),∴a2+b2+(a+b)2=2(a2+b2+ab).26.解:(1)观察已知等式可知:(﹣5)⊙3=﹣5×3﹣5﹣(﹣3)=﹣17;(2)“⊙”运算满足交换律,理由如下:因为a⊙b=ab﹣(﹣a)﹣(﹣b)=ab+a+b;b⊙a=ba﹣(﹣b)﹣(﹣a)=ab+b+a=ab+a+b=a⊙b.所以a⊙b=b⊙a.27.解:(1)∵一列数为1,,,,,,….∴这列数的第n个数为,当n=7时,这个数是=﹣,故答案为:﹣,;(2)设这三个数是4x,﹣2x,x,则4x+(﹣2x)+x=,解得x=﹣,则﹣2x=,4x=﹣,故这三个数中最大的数是.28.解:(1)∵左边的第2项和第3项的分母分别是连续的奇数和偶数,右边的分母为是左边第2项和第3项的分母之积,∴第5个等式为:﹣﹣=﹣;(2)第n个等式为:﹣﹣=﹣,证明:左边==﹣,右边=﹣,∴左边=右边,∴原式成立.29.解:(1)若a k≤1010,且b k≤1010,则a1<a2<…<a k≤1010,1010≥b k>b k+1>…>b1010,则a1,a2,…a k,b k,……,{b1010,共1011个数,不大于1010不可能;(2)若a k>1010,且b k>1010,则a1010>a1009>…>a k+1>a k>1010及b1>b2>…>b k>1010,则${b}_{1},……,{b}_{k},{a}_{k}……{a}_{1010}共1011个数都大于100,也不可能;∴|a1﹣b1|,……,|a1010﹣b1010|中一个数大于1010,一个数不大于1010,∴|a1﹣b1|+|a2﹣b2|+…+|a1010﹣b1010|=1010×1010=1020100.30.解:(1)12+22+32+42+52==55,即12+22+32+42+52的值是55;(2)∵12=;12+22=;12+22+32=;12+22+32+42=;…∴第n个算式是12+22+32+…+n2=;(3)62+72+82+92+…+592+602=12+22+32+…+602﹣(12+22+32+42+52)=﹣=73810﹣55=73755。
【单点训练】规律型:数字的变化类

【单点训练】规律型:数字的变化类【单点训练】规律型:数字的变化类一、选择题(共15小题)2.(2004•荆门)计算机利用的是二进制数,它共有两个数码0、1,将一个十进制数转化为二进制数,只需把该数写成若干个2n数的和,依次写出1或0即可,如19(+)=16+2+1=1×24+0×23+0×22+1×21+1×20=10011(二)为二进制下3.(2007•台湾)将化成小数,则小数点后第122位数为()4.(2005•镇江)一个正整数数表如下(表中下一行中数的个数是上一行中数的个数的2倍):则第6行中的最后一5.(2003•荆门)64名男子乒乓球选手进行单打淘汰赛(胜者进入下一轮,败者淘汰出局),直至决出单打冠军,共6.(2007•孝感)将一正方形按如图方式分成n个全等矩形,上、下各横排两个,中间竖排若干个,则n的值为()8.(2005•淮安)已知一列数:1,﹣2,3,﹣4,5,﹣6,7,…将这列数排成下列形式:第1行1第2行﹣2 3第3行﹣4 5﹣6第4行7﹣8 9﹣10第5行11﹣12 13﹣14 15…按照上述规律排下去,那么第10行从左边数第5个数等于()9.(2007•呼和浩特)观察下列三角形数阵:则第50行的最后一个数是()10.(2006•柳州)请你认真观察和分析图中数字的变化规律,由此得到图中所缺的数字是()11.(2008•赤峰)给定一列按规律排列的数:1,,,,…它的第10个数是().C D.12.(2006•烟台)计算:21﹣1=1,22﹣1=3,23﹣1=7,24﹣1=15,25﹣1=31,…归纳各计算结果中的个位数字规律,200614.(2004•淄博)观察下列数表:15.(2003•郴州)观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,通过观察,用你所发现的规27二、填空题(共15小题)(除非特别说明,请填准确值)16.(2009•南宁)正整数按如图的规律排列.请写出第20行,第21列的数字_________.17.(2009•天水)观察下列计算:•(+1)=(﹣1)(+1)=1,(+)(+1)=[(﹣1)+(﹣)](+1)=2,(++)(+1)=[(﹣1)+(﹣)+(﹣)](+1)=3,…从以上计算过程中找出规律,并利用这一规律进行计算:(+++…+)(+1)=_________.18.(2009•绵阳)将正整数依次按下表规律排成四列,则根据表中的排列规律,数2009应排的位置是第_________行第_________列.19.(2008•遵义)如图是与杨辉三角形有类似性质的三角形数垒,a,b是某行的前两个数,当a=7时,b=_________.20.(2008•宜宾)观察如下一列有规律的数,请在空格处填入合适的数字:1,1,2,3,4,6,9,_________,19,_________…21.(2009•朝阳)下列是有规律排列的一列数:…其中从左至右第100个数是_________.22.(2009•深圳)已知依据上述规律,则a99=_________.23.(2009•鸡西)有一列数﹣,,﹣,,…,那么第7个数是_________.24.(2009•恩施州)观察数表根据表中数的排列规律,则字母A所表示的数是_________.25.(2009•内江)把一张纸片剪成4块,再从所得的纸片中任取若干块,每块又剪成4块,像这样依次地进行下去,到剪完某一次为止.那么2007,2008,2009,2010这四个数中_________可能是剪出的纸片数.26.(2008•永春县)按一定的规律排列的一列数依次为:﹣2,5,﹣10,17,﹣26,…按此规律排下去,这列数中的第9个数是_________.27.(2008•咸宁)观察右表,依据表格数据排列的规律,数2008在表格中出现的次数共有_________次.28.(2008•莆田)观察下列按顺序排列的等式:0+1=12,2×1+2=22,3×2+3=32,4×3+4=42.请你猜想第10个等式应为_________.29.(2008•肇庆)已知21=2,22=4,23=8,24=16,25=32,…,观察上面规律,试猜22008的末位数是_________.30.(2008•烟台)表2是从表1中截取的一部分,则a=_________.三、解答题(共1小题)(选答题,不自动判卷)31.(2007•无锡)图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面﹣层有一个圆圈,以下各层均比上﹣层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n=.如果图1中的圆圈共有12层,(1)我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层最左边这个圆圈中的数是;(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数﹣23,﹣22,﹣21,…,求图4中所有圆圈中各数的绝对值之和.【单点训练】规律型:数字的变化类参考答案与试题解析一、选择题(共15小题)2.(2004•荆门)计算机利用的是二进制数,它共有两个数码0、1,将一个十进制数转化为二进制数,只需把该数写成若干个2n数的和,依次写出1或0即可,如19(+)=16+2+1=1×24+0×23+0×22+1×21+1×20=10011(二)为二进制下3.(2007•台湾)将化成小数,则小数点后第122位数为()=0.7037034.(2005•镇江)一个正整数数表如下(表中下一行中数的个数是上一行中数的个数的2倍):则第6行中的最后一5.(2003•荆门)64名男子乒乓球选手进行单打淘汰赛(胜者进入下一轮,败者淘汰出局),直至决出单打冠军,共6.(2007•孝感)将一正方形按如图方式分成n个全等矩形,上、下各横排两个,中间竖排若干个,则n的值为()8.(2005•淮安)已知一列数:1,﹣2,3,﹣4,5,﹣6,7,…将这列数排成下列形式:第1行1第2行﹣2 3第3行﹣4 5﹣6第4行7﹣8 9﹣10第5行11﹣12 13﹣14 15…+1个数,此行第一个数的绝对值为个数,此行第一个数的绝对值为9.(2007•呼和浩特)观察下列三角形数阵:则第50行的最后一个数是().××个数表示为:个数为:10.(2006•柳州)请你认真观察和分析图中数字的变化规律,由此得到图中所缺的数字是()11.(2008•赤峰)给定一列按规律排列的数:1,,,,…它的第10个数是().C D.个数是.12.(2006•烟台)计算:21﹣1=1,22﹣1=3,23﹣1=7,24﹣1=15,25﹣1=31,…归纳各计算结果中的个位数字规律,200614.(2004•淄博)观察下列数表:15.(2003•郴州)观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,通过观察,用你所发现的规27二、填空题(共15小题)(除非特别说明,请填准确值)20行,第21列的数字420.17.(2009•天水)观察下列计算:•(+1)=(﹣1)(+1)=1,(+)(+1)=[(﹣1)+(﹣)](+1)=2,(++)(+1)=[(﹣1)+(﹣)+(﹣)](+1)=3,…从以上计算过程中找出规律,并利用这一规律进行计算:(+++…+)(+1)=2009.﹣﹣)((+118.(2009•绵阳)将正整数依次按下表规律排成四列,则根据表中的排列规律,数2009应排的位置是第670行第3列.19.(2008•遵义)如图是与杨辉三角形有类似性质的三角形数垒,a,b是某行的前两个数,当a=7时,b=22.20.(2008•宜宾)观察如下一列有规律的数,请在空格处填入合适的数字:1,1,2,3,4,6,9,13,19,28…21.(2009•朝阳)下列是有规律排列的一列数:…其中从左至右第100个数是.,个数,个数,个数可表示为:.个数是22.(2009•深圳)已知依据上述规律,则a99=.=.=.23.(2009•鸡西)有一列数﹣,,﹣,,…,那么第7个数是.个数为﹣.24.(2009•恩施州)观察数表根据表中数的排列规律,则字母A所表示的数是﹣10.25.(2009•内江)把一张纸片剪成4块,再从所得的纸片中任取若干块,每块又剪成4块,像这样依次地进行下去,到剪完某一次为止.那么2007,2008,2009,2010这四个数中2008可能是剪出的纸片数.26.(2008•永春县)按一定的规律排列的一列数依次为:﹣2,5,﹣10,17,﹣26,…按此规律排下去,这列数中的第9个数是﹣82.27.(2008•咸宁)观察右表,依据表格数据排列的规律,数2008在表格中出现的次数共有8次.28.(2008•莆田)观察下列按顺序排列的等式:0+1=12,2×1+2=22,3×2+3=32,4×3+4=42.请你猜想第10个等式应为10×9+10=102.29.(2008•肇庆)已知21=2,22=4,23=8,24=16,25=32,…,观察上面规律,试猜22008的末位数是6.30.(2008•烟台)表2是从表1中截取的一部分,则a=18.三、解答题(共1小题)(选答题,不自动判卷)31.(2007•无锡)图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面﹣层有一个圆圈,以下各层均比上﹣层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n=.如果图1中的圆圈共有12层,(1)我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层最左边这个圆圈中的数是;(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数﹣23,﹣22,﹣21,…,求图4中所有圆圈中各数的绝对值之和.=78+n=。
九年级中考数学考点提升训练——专题:《找规律:数字变化类》(四)(Word版,带答案)

九年级中考数学考点提升训练——专题:《找规律:数字变化类》(四)1.如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着﹣5,﹣2,1,9,且任意相邻四个台阶上的数的和都相等.(1)求前4个台阶上的数的和;(2)求第5个台阶上的数x的值;(3)从下到上前n(n为奇数)个台阶上的数的和能否为2020?若能,求出n的值;若不能,请说明理由.2.仔细观察下列等式:第1个:52﹣12=8×3第2个:92﹣52=8×7第3个:132﹣92=8×11第4个:172﹣132=8×15…(1)请你写出第6个等式:;(2)请写出第n个等式,并加以验证;(3)运用上述规律,计算:8×7+8×11+…+8×399+8×403.3.观察下列数据的规律,完成各题的解答:(1)第8行的最后一个数是;(2)第n行的第一个数是,第n行共有个数.4.你能比较数20182019和20192018的大小吗?为了解决这个问题,可以先将它们一般化,即比较n n+1和(n+1)n的大小(n为正整数)然后从分析n=1,n=2,n=3这些简单的情形入手,从中发现规律,经过归纳猜想得出结论.【观察比较】通过计算、比较下列各组数中两个数的大小(在横线上填“>”“=”或“<”):①1221;②2332;③3443;④4554;⑤5665…【归纳猜想】观察分析上面的结论,猜想n n+1与(n+1)n的大小(直接写出结论);【实际运用】根据上面归纳猜想得到的结论,可以判断2018201920192018.(在横线上填“>”或“<”)5.阅读材料,求值:1+2+22+23+24+…+22019解:设S=1+2+22+23+24+…+22019,将等式两边同时乘以2得:2S=2+22+23+24+…+22019+22020将下式减去上式得2S﹣S=22020﹣1即S=1+2+22+23+24+…+22019=22020﹣1(1)请你仿照此法计算:①1+2+22+23+24+25+26②1+3+32+33+34+…+3n(其中n为正整数)(2)求410+411+412+413+…+420的值.6.观察以下等式:第1个等式:52﹣22=3×7,第2个等式:72﹣42=3×11,第3个等式:92﹣62=3×15,…按照以上规律,解决下列问题:(1)写出第6个等式和第n个等式;(2)证明你写的第n个等式的正确性.7.观察以下等式:第1个等式:;第2个等式:;第3个等式:;第4个等式:;第5个等式:;……按照以上规律,解决下列问题:(1)写出第7个等式: ; (2)写出你猜想的第n 个等式(用含n 的等式表示),并加以证明.8.给定一列数,我们把这列数中的第一个数记为a 1,第二个数记为a 2,第三个数记为a 3,以此类推,第n 个数记为a n (n 为正整数)如下面这列数1,3,5,7,9中,a 1=1,a 2=3,a 3=5,a 4=7,a 5=9.规定运算sum (a 1:a n )=a 1+a 2+a 3+……+a n ,即从这列数的第一个数开始依次加到第n 个数,如在上面这列数中:sum (a 1:a 3)=a 1+a 2+a 3=1+3+5=9.(1)已知一列数1,﹣2,3,﹣4,5,﹣6,7,﹣8,9,﹣10.则sum (a 1:a 10)= .(2)已知一列有规律的数:(﹣1)1×1,(﹣1)2×2,(﹣1)3×3,(﹣1)4×4,……,按照规律,这列数可以无限的写下去sum (a 1:a 2016)= .②是否有正整数n 满足等式sum (a 1:a n )=﹣50成立?如果有,求出n 的值,如果没有,请说明理由9.观察下列算式:①1×3﹣22=3﹣4=﹣1 ②2×4﹣32=8﹣9=﹣1 ③3×5﹣42=15﹣16=﹣1(1)请你按照三个算式的规律写出第④个、第⑤个算式;(2)把这个规律用含字母的式子表示出来,并说明其正确性.10.观察一组数据:2,4,7,11,16,22,29,…,它们有一定的规律,若记第一个数为a 1,第二个数记为a2,…,第n个数记为a n.(1)请写出29后面的第一个数;(2)通过计算a2﹣a1,a3﹣a2,a4﹣a3,…由此推算a100﹣a99的值;(3)根据你发现的规律求a100的值.参考答案1.解:(1)﹣5+(﹣2)+1+9=3,∴前4个台阶上的数的和为3;(2)﹣2+1+9+x=3,∴x=﹣5,∴第5个台阶上的数为﹣5;(3)阶梯上数字为﹣5,﹣2,1,9,﹣5,﹣2,1,9,…由此可得,﹣5,﹣2,1,9四个循环一次,且和是3,∵2020÷3=673…1,∴673×4=2692,∴前2692个台阶上数字之和是2019,∴前2700个台阶上数字之和是2025,∵第2701个台阶上数字是﹣5,∴前2701个台阶上数字之和是2020,∴n=2701,∵n是奇数,∴n存在,n是2701.2.解:(1)根据式子的特点,可知第6个等式是:252﹣212=8×23;故答案为:252﹣212=8×23;(2)第n个等式是:(4n+1)2﹣(4n﹣3)2=8(4n﹣1).验证:左边=(4n+1)2﹣(4n﹣3)2=16n2+8n+1﹣16n2+24n﹣9=32n﹣8=8(4n﹣1)=右边;(3)8×7+8×11+…+8×399+8×403=92﹣52+132﹣92+…+4012﹣3972+4052﹣4012=4052﹣52=(405+50)(405﹣5)=410×400=164000.3.解:(1)观察数据规律可知:第n行最后一个数是n2,则第8行的最后一个数是64;故答案为64;(2)第n行的第一个数是第n﹣1行最后一个数加上1,即(n﹣1)2+1;因为第1行有1个数,第2行有3个数,第3行有5个数,…发现规律,第n行共有(2n﹣1)个数.故答案为:(n﹣1)2+1,(2n﹣1).4.解:【观察比较】分别计算每一项可得:12<21,23<32,34>43,45>54,56>65,故答案为<,<,>,>,>;【归纳猜想】当n=1,n=2时,n n+1<(n+1)n;当n≥3时,n n+1>(n+1)n;【实际运用】当n=2018时,20182019>20192018.故答案为>.5.解:(1)设x=1+2+22+23+24+25+26 ①由①×2得,2x=2+22+23+24+25+26+27 ②由②﹣①得,2x﹣x=27﹣1,即x=27﹣1;设y=1+3+32+33+34+…+3n③由③×3得,3y=3+32+33+34+35+…+3n+1 ④由④﹣③得,3y﹣y=3n+1﹣1,即y=;(2)设m=1+4+42+43+44+ (420)n=1+4+42+43+ (49)由(1)可知,m=,n=,410+411+412+413+…+420=(1+4+42+43+44+...+420)﹣(1+4+42+43+ (49)=m﹣n=﹣=6.解:(1)观察以下等式:第1个等式:52﹣22=3×7,第2个等式:72﹣42=3×11,第3个等式:92﹣62=3×15,…按照以上规律可知:第6个等式:152﹣122=3×27;∴第n个等式:(2n+3)2﹣(2n)2=3(4n+3);(2)证明:第n个等式的左边=(2n+3+2n)(2n+3﹣2n)=3(4n+3)=右边.所以第n个等式正确.7.解:(1)通过观察不难知道等式右边都等于2,等式左边:第一个因式的分子为1,分母与等式序号数相等;第二个因数分子为2,分母是等式的序号数加1;第三个因数是等式序号数与序号数的平方之和.∴写出第7个等式为:故答案为:;(2)第n 个等式:. 证明:左边==右边. 8.解:(1)sum (a 1:a 10)=1﹣2+3﹣4+5﹣6+7﹣8+9﹣10=﹣1×5=﹣5故答案为:﹣5.(2)①sum (a 1:a 2016)=(﹣1)1×1+(﹣1)2×2+(﹣1)3×3+(﹣1)4×4+…+(﹣1)2016×2016=﹣1+2﹣3+4﹣…﹣2015+2016=1×1008=1008故答案为:1008.②若当n 为奇数时,则有:sum (a 1:a n )=﹣n =﹣50解得:n =99,此时等式sum (a 1:a n )=﹣50成立;若当n 为偶数时,则有:sum (a 1:a n )==﹣50解得:n =﹣100,与题意不符∴若当n 为奇数时,等式sum (a 1:a n )=﹣50成立,且n 的值为99;若当n 为偶数时,等式sum (a 1:a n )=﹣50不成立.9.解:(1)①1×3﹣22=3﹣4=﹣1,②2×4﹣32=8﹣9=﹣1,③3×5﹣42=15﹣16=﹣1,④4×6﹣52=24﹣25=﹣1,⑤5×7﹣62=35﹣36=﹣1;(2)第n 个式子是:n ×(n +2)﹣(n +1)2=﹣1.故答案为:4×6﹣52=24﹣25=﹣1;n ×(n +2)﹣(n +1)2=﹣1.10.解:(1)29后面的第一位数是37;(2)由题意:a 2﹣a 1,=2,a 3﹣a 2=3,a 4﹣a 3=4…由此推算a 100﹣a 99=100;(3)a 100=2+2+3+4+…+100=1+×100=5051。
备战2021年九年级中考数学考点提升训练——专题:《找规律:数字变化类》(一)

备战2021年九年级中考数学考点提升训练——专题:《找规律:数字变化类》(一)1.按照一定的规律排列的n个数:﹣2、4、﹣8、16、﹣32、64、…,若最后四个数的和为2560,则n为()A.9 B.10 C.11 D.122.下面表格中的四个数都是按照同一规律填写的,仔细想一想表格中的m是多少?()A.136 B.170 C.191 D.2323.观察等式:1+2+22=23﹣1;1+2+22+23=24﹣1;1+2+22+23+24=25﹣1;若1+2+22+ (29)210﹣1=a,则用含a的式子表示210+211+212+…+218+219的结果是()A.a20﹣1 B.a2+a C.a2+a+1 D.a2﹣a4.如图,平面内有公共端点的六条射线OA、OB、OC、OD、OE、OF,从射线OA开始按逆时针方向依次在射线上写出数字1、2、3、4、5、6、7、…,则数字“2019”在射线()A.OA上B.OC上C.OE上D.OF上5.仔细观察,探索规律:则22019+22018+22017+…+2+1的个位数字是()A.1 B.3 C.5 D.76.按一定规律排列的一列数依次是、1、、、、…按此规律,这列数中第100个数是()A.B.C.D.7.一组数:2,1,3,x,7,y,23,…,满足“前两个数依次为a、b,紧随其后的第三个数是2a﹣b”,例如这组数中的第三个数“3”是由“2×2﹣1”得到的,那么这组数中y 表示的数为()A.9 B.﹣9 C.8 D.﹣88.定义一种对正整数n的“C运算”:①当n为奇数时,结果为3n+1;②当n为偶数时,结果为(其中k是使为奇数的正整数)并且运算重复进行,例如,n=66时,其“C运算”如下:若n=26,则第2019次“C运算”的结果是()A.40 B.5 C.4 D.19.将一列有理数﹣1,2,﹣3,4,﹣5,6,…,如图所示有序排列,根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰5”中C的位置是有理数,﹣2019应排在A、B、C、D、E中的位置.其中两个填空依次为()A.24,C B.24.A C.25,B D.﹣25,E10.将正偶数按表1排成5列:第1列第2列第3列第4列第5列第1行 2 4 6 8第2行16 14 12 10第3行18 20 22 24第4行32 30 28 26………………根据上面的排列规律,2018应在()A.第252行,第1列B.第252行,第4列C.第253行,第2列D.第253行,第5列11.下列一组按规律排列的数1,2,4,8,16,…,第2012个数应是()A.22011B.22012C.22013D.22012﹣112.观察下面的几个算式:1+2+1=4,1+2+3+2+1=9,1+2+3+4+3+2+1=16,1+2+3+4+5+4+3+2+1=25,…根据你所发现的规律,请你直接写出下面式子的结果:1+2+3+…+99+100+99+…+3+2+1=()A.0 B.1250 C.100 D.1000013.几个连续自然数按规律排成如图,根据规律,从2002到2004,箭头方向为()A.B.C.D.14.如图为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始连续的正整数1,2,3,4,…,当字母B第2n+1次出现时(n为正整数).恰好数到的数是()A.4n+2 B.6n+2 C.8n+2 D.12n+215.一列数a1,a2,a3,…,其中(n≥2,且n为整数),则a2012值为()A.B.2 C.﹣1 D.﹣16.如图数表是由从1开始的连续自然数组成:则第n行的第一个数是()A.n2﹣1 B.2n﹣1 C.(n﹣1)2+1 D.n2﹣n17.将1、、、按右侧方式排列.若规定(m,n)表示第m排从左向右第n个数,则(4,2)与(21,2)表示的两数之积是()A.1 B.2 C.2D.618.在一张某月的月历上,任意圈出竖列上的连续三个数的和不可能是()A.57 B.46 C.39 D.2419.我国古代文献《周易》上记载了“八卦”的由来,当时的人们认为世界上的万事万物归根结底是由阴阳两种基本元素构成的,就把它们化成了两种卦爻,阳爻为“﹣”,阴爻为“﹣﹣”.将阳爻和阴爻每次取三个,就会形成8种不同的排列方式,这与德国数学家莱布尼茨(1646﹣1716)创造的二进制竟不谋而合.下表就反映了“八卦”图符与二进制间的对应关系,根据表中的规律,从左到右的空格中应依次填写的数字是()000 110 100 111 001 101A.100,011 B.010,011 C.011,101 D.101,110 20.有2006个数排成一行,其中任意相邻的三个数中,中间的数等于它前后两数的和,若第一个数和第二个数都是1,则这2006个数的和等于()A.2006 B.﹣1 C.0 D.2参考答案1.解:由所给数可得规律:第n个数为(﹣2)n,∴(﹣2)n﹣1+(﹣2)n+(﹣2)n﹣2+(﹣2)n﹣3=2560,∴(﹣2)n﹣3(﹣8﹣2+4+1)=2560,∴n﹣3=9,∴n=12,故选:D.2.解:由题可知:右下方的数是对角两个数相乘减去左上方的数,即m=10×20﹣9=191,故选:C.3.解:由已知可得1+2+22+…+29+210+211+212+…+218+219=220﹣1,∵1+2+22+…+29=210﹣1=a,∴210+211+212+…+218+219=220﹣1﹣210+1=220﹣210,∵210﹣1=a,∴220﹣210=a(a+1),故选:B.4.解:通过观察已知图形,发现共有六条射线,∴数字1﹣2019每六个数字一个循环.∵2019÷6=336…3,∴2019在射线OC上.故选:B.5.解:22019+22018+22017+…+2+1=(2﹣1)×(22019+22018+22017+…+2+1)=22020﹣1,∵21=2,22=4,23=8,24=16,25=32,26=64,…,2020÷4=505,∴22020的末个位数字是6,∴22020﹣1的个位数字是5,故选:C.6.解:由、、、、、、…可得第n个数为.∵n=100,∴第100个数为:故选:B.7.解:解法一:常规解法∵从第三个数起,前两个数依次为a、b,紧随其后的数就是2a﹣b,∴2×3﹣x=7,∴x=﹣1,则2×(﹣1)﹣7=y,解得y=﹣9.解法二:技巧型∵从第三个数起,前两个数依次为a、b,紧随其后的数就是2a﹣b,∴7×2﹣y=23,∴y=﹣9.故选:B.8.解:若n=26,第一次结果为13,第2次结果为:3n+1=40,第3次“C运算”的结果是:=5,第4次结果为:3n+1=16,第5次结果为:,第6次结果为:3n+1=4,第7次结果为:1,…可以看出,从第5次开始,结果就只是1,4两个数轮流出现,且当次数为偶数时,结果是4,次数是奇数时,结果是1,第2019次是奇数,结果是1,故选:D.9.解:∵每个峰需要5个数,∴4×5=20,20+1+3=24,∴“峰5”中C位置的数的是24,∵(2019﹣1)÷5=403余3,∴﹣2019为“峰404”的第3个数,排在C的位置.故选:A.10.解:∵2018÷2=1009,∴201,8是第1009个偶数,而1009÷4=252…1,∴第1009个偶数在第253行,∵奇数行的数从第2列开始向后面排,∴第1009个偶数在第2列,∴2018应在第253行第2列,故选:C.11.解:∵1=20,是第1个数,2=21,是第2个数,4=22,是第3个数,8=23,是第4个数,16=24,是第5个数,…,∴第2012个数是22011.故选:A.12.解:根据所给的数据可得:它的规律是:最中间数的平方,则1+2+3+…+99+100+99+…+3+2+1=1002=10000;故选:D.13.解:观察这n个连续自然数的排列规律,知:从0开始,依4为循环单位;∵2002=500×4+2,2003=500×4+3,2004=501,∴根据规律,从2002到2003再到2004的箭头方向与从2到3再到4箭头方向一致,即可得出答案A正确,故选:A.14.解:按照A→B→C→D→C→B→A→B→C→…的方式进行,每6个字母ABCDCB一循环,每一循环里字母B出现2次,当循环n次时,字母B第2n次出现时(n为正整数),此时数到最后一个数为6n,当字母B第2n+1次出现时(n为正整数),再数2个数为6n+2.故选:B.15.解:∵a1=,a n=,∴a2==2,a3==﹣1,a4==,a5==2,∴数列a1,a2,a3,…a n,以,2,﹣1循环,∵2012÷3=670…2,∴a2012=2.故选:B.16.解:观察发现,第1行共1个数,第2行共3个数,第3行共5个数,第4行共7个数,第5行共9个数,第6行共11个数,…,依此类推,第n行共(2n﹣1)个数,1+3+5+7+9+11+…+(2n﹣1)==n2,所以,第(n﹣1)的最后一个数是(n﹣1)2,第n行的第一个数是(n﹣1)2+1.故选:C.17.解:从图示中知道,(4,2)所表示的数是:;∵第20排最后一个数的序号是:1+2+3+4+…+20=210,则(21,2)表示的是第210+2=212个数,212÷4=53,∴(21,2)表示的数是:,∴(4,2)与(21,2)表示的两数之积是:×=6.故选:D.18.解:设中间一个数为:x,则它上面的数是x﹣7,下面的数是x+7,∴x+x﹣7+x+7=3x,故一定是3的倍数,四个选项中,只有46不是3的倍数,故选:B.19.解:通过观察题中所给表格可知:二个横线代表0,一个横线代表1,∴第三个数字为:010,第四个数字为:011.故选:B.20.解:∵任意相邻的三个数中,中间的数等于它前后两数的和,而且第一个数和第二个数都是1,∴此行数为:1,1,0,﹣1,﹣1,0,1,1,0,﹣1,﹣1,0,1,1…,∴1+1+0﹣1﹣1+0=0,∵2006÷6=334…2,∴第2005个数为1,第2006个数为1,∴这2006个数的和为:334×0+1+1=2.故选:D.。
九年级中考数学考点提升训练——专题:《找规律:数字变化类》(一)(word含答案)

九年级中考数学考点提升训练——专题:《找规律:数字变化类》(一)1.阅读下列材料,完成相应任务:神奇的等式第1个等式:++=1;第2个等式:++=;第3个等式:++=;第4个等式:++=;…第100个等式:++=;…任务:(1)第6个等式为:;(2)猜想第n个等式(用含n的代数式表示),并证明.2.找规律:(1)计算:①2﹣1=;②22﹣2﹣1=;③23﹣22﹣2﹣1=;④24﹣23﹣22﹣2﹣1=;⑤25﹣24﹣23﹣22﹣2﹣1=;(2)根据上面的计算结果猜想:①2200﹣2199﹣2198﹣…﹣22﹣2﹣1的值为;②2n﹣2n﹣1﹣2n﹣2﹣…﹣22﹣2﹣1的值为;(n为正整数)(3)根据上面猜想的结论,试求212﹣211﹣210﹣29﹣28﹣27﹣26的值.3.观察以下等式:第1个等式:2+=22×;第2个等式:3+=32×;第3个等式:4+=42×;第4个等式:5+=52×;……按照以上规律,解决下列问题:(1)写出第5个等式:;(2)写出你猜想的第n个等式:(用含n的等式表示),并证明.4.按如下方式排列正整数,第1行有1个数,第2行有3个数,第3,4行分别有7个、13个数.依此规律.解答下列问题:12 3 43 4 5 6 7 8 94 5 6 7 8 9 10…15 16…(1)第10行有个数,第n行有个数(结果用含n的式子表示)(2)第2,3,4行都含有数4,其中第2行最先出现4.那么2015最先出现在第几行?5.给出下列算式:32﹣12=8=8×1;52﹣32=16=8×2;72﹣52=24=8×3;92﹣72=32=8×4.(1)观察上面一系列式子,你能发现什么规律?(2)用含n的式子表示其规律(n为正整数).(3)计算20192﹣20172的值,此时n是多少?6.观察下列等式①1+=1+②+=+③+=+…………(1)第④个等式为:;(2)请你猜想第n个等式(用含n的式子表示,n为正整数),并证明其正确性.7.观察下列等式:①32﹣31=2×31;②33﹣32=2×32;③34﹣33=2×33;④35﹣34=2×34…根据等式所反映的规律,解答下列问题:(1)直接写出:第⑤个等式为;(2)猜想:第n个等式为(用含n的代数式表示),并证明.8.【概念学习】我们知道:求几个相同加数的和的简便运算是乘法,也可以叫做连加.例如:2+2+2=2×3,5+5+5+5+5+5=5×6类似地,求若干个相同的有理数的减法运算叫做连减,例如2﹣2﹣2,记作2↓3.一般地,把n个a连减记作a↓n,a↓n==(n为整数,且n≥2).【初步探究】直接写出计算结果:2↓4=,3↓5=;=;【深入思考】我们知道,有理数的减法运算可以转化为加法运算,相同加数的加法运算可以转化为乘法运算,那么有理数的连减运算如何转化为乘法运算呢?例如:2↓3=2﹣2﹣2=(﹣2)×1,5↓6=5﹣5﹣5﹣5﹣5﹣5=(﹣5)×4,.(1)试一试:将下列连减运算直接写成两数相乘的形式.8↓7=,(﹣1)↓8=,a↓n=;(n为整数,且n≥2)(2)算一算:÷(﹣2).9.观察以下等式:第1个等式:×(1+)=2﹣,第2个等式:×(1+)=2﹣,第3个等式:×(1+)=2﹣,第4个等式:×(1+)=2﹣.第5个等式:×(1+)=2﹣.…按照以上规律,解决下列问题:(1)写出第6个等式:;(2)写出你猜想的第n个等式:(用含n的等式表示),并证明.10.小东同学在学习多项式乘以多项时发现:(x+4)(2x+5)(3x﹣6)的结果是一个多项式,并且最高次项为:x•2x•3x=3x3,常数项为:4×5×(﹣6)=﹣120,那么一次项是多少呢?要解决这个问题就是要确定该一次项的系数,根据尝试和总结他发现:一次项系数就是:•5•(﹣6)+2•(﹣6)•4+3•4•5=﹣3,即一次项为﹣3x,认真领会小东同学解决问题的思路方法,仔细分析上面等式的结构特征,结合自己对多项式乘法法则的理解,解决以下问题.(1)计算(x+2)(3x+1)(5x﹣3)所得多项式的一次项系数为.(2)(x+6)(2x+3)(5x﹣4)所得多项式的二次项系数为.(3)若计算(x2+x+1)(x2﹣3x+a)(2x﹣1)所得多项式的一次项系数为0,则a=.(4)若(x+1)2021=a0x2021+a1x2020+a2x2019+…+a2020x+a2021,则a2020=.参考答案1.解:(1)第6个等式为:++=;(2)猜想第n个等式(用含n的代数式表示)为:++=;证明:∵左边=++===,∴左边=右边,等式成立.故答案为:++=.2.解:(1)①2﹣1=1;②22﹣2﹣1=1;③23﹣22﹣2﹣1=1;④24﹣23﹣22﹣2﹣1=1;⑤25﹣24﹣23﹣22﹣2﹣1=1;故答案为:1;1;1;1;1.(2)根据上面的计算结果猜想:①2200﹣2199﹣2198﹣…﹣22﹣2﹣1=2199﹣2198﹣…﹣22﹣2﹣1=2198﹣…﹣22﹣2﹣1=2﹣1=1②2n﹣2n﹣1﹣2n﹣2﹣…﹣22﹣2﹣1=2n﹣1﹣2n﹣2﹣…﹣22﹣2﹣1=2n﹣2﹣…﹣22﹣2﹣1=22﹣2﹣1=1故答案为:1;1.(3)212﹣211﹣210﹣29﹣28﹣27﹣26=211﹣210﹣29﹣28﹣27﹣26=210﹣29﹣28﹣27﹣26=29﹣28﹣27﹣26=28﹣27﹣26=27﹣26=26=64.3.解:(1)第1个等式:2+=22×,即2+=22×;第2个等式:3+=32×,即3+=32×;第3个等式:4+=42×,即4+=42×;第4个等式:5+=52×,即5+=52×;……按照以上规律可得,第5个等式:6+,即6+,故答案为:6+;(2)根据题意得,第n个等式:n+1+=(n+1)2•.证明:左边==,右边=,左边=右边,即n+1+=(n+1)2•,故答案为:n+1+=(n+1)2•.4.解:(1)根据题意可知,第2行最后一数为4=22,数字个数是22﹣1;第3行最后一数为9=32,数字个数是32﹣2;第4行最后一数为16=42,数字个数是42﹣3;…,∴第10行最后一数为102=100,数字个数是102﹣9=91;第n行最后一数n2,数字个数是n2﹣(n﹣1)=n2﹣n+1;(2)∵第44行最后一数是442=1936,∴第45行第一个数字是1937,而最后一个数字是452=2025,1937<2015<2025,∴2015最先出现在第45行.故答案为:(1)91,n2﹣n+1.5.解:(1)规律:等式的左边是两个连续奇数的平方差,右边是8的倍数;(2)∵32﹣12=8=8×1,52﹣32=16=8×2,72﹣52=24=8×3,92﹣72=32=8×4,…∴设n(n≥1)表示自然数,用关于n的等式表示这个规律为:(2n+1)2﹣(2n﹣1)2=8n;(3)2n+1=2019,解得:n=1009,∴20192﹣20172=8×1009=8072.答:20192﹣20172的值8072,此时n是1009.6.解:(1)根据上面的规律可得第④个等式为:+=+;故答案为:+=+;(2)根据上面的规律可得第n个等式:+=+,证明:左边=+==,右边=+=,∴左边=右边,∴等式成立,猜想正确.7.解:(1)由①32﹣31=2×31;②33﹣32=2×32;③34﹣33=2×33;④35﹣34=2×34…得出第⑤个等式36﹣35=2×35;故答案为:36﹣35=2×35;(2)由①32﹣31=2×31;②33﹣32=2×32;③34﹣33=2×33;④35﹣34=2×34…得出第n 个等式的底数不变,指数依次分别是n+1、n、n,即3n+1﹣3n=2×3n.证明:左边=3n+1﹣3n=3×3n﹣3n=3n×(3﹣1)=2×3n=右边,所以结论得证.故答案为:3n+1﹣3n=2×3n.8.解:【初步探究】2↓=2﹣2﹣2﹣2=﹣4,4=3﹣3﹣3﹣3﹣3=﹣9,3↓5==﹣4,故答案为:﹣4;﹣9;﹣4;【深入思考】(1)8↓=8﹣8﹣8﹣8﹣8﹣8﹣8=(﹣8)×5,7=(﹣1)﹣(﹣1)﹣(﹣1)﹣(﹣1)﹣(﹣1)﹣(﹣1)﹣(﹣1)﹣(﹣1)↓8(﹣1)=1×6,a↓=.n故答案为:(﹣8)×5;1×6;﹣a(n﹣2);(2)÷(﹣2)=×5×24+(﹣4)×3÷(﹣2)=60+6=66.9.解:(1)第6个等式:×(1+)=2﹣;(2)猜想的第n个等式:×(1+)=2﹣.证明:∵左边=×==2﹣=右边,∴等式成立.故答案为:×(1+)=2﹣;×(1+)=2﹣.10.解:(1)由题意得:一次项系数为:1×1×(﹣3)+2×3×(﹣3)+2×1×5=﹣11;(2)由题干材料知:二次项系数为:×2×(﹣4)+6×2×5+×5×3=63.5;(3)一次项系数为:1×a×(﹣1)+1×(﹣3)×(﹣1)+1×a×2=0,解得a=﹣3;(4)通过题干以及前三问知:a=2021×1=2021.2020故答案为:﹣11;63.5;﹣3;2021.。
2023 年九年级数学中考复习 探索数字的变化规律 填空题专题训练

2022-2023学年九年级数学中考复习《探索数字的变化规律》填空题专题训练(附答案)1.观察下列各数:,,,,,,…则第n个数是.2.观察下面一列数:﹣1,2,﹣3,4,﹣5,6,﹣7,…,将这列数排成下列形式:按照上述规律排下去,那么第10行从左边数第9个数是.3.已知整数a1、a2、a3,a4…a2023满足下列条件a1=﹣1,a2=﹣|a1+1|,a3=﹣|a2+1|,……则a1+a2+a3+a4+…+a2023=.4.我们可以用符号f(a)表示代数式.当a是正整数时,我们规定如果a为偶数,f(a)=0.5a;如果a为奇数,f(a)=5a+1.例如:f(20)=10,f(5)=26.设a1=6,a2=f(a1),a3=f(a2)…;依此规律进行下去,得到一列数:a1,a2,a3,a4…(n为正整数),则2a1﹣a2+a3﹣a4+a5﹣a6+…+a2019﹣a2022=.5.有若干个数,依次记为a1,a2,…,第n个数记为a n.若a1=﹣,从第二个数起,每个数都等于“1与它前面那个数的差的倒数”,那么,a2===,…,则a2022=.6.有一数值转换器,原理如图所示,若开始输入x的值是1,可发现第一次输出的结果是4,第二次输出的结果是2,……,请你探索第2022次输出的结果是.7.观察等式:①2=1×2,②2+4=6=2×3,③2+4+6=12=3×4,…按照这种规律写出第n个等式2+4+6+…+2n=.8.有一列数:1,3,2,﹣1,…,其规律是:从第二个数开始,每一个数都是其前后两个数之和,根据此规律,则第2022个数是.9.若曦对自己上学路线的长度进行了20次测量,得到20个数据x1,x2,…,x20,已知x1+x2+…+x20=2022,当代数式(x﹣x1)2+(x﹣x2)2+…+(x﹣x20)2取得最小值时,x的值为.10.观察下列各式:;;;;…,则a1+a2+a3+…+a200=.11.观察下列等式:……,请根据,上面计算规律计算=.12.a1,a2,a3,a4,a5,a6,…是一列数,已知第1个数a1=1,第5个数a5=﹣1,且任意三个相邻的数之和为2022,则第2022个数a2022的值是.13.1﹣2+3﹣4+5﹣6+…+2021﹣2022的值是.14.观察下列各式的计算过程:(1)(2)(3)根据上面算法,计算:=.15.(1+3+5+…+2017+2019+2021)﹣(2+4+6+…+2018+2020+2022)=.16.正整数按如图的规律排列,请写出:(1)第3行,第6列的数字是;(2)正整数2022在第行,第列.17.如下表,从左到右在每一个小格子中填入一个整数,使得其中任意三个相邻格子所填整数之和都相等3a b c﹣2…那么c=,第2021个数是.18.观察下列等式:3=3,32=9,33=27,34=81,35=243,36=729,37=2187,38=6561,39=19683,…,它们的个位数字有什么规律,用你发现的规律直接写出32021的个位数字是.19.如图,是按一定规律排成的三角形数阵,按图中数阵的排列规律,第5行从左至右第2个数是;第9行从左至右第8个数是.20.如图,每个正方形中的四个数之间都有相同的规律,根据这种规律,可知m的值应是(用a的代数式表示).参考答案1.解:∵,=,,,,,……,第n个数为:,故答案为:.2.解:∵第9行的最后一个数的绝对值为92=81,∴第10行从左边数第9个数的绝对值是81+9=90,∵90是偶数,∴第10行从左边数第9个数是正数,为90,故答案为:90.3.解:根据题意可得,a1=﹣1,a2=﹣|a1+1|=0,a3=﹣|a2+1|=﹣1,a4=﹣|a3+1|=0,…,观察其规律可得,2023÷2=1011……1,∴a2023=﹣1,∴a1+a2+a3+a4+…+a2023=﹣1+0+(﹣1)+0+…+(﹣1)=﹣1×1012=﹣1012.故答案为:﹣1012.4.解:由题意可得,a1=6,a2=f(a1)=0.5×6=3,a3=f(a2)=5×3+1=16,a4=f(a3)=8,a5=f(a4)=4,a6=f(a5)=2,a7=f(a6)=1,a8=f(a7)=6,…,由上可得,上述数列依次以6,3,16,8,4,2,1循环出现,∵2019÷7=288……3,∴a2019=16,∵2020÷14=144……4,∴2a1﹣a2+a3﹣a4+a5﹣a6+…+a2017﹣a2018+a2019﹣a2020=a1+(a1﹣a2+a3﹣a4+a5﹣a6+a7)﹣(a8﹣a9+a10﹣a11+a12﹣a13+a14)…+(a2017﹣a2018+a2019﹣a2020)=6+0+0+…+0+(6﹣3+16﹣8)=6+0+11=17,故答案为:17.5.解:由题意得:a1=﹣,a2=,a3==3,a4=,…则该数据为﹣,,3的循环排列,∵2022÷3=674,∴a2022=a3=3.故答案为:3.6.解:第一次输出的结果是4,第二次输出的结果是2,第三次输出的结果是1,第四次输出的结果是4,第五次输出的结果是1,第六次输出的结果是4,……,∴运算结果每三次计算循环一次,∵2022÷3=674,∴第2022次输出的结果与第三次输出的结果相同,∴第2022次输出的结果是1,故答案为:1.7.解:根据题意2=1×2=1×(1+1);2+4=6=2×3=2×(2+1);2+4+6=12=3×4=3×(3+1);由此得出,第n个等式2+4+6+…+2n=n×(n+1).故答案为:n(n+1).8.解:根据题意可知:一列数是1,3,2,﹣1,﹣3,﹣2,1,3,2…,发现1,3,2,﹣1,﹣3,﹣2,6个数一个循环,所以2022÷6=337,所以第2022个数与第6个数相同,是﹣2.故答案为:﹣2.9.解:==.则当时,y取得最小值,即当x=101.1时,取得最小值;故答案为:101.1.10.解:原式=(1﹣)+(﹣)+(﹣)+...+(﹣)=(1﹣+﹣+﹣+...+﹣)=×(1﹣)=.故答案为:.11.解:=×(1﹣+…+)===.故答案为:.12.解:∵第1个数a1=1,第5个数a5=﹣1,且任意三个相邻的数之和为2022,∴a1+a2+a3=a2+a3+a4,∴a4=a1=4,∵a3+a4+a5=2022,∴a3=2022,∴a2=2022﹣a1﹣a3=﹣1,则这一列数以1,﹣1,2022这三个循环出现,∵2022÷3=674,∴第2022个数a2022的值为:2022.故答案为:2022.13.解:1﹣2+3﹣4+5﹣6+…+2021﹣2022=(1﹣2)+(3﹣4)+(5﹣6)+…+(2021﹣2022)=﹣1+(﹣1)+(﹣1)+…+(﹣1)=﹣1×1011=﹣1011.故答案为:﹣1011.14.解:=××××……××=×=,故答案为:.15.解:(1+3+5+…+2017+2019+2021)﹣(2+4+6+…+2018+2022)=1+3+5+……+2017+2019+2021﹣2﹣4﹣6﹣…﹣2018﹣2022=(1﹣2)+(3﹣4)+(5﹣6)+…+(2017﹣2018)+(2019﹣2020)+(2021﹣2022)==﹣1×1011=﹣1011.故答案为:﹣1011.16.解:(1)由图可知,第六列的第一个数是26,∴第3行,第6列的数字是28,故答案为:28;(2)每行的第一个数n2,∴第45行的第一个数是2025,∵2025﹣2022=3,∴2022在第45行第4列,故答案为:45,4.17.解:由题意可得,3+a+b=a+b+c=b+c+(﹣2),∴c=3,a=﹣2,∵2021÷3=673……2,∴第2021个数和a的值一样,都是﹣2,故答案为:3,﹣2.18.解:∵一列等式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187,38=6561,39=19683,…,∴这列等式的个位数字是3,9,7,1循环出现,∴31的个位数字是3,31+32的个位数字是2,31+32+33的个位数字是9,31+32+33+34的个位数字是0,31+32+33+34+35的个位数字是3,…,∵2021÷4=505……1,∴32021的个位数字是3.19.解:由图形可知,第n行最后一个数为=,∴第4行最后一个数为=,则第5行从左至右第2个数是=2,第9行最后一个数为=;由规律可知第9行有9个数,所以第8个数为:==2.20.解:由正方形中的数字可知,左上角的数字是一些连续的偶数,从0开始,右上角的数字是一些连续的奇数,从4开始,左下角的数字比右上角的数字都小2,右下角的数字都是相对应的左上角的数字的4倍与6的和,故当左上角的数字是a时,右下角的数字是4a+6,即m的值是4a+6,故选:4a+6.。
2021年九年级数学中考复习——专题:找规律之数字变化类(三)

2021年九年级数学中考复习——专题:找规律之数字变化类(三)1.阅读下列材料,然后回答问题:已知a>0,S1=,S2=﹣S1﹣1,S3=,S4=﹣S3﹣1,S5=,….当n为大于1的奇数时,S n=;当n为大于1的偶数时,S n=﹣S n﹣1﹣1.直接写出S2020=(用含a的代数式表示);计算:S1+S2+S3+…+S2022=.2.定义一种关于整数n的“F”运算:(1)当n是奇数时,结果为3n+5;(2)当n是偶数时,结果是(其中k是使是奇数的正整数),并且运算重复进行.例如:取n=58,第一次经F运算是29,第二次经F运算是92,第三次经F运算是23,第四次经F运算是74…;若n=72,则第2019次运算结果是.3.观察下面的变化规律:=1﹣,=﹣,=﹣,=﹣,…根据上面的规律计算:=.4.一组按规律排列的式子:,﹣,,﹣,…(ab≠0),其中第10个式子是.5.按下面一组数的排列规律,在横线上填上适当的数:,,,,,.6.下列各正方形中的四个数之间都有相同的规律,请你仔细观察,找出规律,根据这种规律计算可知:m的值为.7.观察多项式:8x﹣16x2+32x3﹣64x4+128x5…,以此规律,第n项为.8.如表被称为“杨辉三角”或“贾宪三角”.其规律是:从第三行起,每行两端的数都是“1”,其余各数都等于该数“两肩”上的数之和.表中两平行线之间的一列数:1,3,6,10,15,…,我们把第一个数记为a1,第二个数记为a2,第三个数记为a3,…,第n个数记为a n,则a6=,a200=.9.观察下列式子:2=22×,3=32×,4=42×,….你发现它们之间存在的规律是.(用含n的式子表示出来,n表示大于等于2整数)10.给定一列按规律排列的数:,1,,,…,根据前4个数的规律,第2020个数是.11.小磊想编一个循环“插数”程序,对有序的数列:﹣2,0进行有规律的“插数”:对任意两个相邻的数,都用右边的数减去左边的数之差“插”在这相邻的两个数之间,产生一个个新数列.如:第1次“插数”产生的一个新数列是﹣2,2,0;第2次“插数”产生的一个新数列是﹣2,4,2,﹣2,0;第3次“插数”产生的一个新数列是﹣2,6,4,﹣2,2,﹣4,﹣2,2,0;……,第2019次插数产生的一个新数列的所有数之和是.12.观察下列一组数,按规律在横线上填写适当的数,﹣,,﹣,,……,第7个数是.13.在一列数a1,a2,a3,a4,…a n中,已知a1=2,a2=,a3=,a4=,…a n=,则a=.202014.按照一定规律排列的一组数:,,,,…,,,…(其中a,b 为正整数),则a﹣b=.15.已知一列数的和x1+x2+……+x2019=×(1+2+…+2019),|x1﹣3x2+1|=|x2﹣3x3+2|=…=|x2018﹣3x2019+2018|=|x2019﹣3x1+2019|,则x1﹣2x2﹣3x3=.16.如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,当m=99时,则M的值为.17.按一定规律排列的一列数依次为,﹣,,﹣,,﹣,…,按此规律排列下去,这列数中第8个数是,第n个数是(n为正整数).18.一个盒子里装有不多于200颗糖,如果每次2颗,3颗,4颗或6颗的取出,最终盒内都只剩下一颗糖,如果每次以11颗的取出,那么正好取完,则盒子里共有颗糖.19.观察这一列数:﹣1,2,﹣3,4,﹣5,6,﹣7,…,若将这列数排成如图所示的形式,按照这个规律排下去,那么第10行从左边起第8个数是.20.按一定顺序排列的一列数叫做数列,如数列:,,,,…,则这个数列前2018个数的和为.参考答案1.解:∵S1=,S=﹣S1﹣1=,2S==,3S=﹣S3﹣1=,4S==﹣a﹣1,5S=﹣S5﹣1=a,6S==,7….当n为大于1的奇数时,S n=;当n为大于1的偶数时,S n=﹣S n﹣1﹣1.发现规律:每6个结果为一个循环,所以2020÷6=336…4,所以S2020=;因为2022÷6=337,所以S1+S2+S3+…+S2022=337(+++﹣a﹣1+a)=337(﹣1﹣1﹣1)=﹣1011.故答案为:,﹣1011.2.解:由题意n=72时,第一次经F运算是9,第二次经F运算是32,第三次经F运算是1,第四次经F运算是8,第五次经F运算是1…以后出现1、8循环,奇数次是1,偶数次是8,∴第2019次运算结果1,故答案为:1.3.解:由题干信息可抽象出一般规律:(a,b均为奇数,且b=a+2).故=1﹣+﹣+﹣+…+﹣=1﹣=.故答案:.4.解:分子为b,其指数为2,5,8,11,…,其规律为3n﹣1,分母为a,其指数为1,2,3,4,…,其规律为n,分数符号为+、﹣,+,﹣,…,其规律为(﹣1)n+1,…第n个式子是(﹣1)n+1.所以,第10个式子是﹣.故答案是:﹣.5.解:∵,,,,…,∴这列数的第n个数为:,∴当n=5时,=,故答案为:.6.解:由表格可得,左上角的数字是一些连续的奇数,从大到小排列,从3开始,左下角的数字比左上角的数字大2,右上角的数字比左下角的数字大2,右下角的数字等于左下角与右下角的数字的乘积,∴当左上角的数字为﹣3时,左下角的数字为﹣3+2=﹣1,右上角的数字为﹣1+2=1,右下角的数字为(﹣1)×1=﹣1,∴m=﹣1,故答案为:﹣1.7.解:根据分析的规律,得第n项为(﹣1)n+12n+2x n.(n≥1的自然数).故答案为:(﹣1)n+12n+2x n(n≥1的自然数).8.解:由题意可得,a=1,1a=1+2=3,2a=1+2+3=6,3a=1+2+3+4=10,4a=1+2+3+4+5=15,5…,∴a n=1+2+3+…+n=,∴当n=6时,a6==21,当n=200时,a200==20100,故答案为:21,20100.9.解:2=22×,3=32×,4=42×,…∴用含n(n表示大于等于2整数)的代数式表示出来为:n+.故答案为n+.10.解:观察这列数发现,奇数项是负数,偶数项是正数;分子分别为3,5,7,9,…;分母分别为12+1,22+1,32+1,…,∴该列数的第n项是(﹣1)n,∴第2020个数是=,故答案为.11.解:∵第一次操作增加数字:2,第二次操作增加数字:4,2,﹣2,第三次操作增加数字:6,4,﹣2,2,﹣4,﹣2,2,∴第一次操作增加2,第二次操作增加4+2﹣2=4,第三次操作增加6+4﹣2+2﹣4﹣2+2=6,…,即,每次操作加2,第2019次操作后所有数之和为﹣2+0+2019×2=4036.故答案为:4036.12.解:观察一组数,﹣,,﹣,,……,发现规律:第n个数是(﹣1)n,所以第7个数是﹣.故答案为:﹣.13.解:∵a1=2,∴a2==﹣1;a==;3a==2;4…,发现规律:每3个数一个循环,所以2020÷3=673…1,则a2020=a1=2.故答案为:2.14.解:∵一组数:,,,,…,,,…(其中a,b为正整数),∴这组数是:,,,,…,,,,…,∴a=15×16=240,b=17×18=306,∴a﹣b=240﹣306=﹣66,故答案为:﹣66.15.解:因为x1﹣3x2+1+x2﹣3x3+2+...+x2018﹣3x2019+2018+x2019﹣3x1+2019 =x1+x2+......+x2019﹣3(x1+x2+......+x2019)+(1+2+3+ (2019)=×(1+2+...+2019)﹣3××(1+2+...+2019)+(1+2+ (2019)=0.所以绝对值内的2019个式子相加等于0,且它们的绝对值相等,所以|x1﹣3x2+1|=|x2﹣3x3+2|=…=|x2018﹣3x2019+2018|=|x2019﹣3x1+2019|=0,所以x2=3x3﹣2,所以x1=3x2﹣1=3(3x3﹣2)﹣1=9x3﹣7,所以x1﹣2x2﹣3x3=9x3﹣7﹣2(3x3﹣2)﹣3x3=﹣3.故答案为:﹣3.16.解:∵3=2×1+1,15=4×3+3,35=6×5+5,∴M=mn+m,且n=m+1,当m=99时,M=99×100+99=9999,故答案为:9999.17.解:根据分析可知:一列数依次为:,﹣,,﹣,,﹣,…,按此规律排列下去,则这列数中的第8个数是﹣,所以第n个数是:(﹣1)n+1(n是正整数).故答案为:﹣;(﹣1)n+1.18.解:已知如果每次11颗地取出正好取完,则盒子内糖数必为11的倍数.又知盒子里装有不多于200颗糖,则盒子内糖数可能为11、22、33、44、55、66、77、88、99、110、121、132、143、154、165、176、187、198.又已知如果每次2颗,3颗,4颗或6颗地取出,最终盒内都只剩一颗糖,则盒子内糖数为12的倍数+1.又知盒子里装有不多于200颗糖则盒子内糖数可能为13,25,37,49,61,73,85,97,109,121,133,145,157,169,181,193.取上面两组数的交集可得121,故盒子里共有121颗糖.故答案为:121.19.解:∵第n行左边第一个数的绝对值为(n﹣1)2+1,奇数为负,偶数为正,∴第10行从左边数第1个数绝对值为82,即这个数为82,∴从左边数第8个数等于﹣89.故答案为:﹣89.20.解:由数列知第n个数为,则前2018个数的和为++++…+=++++…+=1﹣+﹣+﹣+﹣+…+﹣=1﹣=,故答案为:.。
初三专题---找规律
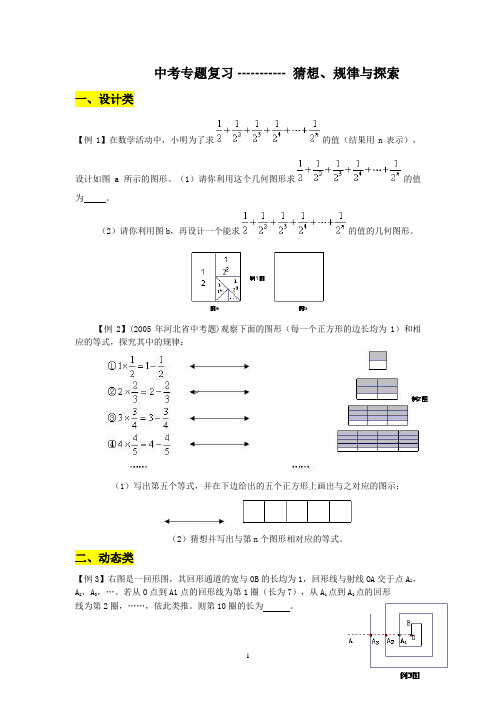
中考专题复习 ----------- 猜想、规律与探索一、设计类【例1】在数学活动中,小明为了求的值(结果用n表示),设计如图a所示的图形。
(1)请你利用这个几何图形求的值为。
(2)请你利用图b,再设计一个能求的值的几何图形。
【例2】(2005年河北省中考题)观察下面的图形(每一个正方形的边长均为1)和相应的等式,探究其中的规律:(1)写出第五个等式,并在下边给出的五个正方形上画出与之对应的图示;(2)猜想并写出与第n个图形相对应的等式。
二、动态类【例3】右图是一回形图,其回形通道的宽与OB的长均为1,回形线与射线OA交于点A1,A 2,A3,…。
若从O点到A1点的回形线为第1圈(长为7),从A1点到A2点的回形线为第2圈,……,依此类推。
则第10圈的长为。
【例4】)已知甲运动方式为:先竖直向上运动1个单位长度后,再水平向右运动2个单位长度;乙运动方式为:先竖直向下运动2个单位长度后,再水平向左运动3个单位长度。
在平面直角坐标系内,现有一动点P 第1次从原点O 出发按甲方式运动到点P 1,第2次从点P 1出发按乙方式运动到点P 2,第3次从点P 2出发再按甲方式运动到点P 3,第4次从点P 3出发再按乙方式运动到点P 4,……。
依此运动规律,则经过第11次运动后,动点P 所在位置P 11的坐标是 。
三、数字类【例5】瑞士中学教师巴尔末成功地从光谱数据,,,,……,中得到巴尔末公式,从而打开了光谱奥妙的大门。
请你按这种规律写出第七个数据是 。
【例6】观察下列算式:122=,224=,328=,4216=,….根据上述算式中的规【例7】按下列规律排列的一列数对(1,2)(4,5)(7,8),…,第5个数对是 。
【例8】一组按规律排列的数:,,,,,…请你推断第9个数是【例9】把数字按如图所示排列起来,从上开始,依次为第一行、第二行、第三行……,中间用虚线围的一列,从上至下依次为1、5、13、25、…,则第10个数为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级中考数学考点提升训练——专题:
《找规律:数字变化类》(三)
1.观察下列三行数:
﹣3,9,﹣27,81,﹣243,… ﹣5,7,﹣29,79,﹣245… ﹣1,3,﹣9,27,﹣81… (1)第一行数按什么规律排列?
(2)第二行、第三行数与第一行数分别有什么关系? (3)分别取这三行数的第6个数,计算这三个数的和.
2.先观察下列等式,然后用你发现的规律解答问题. 第1个等式:a 1==×(1﹣); 第2个等式:a 2==×(﹣); 第3个等式:a 3==×(﹣); 第4个等式:a 4==
×(
﹣
);
…
请回答下列问题:
(1)按以上规律列出第5个等式:a 5= = ;
(2)用含有n 的代数式表示第n 个等式:a n = = (n 为正整数); (3)求a 1+a 2+a 3+a 4+…+a n 的值.3.设f (x )=
,例如f (1)=
=
,f (2)=
=,===,===,…
(1)直接写出结果:f
(4)
=,=;
(2)计算:f
(1)+f
(2)
++f
(3)
++f
(4)
++……+f
(100)
+.
4.将网格中相邻的两个数分别加上同一个数,称为一步变换,比如,我们可以用三步变换将网格1变成网格2,变换过程如图.
(1)请用两步变换将网格3变成网格1.
(2)请用三步变换将网格4变成网格1.
(3)当ab 满足什么条件时,网格5通过若干步变换可以变成网格6,请利用网格7中的字母简要说明理由.
5.将一张边长为1的正方形纸片A ,对折一次可得纸片A 1,再将纸片A 1对折得纸片A 2,依次对折后的纸片A 3、A 4、A 5、…A n .
(1)纸片A 3的面积P 3= ,纸片A 5的面积P 5= ;
(2)设S 5=P 1+P 2+P 3+P 4+P 5,求S 5的值,小东同学再求S 5时用以下方法解: 设 S 5=++++①
2S 5=1+
+
+
+
②
由②﹣①得S 5=
(3)请你模仿小东同学的解题思路求:1+6+62+63+64+…+62015的值.
6.先阅读下列材料,然后解答问题:
材料:从4张不同的卡片中选取2张,有6种不同的选法,抽象成数学问题就是从4个
不同元素中选取2个元素的组合,组合数记为==6.一般地,从n个不同元素中选取m个元素的组合数记作,=(m≤n).
例如:从6个不同元素中选3个元素的组合,组合数记作==20
(1)为迎接国家建设工作检查,学校将举办小型书画展览.王老师在班级8幅优秀书画中选取3幅,共有多少种选法?
(2)探索发现:
计算:=,=,=,=,=,=.
由上述计算,试猜想,,之间有什么关系.(只写结论,不需说明理由)(3)请你直接利用(2)中猜想的结论计算:++++…+.
7.探索规律观察下面由※组成的图案和算式,解答问题
(1)请计算1+3+5+7+9+11=;
(2)请猜想1+3+5+7+9+…+19=;
(3)请猜想1+3+5+7+9+…+(2n﹣1)=;
(4)请用上述规律计算:21+23+25+ (99)
8.研究下列算式,你会发现什么规律?
1×3+1=4=22
2×4+1=9=32
3×5+1=16=42
4×6+1=25=52
…
(1)请你找出规律井计算7×9+1==()2
(2)用含有n的式子表示上面的规律:.
(3)用找到的规律解决下面的问题:
计算:=.
9.计算下列各式:
(1)1﹣=;
(2)=;
(3)=;
你能根据所学知识找到计算上面的算式的简便方法吗?请你利用你找到的简便方法计算下式:.
10.一列火车自A城驶往B城,沿途有n个车站(包括起点站A和终点站B),该列火车挂有一节邮政车厢,运行时需要在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该站的邮包一个,还要装上该站发往下面行程中每个车站的邮包一个.
(1)写出列车在第x车站启程时,邮政车厢上共有邮包的个数y(用x、n表示).(2)当n=20时,列车在第几个车站启程时邮政车厢上邮包的个数最多?
参考答案
1.解:(1)∴﹣3=(﹣1)131,9=(﹣1)232,﹣27=(﹣1)333,81=(﹣1)434,…, ∴第1行第n 个数为(﹣3)n ;
(2)第二行数与第一行数的每一个相对应的数加上﹣2,
即;(﹣1)131﹣2,(﹣1)232﹣2,(﹣1)333﹣2,(﹣1)434﹣2… 第三行数与第一行数的每一个相对应的数乘以,
即×(﹣1)131,
×(﹣1)232,
×(﹣1)333,
×(﹣1)434…
(3)第一行数的第6个数为(﹣1)636=36; 第二行数的第6个数为(﹣1)636﹣2=36﹣2; 第一行数的第6个数为
×(﹣1)1036=35;
这三个数的和为36+36﹣2+35=1699. 2.解:根据观察知, (1)=
×(﹣), 故答案为:,
×(
﹣
);
(2)第n 个等式为=
(﹣);
故答案为:,
(﹣
);
(3)a 1+a 2+a 3+a 4+…+a n =×(1﹣
)+
×(
﹣
)+
×(
﹣
)+
×(
﹣
)+…+
×(
﹣) =×(1﹣+
﹣+
﹣
+…+
﹣
)
=
×(1﹣
)
=×=
3.解:(1)由题意可知:f
(4)==;f
()
=;
(2)f()=,
∴f(x)+f()=1,
∴原式=+1+1…+1=99
故答案为:(1);;(2)99
4.解:(1)如图,
(2)如图,由(1)可得,网格4变成网格1,
所以a﹣2b+k=1,b﹣2+k+m=0,b﹣a+m+n=0,1﹣2b+n=0,解得,k=1﹣a+2b,m=a﹣b,n=2b﹣1;
(3)当满足a=b=0时,交换网格7中的字母a
1和a
2
可得,
由网格5变换成网格6,理由如下:
观察网格6中数字的特点,仅有一格数字为1,其他数字均为0,观察网格5中的整式,仅有一个整式1﹣2b中有常数项1,
所以只要取a=0,b=0,
这时仅有a
2
=1﹣2b=1,其他各网格的值都为0,
所以只要把a
1和a
2
交换,其他都不变.
所以当满足a=b=0时,交换网格7中的字母a
1和a
2
可由网格5变换成网格6,
5.解:(1)纸片A
3的面积P
3
=,纸片A
5
的面积P
5
=;
(2)S
5
=1﹣=;
(3)设S=1+6+62+63+64+ (62015)
则6S=6+62+63+64+ (62016)
5S﹣S=62016﹣1,
S=.
6.解:(1)==56
答:共有56种选法.
(2)=3,=1,=4,=10,=5,=15,因为+=,+=,
所以C k n+∁
n k+1=C
n+1
k+1.
(3)++++…+
=+++…+
=+…+
=
=
=165.
7.解:(1)∵1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,1+3+5+7+9=25=52,∴1+3+5+7+9+11=62=36.
故答案为:36;
(2)∵1+3+5+7+9+…+19共有10个数,
∴1+3+5+7+9+…+19=102=100.
故答案为:100;
(3)由(1)(2)得,1+3+5+7+9+…+(2n﹣1)=n2.
故答案为:n2;
(4)原式=21+23+25+…+99
=(1+3+5+7+...+97+99)﹣(1+3+5+7+ (19)
=()2﹣102
=2500﹣100
=2400.
8.解:(1)7×9+1=64=82;
(2)上述算式有规律,可以用n表示为:n(n+2)+1=n2+2n+1=(n+1)2.(3)原式==.
故答案为:64,8;n(n+2)+1=(n+1)2;.
9.解:(1)1﹣=;
(2)(1﹣)(1﹣)=;
(3)()(1﹣)(1﹣)=;
故答案为:;;;
原式=
=.
10.解:(1)当列车停靠在第x个车站时,
邮政车厢上需要卸下已经通过的(x﹣1)个车站发给该站的邮包共(x﹣1)个,还要装上下面行程中要停靠的(n﹣x)个车站的邮包共(n﹣x)个.
根据题意,完成下表:
车站序号在第x车站启程时邮政车厢邮包总数
1 n﹣1
2 (n﹣1)﹣1+(n﹣2)=2(n﹣2)
3 2(n﹣2)﹣2+(n﹣3)=3(n﹣3)
4 3(n﹣3)﹣3+(n﹣4)=4(n﹣4)
5 4(n﹣4)﹣4+(n﹣5)=5(n﹣5)
……
n0
由上表可得,y=x(n﹣x).
答:列车在第x车站启程时,邮政车厢上共有邮包的个数y=x(n﹣x).
(2)当n=20时,y=x(20﹣x)=﹣x2+20x=﹣(x﹣10)2+100,
当x=10时,y取得最大值.
答:列车在第10个车站启程时,邮政车厢上邮包的个数最多.。
