最小二乘法拟合插值法精品PPT课件
合集下载
最新-数值计算方法课件CH3插值法与最小二乘法—37数据拟合的最小二乘法-PPT文档资料

转化
(a0,a1, 取,an 极)小值
a0*,的a1*问,题,an*
由多元函数取极值的必要条件
得:
(a0,a1,,an) 0
ak
k0,1,,n
ak
m
n
i[2( ajj(xi)yi)k(xi)] 0
i0
j0
移项整理得:
mn
m
i ajj(xi)k(xi) iyik(xi)
i0 j0
i0
交换求和号顺序得:
n[ mij(xi)k(xi)a ]j miyik(xi) (k0,1, ,n) (7)
j0i0
i0
即
m
m
m
a0 i0(xi)k(xi)a1 i1(xi)k(xi) an in(xi)k(xi)
m
Байду номын сангаас
m
((jj,, kk)) ij(xi)k(xi) ik(xi)j(xi)(k,j) (8)
i0
i0
m
(f,k) iyik(xi)
(9)
i0
方程组(7)便可化为:
n
n
(j,k)aj (k,j)aj (f,k)(k0,1, ,n) (10)
一、最小二乘法的基本概念
根据上述实例图中测试点的分布情况,可以画出很多条靠 近这些点的直线,其方程都可表示为:
S(t)atb
(1)
其中: a, b 待定.要从形如(1)式的所有直线中,找出一条用某种 度量标准来衡量最靠近所有数据点 (ti , si ) (的i直0,1线,....m ,)
若 a, b 给定,计算值 S(ti) 与测量数据 si 之差为:
计算机数值方法第三章 插值法与最小二乘法.ppt

《 计 算 机 数 值 方 法 》
(3―1)
使其在给定的n+1个互异的插值结点上满足
插值条件
Pn(xi)=yi (i=0,1,…,n) (3―2)
第三章
插值法与最小二乘法
这样的多项式是否存在并且唯一呢?
根据插值条件,代数多项式(3―1)中的各个系
数a0,a1,…,an应满足下列n+1阶线性方程组
2 n Pn ( x0 ) a0 a1 x0 a2 x0 an x0 y0 2 n Pn ( x1 ) a0 a1 x1 a2 x1 an x1 y1 (3―3) P ( x ) a a x a x2 a xn y n n 0 1 n 2 n n n n
《 计 算 机 数 值 方 法 》
称 l (x),l (x) 为线性插值基函数 k k+1
第三章
插值法与最小二乘法
例1: 已知 100 10 , 121 11 ,求 y 115
代入点斜式插值多项式
y1 y0 L1 ( x) y0 ( x x0 ) x1 x0
得 y=10.71428
第三章
插值法与最小二乘法
下面给出插值多项式Pn(x)余项的表达式。
定理 设函数f(x)在区间[a,b]上具有n+1阶导数,
Pn(x)为次数不高于n的多项式,
且 Pn(xi)=yi (i=0,1,…,n)
则对插值区间上的任何x,都存在ξ∈(a,b),使得
《 计 算 机 数 值 方 法 》
f ( n 1) ( ) Rn ( x ) n 1 ( x ) ( n 1)! 其中,n 1 ( x) ( x x0 )( x x1 ) ( x xn ) ( x xi )
(3―1)
使其在给定的n+1个互异的插值结点上满足
插值条件
Pn(xi)=yi (i=0,1,…,n) (3―2)
第三章
插值法与最小二乘法
这样的多项式是否存在并且唯一呢?
根据插值条件,代数多项式(3―1)中的各个系
数a0,a1,…,an应满足下列n+1阶线性方程组
2 n Pn ( x0 ) a0 a1 x0 a2 x0 an x0 y0 2 n Pn ( x1 ) a0 a1 x1 a2 x1 an x1 y1 (3―3) P ( x ) a a x a x2 a xn y n n 0 1 n 2 n n n n
《 计 算 机 数 值 方 法 》
称 l (x),l (x) 为线性插值基函数 k k+1
第三章
插值法与最小二乘法
例1: 已知 100 10 , 121 11 ,求 y 115
代入点斜式插值多项式
y1 y0 L1 ( x) y0 ( x x0 ) x1 x0
得 y=10.71428
第三章
插值法与最小二乘法
下面给出插值多项式Pn(x)余项的表达式。
定理 设函数f(x)在区间[a,b]上具有n+1阶导数,
Pn(x)为次数不高于n的多项式,
且 Pn(xi)=yi (i=0,1,…,n)
则对插值区间上的任何x,都存在ξ∈(a,b),使得
《 计 算 机 数 值 方 法 》
f ( n 1) ( ) Rn ( x ) n 1 ( x ) ( n 1)! 其中,n 1 ( x) ( x x0 )( x x1 ) ( x xn ) ( x xi )
插值法与最小二乘拟合

5
证 由于Rn(xi) = (xi)-Pn(xi) =0 (i=0,1,…,n), 所以设
Rn(x)=K(x)n+1(x)
对于任一x[a,b],x xi(i=0,1,2,…,n),构造函数 (t)=f(t)-Pn(t)-K(x)n+1(t)
则有
(xi)=0 (i=0,1,2,…,n), (x)=0
4.1.2 插值多项式的截断误差
定理 设(n)(x)在[a,b]连续, (n+1)(x)在(a,b)内存在,在节点a x0<x1<…<xn b上, 满足插值条件(4.2)的插值多项式Pn(x),对 任一x[a,b],插值余项为
Rn (x)
f ( x) Pn ( x)
f (n (n
1) ( )
1)!
ln11.25L2(11.25)
(11.25 11)(11.25 12) 2.302585 (10 11)(10 12)
(11.25 10)(11.25 12) (11 10)(11 12)
2.397895
(11.25 10)(11.25 11) (12 10)(12 11)
xk+1 x
9
待定系数
求 lk-1(x):
令lk 1( x) A ( x xk ) ( x xk 1) ,
由
ll
k k
1( xk ( xk )
1) 1,
1,
lk1( xk ) lk1( xk1 ) 0; l k(xk 1) l k( xk 1) 0;
l
k
1( xk 1)
L2( x j ) = y j
(i, k 0,1,, n)
可知 lk ( x) Ak ( x x0 )( x xk 1 )( x xk 1 )( x xn ),
曲线拟合最小二乘法ppt课件

这里
1( x), ,l ( x)
是线性无关函数系,
为待定常数.
i (i 1, 2, , l)
9
在例1中,设函数
1( x) 1, 2( x) x, 3( x) x2
误 n,
我们希望猜想的数学模型应尽量接近观测数据,
m
2 i
m
[s * ( xi )
f ( xi )]2
i0
i0
m
min
s( x)
[s(
i0
xi
)
f ( xi )]2.
11
(1)直线拟合
设已知数据点 xi , yi , i 1,2,, m ,分布大致为一
条直线。作拟合直线 y(x) a0 a1x ,该直线不是通
的方法称为曲线拟称合为“,残f(差x)”
1
x
x0 x1 x2 …… xn
y
y0
y1
y2
…… yn
y=p(x) y=f(x)
插值
2
求一条曲线,使数据点均在离此曲线的上方或下方不远处, 所求的曲线称为拟合曲线,它既能反映数据的总体分布,又 不至于出现局部较大的波动,更能反映被逼近函数的特性, 使求得的逼近函数与已知函数从总体上来说其偏差按某种 方法度量达到最小。
解得 a0 0.562302 , a1 0.772282
由 a0 ln a 得 a ea0 e0.562302 1.754708,
23
由a1 b 得 b a1 0.772282
于是得到拟合指数函数为 y 1.754708 e0.772282x
(4)超定方程组的最小二乘解
最小二乘法与曲线拟合-PPT

点(xi,yi)带入y=(x) ,便得到以a0,a1,…,am为未知
量的矛盾方程组
0 + 1 1 + 2 12 + ⋯ + 1 = 1
其矩阵形式为
Ԧ =
0 + 1 2 + 2 22 + ⋯ +
其中
1
= 1
⋮
1
1
2
⋮
12
22
⋮
2
⋯
⋯
⋱
最小二乘法与曲线拟合
§5.0 问题的提出
如果实际问题要求解在[a,b]区间的每一点都“很
好地” 逼近f(x)的话,运用插值函数有时就要失败。
另外,插值所需的数据往往来源于观察测量,本身有
一定的误差。要求插值曲线通过这些本身有误差的点,
势必使插值结果更加不准确。
如果由试验提供的数据量比较大,又必然使得插值
不为零,从而有rankA=m+1。由引理2知,正则方程
组有唯一解。
证毕
四、最小二乘法拟合曲线的步骤
1..通过观察、分析得到拟合曲线的数学模型,或
根据经验公式确定数学模型。
2.将拟合曲线的数学模型转换为多项式。
3.写出矛盾方程组。
4.写出正则方程组。(可由多项式模型直接得到)
5.求解正则方程组,得到拟合曲线的待定系数。
多项式的次数过高而效果不理想。
从给定的一组试验数据出发,寻求函数的一个近似
表达式y=(x),要求近似表达式能够反映数据的基本
趋势而又不一定过全部的点(xi,yi),这就是曲线拟合
问题,函数的近似表达式y=(x)称为拟合曲线。本章
介绍用最小二乘法求拟合曲线。
§5.1 用最小二乘法求解矛盾方程组
量的矛盾方程组
0 + 1 1 + 2 12 + ⋯ + 1 = 1
其矩阵形式为
Ԧ =
0 + 1 2 + 2 22 + ⋯ +
其中
1
= 1
⋮
1
1
2
⋮
12
22
⋮
2
⋯
⋯
⋱
最小二乘法与曲线拟合
§5.0 问题的提出
如果实际问题要求解在[a,b]区间的每一点都“很
好地” 逼近f(x)的话,运用插值函数有时就要失败。
另外,插值所需的数据往往来源于观察测量,本身有
一定的误差。要求插值曲线通过这些本身有误差的点,
势必使插值结果更加不准确。
如果由试验提供的数据量比较大,又必然使得插值
不为零,从而有rankA=m+1。由引理2知,正则方程
组有唯一解。
证毕
四、最小二乘法拟合曲线的步骤
1..通过观察、分析得到拟合曲线的数学模型,或
根据经验公式确定数学模型。
2.将拟合曲线的数学模型转换为多项式。
3.写出矛盾方程组。
4.写出正则方程组。(可由多项式模型直接得到)
5.求解正则方程组,得到拟合曲线的待定系数。
多项式的次数过高而效果不理想。
从给定的一组试验数据出发,寻求函数的一个近似
表达式y=(x),要求近似表达式能够反映数据的基本
趋势而又不一定过全部的点(xi,yi),这就是曲线拟合
问题,函数的近似表达式y=(x)称为拟合曲线。本章
介绍用最小二乘法求拟合曲线。
§5.1 用最小二乘法求解矛盾方程组
数值分析3-4(最小二乘法)优秀PPT

i F ( xi ) yi (i 0,1,...,m)
按某种标准最小。
度量标准不同,将导致不同的拟合结果,常用 的准则有如下三种:
(1)使残差的最大绝对值为最小
max i
ei
max i
yi F (xi )
min
(2)使残差的绝对值之和为最小
ei min i
(3)使残差的平方和为最小
min
S ( x )
[S( xi
i0
)
yi
]2
S ( x) a0 a1x ... an xn (n m)
3. 一般定义
已知: 一组数据(xi,yi)(i=0,1,…,m), 求: 在函数类 span{0 ,1,...,n }中找一
个函数 y S ( x) ,使误差平方和最小,
即 这里
解 根据所给数据,在坐标纸上标出,得下图 y
t 从图中可以看出开始时浓度增加较快,后来 逐渐减弱,到一定时间就基本稳定在一个数 值上,即当t→∞时,y趋于某个常数,故有一 水平渐近线。另外 t = 0 时,反应未开始,浓 度为0。概括起来为
(1) y是t的增函数; (2)当t 0 时,y 0; (3)t 时,y趋于一个定值
m
m
2 2
2 i
[S ( xi ) yi ]2
i0
i0
m
min
S ( x )
[S(xi )
i0
yi ]2
S( x) a00 ( x) a11( x) ... ann ( x) (n m)
4. 广义定义
通常把最小二乘法
2 都考虑为加权平方和
2
即
m
2 2
( xi )[S ( xi ) yi ]2
按某种标准最小。
度量标准不同,将导致不同的拟合结果,常用 的准则有如下三种:
(1)使残差的最大绝对值为最小
max i
ei
max i
yi F (xi )
min
(2)使残差的绝对值之和为最小
ei min i
(3)使残差的平方和为最小
min
S ( x )
[S( xi
i0
)
yi
]2
S ( x) a0 a1x ... an xn (n m)
3. 一般定义
已知: 一组数据(xi,yi)(i=0,1,…,m), 求: 在函数类 span{0 ,1,...,n }中找一
个函数 y S ( x) ,使误差平方和最小,
即 这里
解 根据所给数据,在坐标纸上标出,得下图 y
t 从图中可以看出开始时浓度增加较快,后来 逐渐减弱,到一定时间就基本稳定在一个数 值上,即当t→∞时,y趋于某个常数,故有一 水平渐近线。另外 t = 0 时,反应未开始,浓 度为0。概括起来为
(1) y是t的增函数; (2)当t 0 时,y 0; (3)t 时,y趋于一个定值
m
m
2 2
2 i
[S ( xi ) yi ]2
i0
i0
m
min
S ( x )
[S(xi )
i0
yi ]2
S( x) a00 ( x) a11( x) ... ann ( x) (n m)
4. 广义定义
通常把最小二乘法
2 都考虑为加权平方和
2
即
m
2 2
( xi )[S ( xi ) yi ]2
数值计算方法CH插值法与最小二乘法数据拟合的最小二乘法
i0
(1,0 )
6
6
(1,1) i1(xi )1(xi ) xi2 3.64
i0
i0
6
6
( f ,0 ) i yi0 (xi ) yi 25.1
i0
i0
6
6
( f ,1) i yi1(xi ) yi xi 20.18
i0
i0
得法方程组:
7 4.2
34.6.24
a0 a1
2 2
m
i (S (xi ) yi )2
m
n
i (
a j j (xi ) yi )2
i0
i0
j0
为拟合系数 a j ( j 0,1的,函, n数) .因此,可设平方误差为:
m
n
(a0 , a1,, an ) i ( a j j (xi ) yi )2
i0
j0
第7页/共28页
求最小二乘解 S *(的x) 问题
第3页/共28页
一、最小二乘法的基本概念
根据上述实例图中测试点的分布情况,可以画出很多条靠 近这些点的直线,其方程都可表示为:
S(t) at b
(1)
其中: a, b 待定.要从形如(1)式的所有直线中,找出一条用某种 度量标准来衡量最靠近所有数据点 (ti , si ) (的i 直0,1线,...,.m)
9
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
8
9
10
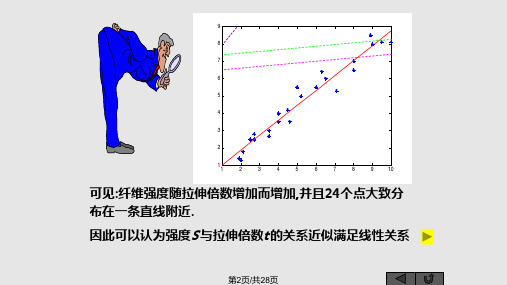
可见:纤维强度随拉伸倍数增加而增加,并且24个点大致分 布在一条直线附近.
因此可以认为强度S 与拉伸倍数t 的关系近似满足线性关系
数值分析课件Chapter7曲线拟合与线性最小二乘问题.ppt

法方程组可写成:GT F T FGx GT F T b
可以验证 x GT (GGT )1(F T F )1 F T b
是法方程组的一个解,故是原方程组的一个最小二乘解
推论7.1.2 若 rankA ,r则方n程组
有无穷多个最小二乘解。
Ax b
Def 2 方程组 Ax b 的所有最小二乘解中2-范数最小
8.9
8.5
10
4
3.5
22
9
8
11
4.5
4.2
23
9.5
8.1
12
4.6
3.5
24
10
8.1
可以看出,纤维强度随 拉伸倍数增加而增加
并且24个点大致分 布在一条直线附近
因此可认为强度与 拉伸倍数之间的主 要关系是线性关系
9
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
8
9
10
y ( x ) a bx
该直线称为这一问题的数学模型。
线性无关,下面讨论正交分解的具体实现方法。
记 A [a1, a2 , , an ],Q [q1, q2 , , qr ] 其中 a1, a2 , , ar线性无关,q1, q2 , , qr两两正交。
Gram-Schmidt正交化方法: 由 A QU 得
a1 u11q1 a2 u12q1 u22q2
y a bx c 1 x
1( x) 1;
2(x)
x;
3(x)
1 x
三、最小二乘问题解的存在性、唯一性
Def 1 设 A R,m若n 存在 x 精R确n地满足
可以验证 x GT (GGT )1(F T F )1 F T b
是法方程组的一个解,故是原方程组的一个最小二乘解
推论7.1.2 若 rankA ,r则方n程组
有无穷多个最小二乘解。
Ax b
Def 2 方程组 Ax b 的所有最小二乘解中2-范数最小
8.9
8.5
10
4
3.5
22
9
8
11
4.5
4.2
23
9.5
8.1
12
4.6
3.5
24
10
8.1
可以看出,纤维强度随 拉伸倍数增加而增加
并且24个点大致分 布在一条直线附近
因此可认为强度与 拉伸倍数之间的主 要关系是线性关系
9
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
8
9
10
y ( x ) a bx
该直线称为这一问题的数学模型。
线性无关,下面讨论正交分解的具体实现方法。
记 A [a1, a2 , , an ],Q [q1, q2 , , qr ] 其中 a1, a2 , , ar线性无关,q1, q2 , , qr两两正交。
Gram-Schmidt正交化方法: 由 A QU 得
a1 u11q1 a2 u12q1 u22q2
y a bx c 1 x
1( x) 1;
2(x)
x;
3(x)
1 x
三、最小二乘问题解的存在性、唯一性
Def 1 设 A R,m若n 存在 x 精R确n地满足
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7
7
1
Xi
7
Xi
2
i 1 i 1
i 1
7
7XiXi 27Xi 3i 1 i 1
i 1
7
7
Xi 2
7
Xi 3
Xi
4
i 1
i 1
i 1
步骤5:根据该求导公式,在Excel 中利用SUM与SUMPRODUCT命令分别求 出:
7 Yi
i 1
7 YiXi
i 1
7
YiXi
2
i 1
步骤6:将求得的数列进行逆矩阵 计算,如图:
最小二乘法拟合插值法
步骤1:根据X与Y对应的值,插入散点 图并做出趋势图,如图:
步骤2:从该图可以看出最接近 这7个点的趋势线为抛物线,所以 设该抛物线方程为:
Y=(A0+A1*X+A2*X2)
步骤3:分别对方程中的A0,A1,A2 进行求导,可得:
步骤4:根据该求导公式,在Excel 中利用SUM与SUMPRODUCT命令分别求 出:
步骤7:将求得的逆矩阵与矩阵B相 乘,求得根,如图:
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
9
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
