CH3 插值法与最小二乘法—3.2 插值多项式中的误差
Ch2_2插值余项与误差估计

一、插值余项
2.2 .3 插值多项式中的误差
从上节可知 , y f ( x )的 Lagrange 插值
Ln ( x )
yl
j0
n
j j
( x)
满足
但
Ln ( xi ) f ( xi )
x [a, b]
i 0 ,1, , n L n ( x ) f ( x ) 不会完全成立
K ( x)
f
( n 1)
( ) f
( n 1)
( n 1)! ( ) ( n 1)!
所以
R n ( x ) K ( x ) n 1 ( x )
n 1 ( x )
称 R n ( x )为插值多项式 Pn ( x )的余项 ( 截断误差 )
定理1. 设 f ( x )在区间 [ a , b ]上 n 1阶可微
0.0167
0.330365.
由(2.17),其截断误差
R1 ( x) M2 2
1 2
( x x0 )( x x1 ) ,
1 2 f ( )( x x0 )( x x1 ),
其中
Байду номын сангаас
R1 ( x)
f ( )2 ( x)
M 2 max f ( x) max sin x sin x1 0.3335,
x0 x x1 x0 x x1
于是
R1 (0.3367) sin 0.3367 L1 (0.3367)
1 2
0.3335 0.0167 0.0033
5
0.92 10 .
用抛物插值计算,由公式(2.5)得
最小二乘法数值分析实验报告

最小二乘法数值分析实验报告最小二乘法数值分析实验报告篇一:数值分析+最小二乘法实验报告数学与信息工程学院实课程名称:实验室:实验台号:班级:姓名:实验日期:验报告数值分析 201X年 4 月 13日篇二:数值分析上机实验最小二乘法数值分析实验报告五最小二乘法一、题目设有如下数据用三次多项式拟合这组数据,并绘出图形。
二、方法最小二乘法三、程序M文件:sy ms x f; xx=input( 请输入插值节点 as [x1,x2...]\n ff=i nput( 请输入插值节点处对应的函数值 as [f1,f 2...]\n m=input(请输入要求的插值次数m= n=leng th(xx); fr i=1:(m+1) syms faix; fai=x^(i-1); fr j=1:n x=xx(j);H(i,j)=eval(fai); end endA=ff*(H) *inv(H*(H) syms x; f=0; fr i=1:(m+1) f=f+A(i)*x^(i-1); end f plt(xx,ff, * ) hldnezplt(f,[xx(1),xx(n)])四、结果 sav e and run之后:请输入插值节点 as [x1,x2...] [-3 -2-1 0 1 2 3] 请输入插值节点处对应的函数值 as[f1,f2...] [-1.76 0.42 1.21.341.432.254.38]请输入要求的插值次数m=3 f =133/100+121469856021/35184372088832*x-8042142191733/450359 9627370496*x^2+1020815915537309/9007199254740992*x^3五、拓展:最小二乘法计算方法比较简单,是实际中常用的一种方法,但是必须经计算机来实现,如果要保证精度则需要对大量数据进行拟合,计算量很大。
插值方法(精品)

第四章插值方法§4.0 引言§4.1 多项式插值问题的一般提法§4.2 拉格朗日(Lagrange)插值§4.3 差商与差分及其性质§4.4 牛顿插值公式§4.5 分段插值法§4.6 三次样条插值§4.7 曲线拟合的最小二乘法引言1 插值法是广泛应用于理论研究和生产实践的重要数值方法,它是用简单函数(特别是多项式或分段多项式)为各种离散数组建立连续模型;为各种非有理函数提供好的逼近方法。
众所周知,反映自然规律的数量关系的函数有三种表示方法:A 解析表达式。
(1865年,瓦里斯Walis ;1690年,Raphson 拉夫逊;1669年,牛顿Newton ;历史悠久的方程)。
,(开普勒(Kepler)方程)。
悬链线方程;。
52)(3−−=x x x f y y x sin ε−=)/cos(λλx y =B图像法C表格法2 事实上,许多数据都是用表格法给出的(如观测和实验而得到的函数数据表格),可是,从一个只提供离散的函数值去进行理论分析和进行设计,是极不方便的甚至是不可能的。
因此需要设法去寻找与已知函数值相符,并且形式简单的插值函数(或近似函数)。
3 另外一种情况是,函数表达式完全给定,但其形式不适宜计算机使用,因为计算机只能执行算术和逻辑操作,因此涉及连续变量问题的计算都需要经过离散化以后才能进行。
如数值积分方法、数值微分方法、差分方程以及有限元法等,都必须直接或间接地应用到插值理论和方法。
1 插值法的概念假设函数y=f (x )是[a , b ]上的实值函数,x 0,x 1,…,x n 是[a ,b ]上n +1个互异的点,f (x )在这些点上的取值分别为y 0,y 1,…,y n 。
求一个确定的函数P (x ),使之满足:P (x i )=y i(i =0,1,2,…,n ) (1)称x 0,x 1,…,x n 为插值节点,关系式(1)称为插值原则,函数P (x )称为函数y=f (x )的插值函数,区间[a , b ]称为插值区间。
拉格朗日插值法理论及误差分析

浅析拉格朗日插值法目录:一、引言二、插值及多项式插值的介绍三、拉格朗日插值的理论及实验四、拉格朗日插值多项式的截断误差及实用估计式五、参考文献一、引言插值在数学发展史上是个古老问题。
插值是和拉格朗日(Lagrange)、牛顿(Newton)、高斯(Gauss)等著名数学家的名字连在一起的。
在科学研究和日常生活中,常常会遇到计算函数值等一类问题。
插值法有很丰富的历史渊源,它最初来源人们对天体研究——有若干观测点(我们称为节点)计算任意时刻星球的位置(插值点和插值)。
现在,人们在诸如机械加工等工程技术和数据处理等科研都有很好的应用,最常见的应用就是气象预报。
插值理论和方法能解决在实际中当许多函数表达式未知或形式复杂,如何去构造近似表达式及求得在其他节点处的值的问题。
二、插值及多项式插值1、插值问题的描述设已知某函数关系y f (x)在某些离散点上的函数值:P m (x)m m 1 a 0xa 1xam 1x插值问题:根据这些已知数据来构造函数 y f (x) 的一种简单的近似表达式, 以便于计算点 x x i ,i 0,1,L , n 的函数值 f ( x) ,或计算函数的一阶、二阶导数 值。
2、插值的几何意义3.1 基本概念假设 y f (x) 是定义在区间 a,b 上的未知或复杂函数,但一直该函数在 点a x 0 x 1 Lx n b 处的函数值 y 0, y 1,L y n 。
找一个简单的函数, 例如函数 P(x),使之满足条件P(x) y i ,i 0,1,2,L ,n, (3.1)通常把上述 x 0 x 1 L x n 称为插值节点,把 P(x)称为 f ( x)的插值多项 式,条件( 3.1)称为插值条件,并把求 P(x) 的过程称为插值法。
3.2 插值多项式的存在性和唯一性如果插值函数是如下 m 次的多项式:那么插值函数的构造就是要确定P m (x)表达式中的 m+1 个系数 a0,a1,L am 1,am 。
教学课件:第三章-插值与逼近

最佳平方逼近
最佳平方逼近是指在平方误差意义下, 函数空间中最佳逼近原函数的逼近元 所在的函数类。
最佳平方逼近在数值分析、计算数学 等领域有广泛应用,如多项式插值、 样条插值等算法都是基于最佳平方逼 近的思想。
图像处理
在图像处理中,插值用于 放大缩小图像,而逼近则 用于图像的平滑和锐化。
物理学模拟
在物理模拟中,插值用于 确定未知点的物理量,而 逼近则用于简化复杂的物 理过程。
02 插值方法
线性插值
总结词
线性插值是最简单的插值方法,通过连接两个已知点的直线来估计中间点的值。
详细描述
线性插值基于两点之间的直线关系,通过已知的x和y坐标计算出中间点的值。 它适用于数据点分布较为均匀的情况,但在数据点分布不均或存在弯曲趋势时, 线性插值的误差较大。
随着科学技术的不断发展,插值与逼近的应用领域也 在不断扩大。未来,插值与逼近将会在人工智能、大 数据分析、机器学习等领域发挥更加重要的作用。
随着教育技术的发展,未来插值与逼近的教学将会更 加注重实践和应用。学生可以通过更多的实践项目和 案例分析,深入理解和掌握插值与逼近的概念和方法 ,提高解决实际问题的能力。
06 总结与展望
总结
• 插值与逼近是数学中重要的概念,广泛应用于实际问题的解决。通过学习插值 与逼近,学生可以更好地理解数学在解决实际问题中的应用,提高数学素养和 解决问题的能力。
• 本章主要介绍了线性插值、多项式插值、样条插值和最小二乘法等插值方法, 以及代数逼近、多项式逼近和样条逼近等逼近方法。这些方法在数值分析、计 算物理、计算机图形学等领域有着广泛的应用。
最小二乘法的基本原理和多项式拟合
最小二乘法的基本原理和多项式拟合一最小二乘法的基本原理从整体上考虑近似函数P(x)同所给数据点(X i,y i)(i=o,i,…,m)误差ri 二呛)—y i(i=0,1,…,m)ri= P(X i)-y i(i=0,1,…,m)绝对值的最大值maX m r i,即误差向量m/ 、T》仃r =(「0,「1,…r m)的X—范数;二是误差绝对值的和 7 ,即误差向量r的1 —m2Z r i范数;三是误差平方和 7 的算术平方根,即误差向量r的2—范数;前两种方法简单、自然,但不便于微分运算,后一种方法相当于考虑2—范数的平方,m2送r i r因此在曲线拟合中常采用误差平方和V 来度量误差r i(i=0 , 1,…,m)的整体大小。
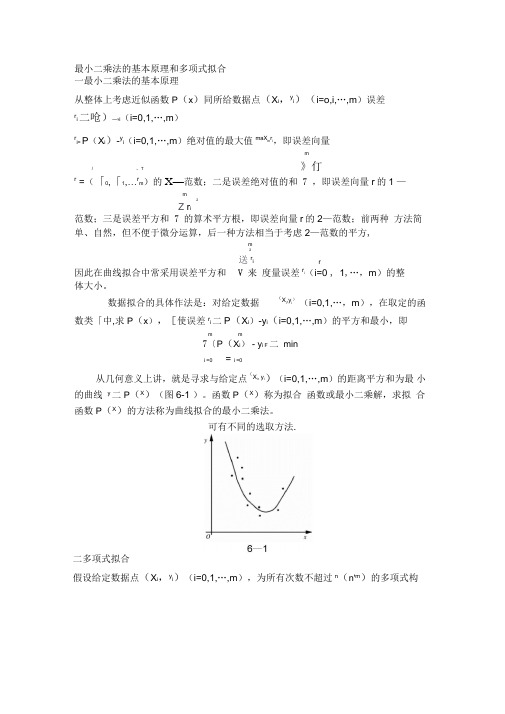
数据拟合的具体作法是:对给定数据(X i,y i)(i=0,1,…,m),在取定的函数类「中,求P(x),[使误差r i二P(X i)-y i(i=0,1,…,m)的平方和最小,即m m7〔P(X i) - y i F 二mini =0 = i =0从几何意义上讲,就是寻求与给定点(X i, y i)(i=0,1,…,m)的距离平方和为最小的曲线y二P(X)(图6-1 )。
函数P(X)称为拟合函数或最小二乘解,求拟合函数P(X)的方法称为曲线拟合的最小二乘法。
可有不同的选取方法.二多项式拟合假设给定数据点(X i,y i)(i=0,1,…,m),为所有次数不超过n(n'm)的多项式构nP n (X )=送 a k X k成的函数类,现求一心m,使得n送 k | a k X i -y i = minV.k=0 丿(1)当拟合函数为多项式时,称为多项式拟合,满足式(1)的P n (X )称为最小二乘 拟合多项式。
特别地,当n=1时,称为线性拟合或直线拟合。
I =送 bn(X i ) —y i 2i =0显然I 7 (' a k X k- y i )2i -0 k -0为a 0,a i ,…a n 的多元函数,因此上述问题即为求1 = l(a 0,a i 「a n )的极值 问题。
插值与拟合(最小二乘法)
二者区别:插值必须精确的经过所给定的点 x,f(x); 但是拟合不需要,拟合允许f(x) , p(x) 之间有误差的存在,但是误差不能太大,要尽可能的 小, 到底怎么来最小化误差,可以: error = |f(x) - p(x)|, min(error), 或者 min(error^2)........ 因为最小化误差的平方和, 所以叫 least square method, 其实翻译的不好,应该叫 最小平方和法。。。。。。
网络错误400请刷新页面重试持续报错请尝试更换浏览器或网络环境
插值与拟合(最小二乘法)
插值与拟合都是给பைடு நூலகம்一组y = f(x)数据的前提下,用函数 p(x) 近似表示 f(x)的方法;
插值用很多种方法,比如多项式插值,三角函数插值等,意思就是选取哪种函数作为插值的函数; 拟合方法很多,其中包括最小二乘法等;
最小二乘法的基本原理和多项式拟合
最小二乘法的基本原理和多项式拟合一 最小二乘法的基本原理从整体上考虑近似函数)(x p 同所给数据点),(i i y x (i=0,1,…,m)误差i i i y x p r -=)((i=0,1,…,m)的大小,常用的方法有以下三种:一是误差i i i y x p r -=)((i=0,1,…,m)绝对值的最大值im i r ≤≤0max ,即误差 向量T m r r r r ),,(10 =的∞—范数;二是误差绝对值的和∑=mi ir 0,即误差向量r 的1—范数;三是误差平方和∑=mi ir02的算术平方根,即误差向量r 的2—范数;前两种方法简单、自然,但不便于微分运算 ,后一种方法相当于考虑 2—范数的平方,因此在曲线拟合中常采用误差平方和∑=mi ir02来 度量误差i r (i=0,1,…,m)的整体大小。
数据拟合的具体作法是:对给定数据 ),(i i y x (i=0,1,…,m),在取定的函数类Φ中,求Φ∈)(x p ,使误差i i i y x p r -=)((i=0,1,…,m)的平方和最小,即∑=mi ir2=从几何意义上讲,就是寻求与给定点),(i i y x (i=0,1,…,m)的距离平方和为最小的曲线)(x p y =(图6-1)。
函数)(x p 称为拟合函数或最小二乘解,求拟合函数)(x p 的方法称为曲线拟合的最小二乘法。
在曲线拟合中,函数类Φ可有不同的选取方法.6—1二 多项式拟合假设给定数据点),(i i y x (i=0,1,…,m),Φ为所有次数不超过)(m n n ≤的多项式构成的函数类,现求一Φ∈=∑=nk k k n x a x p 0)(,使得[]min )(00202=⎪⎭⎫⎝⎛-=-=∑∑∑===mi mi n k i k i k i i n y x a y x p I (1)[ ] ∑ = = - mi ii y x p 02 min ) (当拟合函数为多项式时,称为多项式拟合,满足式(1)的)(x p n 称为最小二乘拟合多项式。
插值法(1)
( x − x0 )( x − x1 )L( x − x j − 1 )( x − x j + 1 )L( x − xn ) l j ( x) = ( x j − x0 )( x j − x1 )L( x j − x j − 1 )( x j − x j + 1 )L( x j − xn )
( x − xi ) =∏ i = 0 ( x j − xi )
虽然线性方程组 (4)推出的插值多项式存在且唯一 但通过解线性方程组(4)求插值多项式却不是好方法
三、Lagrange插值多项式 根据线性空间的理论
所有次数不超过n的多项式构成的线性空间是 n + 1 维的
这个n + 1维线性空间的基底也由 n + 1个多项式组成
并且形式不是唯一的
而任意一个n次多项式可由基底线性表示
本章引例:
Hooker定律
弹簧在力F的作用下伸长 x , 一定范围内服从 Hoo ker 定律: F与x成正比 ,即F = kx , k为弹性系数 , 现在得到下面一组 x , F数据(如表 ),并在( x , F )坐标下作图(如图).可以看出, 当F达到一定数值后, 就不服从Hoo ker 定律.试由数据确 定k ,并给出不服从 Hoo ker 定律时的近似公式.
因此f ( x )的二次Lagrange插值多项式为
L2 ( x ) = y0l0 ( x ) + y1l1 ( x ) + y2l2 ( x )
且
f (175) ≈ L2 (175) = 12l0 ( 175) + 13l1 (175) + 15l2 (175) = 13.230 158 73
在例1中,如果只给出两个节点169和225,也可以作插值 多项式,即1次Lagrange插值多项式,有两个插值基函数, 这种插值方法称为Lagrange线性插值,也可以在n+1个 节点中取相邻的两个节点作线性插值
最小二乘法的基本原理和多项式拟合
最小二乘法的基本原理和多项式拟合Document number:NOCG-YUNOO-BUYTT-UU986-1986UT最小二乘法的基本原理和多项式拟合一最小二乘法的基本原理从整体上考虑近似函数同所给数据点 (i=0,1,…,m)误差(i=0,1,…,m)的大小,常用的方法有以下三种:一是误差(i=0,1,…,m)绝对值的最大值,即误差向量的∞—范数;二是误差绝对值的和,即误差向量r的1—范数;三是误差平方和的算术平方根,即误差向量r的2—范数;前两种方法简单、自然,但不便于微分运算,后一种方法相当于考虑 2—范数的平方,因此在曲线拟合中常采用误差平方和来度量误差 (i=0,1,…,m)的整体大小。
数据拟合的具体作法是:对给定数据 (i=0,1,…,m),在取定的函数类中,求,使误差(i=0,1,…,m)的平方和最小,即=从几何意义上讲,就是寻求与给定点 (i=0,1,…,m)的距离平方和为最小的曲线(图6-1)。
函数称为拟合函数或最小二乘解,求拟合函数的方法称为曲线拟合的最小二乘法。
在曲线拟合中,函数类可有不同的选取方法.6—1二多项式拟合假设给定数据点 (i=0,1,…,m),为所有次数不超过的多项式构成的函数类,现求一,使得(1)当拟合函数为多项式时,称为多项式拟合,满足式(1)的称为最小二乘拟合多项式。
特别地,当n=1时,称为线性拟合或直线拟合。
显然为的多元函数,因此上述问题即为求的极值问题。
由多元函数求极值的必要条件,得(2)即(3)(3)是关于的线性方程组,用矩阵表示为(4)式(3)或式(4)称为正规方程组或法方程组。
可以证明,方程组(4)的系数矩阵是一个对称正定矩阵,故存在唯一解。
从式(4)中解出 (k=0,1,…,n),从而可得多项式(5)可以证明,式(5)中的满足式(1),即为所求的拟合多项式。
我们把称为最小二乘拟合多项式的平方误差,记作由式(2)可得(6)多项式拟合的一般方法可归纳为以下几步:(1) 由已知数据画出函数粗略的图形——散点图,确定拟合多项式的次数n;(2) 列表计算和;(3) 写出正规方程组,求出;(4) 写出拟合多项式。
