分数指数幂运算
分数指数幂证明

分数指数幂证明摘要:一、引言- 分数指数幂的定义- 分数指数幂在数学中的重要性二、分数指数幂的性质- 分数指数幂的运算法则- 分数指数幂的性质三、分数指数幂的证明方法- 基于分数指数幂的性质的证明方法- 基于分数指数幂运算法则的证明方法四、分数指数幂在实际问题中的应用- 分数指数幂在物理学中的应用- 分数指数幂在工程学中的应用五、结论- 分数指数幂证明的重要性- 对分数指数幂证明的展望正文:一、引言分数指数幂是数学中一种重要的概念,它涉及到幂运算和分数的运算。
在数学中,分数指数幂被广泛应用于各种领域,如代数、微积分等。
因此,对分数指数幂的证明方法的研究具有重要的意义。
二、分数指数幂的性质分数指数幂有许多重要的性质,这些性质是进行分数指数幂证明的基础。
首先,我们来看分数指数幂的运算法则:(1)a^(m/n) * a^(n/p) = a^((m*n)/(p*n))(2)a^(m/n) / a^(n/p) = a^((m-n)/(p*n))其次,分数指数幂还有一些重要的性质,如:(1)a^(m/n) = (a^m)^(1/n)(2)a^(-m/n) = (a^m)^(-1/n) = 1 / a^(m/n)三、分数指数幂的证明方法分数指数幂的证明方法主要有两种,一种是基于分数指数幂的性质进行证明,另一种是基于分数指数幂运算法则进行证明。
以基于分数指数幂性质的证明方法为例,假设我们要证明a^(m/n) *a^(n/p) = a^((m*n)/(p*n)),我们可以利用分数指数幂的性质(1):a^(m/n) * a^(n/p) = (a^m)^(1/n) * (a^n)^(1/p)= (a^m)^(1/n * 1/p) * (a^n)^(1/p)= (a^(m*n))^(1/(p*n))= a^((m*n)/(p*n))四、分数指数幂在实际问题中的应用分数指数幂在实际问题中也有很多应用,如在物理学中,分数指数幂常被用于描述放射性衰变的过程;在工程学中,分数指数幂常被用于描述信号处理的过程等。
分数指数幂的同底数运算教案二:灵活应用同底数运算规则求解

亲爱的同学们,大家好!今天,我们将进一步讨论分数指数幂的同底数运算,希望通过今天的学习,能够让大家掌握这个知识点,并且能够熟练运用同底数运算规则求解。
我们来复习一下分数指数幂的定义。
分数指数幂,就是指数为分数的幂,例如2的1/2次方,2的2/3次方等等。
在这种情况下,我们需要首先理解分数指数幂的含义,我们以2的1/2次方为例,这个式子可以写成根号2,也就是2的平方根。
因此,我们也可以推广到其他的分数指数幂中,例如2的2/3次方,可以写成2的3次方根号2。
接下来,我们将讨论同底数运算的规则。
同底数运算的规则非常简单,就是将同一底数的指数相加,例如2的3次方乘以2的5次方,可以写成2的8次方。
用公式表示,就是a的m 次方乘以a的n次方,等于a的m+n次方。
在进行同底数运算的时候,有时候我们需要进行一些化简,例如对于3的1/2次方乘以9的3/2次方,我们可以先将9的3/2次方化简为(3的2次方)的3/2次方,接着可以将3的1/2次方写成3的1次方的1/2次方,然后代入同底数运算的公式中,即可得到3的2次方。
除了同底数运算,我们还需要学习同底数约分的方法。
同底数约分的方法非常简单,就是对于同一底数,将指数相减即可。
例如2的5次方除以2的3次方,可以写成2的(5-3)次方,也就是2的2次方。
在进行同底数约分的时候,有时候我们需要注意,即需要将分数指数幂的平方根或者三次方根化成分数形式,例如8的1/6次方可以写成(2的3次方)的1/6次方,然后化成分数形式,变成(2的1次方)的1/3次方,这样就可以进行同底数运算了。
让我们来看几个例子,来加深理解。
例子1:计算2的2/3次方乘以2的5/3次方。
答案:这个时候我们需要将指数相加,得到2的7/3次方。
例子2:计算3的1/2次方乘以9的3/2次方。
答案:这个时候我们需要进行一些化简,将9的3/2次方化简为(3的2次方)的3/2次方,接着可以将3的1/2次方写成3的1次方的1/2次方,然后代入同底数运算的公式中,即可得到3的2次方。
分数指数幂运算

分数指数幂运算
分数指数幂运算是将一个分数作为底数,另一个分数作为指数进行计算的运算。
如果分数指数是正数,可以按照分数的定义进行计算。
例如,计算2^1/3,可以先计算2的立方根,再将结果与自身相乘,即2^1/3 = (∛2)^3 = 2。
如果分数指数是负数,可以使用倒数的概念进行计算。
例如,计算2^(-1/3),可以先计算2的立方根的倒数,再将结果与自身相乘,即2^(-1/3) = 1/(∛2)。
如果分数指数是分数形式,可以使用乘法的性质进行计算。
例如,计算2^(2/3),可以将指数分解为2×(1/3),然后先计算2的立方根,再将结果平方,即2^(2/3) = (∛2)^2 = 2^(1/3) ×
2^(1/3) = (∛2) × (∛2)。
需要注意的是,分数指数运算可能会得到无理数的结果,因此可能需要进行近似运算或使用特定的表达式表示结果。
指数运算10个公式推导

指数运算10个公式推导1. 同底数幂相乘公式:a^m× a^n = a^m + n(a≠0,m、n为实数)- 推导:设a为底数,m和n为指数。
根据指数的定义,a^m表示m个a相乘,a^n表示n个a相乘。
那么a^m× a^n就是m个a相乘再乘以n个a相乘,总共就是(m + n)个a相乘,所以a^m× a^n=a^m + n。
2. 同底数幂相除公式:a^m÷ a^n = a^m - n(a≠0,m、n为实数且m>n)- 推导:同样设a为底数,m和n为指数。
a^m是m个a相乘,a^n是n个a 相乘。
a^m÷ a^n就是m个a相乘的结果除以n个a相乘的结果,相当于m个a相乘后去掉n个a,所以剩下(m - n)个a相乘,即a^m÷ a^n = a^m - n。
3. 幂的乘方公式:(a^m)^n=a^mn(a≠0,m、n为实数)- 推导:(a^m)^n表示n个a^m相乘,而a^m是m个a相乘,那么n个a^m相乘就是m× n个a相乘,所以(a^m)^n = a^mn。
4. 积的乘方公式:(ab)^n=a^n b^n(a≠0,b≠0,n为实数)- 推导:(ab)^n表示n个ab相乘,即(ab)×(ab)×·s×(ab)(共n个ab)。
根据乘法交换律和结合律,可以将a和b分别相乘,得到a× a×·s× a(共n个a)乘以b×b×·s× b(共n个b),也就是a^n b^n。
5. 商的乘方公式:((a)/(b))^n=(a^n)/(b^n)(a≠0,b≠0,n为实数)- 推导:((a)/(b))^n表示n个(a)/(b)相乘,即(a)/(b)×(a)/(b)×·s×(a)/(b)(共n个(a)/(b))。
指数的运算与指数函数

a>1
图 象
定义域
R 值域 (0,+∞) 性 过定点(0,1),即x=0时,y=1
质
在 R上是减函数
在R上是增函数
☆不同底数的图像
a>b>1
0<b<a<1
归纳:在第一象限总是底大图高
讨论 y a (a 0 a 1)的图像
| x|
(1)a>1 (2)0<a<1
1
2
3
n m
④ a ⑤
n
1 * n (n Z ) a
其中均要求
a0 1
a、b 0
☆平方根
如果 x a ,那么 x 叫做 a 的平方根;
2
a0 a
a a
2
a | a |
2
☆立方根 3 如果 x a ,那么 x 叫做 a 的立方根。
0 0
3 3
aR
3
a
3
a a
指数的运算与指数函数 主讲教师 陈利敏
青春是有限的,智慧是无穷的; 趁短暂的青春,学习无穷的智慧
☆指数的运算
知识梳理
分数指数幂
指数的运算
分数指数幂 的性质
☆分数指数幂
规定: a n a m (a 0, m, n N * , 且n 1)
注意:(1)分数指数幂是根式的另一种表示; (2)根式与分式指数幂可以互化. 规定:
m n
a
m n
1 a
m n
(a 0, m, n N , n 1)
*
注意:0的正分数指数幂等于0; 0的负分数指数幂没意义.
数学分数指数幂

思源个性化学习讲义【知识精要】1.分数指数幂的意义: 一般地,我们规定 n m nm a a = ()1,0>≥n n m a 为正整数,、 ,这就是正数a 的正分数指数幂的意义. 规定nm n maa-=1()1,0>>n n m a 为正整数,、其中的nm nm a a -、叫做分数指数幂,a 是底数整数指数幂和分数指数幂统称为有理数指数幂.注:(1)0的正分数指数幂为0, 0的负分数指数幂无意义. (2)若无特殊说明,底数中的字母均为正数。
2. 当a >0时,整数指数幂的运算性质,对于有理指数幂也同样适用.即对于任意有理数r ,s ,均有下面的运算性质:设q p b a 、,0,0>>为有理数(1)q p q p qp q p a a a a a a -+=÷=⋅,(2)()pq qpa a =(3)()p p pp p pb a b a b a ab =⎪⎭⎫ ⎝⎛=,【热身练习】1. 把下列方根化为分数指数幂的形式(1)310 (2)32101(3)3100 (4)41002. 求值(1)21169 (2)3264 (3) 239- (4)⎪⎪⎭⎫ ⎝⎛-43256( )A.3B.3-C.3±D.81 4.当a _________时,式子23a 有意义 5. 若0>a ,则43a 和53-a 用根式形式表示分别为 和6.56b a 和mm 3用分数指数幂形式表示分别为 和【精解名题】 1. (1)23425-⎪⎭⎫⎝⎛= ;(2) 63125.132⨯⨯= ________2. 计算:631010⨯=__________________3.3151写成幂的形式______________4.化为分数指数幂的形式为 ___________________5. 583221)22(--化为分数指数幂得 _________________________6.式子 ( )7. 已知32121=+-aa ,求下列各式的值。
人教版高一数学必修1第16课时分数指数幂与幂的运算(含解析)
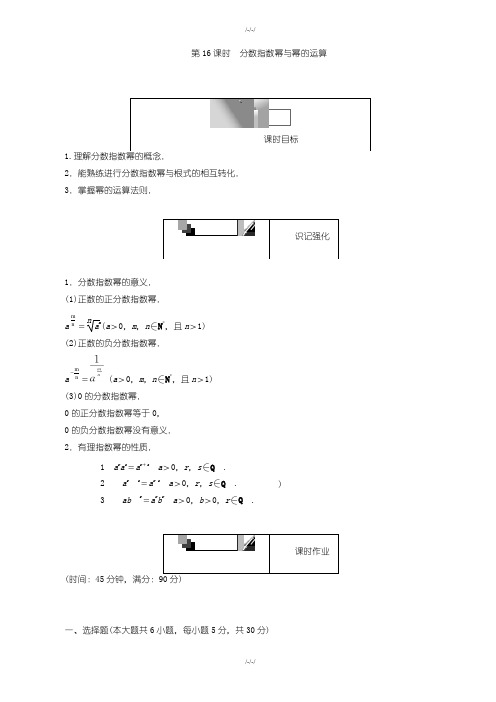
即x -x =± ,
∴x-x-1=(x -x )(x +x )=±3 .
(2)将x+x-1=7两边平方,得x2+x-2+2=49,
∴x2+x-2=47,
∴ = =4.
能力提升
12.(5分)
的值等于()
A.1- B.2-
C. - D.
答案:B
答案:1
解析:设ax=by=cz=k,则k>0,a=k ,b=k ,c=k ,因此abc=k k k =k =k0=1.
三、解答题(本大题共4小题,共45分)
10.(12分)计算:
(1) 0.5-0.752+6-2× ;
(2)(0.25) - 2×[(-2)3] +10(2- )-1-10×30.5;
二、填空题(本大题共3个小题,每小题5分,共15分)
7.用分数指数幂表示: =________.
答案:x y
解析: = =x y =x y
8.若10x=3 ,10y= ,则102x-y=________.
答案:
解析:102x-y=(10x)10y=(3 )2÷ =3 ÷3 = .
9.若a,b,c为正实数,ax=by=cz, + + =0,则abc=________.
解析:设4x=6y=1442=t,则4=t ,6=t ,144=t ,∴36=t .又144=4×36,∴t =t ·t ,即 = + ,选D.
6.已知0<x<1,x2-3x+1=0,则x -x 的值为()
A.1 B.-1
C.1或-1 D.-
答案:B
解析:∵x2-3x+1=0,∴x2+1=3x,∵0<x<1,∴两边除以x,得x+x-1=3,∴(x -x )2=x+x-1-2=3-2=1.又0<x<1,∴x -x = - = <0,∴x -x =-1.故选B.
近似数的精确度 分数指数幂及运算

近似数的精确度分数指数幂及运算
在数学中,我们经常会遇到需要进行近似数的计算,这时候我们需要考虑到近似数的精确度。
近似数的精确度是指我们所得到的近似数与真实值之间的误差大小。
在实际应用中,我们需要根据具体情况来确定近似数的精确度,以保证计算结果的准确性。
在分数的运算中,我们需要注意分母的大小,因为分母越大,分数的精确度就越高。
例如,1/2和1/1000相比,1/2的精确度要高得多。
在进行分数的加减乘除运算时,我们需要先将分数化为相同的分母,然后再进行运算。
这样可以避免分母不同导致的误差。
指数幂是数学中常见的运算方式,它可以用来表示一个数的幂次方。
例如,2的3次方等于8,即2³=8。
在进行指数幂的计算时,我们需要注意底数和指数的大小关系。
如果底数比较大,指数比较小,那么我们可以直接计算出结果。
但如果底数比较小,指数比较大,那么我们需要使用科学计数法来表示结果,以保证精确度。
在运算中,我们还需要注意数值的精确度。
例如,当我们进行小数的加减乘除运算时,我们需要注意小数点后的位数,以保证计算结果的精确度。
如果小数点后的位数太多,我们可以使用四舍五入的方法来保留合适的位数。
在数学中,我们需要根据具体情况来确定近似数的精确度,以保证计算结果的准确性。
在分数、指数幂和运算中,我们需要注意数值
的大小关系和精确度,以避免误差的产生。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学学科导学案
教师: 学生: 年级: 高一日期: 星期: 时段:
③⎝ ⎛⎭⎪⎫n a n =a . ④当n 为奇数时,n a n =a ;
当n 为偶数时,n a n = |a |=⎩⎪⎨⎪⎧ a a ≥0
-a a <0
2.有理数指数幂
(1)幂的有关概念
①正整数指数幂:a n =a ·a ·…·a n 个 (n ∈N *
); ②零指数幂:a 0=1(a ≠0);
③负整数指数幂:a -p =1
a
p (a ≠0,p ∈N *); ④正分数指数幂:a m
n =n
a m (a >0,m 、n ∈ N *,且n >1); ⑤负分数指数幂:a -m n =1a m n
=1n a m (a >0,m 、n ∈N *且n >1). ⑥0的正分数指数幂等于0,0的负分数指数幂没有意义.
(2)有理数指数幂的性质
①a r a s =a r +s (a >0,r 、s ∈Q )
②(a r )s =a rs (a >0,r 、s ∈Q )
③(ab )r =a r b r (a >0,b >0,r ∈Q ).
分数指数幂与根式的关系
根式与分数指数幂的实质是相同的,分数指数幂与根式可以相互转化,通常利用分数指数幂进行根式的化简运算.
指数幂的化简与求值
【例1】►化简下列各式(其中各字母均为正数).
(1)(a 23·b -1)-12·a -12·b 13
6a ·b 5;
(2)56a 13·b -2·(-3a -12b -1)÷(4a 23·b -3)12.
解
化简结果要求
(1)若题目以根式形式给出,则结果用根式表示;
(2)若题目以分数指数幂的形式给出,则结果用分数指数幂表示;
(3)结果不能同时含有根号和分数指数幂,也不能既有分母又有负指数幂.
【训练1】 计算:
(1)0.027-13-⎝ ⎛⎭⎪⎫-17-2+⎝ ⎛⎭
⎪⎫27912-()2-10; (2)⎝ ⎛⎭⎪⎫14-12·(4ab -1)30.1-2(a 3b -3)12
. 解
课内练习与训练
P60-63例题
审阅签字: 时间: 教务主任签字: 时间:。
