第四章 根轨迹方程
自动控制原理 第四章根轨迹

第四章根轨迹法4-1 根轨迹法的基本概念4-2 常规根轨迹的绘制法则4-3 广义根轨迹4-1 根轨迹法的基本概念一、根轨迹的概念根轨迹:系统中某个参数从零到无穷变化时,系统闭环特征根在s平面上移动的轨迹。
根指的是闭环特征根(闭环极点)。
根轨迹法是根据开环传递函数与闭环传递函数的关系,通过开环传递函数直接分析闭环特征根及系统性能的图解法。
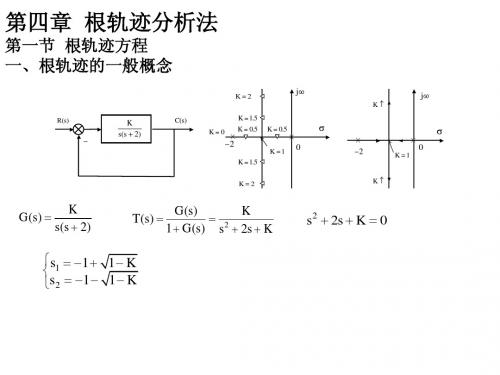
K =0 s 1=0 s 2=-40 < K <1s 1 s 2为不等的负实根K =1s 1=-2 s 2=-21 < K < ∞s 1s2 实部均为-2由根轨迹可知:1)当K =0时,s 1=0,s 2=-1,这两点恰是开环传递函数的极点,同时也是闭环特征方程的极点.2)当0<K < 1 时,s 1,2都是负实根,随着k 的增长,s 1从s 平面的原点向左移,s 2从-1点向右移。
3) 当K = 1时, s 1,2= -2,两根重合在一起,此时系统恰好处在临界阻尼状态。
4) 1 <K <∞,s 1,2为共轭复根,它们的实部恒等于-2,虚部随着K 的增大而增大,系统此时为欠阻尼状态。
★在s平面上,用箭头标明K增大时,闭环特征根移动的方向,以数值表明某极点处的增益大小。
有了根轨迹图就可以分析系统的各种性能:(1)稳定性:根轨迹均在s的左半平面,则系统对所有K>0都是稳定的。
(2)稳态性能:如图有一个开环极点(也是闭环极点)s=0。
说明属于I型系统,阶跃作用下的稳态误差为0。
在速度信号V0t作用下,稳态误差为V0/K,在加速度信号作用下,稳态误差为∞。
(3)动态性能:过阻尼临界阻尼欠阻尼K越大,阻尼比ξ越小,超调量σ%越大。
由此可知:1、利用根轨迹可以直观的分析K的变化对系统性能的影响。
2、根据性能指标的要求可以很快确定出系统闭环特征根的位置;从而确定出可变参数的大小,便于对系统进行设计。
由以上分析知:根轨迹与系统性能之间有着密切的联系,但是,高阶方程很难求解,用直接解闭环特征根的办法来绘制根轨迹是很麻烦的。
第4章 根轨迹法

• 4.4
应用MATLAB绘制根轨迹图
• 使用rlocus命令可以得到连续的单输入单输
出系统的根轨迹。 • (1)Rlocus(num,den)或rlocus(num,
den,k)
• (2)sgrid或sgrid(zeta,wn)
• 解 在图4.11中画出ξ=0.5的射线,与根轨 迹相交得闭环极点的要求位置s0。再画出 Gk(s)的极点到s0的三个向量——
• 得 • 由向量幅值
• 换句话说,如果取K*的值为65,则1+Gk (s) 的一个根将位于s0,另一个根当然是和s0共 轭的。第3个根在何处呢?由根轨迹知道, 第3条根轨迹在负实轴上,在一般情况下, 可以取一试探点,计算相应的K*值,然后 修正试探点直到找出和K*=65相应的点为止。
• ②方法2 根据式(4.14),求出闭环系统特 征方程。
• 由上式可得
• ③方法3
根据式(4.15)有
• d1在根轨迹上,即为所求的分离点,d2不在根 轨迹上,则舍弃。此系统根轨迹如图4.4。
图4.4
• 以上介绍了9条绘制根轨迹的一般规则。为 了熟练应用上述9条规则,并能绘制复杂系 统根轨迹,下面再举一例说明如何绘制一 个复杂系统的完整根轨迹图。
第4章
• 4.1
• 4.1.1
ቤተ መጻሕፍቲ ባይዱ
根轨迹法
根轨迹的基本概念
根轨迹的定义
• 系统参数(如开环增益K *)由零增加到∞ 时,闭环特征根在S平面移动的轨迹称为该 系统的闭环根轨迹。
• 4.1.2
根轨迹方程
• 既然根轨迹是闭环特征根随参数变化的轨迹,
则描述其变化关系的闭环特征方程就是根轨 迹方程。 • 则根轨迹方程(系统闭环特征方程)为: (4.2)
第四章根轨迹法.

9
4.2.1 绘制根轨迹的基本法则 法则 1 根轨迹的分支数和对称性 : 1. 根轨迹对称于实轴(实数根或者复数根) 根轨迹对称于实轴(实数根或者复数根) 2. n阶系统有 条根轨迹 阶方程有 个确定的根,当根由始点 阶系统有n条根轨迹 阶方程有n个确定的根 阶系统有 条根轨迹(n阶方程有 个确定的根, 向终点移动时,必定形成一条根轨迹) 向终点移动时,必定形成一条根轨迹)
24
法则 8 根之和 : 当 n m ≥ 2 时 , 特征方程第二项系数与 K* 无关 , 无论 K* 取 何值 , 开环 n 个极点之和总是等于闭环特征方程 n 个根之和
∑s = ∑ p
i =1 i i =1
n
n
i
(4-25)
25
画出了几种常见的开环零, 在图 4-15 中 , 画出了几种常见的开环零,极点分布及其相应 的根轨迹 , 供绘制概略根轨迹时参考 .
3
4.1.1 根轨迹概念 一, 根轨迹概念 根轨迹简称根迹 , 它是开环系统某一参数从零变到无穷时 , 闭 环系统特征方程的根(闭环极点 在 环系统特征方程的根 闭环极点)在 s 平面上变化的轨迹 . 闭环极点 设控制系统如图4-1所示 设控制系统如图 所示 , 其 闭环传递函数为 C ( s) 2K φ ( s) = = 2 R( s ) s + 2 s + 2 K 显然 , 其特征根为 s1, 2 = 1 ± 1 2 K 其特征根变化如图4-2所示 令 K = 0 → ∞, 其特征根变化如图 所示 . "×"---------表示开环传递函数的极点 × 表示开环传递函数的极点 "°"---------表示开环传递函数的零点 表示开环传递函数的零点 箭头的指向-------表示 增大是根的移动方向 表示K增大是根的移动方向 箭头的指向 表示
第四章:根轨迹法

j=1
确定根轨迹上某点对应的K*值
闭环零、极点与开环零、极点的关系
比较开环传递函数与闭环传递函数:
G (s) H (s) K G K H
( S Z ) ( S Z
i i 1 q j 1 h i i 1 j 1
f
l
f l m j
) K
(S Z
j 1 i i 1
j
)
( S P ) ( S P )
j
qhn
(S P )
Φ(s)=
* KG ∏(s-zi ) ∏(s-pj )
i=1
j=1 * * ∏(s-pi ) ∏(s-pj ) + kG kH ∏(s-zi )∏(s-zj ) i=1 j=1 i=1 j=1 q h f l
相角条件:
m
根轨迹的模值条件与相角条件 n
∑∠(s-zj) -∑∠(s-pj) = (2k+1) π j=1 i=1
k=0, ±1,
±2, … m 绘制根轨迹的充要条件 i=1 m
模值条件:
1+K K = = -1 0 1 n (s ) ∏︱ -p︱
i=1
) ∏︱ - z︱ s -p ( s jn ∏︱ ︱ j=1 i * *
第四章:根轨迹法
教学目的
对于低阶控制系统,我们可以用求解微分方程方法来分析控制 系统,而对于高阶系统,用微分方程的方法求解就比较困难。根轨
迹方法是分析和设计线性定常控制系统的图解方法,使用起来比较
简便,因此在工程设计中获得了广泛应用。 通过本章内容学习,要使学生懂得根轨迹的概念,根轨迹的作 图方法,以及根轨迹与系统性能之间的关系。
自动控制原理第四章根轨迹法

第四章 根轨迹法
第一节 根轨迹与根轨迹方程 根轨迹 系统的某个参数(如开环增益K)由0到∞变化时, 闭环特征根在S平面上运动的轨迹。
例: GK(S)= K/[S(0.5S+1)] = 2K/[S(S+2)] GB(S)= 2K/(S2+2S+2K) 特征方程:S2+2S+2K = 0
-P1)(S-P2)…(S-Pn)
单击此处可添加副标题
当n>m时,只有m条根轨迹趋向于开环零点,还有(n-m)条? m,S→∞,有: (S-Z1)(S-Z2)…(S-Zm) -1 -1 ———————-— = —— = —— P1)(S-P2)…(S-Pn) K* AK 可写成:左边 = 1/Sn-m = 0 当K=∞时,右边 = 0 K=∞(终点)对应于S→∞(趋向无穷远). 即:有(n-m)条根轨迹终止于无穷远。
分解为:
03
例:GK(S)= K/[S(0.05S+1)(0.05S2+0.2S+1)] 试绘制根轨迹。 解: 化成标准形式: GK(S)= 400K/[S(S+20)(S2+4S+20)] = K*/[S(S+20)(S+2+j4)(S+2-j4)] K*=400K——根迹增益 P1=0,P2=-20,P3=-2+j4,P4=-2-j4 n=4,m=0
一点σa。
σa= Zi= Pi
ΣPi-ΣZi = (n-m)σa
σa= (ΣPi-ΣZi)/(n-m)
绘制根轨迹的基本法则
K*(S-Z1)(S-Z2)…(S-Zm)
—————————— = -1 (S-P1)(S-P2)…(S-Pn)
第四章 根轨迹法

nm
0 (1) (2) 30
1
a
(2k 1)
nm
、 、
33
例2
单 位 反 馈 系 统 的G ( s )
s(s2
K* 2s
2)
m
n
pk (2k 1) pk z j pk pi
j1
i 1
ik
p2
(2k
1)
0
2
3 4
4
n
m
σ a
pi zi
i1
i1
nm
j 1
i 1
ik
n
m
o终止角: zk (2k 1) (zk pi ) (zk z j )
i1
j1
jk
• 法则7: 分离点(会合点)坐标d:
o 几条根轨迹在[s]平面上相遇后又分开的点,称为分离点。
o 分离点的坐标d可由方程 dKg (s) 0
例3
D`(s)
N
(s)
N
`(
ds
s)D(s)
j
s1
0
s2
4.3 广义根轨迹
在负反馈系统中, K*变化时的根轨迹叫做常规根轨迹。其他情 况下的根轨迹称广义根轨迹。通常有参数根轨迹和零度根轨迹。
4.3.1 参数根轨迹
• 变化的参数不是开环根轨迹增益K*的根轨迹叫参数根轨迹。将
开环传函变形让变化的参数处于开环增益的位置就可以采用绘制常
规根轨迹时的法则。
1 G(s)H(s) 0即(s3 3s2 2s K* ) 0 s j
j 3 3 2 2j K* 0
ω 2,K * 6 • 开环增益为 K=K*/2 ,K的稳定域为 0<K<3 .
第4章 根轨迹法
m n
sk
s+
jω
s+p
s
j=1 n
=
1 ; K gk
−z j
z
j
i
αj
βi
σ
0
∑ α jk − ∑ βik = ±180 (1 + 2k) (k = 1, 2,⋯)
j=1 i =1
−p i
幅值条件为:
∏ s + zj ∏ s + pi
i =1 j=1 n
m
1 = Kg
幅角条件:
∑ α j − ∑ βi = ±180 (1 + 2k)
j=1 i =1
m
n
(k = 1, 2,⋯)
三、应用幅值条件确定 K g 值
jω
△
某控制系统的开环传递函数为
1 K g (s + ) K(8s + 1) 8 G(s)H(s) = 2 = s (2s + 1) s 2 (s + 1 ) 2
-0.5 L3
sk L 1,2 l 60° σ
1 8 1 p1 = − 2 z1 = −
可见,闭环零点由前向通道的零点和反馈通道的极点组成, 闭环零极点放大系数等于前向通道零极点放大系数 K Gg 。
一、根轨迹的连续性 第二节 绘制根轨迹的一般规则 二、根轨迹的分支数 三、根轨迹的对称性 四、根轨迹的起点和终点
m m
j=1 lim n s→∞ i =1
∏ s + zj ∏ s + pi
六、根轨迹的分离点和会合点
D(s) K g (s) = − N(s)
dK g (s) ds
=0
D' (s)N(s) − N ' (s)D(s) = 0
(自动控制)第四章:根轨迹法

动态性能:从根轨迹图可以分析出系统的工作状态,
如过阻尼状态、欠阻尼状态……
根轨迹增益、闭环零极点与开环零极点的关系 l f
* G(s)= KG
∏( s-p ) i i=1
f i i 1 H q
q
∏( s-z ) i i=1
;
l
j=1 * H (s)= KH h
f l m
∏(s-zj )
C(s)
C ( s) 2k 2 R ( s ) S 2 S 2k
特征方程(闭环):
S2+2s+2k=0
k s(0.5s+1)
特征根:s1,2= -1±√1-2k k=0时, s1=0, s2=-2
K:0 ~ ∞
0<k<0.5 时,两个负实根 ;若s1=-0.25, s2=? k=0.5 时,s1=s2=-1 0.5<k<∞时,s1,2=-1±j√2k-1 j
注意:一组根对应同一个K;
K一变,一组根变; K一停,一组根停;
-2
-1
0
由以上分析,s1、s2两条根轨迹反映了系统特征根随参 数k变化的规律,组成了系统的根轨迹。 1.二阶系统有两个特征根,它的根轨迹有两条分支; 一个n阶系统的根轨迹则应有n条分支。 2.k=0时的闭环极点,s1=0、s2=-2正好是开环传递函 数的两个极点,因此说,系统开环极点就是它各条根轨 迹的起点。 3. k=∞时的闭环极点,是根轨迹的终点。 4.特征方程的重根点是根轨迹的分支离开负实轴进入复 数平面的分支点。
a.系统响应单调上升(ξ>1)系统具有两个不相等的负实根┈ 过阻尼响应。 b.系统响应衰减振荡(0<ξ<1)系统具有一对负实部的共 轭复根┈欠阻尼响应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 根轨迹法4-1 根轨迹的基本概念一. 根轨迹概念:闭环系统的动态性能与闭环极点在s 平面上的位置密切相关,系统的闭环极点也就是特征方程式的根.当系统的某一个或某些参量变化时,特征方程的根在s 平面上运动的轨迹称为根轨迹.根轨迹法: 直接由开环传递函数求取闭环特征根的方法.例: 设控制系统如图4-1所示()()15.0+=s s Ks G()()2220+=+=s s K s s K ,开环极点: 01=p , 22-=p ()()()0202K s s K s R s C s ++==Φ;式中K K 20= 此系统的特征方程式可写为:()02,1121102K s K s s s -±-=⇒=++=∆ 讨论: 200210-===s s K ,时,111210-=-==s s K ,时, j s j s K --=+-==112210,时, ∞--=∞+-=∞=j s j s K 11210,时,令k 为0 ∞.可以用解析的方法求出闭环极点的全部数值,将这些数值图4-1 控制系统的结构图R (s )C (s )K s(0.5s+1)标住在S 平面上,并连成光滑的粗实线,如图4-2所示。
图上,粗实线就称为系统的根轨迹。
分析:1.0K 变化时,根轨迹均位于左半s 平面,系统恒稳定.2.根轨迹有两条,两个起点2,021-==s s3.100<<K 时,闭环特征根为负实根,呈过阻尼状态.4.10=K 时,闭环特征根为一对重根,响应为单调上升的指数曲线.5.10>K 时,闭环特征根为共轭复根,响应为衰减振荡.6.开环增益K 可有根轨迹上对应的0K 值求得.0K 为可变参量绘制的根轨迹,称为常规根轨迹.二、根轨迹的幅值条件和相角条件设单闭环控制系统框图如图:通常有两种表示形式: A .时间常数形式:∏∏==++=ni imj j s T s K s H s G 11)1()1()()(τ图4-3 控制系统的结构图R (s )C (s )H(S)G(S)B .零、极点形式:∏∏==--=ni imj j p s z s K s H s G 110)()()()(则,系统特征方程:1+G(s)H(s)=0 ⇒ G(s)H(s)= -1 ⇒ 幅值条件: |G(s)H(s)|=1相角条件: ∠G(s)H(s)=±(2k+1)π, k=0,1,2,…考虑开环传递函数一般形式:∏∏==--=ni imj j p s z s K s H s G 110)()()()( ,因此幅值条件:1||||110=--∏∏==ni imj j ps z s K 或 ∏∏==--=mj jni izs p s K 110||||相角条件:)()(11∑∑==-∠--∠mj ni j jp s zs =±(2q+1)π, q=0,1,2,…说明:幅值条件与K 0有关,而相角条件与K 0无关。
因此,凡能满足相角条件的点必然满足幅值条件;而满足幅值条件的点不一定满足相角条件!因此,绘制根轨迹的一般步骤是:先找出S 平面上满足相角条件的点,并把它们连成曲线;然后根据实际需要,用幅值条件确定相关点对应的K 值。
例子:P107,例4-1。
4-2 绘制根轨迹的基本规则闭环特征方程:1)()(110-=--∏∏==ni imj j p s z s K上式表明了系统闭环极点和开环零、极点的关系。
基于这种关系,就可以根据开环零、极点的分布确定闭环极点的位置了。
根轨迹是根据系统的开环零、极点去绘制的。
在下面的讨论中,假定所研究的变化是根轨迹增益值K 0,但是当可变参数为系统的其他参数时,这些基本法则仍然适用。
这些基本法则绘出的根轨迹,其相角遵循 1800+2k π条件的称为1800 根轨迹;其相角遵循00+2k π条件的,称为00 根轨迹。
规则1:(对称性法则)根轨迹对称于S 平面的实轴。
规则2:根轨迹的分支数、根轨迹的起点和终点:分支数等于特征方程的阶数,为n 条;根轨从n 个开环极点出发,其中m 条终于开环零点,(n-m)条终点在无穷远处。
∏∏==--=mj jini zs p s K 110||||, K 0=0为根轨迹的起点 s = p i∏∏==--=n i imj jps zs K 110||||1, K 0→∞为根轨迹的终点j 或s →∞规则3:根轨迹在实轴上分布:实轴上某线段右边的实零点和实极点总数为奇数时, 这些线段就是根轨迹的部分。
规则4:根轨迹的渐进线n-m 条趋向无穷远的根轨迹可由渐进线决定:渐进线的倾角为: ,2,1,0)12(=-+±=q mn q a πϕ渐进线与实轴的交点为:开环零点数开环极点数开环零点的实部之和开环极点的实部之和--=--=∑∑==mn zp n i mj ji a 11σ例1:设控制系统的开环传递函数为)22)(3()2(3)()(2++++=s s s s s K s H s G ,求渐进线和与实轴的交点。
解 (1)系统的开环极点为0,-3,(-1+j )和(-1-j ),它们是根轨迹上各分支的起点。
共有四条根轨迹分支。
有一条根轨迹分支终止在有限开环零点-2,其它三条根轨迹分支将趋向于无穷远处。
(2)确定根轨迹的渐近线 渐近线的倾斜角为14180)12()12(-︒⨯+=-+=q m n q a πϕ 取式中的q =0,1,2,得φa =π/3,π,5π/3,或±60°及-180°。
渐近线与实轴的交点为114)2()1130(111-=-----+--=⎥⎦⎤⎢⎣⎡--=∑∑==j j z p m n m i i nj j a σ规则5:根轨迹的分离点、会合点、分离角:两条以上根轨迹的交点。
分离点和会合点必须满足方程00=dsdK ----必要条件 分离角----根轨迹离开重极点处的切线与实轴正方向的夹角分离角=rq π)12(+ , r 为重根数,q=0,1,2… 例2:已知控制系统的开环传递函数为)164)(1()1()()(20++-+=s s s s s K s H s G ,确定根轨迹的分离点。
解 :系统的特征方程式为:0)1()164)(1(02=++++-s K s s s s即:1)164)(1(20+++--=s s s s s K利用0/0=ds dK ,则有0)1(16242110322340=+-+++-=s s s s s ds dK 解之可得,分离点d 1=0.46 和 d 2=-2.22。
规则6:根轨迹的出射角和入射角:出射角:从复数极点出发的角度。
入射角:到达复数零点的角度。
P116, 图4-13:取靠近4P 的点i s ,由相角条件:()()()()()() ,,,,2101243211=+=-∠--∠--∠--∠--∠q q p s p s p s p s z s i i i i i π 4p s i →时,则:()()()()()()143424144412z p p p p p p p q p s i p -∠+-∠--∠--∠-+=-∠=πθ一般情况,出射角:()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-∠--∠+=∑∑≠==nk i i i k m j j k pkp p z p 11πθ同理,入射角:()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-∠--∠-=∑∑=≠=ni i k m k j j j k zkp z z z 11πθ规则7:根轨迹与虚轴的交点两种方法: (1).用劳斯判据求(2).将ωj s =带入特征方程求解例3:设系统的开环传递函数为:)2)(1(2)()(++=s s s Ks H s G ,试绘制系统的根轨迹。
解 根据绘制根轨迹的法则,先确定根轨迹上的一些特殊点,然后绘制其根轨迹图。
(1)系统的开环极点为0,1-,2-是根轨迹各分支的起点。
由于系统没有有限开环零点,三条根轨迹分支均趋向于无穷远处。
(2)系统的根轨迹有3=-m n 条渐进线渐进线的倾斜角为3180)12()12(-︒⨯+=-+=q m n q a πϕ 取式中的q =0,1,2,得φa =π/3,π,5π/3。
渐进线与实轴的交点为: 13)210(111-=--=⎥⎦⎤⎢⎣⎡--=∑∑==m i i nj j a z p m n σ 三条渐近线如图4-13中的虚线所示。
(3)实轴上的根轨迹位于原点与-1点之间以及-2点的左边,如图的粗实线所示。
(4)确定分离点: 系统的特征方程式为:022323=+++K s s s即:)23(2123s s s K ++-= 利用0/=ds dK ,则有:0)26(2123=++-=s s ds dK解得:423.01-=s 和 577.12-=s由于在-1到-2之间的实轴上没有根轨迹,故s 2=-1.577显然不是所要求的分离点。
因此,两个极点之间的分离点应为s 1=-0.423。
(5)确定根轨迹与虚轴的交点 方法一 利用劳斯判据确定劳斯行列表为 3s 1 2 2s32K 1s326K-s2K由劳斯判据,系统稳定时K 的极限值为3。
相应于K =3的频率可由辅助方程0632322=+=+s K s 确定。
解之得根轨迹与虚轴的交点为2j s ±=。
根轨迹与虚轴交点处的频率为41.12±=±=ω方法二 令ωj s =代入特征方程式,可得:02)(2)(3)(23=+++K j j j ωωω 即:0)2()32(22=-+-ωωωj K令上述方程中的实部和虚部分别等于零,即:0322=-ωK ,022=-ωω 所以 :2±=ω 3=K 系统的根轨迹如图所示:规则8:闭环极点的和与积.系统特征方程(n>m 时)为 闭环极点的和:()开环极点之和和∑==ni i p 1闭环极点的积:()()∏∏==+=mj i ni i z K p 101积可利用此性质判闭环极点i s 的分布情况 一些i s 变化后,另一些i s 会做相反变化.例4:在例3中,确定根轨迹各分支上每一点的K 值S 平面σωj根据绘制根轨迹的基本法则,当从开环极点0与-1出发的两条根轨迹分支向右运动时,从另一极点-2出发的根轨迹分支一定向左移动。
当前两条根轨迹分支和虚轴在K =3处相交时,可按式3)41.10()41.10(-=-+++j j x σ(开环极点0,-1,-2之和;即和为定值)求出后一条根轨迹分支上K =3的点为οx =-3。
由(4)知,前两条根轨迹分支离开实轴时的相应根值为-0.423±j 0。
因此,后一条根轨迹分支的相应点为3)423.0()423.0(-=-+-+x σ所以 ,οx =-2.154。
