2016年小升初复习试卷：长方体与正方体

合集下载

小学数学-有答案-小升初综合练习题：长方体正方体表面积

小升初综合练习题：长方体正方体表面积一、填空：（38%，每空2分）1. 长方体和正方体都有________个面，________条棱，________个顶点。

2. 长方体的每个面都是________形或有一组对面是________．它有________条棱，平行的________条棱都相等。

3. 相交于长方体一个顶点的三条棱的长度分别叫做它的________、________和________．4. 长方体有________个面，从不同的角度观察一个长方体，最多能看到________个面。

5. 一个长方体的长是5分米，宽是4分米，高是3分米，6个面中最小的一个面的面积是________，最大的一个面的面积是________．6. 一个长方体长4米，宽3米，高2米，它的占地面积最大是________平方米。

7. 一个长方体模型，从前面看是从上面看是，长方体右面的面积是________平方厘米。

8. 长方体的右侧面面积是12平方厘米，前面面积是8平方厘米，上面面积是6平方厘米，这个长方体的长、宽、高分别是________、________、________．二、选择（8%，每题2分）：一个长方体水池，长20米，宽10米，深2米，占地（）平方米。

A.200B.400C.520下面的图形中，能按虚线折成正方体的是（）A. B. C. D.从一个体积是30立方厘米的长方体木块中，挖掉一小块后（如图），它的表面积（）A.和原来同样大B.比原来小C.比原来大D.无法判断用一根52厘米长的铅丝，正好可以焊成长6厘米，宽4厘米，高（）厘米的长方体教具。

A.2B.3C.4D.5三、解答题（共1小题，满分6分）计算下面每个形体的棱长和。

下面各题，列式计算，不写答．一个长方体，长5分米，宽3分米，高4分米，求它的所有棱长的和。

用钢筋做一个长和宽都是3.5分米，高是10厘米的长方体，需多少分米的钢筋？棱长是4分米的正方体，棱长总和是多少分米？一个长方体的棱长和是36厘米，从一个顶点出发的三条棱的长度和是________厘米。

小学数学-有答案-小升初总复习数学专项练习试卷：长方体和正方体(3)

小升初总复习数学专项练习试卷：长方体和正方体（3）一、填空1.2. 一个正方体的棱长和是12分米，它的体积是________立方分米。

3. 一个长方体的体积是30立方厘米，长是5厘米，高是3厘米，宽是________厘米。

4. 一个长方体的底面积是0.2平方米，高是8分米，它的体积是________立方分米。

5. 一个表面积是54平方厘米的正方体，它的体积是________立方厘米。

（先算出棱长，再计算体积）6. 正方体的棱长缩小3倍，它的体积就缩小________倍。

7. 一个长方体框架长8厘米，宽6厘米，高4厘米，做这个框架共要________厘米铁丝，是求长方体________，在表面贴上塑料板，共要________塑料板是求________，在里面能盛________升水是求________，这个盒子有________立方米是求________．8. 长方体的长是6厘米，宽是4厘米，高是2厘米，它的棱长总和是________厘米，六个面中最大的面积是________平方厘米，表面积是________平方厘米，体积是________立方厘米。

二、判断（对的在括号里面打“√”，错的打“×”）体积单位比面积单位大，面积单位比长度单位大。

________（判断对错）正方体和长方体的体积都可以用底面积乘以高来进行计算。

________．（判断对错）表面积相等的两个长方体，它们的体积一定相等。

________（判断对错）长方体的体积就是长方体的容积________（判断对错）如果一个长方体能锯成四个完全一样的正方体，那么长方体前面的面积是底面积的4倍。

________．（判断对错）三、选择题。

正方体棱长扩大2倍，体积扩大（）倍。

A.2倍B.4倍C.6倍D.8倍一根长方体木料，长1.5米，宽和厚都是2分米，把它锯成4段，表面积最少增加（）平方分米。

A.8B.16C.24D.32一个长方体的长、宽、高都扩大2倍，它的体积扩大（）倍。

六年级下册数学试题-小升初复习讲练：长方体和正方体的表面积(含答案)sc

长方体和正方体的表面积典题探究例1．一个正方体的棱长总和是24米，它的表面积是24平方米．．例2．棱长为6cm的正方体的体积和表面积相等．．（判断对错）例3．一个正方体棱长扩大2倍，则表面积扩大倍，体积扩大倍．例4．一个长方体的棱长总和是108厘米，它的长、宽、高的比为4：3：2，这个长方体的表面积是．例5．一块长方形铁皮（如图），长25厘米，宽15厘米，从四个角分别剪去边长2厘米的小正方形，然后把四周折起来，做成没有盖子的铁盒，请你帮忙计算一下：做这样一个盒子至少需要多少铁皮？铁盒的容积是多少？演练方阵A档（巩固专练）一．选择题（共15小题）1．一个正方体油桶的底面积是9平方厘米，它的表面积是（）A．81cm2B．18cm2C．54cm22．一个正方体的棱长是5厘米，它的表面积是（）A．25平方厘米B．200平方厘米C．125立方厘米D．150平方厘米3．东东从拼好的长方体中拿走了一块（如图），它的表面积（）A．比原来大B．比原来小C．不变4．一根长方体木料，长是8分米，宽是2分米，高是4分米，这根长方体木料的表面积是（）平方分米．A．64 B．56 C．1125．把三个棱长是1cm的正方体拼成一个长方体，表面积减少了（）cm2．A．2B．4C．6D．86．一个长方体水池，长20米，宽10米，深2米，占地（）平方米．A．200 B．400 C．5207．把正方体的棱长扩大4倍，它的表面积扩大（）A．4倍B．8倍C．12倍D．16倍8．（•高邮市）有两盒滋补品，用下面三种方式包装，你认为最省包装纸的是（）A．B．C．9．（•江都市）如图上画了长方体的长、宽、高，这个长方体左面的面积是（）A．15平方厘米B．12平方厘米C．20平方厘米D．无法确定10．（•淳安县）一个棱长2厘米的正方体，挖掉一个棱长1厘米的小正方体后（如图），它的表面积（）A．增大了B．减少了C．不变D．无法断定11．（•恭城县）棱长是6cm的正方体，它的体积和表面积相比（）A．体积大B．表面积大C．一样大D．无法比较12．（•张家港市）把2个棱长4厘米的正方体木块粘合成一个长方体，这个长方体的表面积是（）A．160平方厘米B．128平方厘米C．192平方厘米D．172平方厘米13．（•靖江市）棱长是a米的正方体，它的表面积是（）平方米．A．12a B．a3C．6a2D．a214．（•新邵县）一个正方体的棱长是a分米，它的表面积是（）平方分米．A．a2B．4a2C．6a215．（•雁江区）两块同样的肥皂用三种包装，第（）种包装更省包装纸．A．B．C．二．填空题（共13小题）16．把底面积为25平方厘米的两个相同的正方体，拼成一个长方体，则长方体的表面积是_________平方厘米．17．用铁皮做一个无盖的长方体油箱，要求做一个油箱至少需要多少铁皮，是求油箱的_________，要求油箱能装多少升汽油，是求油箱的_________A、表面积B、底面积C、体积D、容积．18．一个底面半径2cm，高10cm的圆柱的表面积是_________平方厘米．19．一个长方体它的底面是正方形，面积是25平方厘米，它的一个侧面的面积是30平方厘米．这个长方体的表面积是_________平方厘米．20．一个棱长为9分米的正方体的表面积是_________平方分米，把它削成一个最大的圆锥，体积是_________立方厘米．21．正方体棱长总和是24厘米，它的表面积是_________，体积是_________．22．鲜奶盒长6.3厘米，宽4厘米，高10.5厘米．将24盒鲜奶盒包装成一箱，纸箱使用的纸最少是_________平方厘米．23．（•温江区模拟）把两个棱长是2厘米的正方体拼成一个长方体，则长方体的表面积是_________平方厘米．24．（•岚山区模拟）把表面积是54平方厘米的正方体等分成两个长方体，每个长方体的表面积是_________．25．一个正方体木块的棱长为a厘米，把它锯成两个长方体，这两个长方体的棱长总和是_________厘米，表面积总和是_________平方厘米．26．（•北京）一个正方体的棱长为acm，它的棱长总和是_________，它的表面积是_________，它的体积是_________．27．（•满洲里市）在一个长方体中（如图）知道了后面的面积大小还要知道_________的长度，就可以求体积了；同样知道了横截面积，还知道_________的长度，也可以求体积．如果告诉你这个长方体是一个玻璃鱼缸，长是8分米、宽是5分米、高是5分米，那么这个玻璃鱼缸的棱长之和是_________分米，而且做这个鱼缸至少需要_________平方分米的玻璃材料，另外如果在这个鱼缸内放入3分米高的水，这些水有_________升；再放入几条金鱼后水面上升1.2厘米，这些金鱼的体积是_________立方厘米．28．（•静宁县模拟）一个正方体的棱长总和48厘米，它的棱长是_________，表面积是_________，体积是_________．B档（提升精练）一．选择题（共15小题）1．（•岚山区模拟）把一个棱长为a的正方体，任意截成两个长方体，这两个长方体表面积之积是（）A．a×a×6 B．a×a×7 C．a×a×8 D．无法确定2．（•陆良县）如图是一个长3厘米，宽与高都是2厘米的长方体，在它的上面挖掉一个棱长为1厘米的小正方体，这时它的表面积是（）平方厘米．A．32 B．34 C．不能计算3．（•上海）如图中两个物体的表面积比较，结果是（）A．甲＞乙B．甲＜乙C．甲=乙4．（•团风县模拟）一根长方体木料，长2米，宽和厚都是5米，把它锯成1米长的两段，表面积增加了（）平方米．A．50 B．40 C．255．（•中山模拟）把一个正方体的棱长扩大20%，它的表面积就扩大（）A．20% B．40% C．44% D．120%6．（•宜宾县模拟）一个正方体的棱长为1dm，它的表面积是（）A．1 dm2B．1000 dm2C．6 dm27．（•广元模拟）二个同样大小的正方体，组成一个新长方体，表面积是40平方厘米，求一个正方体的表面积（）A．22平方厘米B．24平方厘米C．36平方厘米8．（•宜昌）如图，将一个大正方体，从它的一个顶点处挖去一个小正方体后，剩下物体的表面积和原来的表面积相比较，（）A．变大B．变小C．不变D．无法确定9．（•云阳县）用8个1立方厘米的小方块拼成一个较大正方体，如果拿去一个小方块（如图），它的表面积与拼成的较大正方体的表面积比较（）A．一样大B．减少了C．增大了10．（•顺德区）一个长方体，把它切成3个正方体，一个小正方形的表面积是24平方厘米．原来长方体的表面积是（）A．24平方厘米B．48平方厘米C．56平方厘米D．72平方厘米11．（•芜湖县）把一个棱长为a米的正方体，任意截成两个长方体，这两个长方体的表面积是（）平方米．A．6a2B．8a2C．10a2D．12a212．（•顺德区）把3个棱长为10分米的正方体拼成一个长方体，表面积会减少（）A．200平方分米B．300平方分米C．400平方分米D．600平方分米13．（•湖南模拟）把一个棱长为a的正方体，切成两个长方体表面积为（）A．5a2B．6a2C．7a2D．8a214．（•武胜县）用同样的铝皮制作三个无盖的容器（如图），不计损耗，需要铝皮最少的是（）（单位：厘米）A．B．C．15．（•抚州模拟）在棱长1分米的正方体的一角，挖去一个棱长3cm的小正方体，那么，剩下的部分的表面积与原正方体的表面积相比（）A．比原来大B．比原来小C．一样二．填空题（共13小题）16．（•江岸区）长方体的长、宽、高分别是7cm、6cm、3cm，它的表面积是_________ cm2．17．（•广州模拟）一根长方体的木料，正好可以锯成两个同样的正方体，这时表面积增加了24平方厘米，这根长方体的木料原来的表面积是_________平方厘米．18．（•海曙区）把一个棱长是a厘米的正方体任意截成两个长方体，这两个长方体表面积之和是6a2平方厘米．_________（判断对错）19．（•宿城区模拟）一个正方体的棱长之和是36厘米，它的表面积是_________平方厘米，体积是_________立方厘米．20．（•西安）一个长方体如图，它后面的面的面积是_________dm2，左面的面的面积是_________dm2，顶面的面的面积是_________dm2，这个长方体所占的空间是_________dm3．21．（•陕西）用12个棱长1厘米的小正方体拼成一个长3厘米、宽与高都是2厘米的大长方体，再将它去掉一个小正方体（如图所示），现在它的表面积是_________平方厘米．22．（•临川区模拟）一根长48分米的铁丝做成一个长方体框架，长、宽、高的比为1：2：3，如果用纸把框糊成一个长方体模型，至少需要纸_________平方分米．23．（•上海模拟）图中表示的小正方体的表面积为54平方米，则如图中用8个这样的小正方体组成的正方体的表面积是_________平方米．24．（•东兰县模拟）大小两个正方体的棱长比是3：2；大小正方体的表面积比是_________；大小正方体的体积比是_________．25．（•广州模拟）一个棱长2厘米的正方体橡皮泥，在它的顶点挖去一个棱长1厘米的小正方体后，表面积是原来的_________%，体积是原来的_________%．26．（•孝感模拟）用一根36厘米长的铁丝焊成一个最大的正方形模型，它的表面积好是_________体积是_________．27．（•道里区模拟）把两个一样的正方体拼成一个长方体后，体积和表面积都不变．_________．（判断对错）28．（•无锡）一个长方体的长和宽都是20厘米，高6厘米．这个长方体的表面积是_________平方厘米，体积是_________立方厘米，做这个长方体框架至少要_________厘米长的铁丝．C档（跨越导练）一．填空题（共3小题）1．（•天门）如图所示，把底面周长12.56厘米，高10厘米的圆柱切成若干等分，拼成一个近似的长方体，这个长方体的表面积是_________平方厘米，体积是_________立方厘米．2．（•商州区）一个棱长为6分米的正方体木块的表面积是_________平方分米，把它切削成一个最大的圆锥体，这个圆锥体的体积是_________立方分米．3．（•北京模拟）一个长方体，如果高增加2厘米就成了正方体，而且表面积要增加56平方厘米，原来这个长方体的体积是_________．二．解答题（共3小题）4．（•商州区）棱长是6分米的正方体的体积和表面积相等．_________．（判断对错）5．（•秀屿区）6月1日，全国“限塑令”正式实施一周年．实验小学六年一班学生准备到超市和菜场向顾客赠送自制环保袋．（1）这种环保袋是一个长方体，它的长40厘米，宽10厘米，高50厘米，制作这样的一只环保袋需要多少平方厘米的环保纸？（接头处忽略不计）（2）为确保能在6月1日前完成1500只环保袋，同学们“五一”节过后（5月4日）就开始动工．前7天制作了420只，照这样的速度，能按期完成吗？（用比例解）（3）六（1）班同学把这1500只环保袋按2：3分配给第一、二两个小分队，第二小分队领到多少任务？如果第二小分队有15个同学，他们平均每人要送出几只环保袋？6．（•重庆）有一个长方体，如右图，（单位：厘米）现将它“切成”完全一样的三个长方体．（1）共有_________种切法．（2）怎样切，使切成三块后的长方体的表面积的和比原来长方体的表面积增加得最多，算一算表面积最多增加了多少？长方体和正方体的表面积答案典题探究例1．一个正方体的棱长总和是24米，它的表面积是24平方米．正确．考点：长方体和正方体的表面积．分析：根据题意可得出正方体的棱长为24÷12=2米，有表面积公式计算可得出结论．解答：解：24÷12=2（米），2×2×6=24（平方米），所以原题说法正确．故答案为：正确．点评：此题考查了正方体的表面积公式的应用，可以先借助公式计算出正确答案，再进行判断．例2．棱长为6cm的正方体的体积和表面积相等．错误．（判断对错）考点：长方体和正方体的表面积；长方体和正方体的体积．专题：立体图形的认识与计算．分析：根据正方体的表面积公式：s=6a2，正方体的体积公式：v=a3，因为表面积和体积不是同类量，无法进行比较．由此解答．解答：解：表面积：6×6×6=216（平方厘米）；体积：6×6×6=216（立方厘米）；因为表面积和体积不是同类量，无法进行比较．故答案为：错误．点评：此题解答关键是明确：只有同类量才能进行比较大小，不是同类量无法进行比较．例3．一个正方体棱长扩大2倍，则表面积扩大4倍，体积扩大8倍．考点：长方体和正方体的表面积；长方体和正方体的体积．分析：根据正方体表面积扩大的倍数是棱长扩大倍数的平方，体积扩大的倍数是棱长扩大倍数的立方求解即可．解答：解：一个正方体棱长扩大2倍，则表面积扩大2×2=4倍，体积扩大2×2×2=8倍．故答案为：4，8．点评：考查了正方体的体积，正方体的表面积和正方体棱长的关系，是基础题型，比较简单．例4．一个长方体的棱长总和是108厘米，它的长、宽、高的比为4：3：2，这个长方体的表面积是468平方厘米．考点：长方体和正方体的表面积；按比例分配应用题．分析：根据长方体的特征，12条棱分为互相平行的3组，每组4条棱的长度相等，6个面都是长方形（特殊情况有两个相对的面是正方形），相对的面的面积相等；已知一个长方体的棱长总和是108厘米，它的长、宽、高之比是4：3：2，首先根据按比例分配的方法分别求出长、宽、高；再根据长方体的表面积公式解答．解答：解：4+3+2=9（份），长：108÷4×=27×=12（厘米），宽：108÷4×=27×=9（厘米），高：108÷4×=27×=6（厘米）；表面积：（12×9+12×6+9×6）×2，=（108+72+54）×2，=234×2，=468（平方厘米）；答：这个长方体的表面积是468平方厘米．故答案为：468平方厘米．点评：此题主要考查长方体的特征和表面积的计算，以及了解和掌握长方体的表面积公式：S=2（ab+ah+bh）；解题的关键是根据按比例分配的方法求出长、宽、高．例5．一块长方形铁皮（如图），长25厘米，宽15厘米，从四个角分别剪去边长2厘米的小正方形，然后把四周折起来，做成没有盖子的铁盒，请你帮忙计算一下：做这样一个盒子至少需要多少铁皮？铁盒的容积是多少？考点：长方体和正方体的表面积；长方体和正方体的体积．专题：压轴题．分析：求做这样一个盒子至少需要多少铁皮，用长方形铁皮的面积减去四个边长2厘米的正方形的面积；计算铁盒的容积，需要求出盒子的长、宽，长方形铁皮的长、宽都要减去两个2厘米即是盒子的长、宽，高是2厘米．根据长方体的容积公式解答．解答：解；25×15﹣2×2×4，=375﹣16，=359（平方厘米）；（25﹣2﹣2）×（15﹣2﹣2）×2，=21×11×2，=462（立方厘米）；答：做这样一个盒子至少需要359平方厘米铁皮，铁盒的容积是462立方厘米．点评：此题这样考查长方体的表面积和体积的计算，在计算长方体的表面积的时候，一定要分清求几个面的面积，根据公式解答即可．演练方阵A档（巩固专练）一．选择题（共15小题）1．一个正方体油桶的底面积是9平方厘米，它的表面积是（）A．81cm2B．18cm2C．54cm2考点：长方体和正方体的表面积．专题：立体图形的认识与计算．分析：根据正方体的表面积公式：s=6a2，用正方体的底面积乘6即可．解答：解：9×6=54（平方厘米），答：它的表面积是54平方厘米．故选：C．点评：此题主要考查正方体的表面积公式的灵活运用．2．一个正方体的棱长是5厘米，它的表面积是（）A．25平方厘米B．200平方厘米C．125立方厘米D．150平方厘米考点：长方体和正方体的表面积．专题：立体图形的认识与计算．分析：正方体的表面积=棱长×棱长×6，正方体的棱长已知，代入公式即可求解．解答：解：5×5×6=25×6=150（平方厘米）；答：正方体的表面积是150平方厘米．故选：D．点评：此题主要考查正方体表面积的计算方法．3．东东从拼好的长方体中拿走了一块（如图），它的表面积（）A．比原来大B．比原来小C．不变考点：长方体和正方体的表面积．专题：立体图形的认识与计算．分析：据此即可解答问题．从正方体顶点处拿掉一个小正方体，减少三个面的同时又增加三个面，所以表面积不变；据此解答．解答：解：从正方体顶点处拿掉一个小正方体，减少三个面的同时又增加三个面，所以表面积不变．故选：C．点评：该题主要考查正方体的表面积和立方体的切拼问题．4．一根长方体木料，长是8分米，宽是2分米，高是4分米，这根长方体木料的表面积是（）平方分米．A．64 B．56 C．112考点：长方体和正方体的表面积．分析：根据长方体的表面积公式计算即可求得这根长方体木料的表面积．解答：解：（8×2+8×4+2×4）×2，=（16+32+8）×2，=56×2，=112（平方分米）；答：这根长方体木料的表面积是112平方分米．故选：C．点评：考此题查了长方体的表面积，长方体的表面积公式：S=2（ab+ah+bh），是基础题．5．把三个棱长是1cm的正方体拼成一个长方体，表面积减少了（）cm2．A．2B．4C．6D．8考点：长方体和正方体的表面积．专题：立体图形的认识与计算．分析：由题意可知：三个棱长都是1cm的正方体拼成一个长方体后，减少了4个面，每个面的面积可求，从而可以求出减少的面积．解答：解：1×1×4=4（平方厘米）答：表面积减少了4平方厘米．故选：B．点评：解答此题的关键是明白：三个棱长都是1cm的正方体拼成一个长方体后，减少了4个面．6．一个长方体水池，长20米，宽10米，深2米，占地（）平方米．A．200 B．400 C．520考点：长方体和正方体的表面积．专题：压轴题．分析：求占地面积也就是求长方体的底面积，利用长方形的面积公式计算．解答：解：20×10=200（平方米）；答：占地200平方米．故选：A．点评：此题考查的目的是理解水池的占地面积，实际就是求长方体的底面积，根据长方形的面积公式计算解答．7．把正方体的棱长扩大4倍，它的表面积扩大（）A．4倍B．8倍C．12倍D．16倍考点：长方体和正方体的表面积．分析：根据正方体的表面积的计算方法，正方体的表面积=棱长×棱长×6，再根据积的变化规律，积扩大的倍数等于因数扩大倍数的乘积；由此解答．解答：解：根据积的变化规律，把正方体的棱长扩大4倍，它的表面积扩大：4×4=16倍；故选：D．点评：此题主要根据正方体的表面积的计算方法和积的变化规律解决问题．8．（•高邮市）有两盒滋补品，用下面三种方式包装，你认为最省包装纸的是（）A．B．C．考点：长方体和正方体的表面积．专题：压轴题．分析：由题意可知，哪种方式包装的表面积最小，则最省包装纸．解答：解：假设每盒滋补品三种面的面积分别为1、2、3，则A的表面积=3×4+2×2+1×4=20；B的表面积=3×2+2×4+1×4=18；C的表面积=3×4+2×4+1×2=22；所以B种包装最省包装纸．故选：B．点评：解答此题的关键是，看哪种方式包装的表面积最小，则最省包装纸．9．（•江都市）如图上画了长方体的长、宽、高，这个长方体左面的面积是（）A．15平方厘米B．12平方厘米C．20平方厘米D．无法确定考点：长方体和正方体的表面积．专题：压轴题．分析：由图意可知：左面的长和宽分别为4厘米和3厘米，于是利用长方形的面积公式即可求解．解答：解：4×3=12（平方厘米），故选：B．点评：弄清楚左面的长和宽是正确解答本题的关键．10．（•淳安县）一个棱长2厘米的正方体，挖掉一个棱长1厘米的小正方体后（如图），它的表面积（）A．增大了B．减少了C．不变D．无法断定考点：长方体和正方体的表面积．专题：立体图形的认识与计算．分析：根据正方体的特征，6个面都是正方形，6个面的面积都相等，正方体的表面积=棱长×棱长×6；从一个棱长2厘米的正方体，挖掉一个棱长1厘米的小正方体，因为这个小正方体在顶点上，有3个1平方厘米的把外露，挖掉一个棱长1厘米的小正方体后，又露出与原来相同的3个面，所以表面积不变．解答：解：2×2×6=24（平方厘米）；答：它的表面积不变，还是24平方厘米．故选：C．点评：此题考查的目的是使学生理解掌握正方体的特征及表面积的计算方法．11．（•恭城县）棱长是6cm的正方体，它的体积和表面积相比（）A．体积大B．表面积大C．一样大D．无法比较考点：长方体和正方体的表面积；长方体和正方体的体积．分析：根据体积和表面积的意义进行解答，进而得出结论．解答：解：体积和表面积的意义不同：正方体的体积是正方体所占空间的大小，它的单位是立方米、立方分米、立方厘米；而表面积是指正方体六个面的总面积，它的单位是平方米、平方分米、平方厘米；所以棱长是6cm的正方体，它的体积和表面积没有可比行，无法比较；故选：D．点评：解答此题应根据体积和表面积的意义进行分析即可．12．（•张家港市）把2个棱长4厘米的正方体木块粘合成一个长方体，这个长方体的表面积是（）A．160平方厘米B．128平方厘米C．192平方厘米D．172平方厘米考点：长方体和正方体的表面积．分析：由“把2个棱长4厘米的正方体木块粘合成一个长方体”可知，两个正方体共有12个面，粘合成长方体后，减少了2个面，即还剩10个面，求这10个面的面积就是长方体的表面积．解答：解：4×4×10=160（平方厘米）；故答案为：A．点评：解答此题的关键是明白，粘合成长方体后，减少了2个面，即还剩10个面．13．（•靖江市）棱长是a米的正方体，它的表面积是（）平方米．A．12a B．a3C．6a2D．a2考点：长方体和正方体的表面积．专题：立体图形的认识与计算．分析：根据正方体的特征：它的6个面是完全相同的正方形．由正方体的表面积公式：s=6a2，据此解答．解答：解：棱长是a米的正方形，它的表面积是6a2平方米；故选：C．点评：此题考查的目的是掌握正方体的特征和表面积的计算方法．14．（•新邵县）一个正方体的棱长是a分米，它的表面积是（）平方分米．A．a2B．4a2C．6a2考点：长方体和正方体的表面积．分析：正方体的表面积=棱长×棱长×6，由此可以解决问题．解答：解：正方体的表面积=a×a×6=6a2；故答案为：C．点评：此题考查了正方体表面积公式的应用．15．（•雁江区）两块同样的肥皂用三种包装，第（）种包装更省包装纸．A．B．C．考点：长方体和正方体的表面积．分析：根据把两个相同的长方体拼成一个大长方体，表面积都减少两个面，求哪种包装最省包装纸，只要减少两个最大的面（两个最大的面重合）即可．解答：解：由分析知，求哪种包装最省包装纸，只要减少两个最大的面（两个最大的面重合）即可；由图可知A种包装最省纸；故选：A．点评：解答此题要明确：把两个相同的长方体拼成一个大长方体，表面积减少了两个面的面积．二．填空题（共13小题）16．把底面积为25平方厘米的两个相同的正方体，拼成一个长方体，则长方体的表面积是250平方厘米．考点：长方体和正方体的表面积．分析：两个相同的正方体，拼成一个长方体，则长方体的表面积=两个正方体的表面积的和﹣2个面的面积．解答：解：25×6×2﹣25×2=300﹣50=250（平方厘米）；答：长方体的表面积是250平方厘米．故答案为：250．点评：考查了正方体的表面积公式：正方体的表面积=一个面的面积×6．本题关键是明白两个相同的正方体，拼成一个长方体，长方体的表面积=两个正方体的表面积的和﹣2个面的面积．17．用铁皮做一个无盖的长方体油箱，要求做一个油箱至少需要多少铁皮，是求油箱的A，要求油箱能装多少升汽油，是求油箱的DA、表面积B、底面积C、体积D、容积．考点：长方体和正方体的表面积；长方体和正方体的体积．专题：立体图形的认识与计算．分析：做一个长方体的油箱（无盖），要求至少需要多少铁皮，就是求这个长方体油箱的5个面要用多少（面积单位）的铁皮，实际上就是求这个油箱的表面积．体积是物体所占空间的大小，容积是指容器所能容纳物质的体积，所以容积体积不是一回事．求油箱能装多少升汽油，是求油箱的容积．解答：解：做一个长方体的油箱，要求至少需要多少铁皮，这是求油箱的表面积．求油箱能装多少升汽油，是求油箱的容积．故选：A、D．点评：本题主要是考查体积、容积的意义，面积的意义．注意，求这个油箱能装多少油，是求它的容积，它有多大，求它的体积，求用多少铁皮是求它的表面积．18．一个底面半径2cm，高10cm的圆柱的表面积是150.72平方厘米．考点：长方体和正方体的表面积．专题：立体图形的认识与计算．分析：首先明确条件，已知“圆柱的底面半径是2厘米，高是10厘米”，根据公式表面积=底面积×2+侧面积，解答即可．解答：解：3.14×22×2+2×3.14×2×10=25.12+125.6=150.72（平方厘米）答：这个圆柱的表面积是150.72平方厘米．故答案为：150.72．点评：理解和掌握圆柱体的表面积计算公式是解题的关键．19．一个长方体它的底面是正方形，面积是25平方厘米，它的一个侧面的面积是30平方厘米．这个长方体的表面积是170平方厘米．考点：长方体和正方体的表面积．专题：立体图形的认识与计算．分析：一个底面是正方形的长方体，它的底面积是25平方厘米，可求出这个正方形的边长是5厘米，用30除以5，可求出这个长方体的高，再根据长方体表面积公式计算即可．解答：解：因这个长方体的底面是正方形，且面积是25平方厘米，可知这个正方形的边长是5厘米．30÷5=6（厘米）5×5×2+5×6×4=50+120=170（平方厘米）答：这个长方体的表面积是170平方厘米．点评：本题的关键是求出这个长方体底面的边长和它的高．然后再根据表面积公式进行计算．20．一个棱长为9分米的正方体的表面积是486平方分米，把它削成一个最大的圆锥，体积是190755立方厘米．考点：长方体和正方体的表面积；圆锥的体积．专题：立体图形的认识与计算．分析：（1）正方体的棱长已知，利用正方体的表面积S=6a2，即可求得其表面积．（2）由题意可知：这个最大圆锥的底面直径和高都应等于正方体的棱长，利用圆锥的体积V=Sh，即可求出这个圆锥的体积．解答：解：（1）9×9×6=81×6。

小学数学-有答案-小升初总复习数学专项练习试卷：长方体和正方体

小升初总复习数学专项练习试卷：长方体和正方体一、填空1. 我们学过的几何图形有________、________、________、________、________．2. ________叫做周长。

3. ________叫面积。

4. 长方形的周长=________，字母表示：________．5. 正方形的周长=________，字母表示：________．6. 三角形的周长=________，平行四边形的周长=________，梯形的周长=________．7. 长方形的面积=________；字母表示：s=________．8. 正方形的面积=________；字母表示：s=________．9. 长方体的表面积=________；字母表示：s=________；长方体的体积=________；字母表示：v=________．10. 正方体的表面积=________；字母表示：s=________；正方体的体积=________；字母表示v=________．二、有关计算棱长：有关计算棱长：（1）一个长方体的长6厘米，宽5厘米，高4厘米。

它的棱长和是多少？（2）长方体的棱长和是60厘米，长6厘米，宽5厘米。

高是多少？（3）长方体的棱长和是60厘米，长6厘米，高4厘米。

宽是多少？（4）长方体的棱长和是60厘米，宽5厘米，高4厘米。

长是多少？（1）正方体的棱长是8厘米。

它的棱长和是多少？（2）正方体的棱长和是96厘米。

它的棱长是多少？一个正方体礼盒，棱长为1.5dm，包装这个礼品盒至少要用多少平方分米的包装纸？（接头不计。

）用一根长48厘米的铁丝围成一个长方体，这个长方体长5厘米，宽4厘米，它的高是多少厘米？一个长方体的长是15厘米，宽是12厘米，棱长总和是148厘米，它的高是多少？两根同样长的铁丝焊一个长方体和正方体，长方体长7厘米，宽5厘米，高3厘米，正方体的棱长是多少厘米？三、表面积：一个长方体的长8厘米，宽5厘米，高3厘米。

小升初数学必考题长方体和正方体专题解析

1. 下图可折叠成一个正方体。

依据图意，请你在图上写出另四个正方形分别为哪几个面。

解析既然图中已确定了“后面”、“下面”，从而也就固定了其他四个面的位置。

“后面”的两侧应为正方体的左右面，如下图：再看，与“下面”相对的面为上图右上角的这个正方形，即正方体的“上面”；与“后面”相对的面为上图左下角的正方形，即正方体的“前面”。

如下图：2.下图由五个正方形拼成，如果再添一个同样大小的正方形，应该放置在哪儿，才可将下图折叠成一个正方体？请将添加的正方形拼入下图。

解析可折叠成正方体的六个正方形的摆放结构有3类情况。

其一，以4个正方形（在同一条直线上）为主体，另两个正方形必须分布在两侧，。

其二，以三个正方形为主体，有以下四种结构：其三，以两个正方形为主体，其结构如阶梯状：再回到本题，如果添加一个正方形，使其成为4个正方形为主体，有以下2种添加方法：如果添加一个正方形，使其成为3个正方形为主体，有以下2种添加方法：所以，此题有以上四个答案3.用长299mm，宽为253mm的长方形装饰板拼一个正方形，至少要用多少块？解析由题意知，最少装饰板块数，只能拼出最小的正方形。

这个正方形边长应是装饰板长与宽的最小公倍数。

299与253的公因数不明显，最好用“碾转相除法"(本园地有相关知识专题讲解，可查阅）先求出二者的最大公因数。

299÷253=1 (46)253÷46=5 (23)46÷23=2 （整除为止）最后的除数23就是299与253的最大公因数。

再求299与253的最小公倍数：23×13×11=3289因而，拼出的正方形的边长应为3289mm。

由上式知，用装饰板长299mm拼出正方形边长3289mm所需块数为13；用装饰板宽253mm拼出正方形边长3289mm所需块数为11。

因此，要拼一个边长为3289mm的正方形所用装饰板至少的块数为：13×11=143块4. 一个长方体前面的面积为105平方厘米，右面的面积为56平方厘米，求这个长方体的表面积。

六年级下册数学试题-小升初复习：长方体与正方体表面积全国通用

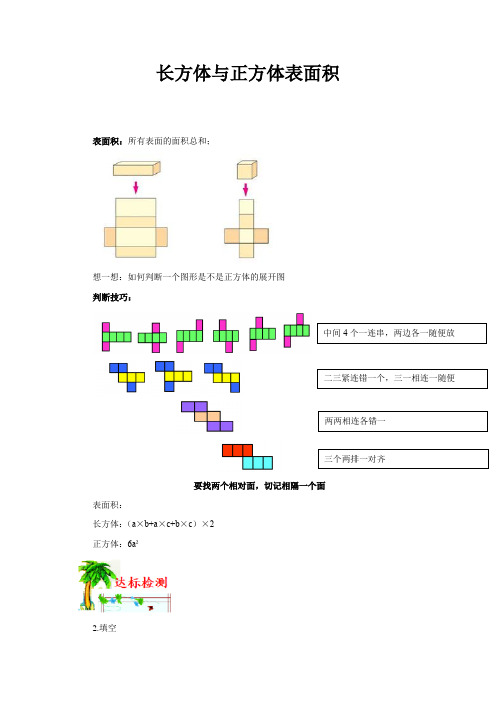
长方体与正方体表面积表面积：所有表面的面积总和；想一想：如何判断一个图形是不是正方体的展开图判断技巧：中间4个一连串，两边各一随便放二三紧连错一个，三一相连一随便两两相连各错一三个两排一对齐要找两个相对面，切记相隔一个面表面积：长方体：（a×b+a×c+b×c）×2正方体：6a²2.填空1、一个长方体的长是6厘米，宽是5厘米，高是4厘米，它的上面的面积是（）平方厘米；前面的面积是（）平方厘米；右面的的面积是（）平方厘米。

这个长方体的表面积是（）平方厘米。

2、用铁丝焊接成一个长12厘米，宽10厘米，高5厘米的长方体的框架，至少需要铁丝（）厘米。

3、一个长方体的长是5分米，宽和高都是4分米，在这个长方体中，长度为4分米的棱有（）条，面积是20平方分米的面有（）个。

4、一个长方体的金鱼缸，长是8分米，宽是5分米，高是6分米，不小心前面的玻璃被打坏了，修理时配上的玻璃的面积是（）。

5、一个正方体的棱长总和是72厘米，它的一个面是边长（）厘米的正方形，它的表面积是（）平方厘米。

三、解决问题1、有一根长52厘米的铁丝，恰好可以焊接成一个长6厘米，宽4厘米，高多少厘米的长方体？2、一间教室长8米，宽5.4米，高4米，门窗面积18平方米。

要粉刷教室四壁和天花板，如果平均每平方米用石灰250克，一共要石灰多少千克?三．一本数学书的长14厘米，宽10厘米，厚1厘米。

如果要把这本数学书的书皮包起来，至少需要多大的纸？四．天天游泳池,长25米,宽10米,深1.6米,在游泳池的四周和池底砌瓷砖,如果瓷砖的边长是1分米的正方形,那么至少需要这种瓷砖多少块？5、一个磁带盒的长是14厘米，宽11厘米，厚3厘米。

现有4盒，按图（1）、图（2）摆放的方式进行包装，哪种包装方式更节约包装纸？为什么？还有其他的包装方式吗？试再画出一种并与前两种进行比较。

—表面积提升一、拆分想一想：将一个棱长是2厘米的正方体分割成两个完全一样的长方体，长方体的表面积总和和原来正方体的表面积是否相等？总结：将一个物体分割成多个物体后表面积总和会增加。

小升初数学《长方形和正方形》专项试题及答案

小升初数学《长方形和正方形》专项试题一、选择题1．一个平行四边形相邻的两条边分别是6cm、4cm，量得一条边上的高是5cm，这个平行四边形的面积是（）平方厘米。

A．36 B．24 C．20 D．152．一个平行四边形的底扩大3倍，高扩大2倍，面积就扩大（）A．5倍B．6倍C．不变3．4个完全相同的正方形拼成一个长方形(如图)．图中阴影三角形的面积的大小是( )．A．甲＞乙＞丙B．乙＞甲＞丙C．甲＝乙＝丙4．正方体的棱长扩大到原来的2倍，它的表面积扩大到原来的（）倍．A．2 B．4 C．8 D．125．两个表面积都是24平方厘米的正方体，拼成一个长方体．这个长方体的表面积是（）平方厘米．A．48 B．44 C．40 D．166．一个正方体的棱长扩大到原来的3倍，它的体积就扩大到原来的（）。

A．3倍B．6倍C．9倍D．27倍7．做一个铁皮烟囱需要多少铁皮，就是求烟囱的（）A．表面积B．体积C．侧面积8．把一团圆柱体橡皮泥揉成与它等底的圆锥体，高将（）。

A．扩大到原来的3倍B．缩小为原来的13C．不变D．扩大到原来的9倍9．压路机的前轮转动一周所压过的路面面积是指（）A．前轮的表面积B．前轮的侧面积C．前轮的底面积10．在长12厘米，宽10厘米，高8厘米的长方体中切出一个体积最大的圆柱，这个圆柱的体积是（）立方厘米．A．1130.4 B．602.88 C．628 D．904.3211．下面说法正确的是（）。

A．圆锥的体积等于圆柱体积的1 3B．把0.56扩大到它的100倍是56C．书的总页数一定，未读的页数与已读的页数成正比例12．把一个棱长1厘米的正方体切成两个完全一样的长方体后，表面积比原来增加（）A．50% B．16C．1313．一底面是正方形的长方体，把它的侧面展开后，正好是一个边长为8分米的正方形，原来长方体的体积是（）立方分米．A．32 B．64 C．1614．有两个表面积都是60平方厘米的正方体，把它们拼成一个长方体．这个长方体的表面积是（）平方厘米．A．90 B．100 C．110 D．12015．奇思用和两种图形拼成了一个图案（如图），这个图案的面积是（）dm2．A．10 B．8 C．616．如下图所示，有（）对面积相等的三角形。

2016年小升初复习试卷：长方体与正方体及参考答案

2016年小升初复习试卷：长方体与正方体一、填空题：（24分，每题2分）1．（8分）1020立方厘米=立方分米5.05升=升毫升3立方分米70立方厘米=毫升平方千米=公顷．20.73立方分米=升毫升4.06公顷=平方米．2．（2分）我在正面看到的是，它可能是．3．（2分）一个长方体和正方体的棱长之和相等，已知长方体的长是6厘米，宽是4厘米，高是2厘米，正方体的体积是立方厘米．4．（2分）1立方分米的1个正方体可以分成个1立方厘米的小正方体，如果把这些小正方体排成一排，一共长分米．5．（2分）将棱长是1分米的正方体铁块镕铸成一个底面是长方形（长20厘米、宽10厘米）的长方体铁块．这个长方体铁块的表面积是平方厘米．6．（2分）一个长方体的长是8分米，把它分成两个相等的正方体后，表面积比原来增加．7．（2分）一个长方体的表面积是40平方厘米，把它平均分开，正好成为两个相等的正方体，每个正方体的表面积是平方厘米；体积是立方厘米．8．（2分）把6个棱长1厘米的正方体木块拼成一个长方体，这个长方体的体积是立方厘米，表面积是平方厘米或平方厘米．9．（2分）把一个长24厘米，宽18厘米，高9厘米的长方体木块截成同样大小的正方体木块（不许有剩余），最少可以截成块．10．（2分）有一个长10厘米、宽8厘米、高5厘米的长方体木块，这个长方体的体积是立方厘米，如果把它锯成棱长是3厘米的小正方体木块，共可以锯成块．11．（2分）一个长方体，体积是200立方分米，若将它沿横截方向截成5段，表面积就增加160平方分米，这个长方体的长是分米．12．（2分）一个长方体的体积是216立方厘米．这个长方体长、宽、高都是合数且互不相等．这个长方体的表面积是平方厘米．二、判断题：（9分，每题1分）13．（1分）站在一个位置上观察物体，最多能看到3个面．．（判断对错）14．（1分）两个正方体的表面积相等，它们体积也一定相等．（判断对错）15．（1分）用4个同样大小的正方体可以拼成一个新的正方体．（判断对错）16．（1分）正方体的棱长扩大2倍，它的体积就扩大8倍．．（判断对错）17．（1分）一个正方体的棱长之和是12厘米．体积是1立方厘米．．（判断对错）18．（1分）一个正方体的棱长是6厘米，它的体积和表面积同样大．（判断对错）19．（1分）一个长方体（非正方体）最多有两个面是正方形．（判断对错）20．（1分）正方体是一种特殊的长方体．．（判断对错）21．（1分）求同一个物体的体积与容积时，计算方法相同，大小也相等．（判断对错）三、选择题：（11分，每题1分）22．（1分）小芳到超市买墨水，看到墨水瓶的包装盒上印有“净含量：60毫升”的字样，这个“60亳升”是指（）A．包装盒的体积B．包装盒的容积C．墨水瓶的体积D．瓶内所装墨水的体积23．（1分）用三块棱长1厘米的小方块拼成一个长方体，它们的表面积减少（）A．6平方厘米B．4平方厘米C．2平方厘米24．（1分）把三个1立方米的正方体拼成一个长方体后，它的棱长总和是（）米．A．32 B．28 C．24 D．2025．（1分）一个长方体的长、宽、高分别是a米、b米、h米，如果高增加3米后，新的长方体体积比原来增加立方米，表面积比原来增加平方米．A.3abB.3abh C．ab（h+3）D.12a．26．（1分）小正方体的棱长是2厘米，大正方体的棱长是4厘米，大正方体的体积是小正方体体积的（）倍．A．2 B．4 C．827．（1分）一段方钢长1米，横截面是边长20厘米的正方形，它的体积是（）立方厘米．A．20 B．2000 C．2500 D．4000028．（1分）下面的图形中，能按虚线折成正方体的是（）A． B． C．D．29．（3分）（1）从侧面看是图A的有．（2）从侧面看是图B的有．（3）从正面和上面看都是图A的有．四、操作题（12分）30．（6分）转动后会形成什么样的图形？31．（6分）从下面的长方形纸上剪下一部分（每格的边长是3厘米），要折成一个棱长为3厘米的正方体，可以怎样剪？设计两种不同的方案，在图中涂色表示．五、解决问题（第2题9分，其余每题5分，共44分）32．（5分）用铁丝做一个长1分米，宽6厘米，高2厘米的长方体框架，至少需要铁丝多少厘米？在这个长方体框架外糊一层纸，至少需要多少平方厘米？（接头处不计）33．（9分）体育馆内挖一个长50米，宽25米，深3米的游泳池．①这个游泳池占地多少平方米？②如果要在池内的四周和池底铺边长为2分米的正方形瓷砖，需要这样的瓷砖多少块？③如果池内的水面距池口60厘米，这个游泳池中所容纳的水是多少吨？（1立方米水重1吨）34．（5分）有一块棱长是40厘米的正方体铁块，现要把它熔铸成一个横截面积是200平方厘米的长方体，这个长方形的长是多少厘米？35．（5分）一个长方体木块的长、宽、高分别是6厘米、5厘米、4厘米．如果把它锯成一个最大的正方体，体积比原来減少了多少？36．（5分）有两个完全一样的长方体，它们的长、宽、高分别是6厘米、5厘米、4厘米．把这两个长方体拼成一个新的长方体后，它们的表面积之和最多减少多少平方厘米？最少减少多少平方厘米？37．（5分）有一个底面积是300平方厘米、高10厘米的长方体，里面盛有5厘米深的水．现在把一块石头浸没到水里，水面上升2厘米．这块石头的体积是多少立方厘米？38．（5分）如图由19个棱长是2厘米的小正方体重叠而成．求这个立体图形的表面积．2016年小升初复习试卷：长方体与正方体参考答案与试题解析一、填空题：（24分，每题2分）1．（8分）1020立方厘米= 1.02立方分米5.05升=5升50毫升3立方分米70立方厘米=3070毫升平方千米=60公顷．20.73立方分米=20升730毫升4.06公顷=40600平方米．【解答】解：（1）1020立方厘米=1.02立方分米（2）5.05升=5 升50 毫升（3）3立方分米70立方厘米=3070 毫升（4）平方千米=60公顷．（5）20.73立方分米=20升730毫升（6）4.06公顷=40600平方米．故答案为：1.02，5，50，3070，60，20，730，10600．2．（2分）我在正面看到的是，它可能是球体或者圆柱体．【解答】解：故答案为：球体或者圆柱体．3．（2分）一个长方体和正方体的棱长之和相等，已知长方体的长是6厘米，宽是4厘米，高是2厘米，正方体的体积是64立方厘米．【解答】解：（6+4+2）×4÷12=12×4÷12=4（厘米），4×4×4=64（立方厘米），答：正方体的体积是64立方厘米．故答案为：64．4．（2分）1立方分米的1个正方体可以分成1000个1立方厘米的小正方体，如果把这些小正方体排成一排，一共长100分米．【解答】解：1立方分米=1000立方厘米，所以：1000÷1=1000（个），1立方厘米的小正方体的棱长是1厘米；则总长度是1×1000=1000（厘米）=100分米，答：1立方分米的1个正方体可以分成1000个1立方厘米的小正方体，把这些小正方体排成一排，一共长100分米．故答案为：1000；100．5．（2分）将棱长是1分米的正方体铁块镕铸成一个底面是长方形（长20厘米、宽10厘米）的长方体铁块．这个长方体铁块的表面积是700平方厘米．【解答】解：1分米=10厘米，10×10×10÷（20×10）=1000÷200=5（厘米）；（20×10+20×5+10×5）×2=（200+100+50）×2=350×2=700（平方厘米）；答：这个长方体铁块的表面积是700平方厘米．故答案为：700．6．（2分）一个长方体的长是8分米，把它分成两个相等的正方体后，表面积比原来增加32平方分米．【解答】解：（8÷2）×（8÷2）×2=4×4×2=16×2=32（平方分米）；答：表面积比原来增加32平方分米．故答案为：32平方分米．7．（2分）一个长方体的表面积是40平方厘米，把它平均分开，正好成为两个相等的正方体，每个正方体的表面积是240平方厘米；体积是8立方厘米．【解答】解：小正方体每个面的面积：40÷（12﹣2）=40÷10=4（平方厘米）小正方体的棱长：因为2的平方是4，所以小正方体的棱长是2厘米，每个小正方体的表面积：40×6=240（平方厘米）每个小正方体的体积：2×2×2=4×2=8（立方厘米）答：每个小正方体的表面积是240平方厘米，体积是8立方厘米．故答案为：240，8．8．（2分）把6个棱长1厘米的正方体木块拼成一个长方体，这个长方体的体积是6立方厘米，表面积是26平方厘米或22平方厘米．【解答】解：1×1×1×6=6（立方厘米）；6×1×4+1×1×2=24+2=26（平方厘米）；（3×1+3×2+1×2）×2=（3+6+2）×2=11×2=22（平方厘米）；答：这个长方体的体积是6立方厘米，表面积是26平方厘米或22平方厘米．故答案为：6、26、22．9．（2分）把一个长24厘米，宽18厘米，高9厘米的长方体木块截成同样大小的正方体木块（不许有剩余），最少可以截成192块．【解答】解：24=2×2×2×318=2×3×39=3×3所以24、18和12的最大公因数是3，即小的正方体的棱长3厘米，（24×18×9）÷（3×3×3）=（24÷3）×（18÷3）×（12÷3）=8×6×4=192（块）答：最少可以截成192块．故答案为：192．10．（2分）有一个长10厘米、宽8厘米、高5厘米的长方体木块，这个长方体的体积是400立方厘米，如果把它锯成棱长是3厘米的小正方体木块，共可以锯成6块．【解答】解：10×8×5=400（立方厘米），10÷3≈3（个），8÷3≈2（个），5÷3≈1（个），3×2×1=6（块）；答：这个长方体的体积是400立方厘米，共可以锯成6块．故答案为：400，6．11．（2分）一个长方体，体积是200立方分米，若将它沿横截方向截成5段，表面积就增加160平方分米，这个长方体的长是10分米．【解答】解：200÷（160÷8）=200÷20=10（分米），答：这个长方体的长是10分米．故答案为：10．12．（2分）一个长方体的体积是216立方厘米．这个长方体长、宽、高都是合数且互不相等．这个长方体的表面积是228平方厘米．【解答】解：216=2×2×2×3×3×3，所以216=4×6×9，（4×6+4×9+6×9）×2=（24+36+54）×2=114×2=228（平方厘米）；答：这个长方体的表面积是228平方厘米．故答案为：228．二、判断题：（9分，每题1分）13．（1分）站在一个位置上观察物体，最多能看到3个面．√．（判断对错）【解答】解：如图，从从长方体的一个面观察（左图），只能看到一个面A；从从长方体的一条棱观察（中图），能看到两个面A、B；从从长方体的一个顶点观察（右图），能看到三个面A、B、C．因此，站一同一个位置上观察物体，最小可看到一个面，最多可看到三个面说法正确．故答案为：√．14．（1分）两个正方体的表面积相等，它们体积也一定相等．√（判断对错）【解答】解：因为两个正方体的表面积相等，则每个面的面积相等，也就可以判定棱长相等，所以体积也相等，所以原题说法正确．故答案为：√．15．（1分）用4个同样大小的正方体可以拼成一个新的正方体．×（判断对错）【解答】解：2×2×2=8（个），所以至少需要8个小正方体才能拼成一个大正方体，原题说法错误，故答案为：×．16．（1分）正方体的棱长扩大2倍，它的体积就扩大8倍．√．（判断对错）【解答】解：正方体的棱长扩大2倍，它的体积就扩大2×2×2=8倍．因此，正方体的棱长扩大2倍，它的体积就扩大8倍．这种说法是正确的．故答案为：√．17．（1分）一个正方体的棱长之和是12厘米．体积是1立方厘米．√．（判断对错）【解答】解；12÷12=1（厘米）；1×1×1=1（立方厘米）；故答案为：√．18．（1分）一个正方体的棱长是6厘米，它的体积和表面积同样大．×（判断对错）【解答】解：因为正方体的表面积和体积单位不相同，没法比较它们的大小，所以原题说法是错误的．故答案为：×．19．（1分）一个长方体（非正方体）最多有两个面是正方形．√（判断对错）【解答】解：根据长方体的特征可知，一般情况6个都是长方形，特殊情况有两个相对的面是正方形．所以“一个长方体（非正方体）最多有两个面是正方形”的说法是正确．故答案为：√．20．（1分）正方体是一种特殊的长方体．√．（判断对错）【解答】解：因为长、宽、高都相等的长方体叫做正方体，正方体是特殊的长方体，所以原题说法正确．故答案为：√．21．（1分）求同一个物体的体积与容积时，计算方法相同，大小也相等．×（判断对错）【解答】解：由分析得：求同一个物体的体积与容积时，计算方法相同，但大小不相等，同一个物体的体积大于它的容积．因此，求同一个物体的体积与容积时，计算方法相同，大小也相等．这种说法是错误的．故答案为：×．三、选择题：（11分，每题1分）22．（1分）小芳到超市买墨水，看到墨水瓶的包装盒上印有“净含量：60毫升”的字样，这个“60亳升”是指（）A．包装盒的体积B．包装盒的容积C．墨水瓶的体积D．瓶内所装墨水的体积【解答】解：由分析知：墨水瓶的包装盒上印有“净含量：60毫升”的字样，这个“60亳升”是指瓶内所装墨水的体积；故选：D．23．（1分）用三块棱长1厘米的小方块拼成一个长方体，它们的表面积减少（）A．6平方厘米B．4平方厘米C．2平方厘米【解答】解：1×1×4=4（平方厘米）；答：它们的表面积减少了4平方厘米．故选：B．24．（1分）把三个1立方米的正方体拼成一个长方体后，它的棱长总和是（）米．A．32 B．28 C．24 D．20【解答】解：1立方米的正方体棱长是1米，3个棱长1米的正方体可以拼成一个长、宽、高分别是3米、1米、1米的长方体；长方体的棱长总和是：（3+1+1）×4=5×4=20（米）答：它的棱长总和是20米．故选：D．25．（1分）一个长方体的长、宽、高分别是a米、b米、h米，如果高增加3米后，新的长方体体积比原来增加3ab立方米，表面积比原来增加6a+6b平方米．A.3abB.3abh C．ab（h+3）D.12a．【解答】解：a×b×3=3ab（立方米）；a×3×2+b×3×2=6a+6b（平方米）；答：新的长方体体积比原来增加3ab立方米，表面积比原来增加6a+6b平方米．故答案为：3ab，6a+6b．26．（1分）小正方体的棱长是2厘米，大正方体的棱长是4厘米，大正方体的体积是小正方体体积的（）倍．A．2 B．4 C．8【解答】解：4÷2=2，因为大正方体的棱长是小正方体棱长的2倍，所以大正方体的体积是小正方体体积的2×2×2=8倍．答：大正方体的体积是小正方体体积的8倍．故选：C．27．（1分）一段方钢长1米，横截面是边长20厘米的正方形，它的体积是（）立方厘米．A．20 B．2000 C．2500 D．40000【解答】解：1米=100厘米，20×20×100=400×100=40000（立方厘米），答：它的体积是40000立方厘米．故选：D．28．（1分）下面的图形中，能按虚线折成正方体的是（）A． B． C．D．【解答】解：各选项的图形中，能按虚线折成正方体的是A，故选：A．29．（3分）（1）从侧面看是图A的有①③．（2）从侧面看是图B的有②．（3）从正面和上面看都是图A的有③．【解答】解：根据题干分析可得：（1）从侧面看是图A的有①③．（2）从侧面看是图B的有②．（3）从正面和上面看都是图A的有③．故答案为：①③；②；③．四、操作题（12分）30．（6分）转动后会形成什么样的图形？【解答】解：根据题干分析可得，平面图形经过旋转一周可以形成几何体，长方形旋转一周，得到的是圆柱；半圆沿直径旋转一周得到的是球体；直角三角形沿一直角边旋转一周得到的是圆锥；直角梯形沿直角边旋转一周得到的是圆台．31．（6分）从下面的长方形纸上剪下一部分（每格的边长是3厘米），要折成一个棱长为3厘米的正方体，可以怎样剪？设计两种不同的方案，在图中涂色表示．【解答】解：根据题意设计如下（“1﹣4﹣1”结构和“2﹣2﹣2”结构）：五、解决问题（第2题9分，其余每题5分，共44分）32．（5分）用铁丝做一个长1分米，宽6厘米，高2厘米的长方体框架，至少需要铁丝多少厘米？在这个长方体框架外糊一层纸，至少需要多少平方厘米？（接头处不计）【解答】解：1分米=10厘米，（10+6+2）×4=18×4=72（厘米）；（10×6+10×2+6×2）×2=（60+20+12）×2=92×2=184（平方厘米）；答：至少需要铁丝72厘米；至少需要纸184平方厘米．33．（9分）体育馆内挖一个长50米，宽25米，深3米的游泳池．①这个游泳池占地多少平方米？②如果要在池内的四周和池底铺边长为2分米的正方形瓷砖，需要这样的瓷砖多少块？③如果池内的水面距池口60厘米，这个游泳池中所容纳的水是多少吨？（1立方米水重1吨）【解答】解：①50×25=1250（平方米）答：这个游泳池占地1250平方米．②2分米=0.2米[50×25+（50×3+25×3）×2]÷（0.2×0.2）=[1250+（150+75）×2]÷0.04=[1250+450]÷0.04=1700÷0.04=42500（块）答：需要这样的瓷砖42500块．③60厘米=0.6米50×25×（3﹣0.6）×1=1250×2.4×1=3000（吨）这个游泳池中所容纳的水是3000吨．34．（5分）有一块棱长是40厘米的正方体铁块，现要把它熔铸成一个横截面积是200平方厘米的长方体，这个长方形的长是多少厘米？【解答】解：40×40×40÷200=64000÷200=320（厘米）答：这个长方体的长是320厘米35．（5分）一个长方体木块的长、宽、高分别是6厘米、5厘米、4厘米．如果把它锯成一个最大的正方体，体积比原来減少了多少？【解答】解：6×5×4﹣4×4×4=120﹣64=56（立方厘米），答：体积比原来减少了56立方厘米．36．（5分）有两个完全一样的长方体，它们的长、宽、高分别是6厘米、5厘米、4厘米．把这两个长方体拼成一个新的长方体后，它们的表面积之和最多减少多少平方厘米？最少减少多少平方厘米？【解答】解：5×4×2=20×2=40（平方厘米）；6×5×2=30×2=60（平方厘米）；答：它们的表面积之和最多减少60平方厘米；最少减少40平方厘米．37．（5分）有一个底面积是300平方厘米、高10厘米的长方体，里面盛有5厘米深的水．现在把一块石头浸没到水里，水面上升2厘米．这块石头的体积是多少立方厘米？【解答】解：300×2=600（立方厘米），答：这块石头的体积是600立方厘米．38．（5分）如图由19个棱长是2厘米的小正方体重叠而成．求这个立体图形的表面积．【解答】解：（2×3）×（2×3）×6=6×6×6=216（平方厘米）答：这个立体图形的表面积是216平方厘米．。

小学数学-有答案-小升初总复习数学专项练习试卷：长方体和正方体(2)

小升初总复习数学专项练习试卷：长方体和正方体（2）一、填空．（（26分，每空2分）1. 2.1平方米=________平方分米2.04立方米=________立方分米0.008立方米=________升=________毫升3.8升=________升________毫升。

2. 长方体和正方体都有________个面，________条棱，________个顶点。

3. 一个长方体相交于一个顶点的三条棱分别长5厘米、3厘米、4厘米，这个长方体的所有棱长之和是________厘米，体积是________．4. 长方体和正方体的体积都可用字母公式________来表示。

5. 一个正方体的底面积是2平方厘米，它的表面积是________平方厘米。

6. 用三个长5厘米、宽3厘米、高2厘米的长方体木块拼成一个表面积最大的长方体，这个大长方体的表面积是________平方厘米。

二、填空题（共18分）填表。

一个长方体木箱，竖着放和横着放时所占的空间不一样大。

________．（判断对错）一个厚度为2毫米的铁皮箱的体积和容积完全相等。

________．（判断对错）正方体的棱长扩大2倍，它的表面积就扩大8倍。

________．（判断对错）体积相等的两个正方体，它们的表面积一定相等。

________．（判断对错）一个棱长为1米的无盖正方体铁箱，它的表面积是5平方米。

________．五、计算下列各题．（16分）计算下列各题。

6.8+6.8×6.8−1.5×6.8；(3.6+12.03÷0.3)×2.5；1.25×0.25×8×0.4；96.356×(5.9+5.1−10)．六、解答题。

一种汽车上的油箱，里面长8分米，宽5分米，高3.5分米，做这个油箱需要多少平方分米的铁皮？这个油箱可以装多少升汽油？用一根长36厘米的铁丝做成一个最大的正方体框架，在框架外面全部糊上白纸，需要白纸多少平方厘米？把一个棱长6分米的正方体钢块，锻造成横截面积为4平方分米的长方体钢锭，这根钢锭长多少米？七、附加题：（10分）一个底面是正方形的长方体，所有棱长的和是100厘米，它的高是7厘米，这个长方体的体积是多少立方厘米？参考答案与试题解析小升初总复习数学专项练习试卷：长方体和正方体（2）一、填空．（（26分，每空2分）1.【答案】210,2040,8,8000,3,800【考点】体积、容积进率及单位换算面积单位间的进率及单位换算【解析】(1)高级单位平方米化低级单位平方分米乘进率100．(2)高级单位立方米化低级单位立方分米乘进率1000．(3)高级单位立方米化低级单位升乘进率1000；高级单位升化低级单位毫升乘进率1000．(4)3.8升看作3升与0.8升之和，把0.8升乘进率1000化成800毫升。

六年级下册数学试题-小升初复习讲练：长方体和正方体的体积 (含答案)sc

长方体和正方体的体积典题探究例1．一个长方体，长扩大到原来的2倍，宽和高不变，体积扩大到原来的倍．例2．正方体的棱长扩大2倍，体积扩大4倍．．（判断对错）例3．有大小两个正方体，它们表面积的比是4：1，则大小正方体的体积之比是．例4．已知长方体货仓长50米，宽30米，高5米，这个长方体货仓最多可以容纳8立方米的正方体货箱个．例5．计算图形的表面积和体积（单位厘米）例6．有一个长方体，它的正面和底面的面积之和是132平方厘米，如果它的长、宽、高都是质数，那么这个长方体的体积是立方厘米．演练方阵A档（巩固专练）一．选择题（共15小题）1．（•苍溪县模拟）一个长方体长、宽、高分别是a米，b米，h米，如果高增加3米后，新的长方体体积比增加了（）立方米．A．a bh B．a bh+3 C．3ab D．3h2．（•常山县）计算一个长方体木箱的容积和体积时，（）是相同的．A．计算公式B．意义C．测量方法3．（•北塘区）一个长方体水池，从里面量长、宽、高都是1米，水池的（）是1立方米．A．体积B．容积C．重量D．面积4．（•扬州）一个长方体的长、宽、高都扩大2倍，它的体积扩大（）倍．A．2B．4C．6D．85．（•福州）一个长方体水池，从里面量长、宽和高都是1米，可以说水池的（）是1立方米．A．容积B．体积C．重量6．（•雁江区）计算正方体、长方体和园柱的（），可用V=sh．A．表面积B．侧面积C．体积7．（•广西）如图，它们的体积公式可以统一成（）A．V=a b h B．V=a3C．V=s h8．（•新泰市）一个正方体的棱长总和是6分米，这个正方体的体积是（）立方分米．A．1B．6C．9．（•廊坊）用一根52厘米长的铅丝，正好可以焊成长6厘米，宽4厘米，高（）厘米的长方体教具．A．2B．3C．4D．510．（•武胜县）一种液体饮料采用长方体塑料盒密封包装，从外面量得盒子长6 厘米，宽4厘米，高10 厘米．盒面注明：“净含量250毫升”．这项说明是否真实？（）A．真实B．不真实C．无法确定11．（•龙海市模拟）正方体棱长扩大2倍，体积扩大（）倍．A．2倍B．4倍C．6倍D．8倍12．（•蓬溪县模拟）一个正方体的棱长扩大2倍，它的表面积要扩大（）A．2倍B．4倍C．8倍13．（•陆良县模拟）一个正方体，如果它的棱长缩小到原来的，那么它的体积缩小到原来的（）A．B．C．14．（•陇川县模拟）大小两个正方体的棱长之比是2：3，则大小正方体的体积之比是（）A．2：3 B．4：6 C．6：9 D．8：2715．（•长寿区）一个正方体的棱长扩大2倍，它的体积扩大（）倍．A．2B．8C．4D．16二．填空题（共13小题）16．一个正方体，高减少4厘米后，表面积就减少80平方厘米，现在长方体体积是_________立方厘米；原来正方体的表面积是_________平方厘米．17．一根3米长的方钢，把它横截成3段时，表面积增加80平方厘米，原来方钢的体积是_________．18．王峰家有一个表面积是24平方分米的正方形纸盒，它的体积是_________立方分米．19．（•南康市模拟）两个长方体棱长和相等，它们的体积相等，表面积也相等．_________．20．（•尚义县）一个长方体的高减少3厘米后，表面积减少48平方厘米，成为一个正方体，正方体的体积是_________立方厘米．21．（•武鸣县模拟）李师傅用12米长的铁丝焊接成一个长方体，长、宽、高的比是3：2：1，这个长方体的体积是_________立方米．22．正方体的棱长增加了两倍，则它的体积增加了_________倍．23．一个长12厘米，宽4厘米，高6厘米的长方体，切割成棱长为2厘米的小正方体，能分成_________个．24．一个长方体的棱长和为272厘米，它的长、宽、高的比是7：6：4，这个长方体的体积是_________立方厘米．25．一个长方体的长扩大2倍，宽扩大3倍，高不变，体积扩大_________倍．26．（•南县）一个长方体和一个正方体的体积相等，它们的表面积也一定相等．_________．（判断对错）27．（•富源县）棱长是6厘米的正方体，它的表面积和体积相等．_________．（判断对错）28．（•中山市模拟）一个长方体棱长的总和是72分米，长、宽、高的比是5：3：1，它的体积是_________立方分米．B档（提升精练）一．选择题（共15小题）1．（•福田区模拟）在一个长、宽、高分别是30厘米、25厘米、60厘米的长方体箱子里，最多能装进棱长为1分米的立方体（）个．A．45 B．30 C．36 D．722．（•道里区模拟）长方体的长、宽、高都变为原来的3倍，它的体积扩大（）倍．A．3倍B．9倍C．27倍D．10倍3．（•道里区模拟）一个长方体水箱的容积是150升，这个水箱底面是一个边长为5分米的正方形，则水箱的高是（）（水箱厚度忽略不计）A．30分米B．10分米C．4分米D．6分米4．（•蓬溪县模拟）两个长方体体积相等，下面说法正确的是（）A．底面积一定相等B．表面积一定相等C．长宽高乘积相等5．（•麻城市模拟）如果把正方体的棱长延长10%，则体积增加（）A．30% B．33% C．33.1% D．无法确定6．（•黄岩区）长方体的长5厘米，宽4厘米，高是3厘米，体积是（）A．60厘米B．60平方厘米C．60立方厘米7．（•萝岗区）一个正方体的底面周长是12cm，它的体积是（）cm3．A．9B．27 C．36 D．728．（•陕西）一个正方体棱长增加20%，它的体积就增加（）A．20% B．44% C．72.8%9．（•永定区模拟）棱长为a厘米的正方体，其体积是（）立方厘米．A．6a2B．6a C．a+a+a D．a310．（•温江区模拟）等底等高的圆柱、正方体、长方体的体积相比较（）A．正方体体积大B．长方体体积大C．圆柱体体积大D．体积一样大11．（•蓬溪县模拟）一个长方体的长、宽、高分别是a米、b米、h米，如果高增加3米后，新的长方体体积比原来增加（）立方米．A．3ab B．3abh C．a b（h+3）D．a bh+3312．（•陆良县模拟）圆柱、正方体和长方体的底面周长相等，高也相等，则（）的体积最大．A．圆柱B．正方体C．长方体D．长方体的体积13．（•萝岗区）如果长方体的长、宽、高都扩大3倍，则它的体积扩大（）A．3B．9C．6D．2714．（•蓝田县模拟）把一个棱长是4分米的立方体钢坯切削成一个最大的圆柱，这个圆柱的体积是（）立方分米．A．50.24 B．64 C．12.56 D．200.9615．（•民乐县模拟）一个正方体棱长为a厘米，如果它的棱长增加4厘米，所得到的正方体的体积比原正方体增加（）立方厘米．A．16 B．64 C．（a+4）3﹣a3D．无法计算二．填空题（共13小题）16．（•萝岗区）一个棱长是6厘米的正方体，它的体积和表面积相等．_________（判断对错）17．（•成都）把一根长12米的长方体木条沿长锯成6段，表面积增加110平方厘米．这段木条原来的体积是_________立方厘米．18．（•萝岗区）一个棱长为6厘米的正方体，它的表面积是_________．体积是_________．19．（•岚山区模拟）棱长1厘米的小正方体至少需要_________个可拼成一个较大的正方体，需要_________个可拼成一个棱长1分米的大正方体．如果把这些小正方体依次排成一排，可以排成_________米．20．（•菏泽模拟）体积相等的两个正方体，表面积也相等．_________（判断对错）21．（•蓝田县模拟）一个棱长是4分米正方体容器装满水后，倒入一个底面积是12平方分米的圆锥体容器里正好装满，这个圆锥体的高是_________分米．22．（•临川区模拟）1米长的方木锯成两段后，表面积比原来增加了8平方厘米，这根方木原来的体积是_________立方厘米．23．（•武平县模拟）如果长方体、正方体、圆柱体的底面积和高都分别相等，那么它们的体积也相等．_________．（判断对错）24．（•荔波县模拟）长方体、正方体和圆柱的体积公式都可以用V=sh表示．…_________．（判断对错）25．（•萧县模拟）一个棱长9cm的正方体，如果它的棱长扩大4倍，那么它的表面积扩大_________倍，体积扩大_________倍．26．（•临川区模拟）棱长和是24分米的正方体体积是_________立方分米．27．（•上海模拟）一个长方体，他的前面和上面的面积之和是108平方厘米，已知长宽高是连续的奇数，这个长方体的体积是_________立方厘米．28．（•永康市模拟）棱长3分米的正方体，它的体积是_________立方分米．3个这样的正方体拼成一个长方体，拼成的长方体的表面积是_________平方分米．C档（跨越导练）一．填空题（共8小题）1．一个长方体的体积是1560，它的长、宽、高均为自然数，它的棱长之和最少是_________．2．（•玉门市）一个长方体和一个圆锥的底面积和高都相等，它们的体积相差18立方厘米．这个长方体的体积是_________立方厘米，圆锥体积是_________立方厘米．3．（•资中县）一个长方体前面和上面的面积之和是91平方厘米，已知长宽高的厘米数都是质数，这个长方体的体积是_________立方厘米或_________立方厘米．4．（•广东）一根长3.6米的长方体木料，其中有一组相对的面是正方形，其余四个面的面积之和是7.2平方米，这根木料的体积是_________立方米．5．（•河西区）一个长方体容器里装水770升，水深15.4分米．现将长方体容器中的水倒一部分给圆柱体容器，并使两个容器中的水高度相同．已知长方体容器的底面积是圆柱体容器底面积的倍（从内侧量），这时两个容器中的水深是_________分米．6．（•射洪县）把6个边长为1cm的小正方体拼成一个较大的长方体．拼成的长方体的体积是_________cm3，表面积最小是_________cm2．7．（•武义县）一个长方体的长、宽、高的比是3：2：5，已知它的宽是4分米，它的体积是_________立方分米．8．（•锦屏县）如图是由两个棱长都是2厘米的正方体拼成的一个长方体，这个长方体的表面积是_________；体积是_________．二．解答题（共10小题）9．把一个横截面为正方形的长方体木块，削成一个最大的圆锥体，已知圆锥的底面周长是12.56厘米，高5厘米，长方体的体积是多少？10．（•浦东新区）一个长方体形状的容器，里面长4分米，宽3分米，高4.5分米．向这个容器里注入30升水，容器里水深多少分米？11．六年的小学生活即将结束，婷婷计划星期天请5名同学到家商量去养老院参加义务劳动的事，家中只有一盒长方体饮料（如图），假如用来招待同学，给每位同学倒上满满一杯（如右图）后，她自己还有饮料吗？（请写出计算过程，箱子、杯子的厚度均忽略不计）（单位：厘米）12．（•沛县）一个圆柱形玻璃水槽，底面直径20厘米，深15厘米，用这个水槽装满水，再倒入一个空的正方体金鱼缸中，已知金鱼缸从里面量的深是30厘米．问：金鱼缸中的水面高度大约是多少厘米？（最后得数保留整厘米数．）13．（•新区）一个学习小组的四名同学观察并测量了一个长方体．刘星说：“如果高再增加2分米，它恰好是一个正方体．”王尘说：“长方体的前后左右四个面的面积之和是96平方分米．”李成说：“它的底面周长是24分米．”张丹说：“这个长方体的棱长总和是64分米．”这四名同学得到的数据都是正确的，你能筛选出必要的数据作条件，求出这个长方体的体积吗？试试看．14．（•华亭县）长方体的棱长之和是96厘米，长、宽、高的比是3：2：1，求这个长方体的体积和表面积？15．（•兰州）有一条长方体木棍，长3米，横截面是边长4分米的正方形，如果把它加工成一根最大的圆木．需要削掉多少立方分米？16．（•资中县）把底面直径为6厘米、高为9厘米的圆柱体可口可乐瓶装满汽水，倒入一个长35厘米、宽20厘米、高6厘米的纸盒中（如下图），这个纸盒最多可以装多少瓶可口可乐汽水？（纸盒和汽水瓶的厚度忽略不计）（保留整数）17．（•龙海市）一个长方体木块，从下部和上部分别截去高为3厘米和2厘米的长方体后，便成为一个正方体，表面积减少了120平方厘米，原来长方体的体积是多少立方厘米？18．（•阳谷县）在一个棱长4分米的正方体水箱中盛满水，全部倒入一个底面积是20平方分米，高4分米的圆柱形水桶中，水深多少分米？长方体和正方体的体积答案典题探究例1．一个长方体，长扩大到原来的2倍，宽和高不变，体积扩大到原来的2倍．考点：长方体和正方体的体积．分析：根据长方体计算的公式代入字母对比就可以了．解答：解：根据题意知：V长=abc；扩大2倍后为：V长变=（2a）bc，=2abc；所以变化后体积扩大2倍；故答案为：2．点评：此题考查了长方体的计算公式的灵活应用．例2．正方体的棱长扩大2倍，体积扩大4倍．错误．（判断对错）考点：长方体和正方体的体积．专题：立体图形的认识与计算．分析：根据正方体体积=棱长3，可得正方体体积扩大的倍数是棱长扩大倍数的立方求解即可．解答：解：正方体的棱长扩大2倍，则体积扩大23=8倍，所以原题说法错误．故答案为：错误．点评：考查了正方体的体积与正方体棱长的关系，是基础题型，比较简单．例3．有大小两个正方体，它们表面积的比是4：1，则大小正方体的体积之比是8：1．考点：长方体和正方体的体积；比的意义．专题：立体图形的认识与计算．分析：正方体的表面积=棱长×棱长×6，正方体的体积=棱长×棱长×棱长，再依据“大小两个正方体表面积的比是4：1”，即可分别求出它们的棱长之比和体积之比．解答：解：因为大小两个正方体表面积的比是4：1，所以大小正方体的棱长比是2：1，所以大小正方体的体积比是8：1．故答案为：8：1．点评：此题主要考查正方体的表面积和体积公式．例4．已知长方体货仓长50米，宽30米，高5米，这个长方体货仓最多可以容纳8立方米的正方体货箱750个．考点：长方体和正方体的体积．分析：先根据8立方米的正方体货箱，可求出正方体木箱的棱长是2米，由于长方体的长为50米，可知沿长边能放（50÷2）个；宽30米，可知沿宽边能放（30÷2）个；高5米，可知竖直方向只能堆两层，也就是说在长方体的货仓里只能用到4米的高度．进一步求出这个长方体货仓最多可以容纳8立方米的正方体货箱个数即可．解答：解：因为8=2×2×2，所以正方体木箱的棱长是2米，50÷2=25（个）（横着放的个数），30÷2=15（个）（竖着放的个数），5÷2=2（层）…1（米）（能放2层，还余1米空间），所以能容纳的木箱的个数为：25×15×2=750（个）．答：这个长方体货仓最多可以容纳8立方米的正方体货箱750个．故答案为：750．点评：此题考查生活中的实际问题，关键是弄明白在这个长方体货仓里能横着装几个、竖着装几个，也就是能装几层，再进一步得解．例5．计算图形的表面积和体积（单位厘米）考点：长方体和正方体的体积；圆柱的侧面积、表面积和体积．专题：压轴题；立体图形的认识与计算．分析：（1）长方体的表面积=（长×宽+宽×高+高×长）×2，长方体的体积=长×宽×高；（2）圆柱的表面积=侧面积+（底面积×2），圆柱的体积=底面积×高，将所给数据分别代入相应的公式，即可分别求出对应图形的表面积和体积．解答：解：（1）长方体的表面积：（10×4+10×6+4×6）×2，=（40+60+24）×2，=124×2，=248（平方厘米）；长方体的体积：10×4×6，=40×6，=240（立方厘米）；答：长方体的表面积是248平方厘米，体积是240立方厘米．（2）圆柱的表面积：3.14×10×8+3.14×（10÷2）2×2，=251.2+157，=408.2（平方厘米）；圆柱的体积：3.14×（10÷2）2×8，=3.14×25×8，=628（立方厘米）；答：圆柱的表面积是408.2平方厘米，体积是628立方厘米．点评：此题主要考查长方体、圆柱的表面积和体积的计算方法．例6．有一个长方体，它的正面和底面的面积之和是132平方厘米，如果它的长、宽、高都是质数，那么这个长方体的体积是385立方厘米．考点：长方体和正方体的体积．专题：压轴题．分析：正面和底面之和为132平方厘米，所以长×宽+长×高=长×（宽+高）=132，把132分解因数为：132=2×2×3×11，又因为长、宽、高都是质数，故长=11，宽+高=12，同样12只能分成5+7，所以这个长方体的三个棱长分别为11、5、7，由此可以解决问题．解答：解：132=11×12=11×（5+7），所以长宽高分别为：11厘米、5厘米、7厘米，体积是：11×5×7=385（立方厘米）；答：这个长方体的体积是385立方厘米．故答案为：385．点评：考查了长方体的体积解答此题的关键：先根据题意，进行分析，判断出长、宽、高的长度，然后根据长方体的体积计算公式进行解答即可．演练方阵A档（巩固专练）一．选择题（共15小题）1．（•苍溪县模拟）一个长方体长、宽、高分别是a米，b米，h米，如果高增加3米后，新的长方体体积比增加了（）立方米．A．a bh B．a bh+3 C．3ab D．3h考点：长方体和正方体的体积；用字母表示数．专题：立体图形的认识与计算．分析：根据长方体的体积公式V=abh，分别求出原来和后来的长方体体积，再相减就是增加的体积．解答：解：原来长方体的体积；V=abh，后来长方体的体积：a×b×（h+3）=abh+3ab，增加的体积：abh+3ab﹣abh=3ab，故选：C．点评：解答此题的关键是把所给出的字母当做已知数，再根据长方体的体积公式分别求出长方体的体积，进而得出答案．2．（•常山县）计算一个长方体木箱的容积和体积时，（）是相同的．A．计算公式B．意义C．测量方法考点：长方体和正方体的体积；立体图形的容积．分析：计算长方体容积是长×宽×高；计算长方体体积是长×宽×高；解答：解：根据题意知：V容=长×宽×高；V体=长×宽×高；所以计算公式相同；故选：A．点评：此题考查了长方体的容积和体积计算．3．（•北塘区）一个长方体水池，从里面量长、宽、高都是1米，水池的（）是1立方米．A．体积B．容积C．重量D．面积考点：长方体和正方体的体积．专题：立体图形的认识与计算．分析：求这个水池可蓄水多少立方米，是求长方体水池的容积，根据体积的计算方法，长方体的体积=长×宽×高来计算．解答：解：因为长方体水池，从里面量长、宽、高都是1米，所以水池的容积是1×1×1=1立方米．故水池的容积是1立方米．故选：B．点评：此题考查长方体的容积，解决此题的关键是分清体积和容积的区别．4．（•扬州）一个长方体的长、宽、高都扩大2倍，它的体积扩大（）倍．A．2B．4C．6D．8考点：长方体和正方体的体积；积的变化规律．分析：根据长方体的体积计算公式和因数与积的变化规律可得：v=abh，三个因数都扩大2倍，积扩大的倍数等于因数扩大倍数的乘积；也就是积扩大8倍．由此解答．解答：解：根据长方体的体积计算方法和因数与积的变化规律得：一个长方体的长、宽、高都扩大2倍，它的体积扩大2×2×2=8倍；故选：D．点评：此题主要考查长方体的体积计算方法和因数与积的变化规律，积扩大的倍数等于因数扩大倍数的乘积．5．（•福州）一个长方体水池，从里面量长、宽和高都是1米，可以说水池的（）是1立方米．A．容积B．体积C．重量考点：长方体和正方体的体积．专题：立体图形的认识与计算．分析：求这个水池可蓄水多少立方米，是求长方体水池的容积，根据体积的计算方法，长方体的体积=长×宽×高来计算．解答：解：因为长方体水池，从里面量长、宽、高都是1米，所以水池的容积是1×1×1=1立方米．故水池的容积是1立方米．故选：B．点评：此题考查长方体的容积，解决此题的关键是分清体积和容积的区别．6．（•雁江区）计算正方体、长方体和园柱的（），可用V=sh．A．表面积B．侧面积C．体积考点：长方体和正方体的体积；圆柱的侧面积、表面积和体积．专题：立体图形的认识与计算．分析：根据正方体、长方体、圆柱的体积公式可得，它们的体积公式都是V=sh．据此即可选择．解答：解：根据题干分析可得，计算正方体、长方体和园柱的体积，可用V=sh，故选：C．点评：此题主要考查正方体、长方体、圆柱的体积公式，熟记公式即可解答．7．（•广西）如图，它们的体积公式可以统一成（）A．V=a b h B．V=a3C．V=s h考点：长方体和正方体的体积；用字母表示数；圆柱的侧面积、表面积和体积．专题：立体图形的认识与计算．分析：长方体的长×宽=它的底面积，正方体的棱长×棱长=它的底面积，长方体和正方体的统一体积公式为：v=sh；再根据圆柱的体积公式的推导过程，把圆柱切拼成近似长方体，正方体的底面积等于圆柱的底面积，长方体的高等于圆柱的高，因为长方体的体积=底面积×高，所以圆柱的体积=底面积×高．由此解答．解答：解：根据分析：长方体、正方体和圆柱体的体积公式可以统一成：v=sh．故选：C．点评：此题考查的目的是使学生理解掌握长方体、正方体和圆柱体的统一体积公式：v=sh．8．（•新泰市）一个正方体的棱长总和是6分米，这个正方体的体积是（）立方分米．A．1B．6C．考点：长方体和正方体的体积．专题：压轴题；立体图形的认识与计算．分析：根据正方体的特征，12条棱的长度都相等，正方体的棱长总和=棱长×12，已知棱长总和是6分米，首先求出棱长，再根据正方体的体积公式：v=a3，把数据代入公式解答．解答：解：棱长是：6÷12=0.5（分米），体积是：0.5×0.5×0.5=0.125（立方分米）；答：这个正方体的体积是0.125立方分米．故选：C．点评：此题主要考查正方体的特征和体积的计算，首先根据棱长总和的计算方法求出棱长，再根据正方体的体积公式解答．9．（•廊坊）用一根52厘米长的铅丝，正好可以焊成长6厘米，宽4厘米，高（）厘米的长方体教具．A．2B．3C．4D．5考点：长方体和正方体的体积．专题：压轴题．分析：根据长方体的棱长的特点，得出长方体是由4条长，4条宽，4条高组成的，（棱长之和﹣长×4﹣宽×4）÷4，即可求出高是多少．解答：解：（52﹣6×4﹣4×4）÷4，=（52﹣24﹣16）÷4，=12÷4，=3（厘米）；故选：B．点评：此题考查了长方体棱长之和的计算方法的灵活应用．10．（•武胜县）一种液体饮料采用长方体塑料盒密封包装，从外面量得盒子长6 厘米，宽4厘米，高10 厘米．盒面注明：“净含量250毫升”．这项说明是否真实？（）A．真实B．不真实C．无法确定考点：长方体和正方体的体积．专题：压轴题；立体图形的认识与计算．分析：先利用长方体的体积公式求出盒子的体积，再与盒子上的标注相比较即可做出判断．解答：解：6×4×10=240（立方厘米）=240（毫升）；答：盒子的体积是240毫升，而净含量为250毫升，不真实．故选：B．点评：此题主要考查长方体的体积计算，一般来说一个容器的容积要小于它的体积．11．（•龙海市模拟）正方体棱长扩大2倍，体积扩大（）倍．A．2倍B．4倍C．6倍D．8倍考点：长方体和正方体的体积．分析：根据正方体的体积计算公式v=a3，以及因数与积的变化规律，正方体棱长扩大2倍，体积扩大2的立方数倍．由此解答．解答：解：根据正方体的体积计算方法可知，正方体棱长扩大2倍，体积扩大2的立方数倍，即扩大8倍．故选：D．点评：此题主要考查正方体的体积计算方法和因数与积的变化规律，由此解决问题．12．（•蓬溪县模拟）一个正方体的棱长扩大2倍，它的表面积要扩大（）A．2倍B．4倍C．8倍考点：长方体和正方体的体积；长方体和正方体的表面积．专题：压轴题．分析：令原正方体棱长为1，棱长扩大2倍，就变成了棱长为2的正方体，利用正方体的表面积公式计算出结果进行选择．解答：解：令正方体棱长为1，则棱长扩大2倍后的正方体棱长为2，1×1×6=6，2×2×6=24，24÷6=4，故选：B．点评：也可以这样思考：正方体的表面积=一个正方形面的面积×6，正方形的面积=边长×边长，当正方体的棱长扩大2倍．根据积的变化规律可得，正方体的一个正方形面的面积就会扩大2×2=4倍，所以正方体的表面积也跟着扩大4倍．13．（•陆良县模拟）一个正方体，如果它的棱长缩小到原来的，那么它的体积缩小到原来的（）A．B．C．考点：长方体和正方体的体积；积的变化规律．专题：立体图形的认识与计算．分析：根据正方体的体积公式：v=a3，再根据积的变化规律，积扩大或缩小的倍数等于因数扩大或缩小倍数的乘积．由此解答．解答：解：正方体的棱长缩小到原来的，它的体积就缩小到原来的××=，答：它的体积缩小到原来的．故选：A．点评：此题主要根据正方体的体积的计算方法和积的变化规律解决问题．14．（•陇川县模拟）大小两个正方体的棱长之比是2：3，则大小正方体的体积之比是（）A．2：3 B．4：6 C．6：9 D．8：27考点：长方体和正方体的体积．专题：立体图形的认识与计算．分析：正方体的体积=棱长×棱长×棱长，再依据“大小两个正方体的棱长比是2：3”，即可分别求出它们的体积之比．解答：解：因为大小两个正方体的棱长比是2：3；所以大小正方体的体积比是（2×2×2）：（3××3）=8：27．故选：D．点评：此题主要考查正方体的体积公式．15．（•长寿区）一个正方体的棱长扩大2倍，它的体积扩大（）倍．A．2B．8C．4D．16考点：长方体和正方体的体积．分析：设原来的正方体的棱长是x，则后来的正方体的棱长是2x，根据“正方体的体积=棱长3”分别求出原来、后来两个正方体的体积，然后根据求一个数是另一个数的几倍用除法解答即可．解答：解：设原来的正方体的棱长是x，则后来的正方体的棱长是2x，则（2x）3÷x3，=8x3÷x3，=8；故选：B．点评：此题考查了正方体体积的计算方法，用到的知识点：求一个数是另一个数的几倍用除法解答．二．填空题（共13小题）16．一个正方体，高减少4厘米后，表面积就减少80平方厘米，现在长方体体积是25立方厘米；原来正方体的表面积是150平方厘米．考点：长方体和正方体的体积；长方体和正方体的表面积．专题：立体图形的认识与计算．分析：根据高减少4厘米，表面积减少80平方厘米，说明减少周围四个相同的面的面积是80平方厘米，根据80÷4=20平方厘米，再根据20÷4=5厘米，可知原来正方体的棱长为5厘米，现在高还是5﹣4=1厘米，根据长方体的体积计算公式可得现在体积为：1×5×5=25立方厘米，根据正方体的表面积计算公式S=6a2可解．解答：解：80÷4÷4=5（厘米）5﹣4=1（厘米）1×5×5=25（立方厘米）5×5×6=150（平方厘米）答：现在长方体的体积是25立方厘米，原来正方体的表面积是150平方厘米．故答案为：25；150．点评：本题理解减少的面积是相同的四个面，且高为4厘米，求出原来正方体的棱长是关键．17．一根3米长的方钢，把它横截成3段时，表面积增加80平方厘米，原来方钢的体积是6000立方厘米．考点：长方体和正方体的体积．分析：根据题意，可知截成3段后增加了4个横截面，表面积增加了80平方厘米，可计算出一个横截面的面积，根据正方体的体积公式底面积乘以高，可计算出原来方钢的体积，列式解答即可得到答案．解答：解：方钢的横截面面积为：80÷4=20（平方厘米），。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。