第十三讲:第九章 梁的弯曲-变形刚度计算解析
合集下载
梁弯曲时的变形和刚度计算
4) 计算最大转角和最大挠度。 有了转角方程和挠曲线方程,可以利用高等数学中求极值的方 法得到最大转角和最大挠度。但一般地,根据梁的受力、边界条件 以及弯矩的正负就能绘出挠曲线的大致形状,从而确定最大转角和 最大挠度发生的位置。在本例中梁的挠曲线应为一上凸曲线,并在 固定端处与梁变形前的轴线相切。由此可知,梁的最大转角和最大 挠度都发生在自由端B处。
目录
弯曲\梁的变形及刚度计算
最大转角发生在支座A (或支座B )处,其值为
max
A
ql3 24EI
()
目录
弯曲\梁的变形及刚度计算
1.4 用叠加法求梁的变形
积分法是求梁变形的基本方法。这种方法的优点是可以求得梁 的转角方程和挠曲线方程,从而求得梁任一横截面的转角和挠度。 其缺点是运算过程比较繁复,特别当梁上荷载复杂时,尤为明显。
2EI 3 2
w q ( x4 lx3 ) Cx D 2EI 12 6
简支梁在铰支座处的挠度均为零,即
x=0,w=0; x=l,w=0
目录
弯曲\梁的变形及刚度计算
将这两个边界条件代入方程,得
C ql3 , D 0 24EI
3) 求转角方程和挠曲线方程。 将所得的积分常数C、D值方程,得转角和挠曲线方程分别为
l
a qa3
6EI
B
C
qa3 6EI
(
)
目录
弯曲\梁的变形及刚度计算
1.5 梁的弯曲刚度计算
在工程中,根据强度条件对梁进行设计后,往往还要对梁进行 刚度计算。梁的刚度条件为
wmax
max
w
式中:wmax、max——梁的最大挠度和最大转角;
[w]、——许用挠度和许用转角。根据梁的用途,其值可在
目录
弯曲\梁的变形及刚度计算
最大转角发生在支座A (或支座B )处,其值为
max
A
ql3 24EI
()
目录
弯曲\梁的变形及刚度计算
1.4 用叠加法求梁的变形
积分法是求梁变形的基本方法。这种方法的优点是可以求得梁 的转角方程和挠曲线方程,从而求得梁任一横截面的转角和挠度。 其缺点是运算过程比较繁复,特别当梁上荷载复杂时,尤为明显。
2EI 3 2
w q ( x4 lx3 ) Cx D 2EI 12 6
简支梁在铰支座处的挠度均为零,即
x=0,w=0; x=l,w=0
目录
弯曲\梁的变形及刚度计算
将这两个边界条件代入方程,得
C ql3 , D 0 24EI
3) 求转角方程和挠曲线方程。 将所得的积分常数C、D值方程,得转角和挠曲线方程分别为
l
a qa3
6EI
B
C
qa3 6EI
(
)
目录
弯曲\梁的变形及刚度计算
1.5 梁的弯曲刚度计算
在工程中,根据强度条件对梁进行设计后,往往还要对梁进行 刚度计算。梁的刚度条件为
wmax
max
w
式中:wmax、max——梁的最大挠度和最大转角;
[w]、——许用挠度和许用转角。根据梁的用途,其值可在
第九章梁弯曲刚度

③物理方程——变形与力的关系
y Bq
=
ql 4 8 EI
; y BR B
=
RB l 3 3 EI
④补充方程
ql 4 - RB l 3 = 0 \ R
3ql =
8 EI 3EI
B
8
⑤求解其它问题(反力、应
力、变形等)
上一页 下一页
q
A l
y q
A EI
l
A
=
=
上一页 下一页
C EA a 例8 q,EI,EA,l 求B的反力。
上一页 下一页
AC段
( ) q = F 4 x 2 - l 2
1 16 EI
1
0 x
l
( ) y =
Fx 1
4 x 2 - 3l 2
1 2
1 48 EI
1
CB段
F
( ) q = 2 16EI
( ) y2
=
Fx2 48EI
4x22 - l 2
- F(2x2 - l) 2
8EI
l2 4x22 - 3l2
max
W
Z
B b
h
3M
得b
max
2 [s ]
=83mm
M图
h=2b=166mm
②按刚度计算
ymax
=
yB
= ql 4 8EI
A
I = bh3 = 2b4 12 3
根据刚度条件 y [y ] , 有 max
ql 4 l 8 EI 250
4
b
3´ 250´ ql3 2´ 8E
= 89.6(mm)
EIy″=M(x) 积分一次得角方程
EIy' = EIq = M (x)dx+ C
材料力学第9章--梁的挠度和刚度计算

3
9.4 叠加法求梁的变形
在小变形条件下,材料服从虎克定律
内力
Fs , M 与外力 q, P, M 0 成线性关系
几个载荷共同作用的变形 === 各个载荷单独作用的变形之和
叠加原理
例9.4
简支梁的EI已知,用叠加法
q
ql
求梁跨中截面的位移和支座B的转角。 A
B
载荷分解如图 均布载荷单独作用时
6 最大挠度
when
0 w1
Fb 2 Fb 2 2 x l b 0 2l 6l
a l b a a 2b l 2 b2 x 3 3 3 if a b then x a Fb wmax w1 ( x ) 9 3EIl if a b then x a wmax Fl 3 48EI
5ql 4 ql 3 wC1 , q B1 384 EI 24 EI ql 4 ql 3 wC 2 , qB2 16EI 3EI 叠加 19ql 4 wC wC1 wC 2 384 EI 7 ql 3 q B q B1 q B 2 24 EI
wmax
挠曲线
P
x
挠曲线方程
挠曲线:梁弯曲后,梁轴线所成的曲线 挠度:梁截面形心在垂直于梁的初始轴线方向的位移
w w( x ) dw x 转角:梁截面相对于变形前的位置转过的角度 q tan q
dx
符号给定:
正值的挠度向下,负值的向上;正值的 转角为顺时针转相,负值的位逆时针转向
2,意义
4
3
7 梁两端的转角
ql 3 EIq A EIq |x 0 24 1 3 ql 2 ql 3 ql 3 EIq B EIq |x l ql l 6 4 24 24
第九章 平面弯曲杆件的变形与刚度计算

若梁上只有第i个载荷单独作用,截面上弯矩 为 M i ( x ) ,转角为 i ,挠度为 yi ,则有:
EIy''i M i ( x)
由弯矩的叠加原理知: M i ( x) M ( x)
i 1
n
所以,
7-4
EI y' 'i EI ( yi )' ' M ( x)
q
C L/2 L/2
2、查梁的简单载荷变形表
=
5(q ) L4 2 yCa ; yCb 0 384EI 3、叠加
q/2
AA
L/2
q/2
C L/2
yC yCa yCb yCa 0
4 5(q ) L4 5 qL 2 384EI 768EI
积分一次得转角方程为:
dy EI z EI z M ( x)dx C dx
再积分一次得挠度方程为:
EI z y M ( x) dxdx C x D
7-3
目录
§9-3 用积分法求弯曲变形
积分常数C、D 由梁的位移边界条件和光滑连续 条件确定。 位移边界条件
M 1 ( x) EIy1 M 2 ( x) EIy2 M 3 ( x) EIy3
叠加法计算梁的变形
EIy M ( x)
y2 y3 y y1 M ( x) M 1 M 2 M 3
一、前提条件:弹性、小变形。 二、叠加原理:各荷载同时作用下,梁任一截面的挠度或转角,等 于各荷载分别单独作用下同一梁同一截面挠度或转角的代数和。
右侧段(a≤x2≤L):
Fb Fb EIy2 x2 F ( x 2 a ) EIy1 x1 L L 2 Fb F ( x a ) Fb 2 2 2 EIw2 x2 C2 EIy1 x1 C1 2L 2 2L Fb 3 Fb 3 F ( x2 a ) 3 EIy1 x1 C1 x1 D1 EIy2 x2 C2 x2 D2 6L 6L 6
工程力学第9章 梁弯曲时的刚度计算
挠曲线
w
x
qx
F
x
9.1 挠曲线近似微分方程
9.1.2 挠度和转角的关系
◆挠曲线方程 : w f x
w
挠曲线
w
x
qx
F
x
tan dw
dx
dw
dx
9.1.3 挠曲线近似微分方程
一、挠曲线的曲率公式
1M EI
1
x
M x
EI
d2w
1
x
6EI 2l
l 2
2l 2
l 2
2
11Fl3 96EI
未知约束力单独作用引起的B处挠度
wB FB
FB 2l 3
48EI
FBl 3 6EI
将上述结果代入式(b),得到补充方程
11Fl3 FBl3 0 96EI 6EI
w Mex x2 l2 6EIl
(c)
Me 3x2 l2 6EIl
(d)
(4)计算最大挠度与截面的转角
作出梁的弯矩图如下图所示,全梁弯矩为正。其最大 挠度处的转角为零。故由式(c)有
dw Me 3x2 l2 0 dx 6EIl
从而得最大挠度所在截面的坐标为
2
在集中力 F 单独作用下,大梁跨度中点C的挠度由教材表
7–1第5栏中查出为
wC
F
Fl 3 48EI
将以上结果叠加,即得在均布载荷 和q 集中力 的F 共同作用
下,大梁跨度中点C的挠度
w
x
qx
F
x
9.1 挠曲线近似微分方程
9.1.2 挠度和转角的关系
◆挠曲线方程 : w f x
w
挠曲线
w
x
qx
F
x
tan dw
dx
dw
dx
9.1.3 挠曲线近似微分方程
一、挠曲线的曲率公式
1M EI
1
x
M x
EI
d2w
1
x
6EI 2l
l 2
2l 2
l 2
2
11Fl3 96EI
未知约束力单独作用引起的B处挠度
wB FB
FB 2l 3
48EI
FBl 3 6EI
将上述结果代入式(b),得到补充方程
11Fl3 FBl3 0 96EI 6EI
w Mex x2 l2 6EIl
(c)
Me 3x2 l2 6EIl
(d)
(4)计算最大挠度与截面的转角
作出梁的弯矩图如下图所示,全梁弯矩为正。其最大 挠度处的转角为零。故由式(c)有
dw Me 3x2 l2 0 dx 6EIl
从而得最大挠度所在截面的坐标为
2
在集中力 F 单独作用下,大梁跨度中点C的挠度由教材表
7–1第5栏中查出为
wC
F
Fl 3 48EI
将以上结果叠加,即得在均布载荷 和q 集中力 的F 共同作用
下,大梁跨度中点C的挠度
材料力学——第9章(平面弯曲杆件的变形与刚度计算)

a
A
x1
F C
b
Fa l
当 a>b 时——
6lEI
B
max
x2
Fab( l a ) max B 6lEI 当 a>b 时——最大挠度发生在AC段
0 x l 2 b2 3 a( a 2b ) 3
xa
最大挠度一定在左侧段
x x
max 1
2 Fb 1 ( x x ) ( l b 2 )3 9 3 EIl
19
Fb l
讨论:1、此梁的最大挠度和最大转角。 左 1 max 1 0 x1 0 右 2 max 2 0 x 2 l 侧 侧 Fab( l b ) Fab( l a ) 段: 1 max A 段: 2 max B 6lEI
§9-1 挠曲线 挠度和转角
§9-2 挠曲线的近似微分方程
§9-3 积分法求梁的变形 §9-4 叠加法求梁的变形 §9-5 梁的刚度条件与合理刚度设计 §9-6 用变形比较法解简单超静定梁
1
研究范围:等直梁在对称弯曲时位移的计算。 研究目的:①对梁作刚度校核; ②解超静定梁(为变形几何条件提供补充方程)。
式中,C1、D1是积分常数,可通过梁的边界条件(支座 的约束条件)确定。
梁上有集中力、集中力偶以及间断性分布荷载作用时,弯 矩方程需分段写出,各梁段的挠曲线近似微分方程也不同。积 分常数还要利用连续性条件,才能求出。 7
二、位移边界条件
A F C B F D
支座位移条件: A 0 B 0 Nhomakorabea
18
⑸跨中点挠度及两端端截面的转角
x L 2
梁的变形与刚度计算
材料——梁的位移与材料的弹性模量 E 成反比; 截面——梁的位移与截面的惯性矩 I 成反比; 跨长——梁的位移与跨长 L 的 n 次幂成正比。 (转角为 L 的 2 次幂,挠度为 L的 3 次幂) 1、增大梁的抗弯刚度(EI) 2、调整跨长和改变结构 方法——同提高梁的强度的措施相同
3、预加反弯度(预变形与受力时梁的变形方向相反,目的起到 一定的抵消作用)
B
查表,得
y
C
y4Biblioteka CqyCm
l
q
A
2 5ql ml 384EI 16 EI
()
Bq
θA θAq θAm
3 ml ql 24 EI 3EI
Aq
m
A
C y cq
(
)
Bm
Am
C ycm
θB θBq θBm
3 ml ql 24 EI 6 EI
(
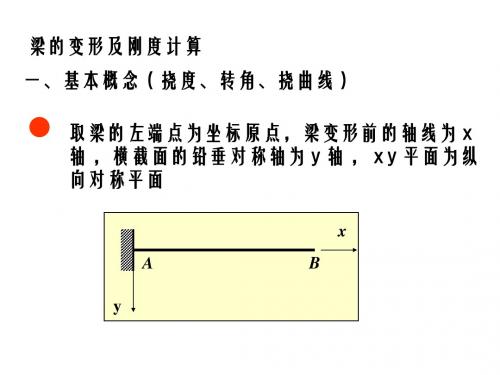
梁的变形及刚度计算 一、基本概念(挠度、转角、挠曲线) 取梁的左端点为坐标原点,梁变形前的轴线为 x 轴 ,横截面的铅垂对称轴为 y 轴 , x y 平面为纵 向对称平面
x
A
y
B
一、基本概念(挠度、转角、挠曲线)
度量梁变形后横截面位移的两个基本量 1、挠度( y): 横截面形心 C (即轴线上的点)在垂直于 x
A C
B
x
C'
y
转角
y挠度
B
转角方程:一般各横截面的转角是不相同的,是位置x的 函数,称为转角方程,记做= (x)
一、基本概念(挠度、转角、挠曲线)
3、挠曲线 :梁变形后的轴线 称为挠曲线 。 挠曲线方程为 y y ( x) ——挠度方程
3、预加反弯度(预变形与受力时梁的变形方向相反,目的起到 一定的抵消作用)
B
查表,得
y
C
y4Biblioteka CqyCm
l
q
A
2 5ql ml 384EI 16 EI
()
Bq
θA θAq θAm
3 ml ql 24 EI 3EI
Aq
m
A
C y cq
(
)
Bm
Am
C ycm
θB θBq θBm
3 ml ql 24 EI 6 EI
(
梁的变形及刚度计算 一、基本概念(挠度、转角、挠曲线) 取梁的左端点为坐标原点,梁变形前的轴线为 x 轴 ,横截面的铅垂对称轴为 y 轴 , x y 平面为纵 向对称平面
x
A
y
B
一、基本概念(挠度、转角、挠曲线)
度量梁变形后横截面位移的两个基本量 1、挠度( y): 横截面形心 C (即轴线上的点)在垂直于 x
A C
B
x
C'
y
转角
y挠度
B
转角方程:一般各横截面的转角是不相同的,是位置x的 函数,称为转角方程,记做= (x)
一、基本概念(挠度、转角、挠曲线)
3、挠曲线 :梁变形后的轴线 称为挠曲线 。 挠曲线方程为 y y ( x) ——挠度方程
第十三讲:第九章 梁的弯曲-变形刚度计算概要

例11
求图示梁的挠曲线方程和转角方程。EI为常量。
Me A
x
e
解:
1.列微分方程并积分
B
M e Me x e M e FAy= M M EIy xx M l l l Me 2 EIy x Me x C 2l Me 3 Me 2 EIy x x Cx D 6l 2
33 5 Fl Fl Fl 2 l 6EI EI 2 EI 3
五、 叠加法求梁的变形
基本原理 由几个外力同时作用时所引起的梁的变形 转角和挠度 等于
由各个外力单独作用时所引起的梁的变形的代数和
q F M
e
y yq y F y M e
例13 求B和yB 解: 1. Me单独作用时 2Mel BM e EI 2 2 2 M l M 2 l e y BM e e EI 2 EI 2. F单独作用时 2 Fl BF CF 2 EI yBF yCF CF l
一、梁的变形度量——挠度与转角
x
1 1'
F
A
C
B
x
y
C'
y
1'
1
y f ( x)
——挠曲线方程
一、梁的变形度量——挠度与转角
x
1 1'
F
A
C
B
x
y
1'
y
C'
1
在小变形下: 即:
dy y tan dx
——转角方程
任一横截面的转角 = 挠曲线在该截面形心处切线的斜率
2.数学方面
A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
FAy=
Me l
6EIl
FBy=
Me l
l
3.求 ymax
由 =0,
x0 1
3 3
l
0.423l
ymax
yx0
0.0642
Mel 2 EI
yC
y
l 2
0.0625
Mel 2 EI
可见:yC与ymax相差很小,两者相差不到ymax的3%。
对于简支梁,只要挠曲线上无拐点,总可以用跨中挠度
工代程替上最通大常挠采度用,中并点且的不挠会度引值起作很为大设误计差依。据
,
yBFBy
FBy l 3 3 EI
A
代入上式,解得
3 FBy 8 ql
B 原结构
B 静定基 FBy
例11 求图示梁的挠曲线方程和转角方程。EI为常量。
解:
Me
4.画挠曲线的大致形状
A
x
FAy=
Me l
l
M Me
B
FBy=
Me l
x
例12 求图示梁的弯曲变形
解:
A
x
F C
x
Me B
l
l
AC段:
CB段:
EIy1 MM1exFl x
EIy1
Fx2 2
Me
Fl x
C1
EIy1
Fx3 6
Me
Flx2
2
C1x
D1
EIy2 Me2x
EIy2 Me x C2
EIy2
Me x2 2
C2x
D2
边界条件: 连续条件:
x 0 1 0
y1 0
x l 1 2
y1 y2
C1 0
D1 0 Fl 2
C2 2 Fl 3
D2 6
B
2Mel EI
Fl 2 2EI
yB
2Mel 2 EI
5Fl 3 6EI
B x
一、梁的变形度量——挠度与转角
x
1 1'
F
A
C
y
C' y
1' 1
B x
y f ( x) ——挠曲线方程
一、梁的变形度量——挠度与转角
在小变形下: 即:
x
1 1'
F
A
C
y
C'
y
1' 1
tan dy y
dx
B x
——转角方程
任一横截面的转角 = 挠曲线在该截面形心处切线的斜率
求梁变形的关键是求挠曲线方程
对于等直杆 转角方程: 挠曲线方程:
EIy Mx
EI Mxdx C EIy Mxdxdx Cx D
四、位移条件
1. 已约知束位条移件条件 2. 位移连续条件
挠度连续——连续性条件 转角连续——光滑性条件
F
x
y
x=l,y=0
=0
F x0
A
1
2B
x
x = 0, y = 0 x = x0 , y 1= y 2 x = l , y = 0
y ( = 0)
1 = 2
( = 0)
例11 求图示梁的挠曲线方程和转角方程。EI为常量。
解:
Me
1.列微分方程并积分
A
EIy
MMe l
xMxl eMxe
Me
FAy=
Me l
x
EIy
Me 2l
x2
Mex C
l
B
FBy=
Me l
EIy Me x3 Me x2 Cx D
6l
2
2.确定积分常数
5Fl 3 6EI
梁的刚度条件与梁的合理设计
一、梁的刚度条件
[ ] max
y [ y] max
式中
[ ]——许用转角 [ y]——许用挠度
二、梁的合理设计
由 EIy Mx出发:
1.提高梁的抗弯刚度 2.减小梁跨度 3.改善梁的受力情况
简单超静定梁的解法
超静定梁 ——仅用平衡方程不能求出全部约束反力的梁 多余约束 ——就维持梁的平衡而言所不必要的约束 多余约束力 ——与多余约束相应的约束反力 超静定次数 ——多余约束的个数
由 y 0, x0
D0
y Me 3x2 6lx 2l 2 6EIl
由 y 0, xl
C Mel 3
y Me x x2 3lx 2l 2 6EIl
例11 求图示梁的挠曲线方程和转角方程。EI为常量。
解:
Me
Me 3x2 6lx Me x x2 3lx 2l 2
第四节 弯曲变形和刚度计算
一、梁的变形度量——挠度与转角 二、挠曲线近似微分方程 三、积分法求梁的变形 四、位移条件
一、梁的变形度量——挠度与转角
x
1 1'
A
C
C' y
1' 1
挠曲线——梁在受力变形后的轴线,
F B x
又称为弹性曲线
若忽略剪力的影响,横截面绕其自身中性轴旋转
一、梁的变形度量——挠度与转角
一次超静定梁
二次超静定梁
变形比较法
超静定梁的解法
1.选择静定基
2.通过比较多余约束处的变形求出多余约束力
例 14 试作图示超静定梁的剪力图和弯矩图。
解: 一次超静定
q
1.取静定基
A
l
设FBy为多余约束力
2.求FBy
q A
列变形几何方程
yB yBq yBFBy 0
q
查表
A
yBq
ql 4 8EI
二、挠曲线近似微分方程
1.力学方面
CD段:纯弯曲
1 M
EI
AC段:横力弯曲
(忽略剪力的影响)
x
1
x
Mx
EI
x
aF
A
C
x y
F
FQ
Fa
M
Fa
D
B
x
F
二、挠曲线近似微分方程
1.力学方面
x Mx
EI
2.数学方面
x
1
y y2
32
x
aF
A
C
x y
3.挠曲线近似微分方程
y
Mx
1 y2 3 2 EI
x
1 1'
F
A
C
y
C'
y
1' 1
B x
挠度(y)
—— 横截面形心沿垂直于轴线方向的线位移 称为该点(横截面的形心)的挠度 向上为正,向下为负
一、梁的变形度量——挠度与转角
x
1 1'
F
A
C
y
C'
y
1' 1
转角()
—— 横截面绕其中性轴旋转的角度 称为该横截面的转角
顺时针转为正,逆时针转为负
挠度与转角是度量梁的变形的两个基本量
A
F C
Me B
l
l
yBMe
BMe B M e
2. F单独作用时
BF
CF
Fl 2 2EI
yBF yCF CF l
5FFl l33 Fl 2 l
36EEII 2EI
3. Me和F共同作用时
F
C
B
A
yBF
BF
B
BMe
BF
2Mel EI
Fl 2 2EI
yB
y BM e
yBF
2Mel 2 EI
Fa
D
B
x
二、挠曲线近似微分方程
y
Mx
1 y2 3 2 EI
O
x
M
M
y
符号处理: y"与M(x)恒异号
O
x
1
y y2
32
Mx
EI
M
M
y
——挠曲线微分方程
在小变形情况下,通常 <1,而tan1=0.017, y'2<<1
EIy M x ——挠曲线近似微分方程
三、积分法求梁的变形
五、 叠加法求梁的变形
基本原理 由几个外力同时作用时所引起的梁的变形
等于
转角和挠度
由各个外力单独作用时所引起的梁的变形的代数和
q F Me y yq yF yMe
例13 求B和yB
解:1. Me单独作用时
A
BM e
2Mel EI
yBM e
Me 2l
2EI
2
2Mel EI
2
