第8章习题解答

合集下载

初二物理第八章练习题含答案

初二物理第八章练习题含答案1. 选择题(1) 以下属于力的性质是:A. 大小B. 方向C. 作用点D. 面积答案：A、B、C(2) 能够使物体发生位移的只有:A. 摩擦力B. 重力C. 弹力和悬挂力D. 正确答案全部都对答案：C(3) 法拉第一定律指出的是:A. 外力作用于物体上时，物体一定保持静止或匀速直线运动B. 外力作用于物体上时，物体的速度将发生变化C. 物体受到的合力为零时，物体一定保持静止或匀速直线运动D. 物体受到的合力为零时，物体的速度将发生变化答案：C2. 填空题(1) 一个力从右往左作用于一个物体，这个物体产生的反作用力的方向是______。

答案：从左往右(2) 一个力从上往下作用于一个物体，这个物体产生的反作用力的方向是______。

答案：从下往上(3) 一个物体受到A力的作用产生加速度a，如果力A的大小不变，改变作用方向，则产生的加速度为______。

答案：-a3. 解答题(1) 什么是力？力的三要素是什么？解答：力是物体之间相互作用的结果，是导致物体发生变化的原因。

力的三要素包括大小、方向和作用点。

大小表示力的强弱程度，方向表示力作用的直线方向，作用点表示力作用的具体位置。

(2) 什么是合力？如何求合力？解答：合力是同时作用在物体上的多个力的共同效果。

求合力的方法是将所有作用在物体上的力按照大小和方向合成，可以通过向量法或图示法来求解。

(3) 描述牛顿第一定律，并用实例说明其应用。

解答：牛顿第一定律也称为惯性定律，指出在没有外力作用时，物体将保持静止或匀速直线运动的状态。

例如，当我们用力推动一张光滑的桌子上的书时，如果力的大小和方向适当，书就会保持匀速直线运动，直到受到其他力的作用。

这说明物体在没有外力干扰时具有惯性，保持原来的状态不发生变化。

总结：初二物理第八章练习题主要涉及力的性质和作用、法拉第一定律等内容。

通过选择题和填空题加深对知识点的理解，同时通过解答题展开思考和拓展。

高等数学习题详解-第8章二重积分

习题8-11. 设有一平面薄片，在xOy 平面上形成闭区域D ，它在点(x ,y )处的面密度为μ(x ,y )，且μ(x ,y )在D 连续，试用二重积分表示该薄片的质量. 解：(,)Dm x y d μσ=⎰⎰.2. 试比较下列二重积分的大小：(1) 2()Dx y d σ+⎰⎰与3()Dx y d σ+⎰⎰，其中D 由x 轴、y 轴及直线x +y =1围成；(2)ln()Dx y d σ+⎰⎰与2ln()Dx y d σ+⎡⎤⎣⎦⎰⎰，其中D 是以A (1,0)，B (1,1)，C (2，0）为顶点的三角形闭区域.解：(1)在D 内，()()2301x y x y x y ≤+≤+≥+，故，23()()DDx y d x y d σσ+≥+⎰⎰⎰⎰.(2) 在D 内，212ln()1,ln()ln ()x y x y x y x y ≤+≤≤+≤+≥+，故0从而, 2ln()[ln()]DDx y d x y d σσ+≥+⎰⎰⎰⎰习题8-21. 画出积分区域，并计算下列二重积分：(1) ()Dx y d σ+⎰⎰，其中D 为矩形闭区域：1,1x y ≤≤；(2) (32)Dx y d σ+⎰⎰，其中D 是由两坐标轴及直线x +y =2所围成的闭区域；(3) 22()D xy x d σ+-⎰⎰,其中D 是由直线y =2,y =x ,y =2x 所围成的闭区域；(4) 2Dx y d σ⎰⎰,其中D 是半圆形闭区域:x 2+y 2≤4,x ≥0；(5) ln Dx y d σ⎰⎰,其中D 为:0≤x ≤4,1≤y ≤e ；(6)22Dx d σy ⎰⎰其中D 是由曲线11,,2xy x y x ===所围成的闭区域. 解：(1) 111111()()20.Dx y d dx x y dy xdx σ---+=+==⎰⎰⎰⎰⎰ (2) 222200(32)(32)[3(2)(2)]x Dx y d dx x y dy x x x dx σ-+=+=-+-⎰⎰⎰⎰⎰223202220[224]4.330x x dx x x x =-++=-++=⎰(3) 32222222002193()()()248yy Dy x y x d dy x y x dx y dy σ+-=+-=-⎰⎰⎰⎰⎰43219113.96860y y -= (4) 因为被积函数是关于y 的奇函数，且D 关于x 轴对称，所以20.Dx yd σ=⎰⎰(5) 44201041ln ln (ln ln )2(1)2110e De e e x yd dx x ydy x y y y dx x e σ-==-==-⎰⎰⎰⎰⎰.(6) 122224111311122222119()()124642x x Dx x x x x x d dx dy dx x x dx y y y x σ==-=-=-=⎰⎰⎰⎰⎰⎰.2. 将二重积分(,)Df x y d σ⎰⎰化为二次积分（两种次序）其中积分区域D 分别如下：(1) 以点(0,0),(2,0),(1,1)为顶点的三角形；(2) 由直线y =x 及抛物线y 2=4x 所围成的闭区域；(3) 由直线y =x ,x =2及双曲线1y x=所围成的闭区域；(4) 由曲线y =x 2及y =1所围成的闭区域. 解：(1) 1221201(,)(,)(,).xx y ydx f x y dy dx f x y dy dy f x y dx --+=⎰⎰⎰⎰⎰⎰(2) 2441004(,)(,).y x y dx f x y dy dy f x y dx =⎰⎰⎰⎰(3) 12222111112(,)(,)(,).xyyxdy f x y dx dy f x y dx dx f x y dy +=⎰⎰⎰⎰⎰⎰(4) 21111(,)(,).xdx f x y dy dy f x y dx -=⎰⎰⎰3. 交换下列二次积分的积分次序：(1) 10(,)ydy f x y dx ⎰⎰；（2）2220(,)yydy f x y dx ⎰⎰；(3) ln 10(,)e xdx f x y dy ⎰⎰； (4) 123301(,)(,)y ydy f x y dx dy f x y dx -+⎰⎰⎰⎰.解：(1) 111(,)(,)yxdy f x y dx dx f x y dy =⎰⎰⎰⎰.(2) 222402(,)(,).y x ydy f x y dx dx f x y dy =⎰⎰⎰⎰(3) ln 11(,)(,)y e xeedx f x y dy dy f x y dx =⎰⎰⎰⎰(4) 123323012(,)(,)(,)yyxxdy f x y dx dy f x y dx dx f x y dy --+=⎰⎰⎰⎰⎰⎰.4. 求由平面x =0,y =0,x =1,y =1所围成的柱体被平面z =0及2x +3y +z =6截得的立体体积.解：11100037(623)(62).22V dx x y dy x dx =--=--=⎰⎰⎰5. 求由平面x =0,y =0,x +y =1所围成的柱体被平面z =0及曲面x 2+y 2=6－z 截得的立体体积.解：3111222000(1)34(6)[6(1)(1)).312x x V dx x y dy x x x dx --=--=----=⎰⎰⎰习题8-31. 画出积分区域，把二重积分(,)Df x y d σ⎰⎰化为极坐标系下的二次积分,其中积分区域D是：(1) x 2+y 2≤a 2 (a >0)； (2) x 2+y 2≤2x ；(3) 1≤x 2+y 2≤4； (4) 0≤y ≤1－x ,0≤x ≤1. 解：(1) 20(,)(cos ,sin ).aDf x y d d f r r rdr πσθθθ=⎰⎰⎰⎰(2) 2cos 202(,)(cos ,sin ).Df x y d d f r r rdr πθπσθθθ-=⎰⎰⎰⎰(3) 221(,)(cos ,sin ).D f x y d d f r r rdr πσθθθ=⎰⎰⎰⎰(4)12cos sin 0(,)(cos ,sin ).Df x y d d f r r rdr πθθσθθθ+=⎰⎰⎰⎰2. 把下列积分化为极坐标形式，并计算积分值：(1)22220()aa y dy x y dx -+⎰⎰；(2)21220;xxdx x y dx +⎰⎰解：(1)224422320()248aa y aa a dy x y dx d r dr πππθ-+==⋅=⎰⎰⎰⎰. (2) 22sin 3122244cos 600001sin 3cos x x dx x y dx d r dr d πθπθθθθθ+==⎰⎰⎰⎰⎰244466400011cos 111(cos )[(cos )(cos )]33cos cos cos d d d πππθθθθθθθ-=-=--⎰⎰⎰ 532(21)1cos cos 4().3530πθθ--+=--+= 3. 在极坐标系下计算下列二重积分：(1)22x y De d σ+⎰⎰,其中D 是圆形闭区域: x 2+y 2≤1；(2) 22ln(1)Dxy d σ++⎰⎰,其中D 是由圆周x 2+y 2=1及坐标轴所围成的在第一象限内的闭区域；(3)arctanDyd σx⎰⎰，其中D 是由圆周x 2+y 2=1,x 2+y 2=4及直线y =0,y =x 所围成的在第一象限内的闭区域；(4)222DR x y d σ--其中D 由圆周x 2+y 2=Rx (R >0)所围成.解：(1) 22222100112(1).20xy r r De d d e rdr e e πσθππ+==⋅=-⎰⎰⎰⎰(2)23112222221ln(1)ln(1)[ln(1)]221Dr r xy d d r rdr r dr rππσθ++=+=+-+⎰⎰⎰⎰⎰ 212(1)[ln 22](2ln 21)441r r r dr rππ+-=-=-+⎰. (3) 222244010133arctan arctan(tan ).32264Dy d d rdr d rdr x ππππσθθθθ=⋅==⋅=⎰⎰⎰⎰⎰⎰(4)222DR x y d σ--3cos 2222222022cos 12()230R R d R r rdr R r d ππθππθθθ--=-=--⎰⎰⎰3333221(sin )33R R R d πππθθ-=--=⎰.4. 求由曲面z =x 2+y 2与22z x y =+所围成的立体体积.解：两条曲线的交线为x 2+y 2=1，因此，所围成的立体体积为：21222220[()]().6DV x y x y d d r r rdr ππσθ=++=-=⎰⎰⎰⎰习题8-41. 计算反常二重积分()x y De dx dy -+⎰⎰，其中D ：x ≥0,y ≥x .2. 计算反常二重积分222()Ddx dyx y +⎰⎰，其中D ：x 2+y 2≥1. 解：1.22201()2a aaax yx x aaa xe dx edy eedx e e ---------=-=-+-⎰⎰⎰所以2()211lim ().22a x y a a a De edxdy e e --+--→+∞-=-+-=⎰⎰2. 由232011112()22R d dr r R πθπ=-⎰⎰，得222211lim 2().2()2R Ddxdy x y R ππ→+∞=-=+⎰⎰复习题8（A ）1. 将二重积分d d (,)Df x y x y ⎰⎰化为二次积分(两种次序都要)，其中积分区域D 是：(1) ︱x ︱≤1,︱y ︱≤2;(2) 由直线y =x 及抛物线y 2=4x 所围成. 解：(1) 12211221(,)(,).dx f x y dy dy f x y dx ----=⎰⎰⎰⎰(2) 2424004(,)(,).xyy xdx f x y dy dy f x y dx =⎰⎰⎰⎰2. 交换下列两次积分的次序： (1)d d 10(,)yyy f x y x ⎰⎰;(2)d d 2220(,)a ax x x f x y y -⎰⎰;(3)d d +d d 12201(,)(,)xxx f x y y x f x y y -⎰⎰⎰⎰．解：(1) 211d (,)d d (,)d y x yxy f x y x x f x y y =⎰⎰⎰⎰.(2) 222222200d (,)d d (,)d aax x aa a y a a y x f x y y y f x y x -+---=⎰⎰⎰⎰.(3)1221201d (,)d +d (,)d d (,)d xxy yx f x y y x f x y y y f x y x --=⎰⎰⎰⎰⎰⎰.3. 计算下列二重积分：(1) e d x y Dσ+⎰⎰， D : ︱x ︱≤1,︱y ︱≤1;(2) d d 2D xy x y ⎰⎰,D 由直线y =1,x =2及y =x 围成；(3) d d (1)Dx x y -⎰⎰,D 由y =x 和y =x３围成；(4) d d 22()Dx y x y +⎰⎰，D :︱x ︱+︱y ︱≤1; (5) d 1sin Dy σy ⎰⎰，D 由22y x π=与y =x 围成； (6)d (4)Dx y σ--⎰⎰，D 是圆域x 2＋y 2≤R 2；解: (1) 1111111211111e d ()()()1x y x y x x x x Ddx e dy e e dx e e e e σ+++-+----==-=-=--⎰⎰⎰⎰⎰.(2)5322224211121129d d ()()2253151xDx x xy x y dx x ydy x x dx ==-=-=⎰⎰⎰⎰⎰.(3) 3112430011117(1)d d (1)()325460x x Dx x y dx x dy x x x x dx -=-=--+=--+=-⎰⎰⎰⎰⎰.(4)1122220()d d 4()xDx y x y dx x y dy -+=+⎰⎰⎰⎰33241201412124(2)4()33323330x x x x x x dx x =--+=--+=⎰. (5) 222200sin 12sin d (sin sin )y y Dy y dy dx y y y dy y y πππσπ==-⎰⎰⎰⎰⎰222222sin (cos )1(cos sin )10ydy yd y y y y ππππππ=+=+-=-⎰⎰. (6)322200(4)d (4cos sin )[2(cos sin )]3RDR x y d r r rdr R d ππσθθθθθθ--=--=-+⎰⎰⎰⎰⎰3222[2(sin cos )]430R R R πθθθπ=--=.4. 已知反常二重积分e d 2y Dx σ-⎰⎰收敛，求其值．其中D 是由曲线y =4x 2与y =9x 2在第一象限所围成的区域．解：设2249(0)a D y x y x y a a ===>是由曲线、和在第一象限所围成.则22222200015555ed ()236144144144aaa a y y y y a D x dy dx ye dy e d y e σ-----==⋅=--=-⎰⎰⎰⎰⎰. 所以225e d lime d 144ay ya DD x x σσ--→+∞==⎰⎰⎰⎰. 5. 计算e d 2x x +∞--∞⎰．解：由第四节例2以及2y =e x -是偶函数，可知2e d x x +∞--∞=⎰.6. 求由曲面z =0及z =4-x 2-y 2所围空间立体的体积．解：曲面z =0和z =4-x 2-y 2的交线为x 2+y 2 =4.因此，所围空间立体的体积为：222220016(4)d d (4)2(8)84D x y x y d r rdr πθππ--=-=-=⎰⎰⎰⎰.7. 已知曲线y =ln x 及过此曲线上点(e ，1）的切线ey x 1=．(1) 求由曲线y =ln x ，直线ey x 1=和y =0所围成的平面图形D 的面积；(2) 求以平面图形D 为底，以曲面z =e y 为顶的曲顶柱体的体积．解：(1) 1ln (ln )12221e e e ee S xdx x x x =-=--=-⎰.(2) 221120013()()2220y y e yyyy y ye e V dy e dx e ye dy ye e ==-=-+=-⎰⎰⎰.（B ）1. 交换积分次序：(1) 311(,)xxdx f x y dy -⎰⎰；（2）0112(,)y dy f x y dx --⎰⎰；(3) 224(,)x x f x y dy -⎰；(4) 110(,)dx f x y dy ⎰.解：(1) 3111(,)(,)x xydx f x y dy dy f x y dx -=⎰⎰⎰.(2) 01101221(,)(,)yxdy f x y dx dx f x y dy ---=⎰⎰⎰⎰.(3) 2242402(,)(,)(,)x x f x y dy dy f x y dx dy f x y dx -=+⎰⎰⎰.(4) 211121(,)(,)(,)y dx f x y dy dy f x y dx dy f x y dx =+⎰⎰⎰⎰.2. 计算积分2122x xxdx dy x y +⎰⎰.解：222sin sin 144cos cos 2220000cos cos xxx r dx dy d rdr d dr x y r πθπθθθθθθθ==+⎰⎰⎰⎰⎰⎰ 40sin ln 24(ln cos )cos 2d ππθθθθ==-=⎰. 3. 计算积分112201yy dy dx x y ++⎰⎰.解：111114cos 4cos cos 2222000sin sin [sin ]111yy r dy dx d rdr d dr dr x y r r ππθθθθθθθθ==-++++⎰⎰⎰⎰⎰⎰⎰ 44001ln 21(tan sin arctan )arctan (cos )cos 2cos d d ππθθθθθθ=-⋅=+⎰⎰令cos t θ=,则原式211ln 21ln 21ln 211(arctan ln(12222dt dt t t t t t =+=+=+++ln 213ln 213ln ln 22242224ππ=+--=-. 4. 设函数f (x )在区间0,1⎡⎤⎣⎦上连续，且1()f x dx A =⎰，求11()()xdx f x f y dy ⎰⎰. 解：设1'()()()(1)(0)F x f x f x dx F F A ==-=⎰，则.11111()()()[(1)()](1)()()(())xdx f x f y dy f x F F x dx F f x dx F x d F x =-=-⎰⎰⎰⎰⎰21()111(1)(1)[(1)(0)][(1)(0)](1)(1)(0)22220F x F A F A F F F F F A AF AF =-=--+=--21[(1)(0)]22A A F F =-=. 5. 计算2Dx y d σ⎰⎰，其中D 是由直线y =0,y =1及双曲线x 2－y 2=1所围成的闭区域.解：11222022(13Dx yd dy ydx y y σ==+⎰⎰⎰⎰35122222011122(1)(1)(1)1)335150y d y y =++=⋅+=⎰. 6. 计算222y xdx e dy ⎰⎰.解：2222222240000211(1)220y y y y y x dx e dy dy e dx ye dy e e ====-⎰⎰⎰⎰⎰.7. 证明211()()d ()()d 1b x bn n a a adx x y f y y b y f y y n ---=--⎰⎰⎰，其中n 为大于1的正整数. 证：22()()d ()()b x b bn n aaaydx x y f y y dy x y f y dx ---=-⎰⎰⎰⎰11()()1bn b yax y f y dy n -=--⎰11()()d 1bn ab y f y y n -=--⎰。

第8章习题答案

第八章多态1.单选题（1）．下列关于运算符重载的描述中，( D )是正确的。

(A) 可以改变参与运算的操作数个数 (B) 可以改变运算符原来的优先级(C) 可以改变运算符原来的结合性(D) 不能改变原运算符的语义（2）．下列函数中，不能重载运算符的函数是( b )。

(A) 成员函数(B) 构造函数(C) 普通函数 (D) 友员函数（3）．要求用成员函数重载的运算符是( A )。

(A) =(B) == (C) <= (D) ++（4）．要求用友员函数重载的运算符是( C )。

(A) = (B) [] (C) <<(D) ()（5）．在C++中，要实现动态联编，必须使用( D )调用虚函数。

(A) 类名(B) 派生类指针(C) 对象名(D) 基类指针（6）．下列函数中，不能说明为虚函数的是( C )。

(A) 私有成员函数(B) 公有成员函数(C) 构造函数(D) 析构函数（7）．在派生类中，重载一个虚函数时，要求函数名、参数的个数、参数的类型、参数的顺序和函数的返回值( A )。

(A) 相同(B)不同(C) 相容(D) 部分相同（8）．C++中，根据（D ）识别类层次中不同类定义的虚函数版本。

(A) 参数个数(B) 参数类型(C) 函数名(D) this指针类型（9）．虚析构函数的作用是（C ）。

(A) 虚基类必须定义虚析构函数(B) 类对象作用域结束时释放资源(C)delete动态对象时释放资源(D) 无意义（10）．下面函数原型中，( B )声明了fun为纯虚函数。

(A) void fun()=0; (B) virtual void fun()=0;(C) virtual void fun(); (D) virtual void fun(){ };（11）．若一个类中含有纯虚函数，则该类称为( C )。

(A) 基类(B)纯基类(C) 抽象类(D) 派生类（12）．假设Aclass为抽象类，下列正确的说明语句是( B )。

课后习题答案第8章_存储器和可编程逻辑器件

第8章半导体存储器和可编程逻辑器件8-1存储器按读写功能以及信息的可保存性分别分为哪几类？并简述各自的特点。

解答：存储器按读写功能可分为只读存储器（ROM）和随机存储器（RAM）。

随机存取存储器在工作过程中，既可从其任意单元读出信息，又可以把外部信息写入任意单元。

因此，它具有读、写方便的优点，但由于具有易失性，所以不利于数据的长期保存。

只读存储器在正常工作时其存储的数据固定不变，只能读出，不能随时写入。

ROM为非易失性器件，当器件断电时，所存储的数据不会丢失。

存储器按信息的可保存性可分为易失性存储器和非易失性存储器。

易失性存储器在系统关闭时会失去存储的信息，它需要持续的电源供应以维持数据。

非易失存储器在系统关闭或无电源供应时仍能保持数据信息。

8-2什么是SRAM？什么是DRAM？它们在工作原理、电路结构和读/写操作上有何特点？解答：SRAM（Static Random Access Memory）为静态随机存储器，其存储单元是在静态触发器的基础上附加控制电路构成的。

DRAM（Dynamic Random Access Memory）为动态随机存储器，常利用MOS管栅极电容的电荷存储效应来组成动态存储器，为了避免存储信息的丢失，必须定时地对电路进行动态刷新。

SRAM的数据由触发器记忆，只要不断电，数据就能保存，但其存储单元所用的管子数目多，因此功耗大，集成度受到限制。

DRAM一般采用MOS管的栅极电容来存储信息，由于电荷保存时间有限，为避免存储数据的丢失，必须由刷新电路定期刷新，但其存储单元所用的管子数目少，因此功耗小，集成度高。

SRAM速度非常快，但其价格较贵；DRAM的速度比SRAM慢，不过它比ROM 快。

8-3若RAM的存储矩阵为256字⨯4位，试问其地址线和数据线各为多少条？解答：存储矩阵为256字⨯4位的RAM地址线为8根，数据线为4根。

8-4某仪器的存储器有16位地址线，8位数据线，试计算其最大存储容量是多少？解答：最大存储容量为216⨯8=524288=512k bit（位）8-5用多少片256⨯4位的RAM可以组成一片2K⨯8位的RAM？试画出其逻辑图。

基础电子技术习题解答第8章组合数字电路习题解答

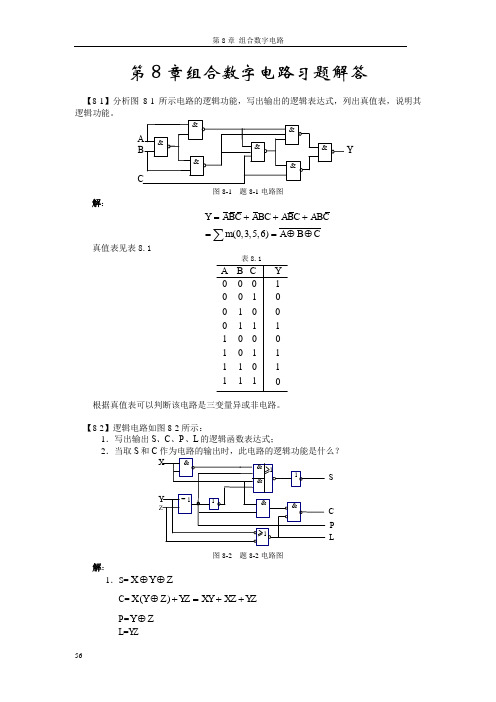
第8章组合数字电路习题解答【8-1】分析图8-1所示电路的逻辑功能，写出输出的逻辑表达式，列出真值表，说明其逻辑功能。

A B &&&&&&&CY图8-1 题8-1电路图解：(0,3,5,6)Y ABC ABC ABC ABC m A B C=+++==⊕⊕∑真值表见表8.1表8.1Y C B A 10001000010011100101110111111000根据真值表可以判断该电路是三变量异或非电路。

【8-2】逻辑电路如图8-2所示：1．写出输出S 、C 、P 、L 的逻辑函数表达式；2．当取S 和C 作为电路的输出时，此电路的逻辑功能是什么？=1&&1&&11&1XYZSC P L图8-2 题8-2电路图解：1．S=X Y Z ⊕⊕C =()X Y Z YZ XY XZ YZ ⊕+=++ P =Y Z ⊕ L =YZ2．当取S 和C 作为电路的输出时，此电路为全加器。

【8-3】图8-3为由三个全加器构成的电路，试写出其输出F 1，F 2，F 3，F 4的表达式。

A iB iC i-1S i C iA iB iC S i C iA iB iC i-1S i C iX YZ12F 3F 4i-1图8-3 题8-3电路图解：F 1=X Y Z ⊕⊕ 2()F X Y Z =⊕⋅3F XY Z =⊕ 4F XYZ =【8-4】图8-4为集成4位全加器74LS283和或非门构成的电路，已知输入DCBA 为BCD8421码，写出B 2 B 1的表达式，并列表说明输出''''A B C D 为何种编码？A 3A 2A 1A 0S 3 S 2S 1 S 0C 0C 4D' C' B' A'74LS283D C B AB 3 B 2B 1B 041>1>1>图8-4 题8-4电路图解：21B B D B A D C D CB CA ==++++=++若输入DCBA 为BCD8421码，列表可知D 'C 'B 'A '为BCD2421码。

福州大学大学物理习题解答-第8章气体动理论

第八章气体动理论习题解答8-1 设想太阳是由氢原子组成的理想气体，其密度可当成是均匀的。

若此理想气体的压强为1.35×1014 Pa 。

试估计太阳的温度。

（已知氢原子的质量m = 1.67×10-27kg ，太阳半径R = 6.96×108 m ，太阳质量M = 1.99×1030kg ）解：mR MVm M mn 3π)3/4(===ρK 1015.1)3/4(73⨯===Mkm R nk p T π8-2 目前已可获得1.013×10-10 Pa 的高真空，在此压强下温度为27℃的1cm 3体积内有多少个气体分子？解：3462310/cm 1045.2103001038.110013.1⨯=⨯⨯⨯⨯===---V kT p nV N 8-3 容积V ＝1 m 3的容器内混有N 1＝1.0×1023个氢气分子和N 2＝4.0×1023个氧气分子，混合气体的温度为 400 K ，求：（1）气体分子的平动动能总和；（2）混合气体的压强。

解：（1）J 1014.41054001038.123)(233232321⨯=⨯⨯⨯⨯⨯=+=-∑N N kT tε（2）Pa kT n p i323231076.21054001038.1⨯=⨯⨯⨯⨯==-∑8-4 储有1mol 氧气、容积为1 m 3的容器以v =10 m/s 的速率运动。

设容器突然停止，其中氧气的80%的机械运动动能转化为气体分子热运动动能。

问气体的温度及压强各升高多少？（将氧气分子视为刚性分子）解：1mol 氧气的质量kg 10323-⨯=M ，5=i 由题意得T R Mv ∆=⋅ν25%80212K 102.62-⨯=∆⇒TT R V p RT pV ∆=⋅∆⇒=νν pa 52.0102.631.82=⨯⨯=∆=∆∴-VTR p 8-5 一个具有活塞的容器中盛有一定量的氧气，压强为1 atm 。

教材第八章习题解答

第八章氧化还原反应和电化学习题解答1．回答下列问题。

（1）怎样利用电极电势来确定原电池的正负极，并计算原电池的电动势？（2）怎样理解介质的酸性增强，KMnO 4的电极电势代数值增大、氧化性增强？（3）Nernst 方程式中有哪些影响因素？它与氧化态及还原态中的离子浓度、气体分压和介质的关系如何？（4）区别概念：一次电池与二次电池、可逆电池与不可逆电池。

（5）介绍几种不同原电池的性能和使用范围。

（6）什么是电化学腐蚀，它与化学腐蚀有何不同？（7）防止金属腐蚀的方法主要有哪些？各根据什么原理？【解答】（1）电极电势值高的电极做正极，电极电势值低的电极做负极。

原电池的电动势等于正极的电动电势减去负极的电极电势。

（2）根据电极反应：-+-2+42M nO +8H +5e =M n +4H O2442284c(M n)0.0592M nO M nO c ()()lg M nM nc(M nO )5c(H )()cc+--ΘΘ++-ΘΘϕ=ϕ-+⋅由电极电势的能斯特公式可知，介质酸性增强时，H +浓度增大，42M nO ()M n-+ϕ代数值增大，电对中MnO 4-的氧化性增强。

（3）对于电极反应 -a(O x)+ze b(R ed) 电极电势的Nernst 方程为：bR e d aO x (c /c )R T (O x /R e d )(O x /R e d )lnzF(c /c )ΘΘΘϕ=ϕ-影响电极电势大小的因素：a ）浓度对电极电势的影响电对中氧化态的离子浓度(或气体分压)增大时，电极电势增加；还原态的离子浓度(或气体分压)增大时，电极电势降低。

b ）酸度对电极电势的影响对于有H +或OH -参加的电极反应，溶液酸度的变化会对电极电势产生影响，对于没有H +或OH -参加的电极反应，溶液酸度的变化对电极电势的影响很小。

（4）一次电池是指电池放电到活性物质耗尽只能废弃而不能再生和重复使用的电池。

物理学第3版习题解答_第8章光的波动性

. B
解：（1）以 A 为原点
x1
B
. A
x
A
图 8-35 习题 8-5 用图
-1
本题需补充一平面简谐波以速度 u = 20 m ⋅ s 沿直线传播
t x y = A cos[ 2 π( − ) + ϕ ] λ = uT = 10 m ，根据 T λ ，有
y = A cos[2π(
t x π − )− ] 0.5 10 2
x1 = 0.04 cos(2t + π 6) x 2 = 0.03 cos(2t − π 6)
试写出合振动的表达式。
解合振动的振幅为
2 A = A12 + A2 + 2 A1 A2 cos(ϕ 2 − ϕ1 )
⎛ π π⎞ = 0.04 2 + 0.03 2 + 2 × 0.03 × 0.04 × cos⎜ − − ⎟ ⎝ 6 6⎠ = 0.06m
第八章习题解答
8-1 一物体沿 x 轴作简谐振动，振幅为 0.12m，周期为 2s。当 t = 0 时，位移为 0.06m，且向 x 轴正方向运动。求：(1)初相；(2) t = 0.5s 时，物体的位置；(3)在 x = -0.06m 处，且向 x 轴负向方向运动。物体从这一状态回到平衡位置的最短时间。解：
−1
8-8 波长为 589.3nm 的钠光照在一双缝上，在距双缝 200cm 的观察屏幕上测量 10 个条纹的宽度为 2.2cm，试计算双缝之间的距离。
解：根据 ∆x =
D λ 有 d = 0.536 mm d
8-9 在杨氏干涉实验中，若双缝间距为 0.40mm，在距双缝 100cm 的光屏上出现干涉条纹。现测得相邻两条明纹中心的间距为 1.5mm，求入射光的波长。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第8章思考题及习题8参考答案
一、填空
1. 单片机存储器的主要功能是存储和。

答：程序、数据。

2．假设外部数据存储器2000H单元的内容为80H，执行下列指令后累加器A中的内容为。

MOV P2，#20H
MOV R0，#00H
MOVX A，@R0
答：80H。

3．在存储器扩展中，无论是线选法还是译码法最终都是为扩展芯片的端提供控制信号。

答：片选。

4．起止范围为0000H～3FFFH的数据存储器的容量是KB。

答：16KB。

5．在AT89S52单片机中，PC和DPTR都用于提供地址，但PC是为访问存储器提供地址，而DPTR是为访问存储器提供地址。

答：程序、数据。

6．11条地址线可选个存储单元，16KB存储单元需要条地址线。

答：2K，14。

7．4KB RAM存储器的首地址若为0000H，则末地址为H。

答：0FFF。

8．若单片机外扩32KB 数据存储器的首地址若为4000H，则末地址为H。

答：BFFF
9. 设计一个以AT89S52单片机为核心的系统，如果不外扩程序存储器，使其内部8KB闪烁程序存储器有效，则其引脚应该接。

答：EA*，+5V
10．74LS138是具有3个输入的译码器芯片，其输出常作片选信号，可选中片芯片中的任一芯片，并且只有1路输出为电平，其它输出均为电平。

答：8，低，高；
二、单选
1．区分AT89S51单片机片外程序存储器和片外数据存储器的最可靠方法是。

A．看其位于地址范围的低端还是高端
B．看其离AT89S51单片机芯片的远近
C．看其芯片的型号是ROM还是RAM
D．看其是与RD信号连接还是与PSEN信号连接
答：D
2．访问片外数据存储器的寻址方式是。

A.立即寻址
B.寄存器寻址
C.寄存器间接寻址
D.直接寻址
答：C
3．若要同时扩展4片2KB的RAM和4片4KB的ROM，则最少需要根地址线。

A、12
B、13
C、14
D、15
4．当EA=1时，AT89S52单片机可以扩展的外部程序存储器的最大容量为。

A．64KB B．60KB C．58KB D．56KB
答：D
5. 若某数据存储器芯片地址线为12根,那么它的存储容量为。

A、1KB B.4KB C.2KB D.8KB
答：B
三、编程
1．试编写一个程序（如将05H和06H拼为56H），设原始数据放在片外数据区2001H单元和2002H单元中，按顺序拼装后的单字节数放入2002H。

答：本题主要考察对外部存储器的读、写操作，只要记住正确使用MOVX指令就可以了。

编程思路：首先读取2001H的值，保存在寄存器A中，将寄存器A的高四位和低四位互换，再屏蔽掉低四位然后将寄存器A的值保存到30H中，然后再读取2002H的值，保存在寄存器A 中，屏蔽掉高四位，然后将寄存器A的值与30H进行或运算，将运算后的结果保存在2002H 中。

ORG 0000H
MAIN：MOV DPTR，#2001H ；设置数据指针的初值
MOVX A，@DPTR ；读取2001H的值
SWAP A
ANL A，#0F0H ；屏蔽掉低四位
MOV 30H，A ；保存A
INC DPTR ；指针指向下一个
MOVX A，@DPTR ；读取2002H的值
ANL A，#0FH ；屏蔽掉高四位
ORL A，30H ；进行拼装
MOVX @DPTR，A ；保存到2002H
END
2．编写程序，将外部数据存储器中的4000H～40FFH单元全部清“0”。

答：本题主要考察对外部数据块的写操作；编程时只要注意循环次数和MOVX指令的使用就可以了。

ORG 0000H
MAIN：MOV A，#0 ；送预置数给A
MOV R0，#0FFH ；设置循环次数
MOV DPTR，#4000H ；设置数据指针的初值
LOOP：MOVX @DPTR，A ；当前单元清零
INC DPTR ；指向下一个单元
DJNZ R0，LOOP ；是否结束
END
四、简答
1．在AT89S52单片机系统中，外接程序存储器和数据存储器共用16位地址线和8位数据线，为何不会发生冲突？
答：因为控制信号线的不同：外扩的RAM芯片既能读出又能写入，所以通常都有读写控制引脚，记为OE*和WE*。

外扩RAM的读、写控制引脚分别与AT89S51的RD*和WR*引脚相连。

外扩的EPROM在正常使用中只能读出，不能写入，故EPROM芯片没有写入控制引脚，只有读出引脚，记为OE*，该引脚与AT89S52单片机的PSEN*相连。

2．题图8-1（a）所示为AT89S51单片机中存储器的地址空间分布图。

题图8-1（b）
题图8-1
为存储器的地址译码电路，为使地址译码电路按题图8-1（a）所示的要求进行正确寻址，要求画出：
（1）A组跨接端子的内部正确连线图。

（2）B组跨接端子的内部正确连线图。

答：（1）A组跨接端子的内部正确连线图
（2）B组跨接端子的内部正确连线图
注意：答案不唯一，还有其他连接方法，也可满足题目要求。

如有侵权请联系告知删除，感谢你们的配合！。