电动力学 4章 菲涅耳公式讲解
Fresnel(菲涅尔)公式

d=z=
2π
λ0
n12 sin2 i1 − n22 ;(3)波矢常数: k2 sin i2 > k2 。
应用:近场光学
15
1.3 反射率和透射率
W1
=
I1σ
cos i1
=
n1 2
ε0 μ0
A1 2 cos i1
W1′ =
I1′σ
cos i1
=
n1 2
ε0 μ0
A1′ 2 cos i1
W2
=
I2σ
cos i2
2.4
2.2
n =1.33 1
n =1
2.0
2
r
r
s
p
1.8
t
t
s
p
1.6
1.4
1.2
i
c
1.0
0.8
0.6
0.4
0.2
i
B
0.0
-0.2 0
10
20
30
40
50
60
i
1
12
全内反射的应用: 1、导波光学 Waveguide / Optical fiber
n 1
n <n , n <n 12 32
n 2
1
Stocks 公式:
A
Ar
Att'
Ar
Arr
Art
At
Atr'
At
Arr + Att′ = A 可知: Art + Atr′ = 0
r2 + tt′ = 1 r + r′ = 0
2
1.2 振幅反射(透射)比 相位跃变(相移) 1、透射比与相位跃变
菲涅耳公式

讨论: A
i1 iB
i1 i2 / 2
rp 0 rp 0
当
n1 n2 , i1 i2 时
1
rs 0 rs 0
当n
n2 , i1 i2
时
当光从光疏介质向光密介质入射时, 反射光发生相位突变。 B
当
i1 iB
i1 i2 / 2
n1 n2 , i1 i2
反射、折射时的偏振现象
入 射 角 i1 0 反射光偏振态 自然光 部分偏振光(自然光+S 光) 折射光偏振态 自然光 部 分 偏 振 部分偏振光(自然光+S 光) 光 自然光
iB
线偏振光(S 光)
2
(ic )
自然光
三、维纳(O.Wiener 1890年)实验证明—— 电场是主要的
光与物质的相互作用,本质上是光与电子的相互作用。运 动的电子既有电荷亦有磁矩,光是电磁波。在光与电子的相互 作用中,是电场起主要作用,还是磁场起主要作用,还是电场 和磁场起等同的作用?-----维纳实验回答了这个问题。
, ,
E 2 s y 0 A2 s
exp i ( k r ' t ) exp i ( k r t )
2 2
其中:
k1 x 0 k1 sin i1 z 0 k1 cos i1 k1 ' x 0 k1 ' cos i1x ' y 0 k1 ' cos i1 y ' z 0 k1 ' cos i1z ' k 2 x 0 k 2 cos i2 x y 0 k 2 cos i2 y z 0 k 2 cos i2 z
第4章光的偏振4(菲涅耳公式)_905507819

sini2 sini2
i1 i1
~ts
EE~~12ss
2n1 cos i1
n1 cos i1 n2 cos i2
2sin i2
sini1
cos i1
i2
6
菲涅耳公式
半波
~rs
EE~~11ss
n1 cos i1 n2 cos i2 n1 cos i1 n2 cos i2
sini2 sini2
1
光波分解为两种线偏振光 s光:偏振方向垂直于入射面 p光:偏振方向平行于入射面
2
符号规定
S:垂直分量 为正
pˆ1
sˆ1 kˆ1
P:平行分量 三矢量关系
pˆ1 sˆ1 kˆ1 pˆ1 sˆ1 kˆ1 pˆ 2 sˆ2 kˆ2
时为正
pˆ1
kˆ1
sˆ1
sˆ2
pˆ 2
kˆ2
z
n1
x
i1 i1
~rp
E~1p E~1 p
n2 cos i1 n1 cos i2 n2 cos i1 n1 cos i2
tani1 tani1
i2 i2
损失
可正 可负
~
~ts
~tp
EE~12ss
2n1 cos i1
n1 cos i1 n2 cos i2
2sin i2 cos i1 sin i1 i2
n2
3
pˆ1
sˆ1 kˆ1
pˆ1
kˆ1
i1 i1 sˆ1
i2
sˆ2
pˆ 2
kˆ2
n1
x
n2
z
根据电磁场量的边界条件,得到如下结果
详细推导参见赵凯华《光学》p. 286
菲涅耳公式——精选推荐

§1-6 菲涅耳公式一.菲涅耳公式电磁波通过不同介质的分界面时会发生反射和折射,在电动力学中将讲到入射、反射和折射三束波在分界面上振幅的大小和方向之间的关系,这一关系可由菲涅耳公式表达出来,上节提到的在反射过程中发生的半波损失问题,就可以用这个公式来解释,这一公式对以后讲到的许多光学现象,都能圆满地加以说明。
菲涅耳公式的内容说明如下:在任何时刻,我们都可以把入射波、反射波和折射波的电矢量分成两个分量,一个平行于入射面,另一个垂直于入射面。
有关各量的平等分量与垂直分量依次用指标P 和S 来表示。
以1i 、'1i 和2i 分别表示入射角、反射角和折射角,它们确定了各波的传播方向(在大多数情况下,只要注意各波的磁场矢量即可,因为知道了各个波的传播方向,各波的磁场矢量就可按右螺旋关系确定)。
以1A 、'1A 和2A 来依次表示入射波、反射波和折射波的电矢量的振幅,它们的分量相应就是1P A 、1'P A 、2P A 和1s A 、1's A 、2s A 。
由于三个波的传播方向各不相同,必须分别规定各分量的某一个方向作为正方向,这种规定当然是任意的。
但是只要在一个问题材的全部讨论过程中始终采取同一种正方向的选择,由此得到的各个关系式就具有普遍的意义,(a)(b)(图1-16)图1-16中xy 平面为两介质的分界面,z 轴为法线方向,xz 平面为入射面,规定电矢量的s 分量以沿着y +方向的为正,这对于入射、反射和折射三个波都相同,图中III II I 、、三个面依次表示入射、反射和折射三个波的波面。
电矢量的P 分量沿着这三个波面与入射面的交线,它们的正方向分别规定为如图1-16)()(b a 、所示,且S 分量、P 分量和传播方向三者构成右螺旋关系。
在传播过程中,电矢量的方向是在不断变化的,我们所注意的仅是在反射、折射过程这一瞬时的变化,所以菲涅耳公式所表示的有关各量的方向都是指紧靠两介质分界面O 点处而言的(在图中为清楚起见,将通过O 点的三个波面画III II I 、、画在离开O 点较远之处)。
菲涅耳公式推导课件

菲涅耳公式的推导
菲涅耳公式
描述光波在界面上反射和折射行为的公式,包括反射系数和 折射系数的计算。
推导过程
基于光的波动方程、波前的传播和波前的叠加原理,通过数 学推导得到菲涅耳公式。
04
菲涅耳公式的解析
半波损失现象的解释
Hale Waihona Puke 1 2 3半波损失现象
当光从光密介质射向光疏介质时,反射光在离开 分界面处会额外损失半个波长的光程。
波动方程的形式
$frac{partial^2 A}{partial x^2} + frac{partial^2 A}{partial y^2} + frac{partial^2 A}{partial z^2} = frac{1}{c^2} frac{partial^2 A}{partial t^2}$ ,其中$A$表示光波的振幅,$c$表示光速。
THANKS
感谢观看
菲涅耳公式推导课件
目 录
• 菲涅耳公式的背景和意义 • 光的干涉原理 • 菲涅耳公式的推导过程 • 菲涅耳公式的解析 • 菲涅耳公式的应用实例
01
菲涅耳公式的背景和意义
光的波动理论
01
光的波动理论认为光是一种波动 现象,具有波长、频率和相位等 特征。
02
该理论解释了光的干涉、衍射和 偏振等现象,为光学研究奠定了 基础。
全息照相技术
总结词
全息照相技术是菲涅耳公式的又一重要 应用,通过该公式可以实现高质量的全 息成像,并拓展全息技术的应用领域。
VS
详细描述
全息照相技术是一种记录和重现三维物体 光波前的方法。在全息照相中,菲涅耳公 式被用来计算物光波和参考光波在全息板 上的干涉场,从而得到全息图像。通过优 化菲涅耳公式的参数和应用,可以提高全 息图像的质量和稳定性,进一步拓展全息 技术的应用领域。
(三)菲涅耳公式及其讨论(电磁场的连续条件) 表示反射波、折.

rs
对所有的θ1都是负值,表明反射时s波在界面上发生 了 的位相变化。
tg (1 2 ) n2 cos1 n1 cos 2 rp A1 p tg (1 2 ) n2 cos1 n1 cos 2
A1' p
rp
当 1 B 时为正值,表明其相位变化为0。 当 1 B 时为负值,表明在界面上,反射光的p波有 相位变化。
6块透镜系统,反射面12面,若n=1.52,光在各面入射
角很小,透过这一系统的光能量为
W2 (1 0.043)12W1 0.59W1
W1为入射光能量,由于反射而损失的能量占41%。 为减少光能量损失,近代光学技术普遍采用在光学元 件表面镀增透膜。
(五)反射和折射时的偏振关系
一束自然光可分解为两束振动方向相互垂直的、 等幅的、不相干的线偏振光。 将自然光中两个相互垂直的等幅振动之一完全移去得到 的光,称为完全偏振光,也可称为线偏振光或平面偏振光。 部分偏振光在垂直于光传播方向的平面内沿各方向振动 的光矢量都有,但振幅不对称,在某一方向振动较强,而与
对于反射波,应区分n1>n2和n1<n2两种情况,并注意
1 B和1 B 时的不同。
(1)当光从光疏介质射到光密介质时,
A1' s sin(1 2 ) n1 cos1 n2 cos 2 rs A1s sin(1 2 ) n1 cos1 n2 cos 2
n 1 rp A1 p n 1 tp A2 p A1 p 2 n 1
A1' p
A2 s 2 ts A1s n 1
相对折射率
n
n2
n1
(二)反射和折射时的振幅关系 菲涅耳公式给出反射波或折射波与入射波的振幅的相对变 化,用振幅反射、透射系数来表示,并随入射角而变。
菲涅耳公式推导

菲涅耳公式推导一、引言菲涅耳公式是描述光在两介质交界面上的光线反射和折射的定律,对理解光的传播和光学现象具有重要意义。
它的推导基于麦克斯韦方程组和边界条件,通过数学方法得到了反射和折射的强度和角度之间的关系。
二、麦克斯韦方程组我们需要了解一些麦克斯韦方程组的基本知识。
麦克斯韦方程组是描述电磁场的基本方程,包括四个方程:电场的高斯定律、磁场的高斯定律、法拉第电磁感应定律和安培环路定律。
这些方程描述了电场和磁场的变化规律和相互作用关系,为推导菲涅耳公式提供了理论基础。
三、边界条件在光在两介质交界面上的反射和折射过程中,有一些边界条件需要满足。
首先,电场和磁场的切向分量在界面上必须连续,即电场和磁场的切向分量在界面上的值相等。
其次,法向分量的电场和磁场的导数在界面上必须连续,即电场和磁场的法向分量在界面上的导数值相等。
这些边界条件保证了光的连续性和一致性。
四、推导过程根据麦克斯韦方程组和边界条件,可以推导出菲涅耳公式。
首先考虑入射光线和界面法线的夹角,利用电场和磁场的边界条件,可以得到反射光的电场和磁场的幅度与入射光的关系。
然后考虑入射光线和界面法线的夹角,利用电场和磁场的边界条件,可以得到折射光的电场和磁场的幅度与入射光的关系。
最后,根据反射和折射的电场和磁场幅度,可以得到反射光和折射光的强度和角度之间的关系,即菲涅耳公式。
五、菲涅耳公式的应用菲涅耳公式在光学中有广泛的应用。
首先,它可以用于计算反射率和透射率,即入射光的一部分被反射,一部分被折射。
这对于设计反射镜、透镜和光学薄膜具有重要意义。
其次,菲涅耳公式可以用于计算反射和折射的角度,根据入射角度和介质折射率的关系,可以确定折射光线的方向。
此外,菲涅耳公式还可以用于研究偏振光的反射和折射现象,对于光的偏振性质研究具有重要意义。
六、总结菲涅耳公式是描述光在两介质交界面上的反射和折射现象的定律,通过麦克斯韦方程组和边界条件的推导得到。
它在光学研究中具有重要的理论和实际应用价值,可以用于计算反射率、透射率和光线的角度,对于光学器件设计和光学现象的解释具有重要意义。
1-6 菲涅耳公式_投影稿
next
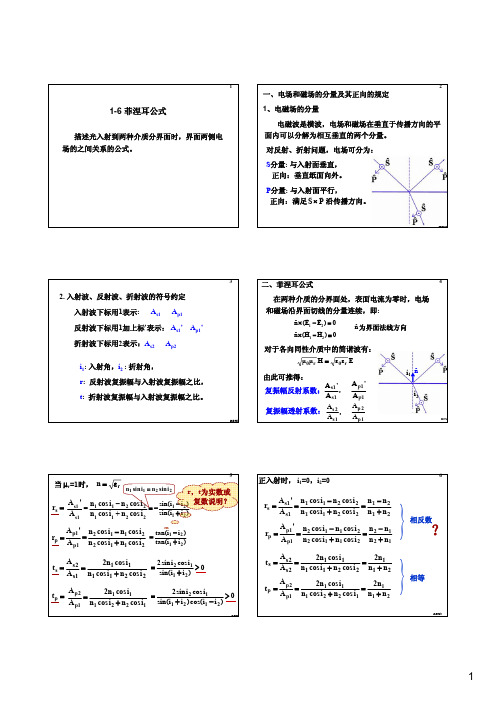
n1 <n2< n3
next
3
rs
A 'S1 A S1
A p tan( i 1 i 2 ) sin( i 1 i 2 ) rp 1 sin( i 1 i 2 ) A p1 tan( i 1 i 2 )
'
19
20
光以小角度(i1<ip)入射到介质薄膜时,薄膜上、 下表面反射(透射)的光之间的额外程差: n1 <n2< n3 n1<n2 且 n2>n3 或: n 或:n1> n2 且 n2< n3 1> n2>n3 反射光 透射光 有 无 n1 n2 n3
当r=1时, n r
5
n1 sin i1 n2 sin i 2
正入射时, i1=0,i2=0
6
rs
A s1 ' n 1 cos i1 n 2 cos i 2 n 1 n 2 A s1 n 1 cos i1 n 2 cos i 2 n 1 n 2
rp
A p1 ' A p1
next
2、透射光的额外程差 用同样的讨论方法可以得到,对于小角度入射: 当n1<n2 ,n2>n3 或 n1 > n2 ,n2< n3时:没有额外程差 当n1> n2>n3 或 n1 <n2< n3 时: 有额外程差
无 有
透射光的结论正好 与反射光的结论相反。 n1<n2<n3
介质薄膜
next
21
22
六、光正、逆向入射时菲涅耳系数之间的关系 符号约定: r 、t表示光正向传播时的菲涅耳系数 r' 、t'表示光逆向传播时的菲涅耳系数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
?
2n1 cos i1 n1 cos i1 ? n2 cos i2
?
2cos i1 sin i2 sin( i1 ? i2 )
关于菲涅耳公式的讨论
一、菲涅耳公式中的能量守恒
既然 E02 表示光的能量流动,为什么
2
2
2
E1s ? E1s ' ? E 2s ?
平面电磁波的能流密度:
S? 1 2
? ?
E02
这就是著名的反射定律和折射定律(Snell定律),它包 括两个内容:
(1)入射、反射和折射光线在同一个面内。
(2)反射角等于入射角;以及, n1 sin i1 ? n2 sin i2
再由磁矢量在界面(即z=0)处的条件: H1s ? H1s ' ? H 2s
并利用在非铁磁质中的关系: ? r ? 1, n ? ?r ? r ? ?r
? 根据叠加原理:可以只研究入射波电场仅含s 分量和仅含p分量这两种特殊情况;当两种 分量同时存在时,则只要先分别计算由单个 分量所造成的折、反射波电场,然后再作矢 量相加即可得到结果。
把电矢量分成两个分量 :
E1 p
p分量—— 平行于入射面
E1s
(光线方向与界面法线所确定的平面,
E1?p
i1 i1?
E1?s
如图中 xy面为界面,z轴为法线。) s分量—— 垂直于入射面。
图中的y轴方向。
规定s 分量的正方向为沿y 轴正方
O i2
x
E2 p
E2 s
z
向,p 分量的正方向为与s 分量和传播 方向构成右手螺旋关系:
p? ? s? ? k?
对于s分量,设:
? ? E 1s
?
y 0 ? A1s exp
? i(k1
? 菲涅尔公式描述折、反射波(复)振幅与入射波 (复)振幅之间的关系,是物理光学中的又一组基 本公式:
rp
?
tg (i1 tg (i1
? ?
i2 ) i2 )
tp
?
2 sin i2 cos i1 sin(i1 ? i2 ) cos(i1 ?
i2 )
rs
?
?
sin(i1 sin(i1
? ?
i2 ) i2 )
? n? ?
? (E2
?
? E1 )
?
0
? ? ? ?
? ?
n? n? n?
?
? (H
?
?(
D ?
2
?( B2
?
2
?
H ?
1
)
? D? 1 ) ?
? B1 ) ?
?
?
0
J
s
s
在绝缘介质界面,无自由电荷和传导电流
注:Js 为表 面传导电流 密度;
? s 为表 面自由电荷
密度。
??1E1n ? ?2E2n
ts
?
2 sin i2 cos i1 sin(i1 ? i2 )
(1)p分量的振幅反射率:
rp
?
E1?p E1 p
?
n2 cos i1 ? n1 cos i2 n2 cos i1 ? n1 cos i2
?
tan( i1 ? i2 ) tan( i1 ? i2 )
(2)s分量的振幅反射率:
rs
?
E1?s E1s
由电磁场边界条件,在界面(即z=0)处有: E1s ? E1s ' ? E2s
因对于所有时间t,和所有x、y上式成立,所以: ? 1 ? ? 1 ' ? ? 2
cos i1y ' ? 0 , cos i2 y ? 0
由此可知道,(1)入射、反射和折射光线在同一个面内。
因而,
? k1
'
和
? k2
可表达为:
?r?
?
?
1t )
? ? ,
E 1s
?
y 0 ? A1,s exp
? i(k1
?r?
?
?
'1 t )
? ? E 2 s
?
y 0 ? A2 s exp
? i(k2
?r?
?
?
2t)
其中:
? k?1 ? x0 ?k1 sin i1 ? z0 ?k1 cosi1 k?1'? x0 ?k1'cosi1x '? y0 ?k1'cosi1y '? z0 ?k1'cosi1z ' k2 ? x0 ?k2 cosi2x ? y0 ?k2 cosi2y ? z0 ?k2 cosi2z
?? E1t ? E2t
? ?
?
1 H 1n
?
? 2H2n
?? H1t ? H 2t
电位移矢量法线分量连续 电场强度矢量切线分量连续 磁感应强度矢量法线分量连续 磁场强度切线分量连续
? 研究该问题的基本思路:我们可以把入射波 电场的振幅矢量分解成两个分量,一个分量 垂直于入射面,称为“s”分量;另一个分量 位在入射面内,称为“p”分量。
?
n1 cos i1 ? n2 cos i2 n1 cos i1 ? n2 cos i2
?
sin( i2 ? i1 ) sin( i2 ? i1 )
(3)p分量的振幅透射率:
tp
?
E2 p E1 p
?
2n1 cos i1 n2 cos i1 ? n1 cos i2
(4)s分量的振幅透射率:
ts
?
E2s E1s
? 菲涅耳给出在分界面处,入射波、反射波、折; 1s
A1s
?
sin(i2 ? i1) sin(i2 ? i1)
ts
?
A2 s A1s
?
2sin i2 cos i1 sin(i1 ? i2 )
? 同理可得出在分界面处,p分量的振幅关系。
? 折射、反射定律只解决了平面光波在两个介质分界 面上的传播方向问题。
? ?k1'? x0 ?k1 sin i1'? z0 ?k1 cosi1'
k2 ? x0 ?k2 sin i2 ? z0 ?k2 cosi2
从而, k1 sin i1 ? k1 sin i1'? k2 sin i2
得到,(2) i1 ? i1' ,即反射角等于入射角; 以及, n1 sin i1 ? n2 sin i2
菲涅耳在麦克斯韦之前得到了反射、折射公式 .
电磁场边界条件:电磁场边值关系由麦克斯韦积分方程给出,反 映了电磁场在两种介质分界面处的突变的规律。
? ?
?L
? E
?dl
?
?
d dt
?
??SB ?dS
? ?? ?
?L
? H
?dl
?
If
?
d dt
?
??SD ?dS
? ?
?
??S D
?dS
?
Qf
?
????SB ?dS ? 0
1.4 菲涅耳公式
(Augustin-Jean Fresnel 1788-1827 )
光射在两种介质的界面上时,将发生反射和折 射。能流的分配与入射角有关,还存在相位的跃变 和偏振态的变化。
从电磁场的边界条件出发,可以得到 反射和折 射定律,以及入射与反射、折射的振幅关系 ——解
决光在界面上的强度分配问题。
一般 ? r? 1
n? ?r
S? 1 2
?0 ?0
?(n ?E02 )
平面电磁波的能流密度与 (n?E02) 成正比。
