20170807-峰值电流型控制Buck等效功率级的小信号传递函数
20170809-峰值电流型控制Buckoost等效功率级的小信号传递函数

峰值电流型控制Buckboost 等效功率级的小信号传递函数
普高(杭州)科技开发有限公司 张兴柱 博士
Buckboost 变换器在峰值电流型控制下的等效功率级小信号传递函数(CCM ): )
1)(1()1()1()(220n n p p zc a vc vc s Q s s s s G s G ωωωωω++++−′≈′ )1)(1()1)(1()(220
n n p p zc a vg vg s Q s s s s G s G ωωωωω++++′+′≈′ )1()1()(0
p zc out s s R s Z ωω++′≈′ 其中:10F D R R G i vc ′=′,120F F L RT G s vg =′,1
0F R R =′ 11F RC p =ω,DL R D a 2′=ω,)5.0(1−′=D m Q c p π,C R c zc 1=ω,s
n T πω=, a a D D D F ωω)
21(2−′=′,n e c S S m +=1,i g n R L V S ×= )5.0(131−′++=c s m D L
RT D F ,)]21([22D D m D D D D RT L F c s −−′′+′=
Buckboost 的峰值电流控制等效功率级小信号传递函数,与Buck 的差别是在控制电压到输出电压这个小信号传递函数中增加了一个右半平面零点,其它的特性很类似,但由于其极点数少了,所以相比于电压型控制而言,它的补偿电路也是比较容易设计的。
1。
15、buck变换器DCM小信号建模
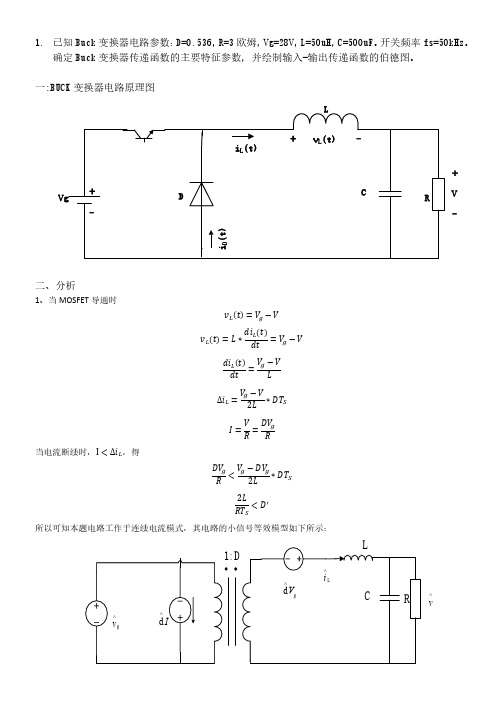
一:BUCK 变换器电路原理图 L
+ Vg
-
iL(t)
+ vL(t) -
D
C
+
带入参数得:
0.536 ∗ 3 ������ (������) =
7.5 ∗ 10 ∗ ������ + 5 ∗ 10 ∗ ������ + 3
② 、控制扰动与输出扰动的传递函数: 忽略输入扰动的作用,其小信号模型等效电路图为:
L
iL
d Vg
C
R
v
������
∗
1 ������������
������(������) ������ ������(������)
MATLAB 程序如下: >>num=[0.536*3]; >>den=[7.5*10^(-8),5*10^(-5),3]; >>figure(1);bode(num,den);grid; Bode 图如下:
RV -
iD(t)
二、分析
1、当 MOSFET 导通时
������ (������) = ������ − ������
������������ (������)
������ (������) = ������ ∗
= ������ − ������
������������
������������ (������) ������ − ������
带补偿网络的Buck变换器小信号模型

通过 OrCAD 的建模, 分析并完成系统设计。 统线性反馈控制对开关电源性能的影响 。最后, 关键词:Buck 变换器; 小信号; 补偿网络; OrCAD 中图分类号:TN624 文献标识码:B
2
占空比到输出的传递函数为: V0 / D G2 ( s) = L LC ·s2 + s + 1 R
( 17 )
5
PID 补偿网络
为了 全 面 提 高 系 统 的 控 制 性 能, 补偿网络采用 PID 调节。 由于微分环节能预测系统输出的变化趋 势, 可以补偿由低通滤波器引起的时间滞后 , 从而增加 系统的快速性和有效的抑制超调, 使系统的动态性能 得以改善, 并使系统的性能的改善不再受到低通滤波 。 器的限制 此补偿网络的传递函数是: G0 ( s) = ( 1 + x1 s ) ( 1 + x2 s ) s ( 1 + x3 s ) ( 1 + x4 s ) ( 18 ) C2 C3 ; C2 + C3
0 A= 1 C
1 L 1 - RC -
d L b= 0
C =
T
[ d 0]
0 1
其中: G vs =
( 2 ) 施加扰动, 扰动是在稳态量的基础上进行的 , D、 X、 Y 施加扰动, 令 d = D, 对 Vs 、 并将稳态分量与暂 态分量分离, 应先从式( 7 ) 中求出稳态解, 则稳态方程 变为 AX + bV s = 0 Y = CT X ( 8) X, Y 分别表示 x 和 y 的稳态值。 式 ( 8 ) 就是我们 想要获得的变换器的稳态状态空间平均方程 。由此方 程, 可解得其稳态值为 X = - A - 1 bV s Y = - C T A - 1 bV s ( 9)
20170803-峰值电流型控制等效功率级的小信号传递函数
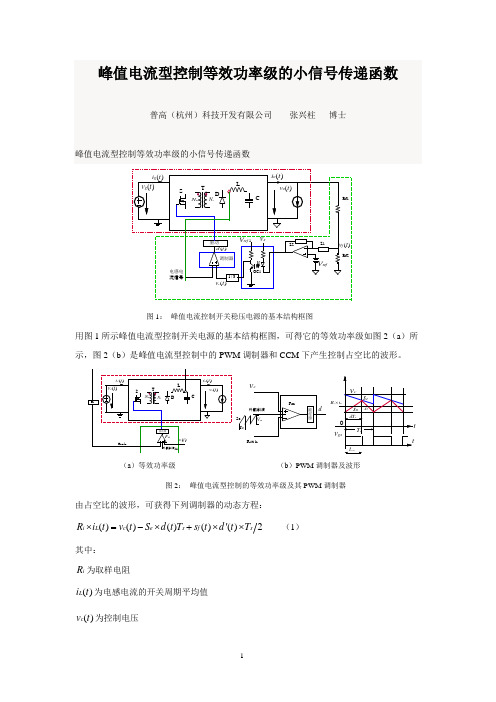
图1: 峰值电流控制开关稳压电源的基本结构框图用图1所示峰值电流型控制开关电源的基本结构框图,可得它的等效功率级如图2(a )所(a )等效功率级 (b )PWM 调制器及波形图2: 峰值电流型控制的等效功率级及其PWM 调制器由占空比的波形,可获得下列调制器的动态方程:2)()()()()(s f s e c L i T t d t s T t d S t v t i R ×′×+×−=× (1)其中:i R 为取样电阻)(t i L 为电感电流的开关周期平均值 )(t v c 为控制电压)(t d 为控制占控比 e S 为外部斜波的斜率)(t s f 为电感电流取样信号的下降斜率 )(t s n 为电感电流取样信号的上升斜率 )(1)(t d t d −=′ s T 为开关周期将上述调制器动态方程中的动态变量,用稳态工作点+小扰动这种动态变量,即:)(ˆ)(t i I t i L L L += )(ˆ)(t dD t d += )(ˆ)(t s S t s f f f += )(ˆ)(t vV t v c c c += 和)(ˆ)(t dD t d −′=′ 代入,并忽略小信号的乘积项,可得下面的稳态调制器方程和小信号调制器方程:2s f s e c L i T D S DT S V I R ×′×+×−=× (2)2])(ˆ)(ˆ[)(ˆ)(ˆ)(ˆs f f s e c L i T D t s t d S T t d S t v t iR ×′×+×−+×−=× (3) 对(3)的小信号调制器方程进行一定的处理,便可得调制器的小信号关系。
其中R.Ridely 在处理时,引入了采样函数,并将最终的调制器小信号方程写成了下面的关系:]ˆˆ)(ˆ)(ˆ[)(ˆg f o r L e i c m v k v k s i s H R v F s d×+×+××−= (4) 其中:s n c m T S m F 1=,ne c S S m +=1n S 为电感电流取样信号的稳态上升斜率221)(n n n e s Q s s H ω++=,是R.Ridely 引入的采样函数s n πω=或2s n f f =,π2−=n Qr k 和f k 是与拓扑结构有关的系数,r k 是正数、f k 是负数。
基于峰值电流控制的Buck—Boost型LED驱动器设计

彩、 长寿命 的新 型光 源 .理 论 上 ,E 的使 用 寿 命 LD 在 1 小 时 以上 , 是 在 实 际应 用 过程 中 , 为 0万 但 因 L D正 向伏 安 特 性 非 常 陡 ( 向 动 态 电 阻 非 常 E 正 小 )所 以要 给 L D供 电就 比较 困难 , 能 像 普通 , E 不 白炽灯 一样 , 直接用 电压 源 供 电 , 否则 电压 波 动稍
成 把 直 流 电压 转 换 成 直流 电压 % 的功 能 .输 出 电压 , o=D , <1 故 称 B c V D , u k电路 为 降压
电路 .
1 L D恒流驱 动器简介 E
L D照 明 系统 需 要 借 助 于 恒 流 供 电 , E 目前 主 流 的恒 流驱动设 计方 案 是利 用 线性 或 开 关 型 D / C
Fi. Th o tc n e r g2 e Bo s o v yo
的 电压 经 开关 管 S对 负载 R、 : £ 放 电.因 C和 : 此: = 一 , 流 的 增 量 △ L 电 += 2
( ) u kB ot 3 B c — os —— 升 降 压 电 路. 的输 出平 它 均 电 V :D ( D) o / 1一 压大 于或小 于输入 电压 ,
又可 以分 为电感 型 L D驱动 器和 开关 电容型 L D E E 驱 动器 .电感 型驱 动 器 方案 的优 点 是 驱 动 电流
( ) os 2 B ot 升 压 电路 . 的输 出 平 均 电压 —— 它
较 高 ,E L D端 电压 较低 、 耗较 低 、 率保 持 不 变 , 功 效
第 9卷 第 4期 21 0 0年 8月
广州 大学 学报 ( 自然科 学 版 )
峰值电流模式控制总结(完整版).

峰值电流模式控制总结PWM (Peak Current-mode Control PWM)峰值电流模式控制简称电流模式控制。
它的概念在60年代后期来源于具有原边电流保护功能的单端自激式反激开关电源。
在70年代后期才从学术上作深入地建模研究 。
直至80年代初期,第一批电流模式控制PWM集成电路(UC3842、UC3846)的出现使得电流模式控制迅速推广应用,主要用于单端及推挽电路。
近年来,由于大占空比时所必需的同步不失真斜坡补偿技术实现上的难度及抗噪声性能差,电流模式控制面临着改善性能后的电压模式控制的挑战。
如图1所示,误差电压信号 Ue 送至PWM比较器后,并不是象电压模式那样与振荡电路产生的固定三角波状电压斜坡比较,而是与一个变化的其峰比较,然后得到PWM 值代表输出电感电流峰值的三角状波形或梯形尖角状合成波形信号UΣ脉冲关断时刻。
因此(峰值)电流模式控制不是用电压误差信号直接控制PWM脉冲宽度,而是直接控制峰值输出侧的电感电流大小,然后间接地控制PWM脉冲宽度。
图1采用斜坡补偿的BUCK电流型控制1. 峰值电流模式控制PWM的优点:①暂态闭环响应较快,对输入电压的变化和输出负载的变化的瞬态响应均快;峰值电流模式控制PWM是双闭环控制系统,电压外环控制电流内环。
电流内环是瞬时快速按照逐个脉冲工作的。
功率级是由电流内环控制的电流源,而电压外环控制此功率级电流源。
在该双环控制中,电流内环只负责输出电感的动态变化,因而电压外环仅需控制输出电容,不必控制LC储能电路。
由于这些,峰值电流模式控制PWM具有比起电压模式控制大得多的带宽。
②虽然电源的L-C滤波电路为二阶电路,但增加了电流内环控制后,只有当误差电压发生变化时,才会导致电感电流发生变化。
即误差电压决定电感电流上升的程度,进而决定功率开关的占空比。
因此,可看作是一个电流源,电感电流与负载电流之间有了一定的约束关系,使电感电流不再是独立变量,整个反馈电路变成了一阶电路,由于反馈信号电路与电压型相比,减少了一阶,因此误差放大器的控制环补偿网络得以简化,稳定度得以提高并且改善了频响,具有更大的增益带宽乘积。
Buck型变换器的线性化小信号补偿前馈控制

Buck型变换器的线性化小信号补偿前馈控制石安辉;吴强【摘要】To improve the dynamic performance of DC/DC converter against input voltage disturbance, and reduce the low frequency ripple of output voltage, a uniform average equivalent circuit is established for buck series converters under voltage mode PWM control and in continuous conduction mode. According to the invariance principle of feedforward control and the equivalent circuit analysis, linearized small- signal compensation feedforward control method and its implementation are presented. The buck series converter using this control method can quickly compensate for the input voltage disturbance deviation, accelerate the speed of dynamic response against the input disturbance, significantly reduce the low frequency ripple of the output voltage, and improve the dynamic performance of buck series converters. Simulation results ver- ify the correctness of the linearized small-signal compensation feedforward control method and its analysis.%为减小由输入电源扰动引起的输出电压工频纹波,改善DC/DC变换器动态性能,根据平均变量建模思想,为电压型PWM控制的Buck型变换器建立连续导电工作模式(CCM)下统一的平均变量等效电路。
ZVT-PWM Buck变换器的小信号建模及数字控制

ZVT-PWM Buck变换器的小信号建模及数字控制
马聪;王俊峰;王凯;陈瑾怡
【期刊名称】《电力电子技术》
【年(卷),期】2024(58)5
【摘要】首先介绍了零电压转换-脉宽调制(ZVT-PWM)Buck变换器的工作原理。
接着采用等效可控源平均法推导出了变换器的小信号模型以及传递函数的表达式。
对小信号模型分析表明,ZVT-PWM Buck变换器比传统Buck变换器的瞬态响应特性更好。
然后依据该小信号模型,设计了数字控制器的参数。
最后对原理样机进行测试,实测的功率级传递函数验证了小信号模型的正确性,闭环下的负载瞬态响应测试过冲电压为410mV,恢复时间为150μs,优于传统Buck变换器的负载瞬态响应特性。
【总页数】4页(P129-132)
【作者】马聪;王俊峰;王凯;陈瑾怡
【作者单位】西安微电子技术研究所
【正文语种】中文
【中图分类】TM46
【相关文献】
1.改进型ZVT-PWM Buck变换器的研究
2.输出本安型准Z源Buck变换器CCM 模式小信号建模与控制
3.一种改进型ZVT-PWM Buck变换器的设计
4.ZVT-
PWM Buck变换器的改进电路仿真研究5.基于耦合电感高增益Buck-Boost变换器小信号建模
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
峰值电流型控制Buck 等效功率级的小信号传递函数
普高(杭州)科技开发有限公司 张兴柱 博士
Buck 变换器在峰值电流型控制下的等效功率级小信号传递函数(CCM ): )
1)(1()1()(220n n p p zc vc vc s Q s s s G s G ωωωω++++′≈′ )1)(1()1()(220
n n p p zc vg vg s Q s s s G s G ωωωω++++′≈′ )
1()1()(0p zc out s s R s Z ωω++′≈′ 其中:101F R R G i vc =
′,120F F L RT G s vg =′,10F R R =′ 11F RC p =ω,)5.0(1−′=D m Q c p π,C R c zc 1=ω,s
n T πω= )5.0(11−′+
=D m L
RT F c s ,)]21([2D D m D F c −−′=,n e c S S m +=1 i o g n R L V V S ×−= 从求得的峰值电流控制Buck 等效功率级的三个CCM 小信号传递函数,我们可以来分析这种控制的特点。
其峰值电流控制等效功率级的控制电压到输出电压小信号传递函数)(s G vc ′,和输入电压到输出电压小信号传递函数)(s G vg ′,形式完全相同,所不同的只是零频分量。
它由一个左半平面单极点,一个1/2开关频率处的双极点和一个因输出滤波电容ESR 引起的左半平面单零点组成。
双极点的频率在1/2开关频率,比起开关电源的带宽要高得多,故一般情况下可将其忽略。
在R.Ridely 引入采样函数之前的分析文章中,所得到的结果都是用一阶小信号传递函数近似,所以就不能解释在实验中出现的子谐波振荡现象。
所谓的子谐波振荡是峰值电流型控制的等效功率级,在工作占空比大于0.5时和无外部补偿斜波时,会在输出产生一种1/2开关频率的有规则的振荡,可在MOSFET 的ds V 波形上反映出来,它在时钟的相邻开关周期内,具有不同的导通时间和截止时间,一长一短,其波形示意图如图1所示。
虽然这种振荡波形,人耳一般听不到,但它会影响开关电源长期工作的可靠性,所以必须避免。
图1: 峰值电流等效功率级中MOSFET 在D>0.5时的波形
解释子谐波振荡的原因,可以从稳态工作点上,对电流作一个小扰动,看看其扰动后,该电流的变化,这种解释是在R.Ridely 发表文章之前所采用的,如图2所示。
从图2,很容易看 Vc Black----
稳态Red------
有子谐波振荡Vc S n
S f
S n
S f
S n <S f S n >S f D>0.5
Black----
稳态Red------
无子谐波振荡
D<0.5(a)(b)
图2: 解释子谐波振荡的图示法
出,当占空比大于0.5时,因为电感电流取样信号的上升斜率小于下降斜率,使得电感电流的微小扰动,在每一个开关周期后,会被不断地放大,这种结果便是振荡,由于外部时钟的缘故,这种振荡最终表现为子谐波振荡。
而在占空比小于0.5时,从图2的波形中也可以看出,即使电感电流上有了一个小的扰动,在每一个开关周期后,这个扰动就被减小,最终收敛到零,所以占空比小于0.5时,不会产生子谐波振荡。
现在再回顾头来,看看峰值电流控制等效功率级在CCM 下的小信号传递函数,其有一个1/2开关频率的双极点,为了让等效功率级稳定,这个双极点必须位于左半平面。
但从这个双极点的)
5.0(1−′=D m Q c p π可知,在不加外部补偿斜波时,它的1011=+=+=n n e c S S S m ,所以当5.0>D 时,有0)
5.0(1)5.0(1<−=−′=D D Q p ππ,因此这时的双极点将位于右半平面,所以这个等效功率级是不稳定的。
而在5.0<D 时,有
0)
5.0(1)5.0(1>−=−′=D D Q p ππ,此时的双极点将位于左半平面,所以其等效功率级是稳定的。
这个结论与实验观察到的结果一致,要避免占空比大于0.5时,峰值电流控制等效功率级在CCM 下的子谐波振荡,最简单的办法就是控制n e c S S m +
=1大于1,或加上一个外部补偿斜波,来保证在最大占空比(当大于0.5时)下的0]
5.0)1([1max >−−=D m Q c p π。
所加的补偿斜波应合理设计,不要太大,否则峰值电流型控制中的电感电流信息将被外部斜波所淹没,控制就将等效于电压型控制。
在合理设计了外部补偿斜波后,还要对开关电流的取样进行高频滤波,以免MOSFET 开通瞬间因副边二极管反向恢复引起的尖峰电流将MOSFET 提前关断。
当这些措施保证无子谐波振荡后,在进行动态分析时,因双极点的频率很高,就可将这个双极点忽略不计了。
因此峰值电流控制等效功率级在CCM 下的控制电压到输出电压的小信号传递函数可看作是一个一阶的传递函数,它比前面介绍的电压型控制等效功率级在CCM 下的同一个小信号传递函数要低一阶,所以其电压环应该更容易设计,或者说,峰值电流型控制的开关电源比电压型控制的开关电源,可以做更高的环增益带宽。
从Buck 变换器在峰值电流控制等效功率级的另一个小信号传递函数)(s G vg ′的表达式,
我们也可以分析当内环闭合后,等效功率级的电压音频隔离度是变好了,还是变坏了?这可以看一下它的零频分量:120F F L RT G s vg =′,其中)]2
1([2D D m D F c −−′=,公式中其它的值都为正数。
如果取i o f e R L V S S 2121==,则有:D D D D R L
V V R L V S S m i o g i o n e c −−=−+=−+=+=121121211,所以有:0)]2
1(121[)]21([2=−−′−−=−−′=D D D D D D D m D F c ,因此就有:0)(≈′s G vg 。
这说明,采用峰值电流型控制后,Buck 变换器即使不加外环,其输出电压对输入电压扰动的低频抑制能力就可以大大增加。
这也是前面对峰值电流调制器小信号方程分析时得出的结论。
上面的斜波补偿,在实际电路中是不能取的,这可从实验中证实,因为取这种外部斜波补偿时,开关电源的抗高频干扰能力非常差,电源很难正常工作。
所以一般情况下,外部补偿斜波要比上述理想的补偿斜波大,以避免干扰。
尽管如此,也足以说明,峰值电流型控制对输出电压抗输入电压的低频抑制能力是非常有利的。
利用同样的分析,可以对峰值电流控制等效功率级的小信输出阻抗)(s Z out ′,看是变好了,还是变坏了?在Buck 变换器的峰值电流控制等效功率级中,输出阻抗中的零频分量为1
0F R R =′,这与电压型控制等效功率级中的零频分量L R 相比,要大许多(因为R 要远远大于L R )。
所以在峰值电流型控制中,其输出电压抗负载电流的低频抑制能力是变坏了。
